Simulation 3: Two-dimensional Non-linear Regression
Dayi Li
2025-04-19
Last updated: 2025-04-19
Checks: 6 1
Knit directory: BOSS_website/
This reproducible R Markdown analysis was created with workflowr (version 1.7.1). The Checks tab describes the reproducibility checks that were applied when the results were created. The Past versions tab lists the development history.
Great! Since the R Markdown file has been committed to the Git repository, you know the exact version of the code that produced these results.
Great job! The global environment was empty. Objects defined in the global environment can affect the analysis in your R Markdown file in unknown ways. For reproduciblity it’s best to always run the code in an empty environment.
The command set.seed(20250415) was run prior to running
the code in the R Markdown file. Setting a seed ensures that any results
that rely on randomness, e.g. subsampling or permutations, are
reproducible.
Great job! Recording the operating system, R version, and package versions is critical for reproducibility.
- unnamed-chunk-3
- unnamed-chunk-5
- unnamed-chunk-7
- unnamed-chunk-8
To ensure reproducibility of the results, delete the cache directory
sim3_cache and re-run the analysis. To have workflowr
automatically delete the cache directory prior to building the file, set
delete_cache = TRUE when running wflow_build()
or wflow_publish().
Great job! Using relative paths to the files within your workflowr project makes it easier to run your code on other machines.
Great! You are using Git for version control. Tracking code development and connecting the code version to the results is critical for reproducibility.
The results in this page were generated with repository version 2011696. See the Past versions tab to see a history of the changes made to the R Markdown and HTML files.
Note that you need to be careful to ensure that all relevant files for
the analysis have been committed to Git prior to generating the results
(you can use wflow_publish or
wflow_git_commit). workflowr only checks the R Markdown
file, but you know if there are other scripts or data files that it
depends on. Below is the status of the Git repository when the results
were generated:
Ignored files:
Ignored: .DS_Store
Ignored: .Rproj.user/
Ignored: analysis/sim3_cache/
Ignored: data/sim3/
Ignored: output/sim3/
Untracked files:
Untracked: code/nlreg.stan
Unstaged changes:
Modified: BOSS_website.Rproj
Note that any generated files, e.g. HTML, png, CSS, etc., are not included in this status report because it is ok for generated content to have uncommitted changes.
These are the previous versions of the repository in which changes were
made to the R Markdown (analysis/sim3.Rmd) and HTML
(docs/sim3.html) files. If you’ve configured a remote Git
repository (see ?wflow_git_remote), click on the hyperlinks
in the table below to view the files as they were in that past version.
| File | Version | Author | Date | Message |
|---|---|---|---|---|
| Rmd | 2011696 | david.li | 2025-04-19 | wflow_publish("analysis/sim3.Rmd") |
Data
library(tidyverse)
library(tikzDevice)
library(rstan)
library(INLA)
library(inlabru)
library(modeest)
function_path <- "./code"
output_path <- "./output/sim3"
data_path <- "./data/sim3"
source(paste0(function_path, "/00_BOSS.R"))We simulate \(n = 200\) data points based on the above model with \(\rho_0 = 10\), \(R = 2\), \(\beta = 2\), \(\gamma = -2.5\), and \(\sigma = 0.5\). The inferential goal is the nuisance parameters \(R\) and \(\beta\).
r <- seq(0, 20, length.out = 200)
beta <- 10
a <- 2
b <- 2
c <- -2.5
set.seed(1234)
Ir <- beta*(1 + (r/a)^b)^c
lr <- log(Ir) + rnorm(length(r), 0, 0.5)
data <- data.frame(r, lr)
ggplot(data, aes(r, lr)) + geom_point() + ylab('y')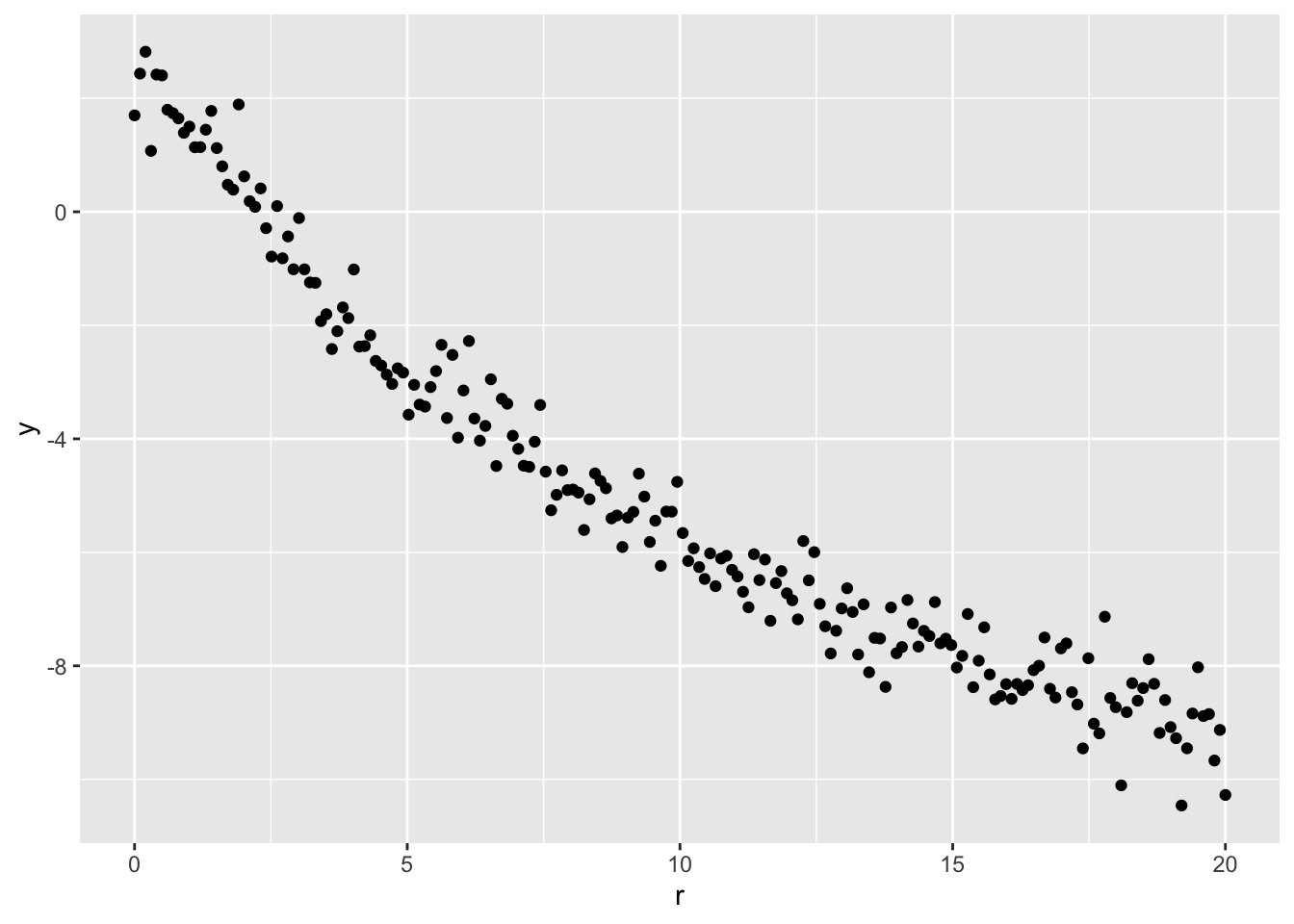
inlabru
We first runinlabru to to fit the model. We set the
following priors for the parameters:
inlabru version: 2.11.1
INLA version: 24.06.27
Components:
a: main = linear(1), group = exchangeable(1L), replicate = iid(1L)
b: main = linear(1), group = exchangeable(1L), replicate = iid(1L)
c: main = linear(1), group = exchangeable(1L), replicate = iid(1L)
Intercept: main = linear(1), group = exchangeable(1L), replicate = iid(1L)
Likelihoods:
Family: 'gaussian'
Data class: 'data.frame'
Predictor: lr ~ Intercept + c * log(1 + (r/a_fun(a))^b_fun(b))
Time used:
Pre = 0.716, Running = 0.256, Post = 0.0213, Total = 0.994
Fixed effects:
mean sd 0.025quant 0.5quant 0.975quant mode kld
a -0.255 0.096 -0.443 -0.255 -0.066 -0.255 0
b -0.179 0.180 -0.533 -0.179 0.176 -0.179 0
c -2.812 0.553 -3.898 -2.813 -1.727 -2.813 0
Intercept 2.220 0.216 1.797 2.220 2.643 2.220 0
Model hyperparameters:
mean sd 0.025quant 0.5quant
Precision for the Gaussian observations 3.95 0.397 3.21 3.94
0.975quant mode
Precision for the Gaussian observations 4.76 3.91
Deviance Information Criterion (DIC) ...............: 300.84
Deviance Information Criterion (DIC, saturated) ....: 207.37
Effective number of parameters .....................: 4.96
Watanabe-Akaike information criterion (WAIC) ...: 301.63
Effective number of parameters .................: 5.47
Marginal log-Likelihood: -173.54
is computed
Posterior summaries for the linear predictor and the fitted values are computed
(Posterior marginals needs also 'control.compute=list(return.marginals.predictor=TRUE)')BOSS
Now let’s run BOSS. We first specify the (unnormalized) log-posterior for \((R,\beta)\). Note that for this specific problem, the unnormalized log-posterior has a closed-form expression:
# specify the objective function for BOSS: unnormalized log posterior of (R, beta)
eval_func <- function(par, x = r, y = lr){
a <- par[1]
b <- par[2]
n <- length(r)
X <- matrix(cbind(rep(1, n), log(1 + (r/a)^b)), ncol = 2)
Vb <- solve(t(X) %*% X + diag(1/1000, 2))
P <- diag(n) - X %*% Vb %*% t(X)
mlik <- log(det(Vb))/2 - log(1000) + lgamma((n+1)/2) - (n+1)/2*log(1e-5 + t(y) %*% P %*% y/2) -
n/2*log(pi) -5*log(10)
return(mlik)
}Next, we run the BOSS algorithm where the stopping criteria is based on the convergence of the posterior mode. Specifically, we check the modal convergence every \(5\) BO iteration, and consider the convergence statistics of the average \(5\) nearest neighbor distance around the current mode.
[1] "Initial evaluation phase..."
[1] "Using Latin Hypercube Sampling for initial design for D > 1."
[1] "The new length.scale: 0.0125392075378212"
[1] "The new signal_var: 1490.69579151025"
[1] "Iteration: 1"
[1] "Maximize Acquisition Function"
[1] "Next point: 3.39247762995756" "Next point: 2.53528069773033"
[1] "Function value: -155.435229295696"
[1] "Iteration: 2"
[1] "Maximize Acquisition Function"
[1] "Next point: 3.8038475325644" "Next point: 2.68330346171062"
[1] "Function value: -176.520015381528"
[1] "Iteration: 3"
[1] "Maximize Acquisition Function"
[1] "Next point: 0.549059004499577" "Next point: 3.34522031943779"
[1] "Function value: -198.867873858364"
[1] "Iteration: 4"
[1] "Maximize Acquisition Function"
[1] "Next point: 4.34095398883801" "Next point: 3.12408960633911"
[1] "Function value: -207.733139142784"
[1] "Iteration: 5"
[1] "Time to update the parameters!"
[1] "The new length.scale: 0.207814698862999"
[1] "The new signal_var: 1046.08277544569"
[1] "Maximize Acquisition Function"
[1] "Next point: 3.15009375265262" "Next point: 0.996414395629452"
[1] "Function value: -107.708793536351"
[1] "Iteration: 6"
[1] "Maximize Acquisition Function"
[1] "Next point: 1.71046628215391" "Next point: 2.51697806578914"
[1] "Function value: -104.326360329238"
[1] "Iteration: 7"
[1] "Maximize Acquisition Function"
[1] "Next point: 4.36852546944587" "Next point: 0.1"
[1] "Function value: -396.973541298251"
[1] "Iteration: 8"
[1] "Maximize Acquisition Function"
[1] "Next point: 2.30835956213877" "Next point: 1.30898294385526"
[1] "Function value: -102.70179669635"
[1] "Iteration: 9"
[1] "Maximize Acquisition Function"
[1] "Next point: 2.49420255380714" "Next point: 0.268285686213857"
[1] "Function value: -276.388547441321"
[1] "Iteration: 10"
[1] "Time to update the parameters!"
[1] "The new length.scale: 0.224903553551365"
[1] "The new signal_var: 6295.50805467058"
[1] "Maximize Acquisition Function"
[1] "Next point: 0.1" "Next point: 0.1"
[1] "Function value: -405.65430254406"
[1] "Iteration: 11"
[1] "Maximize Acquisition Function"
[1] "Next point: 0.1" "Next point: 2.25899188860582"
[1] "Function value: -268.335694832807"
[1] "Iteration: 12"
[1] "Maximize Acquisition Function"
[1] "Next point: 5" "Next point: 4"
[1] "Function value: -244.726383759173"
[1] "Iteration: 13"
[1] "Maximize Acquisition Function"
[1] "Next point: 5" "Next point: 1.28725801439757"
[1] "Function value: -132.314300517847"
[1] "Iteration: 14"
[1] "Maximize Acquisition Function"
[1] "Next point: 1.48980336640252" "Next point: 4"
[1] "Function value: -114.420300855258"
[1] "Iteration: 15"
[1] "Time to update the parameters!"
[1] "The new length.scale: 0.208918285076918"
[1] "The new signal_var: 8143.76319105878"
[1] "Maximize Acquisition Function"
[1] "Next point: 1.83398473313779" "Next point: 3.28484746059395"
[1] "Function value: -106.274654633996"
[1] "Iteration: 16"
[1] "Maximize Acquisition Function"
[1] "Next point: 0.1" "Next point: 4"
[1] "Function value: -271.530250317145"
[1] "Iteration: 17"
[1] "Maximize Acquisition Function"
[1] "Next point: 3.88295426616959" "Next point: 1.51247681276012"
[1] "Function value: -128.686069084485"
[1] "Iteration: 18"
[1] "Maximize Acquisition Function"
[1] "Next point: 3.75343341910618" "Next point: 4"
[1] "Function value: -196.057382251179"
[1] "Iteration: 19"
[1] "Maximize Acquisition Function"
[1] "Next point: 0.1" "Next point: 1.19396687831867"
[1] "Function value: -261.826866746668"
[1] "Iteration: 20"
[1] "Time to update the parameters!"
[1] "The new length.scale: 0.207371432810264"
[1] "The new signal_var: 7356.37154505985"
[1] "Maximize Acquisition Function"
[1] "Next point: 2.47742252037393" "Next point: 2.83052560216642"
[1] "Function value: -120.083076060318"
[1] "Time to check modal difference!"
[1] "Modal rel-difference: 18.6313868001438"
[1] "Hessian rel-difference in second moment: Inf"
[1] "Iteration: 21"
[1] "Maximize Acquisition Function"
[1] "Next point: 2.22858690087297" "Next point: 4"
[1] "Function value: -118.54453991616"
[1] "Iteration: 22"
[1] "Maximize Acquisition Function"
[1] "Next point: 5" "Next point: 1.88177503666484"
[1] "Function value: -181.175894354487"
[1] "Iteration: 23"
[1] "Maximize Acquisition Function"
[1] "Next point: 3.02894473930322" "Next point: 1.49299299865655"
[1] "Function value: -109.510719723527"
[1] "Iteration: 24"
[1] "Maximize Acquisition Function"
[1] "Next point: 2.00673690804772" "Next point: 1.9004720383616"
[1] "Function value: -100.9154002351"
[1] "Iteration: 25"
[1] "Time to update the parameters!"
[1] "The new length.scale: 0.211094658250803"
[1] "The new signal_var: 6896.12903814478"
[1] "Maximize Acquisition Function"
[1] "Next point: 5" "Next point: 0.722783361803266"
[1] "Function value: -122.632726399684"
[1] "Time to check modal difference!"
[1] "Modal rel-difference: 10.606299297602"
[1] "Hessian rel-difference in second moment: 0.235037077663795"
[1] "Iteration: 26"
[1] "Maximize Acquisition Function"
[1] "Next point: 1.52447832246582" "Next point: 1.06977724103305"
[1] "Function value: -129.586642938453"
[1] "Iteration: 27"
[1] "Maximize Acquisition Function"
[1] "Next point: 1.1794259251906" "Next point: 2.89246424228203"
[1] "Function value: -129.890076314455"
[1] "Iteration: 28"
[1] "Maximize Acquisition Function"
[1] "Next point: 5" "Next point: 2.76507175759142"
[1] "Function value: -220.855268187938"
[1] "Iteration: 29"
[1] "Maximize Acquisition Function"
[1] "Next point: 4.2820818511709" "Next point: 0.966798998553444"
[1] "Function value: -107.900563656775"
[1] "Iteration: 30"
[1] "Time to update the parameters!"
[1] "The new length.scale: 0.197803601064826"
[1] "The new signal_var: 6314.82272327829"
[1] "Maximize Acquisition Function"
[1] "Next point: 1.27730941101984" "Next point: 3.55884720621139"
[1] "Function value: -124.744833127496"
[1] "Time to check modal difference!"
[1] "Modal rel-difference: 8.336501296134"
[1] "Hessian rel-difference in second moment: 0.196142720821809"
[1] "Iteration: 31"
[1] "Maximize Acquisition Function"
[1] "Next point: 1.89601662674166" "Next point: 3.72504379277639"
[1] "Function value: -108.389481842152"
[1] "Iteration: 32"
[1] "Maximize Acquisition Function"
[1] "Next point: 1.31929188110382" "Next point: 2.13377703987779"
[1] "Function value: -118.994812447546"
[1] "Iteration: 33"
[1] "Maximize Acquisition Function"
[1] "Next point: 3.68478937490418" "Next point: 1.08715377632225"
[1] "Function value: -106.403166673593"
[1] "Iteration: 34"
[1] "Maximize Acquisition Function"
[1] "Next point: 1.72787835143582" "Next point: 1.57006941391746"
[1] "Function value: -106.246531564902"
[1] "Iteration: 35"
[1] "Time to update the parameters!"
[1] "The new length.scale: 0.206223295085481"
[1] "The new signal_var: 5966.60112951376"
[1] "Maximize Acquisition Function"
[1] "Next point: 4.4651995474428" "Next point: 1.20986077947489"
[1] "Function value: -118.524893357631"
[1] "Time to check modal difference!"
[1] "Modal rel-difference: 6.87934296310509"
[1] "Hessian rel-difference in second moment: 0.0524670519040056"
[1] "Iteration: 36"
[1] "Maximize Acquisition Function"
[1] "Next point: 2.33124534904226" "Next point: 0.966486461728774"
[1] "Function value: -117.135493951319"
[1] "Iteration: 37"
[1] "Maximize Acquisition Function"
[1] "Next point: 2.86322708709954" "Next point: 1.19321201448268"
[1] "Function value: -103.524382274893"
[1] "Iteration: 38"
[1] "Maximize Acquisition Function"
[1] "Next point: 2.08269051036145" "Next point: 2.34230541030725"
[1] "Function value: -103.759025478286"
[1] "Iteration: 39"
[1] "Maximize Acquisition Function"
[1] "Next point: 2.39721734353278" "Next point: 1.74644124756321"
[1] "Function value: -103.32083196326"
[1] "Iteration: 40"
[1] "Time to update the parameters!"
[1] "The new length.scale: 0.197625240659466"
[1] "The new signal_var: 5647.27870613666"
[1] "Maximize Acquisition Function"
[1] "Next point: 1.94168595126276" "Next point: 2.8256261097899"
[1] "Function value: -104.902400165752"
[1] "Time to check modal difference!"
[1] "Modal rel-difference: 5.06550431878812"
[1] "Hessian rel-difference in second moment: 0.0820968226973386"
[1] "Iteration: 41"
[1] "Maximize Acquisition Function"
[1] "Next point: 1.60085351748808" "Next point: 3.10921137193474"
[1] "Function value: -108.350695937393"
[1] "Iteration: 42"
[1] "Maximize Acquisition Function"
[1] "Next point: 3.46577915706282" "Next point: 3.40228397935202"
[1] "Function value: -175.295537591055"
[1] "Iteration: 43"
[1] "Maximize Acquisition Function"
[1] "Next point: 4.80448578334332" "Next point: 0.945793312533219"
[1] "Function value: -109.025395775071"
[1] "Iteration: 44"
[1] "Maximize Acquisition Function"
[1] "Next point: 1.78091258513324" "Next point: 2.05667769938974"
[1] "Function value: -102.501760732702"
[1] "Iteration: 45"
[1] "Time to update the parameters!"
[1] "The new length.scale: 0.203351068001825"
[1] "The new signal_var: 5306.19280452682"
[1] "Maximize Acquisition Function"
[1] "Next point: 2.14725118987313" "Next point: 1.62258591259679"
[1] "Function value: -100.772483122748"
[1] "Time to check modal difference!"
[1] "Modal rel-difference: 3.7445126388009"
[1] "Hessian rel-difference in second moment: 0.0336570040147993"
[1] "Iteration: 46"
[1] "Maximize Acquisition Function"
[1] "Next point: 1.80996980795622" "Next point: 4"
[1] "Function value: -108.675300386845"
[1] "Iteration: 47"
[1] "Maximize Acquisition Function"
[1] "Next point: 2.04656552355355" "Next point: 1.7469170140111"
[1] "Function value: -100.738664336894"
[1] "Iteration: 48"
[1] "Maximize Acquisition Function"
[1] "Next point: 2.10323212157741" "Next point: 1.72382676887338"
[1] "Function value: -100.726488683073"
[1] "Iteration: 49"
[1] "Maximize Acquisition Function"
[1] "Next point: 2.08895278767657" "Next point: 1.67832179727633"
[1] "Function value: -100.733361742925"
[1] "Iteration: 50"
[1] "Time to update the parameters!"
[1] "The new length.scale: 0.205738136133142"
[1] "The new signal_var: 5071.46893785769"
[1] "Maximize Acquisition Function"
[1] "Next point: 2.09091125346518" "Next point: 1.71160044883931"
[1] "Function value: -100.714732952287"
[1] "Time to check modal difference!"
[1] "Modal rel-difference: 0.855822352404627"
[1] "Hessian rel-difference in second moment: 0.00698728537360029"
[1] "Iteration: 51"
[1] "Maximize Acquisition Function"
[1] "Next point: 2.0906142448018" "Next point: 1.71171861964949"
[1] "Function value: -100.714718354458"
[1] "Iteration: 52"
[1] "Maximize Acquisition Function"
[1] "Next point: 2.090479033876" "Next point: 1.71174679641881"
[1] "Function value: -100.714712474601"
[1] "Iteration: 53"
[1] "Maximize Acquisition Function"
[1] "Next point: 2.09031337717031" "Next point: 1.71186204179447"
[1] "Function value: -100.714706823286"
[1] "Iteration: 54"
[1] "Maximize Acquisition Function"
[1] "Next point: 2.09023645066086" "Next point: 1.71187902701174"
[1] "Function value: -100.71470421998"
[1] "Iteration: 55"
[1] "Time to update the parameters!"
[1] "The new length.scale: 0.203530384075413"
[1] "The new signal_var: 4848.3838172548"
[1] "Maximize Acquisition Function"
[1] "Next point: 5" "Next point: 0.947409356531545"
[1] "Function value: -109.5614389765"
[1] "Time to check modal difference!"
[1] "Modal rel-difference: 0.0365436900528706"
[1] "Hessian rel-difference in second moment: 0.000554510847286941"
[1] "Iteration: 56"
[1] "Maximize Acquisition Function"
[1] "Next point: 2.0901984028146" "Next point: 1.71186750265419"
[1] "Function value: -100.714702936014"
[1] "Iteration: 57"
[1] "Maximize Acquisition Function"
[1] "Next point: 2.09015186986032" "Next point: 1.7118625695627"
[1] "Function value: -100.714701534366"
[1] "Iteration: 58"
[1] "Maximize Acquisition Function"
[1] "Next point: 2.0900827092144" "Next point: 1.7119503329025"
[1] "Function value: -100.714699852479"
[1] "Iteration: 59"
[1] "Maximize Acquisition Function"
[1] "Next point: 2.09004487281399" "Next point: 1.71196819738118"
[1] "Function value: -100.714698894933"
[1] "Iteration: 60"
[1] "Time to update the parameters!"
[1] "The new length.scale: 0.202730673019302"
[1] "The new signal_var: 4618.78817798718"
[1] "Maximize Acquisition Function"
[1] "Next point: 2.09008958727693" "Next point: 1.71188588871192"
[1] "Function value: -100.714699890451"
[1] "Time to check modal difference!"
[1] "Modal rel-difference: 0.00127626501053311"
[1] "Hessian rel-difference in second moment: 2.32759716121696e-05"
[1] "Posterior surrogate converged based on modal criteria!"We then run BOSS using AGHQ as convergence statistics. Again, we check for convergence every \(5\) iterations. The convergence criteria is relative difference in AGHQ statstics being less than \(0.05\).
[1] "Initial evaluation phase..."
[1] "Using Latin Hypercube Sampling for initial design for D > 1."
[1] "The new length.scale: 0.01"
[1] "The new signal_var: 1491.51089195998"
[1] "Iteration: 1"
[1] "Maximize Acquisition Function"
[1] "Next point: 3.36788724163691" "Next point: 2.52442875164072"
[1] "Function value: -154.10262736454"
[1] "Iteration: 2"
[1] "Maximize Acquisition Function"
[1] "Next point: 0.899374804314845" "Next point: 2.52532386731604"
[1] "Function value: -154.093241323996"
[1] "Iteration: 3"
[1] "Maximize Acquisition Function"
[1] "Next point: 4.17436119321284" "Next point: 0.939393288116017"
[1] "Function value: -108.206634007251"
[1] "Iteration: 4"
[1] "Maximize Acquisition Function"
[1] "Next point: 2.64365055186682" "Next point: 3.72777301374244"
[1] "Function value: -136.54175465231"
[1] "Iteration: 5"
[1] "Time to update the parameters!"
[1] "The new length.scale: 0.153306325677533"
[1] "The new signal_var: 1139.75125687272"
[1] "Maximize Acquisition Function"
[1] "Next point: 4.84797043884089" "Next point: 0.10039"
[1] "Function value: -396.360588927968"
[1] "Iteration: 6"
[1] "Maximize Acquisition Function"
[1] "Next point: 1.16988967634189" "Next point: 3.85052065164225"
[1] "Function value: -133.501288693767"
[1] "Iteration: 7"
[1] "Maximize Acquisition Function"
[1] "Next point: 3.33723585303201" "Next point: 1.24655140848289"
[1] "Function value: -106.842429329463"
[1] "Iteration: 8"
[1] "Maximize Acquisition Function"
[1] "Next point: 4.25572202910418" "Next point: 1.50601168021124"
[1] "Function value: -136.642962678151"
[1] "Iteration: 9"
[1] "Maximize Acquisition Function"
[1] "Next point: 4.99951" "Next point: 3.99961"
[1] "Function value: -244.705618605336"
[1] "Iteration: 10"
[1] "Time to update the parameters!"
[1] "The new length.scale: 0.153658263188958"
[1] "The new signal_var: 5746.02513323413"
[1] "Maximize Acquisition Function"
[1] "Next point: 2.87689329705555" "Next point: 0.131930307477416"
[1] "Function value: -368.541623558057"
[1] "Iteration: 11"
[1] "Maximize Acquisition Function"
[1] "Next point: 2.23000585587537" "Next point: 1.71057681264356"
[1] "Function value: -101.208170803435"
[1] "Iteration: 12"
[1] "Maximize Acquisition Function"
[1] "Next point: 0.10049" "Next point: 3.43087782498012"
[1] "Function value: -270.770258051378"
[1] "Iteration: 13"
[1] "Maximize Acquisition Function"
[1] "Next point: 1.956385701943" "Next point: 2.92703318148592"
[1] "Function value: -105.591058610638"
[1] "Iteration: 14"
[1] "Maximize Acquisition Function"
[1] "Next point: 0.10049" "Next point: 0.10039"
[1] "Function value: -405.328591854816"
[1] "Iteration: 15"
[1] "Time to update the parameters!"
[1] "The new length.scale: 0.180577755317966"
[1] "The new signal_var: 9951.0700347438"
[1] "Maximize Acquisition Function"
[1] "Next point: 1.98100074628061" "Next point: 0.945400406625028"
[1] "Function value: -125.506950160981"
[1] "Iteration: 16"
[1] "Maximize Acquisition Function"
[1] "Next point: 0.10049" "Next point: 1.73440262353716"
[1] "Function value: -265.789554328639"
[1] "Iteration: 17"
[1] "Maximize Acquisition Function"
[1] "Next point: 3.76234068526845" "Next point: 3.99961"
[1] "Function value: -196.465134780487"
[1] "Iteration: 18"
[1] "Maximize Acquisition Function"
[1] "Next point: 1.76310770221691" "Next point: 2.26937869125943"
[1] "Function value: -102.977494605348"
[1] "Iteration: 19"
[1] "Maximize Acquisition Function"
[1] "Next point: 4.99951" "Next point: 3.08249258418982"
[1] "Function value: -229.184909424024"
[1] "Iteration: 20"
[1] "Time to update the parameters!"
[1] "The new length.scale: 0.198530208408444"
[1] "The new signal_var: 8620.2433453076"
[1] "Maximize Acquisition Function"
[1] "Next point: 0.10049" "Next point: 3.99961"
[1] "Function value: -271.418348675716"
[1] "Time to check AGHQ difference!"
[1] "AGHQ rel-difference in first moment: Inf"
[1] "AGHQ rel-difference in second moment: Inf"
[1] "AGHQ rel-difference in range: Inf"
[1] "Iteration: 21"
[1] "Maximize Acquisition Function"
[1] "Next point: 4.99951" "Next point: 1.23668938938927"
[1] "Function value: -127.70029855752"
[1] "Iteration: 22"
[1] "Maximize Acquisition Function"
[1] "Next point: 4.99951" "Next point: 2.01071779474845"
[1] "Function value: -189.100734305873"
[1] "Iteration: 23"
[1] "Maximize Acquisition Function"
[1] "Next point: 1.67719342389818" "Next point: 0.10039"
[1] "Function value: -398.768880580251"
[1] "Iteration: 24"
[1] "Maximize Acquisition Function"
[1] "Next point: 0.401273270129821" "Next point: 0.994851925818134"
[1] "Function value: -208.29300499339"
[1] "Iteration: 25"
[1] "Time to update the parameters!"
[1] "The new length.scale: 0.193752399960311"
[1] "The new signal_var: 8942.57411879633"
[1] "Maximize Acquisition Function"
[1] "Next point: 1.24181139918099" "Next point: 3.20939749237754"
[1] "Function value: -126.201328197186"
[1] "Time to check AGHQ difference!"
[1] "AGHQ rel-difference in first moment: 0.034015196520544"
[1] "AGHQ rel-difference in second moment: 0.211694300042735"
[1] "AGHQ rel-difference in range: 0.096480401772991"
[1] "Iteration: 26"
[1] "Maximize Acquisition Function"
[1] "Next point: 2.47849138359572" "Next point: 2.56611783889685"
[1] "Function value: -116.874660008452"
[1] "Iteration: 27"
[1] "Maximize Acquisition Function"
[1] "Next point: 1.35236947926919" "Next point: 1.063776385202"
[1] "Function value: -136.880215866144"
[1] "Iteration: 28"
[1] "Maximize Acquisition Function"
[1] "Next point: 4.12685192692566" "Next point: 3.37486722553263"
[1] "Function value: -204.054490427246"
[1] "Iteration: 29"
[1] "Maximize Acquisition Function"
[1] "Next point: 3.37442109770312" "Next point: 0.767472700745922"
[1] "Function value: -126.00995287392"
[1] "Iteration: 30"
[1] "Time to update the parameters!"
[1] "The new length.scale: 0.182131938587331"
[1] "The new signal_var: 8158.31625373167"
[1] "Maximize Acquisition Function"
[1] "Next point: 2.66680235334015" "Next point: 1.14586484146277"
[1] "Function value: -104.514408829287"
[1] "Time to check AGHQ difference!"
[1] "AGHQ rel-difference in first moment: 0.133634861935483"
[1] "AGHQ rel-difference in second moment: 0.0685591407036774"
[1] "AGHQ rel-difference in range: 0.168981010465047"
[1] "Iteration: 31"
[1] "Maximize Acquisition Function"
[1] "Next point: 1.84838094951402" "Next point: 3.60975329062009"
[1] "Function value: -107.559968446437"
[1] "Iteration: 32"
[1] "Maximize Acquisition Function"
[1] "Next point: 3.84999417756193" "Next point: 0.10039"
[1] "Function value: -396.879407703669"
[1] "Iteration: 33"
[1] "Maximize Acquisition Function"
[1] "Next point: 1.82065009986094" "Next point: 1.46482984266919"
[1] "Function value: -105.788583158653"
[1] "Iteration: 34"
[1] "Maximize Acquisition Function"
[1] "Next point: 1.79608535447827" "Next point: 3.99961"
[1] "Function value: -108.647070144177"
[1] "Iteration: 35"
[1] "Time to update the parameters!"
[1] "The new length.scale: 0.19081861892336"
[1] "The new signal_var: 8935.54458717079"
[1] "Maximize Acquisition Function"
[1] "Next point: 1.31894420091323" "Next point: 2.08698011332237"
[1] "Function value: -119.0706064872"
[1] "Time to check AGHQ difference!"
[1] "AGHQ rel-difference in first moment: 0.273766102739537"
[1] "AGHQ rel-difference in second moment: 0.410700686548536"
[1] "AGHQ rel-difference in range: 0.313185989452447"
[1] "Iteration: 36"
[1] "Maximize Acquisition Function"
[1] "Next point: 4.99951" "Next point: 0.816742674904655"
[1] "Function value: -112.813833290136"
[1] "Iteration: 37"
[1] "Maximize Acquisition Function"
[1] "Next point: 3.02840226087854" "Next point: 3.99961"
[1] "Function value: -159.400681046729"
[1] "Iteration: 38"
[1] "Maximize Acquisition Function"
[1] "Next point: 0.10049" "Next point: 2.59820572293399"
[1] "Function value: -269.226356324172"
[1] "Iteration: 39"
[1] "Maximize Acquisition Function"
[1] "Next point: 3.63320261214955" "Next point: 1.8628616400187"
[1] "Function value: -140.886117535146"
[1] "Iteration: 40"
[1] "Time to update the parameters!"
[1] "The new length.scale: 0.188509900268282"
[1] "The new signal_var: 8348.12054975627"
[1] "Maximize Acquisition Function"
[1] "Next point: 1.55017615377562" "Next point: 2.69009420148062"
[1] "Function value: -108.694911845645"
[1] "Time to check AGHQ difference!"
[1] "AGHQ rel-difference in first moment: 0.0158058955892352"
[1] "AGHQ rel-difference in second moment: 0.0840472188164307"
[1] "AGHQ rel-difference in range: 0.0199740439061026"
[1] "Iteration: 41"
[1] "Maximize Acquisition Function"
[1] "Next point: 2.53412627255598" "Next point: 3.10504302657025"
[1] "Function value: -125.532548886976"
[1] "Iteration: 42"
[1] "Maximize Acquisition Function"
[1] "Next point: 4.66180376231102" "Next point: 1.0101124529838"
[1] "Function value: -109.642839504439"
[1] "Iteration: 43"
[1] "Maximize Acquisition Function"
[1] "Next point: 2.24250270848787" "Next point: 1.31287928194822"
[1] "Function value: -103.0464683244"
[1] "Iteration: 44"
[1] "Maximize Acquisition Function"
[1] "Next point: 2.82267005915753" "Next point: 1.79492164893319"
[1] "Function value: -113.433344515613"
[1] "Iteration: 45"
[1] "Time to update the parameters!"
[1] "The new length.scale: 0.194943290594159"
[1] "The new signal_var: 7970.71067301064"
[1] "Maximize Acquisition Function"
[1] "Next point: 3.93405693656846" "Next point: 1.15337784511907"
[1] "Function value: -109.666489000288"
[1] "Time to check AGHQ difference!"
[1] "AGHQ rel-difference in first moment: 0.201629214228545"
[1] "AGHQ rel-difference in second moment: 0.627356195977988"
[1] "AGHQ rel-difference in range: 0.919309137010468"
[1] "Iteration: 46"
[1] "Maximize Acquisition Function"
[1] "Next point: 2.25622324823438" "Next point: 2.09255258336871"
[1] "Function value: -104.633147057339"
[1] "Iteration: 47"
[1] "Maximize Acquisition Function"
[1] "Next point: 1.84386933449412" "Next point: 1.88893579506439"
[1] "Function value: -101.819483683482"
[1] "Iteration: 48"
[1] "Maximize Acquisition Function"
[1] "Next point: 2.660363725821" "Next point: 1.38199030500778"
[1] "Function value: -102.687097295759"
[1] "Iteration: 49"
[1] "Maximize Acquisition Function"
[1] "Next point: 1.93432899851485" "Next point: 2.56028338642914"
[1] "Function value: -103.473481271178"
[1] "Iteration: 50"
[1] "Time to update the parameters!"
[1] "The new length.scale: 0.188902913606183"
[1] "The new signal_var: 7667.71969198605"
[1] "Maximize Acquisition Function"
[1] "Next point: 3.54883345115633" "Next point: 1.00628227957786"
[1] "Function value: -106.612853400076"
[1] "Time to check AGHQ difference!"
[1] "AGHQ rel-difference in first moment: 0.624414234025311"
[1] "AGHQ rel-difference in second moment: 0.865941214033516"
[1] "AGHQ rel-difference in range: 2.57531416402589"
[1] "Iteration: 51"
[1] "Maximize Acquisition Function"
[1] "Next point: 1.65341609373487" "Next point: 3.31387170432528"
[1] "Function value: -107.798086838751"
[1] "Iteration: 52"
[1] "Maximize Acquisition Function"
[1] "Next point: 1.45880686995731" "Next point: 3.99961"
[1] "Function value: -115.716084725852"
[1] "Iteration: 53"
[1] "Maximize Acquisition Function"
[1] "Next point: 2.01965807876835" "Next point: 1.93720826916132"
[1] "Function value: -101.020771776922"
[1] "Iteration: 54"
[1] "Maximize Acquisition Function"
[1] "Next point: 2.07727606184602" "Next point: 1.64166568316299"
[1] "Function value: -100.826110585672"
[1] "Iteration: 55"
[1] "Time to update the parameters!"
[1] "The new length.scale: 0.192460021446482"
[1] "The new signal_var: 7329.65835506151"
[1] "Maximize Acquisition Function"
[1] "Next point: 2.05574349412511" "Next point: 1.76298911168769"
[1] "Function value: -100.731965345108"
[1] "Time to check AGHQ difference!"
[1] "AGHQ rel-difference in first moment: 0.14348127384152"
[1] "AGHQ rel-difference in second moment: 0.535117268070077"
[1] "AGHQ rel-difference in range: 0.505130242813836"
[1] "Iteration: 56"
[1] "Maximize Acquisition Function"
[1] "Next point: 2.09950664394677" "Next point: 1.70143395247346"
[1] "Function value: -100.7159745638"
[1] "Iteration: 57"
[1] "Maximize Acquisition Function"
[1] "Next point: 2.08874769213455" "Next point: 1.71266608032567"
[1] "Function value: -100.714692289515"
[1] "Iteration: 58"
[1] "Maximize Acquisition Function"
[1] "Next point: 2.08826286318168" "Next point: 1.71336800888567"
[1] "Function value: -100.714695934487"
[1] "Iteration: 59"
[1] "Maximize Acquisition Function"
[1] "Next point: 2.08800829313877" "Next point: 1.71372006588728"
[1] "Function value: -100.714700737904"
[1] "Iteration: 60"
[1] "Time to update the parameters!"
[1] "The new length.scale: 0.193540988710602"
[1] "The new signal_var: 7047.6100162569"
[1] "Maximize Acquisition Function"
[1] "Next point: 2.0885262639402" "Next point: 1.71323561326753"
[1] "Function value: -100.714690905073"
[1] "Time to check AGHQ difference!"
[1] "AGHQ rel-difference in first moment: 0.15649123389114"
[1] "AGHQ rel-difference in second moment: 0.296425215944875"
[1] "AGHQ rel-difference in range: 0.798053519069554"
[1] "Iteration: 61"
[1] "Maximize Acquisition Function"
[1] "Next point: 2.08793161428284" "Next point: 1.71382817640228"
[1] "Function value: -100.714702530674"
[1] "Iteration: 62"
[1] "Maximize Acquisition Function"
[1] "Next point: 2.08767635542202" "Next point: 1.71437287426977"
[1] "Function value: -100.714709846605"
[1] "Iteration: 63"
[1] "Maximize Acquisition Function"
[1] "Next point: 2.08778387157118" "Next point: 1.71420860784399"
[1] "Function value: -100.714706326235"
[1] "Iteration: 64"
[1] "Maximize Acquisition Function"
[1] "Next point: 2.08898033963739" "Next point: 1.71353629327241"
[1] "Function value: -100.714692395357"
[1] "Iteration: 65"
[1] "Time to update the parameters!"
[1] "The new length.scale: 0.191912946317129"
[1] "The new signal_var: 6766.83209355115"
[1] "Maximize Acquisition Function"
[1] "Next point: 2.08723113746063" "Next point: 1.71415465070014"
[1] "Function value: -100.714731019461"
[1] "Time to check AGHQ difference!"
[1] "AGHQ rel-difference in first moment: 0.0532596662649209"
[1] "AGHQ rel-difference in second moment: 0.0147251306070371"
[1] "AGHQ rel-difference in range: 0.118328629942979"
[1] "Iteration: 66"
[1] "Maximize Acquisition Function"
[1] "Next point: 4.99951" "Next point: 0.970964082457995"
[1] "Function value: -110.027750759884"
[1] "Iteration: 67"
[1] "Maximize Acquisition Function"
[1] "Next point: 2.08873494238375" "Next point: 1.71450118073306"
[1] "Function value: -100.714713824974"
[1] "Iteration: 68"
[1] "Maximize Acquisition Function"
[1] "Next point: 2.08890406336359" "Next point: 1.71276970441865"
[1] "Function value: -100.714688439608"
[1] "Iteration: 69"
[1] "Maximize Acquisition Function"
[1] "Next point: 2.08371911050609" "Next point: 1.7153917188881"
[1] "Function value: -100.715145614819"
[1] "Iteration: 70"
[1] "Time to update the parameters!"
[1] "The new length.scale: 0.190138111640216"
[1] "The new signal_var: 6482.78072929501"
[1] "Maximize Acquisition Function"
[1] "Next point: 3.06837209769682" "Next point: 1.12285688803058"
[1] "Function value: -104.478234514814"
[1] "Time to check AGHQ difference!"
[1] "AGHQ rel-difference in first moment: 0.0285529650258671"
[1] "AGHQ rel-difference in second moment: 0.0482617328407285"
[1] "AGHQ rel-difference in range: 0.0404881523834777"
[1] "Posterior surrogate converged based on AGHQ criteria!"MCMC
Lastly, we implement the MCMC-based method using stan to
obtain the oracle.
Trying to compile a simple C fileRunning /Library/Frameworks/R.framework/Resources/bin/R CMD SHLIB foo.c
using C compiler: ‘Apple clang version 15.0.0 (clang-1500.3.9.4)’
using SDK: ‘’
clang -arch arm64 -I"/Library/Frameworks/R.framework/Resources/include" -DNDEBUG -I"/Library/Frameworks/R.framework/Versions/4.4-arm64/Resources/library/Rcpp/include/" -I"/Library/Frameworks/R.framework/Versions/4.4-arm64/Resources/library/RcppEigen/include/" -I"/Library/Frameworks/R.framework/Versions/4.4-arm64/Resources/library/RcppEigen/include/unsupported" -I"/Library/Frameworks/R.framework/Versions/4.4-arm64/Resources/library/BH/include" -I"/Library/Frameworks/R.framework/Versions/4.4-arm64/Resources/library/StanHeaders/include/src/" -I"/Library/Frameworks/R.framework/Versions/4.4-arm64/Resources/library/StanHeaders/include/" -I"/Library/Frameworks/R.framework/Versions/4.4-arm64/Resources/library/RcppParallel/include/" -I"/Library/Frameworks/R.framework/Versions/4.4-arm64/Resources/library/rstan/include" -DEIGEN_NO_DEBUG -DBOOST_DISABLE_ASSERTS -DBOOST_PENDING_INTEGER_LOG2_HPP -DSTAN_THREADS -DUSE_STANC3 -DSTRICT_R_HEADERS -DBOOST_PHOENIX_NO_VARIADIC_EXPRESSION -D_HAS_AUTO_PTR_ETC=0 -include '/Library/Frameworks/R.framework/Versions/4.4-arm64/Resources/library/StanHeaders/include/stan/math/prim/fun/Eigen.hpp' -D_REENTRANT -DRCPP_PARALLEL_USE_TBB=1 -I/opt/R/arm64/include -fPIC -falign-functions=64 -Wall -g -O2 -c foo.c -o foo.o
In file included from <built-in>:1:
In file included from /Library/Frameworks/R.framework/Versions/4.4-arm64/Resources/library/StanHeaders/include/stan/math/prim/fun/Eigen.hpp:22:
In file included from /Library/Frameworks/R.framework/Versions/4.4-arm64/Resources/library/RcppEigen/include/Eigen/Dense:1:
In file included from /Library/Frameworks/R.framework/Versions/4.4-arm64/Resources/library/RcppEigen/include/Eigen/Core:19:
/Library/Frameworks/R.framework/Versions/4.4-arm64/Resources/library/RcppEigen/include/Eigen/src/Core/util/Macros.h:679:10: fatal error: 'cmath' file not found
#include <cmath>
^~~~~~~
1 error generated.
make: *** [foo.o] Error 1
SAMPLING FOR MODEL 'anon_model' NOW (CHAIN 3).
SAMPLING FOR MODEL 'anon_model' NOW (CHAIN 4).
SAMPLING FOR MODEL 'anon_model' NOW (CHAIN 2).
SAMPLING FOR MODEL 'anon_model' NOW (CHAIN 1).
Chain 3:
Chain 3: Gradient evaluation took 0.000135 seconds
Chain 3: 1000 transitions using 10 leapfrog steps per transition would take 1.35 seconds.
Chain 3: Adjust your expectations accordingly!
Chain 3:
Chain 3:
Chain 4:
Chain 4: Gradient evaluation took 0.000104 seconds
Chain 4: 1000 transitions using 10 leapfrog steps per transition would take 1.04 seconds.
Chain 4: Adjust your expectations accordingly!
Chain 4:
Chain 4:
Chain 1:
Chain 1: Gradient evaluation took 6.6e-05 seconds
Chain 1: 1000 transitions using 10 leapfrog steps per transition would take 0.66 seconds.
Chain 1: Adjust your expectations accordingly!
Chain 1:
Chain 1:
Chain 2:
Chain 2: Gradient evaluation took 8.9e-05 seconds
Chain 2: 1000 transitions using 10 leapfrog steps per transition would take 0.89 seconds.
Chain 2: Adjust your expectations accordingly!
Chain 2:
Chain 2:
Chain 3: Iteration: 1 / 20000 [ 0%] (Warmup)
Chain 4: Iteration: 1 / 20000 [ 0%] (Warmup)
Chain 1: Iteration: 1 / 20000 [ 0%] (Warmup)
Chain 2: Iteration: 1 / 20000 [ 0%] (Warmup)
Chain 1: Iteration: 1001 / 20000 [ 5%] (Sampling)
Chain 4: Iteration: 1001 / 20000 [ 5%] (Sampling)
Chain 2: Iteration: 1001 / 20000 [ 5%] (Sampling)
Chain 3: Iteration: 1001 / 20000 [ 5%] (Sampling)
Chain 3: Iteration: 3000 / 20000 [ 15%] (Sampling)
Chain 1: Iteration: 3000 / 20000 [ 15%] (Sampling)
Chain 2: Iteration: 3000 / 20000 [ 15%] (Sampling)
Chain 4: Iteration: 3000 / 20000 [ 15%] (Sampling)
Chain 3: Iteration: 5000 / 20000 [ 25%] (Sampling)
Chain 2: Iteration: 5000 / 20000 [ 25%] (Sampling)
Chain 1: Iteration: 5000 / 20000 [ 25%] (Sampling)
Chain 4: Iteration: 5000 / 20000 [ 25%] (Sampling)
Chain 3: Iteration: 7000 / 20000 [ 35%] (Sampling)
Chain 2: Iteration: 7000 / 20000 [ 35%] (Sampling)
Chain 1: Iteration: 7000 / 20000 [ 35%] (Sampling)
Chain 4: Iteration: 7000 / 20000 [ 35%] (Sampling)
Chain 3: Iteration: 9000 / 20000 [ 45%] (Sampling)
Chain 2: Iteration: 9000 / 20000 [ 45%] (Sampling)
Chain 1: Iteration: 9000 / 20000 [ 45%] (Sampling)
Chain 4: Iteration: 9000 / 20000 [ 45%] (Sampling)
Chain 3: Iteration: 11000 / 20000 [ 55%] (Sampling)
Chain 2: Iteration: 11000 / 20000 [ 55%] (Sampling)
Chain 1: Iteration: 11000 / 20000 [ 55%] (Sampling)
Chain 4: Iteration: 11000 / 20000 [ 55%] (Sampling)
Chain 3: Iteration: 13000 / 20000 [ 65%] (Sampling)
Chain 2: Iteration: 13000 / 20000 [ 65%] (Sampling)
Chain 1: Iteration: 13000 / 20000 [ 65%] (Sampling)
Chain 4: Iteration: 13000 / 20000 [ 65%] (Sampling)
Chain 3: Iteration: 15000 / 20000 [ 75%] (Sampling)
Chain 2: Iteration: 15000 / 20000 [ 75%] (Sampling)
Chain 1: Iteration: 15000 / 20000 [ 75%] (Sampling)
Chain 4: Iteration: 15000 / 20000 [ 75%] (Sampling)
Chain 3: Iteration: 17000 / 20000 [ 85%] (Sampling)
Chain 2: Iteration: 17000 / 20000 [ 85%] (Sampling)
Chain 1: Iteration: 17000 / 20000 [ 85%] (Sampling)
Chain 4: Iteration: 17000 / 20000 [ 85%] (Sampling)
Chain 3: Iteration: 19000 / 20000 [ 95%] (Sampling)
Chain 2: Iteration: 19000 / 20000 [ 95%] (Sampling)
Chain 1: Iteration: 19000 / 20000 [ 95%] (Sampling)
Chain 3: Iteration: 20000 / 20000 [100%] (Sampling)
Chain 3:
Chain 3: Elapsed Time: 2.744 seconds (Warm-up)
Chain 3: 56.923 seconds (Sampling)
Chain 3: 59.667 seconds (Total)
Chain 3:
Chain 2: Iteration: 20000 / 20000 [100%] (Sampling)
Chain 2:
Chain 2: Elapsed Time: 2.635 seconds (Warm-up)
Chain 2: 57.93 seconds (Sampling)
Chain 2: 60.565 seconds (Total)
Chain 2:
Chain 4: Iteration: 19000 / 20000 [ 95%] (Sampling)
Chain 1: Iteration: 20000 / 20000 [100%] (Sampling)
Chain 1:
Chain 1: Elapsed Time: 2.521 seconds (Warm-up)
Chain 1: 58.831 seconds (Sampling)
Chain 1: 61.352 seconds (Total)
Chain 1:
Chain 4: Iteration: 20000 / 20000 [100%] (Sampling)
Chain 4:
Chain 4: Elapsed Time: 2.599 seconds (Warm-up)
Chain 4: 60.806 seconds (Sampling)
Chain 4: 63.405 seconds (Total)
Chain 4: Warning: There were 42 divergent transitions after warmup. See
https://mc-stan.org/misc/warnings.html#divergent-transitions-after-warmup
to find out why this is a problem and how to eliminate them.Warning: Examine the pairs() plot to diagnose sampling problems user system elapsed
263.387 5.942 97.522 Results Comparison
We now compare the results of the posterior distributions from
inlabru, modal-based BOSS, and AGHQ-based BOSS, and
MCMC.
inlabru posterior distribution:
# get joint posterior of (R, beta) from inlabru
joint_samp <- inla.posterior.sample(10000, fit, selection = list(a = 1, b = 1), seed = 12345)Warning in inla.posterior.sample(n, rfake, intern = intern, use.improved.mean =
use.improved.mean, : Since 'seed!=0', parallel model is disabled and serial
model is selected, num.threads='1:1'joint_samp <- do.call('rbind', lapply(joint_samp, function(x) matrix(x$latent, ncol = 2)))
inla.joint.samps <- data.frame(a = a_fun(joint_samp[,1]), b = b_fun(joint_samp[,2]))
# plot joint posterior of (R, beta) from inlabru
ggplot(inla.joint.samps, aes(a, b)) + stat_density_2d(
geom = "raster",
aes(fill = after_stat(density)), n = 500,
contour = FALSE) +
geom_point(data = data.frame(a = a_fun(fit$summary.fixed$mode[1]), b = b_fun(fit$summary.fixed$mode[2])), color = 'red', shape = 1, size =0.5) +
geom_point(data = data.frame(a = 2, b = 2), color = 'orange', size =0.5) +
coord_fixed() + scale_fill_viridis_c(name = 'Density') + theme_minimal() + xlab('$R$') + ylab('$\\beta$') + xlim(c(0.1, 5)) + ylim(c(0.1, 4))Warning: Removed 1996 rows containing missing values or values outside the scale range
(`geom_raster()`).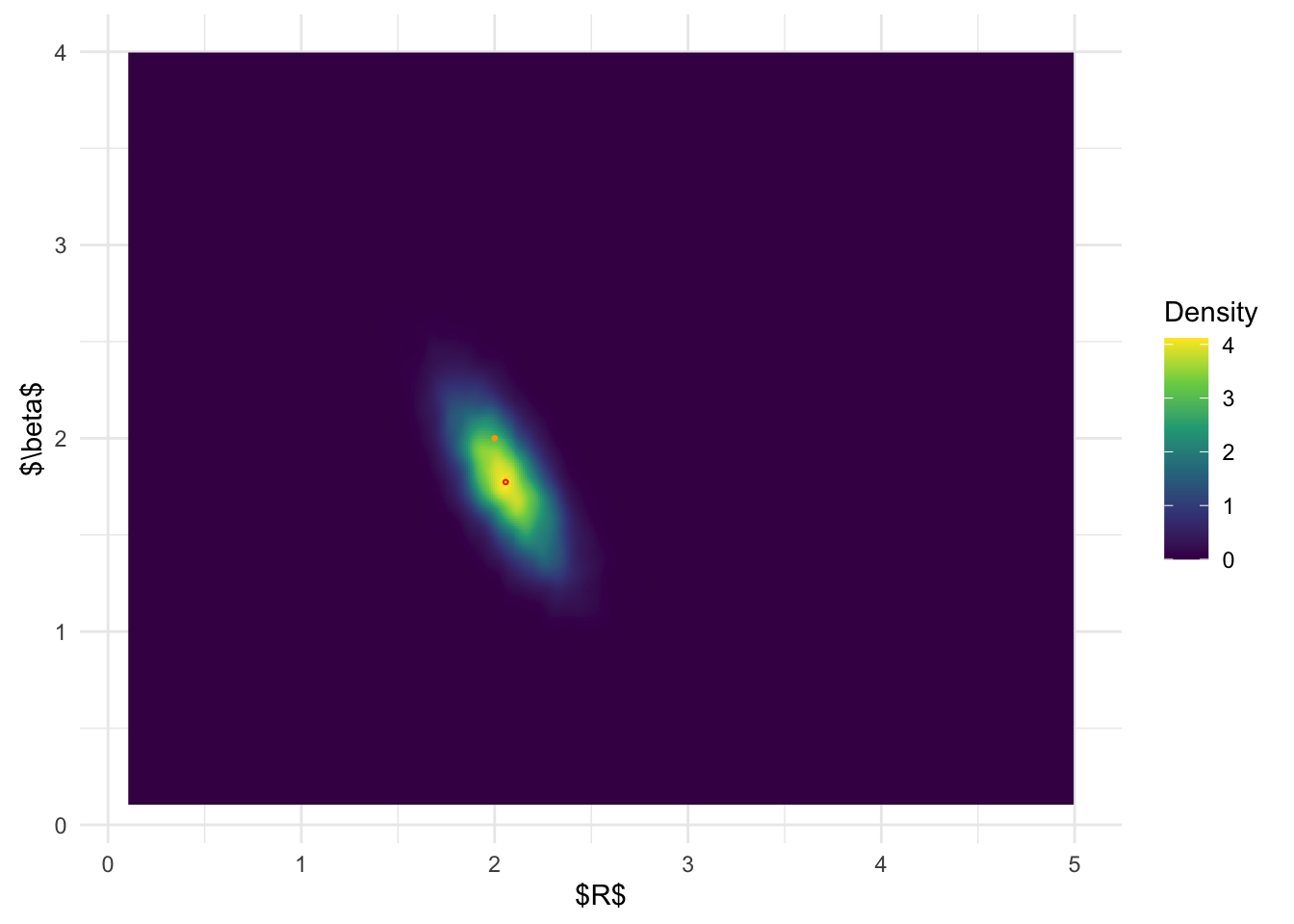
BOSS-modal posterior distribution:
# get the design points data from BOSS
data_to_smooth <- list()
unique_data <- unique(data.frame(x = res_opt_modal$result$x, y = res_opt_modal$result$y))
data_to_smooth$x <- as.matrix(dplyr::select(unique_data, -y))
data_to_smooth$y <- (unique_data$y - mean(unique_data$y))
square_exp_cov <- square_exp_cov_generator_nd(length_scale = res_opt_modal$length_scale, signal_var = res_opt_modal$signal_var)
surrogate <- function(xvalue, data_to_smooth, cov){
predict_gp(data_to_smooth, x_pred = xvalue, choice_cov = cov, noise_var = 1e-6)$mean
}
ff <- list()
ff$fn <- function(x) as.numeric(surrogate(x, data_to_smooth = data_to_smooth, cov = square_exp_cov))
x.1 <- (seq(from = 0.1, to = 5, length.out = 300) - 0.1)/4.9
x.2 <- (seq(from = 0.1, to = 4, length.out = 300) - 0.1)/3.9
x_vals <- expand.grid(x.1, x.2)
names(x_vals) <- c('x.1','x.2')
x_original <- t(t(x_vals)*(c(5, 4) - c(0.1, 0.1)) + c(0.1, 0.1))
fn_vals <- apply(x_vals, 1, function(x) ff$fn(x = matrix(x, ncol = 2))) + mean(unique_data$y)
# normalize
lognormal_const <- log(sum(exp(fn_vals))*0.0098*0.0078*25/9)
post_x_modal <- data.frame(x_original, pos = exp(fn_vals - lognormal_const))
# plot joint posterior of (R, beta) from BOSS
ggplot(post_x_modal, aes(x.1,x.2)) + geom_raster(aes(fill = (pos))) +
geom_point(data = data.frame(x.1 = post_x_modal$x.1[which.max(post_x_modal$pos)], x.2 = post_x_modal$x.2[which.max(post_x_modal$pos)]), color = 'red', shape = 1, size =0.5) +
geom_point(data = data.frame(x.1 = 2, x.2 = 2), color = 'orange', size =0.5) + coord_fixed() + scale_fill_viridis_c(name = 'Density') + theme_minimal() + xlab('$R$') + ylab('$\\beta$')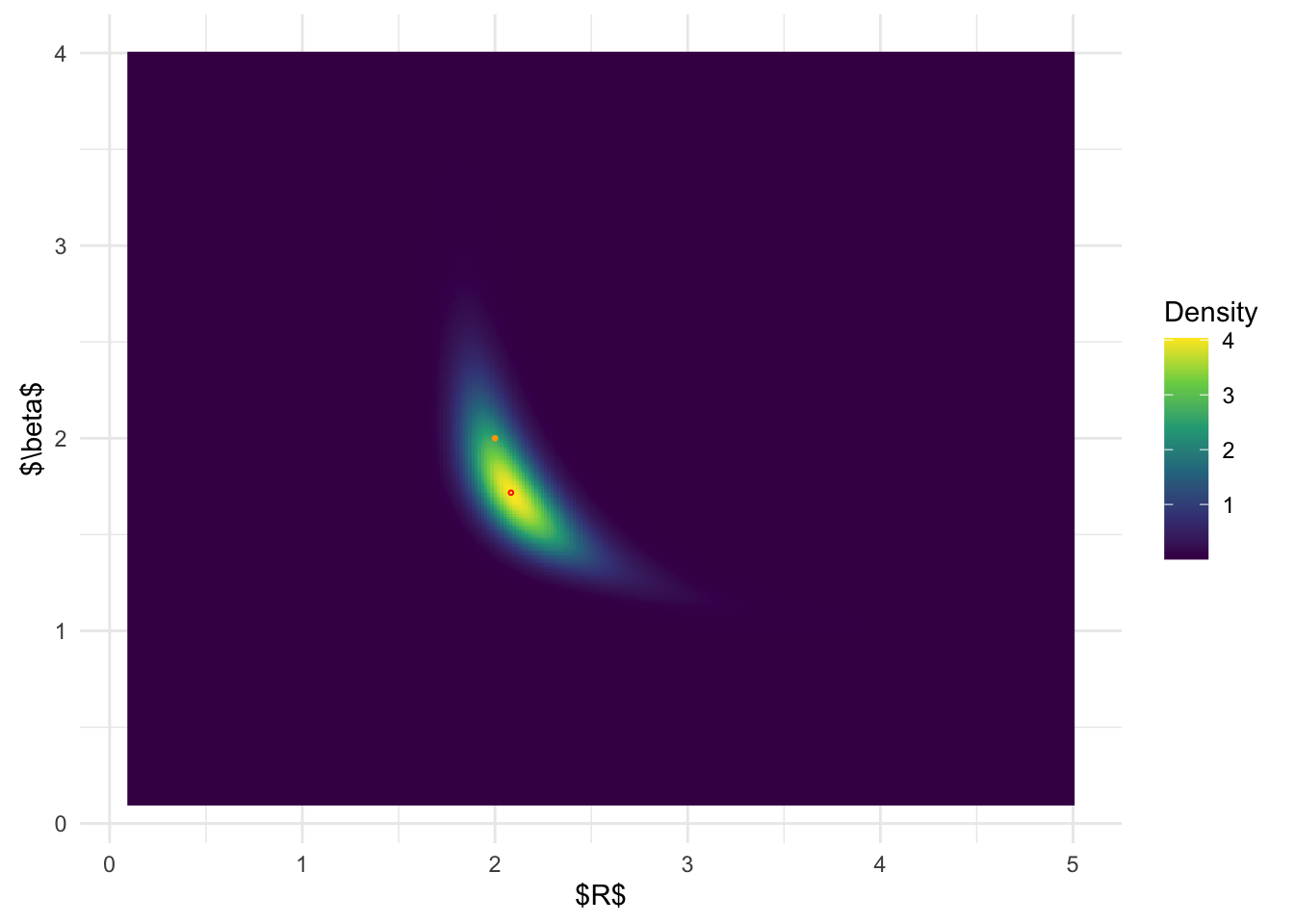
BOSS-AGHQ posterior distribuiton:
# get the design points data from BOSS
data_to_smooth <- list()
unique_data <- unique(data.frame(x = res_opt_aghq$result$x, y = res_opt_aghq$result$y))
data_to_smooth$x <- as.matrix(dplyr::select(unique_data, -y))
data_to_smooth$y <- (unique_data$y - mean(unique_data$y))
square_exp_cov <- square_exp_cov_generator_nd(length_scale = res_opt_aghq$length_scale, signal_var = res_opt_aghq$signal_var)
surrogate <- function(xvalue, data_to_smooth, cov){
predict_gp(data_to_smooth, x_pred = xvalue, choice_cov = cov, noise_var = 1e-6)$mean
}
ff <- list()
ff$fn <- function(x) as.numeric(surrogate(x, data_to_smooth = data_to_smooth, cov = square_exp_cov))
x.1 <- (seq(from = 0.1, to = 5, length.out = 300) - 0.1)/4.9
x.2 <- (seq(from = 0.1, to = 4, length.out = 300) - 0.1)/3.9
x_vals <- expand.grid(x.1, x.2)
names(x_vals) <- c('x.1','x.2')
x_original <- t(t(x_vals)*(c(5, 4) - c(0.1, 0.1)) + c(0.1, 0.1))
fn_vals <- apply(x_vals, 1, function(x) ff$fn(x = matrix(x, ncol = 2))) + mean(unique_data$y)
# normalize
lognormal_const <- log(sum(exp(fn_vals))*0.0098*0.0078*25/9)
post_x_aghq <- data.frame(x_original, pos = exp(fn_vals - lognormal_const))
# plot joint posterior of (R, beta) from BOSS
ggplot(post_x_aghq, aes(x.1,x.2)) + geom_raster(aes(fill = (pos))) +
geom_point(data = data.frame(x.1 = post_x_aghq$x.1[which.max(post_x_aghq$pos)], x.2 = post_x_aghq$x.2[which.max(post_x_aghq$pos)]), color = 'red', shape = 1, size =0.5) +
geom_point(data = data.frame(x.1 = 2, x.2 = 2), color = 'orange', size =0.5) + coord_fixed() + scale_fill_viridis_c(name = 'Density') + theme_minimal() + xlab('$R$') + ylab('$\\beta$')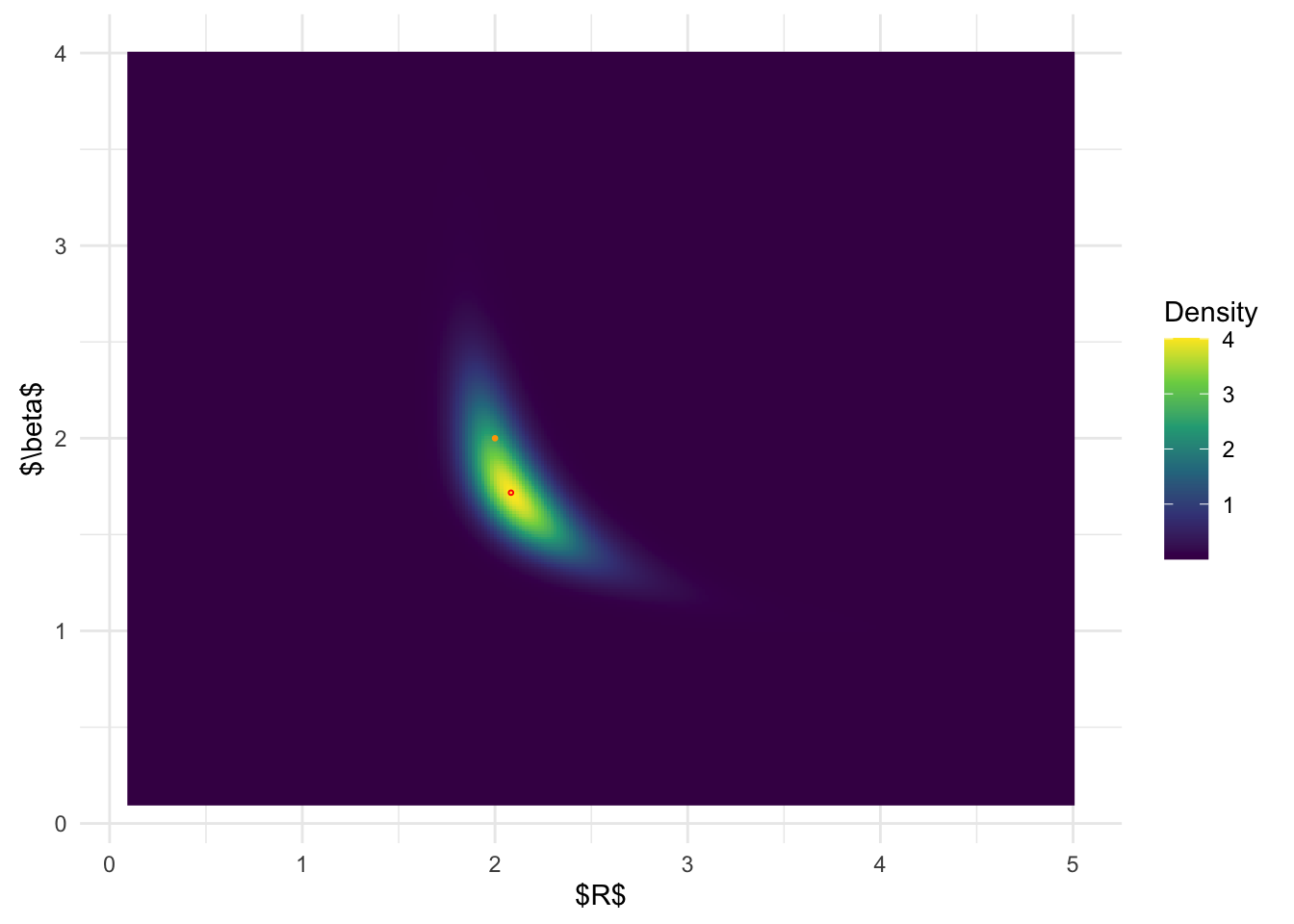
MCMC posterior distribution:
ggplot(MCMC_samp, aes(a, b)) + stat_density_2d(
geom = "raster",
aes(fill = after_stat(density)), n = 300,
contour = FALSE) +
geom_point(data = data.frame(a = post_x_aghq$x.1[which.max(post_x_aghq$pos)], b = post_x_aghq$x.2[which.max(post_x_aghq$pos)]), color = 'red', shape = 1, size =0.5) +
geom_point(data = data.frame(a = 2, b = 2), color = 'orange', size =0.5) + coord_fixed() + scale_fill_viridis_c(name = 'Density') + theme_minimal() + xlab('$R$') + ylab('$\\beta$') + xlim(c(0.1, 5)) + ylim(c(0.1, 4))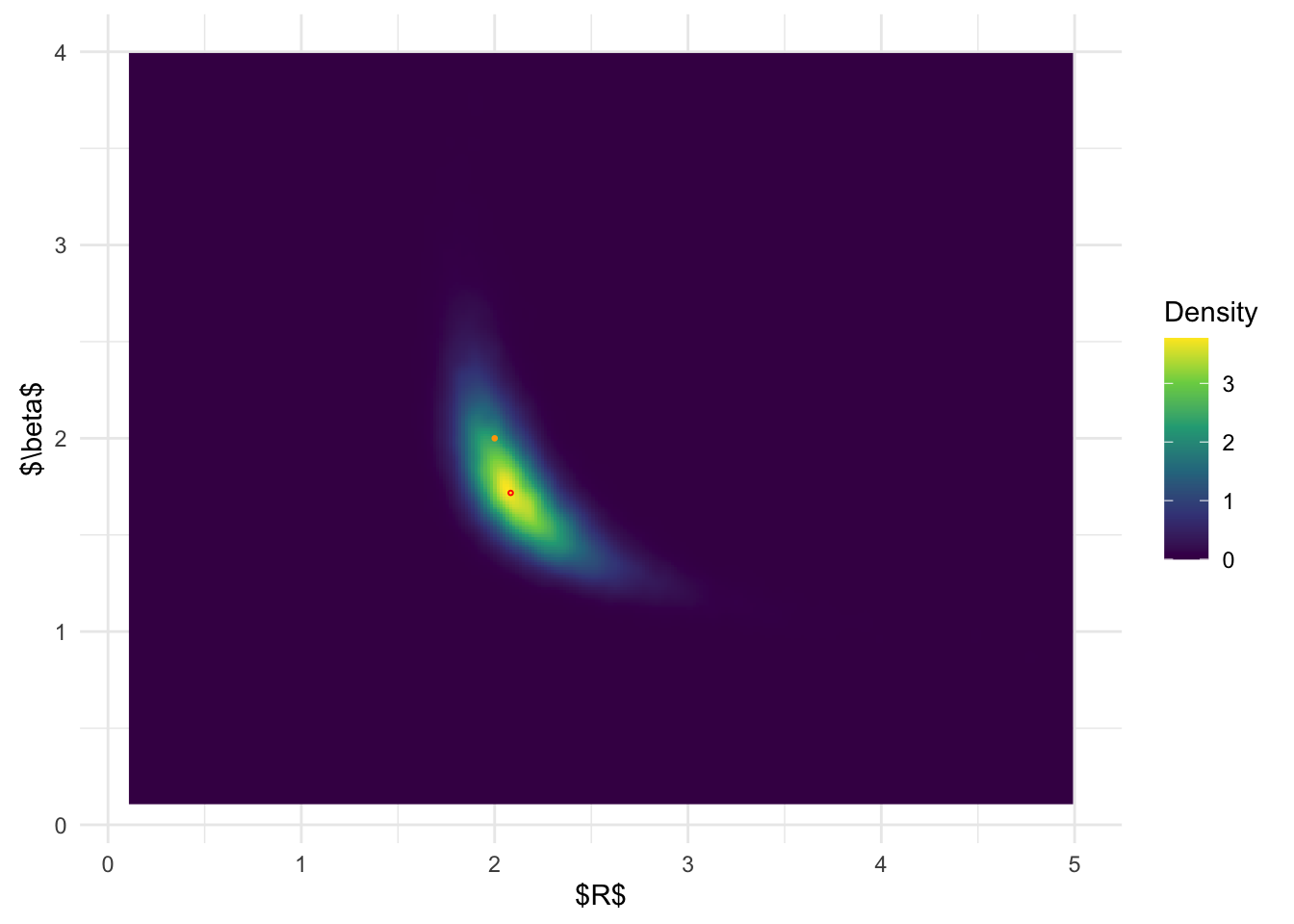
From the above results, it is clear that BOSS is much better at
depicting the joint posterior distribution than
inlabru.
sessionInfo()R version 4.4.1 (2024-06-14)
Platform: aarch64-apple-darwin20
Running under: macOS 15.0
Matrix products: default
BLAS: /Library/Frameworks/R.framework/Versions/4.4-arm64/Resources/lib/libRblas.0.dylib
LAPACK: /Library/Frameworks/R.framework/Versions/4.4-arm64/Resources/lib/libRlapack.dylib; LAPACK version 3.12.0
locale:
[1] en_US.UTF-8/en_US.UTF-8/en_US.UTF-8/C/en_US.UTF-8/en_US.UTF-8
time zone: America/Toronto
tzcode source: internal
attached base packages:
[1] stats graphics grDevices utils datasets methods base
other attached packages:
[1] modeest_2.4.0 inlabru_2.11.1 fmesher_0.1.7
[4] INLA_24.06.27 sp_2.1-4 Matrix_1.7-0
[7] rstan_2.32.6 StanHeaders_2.32.10 tikzDevice_0.12.6
[10] lubridate_1.9.3 forcats_1.0.0 stringr_1.5.1
[13] dplyr_1.1.4 purrr_1.0.2 readr_2.1.5
[16] tidyr_1.3.1 tibble_3.2.1 ggplot2_3.5.1
[19] tidyverse_2.0.0 workflowr_1.7.1
loaded via a namespace (and not attached):
[1] mnormt_2.1.1 DBI_1.2.3 gridExtra_2.3
[4] inline_0.3.19 rlang_1.1.4 magrittr_2.0.3
[7] clue_0.3-65 git2r_0.33.0 matrixStats_1.4.1
[10] e1071_1.7-16 compiler_4.4.1 getPass_0.2-4
[13] loo_2.8.0 callr_3.7.6 vctrs_0.6.5
[16] lhs_1.2.0 rmutil_1.1.10 pkgconfig_2.0.3
[19] fastmap_1.2.0 labeling_0.4.3 utf8_1.2.4
[22] promises_1.3.0 rmarkdown_2.28 pracma_2.4.4
[25] tzdb_0.4.0 nloptr_2.1.1 ps_1.8.0
[28] MatrixModels_0.5-3 xfun_0.47 cachem_1.1.0
[31] jsonlite_1.8.9 highr_0.11 later_1.3.2
[34] parallel_4.4.1 cluster_2.1.6 R6_2.5.1
[37] bslib_0.8.0 stringi_1.8.4 mvQuad_1.0-8
[40] rpart_4.1.23 numDeriv_2016.8-1.1 jquerylib_0.1.4
[43] Rcpp_1.0.13 knitr_1.48 filehash_2.4-6
[46] httpuv_1.6.15 splines_4.4.1 timechange_0.3.0
[49] tidyselect_1.2.1 rstudioapi_0.16.0 yaml_2.3.10
[52] timeDate_4041.110 codetools_0.2-20 processx_3.8.4
[55] pkgbuild_1.4.4 lattice_0.22-6 plyr_1.8.9
[58] withr_3.0.1 evaluate_1.0.0 stable_1.1.6
[61] sf_1.0-19 units_0.8-5 proxy_0.4-27
[64] RcppParallel_5.1.10 pillar_1.9.0 whisker_0.4.1
[67] KernSmooth_2.23-24 stats4_4.4.1 sn_2.1.1
[70] generics_0.1.3 rprojroot_2.0.4 hms_1.1.3
[73] munsell_0.5.1 scales_1.3.0 timeSeries_4041.111
[76] class_7.3-22 glue_1.7.0 statip_0.2.3
[79] tools_4.4.1 data.table_1.16.0 spatial_7.3-17
[82] fBasics_4041.97 fs_1.6.4 grid_4.4.1
[85] QuickJSR_1.6.0 colorspace_2.1-1 cli_3.6.3
[88] optimx_2025-4.9 fansi_1.0.6 viridisLite_0.4.2
[91] gtable_0.3.5 stabledist_0.7-2 sass_0.4.9
[94] digest_0.6.37 classInt_0.4-10 aghq_0.4.1
[97] farver_2.1.2 htmltools_0.5.8.1 lifecycle_1.0.4
[100] httr_1.4.7 statmod_1.5.0 MASS_7.3-61