poisson log normal distribution

Introduction

Consider the model $$x\sim Poisson(s\exp(\mu)),\mu\sim N(0,\sigma2).$$

There are two approaches to estimate $\sigma^2$ and get the posterior of $\mu$.

A. estimate $\sigma^2$ by maximizing the marginal likelihood then obtain $p(\mu|x;\hat\sigma^2)$.

B. estimate $\sigma^2$ and $q(\mu)$ iteratively in a variational empirical Bayes algorithm.

ANother question is: is $q(\mu)=M(\mu;\cdot,\cdot)$ a good approximation to the true posterior?

Let’s answer the last question first. Assume $\sigma^2$ is known. THe true posterior of $\mu$ is $$p(\mu|x) = \frac{p(x|\mu)p(\mu)}{p(x)} \propto e^{\mu x - se^\mu-\frac{\mu^2}{2\sigma^2}}$$ . Apparently there’s no closed form of the posterior.

Here I use quadrature to calculate the posterior density.

library(fastGHQuad)

Loading required package: Rcpp

library(vebpm)
pois_pmf = function(mu,x){
  dpois(x,exp(mu))
}
pln_marginal = function(x,sigma2,n_gh=20){
  gh_points = gaussHermiteData(n_gh)
  1/sqrt(pi)*sum(gh_points$w*pois_pmf(sqrt(2*sigma2)*gh_points$x,x))
}
mu_true_post = function(mu,x,sigma2){
  pois_pmf(mu,x)*dnorm(mu,0,sqrt(sigma2))/pln_marginal(x,sigma2)
}
mu_true_post_vec = function(mu,x,sigma2){
  n = length(mu)
  res = c()
  for(i in 1:n){
    res[i] =  mu_true_post(mu[i],x,sigma2)
  }
  res
}

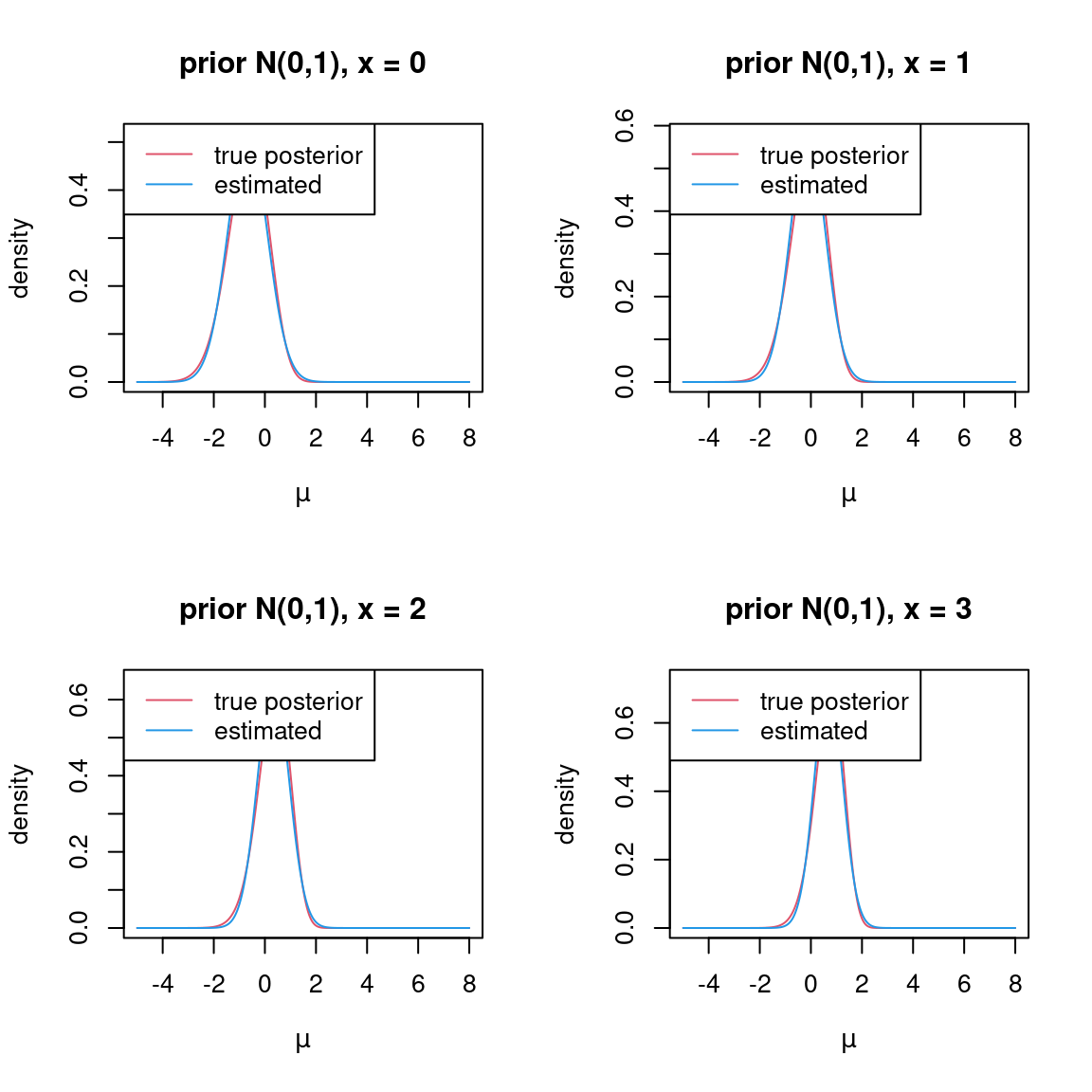
Let’s plot the true posterior density, setting $\sigma^2=1$: I also plot the posterior $q(\mu) = N(m,v)$ fitted by variational inference.

plot_posterior = function(mu_seq,x,prior_var=1){
  d_true = mu_true_post_vec(mu_seq,x,prior_var)
  fit = pois_mean_GG(x,prior_mean = 0,prior_var = prior_var,)
  d_hat = dnorm(mu_seq,mean=fit$posterior$mean_log,sd=sqrt(fit$posterior$var_log))
  plot(mu_seq,d_true,type='l',xlab=expression(mu),ylab='density',main=paste('prior N(0,',prior_var,'), x = ',x,sep=''),col=2,ylim=range(c(d_true,d_hat)))
  lines(mu_seq,d_hat,col=4)
  legend('topleft',c('true posterior','estimated'),lty=c(1,1),col=c(2,4))
}

sigma2 = 1
mu_seq = seq(-5,8,length.out = 500)
par(mfrow=c(2,2))
for(x in 0:11){
  plot_posterior(mu_seq,x,prior_var=sigma2)
}

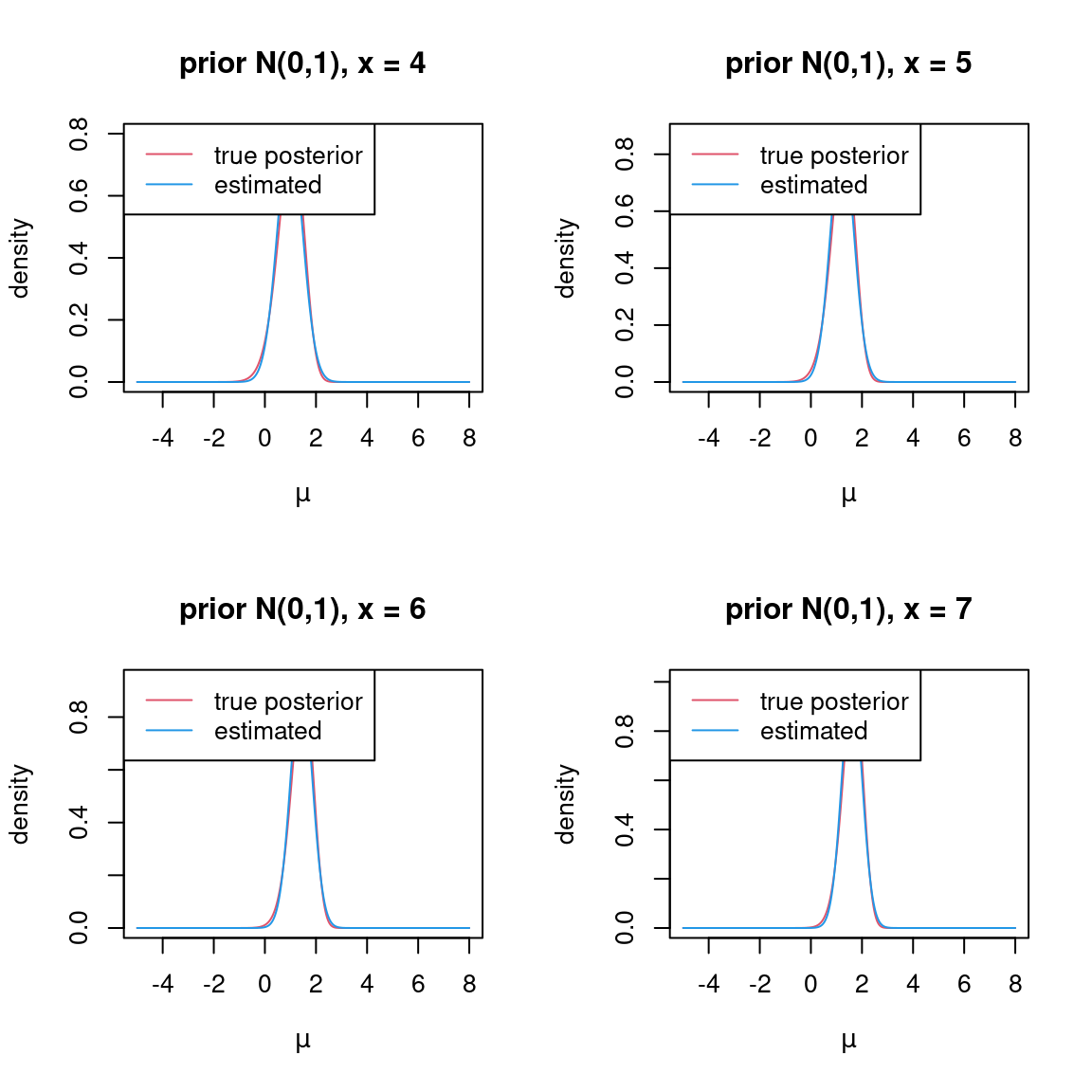
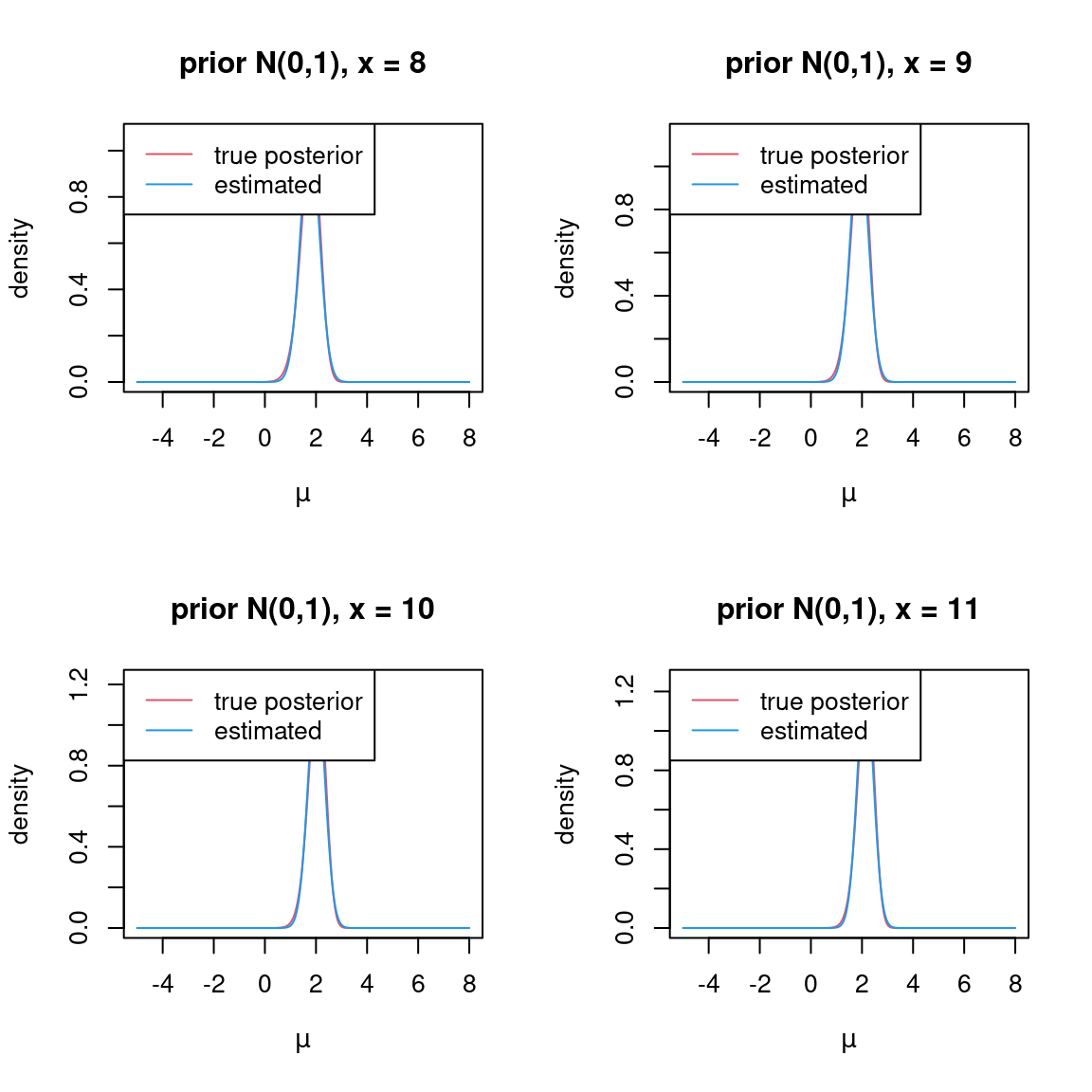
The normal posterior is a reasonable choice.

Now about estimating the variance, we are interested in the accuracy and the speed. We can either use quadrature or numerical integration to evaluate the marginal likelihood.

f = function(mu,x,lsigma2){
  dpois(x,exp(mu))*dnorm(mu,0,sqrt(exp(lsigma2)))
}
pln_marginal_loglik = function(lsigma2,x){
  # quadrature
  res = 0
  for(i in 1:length(x)){
    res = res + log(pln_marginal(x[i],exp(lsigma2)))
  }
  -res
}
pln_mle = function(x){
  exp(optim(0,pln_marginal_loglik,x=x,method = "L-BFGS-B")$par)
}

par(mfrow=c(1,1))
n = 1000
mu = rnorm(n)
x = rpois(n,exp(mu))
s_seq = seq(0.001,3,length.out=100)
l = c()
for(i in 1:length(s_seq)){
  l[i] = pln_marginal_loglik(log(s_seq[i]),x)
}
plot(s_seq,l,ylab='negative llik')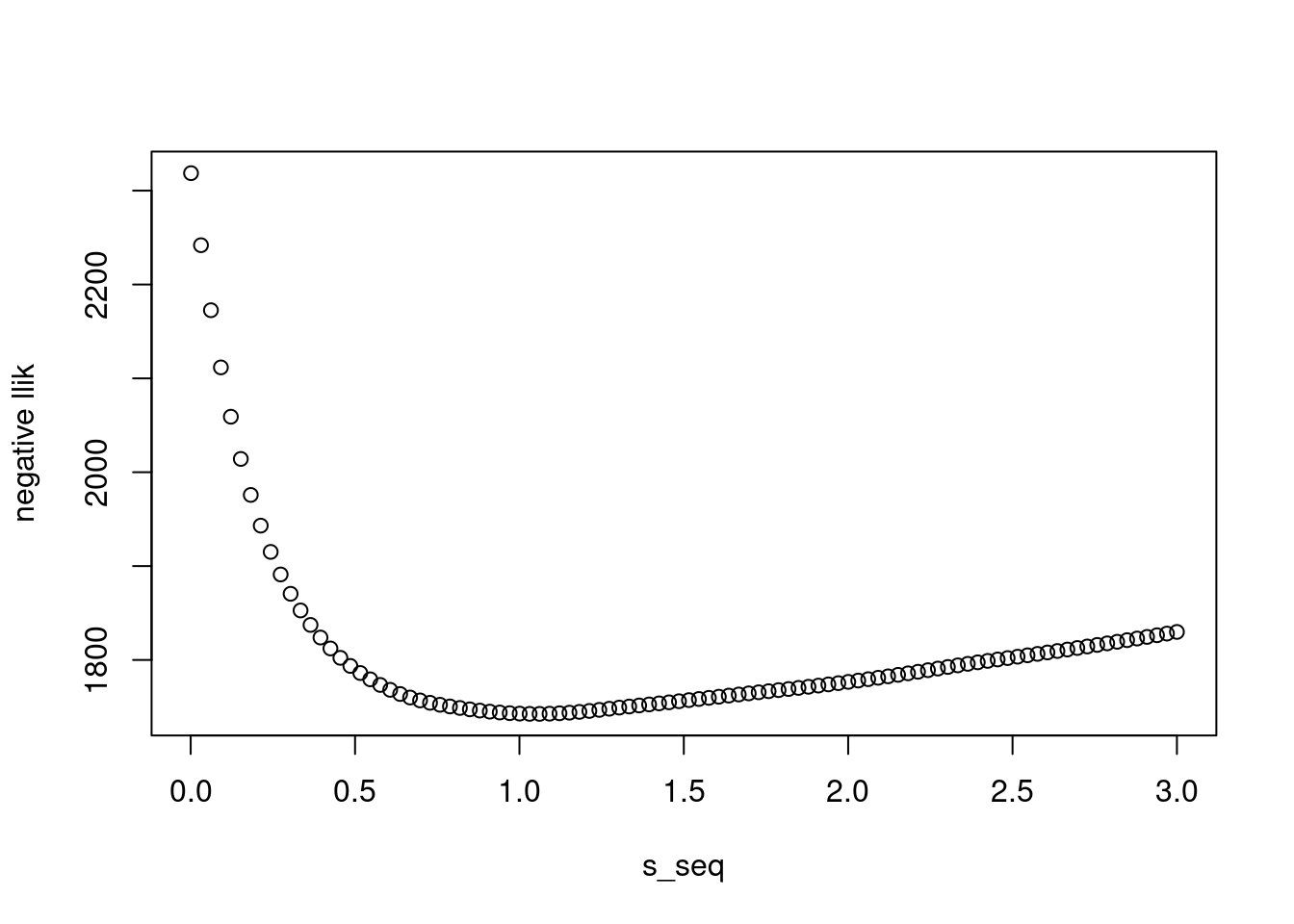

pln_mle(x)

[1] 1.0492

exp(optimize(pln_marginal_loglik,interval = c(-1,1),x=x)$minimum)

[1] 1.049207

The numerical integration is a bottleneck of the computation. If we could get rid of the integration…?

Session information

sessionInfo()

R version 4.2.2 Patched (2022-11-10 r83330)
Platform: x86_64-pc-linux-gnu (64-bit)
Running under: Ubuntu 22.04.1 LTS

Matrix products: default
BLAS:   /usr/lib/x86_64-linux-gnu/openblas-pthread/libblas.so.3
LAPACK: /usr/lib/x86_64-linux-gnu/openblas-pthread/libopenblasp-r0.3.20.so

locale:
 [1] LC_CTYPE=en_US.UTF-8       LC_NUMERIC=C              
 [3] LC_TIME=en_US.UTF-8        LC_COLLATE=en_US.UTF-8    
 [5] LC_MONETARY=en_US.UTF-8    LC_MESSAGES=en_US.UTF-8   
 [7] LC_PAPER=en_US.UTF-8       LC_NAME=C                 
 [9] LC_ADDRESS=C               LC_TELEPHONE=C            
[11] LC_MEASUREMENT=en_US.UTF-8 LC_IDENTIFICATION=C       

attached base packages:
[1] stats     graphics  grDevices utils     datasets  methods   base     

other attached packages:
[1] vebpm_0.3.4      fastGHQuad_1.0.1 Rcpp_1.0.9       workflowr_1.7.0 

loaded via a namespace (and not attached):
 [1] horseshoe_0.2.0    invgamma_1.1       lattice_0.20-45    getPass_0.2-2     
 [5] ps_1.7.2           rprojroot_2.0.3    digest_0.6.31      utf8_1.2.2        
 [9] truncnorm_1.0-8    R6_2.5.1           evaluate_0.19      highr_0.9         
[13] httr_1.4.4         ggplot2_3.4.0      pillar_1.8.1       rlang_1.0.6       
[17] rstudioapi_0.14    ebnm_1.0-11        irlba_2.3.5.1      whisker_0.4.1     
[21] callr_3.7.3        jquerylib_0.1.4    nloptr_2.0.3       Matrix_1.5-3      
[25] rmarkdown_2.19     splines_4.2.2      stringr_1.5.0      munsell_0.5.0     
[29] mixsqp_0.3-48      compiler_4.2.2     httpuv_1.6.7       xfun_0.35         
[33] pkgconfig_2.0.3    SQUAREM_2021.1     htmltools_0.5.4    tidyselect_1.2.0  
[37] tibble_3.1.8       matrixStats_0.63.0 fansi_1.0.3        dplyr_1.0.10      
[41] later_1.3.0        grid_4.2.2         jsonlite_1.8.4     gtable_0.3.1      
[45] lifecycle_1.0.3    git2r_0.30.1       magrittr_2.0.3     scales_1.2.1      
[49] ebpm_0.0.1.3       cli_3.4.1          stringi_1.7.8      cachem_1.0.6      
[53] fs_1.5.2           promises_1.2.0.1   bslib_0.4.2        generics_0.1.3    
[57] vctrs_0.5.1        trust_0.1-8        tools_4.2.2        glue_1.6.2        
[61] parallel_4.2.2     processx_3.8.0     fastmap_1.1.0      yaml_2.3.6        
[65] colorspace_2.0-3   ashr_2.2-54        deconvolveR_1.2-1  knitr_1.41        
[69] sass_0.4.4