Last updated: 2022-09-14

Checks: 7 0

Knit directory: misc/

This reproducible R Markdown analysis was created with workflowr (version 1.7.0). The Checks tab describes the reproducibility checks that were applied when the results were created. The Past versions tab lists the development history.

R Markdown file: up-to-date

Great! Since the R Markdown file has been committed to the Git repository, you know the exact version of the code that produced these results.

Environment: empty

Great job! The global environment was empty. Objects defined in the global environment can affect the analysis in your R Markdown file in unknown ways. For reproduciblity it’s best to always run the code in an empty environment.

Seed: set.seed(20191122)

The command set.seed(20191122) was run prior to running the code in the R Markdown file. Setting a seed ensures that any results that rely on randomness, e.g. subsampling or permutations, are reproducible.

Session information: recorded

Great job! Recording the operating system, R version, and package versions is critical for reproducibility.

Cache: none

Nice! There were no cached chunks for this analysis, so you can be confident that you successfully produced the results during this run.

File paths: relative

Great job! Using relative paths to the files within your workflowr project makes it easier to run your code on other machines.

Repository version: 3be295f

Great! You are using Git for version control. Tracking code development and connecting the code version to the results is critical for reproducibility.

The results in this page were generated with repository version 3be295f. See the Past versions tab to see a history of the changes made to the R Markdown and HTML files.

Note that you need to be careful to ensure that all relevant files for the analysis have been committed to Git prior to generating the results (you can use wflow_publish or wflow_git_commit). workflowr only checks the R Markdown file, but you know if there are other scripts or data files that it depends on. Below is the status of the Git repository when the results were generated: 


Ignored files:
    Ignored:    .Rhistory
    Ignored:    .Rproj.user/

Note that any generated files, e.g. HTML, png, CSS, etc., are not included in this status report because it is ok for generated content to have uncommitted changes.

These are the previous versions of the repository in which changes were made to the R Markdown (analysis/nb.Rmd) and HTML (docs/nb.html) files. If you’ve configured a remote Git repository (see ?wflow_git_remote), click on the hyperlinks in the table below to view the files as they were in that past version.

File Version Author Date Message
Rmd 3be295f Dongyue Xie 2022-09-14 wflow_publish("analysis/nb.Rmd")
html e58b698 DongyueXie 2020-04-12 Build site.
Rmd d3a2bcd DongyueXie 2020-04-12 wflow_publish("analysis/nb.Rmd")

Introduction

In its very original form, negative binomial distribution \(NB(r,p)\) has pmf \(P(X=k;r,p) = {k+r-1 \choose k}p^r(1-p)^k\), where \(k\) is number of failures observed in a sequence of Bernoulli trials that are stopped at \(r\) successes, and \(p\) is the paprameter of the Bernnouli dsitrbution. It’s mean is \(\mu = \frac{pr}{1-p}\) and variance is \(\sigma^2 = \frac{pr}{(1-p)^2} = \mu + \frac{1}{r}\mu^2\). On the other hand, if the distribution is charaterized by mean and variance, then \(p = \frac{\sigma^2-\mu}{\sigma^2}\) and \(r=\frac{\mu^2}{\sigma^2-\mu}\).

Sometimes people write \(NB(\mu,\alpha)\), where \(\mu\) is the mean and \(\alpha\) is called dispersion parameter. Obviously, \(\alpha = \frac{1}{r}\).

In R function rnbinom, size is the \(r\), prob is the \(p\) and \(\mu\) is the mean.

Poisson-gamma

It’s well known that the marginal distribution of a Poisson-gamma random variable is negative bionomial. Suppose \(X\sim Poisson(\lambda)\) and the Poisson parameter \(\lambda\) itself is distributed as \(Gamma(r,\frac{1-p}{p})\), where \(r\) is the shape parameter and \(\frac{1-p}{p}\) is the rate parameter of gamma distribution(note: A gamma distribution with shape a and rate b has pdf \(\frac{b^a}{\Gamma(a)}x^{a-1}\exp(-bx)\), mean \(a/b\) and variance \(a/b^2\)), then the marginal distribution of \(X\) is \(NB(r,p)\).

On the other hand, if \(\lambda\sim Gamma(a,\mu)\), where \(\mu=a/b\), then \(X\sim NB(\mu,1/\alpha)\); if further let \(p = \frac{\mu}{\mu+\alpha}\), then \(X\sim NB(\alpha,p)\).

Estimation

Consider a \(NB(r,p)\) with pmf \(P(X=k;r,p) = {k+r-1 \choose k}p^r(1-p)^k\).

If we have one observation from a NB and \(r\) is known, then mle is \(\hat p = \frac{r}{r+k}\) and an unbiased estimator is \(\hat p = \frac{r-1}{r+k-1}\).

The log-likelihood for \(N\) iid observations \((y_1,...,y_n)\) is \[l(r,p) = \sum_i \left(\log\Gamma(y_i+r)+y_i\log p\right) + Nr\log(1-p) -N\log\Gamma(r).\]

The partial derivatives of \(l(r,p)\) w.r.t r and p are \[\frac{\partial l}{\partial p} = \frac{\sum_i y_i}{p} - \frac{nr}{1-p} = 0\] \[p = \frac{\sum_i y_i}{nr+\sum_i y_i}\] \[\frac{\partial l}{\partial r} = \sum_i\psi(y_i+r) - n\psi(r)+n\log(1-p) = 0\] \[\psi(y) = \frac{\Gamma'(y)}{\Gamma(y)}\]

set.seed(12345)
r = 10
p = 0.3
n = 1000
x = rnbinom(n,r,1-p)

lr = function(r,x){
  n = length(x)
  p = sum(x)/(sum(x)+n*exp(r))
  temp = (sum(lgamma(x+exp(r))+x*log(p)) + n*exp(r)*log(1-p) - n*lgamma(exp(r)))
  return(-temp)
}

lr_d1 = function(r,x){
  n = length(x)
  p = sum(x)/(sum(x)+n*exp(r))
  temp = (sum(digamma(x+exp(r)))-n*digamma(exp(r))+n*log(1-p))
  return(-temp)
}

r_vec = 1:50
l_value = c()
for(rr in r_vec){
  l_value = c(l_value,lr(log(rr),x))
}
plot(r_vec,l_value,type='l')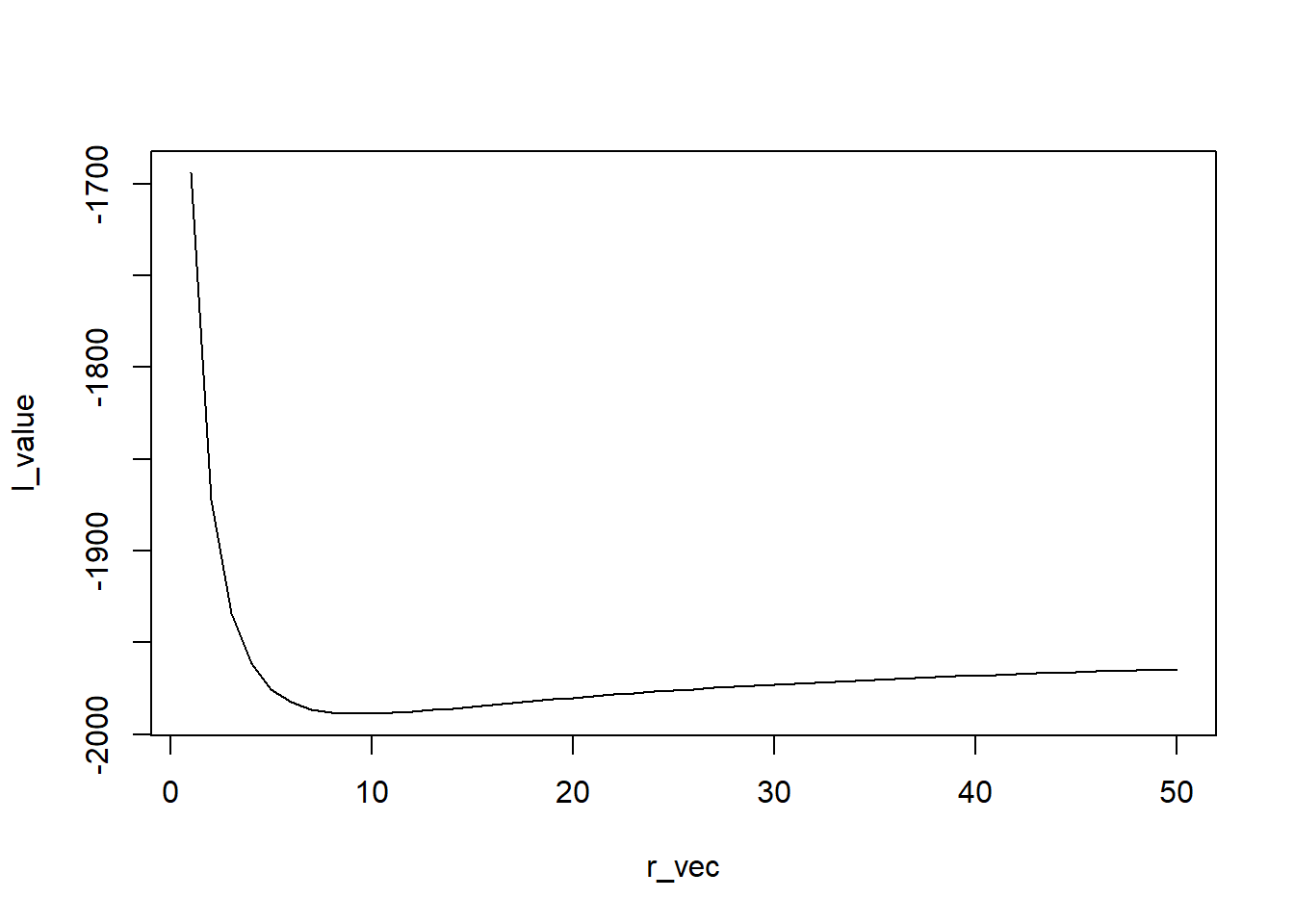

res = optim(par=log(20),fn=lr,gr=lr_d1,method ='BFGS',x=x)
exp(res$par)
[1] 9.412021

Negative binomial glm

Now we focus on the parameterization with mean \(\mu\) and dispersion parameter \(\alpha\). With \(\alpha\) fixed, this is a member of an exponential dispersion family appropriate for discrete variables, with natural parameter \(\log(\frac{\mu}{\mu+1/\alpha})\).

In nbglm, the dispersion parameter \(\alpha\) is common for all observations. We can test \(H_0: \alpha=0\) to see if Poisson is enough. This quadratuc mean-variance relationship model is called NB2.

NB1(linear) instead uses another paramaterization of the gamma mixture which yields a negative binomial distribution with with mean \(\mu\) and variance \(\frac{\mu(1+r)}{r}\). See Foundations of Linear and Generalized Linear Models, p250.


sessionInfo()
R version 4.2.1 (2022-06-23 ucrt)
Platform: x86_64-w64-mingw32/x64 (64-bit)
Running under: Windows 10 x64 (build 22000)

Matrix products: default

locale:
[1] LC_COLLATE=English_United States.utf8 
[2] LC_CTYPE=English_United States.utf8   
[3] LC_MONETARY=English_United States.utf8
[4] LC_NUMERIC=C                          
[5] LC_TIME=English_United States.utf8    

attached base packages:
[1] stats     graphics  grDevices utils     datasets  methods   base     

other attached packages:
[1] workflowr_1.7.0

loaded via a namespace (and not attached):
 [1] Rcpp_1.0.9       highr_0.9        compiler_4.2.1   pillar_1.8.1    
 [5] bslib_0.4.0      later_1.3.0      git2r_0.30.1     jquerylib_0.1.4 
 [9] tools_4.2.1      getPass_0.2-2    digest_0.6.29    jsonlite_1.8.0  
[13] evaluate_0.16    tibble_3.1.8     lifecycle_1.0.2  pkgconfig_2.0.3 
[17] rlang_1.0.5      cli_3.3.0        rstudioapi_0.14  yaml_2.3.5      
[21] xfun_0.32        fastmap_1.1.0    httr_1.4.4       stringr_1.4.1   
[25] knitr_1.40       fs_1.5.2         vctrs_0.4.1      sass_0.4.2      
[29] rprojroot_2.0.3  glue_1.6.2       R6_2.5.1         processx_3.7.0  
[33] fansi_1.0.3      rmarkdown_2.16   callr_3.7.2      magrittr_2.0.3  
[37] whisker_0.4      ps_1.7.1         promises_1.2.0.1 htmltools_0.5.3 
[41] httpuv_1.6.5     utf8_1.2.2       stringi_1.7.8    cachem_1.0.6