Code
from matplotlib.ticker import MultipleLocator, AutoMinorLocator
from matplotlib.dates import YearLocator
import matplotlib.pyplot as plt
import pandas as pd
data = pd.read_csv('../presentation/01_data/tidy_svr.csv')
data['ds'] = pd.to_datetime(data['ds'])
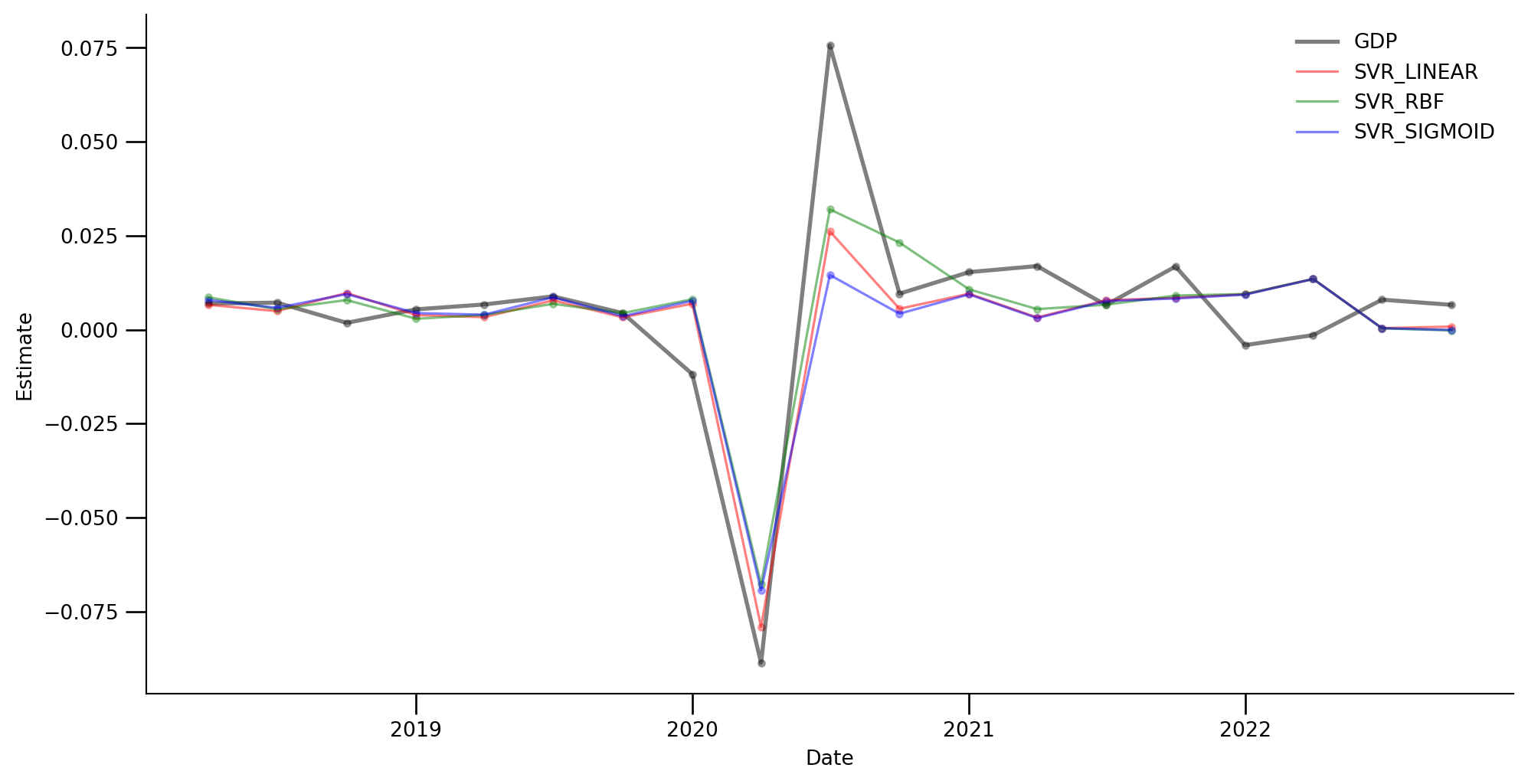
models_to_plot = ['SVR_LINEAR', 'SVR_RBF',
'SVR_SIGMOID', 'GDP']
filtered_data = data[data['Model'].isin(models_to_plot)]
grouped = filtered_data.groupby('Model')
selected_data = pd.concat([group.iloc[::3] for _, group in grouped])
model_color_dict = {
'SVR_LINEAR': 'red',
'SVR_RBF': 'green',
'SVR_SIGMOID': 'blue',
'GDP': 'black'
}
fig, ax = plt.subplots(figsize=(12, 6))
ax.xaxis.set_major_locator(YearLocator())
ax.spines['top'].set_visible(False)
ax.spines['right'].set_visible(False)
ax.tick_params(which="major", width=1.0)
ax.tick_params(which="major", length=10)
ax.tick_params(which="minor", width=1.0, labelsize=10)
ax.tick_params(which="minor", length=5, labelsize=10, labelcolor="0.25")
ax.set_ylabel("Estimate", weight="medium")
ax.set_xlabel("Date", weight="medium")
default_linewidth = 1.2
gdp_linewidth = 2
for model in selected_data['Model'].unique():
subset = selected_data[selected_data['Model'] == model]
ax.scatter(subset['ds'], subset['Estimate'], s=10, color=model_color_dict[model],
edgecolor=model_color_dict[model], linewidth=1, zorder=-20, alpha=0.3)
linewidth = gdp_linewidth if model == 'GDP' else default_linewidth
ax.plot(subset['ds'], subset['Estimate'],
c=model_color_dict[model], linewidth=linewidth, alpha=0.5, label=model)
ax.legend(frameon=False)
plt.show()