The Poisson distribution
2024-07-30
Last updated: 2024-07-30
Checks: 7 0
Knit directory: muse/
This reproducible R Markdown analysis was created with workflowr (version 1.7.1). The Checks tab describes the reproducibility checks that were applied when the results were created. The Past versions tab lists the development history.
Great! Since the R Markdown file has been committed to the Git repository, you know the exact version of the code that produced these results.
Great job! The global environment was empty. Objects defined in the global environment can affect the analysis in your R Markdown file in unknown ways. For reproduciblity it’s best to always run the code in an empty environment.
The command set.seed(20200712) was run prior to running
the code in the R Markdown file. Setting a seed ensures that any results
that rely on randomness, e.g. subsampling or permutations, are
reproducible.
Great job! Recording the operating system, R version, and package versions is critical for reproducibility.
Nice! There were no cached chunks for this analysis, so you can be confident that you successfully produced the results during this run.
Great job! Using relative paths to the files within your workflowr project makes it easier to run your code on other machines.
Great! You are using Git for version control. Tracking code development and connecting the code version to the results is critical for reproducibility.
The results in this page were generated with repository version 482856c. See the Past versions tab to see a history of the changes made to the R Markdown and HTML files.
Note that you need to be careful to ensure that all relevant files for
the analysis have been committed to Git prior to generating the results
(you can use wflow_publish or
wflow_git_commit). workflowr only checks the R Markdown
file, but you know if there are other scripts or data files that it
depends on. Below is the status of the Git repository when the results
were generated:
Ignored files:
Ignored: .Rhistory
Ignored: .Rproj.user/
Ignored: r_packages_4.3.3/
Ignored: r_packages_4.4.0/
Note that any generated files, e.g. HTML, png, CSS, etc., are not included in this status report because it is ok for generated content to have uncommitted changes.
These are the previous versions of the repository in which changes were
made to the R Markdown (analysis/poisson.Rmd) and HTML
(docs/poisson.html) files. If you’ve configured a remote
Git repository (see ?wflow_git_remote), click on the
hyperlinks in the table below to view the files as they were in that
past version.
| File | Version | Author | Date | Message |
|---|---|---|---|---|
| Rmd | 482856c | Dave Tang | 2024-07-30 | Sampling from a sequencing library |
| html | 7efed52 | Dave Tang | 2024-07-30 | Build site. |
| Rmd | 67813b6 | Dave Tang | 2024-07-30 | Fix LaTeX |
| html | e49a794 | Dave Tang | 2024-07-30 | Build site. |
| Rmd | 2dceb55 | Dave Tang | 2024-07-30 | The Poisson distribution |
Introduction
A Poisson distribution is the probability distribution that results from a Poisson experiment. A probability distribution assigns a probability to possible outcomes of a random experiment. A Poisson experiment has the following properties:
- The outcomes of the experiment can be classified as either successes or failures.
- The average number of successes that occurs in a specified region is known.
- The probability that a success will occur is proportional to the size of the region.
- The probability that a success will occur in an extremely small region is virtually zero.
A Poisson random variable is the number of successes that result from a Poisson experiment. Given the mean number of successes that occur in a specified region, we can compute the Poisson probability based on the following formula:
\[ P(x; \mu) = \frac{(e^{-\mu})(\mu^x)}{x!} \]
which is also written as:
\[ Pr(X = k) = e^{-\lambda} \frac{\lambda^k}{k!} \ \ k = 0, 1, 2, \dotsc \]
Examples
Homes sold
The average number of homes sold is 2 homes per day. What is the probability that exactly 3 homes will be sold tomorrow?
\[ P(3; 2) = \frac{(e^{-2}) (2^3)}{3!} \]
Calculating this manually in R:
e <- exp(1)
((e^-2)*(2^3))/factorial(3)[1] 0.180447Using dpois():
dpois(x = 3, lambda = 2)[1] 0.180447RNA-seq
The Poisson distribution can be used to estimate the technical variance in high-throughput sequencing experiments. My basic understanding is that the variance between technical replicates can be modelled using the Poisson distribution. Check out Why Does Rna-Seq Read Count Fit Poisson Distribution? on Biostars.
From Chris Miller:
Picture a process whereby you take the genome and choose a location at random to produce a read. This is a Poisson process. If you plot the depth of sequence along this theoretical genome, it will be a poisson distribution.
Expanding on the idea above in Modern Statistics for Modern Biology:
Consider a sequencing library that contains \(n_1\) fragments corresponding to gene 1, \(n_2\) fragments for gene 2, and so on, with a total library size of \(n = n_1 + n_2 + \ldots\). This library is then sequenced and the identity of \(r\) randomly sampled fragments are determined. To paint a better mental picture, the following are some typical numbers. The number of genes will be in the order of tens of thousands; the value of \(n\) depends on the amount of cells that were used to prepare the library and typically this is in the order of billions or trillions; and the number of reads \(r\) is usually in the tens of millions, which is much smaller than \(n\). Sequencing is sampling from \(n\).
From this we can conclude that the probability that a given read maps to the \(i\) th gene is \(p_i = n_i/n\) (ratio of a specific fragment to all fragments) and this is independent of the outcomes for all the other reads. So we can model the number of reads for gene \(i\) by a Poisson distribution, where the rate of the Poisson process is the product of \(p_i\), the initial proportion of fragments for the \(i\) th gene, times \(r\), the number of reads sequenced; that is \(\lambda_i = rp_i\).
In practice, we are usually not interested in modeling the read counts within a single library, but in comparing the counts between libraries. That is, we want to know whether any differences that we see between different biological conditions are larger than what we might expect even between biological replicates. Empirically, it turns out that replicate experiments vary more than the Poisson distribution predicts.
Intuitively, what happens is that \(p_i\), and therefore also \(\lambda_i\), varies even between biological replicates. To account for that variation, we need to add another layer of modeling on top and it turns out that the gamma-Poisson (a.k.a. negative binomial) distribution suits our modeling requirements. Instead of a single \(\lambda\), which represents both mean and variance, this distribution has two parameters. In principle, these can be different for each gene and we can estimate them from the data.
Calculating confidence intervals
Calculate the confidence intervals using R. Create data with 1,000,000 values that follow a Poisson distribution with lambda = 20.
set.seed(1984)
n <- 1000000
data <- rpois(n, 20)Functions for calculating the lower and upper tails.
poisson_lower_tail <- function(n) {
qchisq(0.025, 2*n)/2
}
poisson_upper_tail <- function(n) {
qchisq(0.975, 2*(n+1))/2
}Lower limit for lambda = 20.
poisson_lower_tail(20)[1] 12.21652Upper limit for lambda = 20.
poisson_upper_tail(20)[1] 30.88838How many values in data are lower than the lower limit?
table(data<poisson_lower_tail(20))
FALSE TRUE
961213 38787 How many values in data are higher than the upper limit?
table(data>poisson_upper_tail(20))
FALSE TRUE
986239 13761 What percentage of values were outside of the 95% CI?
(sum(data<poisson_lower_tail(20)) + sum(data>poisson_upper_tail(20))) * 100 / n[1] 5.2548Plot.
hist(data)
abline(v=poisson_lower_tail(20))
abline(v=poisson_upper_tail(20))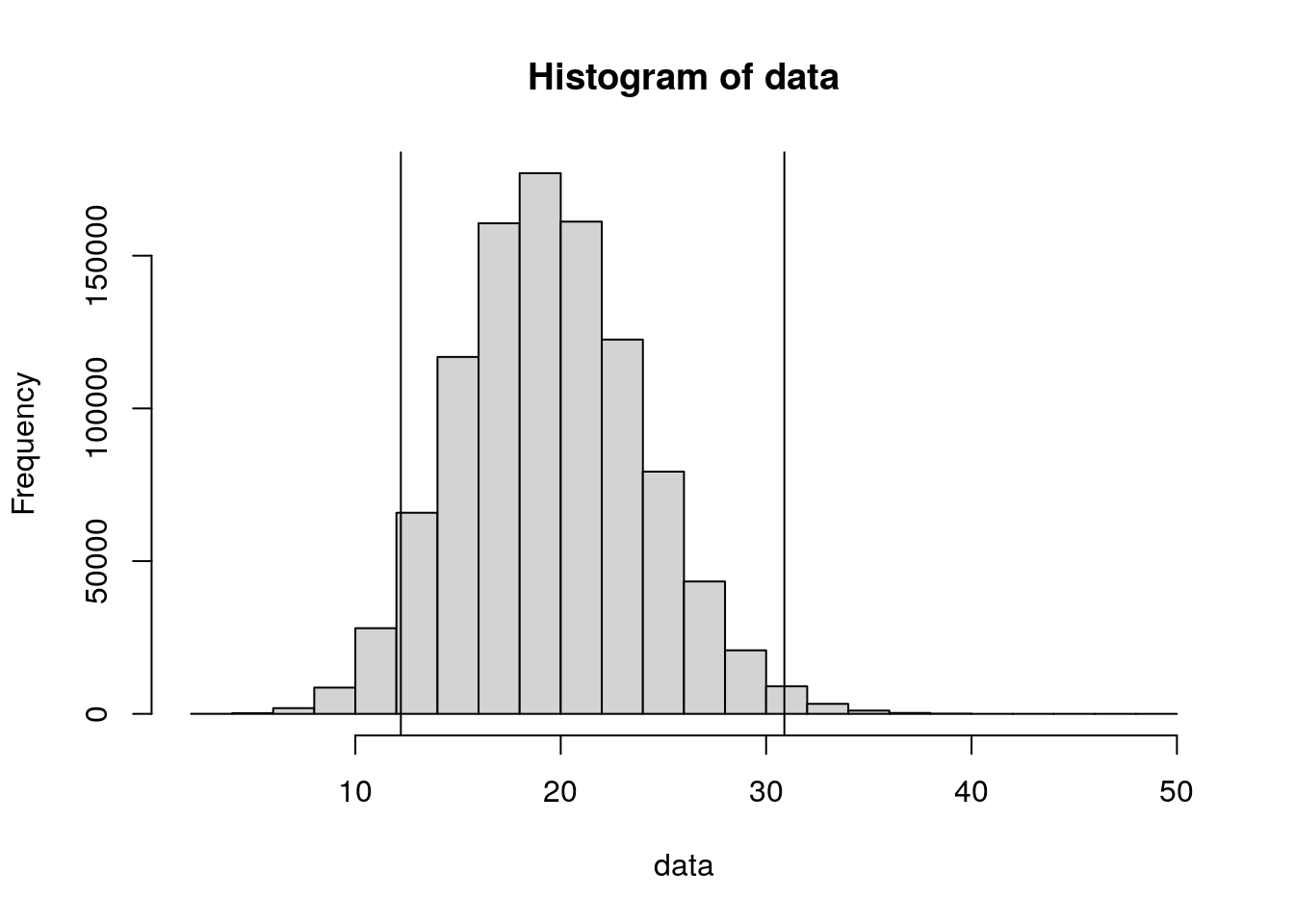
| Version | Author | Date |
|---|---|---|
| e49a794 | Dave Tang | 2024-07-30 |
Webtool
Using the Poisson Confidence Interval Calculator and lambda = 20 returns:
- 99% confidence interval: 10.35327 - 34.66800
- 95% confidence interval: 12.21652 - 30.88838
- 90% confidence interval: 13.25465 - 29.06202
which matches our 95% CI values.
sessionInfo()R version 4.4.0 (2024-04-24)
Platform: x86_64-pc-linux-gnu
Running under: Ubuntu 22.04.4 LTS
Matrix products: default
BLAS: /usr/lib/x86_64-linux-gnu/openblas-pthread/libblas.so.3
LAPACK: /usr/lib/x86_64-linux-gnu/openblas-pthread/libopenblasp-r0.3.20.so; LAPACK version 3.10.0
locale:
[1] LC_CTYPE=en_US.UTF-8 LC_NUMERIC=C
[3] LC_TIME=en_US.UTF-8 LC_COLLATE=en_US.UTF-8
[5] LC_MONETARY=en_US.UTF-8 LC_MESSAGES=en_US.UTF-8
[7] LC_PAPER=en_US.UTF-8 LC_NAME=C
[9] LC_ADDRESS=C LC_TELEPHONE=C
[11] LC_MEASUREMENT=en_US.UTF-8 LC_IDENTIFICATION=C
time zone: Etc/UTC
tzcode source: system (glibc)
attached base packages:
[1] stats graphics grDevices utils datasets methods base
other attached packages:
[1] lubridate_1.9.3 forcats_1.0.0 stringr_1.5.1 dplyr_1.1.4
[5] purrr_1.0.2 readr_2.1.5 tidyr_1.3.1 tibble_3.2.1
[9] ggplot2_3.5.1 tidyverse_2.0.0 workflowr_1.7.1
loaded via a namespace (and not attached):
[1] sass_0.4.9 utf8_1.2.4 generics_0.1.3 stringi_1.8.4
[5] hms_1.1.3 digest_0.6.35 magrittr_2.0.3 timechange_0.3.0
[9] evaluate_0.24.0 grid_4.4.0 fastmap_1.2.0 rprojroot_2.0.4
[13] jsonlite_1.8.8 processx_3.8.4 whisker_0.4.1 ps_1.7.6
[17] promises_1.3.0 httr_1.4.7 fansi_1.0.6 scales_1.3.0
[21] jquerylib_0.1.4 cli_3.6.2 rlang_1.1.4 munsell_0.5.1
[25] withr_3.0.0 cachem_1.1.0 yaml_2.3.8 tools_4.4.0
[29] tzdb_0.4.0 colorspace_2.1-0 httpuv_1.6.15 vctrs_0.6.5
[33] R6_2.5.1 lifecycle_1.0.4 git2r_0.33.0 fs_1.6.4
[37] pkgconfig_2.0.3 callr_3.7.6 pillar_1.9.0 bslib_0.7.0
[41] later_1.3.2 gtable_0.3.5 glue_1.7.0 Rcpp_1.0.12
[45] highr_0.11 xfun_0.44 tidyselect_1.2.1 rstudioapi_0.16.0
[49] knitr_1.47 htmltools_0.5.8.1 rmarkdown_2.27 compiler_4.4.0
[53] getPass_0.2-4