GSVA: gene set variation analysis

workflowr

• Summary
• Checks
• Past versions

Last updated: 2023-12-18

Checks: 7 0

Knit directory: muse/

This reproducible R Markdown analysis was created with workflowr (version 1.7.1). The Checks tab describes the reproducibility checks that were applied when the results were created. The Past versions tab lists the development history.

---

R Markdown file: up-to-date

Great! Since the R Markdown file has been committed to the Git repository, you know the exact version of the code that produced these results.

Environment: empty

Great job! The global environment was empty. Objects defined in the global environment can affect the analysis in your R Markdown file in unknown ways. For reproduciblity it’s best to always run the code in an empty environment.

Seed: set.seed(20200712)

The command set.seed(20200712) was run prior to running the code in the R Markdown file. Setting a seed ensures that any results that rely on randomness, e.g. subsampling or permutations, are reproducible.

Session information: recorded

Great job! Recording the operating system, R version, and package versions is critical for reproducibility.

Cache: none

Nice! There were no cached chunks for this analysis, so you can be confident that you successfully produced the results during this run.

File paths: relative

Great job! Using relative paths to the files within your workflowr project makes it easier to run your code on other machines.

Repository version: af7bbbe

Great! You are using Git for version control. Tracking code development and connecting the code version to the results is critical for reproducibility.

The results in this page were generated with repository version af7bbbe. See the Past versions tab to see a history of the changes made to the R Markdown and HTML files.

Note that you need to be careful to ensure that all relevant files for the analysis have been committed to Git prior to generating the results (you can use wflow_publish or wflow_git_commit). workflowr only checks the R Markdown file, but you know if there are other scripts or data files that it depends on. Below is the status of the Git repository when the results were generated:

Ignored files:
    Ignored:    .Rproj.user/
    Ignored:    r_packages_4.3.2/

Note that any generated files, e.g. HTML, png, CSS, etc., are not included in this status report because it is ok for generated content to have uncommitted changes.

---

These are the previous versions of the repository in which changes were made to the R Markdown (analysis/gsva.Rmd) and HTML (docs/gsva.html) files. If you’ve configured a remote Git repository (see ?wflow_git_remote), click on the hyperlinks in the table below to view the files as they were in that past version.

File	Version	Author	Date	Message
Rmd	af7bbbe	Dave Tang	2023-12-18	Implementation
html	0851e8a	Dave Tang	2023-12-18	Build site.
Rmd	7a818f5	Dave Tang	2023-12-18	Include background from paper
html	39a8474	Dave Tang	2023-11-08	Build site.
Rmd	b774382	Dave Tang	2023-11-08	ssGSEA molecular signature
html	38ae3bc	Dave Tang	2023-11-08	Build site.
Rmd	d80c8a1	Dave Tang	2023-11-08	Molecular signature identification
html	834452d	Dave Tang	2023-11-08	Build site.
Rmd	525a52a	Dave Tang	2023-11-08	GSVA on microarray and RNA-seq data
html	3f0f517	Dave Tang	2023-11-08	Build site.
Rmd	3f1aa75	Dave Tang	2023-11-08	Elaborate on the different methods
html	d6d78a0	Dave Tang	2023-11-07	Build site.
Rmd	794b249	Dave Tang	2023-11-07	All available methods
html	00b6361	Dave Tang	2023-11-07	Build site.
Rmd	2ed827f	Dave Tang	2023-11-07	Use Param object
html	a0a232a	Dave Tang	2023-11-07	Build site.
Rmd	748c6d1	Dave Tang	2023-11-07	Enrichment scores
html	a077e6c	Dave Tang	2023-10-23	Build site.
Rmd	115752b	Dave Tang	2023-10-23	Technical notes
html	14e3e6b	Dave Tang	2023-10-23	Build site.
Rmd	9b9327a	Dave Tang	2023-10-23	No progress bar
html	b0af093	Dave Tang	2023-10-23	Build site.
Rmd	aeb90e1	Dave Tang	2023-10-23	GSVA

---

Background

Notes from the paper GSVA: gene set variation analysis for microarray and RNA-Seq data.

Gene Set Enrichment (GSE) analyses begin by obtaining a ranked gene list, typically derived from a microarray experiment that studies gene expression changes between two groups.

The genes are then mapped into predefined gene sets and their gene expression statistic is summarized into a single enrichment score for each gene set.

Many methodological variations of GSE methods have been proposed, including non-parametric enrichment statistics, battery testing, and focused gene set testing.

Battery testing methods aim at identifying gene sets standing out from a large collection of annotated pathways and gene signatures.

Focused gene set testing methods try to carefully evaluate a few gene sets that are relevant to the experiment being analyzed.

An important distinction among many of the GSE methods is the definition of the null hypothesis that is tested. The null hypothesis of a competitive test declares that there are no differences between genes inside and outside the gene set.

A self-contained test defines its null hypothesis only in terms of the genes inside the gene set being tested. More concretely, for a self-contained test on a gene set, the differential expression of just one of its genes allows one to reject the null hypothesis of no differential expression for that gene set. It follows, that self-contained tests provide higher power than competitive tests to detect subtle changes of expression in a gene set. But they may not be useful to single out a few gene sets in a battery testing setting because of the potentially large number of reported results.

Finally, many GSE methods assume two classes (e.g. case/control) and evaluate enrichment within this context.

The limits imposed by this assumption become evident with the rise of large genomic studies, such as The Cancer Genome Atlas project (TCGA - http://cancergenome.nih.gov), an ambitious project with the goal to identify the molecular determinants of multiple cancer types. In contrast to case-control studies with small sample sizes, the TCGA project has large patient cohorts with multiple phenotypes, structured with hierarchical, multi-class, and censored data. Hence, GSE methods are needed that can assess pathway variation across large, heterogeneous populations with complex phenotypic traits.

To address these challenges, we present a non-parametric, unsupervised method called Gene Set Variation Analysis (GSVA).

GSVA calculates sample-wise gene set enrichment scores as a function of genes inside and outside the gene set, analogously to a competitive gene set test. Further, it estimates variation of gene set enrichment over the samples independently of any class label.

Conceptually, this methodology can be understood as a change in coordinate systems for gene expression data, from genes to gene sets. This transformation facilitates post-hoc construction of pathway-centric models, such as differential pathway activity identification or survival prediction. Further, we demonstrate the flexibility of GSVA by applying it to RNA-seq data.

Implementation

The GSVA method requires two main inputs:

1. A matrix \(X = {\{x_{ij}\}}_{p \times n}\) of normalised expression values for \(p\) genes and \(n\) samples and
2. A collection of gene sets \(\Gamma = \{\gamma_1,\ldots,\gamma_m\}\).

Figure 1

Step 1. Kernel estimation of the cumulative density function (kcdf). The two plots show two simulated expression profiles mimicking 6 samples from microarray and RNA-seq data. The x-axis corresponds to expression values where each gene is lowly expressed in the four samples with lower values and highly expressed in the other two. The scale of the kcdf is on the left y-axis and the scale of the Gaussian and Poisson kernels is on the right y-axis.

In statistics, kernel density estimation (KDE) is the application of kernel smoothing for probability density estimation, i.e., a non-parametric method to estimate the probability density function of a random variable based on kernels as weights.

Step 2. The expression-level statistic is rank ordered for each sample. This is to bring distinct expression profiles to a common scale.

Step 3. For every gene set, the Kolmogorov-Smirnov-like rank statistic is calculated. The plot illustrates a gene set consisting of 3 genes out of a total number of 10 with the sample-wise calculation of genes inside and outside of the gene set.

Step 4. The GSVA enrichment score is either the maximum deviation from zero (top) or the difference between the two sums (bottom). The two plots show two simulations of the resulting scores under the null hypothesis of no gene expression change. The output of the algorithm is a matrix containing pathway enrichment scores for each gene set and sample.

Vignette

Following the vignette.

Gene set variation analysis (GSVA) is a particular type of gene set enrichment method that works on single samples and enables pathway-centric analyses of molecular data by performing a conceptually simple but powerful change in the functional unit of analysis, from genes to gene sets. The GSVA package provides the implementation of four single-sample gene set enrichment methods, concretely zscore, plage, ssGSEA and its own called GSVA. While this methodology was initially developed for gene expression data, it can be applied to other types of molecular profiling data. In this vignette we illustrate how to use the GSVA package with bulk microarray and RNA-seq expression data.

Gene set variation analysis (GSVA) provides an estimate of pathway activity by transforming an input gene-by-sample expression data matrix into a corresponding gene-set-by-sample expression data matrix.

This resulting expression data matrix can be then used with classical analytical methods such as differential expression, classification, survival analysis, clustering or correlation analysis in a pathway-centric manner. One can also perform sample-wise comparisons between pathways and other molecular data types such as microRNA expression or binding data, copy-number variation (CNV) data or single nucleotide polymorphisms (SNPs).

Package

Install GSVA. (Dependencies are listed in the Imports section in the DESCRIPTION file.)

if (!require("BiocManager", quietly = TRUE))
  install.packages("BiocManager")

if (!require("GSVA", quietly = TRUE))
  BiocManager::install("GSVA")

if (!require("GSVAdata", quietly = TRUE))
  BiocManager::install("GSVAdata")

Load package.

library(GSVA)
packageVersion("GSVA")

[1] '1.50.0'

Quick start

Generate example expression matrix with 10,000 genes across 30 samples.

p <- 10000
n <- 30
set.seed(1984)
X <- matrix(
  rnorm(p*n),
  nrow=p,
  dimnames=list(paste0("g", 1:p), paste0("s", 1:n))
)
X[1:5, 1:5]

           s1         s2         s3          s4           s5
g1  0.4092032  1.4676435  0.3515056  1.53512312 -1.279009469
g2 -0.3230250 -1.8501416 -0.9198650  1.40036448  0.086613315
g3  0.6358523  1.6084120  1.6380322  0.23799146  0.216628121
g4 -1.8461288 -0.2928844  0.4651573 -0.09766558 -0.009887299
g5  0.9536474 -0.4816006  0.1807824  1.03141311  0.206414282

Generate 100 gene sets that are contain from 10 to up to 100 genes sampled from 1:p.

set.seed(1984)
gs <- as.list(sample(10:100, size=100, replace=TRUE))

gs <- lapply(gs, function(n, p){
  paste0("g", sample(1:p, size=n, replace=FALSE))
}, p)
names(gs) <- paste0("gs", 1:length(gs))

sapply(gs, length)

  gs1   gs2   gs3   gs4   gs5   gs6   gs7   gs8   gs9  gs10  gs11  gs12  gs13 
   49    29    67    90    94    87    41    26    86    77    97    90    45 
 gs14  gs15  gs16  gs17  gs18  gs19  gs20  gs21  gs22  gs23  gs24  gs25  gs26 
   47    54    83    11    75    95    99    94    89    93    50    49    87 
 gs27  gs28  gs29  gs30  gs31  gs32  gs33  gs34  gs35  gs36  gs37  gs38  gs39 
   36    61    84    99    58    30    63    29    35    29    69    41    46 
 gs40  gs41  gs42  gs43  gs44  gs45  gs46  gs47  gs48  gs49  gs50  gs51  gs52 
   38    17    48    72    15    81   100    93    37    99    89    43    36 
 gs53  gs54  gs55  gs56  gs57  gs58  gs59  gs60  gs61  gs62  gs63  gs64  gs65 
   84    83    40    72    90    86    37    23    69    96    20    93    36 
 gs66  gs67  gs68  gs69  gs70  gs71  gs72  gs73  gs74  gs75  gs76  gs77  gs78 
   21    46    76    71    57    48    25    73    26    46    29    53    69 
 gs79  gs80  gs81  gs82  gs83  gs84  gs85  gs86  gs87  gs88  gs89  gs90  gs91 
   69    42    76    30    16    49    35    12    83    99    88    66    10 
 gs92  gs93  gs94  gs95  gs96  gs97  gs98  gs99 gs100 
   51    82    73    97    59    59    42    10    64 

Calculate GSVA enrichment scores using the gsva() function, which does all the work and requires the following two input arguments:

1. A normalised gene expression dataset, which can be provided in one of the following containers:
   • A matrix of expression values with genes corresponding to rows and samples corresponding to columns.
   • An ExpressionSet object; see package Biobase.
   • A SummarizedExperiment object, see package SummarizedExperiment.
2. A collection of gene sets; which can be provided in one of the following containers:
   • A list object where each element corresponds to a gene set defined by a vector of gene identifiers, and the element names correspond to the names of the gene sets.
   • A GeneSetCollection object; see package GSEABase.

The first argument to the gsva() function is the gene expression data matrix and the second the collection of gene sets. The gsva() function can take the input expression data and gene sets using different specialized containers that facilitate the access and manipulation of molecular and phenotype data, as well as their associated metadata. Another advanced features include the use of on-disk and parallel backends to enable, respectively, using GSVA on large molecular data sets and speed up computing time.

The gsva() function will apply the following filters before the actual calculations take place:

1. Discard genes in the input expression data matrix with constant expression.
2. Discard genes in the input gene sets that do not map to a gene in the input gene expression data matrix.
3. Discard gene sets that, after applying the previous filters, do not meet a minimum and maximum size, which by default is 1 for the minimum size and Inf for the maximum size.

When method="gsva" is used (the default), the following parameters can be tuned:

• kcdf: The first step of the GSVA algorithm brings gene expression profiles to a common scale by calculating an expression statistic through a non-parametric estimation of the CDF across samples. Such a non-parametric estimation employs a kernel function and the kcdf parameter allows the user to specify three possible values for that function:

1. “Gaussian”, the default value, which is suitable for continuous expression data, such as microarray fluorescent units in logarithmic scale and RNA-seq log-CPMs, log-RPKMs or log-TPMs units of expression;
2. “Poisson”, which is suitable for integer counts, such as those derived from RNA-seq alignments;
3. “none”, which will enforce a direct estimation of the CDF without a kernel function.

• mx.diff: The last step of the GSVA algorithm calculates the gene set enrichment score from two Kolmogorov-Smirnov random walk statistics. This parameter is a logical flag that allows the user to specify two possible ways to do such calculation:

1. TRUE, the default value, where the enrichment score is calculated as the magnitude difference between the largest positive and negative random walk deviations;
2. FALSE, where the enrichment score is calculated as the maximum distance of the random walk from zero.

• abs.ranking: Logical flag used only when mx.diff=TRUE. By default, abs.ranking=FALSE and it implies that a modified Kuiper statistic is used to calculate enrichment scores, taking the magnitude difference between the largest positive and negative random walk deviations. When abs.ranking=TRUE the original Kuiper statistic is used, by which the largest positive and negative random walk deviations are added together. In this case, gene sets with genes enriched on either extreme (high or low) will be regarded as highly activated.

• tau: Exponent defining the weight of the tail in the random walk. By default tau=1. When method="ssgsea", this parameter is also used and its default value becomes then tau=0.25 to match the methodology described in (Barbie et al. 2009).

In general, the default values for the previous parameters are suitable for most analysis settings, which usually consist of some kind of normalized continuous expression values.

es_gsva <- gsva(gsvaParam(X, gs), verbose=FALSE)
dim(es_gsva)

[1] 100  30

Median enrichment scores.

apply(es_gsva, 2, median)

          s1           s2           s3           s4           s5           s6 
 0.009061514 -0.008458424 -0.005713628 -0.021937531  0.006417182  0.019422486 
          s7           s8           s9          s10          s11          s12 
 0.010140618  0.005812097  0.006495584  0.008887644  0.024577619 -0.031697634 
         s13          s14          s15          s16          s17          s18 
 0.001642502  0.008919786 -0.022622470  0.027695420 -0.015799537 -0.011108686 
         s19          s20          s21          s22          s23          s24 
-0.013956442 -0.015493300 -0.004809844 -0.014081494  0.026845336  0.023895676 
         s25          s26          s27          s28          s29          s30 
 0.006358240  0.010642450 -0.012690144 -0.005999451 -0.005058572 -0.012403422 

ssgsea (Barbie et al. 2009). Single sample GSEA (ssGSEA) is a non-parametric method that calculates a gene set enrichment score per sample as the normalized difference in empirical cumulative distribution functions (CDFs) of gene expression ranks inside and outside the gene set. By default, the implementation in the GSVA package follows the last step described in (Barbie et al. 2009, online methods, pg. 2) by which pathway scores are normalized, dividing them by the range of calculated values. This normalization step may be switched off using the argument ssgsea.norm in the call to the gsva() function; see below.

es_ssgsea <- gsva(ssgseaParam(X, gs), verbose=FALSE)

[1] "Calculating ranks..."
[1] "Calculating absolute values from ranks..."
[1] "Normalizing..."

apply(es_ssgsea, 2, median)

       s1        s2        s3        s4        s5        s6        s7        s8 
0.1056332 0.1105148 0.1149790 0.1045303 0.1192256 0.1274702 0.1192217 0.1287768 
       s9       s10       s11       s12       s13       s14       s15       s16 
0.1316429 0.1257247 0.1293241 0.1083643 0.1222038 0.1012195 0.1018693 0.1174057 
      s17       s18       s19       s20       s21       s22       s23       s24 
0.1103184 0.1112410 0.1164373 0.1126160 0.1212393 0.1067666 0.1167117 0.1418775 
      s25       s26       s27       s28       s29       s30 
0.1221909 0.1235449 0.1112199 0.1012381 0.1254514 0.1210392 

Investigating the scores

Create another test matrix.

p <- 10000
n <- 2
set.seed(1984)
X <- matrix(
  rnorm(n = p*n, mean = 10, sd = 10),
  nrow=p,
  dimnames=list(paste0("g", 1:p), paste0("s", 1:n))
)

X[1:50, 's1'] <- rnorm(n = 50, mean = 50, sd = 55)
X[51:100, 's1'] <- rnorm(n = 50, mean = 2, sd = 2)

X[1:50, 's2'] <- rnorm(n = 50, mean = 100, sd = 5)
X[51:100, 's2'] <- rnorm(n = 50, mean = 2, sd = 0.5)

X[1:5, ]

            s1        s2
g1  69.3328103  96.46911
g2  -0.5925752  96.19110
g3 140.0917737 102.47525
g4  75.5836499 103.64442
g5  59.9430328  99.50861

Create testing gene lists with higher and lower expression patterns and check their enrichment scores.

gene_set <- list(
  gs1 = paste0("g", 1:50),
  gs2 = paste0("g", 51:100),
  gs3 = paste0("g", 101:150)
)

ssgsea (Barbie et al. 2009). Single sample GSEA (ssGSEA) is a non-parametric method that calculates a gene set enrichment score per sample as the normalized difference in empirical cumulative distribution functions (CDFs) of gene expression ranks inside and outside the gene set. By default, the implementation in the GSVA package follows the last step described in (Barbie et al. 2009, online methods, pg. 2) by which pathway scores are normalized, dividing them by the range of calculated values. This normalization step may be switched off using the argument ssgsea.norm in the call to the gsva() function.

test_ssgsea <- gsva(ssgseaParam(X, gene_set), verbose=FALSE)

[1] "Calculating ranks..."
[1] "Calculating absolute values from ranks..."
[1] "Normalizing..."

test_ssgsea

             s1          s2
gs1  0.50202664  0.62745511
gs2 -0.35383441 -0.37254489
gs3  0.01605471  0.08617871

No normalisation.

test_ssgsea <- gsva(ssgseaParam(X, gene_set, normalize = FALSE), verbose=FALSE)

[1] "Calculating ranks..."
[1] "Calculating absolute values from ranks..."

test_ssgsea

            s1         s2
gs1  4000.5026  5000.0052
gs2 -2819.6024 -2968.7007
gs3   127.9353   686.7328

gsva (Hanzelmann, Castelo, and Guinney 2013). This is the default method of the package and similarly to ssGSEA, is a non-parametric method that uses the empirical CDFs of gene expression ranks inside and outside the gene set, but it starts by calculating an expression-level statistic that brings gene expression profiles with different dynamic ranges to a common scale.

test_gsva <- gsva(gsvaParam(X, gene_set), verbose=FALSE)
test_gsva

           s1        s2
gs1 0.9771127 0.9994906
gs2 0.9869514 0.9896900
gs3 0.9716955 0.9815203

zscore (Lee et al. 2008). The z-score method standardizes expression profiles over the samples and then, for each gene set, combines the standardized values as follows. Given a gene set \(\gamma = \{1, \ldots ,k\}\) with standardized values \(\{z_1,\ldots,z_k\}\) for each gene in a specific sample, the combined z-score \(Z_\gamma\) for the gene set \(\gamma\) is defined as:

\[ Z_\gamma = \frac{\sum^k_{i=1} z_i}{\sqrt{k}}.\]

test_zscore <- gsva(zscoreParam(X, gene_set), verbose=FALSE)
test_zscore

      s1   s2
gs1 -2.8  2.8
gs2  0.4 -0.4
gs3 -0.4  0.4

plage (Tomfohr, Lu, and Kepler 2005). Pathway level analysis of gene expression (PLAGE) standardizes expression profiles over the samples and then, for each gene set, it performs a singular value decomposition (SVD) over its genes. The coefficients of the first right-singular vector are returned as the estimates of pathway activity over the samples. Note that, because of how SVD is calculated, the sign of its singular vectors is arbitrary.

test_plage <- gsva(plageParam(X, gene_set), verbose=FALSE)
test_plage

            s1         s2
gs1  0.7071068 -0.7071068
gs2 -0.7071068  0.7071068
gs3  0.7071068 -0.7071068

Enrichment scores on microarray and RNA-seq data

Gene expression data of lymphoblastoid cell lines (LCL) from HapMap individuals that have been profiled using microarray and RNA-seq.

library(Biobase)
library(GSVAdata)
data(c2BroadSets)
data(commonPickrellHuang)

stopifnot(
  identical(
    featureNames(huangArrayRMAnoBatchCommon_eset),
    featureNames(pickrellCountsArgonneCQNcommon_eset)
  )
)

stopifnot(
  identical(
    sampleNames(huangArrayRMAnoBatchCommon_eset),
    sampleNames(pickrellCountsArgonneCQNcommon_eset)
  )
)

pickrellCountsArgonneCQNcommon_eset

ExpressionSet (storageMode: lockedEnvironment)
assayData: 11508 features, 36 samples 
  element names: exprs 
protocolData
  rowNames: NA19099 NA18523 ... NA19171 (36 total)
  varLabels: exprs dates
  varMetadata: labelDescription channel
phenoData
  rowNames: NA19099 NA18523 ... NA19171 (36 total)
  varLabels: CoriellCellLineID Population ... FamilyRelationship (5
    total)
  varMetadata: channel labelDescription
featureData: none
experimentData: use 'experimentData(object)'
Annotation: org.Hs.eg.db 

For the current analysis we use the subset of canonical pathways from the C2 collection of MSigDB Gene Sets. These correspond to the following pathways from KEGG, REACTOME and BIOCARTA.

canonicalC2BroadSets <- c2BroadSets[
  c(
    grep("^KEGG", names(c2BroadSets)),
    grep("^REACTOME", names(c2BroadSets)),
    grep("^BIOCARTA", names(c2BroadSets))
  )
]

canonicalC2BroadSets

GeneSetCollection
  names: KEGG_GLYCOLYSIS_GLUCONEOGENESIS, KEGG_CITRATE_CYCLE_TCA_CYCLE, ..., BIOCARTA_ACTINY_PATHWAY (833 total)
  unique identifiers: 55902, 2645, ..., 8544 (6744 total)
  types in collection:
    geneIdType: EntrezIdentifier (1 total)
    collectionType: BroadCollection (1 total)

We calculate the GSVA enrichment scores for these gene sets using first the normalized microarray data and then the normalized RNA-seq integer count data. Note that the only requirement to do the latter is to set the argument kcdf="Poisson", which is "Gaussian" by default. However, if the RNA-seq normalized expression levels is continuous, such as log-CPMs, log-RPKMs or log-TPMs, use "Gaussian".

Microarray.

huangPar <- gsvaParam(
  exprData = huangArrayRMAnoBatchCommon_eset,
  geneSets = canonicalC2BroadSets,
  minSize=5,
  maxSize=500
)

esmicro <- gsva(huangPar, verbose=FALSE)

Mapping identifiers between gene sets and feature names

exprs(esmicro)[1:6, 1:6]

                                                  NA19099    NA18523
KEGG_GLYCOLYSIS_GLUCONEOGENESIS               -0.14418012 -0.3133817
KEGG_CITRATE_CYCLE_TCA_CYCLE                  -0.20263269  0.2546732
KEGG_PENTOSE_PHOSPHATE_PATHWAY                 0.13384996 -0.3426199
KEGG_PENTOSE_AND_GLUCURONATE_INTERCONVERSIONS -0.04814412  0.2649390
KEGG_FRUCTOSE_AND_MANNOSE_METABOLISM          -0.05277464 -0.2559473
KEGG_GALACTOSE_METABOLISM                     -0.51060398 -0.3263793
                                                  NA19144     NA19137
KEGG_GLYCOLYSIS_GLUCONEOGENESIS               -0.39117167  0.21340339
KEGG_CITRATE_CYCLE_TCA_CYCLE                   0.01268519 -0.23423639
KEGG_PENTOSE_PHOSPHATE_PATHWAY                 0.01105565  0.10473591
KEGG_PENTOSE_AND_GLUCURONATE_INTERCONVERSIONS -0.24778162 -0.57051071
KEGG_FRUCTOSE_AND_MANNOSE_METABOLISM          -0.27260660  0.02654463
KEGG_GALACTOSE_METABOLISM                     -0.33944553  0.18058711
                                                 NA18861     NA19116
KEGG_GLYCOLYSIS_GLUCONEOGENESIS                0.3989804 -0.03179434
KEGG_CITRATE_CYCLE_TCA_CYCLE                   0.1669631 -0.19060735
KEGG_PENTOSE_PHOSPHATE_PATHWAY                 0.5331964  0.08319882
KEGG_PENTOSE_AND_GLUCURONATE_INTERCONVERSIONS -0.1518934 -0.12257602
KEGG_FRUCTOSE_AND_MANNOSE_METABOLISM           0.4662563 -0.07516578
KEGG_GALACTOSE_METABOLISM                      0.5901477 -0.05433206

RNA-seq.

pickrellPar <- gsvaParam(
  exprData = pickrellCountsArgonneCQNcommon_eset,
  geneSets = canonicalC2BroadSets,
  minSize=5,
  maxSize=500,
  kcdf="Poisson"
)

esrnaseq <- gsva(pickrellPar, verbose=FALSE)

Mapping identifiers between gene sets and feature names

exprs(esrnaseq)[1:6, 1:6]

                                                NA19099     NA18523     NA19144
KEGG_GLYCOLYSIS_GLUCONEOGENESIS               0.2292013 -0.26418772 -0.37401687
KEGG_CITRATE_CYCLE_TCA_CYCLE                  0.1953447 -0.20215701 -0.31886736
KEGG_PENTOSE_PHOSPHATE_PATHWAY                0.3957182 -0.35222123 -0.14016244
KEGG_PENTOSE_AND_GLUCURONATE_INTERCONVERSIONS 0.3043138 -0.23429588 -0.27059673
KEGG_FRUCTOSE_AND_MANNOSE_METABOLISM          0.1123176 -0.06274804 -0.04494400
KEGG_GALACTOSE_METABOLISM                     0.0606202 -0.42485552 -0.03930301
                                                 NA19137     NA18861    NA19116
KEGG_GLYCOLYSIS_GLUCONEOGENESIS                0.2913508  0.17081880 -0.4570259
KEGG_CITRATE_CYCLE_TCA_CYCLE                   0.2573530  0.09452472 -0.1433765
KEGG_PENTOSE_PHOSPHATE_PATHWAY                 0.3585130  0.16414025 -0.2658944
KEGG_PENTOSE_AND_GLUCURONATE_INTERCONVERSIONS -0.2453460 -0.06027442  0.0470686
KEGG_FRUCTOSE_AND_MANNOSE_METABOLISM           0.4431209 -0.43879510 -0.2629824
KEGG_GALACTOSE_METABOLISM                      0.3496528 -0.12188569 -0.4629607

Correlation of enrichment scores between the two technologies.

library(corrplot)

corrplot 0.92 loaded

corrplot(cor(exprs(esrnaseq), exprs(esmicro)), type="lower")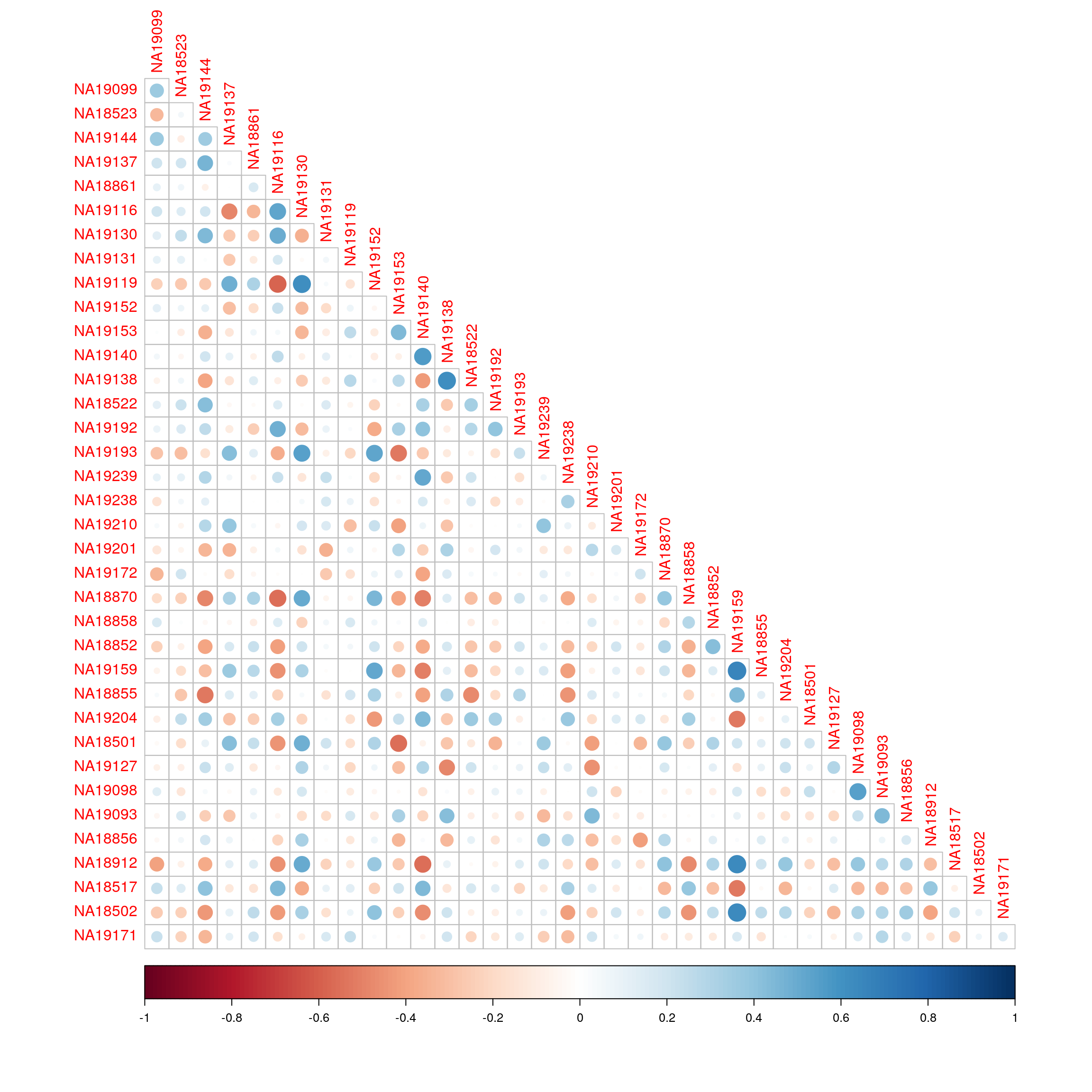

Past versions of correlation_enrichment_scores-1.png

Version	Author	Date
834452d	Dave Tang	2023-11-08

Correlation of enrichment scores between just the RNA-seq samples ordered using hierarchical clustering.

corrplot(cor(exprs(esrnaseq), exprs(esrnaseq)), type="lower", diag = FALSE, order = "hclust")

Past versions of correlation_enrichment_scores_rnaseq-1.png

Version	Author	Date
834452d	Dave Tang	2023-11-08

Molecular signature identification

Verhaak et al. 2010 identified four subtypes of glioblastoma multiforme (GBM) using gene expression patterns:

1. Proneural
2. Classical
3. Neural
4. Mesenchymal

Here we will try to replicate the study using four gene set signatures specific to brain cell types that were derived using mouse models by Cahoy et al. 2008:

1. Astrocytes
2. Oligodendrocytes
3. Neurons
4. Cultured astroglial cells

data(gbm_VerhaakEtAl)
gbm_eset

ExpressionSet (storageMode: lockedEnvironment)
assayData: 11861 features, 173 samples 
  element names: exprs 
protocolData: none
phenoData
  rowNames: TCGA.02.0003.01A.01 TCGA.02.0010.01A.01 ...
    TCGA.12.0620.01A.01 (173 total)
  varLabels: subtype
  varMetadata: labelDescription channel
featureData: none
experimentData: use 'experimentData(object)'
Annotation:  

Feature names are gene symbols.

head(featureNames(gbm_eset))

[1] "AACS"    "FSTL1"   "ELMO2"   "CREB3L1" "RPS11"   "PNMA1"  

Subtypes.

table(gbm_eset$subtype)

  Classical Mesenchymal      Neural   Proneural 
         38          56          26          53 

Length of the signatures.

data(brainTxDbSets)
lengths(brainTxDbSets)

      astrocytic_up        astroglia_up         neuronal_up oligodendrocytic_up 
                 85                  88                  98                  70 

Check out the signatures.

lapply(brainTxDbSets, head)

$astrocytic_up
[1] "GRHL1"   "GPAM"    "PAPSS2"  "MERTK"   "BTG1"    "SLC46A1"

$astroglia_up
[1] "BST2"     "SERPING1" "ACTA2"    "C9orf167" "C1orf31"  "ANXA4"   

$neuronal_up
[1] "STXBP1"  "JPH4"    "CACNG3"  "BRUNOL6" "CLSTN2"  "FAM123C"

$oligodendrocytic_up
[1] "DCT"    "ZNF536" "GNG8"   "ELOVL6" "NR2C1"  "RCBTB1"

GSVA enrichment scores are calculated using the gene sets contained in brainTxDbSets; maxDiff is set to FALSE. Here’s a reminder of what this parameter does:

max.diff: The last step of the GSVA algorithm calculates the gene set enrichment score from two Kolmogorov-Smirnov random walk statistics. This parameter is a logical flag that allows the user to specify two possible ways to do such calculation:

1. TRUE, the default value, where the enrichment score is calculated as the magnitude difference between the largest positive and negative random walk deviations;
2. FALSE, where the enrichment score is calculated as the maximum distance of the random walk from zero.

gbmPar <- gsvaParam(gbm_eset, brainTxDbSets, maxDiff=FALSE)
gbm_es <- gsva(gbmPar, verbose=FALSE)

Prepare data frame for plotting.

my_df <- data.frame(
  sample = colnames(gbm_eset),
  subtype = gbm_eset$subtype
)

t(exprs(gbm_es)) |>
  as.data.frame() |>
  tibble::rownames_to_column('sample') |>
  dplyr::inner_join(my_df, by = "sample") |>
  dplyr::mutate(sample = factor(sample, levels = sample)) |>
  tidyr::pivot_longer(cols = c(-sample, -subtype), names_to = "signature", values_to = "enrichment") -> my_df

head(my_df)

# A tibble: 6 × 4
  sample              subtype   signature           enrichment
  <fct>               <fct>     <chr>                    <dbl>
1 TCGA.02.0003.01A.01 Proneural astrocytic_up           -0.305
2 TCGA.02.0003.01A.01 Proneural astroglia_up            -0.515
3 TCGA.02.0003.01A.01 Proneural neuronal_up              0.554
4 TCGA.02.0003.01A.01 Proneural oligodendrocytic_up      0.332
5 TCGA.02.0010.01A.01 Proneural astrocytic_up           -0.295
6 TCGA.02.0010.01A.01 Proneural astroglia_up            -0.541

Plot.

library(ggplot2)
ggplot(my_df, aes(sample, signature, fill = enrichment)) +
  geom_tile() +
  facet_grid(~subtype, scales = "free") +
  theme(
    axis.text.x = element_blank(), axis.ticks.x = element_blank()
  ) +
  scale_fill_gradient(low = "skyblue", high = "red")

Past versions of plot_gbm-1.png

Version	Author	Date
38ae3bc	Dave Tang	2023-11-08

Results using maxDiff=TRUE.

gbmPar <- gsvaParam(gbm_eset, brainTxDbSets, maxDiff=TRUE)
gbm_es_max <- gsva(gbmPar, verbose=FALSE)

my_df <- data.frame(
  sample = colnames(gbm_eset),
  subtype = gbm_eset$subtype
)

t(exprs(gbm_es_max)) |>
  as.data.frame() |>
  tibble::rownames_to_column('sample') |>
  dplyr::inner_join(my_df, by = "sample") |>
  dplyr::mutate(sample = factor(sample, levels = sample)) |>
  tidyr::pivot_longer(cols = c(-sample, -subtype), names_to = "signature", values_to = "enrichment") -> my_df2

ggplot(my_df2, aes(sample, signature, fill = enrichment)) +
  geom_tile() +
  facet_grid(~subtype, scales = "free") +
  theme(
    axis.text.x = element_blank(), axis.ticks.x = element_blank()
  ) +
  scale_fill_gradient(low = "skyblue", high = "red")

Past versions of gbm_es_max_diff_true-1.png

Version	Author	Date
38ae3bc	Dave Tang	2023-11-08

Results using ssgsea.

gbm_ssgsea <- gsva(ssgseaParam(gbm_eset, brainTxDbSets), verbose=FALSE)

[1] "Calculating ranks..."
[1] "Calculating absolute values from ranks..."
[1] "Normalizing..."

my_df <- data.frame(
  sample = colnames(gbm_eset),
  subtype = gbm_eset$subtype
)

t(exprs(gbm_ssgsea)) |>
  as.data.frame() |>
  tibble::rownames_to_column('sample') |>
  dplyr::inner_join(my_df, by = "sample") |>
  dplyr::mutate(sample = factor(sample, levels = sample)) |>
  tidyr::pivot_longer(cols = c(-sample, -subtype), names_to = "signature", values_to = "enrichment") -> my_df3

ggplot(my_df3, aes(sample, signature, fill = enrichment)) +
  geom_tile() +
  facet_grid(~subtype, scales = "free") +
  theme(
    axis.text.x = element_blank(), axis.ticks.x = element_blank()
  ) +
  scale_fill_gradient(low = "skyblue", high = "red")

Past versions of gbm_es_ssgsea-1.png

Version	Author	Date
39a8474	Dave Tang	2023-11-08

Session information

sessionInfo()

R version 4.3.2 (2023-10-31)
Platform: x86_64-pc-linux-gnu (64-bit)
Running under: Ubuntu 22.04.3 LTS

Matrix products: default
BLAS:   /usr/lib/x86_64-linux-gnu/openblas-pthread/libblas.so.3 
LAPACK: /usr/lib/x86_64-linux-gnu/openblas-pthread/libopenblasp-r0.3.20.so;  LAPACK version 3.10.0

locale:
 [1] LC_CTYPE=en_US.UTF-8       LC_NUMERIC=C              
 [3] LC_TIME=en_US.UTF-8        LC_COLLATE=en_US.UTF-8    
 [5] LC_MONETARY=en_US.UTF-8    LC_MESSAGES=en_US.UTF-8   
 [7] LC_PAPER=en_US.UTF-8       LC_NAME=C                 
 [9] LC_ADDRESS=C               LC_TELEPHONE=C            
[11] LC_MEASUREMENT=en_US.UTF-8 LC_IDENTIFICATION=C       

time zone: Etc/UTC
tzcode source: system (glibc)

attached base packages:
[1] stats4    stats     graphics  grDevices utils     datasets  methods  
[8] base     

other attached packages:
 [1] ggplot2_3.4.4        corrplot_0.92        GSVAdata_1.38.0     
 [4] hgu95a.db_3.13.0     org.Hs.eg.db_3.18.0  GSEABase_1.64.0     
 [7] graph_1.80.0         annotate_1.80.0      XML_3.99-0.16       
[10] AnnotationDbi_1.64.1 IRanges_2.36.0       S4Vectors_0.40.2    
[13] Biobase_2.62.0       BiocGenerics_0.48.1  GSVA_1.50.0         
[16] BiocManager_1.30.22  workflowr_1.7.1     

loaded via a namespace (and not attached):
 [1] DBI_1.1.3                   bitops_1.0-7               
 [3] rlang_1.1.2                 magrittr_2.0.3             
 [5] git2r_0.33.0                matrixStats_1.2.0          
 [7] compiler_4.3.2              RSQLite_2.3.4              
 [9] getPass_0.2-4               DelayedMatrixStats_1.24.0  
[11] png_0.1-8                   callr_3.7.3                
[13] vctrs_0.6.5                 stringr_1.5.1              
[15] pkgconfig_2.0.3             crayon_1.5.2               
[17] fastmap_1.1.1               XVector_0.42.0             
[19] labeling_0.4.3              utf8_1.2.4                 
[21] promises_1.2.1              rmarkdown_2.25             
[23] ps_1.7.5                    purrr_1.0.2                
[25] bit_4.0.5                   xfun_0.41                  
[27] zlibbioc_1.48.0             cachem_1.0.8               
[29] beachmat_2.18.0             GenomeInfoDb_1.38.2        
[31] jsonlite_1.8.8              blob_1.2.4                 
[33] highr_0.10                  later_1.3.2                
[35] rhdf5filters_1.14.1         DelayedArray_0.28.0        
[37] Rhdf5lib_1.24.1             BiocParallel_1.36.0        
[39] irlba_2.3.5.1               parallel_4.3.2             
[41] R6_2.5.1                    bslib_0.6.1                
[43] stringi_1.8.3               GenomicRanges_1.54.1       
[45] jquerylib_0.1.4             Rcpp_1.0.11                
[47] SummarizedExperiment_1.32.0 knitr_1.45                 
[49] tidyselect_1.2.0            httpuv_1.6.13              
[51] Matrix_1.6-1.1              rstudioapi_0.15.0          
[53] abind_1.4-5                 yaml_2.3.8                 
[55] codetools_0.2-19            processx_3.8.3             
[57] lattice_0.21-9              tibble_3.2.1               
[59] withr_2.5.2                 KEGGREST_1.42.0            
[61] evaluate_0.23               Biostrings_2.70.1          
[63] pillar_1.9.0                MatrixGenerics_1.14.0      
[65] whisker_0.4.1               generics_0.1.3             
[67] rprojroot_2.0.4             RCurl_1.98-1.13            
[69] munsell_0.5.0               scales_1.3.0               
[71] sparseMatrixStats_1.14.0    xtable_1.8-4               
[73] glue_1.6.2                  tools_4.3.2                
[75] ScaledMatrix_1.10.0         fs_1.6.3                   
[77] rhdf5_2.46.1                grid_4.3.2                 
[79] tidyr_1.3.0                 colorspace_2.1-0           
[81] SingleCellExperiment_1.24.0 GenomeInfoDbData_1.2.11    
[83] BiocSingular_1.18.0         HDF5Array_1.30.0           
[85] cli_3.6.2                   rsvd_1.0.5                 
[87] fansi_1.0.6                 S4Arrays_1.2.0             
[89] dplyr_1.1.4                 gtable_0.3.4               
[91] sass_0.4.8                  digest_0.6.33              
[93] SparseArray_1.2.2           farver_2.1.1               
[95] memoise_2.0.1               htmltools_0.5.7            
[97] lifecycle_1.0.4             httr_1.4.7                 
[99] bit64_4.0.5