In [3]:
from IPython.display import Image, display, HTML
css_link_fontawesome = '<link rel="stylesheet" href="https://cdnjs.cloudflare.com/ajax/libs/font-awesome/6.2.0/css/all.min.css">'
css_rise = '<link rel="stylesheet" href="rise.css">'
display(HTML(css_link_fontawesome))
display(HTML(css_rise))

Leveraging Python for Spatial Data Science

Spatial Data Science Bootcamp Paris October 26th, 2023¶

Florian Bayer, PhD in Public Health, MSc in Geography

Health geographer at Agence de la biomédecine, University lecturer at Paris Panthéon Sorbonne and ENSG

Objectives

The aim of this workshop is to deliver an overview of spatial analysis tools that enable leveraging spatial dimension in your analyses.

Our primary focus will revolve around examining the spatial distribution of self-employed general practitioners (GPs), distinct from those employed by healthcare institutions, within the Paris metropolitan area and its surrounding regions.

The primary objective is to ascertain the presence of spatial disparities in the distribution of general practitioners throughout the Parisian region.

The data comes from the french health ministry.

Workshop Outline

  • Spatial data management and geocoding
  • Introduction to the Modifiable Areal Unit Problem (MAUP)
  • Spatial autocorrelation and Hot Spot Detection
  • Appendix : travel time computing
In [4]:
import pandas as pd
import matplotlib.pyplot as plt

import os
import warnings
warnings.filterwarnings("ignore", category=UserWarning)

class Colors:
    white = '#eee8d5'
    red = '#e63946'
    blue = '#152744'
    gray = "#777777"
    lightgray="#F4F4F4"
    darkgray="#4d4d4d"
    legend_text = '#002b36'

Requirements

This workshop requires Python 3.x (specifically tested with version 3.9). The primary packages utilized in this workshop include:

  • geopandas for efficient geographic data handling
  • h3pandas for spatial aggregation
  • matplotlib for creating maps and visualizations
  • scipy and splot and esda for performing statistical calculations
  • libpysal for constructing spatial weight matrices
  • geopy for distance calculations based on geographic coordinates
  • Additionally, Jupyter lab is recommended for an interactive environment

Feel free to clone the repository : https://github.com/fbxyz/SDS_Bootcamp

Data Management

Data have been preprocessed, see BC_0_data_processing.ipynb for more details

In [5]:
data_dir = "data"
file="data_bootcamp.pckl"
pckl_path = os.path.join(data_dir, file)

gp_data = pd.read_pickle(pckl_path) 
gp_data.head()
Out[5]:
GPid lastname firstname name citycode state q
0 810000231778 SENBEL CLAUDE CDS MEDIKSANTE 75117 75 206 Boulevard PEREIRE 75017 PARIS Paris
1 810000459833 DAVEAU PASCALE CABINET DU DR PASCALE DAVEAU 75056 75 11 RUE DE REIMS 75013 PARIS Paris
2 810000556125 PENDOLA-LUCHEL ISABELLE CABINET DU DR ISABELLE PENDOLA-LUCHEL 75056 75 37 RUE CHARCOT 75013 PARIS Paris
3 810000571660 CHIAVERINI PHILIPPE CABINET DU DR PHILIPPE CHIAVERINI 75056 75 52 RUE MADEMOISELLE 75015 PARIS Paris
4 810000582683 GUEDJ CHANTAL CABINET DU DR CHANTAL GUEDJ 92051 92 113 AVENUE CHARLES DE GAULLE 92200 NEUILLY SUR...

Geocoding GPs

For geocoding, we employ the free addok service, which is particularly optimized for French adresses. It is also possible to use OSM's Nominatim.

To speed up geocoding, we use the CSV plugin of addok. An intermediate CSV file is required. However, it is also possible to use the /search/ endpoint for more options (result types, filters, etc.).

CSV overview

Only the 'q' column is utilized for geocoding.

This consists of a combination of the building number, street name, postal code, city, and department. Additional addressing elements can be incorporated for enhanced functionality.

In [6]:
source_path = os.path.join(data_dir, 'GP_adress.csv')
gp_data.q.to_csv(source_path, index=False)
gp_data.head()
Out[6]:
GPid lastname firstname name citycode state q
0 810000231778 SENBEL CLAUDE CDS MEDIKSANTE 75117 75 206 Boulevard PEREIRE 75017 PARIS Paris
1 810000459833 DAVEAU PASCALE CABINET DU DR PASCALE DAVEAU 75056 75 11 RUE DE REIMS 75013 PARIS Paris
2 810000556125 PENDOLA-LUCHEL ISABELLE CABINET DU DR ISABELLE PENDOLA-LUCHEL 75056 75 37 RUE CHARCOT 75013 PARIS Paris
3 810000571660 CHIAVERINI PHILIPPE CABINET DU DR PHILIPPE CHIAVERINI 75056 75 52 RUE MADEMOISELLE 75015 PARIS Paris
4 810000582683 GUEDJ CHANTAL CABINET DU DR CHANTAL GUEDJ 92051 92 113 AVENUE CHARLES DE GAULLE 92200 NEUILLY SUR...

Geocoding with ADDOK

We use the example from addok doc to geocode 'GP_adress.csv'.

Note: on 24/10/2023, the http://api-adresse.data.gouv.fr/search/csv/ API appears to be broken.

You can easily deploy ADDOK with Docker https://github.com/BaseAdresseNationale/addok-docker

In [7]:
import requests

addok_url = 'http://api-adresse.data.gouv.fr/search/csv/'

def geocode(filepath_in):
    output_dir = os.path.dirname(filepath_in)  
    with open(filepath_in, 'rb') as f:
        filename, response = post_to_addok(filepath_in, f.read())
        output_path = os.path.join(output_dir, filename)  
        write_response_to_disk(output_path, response)

def write_response_to_disk(filename, response, chunk_size=1024):
    with open(filename, 'wb') as fd:
        for chunk in response.iter_content(chunk_size=chunk_size):
            fd.write(chunk)

def post_to_addok(filename, filelike_object):
    files = {'data': (filename, filelike_object)}
    response = requests.post(addok_url, files=files)
    content_disposition = response.headers['content-disposition']
    filename = content_disposition[len('attachment; filename="'):-len('"')]
    return filename, response

geocode_path = os.path.join(data_dir, 'geocoded.csv')

if not os.path.exists(geocode_path) : 
    geocode(source_path)

Checking the results (1)

A significant number of users tend to neglect the post-processing of geocoding results. It is imperative to assess the quality of geocoding

ADDOK offers several tools for this purpose, with result_score being one of them.

This score ranges from 0 to 1, where a score of 1 indicates a perfect match between the input string and the one stored in the database.

In [8]:
geocoded = pd.read_csv(geocode_path,dtype={"result_citycode":object, 'result_oldcitycode':object})
geocoded["result_score"] = round(geocoded["result_score"],2)
geocoded.head()
Out[8]:
q latitude longitude result_label result_score result_score_next result_type result_id result_housenumber result_name result_street result_postcode result_city result_context result_citycode result_oldcitycode result_oldcity result_district result_status
0 206 Boulevard PEREIRE 75017 PARIS Paris 48.880461 2.288405 206 Boulevard Pereire 75017 Paris 0.84 NaN housenumber 75117_7258_00206 206 206 Boulevard Pereire Boulevard Pereire 75017 Paris 75, Paris, Île-de-France 75117 NaN NaN Paris 17e Arrondissement ok
1 11 RUE DE REIMS 75013 PARIS Paris 48.828374 2.371458 11 Rue de Reims 75013 Paris 0.80 NaN housenumber 75113_8109_00011 11 11 Rue de Reims Rue de Reims 75013 Paris 75, Paris, Île-de-France 75113 NaN NaN Paris 13e Arrondissement ok
2 37 RUE CHARCOT 75013 PARIS Paris 48.829844 2.369682 37 Rue Charcot 75013 Paris 0.80 NaN housenumber 75113_1786_00037 37 37 Rue Charcot Rue Charcot 75013 Paris 75, Paris, Île-de-France 75113 NaN NaN Paris 13e Arrondissement ok
3 52 RUE MADEMOISELLE 75015 PARIS Paris 48.843300 2.299716 52 Rue Mademoiselle 75015 Paris 0.83 NaN housenumber 75115_5893_00052 52 52 Rue Mademoiselle Rue Mademoiselle 75015 Paris 75, Paris, Île-de-France 75115 NaN NaN Paris 15e Arrondissement ok
4 113 AVENUE CHARLES DE GAULLE 92200 NEUILLY SUR... 48.881485 2.269683 113 Avenue Charles de Gaulle 92200 Neuilly-sur... 0.77 NaN housenumber 92051_1436_00113 113 113 Avenue Charles de Gaulle Avenue Charles de Gaulle 92200 Neuilly-sur-Seine 92, Hauts-de-Seine, Île-de-France 92051 NaN NaN NaN ok

Checking the results (2)

We can represent the results using a box plot. Some of the matches have scores that fall below 0.5. Let's search deeper into this.

In [9]:
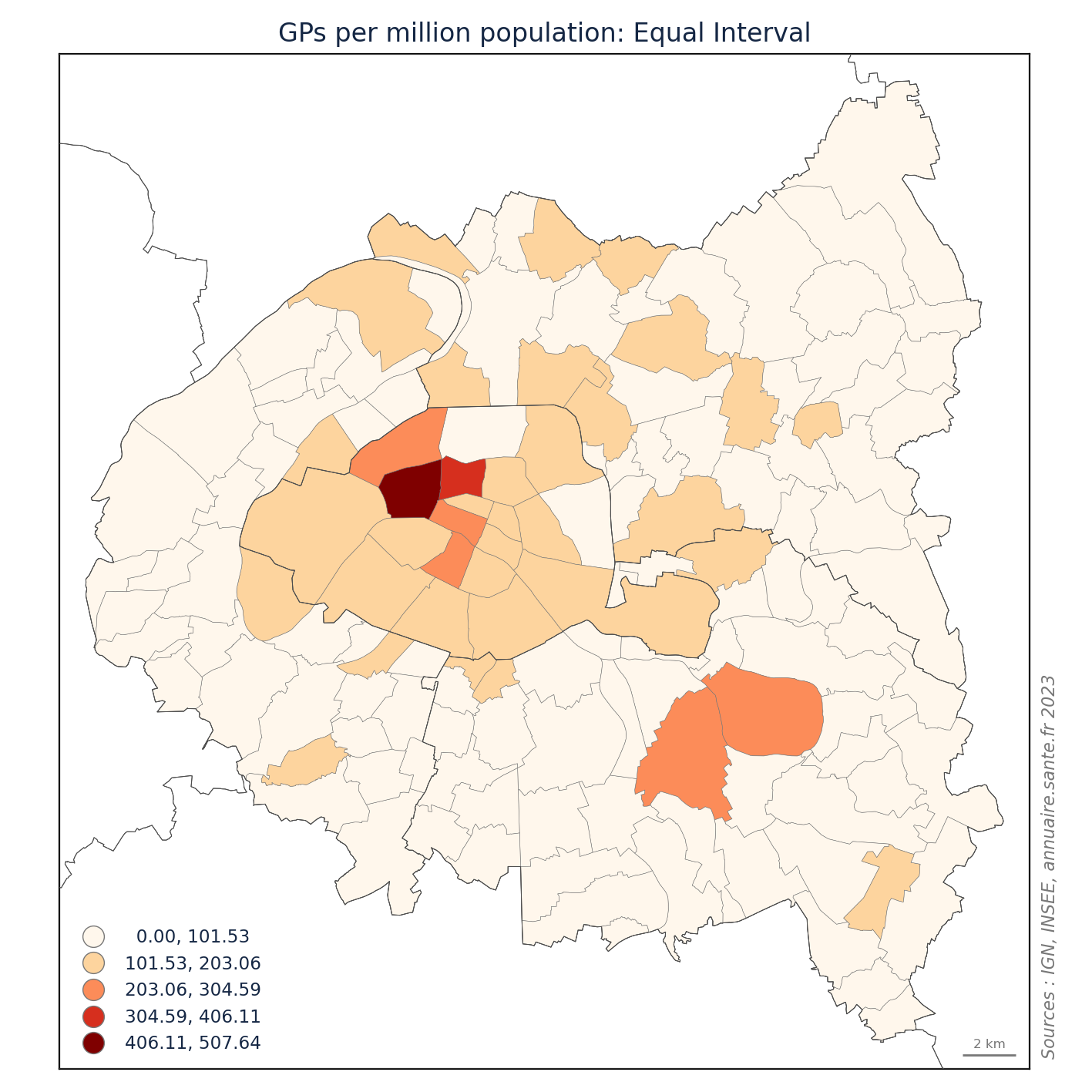
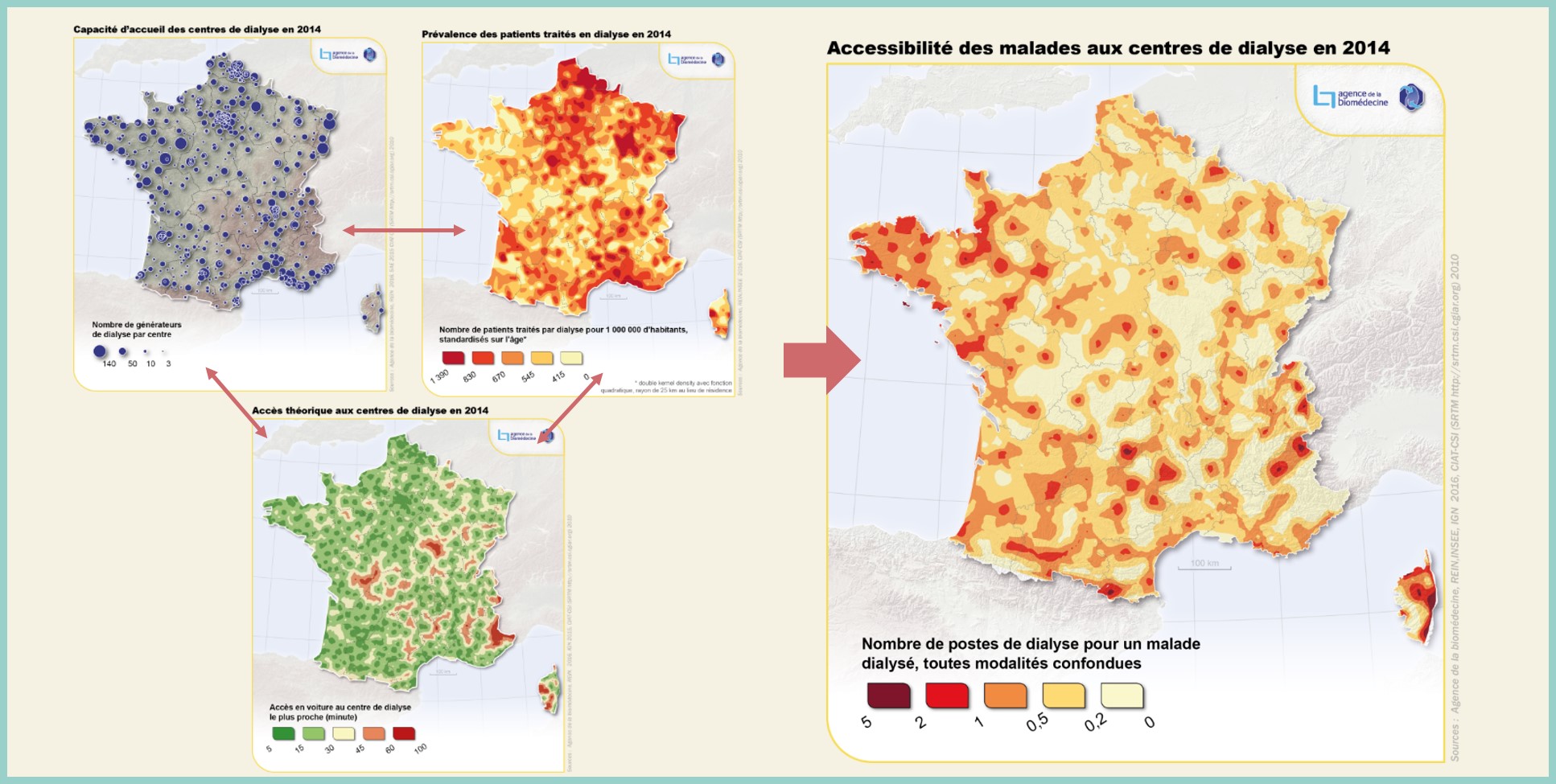
import matplotlib.pyplot as plt

def customize_axes(_ax, _fig):
    for spine in ['top', 'right']:
        _ax.spines[spine].set_visible(False)

    for spine in _ax.spines.values():
        spine.set_edgecolor(Colors.white)

    _ax.tick_params(axis='x', colors=Colors.white, rotation=45) 
    _ax.tick_params(axis='y', colors=Colors.white)
    _ax.set_facecolor('none')
    _fig.patch.set_facecolor('none')

fig_box, ax_box = plt.subplots()
boxplot = geocoded.boxplot(column=['result_score'], vert=False, grid=False, ax=ax_box,
                          flierprops={'marker': 'o', 'markersize': 5, 'markerfacecolor': Colors.red, 'markeredgecolor': 'none'},
                          boxprops={'color': Colors.white}, medianprops={'color': Colors.red}, whiskerprops={'color':  Colors.white})

ax_box.set_xlabel('')
ax_box.set_yticklabels([])
ax_box.set_xlim(0, 1)

ax_box.set_title('Geocoding results scores', color=Colors.white)

customize_axes(ax_box,fig_box)
fig_box.set_size_inches(fig_box.get_size_inches()[0]*1.5, fig_box.get_size_inches()[1] / 3)
plt.show()

Checking the results (3)

These are false negatives. Noise in the character strings (e.g., CEDEX) is causing the matching to decrease.

In [10]:
geocoded[['q','result_label','result_score']].sort_values("result_score", ascending=True).query("result_score<0.5")
Out[10]:
q result_label result_score
1242 48 Avenue DU PRESIDENT ROOSEVELT 94320 THIAIS ... 48 Av du Pdt Franklin Roosevelt 94320 Thiais 0.47
4890 48 Avenue DU PRESIDENT ROOSEVELT 94320 THIAIS ... 48 Av du Pdt Franklin Roosevelt 94320 Thiais 0.47
603 2 Boulevard DE L'EUROPE 91022 EVRY CEDEX Essonne 2 Boulevard de l'Europe - Valéry Giscard d'Est... 0.47
9806 2 Boulevard DE L'EUROPE 91022 EVRY CEDEX Essonne 2 Boulevard de l'Europe - Valéry Giscard d'Est... 0.47
2722 2 Boulevard DE L'EUROPE 91022 EVRY CEDEX Essonne 2 Boulevard de l'Europe - Valéry Giscard d'Est... 0.47
7092 2 Boulevard DE L'EUROPE 91022 EVRY CEDEX Essonne 2 Boulevard de l'Europe - Valéry Giscard d'Est... 0.47
2224 2 Boulevard DE L'EUROPE 91022 EVRY CEDEX Essonne 2 Boulevard de l'Europe - Valéry Giscard d'Est... 0.47
212 Allee D'ESTIENNE D ORVES 93701 DRANCY CEDEX Se... Rue d’Estienne d’Orves 93700 Drancy 0.48
330 Allee D'ESTIENNE D ORVES 93701 DRANCY CEDEX Se... Rue d’Estienne d’Orves 93700 Drancy 0.48
5255 Allee D'ESTIENNE D ORVES 93701 DRANCY CEDEX Se... Rue d’Estienne d’Orves 93700 Drancy 0.48
6963 Allee D'ESTIENNE D ORVES 93701 DRANCY CEDEX Se... Rue d’Estienne d’Orves 93700 Drancy 0.48
5377 Allee D'ESTIENNE D ORVES 93701 DRANCY CEDEX Se... Rue d’Estienne d’Orves 93700 Drancy 0.48
554 Allee D'ESTIENNE D ORVES 93701 DRANCY CEDEX Se... Rue d’Estienne d’Orves 93700 Drancy 0.48
5003 Allee D'ESTIENNE D ORVES 93701 DRANCY CEDEX Se... Rue d’Estienne d’Orves 93700 Drancy 0.48
7399 LIEU DIT FORCILLES 77150 FEROLLES ATTILLY Sein... Chemin de Forcil 77150 Férolles-Attilly 0.49
9977 8 PLACE DES TOULEUSES 95011 CERGY PONTOISE CED... 8 Place des Touleuses 95000 Cergy 0.49
4178 20 R H BENEDICT DE SAUSSURE 94000 CRETEIL Val-... 20 Rue Saussure 94000 Créteil 0.49
10442 LIEU DIT FORCILLES 77150 FEROLLES ATTILLY Sein... Chemin de Forcil 77150 Férolles-Attilly 0.49

Checking the geocoding accuracy (1)

Geocoding accuracy is often crucial regardless of the purpose of your project.

For our GPs, the vast majority of the results are localized at the house number :

In [11]:
result_counts = geocoded['result_type'].value_counts()

fig_bar, ax_bar = plt.subplots()

bars = result_counts.plot(kind='bar', color=Colors.red, edgecolor=Colors.white, ax=ax_bar)  
customize_axes(ax_bar,fig_bar)
ax_bar.set_title('Geocoding accuracy (n)', color=Colors.white)
fig_bar;

Checking the geocoding accuracy (2)

Relying solely on the result score may not be adequate. There are instances where the scores seem acceptable, but the point is geocoded in the wrong city, especially in cases involving streets with identical names.

Hence, it's important to verify whether the points are correctly located within the municipalities. To accomplish this, we compare the citycodes from the input source with the geocoded citycodes.

In [12]:
gp_data_xy = pd.concat([gp_data,geocoded[['latitude','longitude','result_label','result_score','result_type', 'result_citycode','result_oldcitycode']]], axis = 1)
gp_data_xy.query("citycode!=result_citycode")
Out[12]:
GPid lastname firstname name citycode state q latitude longitude result_label result_score result_type result_citycode result_oldcitycode
1 810000459833 DAVEAU PASCALE CABINET DU DR PASCALE DAVEAU 75056 75 11 RUE DE REIMS 75013 PARIS Paris 48.828374 2.371458 11 Rue de Reims 75013 Paris 0.80 housenumber 75113 NaN
2 810000556125 PENDOLA-LUCHEL ISABELLE CABINET DU DR ISABELLE PENDOLA-LUCHEL 75056 75 37 RUE CHARCOT 75013 PARIS Paris 48.829844 2.369682 37 Rue Charcot 75013 Paris 0.80 housenumber 75113 NaN
3 810000571660 CHIAVERINI PHILIPPE CABINET DU DR PHILIPPE CHIAVERINI 75056 75 52 RUE MADEMOISELLE 75015 PARIS Paris 48.843300 2.299716 52 Rue Mademoiselle 75015 Paris 0.83 housenumber 75115 NaN
20 810100025484 YOKA HUGUETTE CABINET DU DR HUGUETTE YOKA 75056 75 36 AVENUE NIEL 75017 PARIS Paris 48.881717 2.296001 36 Avenue Niel 75017 Paris 0.80 housenumber 75117 NaN
26 810101079472 SOOBRON Sarvesh CABINET DU DR SARVESH SOOBRON 75056 75 42 RUE CURIAL 75019 PARIS Paris 48.892155 2.372772 42 Rue Curial 75019 Paris 0.80 housenumber 75119 NaN
... ... ... ... ... ... ... ... ... ... ... ... ... ... ...
10860 810100216117 SAUVAGE-RIGAL SOPHIE CABINET DU DR SOPHIE SAUVAGE-RIGAL 75056 75 1 RUE OLIVIER DE SERRES 75015 PARIS Paris 48.837089 2.298739 1 Rue Olivier de Serres 75015 Paris 0.85 housenumber 75115 NaN
10861 810100373447 FIORINA EMILY CABINET DU DR EMILY FIORINA 75056 75 47 RUE FESSART 75019 PARIS Paris 48.876723 2.383698 47 Rue Fessart 75019 Paris 0.80 housenumber 75119 NaN
10862 810100387579 DUPUI Julien CABINET DU DR Julien DUPUI 75056 75 38 BOULEVARD SAINT MARCEL 75005 PARIS Paris 48.838847 2.357659 38 Boulevard Saint-Marcel 75005 Paris 0.84 housenumber 75105 NaN
10863 810100413664 DODILLE LAURENCE CABINET DU DR ALAIN AMSLEM 75056 75 94 RUE BRILLAT SAVARIN 75013 PARIS Paris 48.824532 2.343058 94 Rue Brillat-Savarin 75013 Paris 0.84 housenumber 75113 NaN
10872 810101116308 VERCOUSTRE BEATRICE CABINET DU DR BEATRICE VERCOUSTRE 75056 75 105 RUE DE MAUBEUGE 75010 PARIS Paris 48.881986 2.354295 105 Rue de Maubeuge 75010 Paris 0.82 housenumber 75110 NaN

2286 rows × 14 columns

Checking the geocoding accuracy (3)

There seems to be a concern regarding the department of Paris. Specifically with the city code of Paris (75056) in comparison to the codes of the 20 districts (arrondissements) of Paris (751xx).

As a preliminary measure, we can manually inspect the results with the lowest scores to ascertain their accuracy in geocoding.

In [13]:
gp_data_xy[['q','result_label','result_score','state']].query("state=='75' and result_score<0.65").drop_duplicates()
Out[13]:
q result_label result_score state
54 178 Rue DE VAUGIRARD 75738 PARIS CEDEX 15 Paris 178 Rue de Vaugirard 75015 Paris 0.63 75
321 12 Rue ARMAND MOISANT 75731 PARIS CEDEX 15 Paris 12 Rue Armand Moisant 75015 Paris 0.62 75
410 37 Rue DES VOLONTAIRES 75730 PARIS CEDEX 15 Paris 37 Rue des Volontaires 75015 Paris 0.63 75
525 18 Place LACHAMBEAUDIE 75570 PARIS CEDEX 12 Paris 18 Place Lachambeaudie 75012 Paris 0.63 75
542 44 Rue D AMSTERDAM 75311 PARIS CEDEX 09 Paris 44 Rue d'Amsterdam 75009 Paris 0.60 75
796 3 Rue DU MAROC 75954 PARIS CEDEX 19 Paris 3 Rue du Maroc 75019 Paris 0.56 75
997 2 Rue AMBROISE PARE 75462 PARIS CEDEX 10 Paris 2 Rue Ambroise Paré 75010 Paris 0.60 75
1166 20 BIS RUE DARU 75008 PARIS Paris 20b Rue Daru 75008 Paris 0.62 75
2729 29 BIS RUE MONGE 75005 PARIS Paris 29b Rue Monge 75005 Paris 0.64 75
3878 34 BIS RUE VIGNON 75009 PARIS Paris 34b Rue Vignon 75009 Paris 0.64 75
5007 211 Rue DE VAUGIRARD 75724 PARIS CEDEX 15 Paris 211 Rue de Vaugirard 75015 Paris 0.63 75
5374 26 RUE ARNOLD NETTER 75012 PARIS Paris 26 Avenue du Docteur Arnold Netter 75012 Paris 0.57 75
10450 71 BIS RUE PETIT 75019 PARIS Paris 71b Rue Petit 75019 Paris 0.64 75

Checking the geocoding accuracy (4)

Now let's check that the GPs coordinates outside of Paris are correctly assigned to the respective municipalities.

In [14]:
gp_data_xy[~((gp_data_xy['citycode'] == gp_data_xy['result_citycode']) | (gp_data_xy['citycode'] == gp_data_xy['result_oldcitycode'])) & (gp_data_xy['state'] != '75')]
Out[14]:
GPid lastname firstname name citycode state q latitude longitude result_label result_score result_type result_citycode result_oldcitycode

The geocoding appears to be exceptionally accurate, which is a rare occurrence.

It is highly likely that the source file has undergone a data management process, and the reference data for the source and ADDOK addresses are closely aligned

Dataframe to Geodataframe

With the geocoding now validated, we can proceed to create geodataframes using GeoPandas.

These geodataframes are essentially Pandas dataframes with a 'geometry' column and a defined projection system.

They provide the capability to perform common GIS operations, including spatial joins, spatial clipping, entity merging, reprojections, and various other spatial analyses.

In [15]:
import geopandas as gpd 

geo_gp = gpd.GeoDataFrame(
    gp_data_xy[['GPid','lastname','firstname','name','result_label','result_citycode','state','latitude','longitude']],
    geometry=gpd.points_from_xy(gp_data_xy.longitude, gp_data_xy.latitude),
    crs="EPSG:4326" # ADDOK returns the results in the World Geodetic System 1984 coordinate system
)

geo_gp = geo_gp.to_crs(2154) # But we are reprojecting the geodataframe into the French Metropole coordinate system.

geo_gp['latitude'] = geo_gp.geometry.centroid.y
geo_gp['longitude'] = geo_gp.geometry.centroid.x

#To avoid any unpleasant surprises during the workshop, let's export the geocoded data...
source_path = os.path.join(data_dir, 'geocoded.geojson')
geo_gp.to_file(source_path)

geo_gp.head()
Out[15]:
GPid lastname firstname name result_label result_citycode state latitude longitude geometry
0 810000231778 SENBEL CLAUDE CDS MEDIKSANTE 206 Boulevard Pereire 75017 Paris 75117 75 6.864729e+06 647812.228635 POINT (647812.229 6864728.696)
1 810000459833 DAVEAU PASCALE CABINET DU DR PASCALE DAVEAU 11 Rue de Reims 75013 Paris 75113 75 6.858885e+06 653857.025463 POINT (653857.025 6858885.388)
2 810000556125 PENDOLA-LUCHEL ISABELLE CABINET DU DR ISABELLE PENDOLA-LUCHEL 37 Rue Charcot 75013 Paris 75113 75 6.859050e+06 653727.951994 POINT (653727.952 6859049.875)
3 810000571660 CHIAVERINI PHILIPPE CABINET DU DR PHILIPPE CHIAVERINI 52 Rue Mademoiselle 75015 Paris 75115 75 6.860589e+06 648605.100157 POINT (648605.100 6860589.305)
4 810000582683 GUEDJ CHANTAL CABINET DU DR CHANTAL GUEDJ 113 Avenue Charles de Gaulle 92200 Neuilly-sur... 92051 92 6.864855e+06 646440.264871 POINT (646440.265 6864855.094)

Mapping the geocoding results

GeoPandas allows for direct exploration of the geodataframe on an interactive map.

In [16]:
import geopandas as gpd

style_kwdsdict = {
    "fillOpacity": 0.5,  
    "fillColor": Colors.red, 
    "stroke": False, 
}

geo_gp['geometry'].explore(tiles='CartoDB Dark-matter', style_kwds=style_kwdsdict)
Out[16]:
Make this Notebook Trusted to load map: File -> Trust Notebook

Reading and loading the Ile-de-France municipalities (1)

Additionally, we will require a basemap of the municipalities in the Ile-de-France region.

This basemap is available in GeoJSON format and utilizes the WGS84 coordinate system (EPSG 4326).

For information on various projection systems, the website https://epsg.io/ serves as a valuable resource.

In [17]:
url_cities = "./data/com_idf.geojson"

# To simplify the workshop, we only load the municipalities near Paris with a bounding box
bbox_4326 = [2.08, 48.64, 2.7, 49.04] 
b = (bbox_4326[0], bbox_4326[1], bbox_4326[2], bbox_4326[3])

gdf_cities = gpd.read_file(url_cities, bbox=(b), crs=4326)

gdf_cities = gdf_cities.to_crs(2154)
bbox_2154 = gdf_cities.total_bounds
In [18]:
gdf_cities.explore(tiles='CartoDB Dark-matter')
Out[18]:
Make this Notebook Trusted to load map: File -> Trust Notebook

Reading and loading the Ile-de-France municipalities (2)

For this initial phase, we will retain only the municipalities located within the departments bordering the city of Paris.

Additionally, we will compute the coordinates of centroids, including longitude and latitude.

In [19]:
gdf_parispc = gdf_cities.query("insee_dep in ('75','92','93','94')").copy()

gdf_parispc["longitude"] = gdf_parispc.centroid.x
gdf_parispc["latitude"] = gdf_parispc.centroid.y
    
gdf_parispc.explore(tiles='CartoDB Dark-matter', column='insee_dep', legend=False)
Out[19]:
Make this Notebook Trusted to load map: File -> Trust Notebook

Reading and loading departments

Now, let's create a layer for the departments

In [20]:
gdf_dep = gdf_cities[['insee_dep','geometry']].dissolve(by='insee_dep')
bbox_parispc = gdf_parispc.buffer(1000).total_bounds
gdf_dep = gdf_dep.clip(bbox_parispc)

The bounding box will be precious for furthers analysis.

In [21]:
bbox_parispc
Out[21]:
array([ 636299.0812222 , 6842146.01796456,  672750.28085618,
       6880244.92629093])

Mapping the General Practitioners (1)

Let's count and map the number of GPs per municipality.

In [22]:
city_gp = geo_gp.groupby(['result_citycode']).agg({'GPid':'count'}).reset_index()
city_gp.columns = ['insee_com','GPcount']
city_map = gdf_parispc.merge(city_gp,on='insee_com',how='left')
city_map.query("insee_com=='75101'")
Out[22]:
nom insee_com population insee_dep geometry longitude latitude GPcount
137 Paris 1er Arrondissement 75101 15917 75 MULTIPOLYGON (((651911.600 6861760.600, 651787... 651316.800507 6.862706e+06 34.0

A spatial method with GeoPandas would have been :

In [23]:
result = gdf_parispc.sjoin(geo_gp).groupby('insee_com').size()
result
Out[23]:
insee_com
75101     34
75102     37
75103     53
75104     33
75105    118
        ... 
94077     10
94078     28
94079     11
94080     41
94081     65
Length: 142, dtype: int64

Mapping the General Practitioners (2)

We will now use matplotlib to map the results.

The main_map() function will generate a basemap that encompasses Paris and the municipalities in its immediate suburbs. This basemap will serve as a foundation for creating multiple figures using Matplotlib.

In [24]:
from mpl_toolkits.axes_grid1.anchored_artists import AnchoredSizeBar

def main_map(bbox):
    """
    Create a main map using Matplotlib.

    Parameters:
        bbox (list): A list containing the bounding box coordinates [left, bottom, right, top].

    Returns:
        fig (matplotlib.figure.Figure): The Matplotlib figure.
        ax_main (matplotlib.axes.Axes): The main axis for the map.
    """
    
    cm = 1 / 2.54
    fig_main, ax_main = plt.subplots(sharex='all', sharey='all', figsize=(18 * cm, 18 * cm))
    ax_main.axes.get_xaxis().set_visible(False) 
    ax_main.axes.get_yaxis().set_visible(False)  
    ax_main.set_xlim(left=bbox[0], right=bbox[2])
    ax_main.set_ylim(bottom=bbox[1], top=bbox[3])
    city_map.plot(ax=ax_main, color=Colors.lightgray, edgecolor=Colors.gray, linewidth=0.25, zorder=0)
    
    gdf_dep.boundary.plot(ax=ax_main, color=Colors.darkgray, linewidth=0.35, linestyle='-', facecolor="none", zorder=5)
    
    scalebar = AnchoredSizeBar(ax_main.transData,
                           2000, '2 km',
                           loc='lower right',
                           pad=1,
                           color=Colors.gray,
                           label_top=True,
                           frameon=False,
                           prop={'size': 6},
                           zorder=6)
    ax_main.add_artist(scalebar)

    ax_main.text(1.03, 0.01, 'Sources : IGN, INSEE, annuaire.sante.fr 2023', transform=ax_main.transAxes,
                 va='bottom', ha='right', fontsize=8, color=Colors.gray, rotation='vertical',
                 fontdict={'style': 'italic'})

    return fig_main, ax_main

Mapping the General Practitioners (3)

Our basemap

In [25]:
fig_gp, ax_gp = main_map(bbox_parispc)

Mapping the General Practitioners (4)

plot_scattermap() adds a scattermap to an existing ax created with main_map().

In [26]:
from mpl_toolkits.axes_grid1.anchored_artists import AnchoredSizeBar

def plot_scattermap(ax, data, size_column, title, legend_title, text_color, scatter_color, scale=1, legend=True):
    """
    Create a scatter plot and a custom legend on the given axis.

    Parameters:
        ax (matplotlib.axes.Axes): The axis where the scatter plot and legend will be created.
        data (pandas.DataFrame): The data containing coordinates and size information.
        size_column (str): The name of the column in 'data' that contains the point sizes.
        title (str): The title for the scatter plot.
        legend_title (str): The title for the legend.
        text_color (str): The color of the text.
        scatter_color (str): The fill color of the scatter plot.
        scale (float): Scaling factor for point sizes in the scatter plot.

    Returns:
        scatter (matplotlib.collections.PathCollection): The scatter plot.
        legend_points (list of matplotlib.collections.PathCollection): List of points in the legend.
    """
    min_size = data[size_column].min()
    median_size = data[size_column].median()
    max_size = data[size_column].max()
    
    data.sort_values(size_column, inplace=True, ascending=False)
    
    scatter = ax.scatter(data['longitude'], data['latitude'], c=scatter_color,
                          edgecolor='w', linewidths=0.2,
                          s=data[size_column]*scale, label='Scatter Points', zorder=6)
    
    ax.set_title(title, color=text_color)
    
    if legend : 
        leg_val = [max_size, median_size, min_size]
        legend_points = [
            ax.scatter([], [], c=scatter_color, edgecolor='w', linewidths=0.2, s=size*scale, label=f'{int(size)}', zorder=2) for size in leg_val
        ]
        legend_ax = ax.legend(handles=legend_points, title=legend_title, loc='lower left', frameon=True)

        for text in legend_ax.get_texts():
            text.set_color(text_color) 

        title_text = legend_ax.get_title()
        title_text.set_position((0, 15)) 
        title_text.set_color(text_color) 
        title_text.set_backgroundcolor('w')

        legend_ax.get_frame().set_facecolor('w')
        legend_ax.get_frame().set_edgecolor('w')
    
    return scatter
In [27]:
fig_pop, ax_pop = main_map(bbox_parispc);

Mapping GPs and population

Indeed, this map may not provide much informative value, as the distribution of GPs closely mirrors the distribution of the population in the area.

In [28]:
def save_scattermap_plot(ax, data, column, title, xlabel, color1, color2, scale, filename):
    plot_scattermap(ax, data, column, title, xlabel, color1, color2, scale)
    fig = ax.get_figure()
    fig.tight_layout()
    fig.savefig(filename, dpi=200)
    
output_directory = "./assets/"
file_names = ["fig_gp.png", "fig_pop.png"]

file_paths = [os.path.join(output_directory, filename) for filename in file_names]

save_scattermap_plot(ax_gp, city_map, 'GPcount', "General practitioners in Paris area (aug. 2023)", "Number of GPs", Colors.blue, Colors.blue, 1, file_paths[0])
save_scattermap_plot(ax_pop, city_map, 'population', "Population in Paris area, 2022", "Population", Colors.blue, Colors.red, 0.002, file_paths[1])

html_code = f"""
<div style="display: flex; align-items: center;">
    {" ".join([f'<div style="flex: 1;"><img src="{filepath}" width="600"></div>' for filepath in file_paths])}
</div>
"""
In [29]:
display(HTML(html_code))

MAUP

We have just demonstrated that the most populated areas are also the areas with the highest number of GPs...

Faced with this remarkable revelation, it might be necessary to question the relevance and limitations of administrative boundaries when we are focusing on a spatial approach : The Modifiable Areal Unit Problem or MAUP.

MAUP : Issue

The MAUP is a concern that demonstrates how administrative boundaries can create the illusion of patterns that are, in reality, artifacts.

To illustrate this concept, we will generate a 10-kilometer grid and a fictional administrative mesh. This will help demonstrate how the choice of spatial units or boundaries can influence the interpretation of data and potentially lead to misleading conclusions.

In [30]:
from shapely.geometry import box, Point, MultiPoint
from shapely.ops import orient, voronoi_diagram
import random


def create_grid(epsg_code, bounding_box, resolution, return_centroids=False):
    """
    Create a grid of squares within a specified bounding box with a given resolution.

    Parameters:
        epsg_code (int): The EPSG code specifying the coordinate reference system (CRS) of the grid.
        bounding_box (list): A list containing the coordinates of the bounding box in the form [xmin, ymin, xmax, ymax].
        resolution (float): The resolution of each square in units of the specified CRS.
        return_centroids (bool): If True, return only the centroids of the squares.

    Returns:
        geopandas.GeoDataFrame: A GeoDataFrame containing the grid of squares or centroids.
    
    Example:
        epsg = 2154
        bounding_box = [632217, 6882276, 678065, 6838152]
        resolution = 10000  # Resolution of each square in CRS units
        grid = create_grid(epsg, bounding_box, resolution)
    """
    crs = f"EPSG:{epsg_code}"
    
    xmin, ymin, xmax, ymax = bounding_box
    
    x_coords = list(range(int(xmin), int(xmax), int(resolution)))
    y_coords = list(range(int(ymin), int(ymax), int(resolution)))
    
    features = []
    for x in x_coords:
        for y in y_coords:
            square = box(x, y, x + resolution, y + resolution)
            if return_centroids:
                centroid = square.centroid
                features.append(centroid)
            else:
                features.append(square)
    
    grid_gdf = gpd.GeoDataFrame({'geometry': features}, crs=crs)
    grid_gdf.geometry = grid_gdf.geometry.apply(orient, args=(-1,)) # to avoid errors with Altair
    
    if return_centroids:
        grid_gdf["latitude"] = grid_gdf.geometry.y
        grid_gdf["longitude"] = grid_gdf.geometry.x
    else :
        grid_gdf["latitude"] = grid_gdf.centroid.y
        grid_gdf["longitude"] = grid_gdf.centroid.x
        
    grid_gdf['OBJECTID'] = grid_gdf.index
    
    return grid_gdf

MAUP : Illustration (1)

We will generate a grid consisting of 16 squares, each measuring 10 kilometers by 10 kilometers, and distribute points evenly within this grid.

In [31]:
epsg=2154

bbox_city = city_map.total_bounds
grid_10km = create_grid(epsg, bbox_city, 10000)

bbox_grid = grid_10km.total_bounds
point_1km = create_grid(epsg, bbox_grid, 2000, True)

MAUP : Illustration (2)

Additionally, we will construct a fictional administrative mesh by creating 16 Voronoi diagrams to partition the area.

This mesh will serve as a representation of how administrative boundaries can be artificially imposed on a geographical area.

In [32]:
def generate_random_points_voronoi(bbox, num_points, output_epsg):
    """
    Generate a GeoDataFrame representing Voronoi polygons for random points within a specified bounding box.

    Parameters:
        bbox (tuple): A tuple containing the bounding box coordinates (bbox_min_x, bbox_min_y, bbox_max_x, bbox_max_y).
        num_points (int): The number of random points to generate.
        output_epsg (int): The EPSG code for the output coordinate reference system (CRS).

    Returns:
        geopandas.GeoDataFrame: A GeoDataFrame containing Voronoi polygons within the specified bounding box.
    """
    random.seed(2)
    
    bbox_min_x, bbox_min_y, bbox_max_x, bbox_max_y = bbox
    random_points = []
    
    for _ in range(num_points):
        x = random.uniform(bbox_min_x, bbox_max_x)
        y = random.uniform(bbox_min_y, bbox_max_y)
        random_points.append(Point(x, y))
    
    points = MultiPoint(random_points)
    regions = voronoi_diagram(points)
    
    # Create a GeoDataFrame from the Voronoi regions
    gdf = gpd.GeoDataFrame(geometry=[regions], crs=f'EPSG:{output_epsg}')
    
    # Use intersection to clip the GeoDataFrame with the bounding box
    gdf = gdf.clip(bbox)
    gdf = gdf.explode(index_parts=False).reset_index(drop=True)
    gdf['OBJECTID'] = gdf.index
    
    gdf["latitude"] = gdf.centroid.y
    gdf["longitude"] = gdf.centroid.x
    
    return gdf
In [33]:
voronoi_gdf = generate_random_points_voronoi(bbox_grid, 16, epsg)
In [34]:
def configure_axis(ax):
    ax.title.set_color(Colors.blue)
    ax.axes.get_xaxis().set_visible(False)
    ax.axes.get_yaxis().set_visible(False)

    for spine in ['top', 'right', 'bottom', 'left']:
        ax.spines[spine].set_visible(False)

def main_maup(cm = 1 / 2.54, title1="10 km by 10 km grid", title2="Fictional administrative mesh", double_grid=False):
    
    fig_mp, (ax1, ax2) = plt.subplots(1, 2, sharex='all', sharey='all', figsize=(25 * cm, 25 * cm))

    configure_axis(ax1)
    configure_axis(ax2)

    grid_10km.plot(ax=ax1, color=Colors.lightgray, edgecolor=Colors.gray, linewidth=2, zorder=0)
    ax1.set_title(title1)
    
    if not double_grid : 
        voronoi_gdf.plot(ax=ax2, color=Colors.lightgray, edgecolor=Colors.gray, linewidth=2, zorder=0)
    else : 
        grid_10km.plot(ax=ax2, color=Colors.lightgray, edgecolor=Colors.gray, linewidth=2, zorder=0)
    ax2.set_title(title2)

    return fig_mp, ax1, ax2

MAUP : Illustration (3)

In both the grid and the fictional administrative mesh, we have evenly distributed several points.

In [35]:
fig_maup, ax_regu, ax_voro = main_maup()
    
point_1km.plot(ax=ax_regu, color=Colors.red, zorder=1, markersize=2)
point_1km.plot(ax=ax_voro, color=Colors.red, zorder=1, markersize=2)

fig_maup;

MAUP : Illustration (4)

Now, let's aggregate these points within each administrative boundary.

In [36]:
grid_10km['count'] = grid_10km.sjoin(point_1km).groupby('OBJECTID_left').size()
voronoi_gdf['count'] = voronoi_gdf.sjoin(point_1km).groupby('OBJECTID_left').size()
In [37]:
fig_maup_s, ax_regu_s, ax_voro_s = main_maup()

plot_scattermap(ax_regu_s, grid_10km, 'count', "10 km by 10 km grid", "Population", Colors.blue, Colors.red, scale=15, legend=False)
plot_scattermap(ax_voro_s, voronoi_gdf, 'count', "Fictional administrative mesh", "Population", Colors.blue, Colors.red, scale=15, legend=False)
fig_maup_s;

This example highlights how the observed phenomenon can appear more significant in the northwest and weaker in the southeast due to the artificial administrative boundaries, even though in reality, it is evenly distributed across the entire study area.

MAUP : Illustration (5)

And it's even worse if you don't adhere to the rules of graphic semiology (your eye cannot perceive proportionality with different shades of gray. Only size can convey this information).

In [38]:
def customize_legend(_legend):
    _legend.set_frame_on(True)
    _legend.get_frame().set_facecolor('w')
    _legend.get_frame().set_edgecolor('w')
    _legend.get_title().set_color(Colors.blue)

    for line in _legend.get_lines():
        line.set_markeredgecolor(Colors.gray)
        line.set_markeredgewidth(0.5)

    for text in _legend.get_texts():
        text.set_color(Colors.blue)

    title_text = _legend.get_title()
    title_text.set_position((0, 15)) 
    title_text.set_color(Colors.blue)
    title_text.set_backgroundcolor('w')
In [39]:
fig_maup_c, ax_regu_c, ax_voro_c = main_maup()

legend = {'loc':'lower left', 'bbox_to_anchor':(0, -.35), 'markerscale':1, 
          'title_fontsize':'medium', 'fontsize':'small', 'title' : 'Population','labelcolor': Colors.legend_text, }

grid_10km.plot(ax=ax_regu_c, column='count', cmap='OrRd', scheme='quantiles', edgecolor=Colors.gray, 
               legend=True, legend_kwds=legend )
customize_legend(ax_regu_c.get_legend())

voronoi_gdf.plot(ax=ax_voro_c, column='count', cmap='OrRd', scheme='FisherJenks', k=4, edgecolor=Colors.gray, legend=True, legend_kwds=legend )
customize_legend(ax_voro_c.get_legend())
fig_maup_c;

MAUP : Solution (1)

An alternative approach is to normalize the results by introducing a denominator, such as area for density computation.

In [40]:
grid_10km['area'] = grid_10km.geometry.area /1000000
voronoi_gdf['area'] = voronoi_gdf.geometry.area /1000000

grid_10km['density'] = grid_10km['count'] / grid_10km['area'] 
voronoi_gdf['density'] = voronoi_gdf['count'] / voronoi_gdf['area']

MAUP : Solution (2)

In [41]:
fig_maup_d, ax_regu_d, ax_voro_d = main_maup()

legend['title']="Density (km²)"

grid_10km.plot(ax=ax_regu_d, column='density', cmap='OrRd', scheme='quantiles', edgecolor=Colors.gray, 
               legend=True, 
               legend_kwds=legend )
customize_legend(ax_regu_d.get_legend())

voronoi_gdf.plot(ax=ax_voro_d, column='density', cmap='OrRd', scheme='FisherJenks', k=4, edgecolor=Colors.gray,
                 legend=True, 
                 legend_kwds=legend )
customize_legend(ax_voro_d.get_legend())

fig_maup_d;

MAUP : GPs' number

Here is the result after applying the normalization method to our study area.

In [42]:
city_map['area'] = city_map.geometry.area /1000000

fig_gp_n, ax_gp_n = main_map(bbox_parispc)

legend = {'loc':'lower left', 'markerscale':1, 'title_fontsize':'medium', 'fontsize':'small'}

city_map.plot(ax=ax_gp_n, column='GPcount', cmap='OrRd', scheme='FisherJenks', k=4,
              edgecolor=Colors.gray,  linewidth=0.2, legend=True, legend_kwds=legend )
customize_legend(ax_gp_n.get_legend())

ax_gp_n.set_title("Number of GPs (avoid this representation)", color=Colors.blue)
fig_gp_n;

MAUP : GPs' density

In [43]:
city_map['area'] = city_map.geometry.area /1000000
city_map["GP_density"] = city_map["GPcount"] / city_map['area']
city_map['GP_density'] = city_map['GP_density'].fillna(0)

fig_gp_d, ax_gp_d = main_map(bbox_parispc)

city_map.plot(ax=ax_gp_d, column='GP_density', cmap='OrRd', scheme='FisherJenks', k=4,
              edgecolor=Colors.gray,  linewidth=0.2,
              legend=True, legend_kwds=legend )
customize_legend(ax_gp_d.get_legend())

ax_gp_d.set_title("Density of GPs (km²)", color=Colors.blue)
fig_gp_d;

MAUP : GPs per population

Another more common solution is to divide by the population size of each area. While this operation may be closer to the issue at hand, it no longer standardizes the size of spatial units. Consequently, it may reintroduce the MAUP.

In [44]:
city_map["GP_pop"] = city_map["GPcount"] / city_map['population'] * 100000
city_map['GP_pop'] = city_map['GP_pop'].fillna(0)

fig_gp_p, ax_gp_p = main_map(bbox_parispc)

city_map.plot(ax=ax_gp_p, column='GP_pop', cmap='OrRd', scheme='FisherJenks', k=4,
              edgecolor=Colors.gray,  linewidth=0.2,
              legend=True, legend_kwds=legend )
customize_legend(ax_gp_p.get_legend())

ax_gp_p.set_title("GPs per million population", color=Colors.blue)
fig_gp_p;

Map Classification

You might have noticed that the choropleth maps produced are classified using the Fisher-Jenks algorithm. This choice is non-trivial as it seeks to minimize the variance within each class while maximizing the variance between classes.

In essence, the values within the same class are grouped in a highly similar manner, ensuring significant dissimilarity between the classes themselves.

This methodology yields a visual representation that closely approximates reality. However, the objectives of your maps may steer you towards employing alternative techniques, particularly when conducting comparisons between maps.

While this issue of discretization goes beyond the scope of the MAUP, it is nevertheless a crucial step in creating a map. Inadequate discretization has the potential to result in misinterpretations of your findings.

Effect of classification on maps interpretation

We will visualize the distribution of general practitioners per million inhabitants using three distinct classification methods.

In [45]:
schemes = [
    {"scheme": "quantiles", "file_name": "fig_class_q5.png", "title": "Quantiles"},
    {"scheme": "fisherjenks", "file_name": "fig_class_j5.png", "title": "Fisher Jenks"},
    {"scheme": "equalinterval", "file_name": "fig_class_e5.png", "title": "Equal Interval"}
]

for scheme_params in schemes:
    fig_gp_mc, ax_gp_mc = main_map(bbox_parispc)
    plt.close()
    
    city_map.plot(ax=ax_gp_mc, column='GP_pop', cmap='OrRd', scheme=scheme_params["scheme"], k=5,
                  edgecolor=Colors.gray,  linewidth=0.2, legend=True, legend_kwds=legend)
    
    customize_legend(ax_gp_mc.get_legend())
    ax_gp_mc.set_title(f"GPs per million population: {scheme_params['title']}", color=Colors.blue)

    file_path = f"./assets/{scheme_params['file_name']}"
    fig_gp_mc.tight_layout()
    fig_gp_mc.savefig(file_path, dpi=200)
    plt.close()

Quantiles, Fisher Jenks and Equal Interval

With the same dataset, we can convey various messages by employing different classification methods.

In [46]:
html_code = f"""
<div style="display: flex; align-items: center;">
    {" ".join([f'<div style="flex: 1;"><img src="./assets/{scheme_params["file_name"]}" width="600"></div>' for scheme_params in schemes])}
</div>
"""
display(HTML(html_code))

Kernel Density Estimation (KDE)

Another approach to mitigate the Modifiable Areal Unit Problem (MAUP) is to employ Kernel Density Estimation (KDE). However, it is essential for your source data to be on a relatively fine grid for this method to be effective.

KDE is a non-parametric technique used to estimate the probability density function of a continuous random variable. It serves as an alternative to histogram-based density estimation.

The process involves positioning a kernel with a specific function (e.g., Normal, Negative Exponential, Quartic, etc.) at each data point and then summing them to create a continuous and smooth density estimate.

The bandwidth parameter plays a critical role in this method, as it determines the width of the kernels and influences the smoothness of the estimate. A higher bandwidth value results in a smoother density estimate.

In [47]:
import numpy as np
from scipy.stats import gaussian_kde

def create_bimodal_kernel_density_plot(data_mode1_params, data_mode2_params, bw=0.5):
    """
    Generate a bimodal kernel density plot using Matplotlib and SciPy.

    Args:
        data_mode1_params (tuple): Parameters for the first normal distribution (mean, standard deviation, number of samples).
        data_mode2_params (tuple): Parameters for the second normal distribution (mean, standard deviation, number of samples).
        bw(float): Estimator bandwidth

    Returns:
        tuple: A tuple containing the Matplotlib figure and axis objects representing the bimodal kernel density plot.
    """
    np.random.seed(42)
    
    data_mode1 = np.random.normal(data_mode1_params[0], data_mode1_params[1], data_mode1_params[2])
    data_mode2 = np.random.normal(data_mode2_params[0], data_mode2_params[1], data_mode2_params[2])
    data = np.concatenate((data_mode1, data_mode2))

    kde = gaussian_kde(data,bw_method=bw)

    x_values = np.linspace(min(data), max(data), 1000)
    density_values = kde(x_values)

    fig_kde, ax_kde = plt.subplots(figsize=(8, 6))

    ax_kde.fill_between(x_values, density_values, alpha=0.5, label='Density', color=Colors.white)
    ax_kde.scatter(data, np.zeros_like(data), color=Colors.red, s=20, label='Points at Y=0')

    ax_kde.set_xlabel('X')
    ax_kde.set_ylabel('Density estimation')
    ax_kde.set_title(f'Bimodal Kernel Density Plot, bandwith: {bw}, Gaussian function', color=Colors.white)
    ax_kde.legend(frameon=False, labelcolor=Colors.white)

    return fig_kde, ax_kde

One dimensional KDE with an estimator bandwidth of 0.5

In this example, the density curve provides a succinct summary of the distribution of points' arrangement along a single dimension.

In [48]:
data1 = (-2, 1, 25)
data2 = (2, 1, 100)
fig_kde_uni, ax_kde_uni = create_bimodal_kernel_density_plot(data1, data2)
customize_axes(ax_kde_uni,fig_kde_uni)
fig_kde_uni;

One dimensional KDE with an estimator bandwidth of 0.05

Conversely, using a lower bandwidth captures finer details but can introduce noise into the density estimation:

In [49]:
fig_kde_uni2, ax_kde_uni2 = create_bimodal_kernel_density_plot(data1, data2, 0.05)
customize_axes(ax_kde_uni2,fig_kde_uni2)
fig_kde_uni2;

KDE with spatial data

When the KDE function is applied to both spatial dimensions, it becomes feasible to circumvent the constraints imposed by territorial boundaries, allowing for the visualization of the distribution of points.

KDE with spatial data : GPs location

In [50]:
geo_gp_pc = geo_gp.clip(bbox_parispc)
In [51]:
fig_gp_frontier, ax_gp_frontier = main_map(bbox_parispc)

geo_gp_pc.plot(ax=ax_gp_frontier,markersize=0.1,color=Colors.red)
ax_gp_frontier.set_title('Geocoded General Practitionners', color=Colors.blue)
fig_gp_frontier;

KDE with spatial data : density contour function

This function will generate a spatial Kernel Density Estimation (KDE) using the gaussian_kde() function from the SciPy library.

A mobile window traverses the study area, assigning weights to the encountered points based on the density function.

In [52]:
def generate_density_contour(longitude, latitude, bw_method=0.12, area=150, weight=None):
    """
    Generate a density contour plot of geographical data.

    Parameters:
        longitude (numpy.ndarray): Array of longitude values.
        latitude (numpy.ndarray): Array of latitude values.
        bw_method (float): Bandwidth for kernel density estimation (default is 0.12).
        area (int): The number of points in the meshgrid for the contour plot (default is 150).
        weight (numpy.ndarray, optional): An array of weights for kernel density estimation (default is None).

    Returns:
        x (numpy.ndarray): Meshgrid for longitude values.
        y (numpy.ndarray): Meshgrid for latitude values.
        z (numpy.ndarray): Density values for the contour plot.
    """
    if weight is not None:
        kde = gaussian_kde([longitude, latitude], bw_method=bw_method, weights=weight)
    else:
        kde = gaussian_kde([longitude, latitude], bw_method=bw_method)
    
    x, y = np.meshgrid(np.linspace(longitude.min(), longitude.max(), area), np.linspace(latitude.min(), latitude.max(), area))

    z = kde(np.vstack([x.ravel(), y.ravel()])) 
    relative_z =  z / np.sum(z) 
    relative_z = relative_z.reshape(x.shape)

    return x, y, relative_z

Two dimensionals KDE with an estimator bandwidth of 0.2

We will begin by creating an initial Kernel Density Estimation (KDE) with a broad bandwidth. Please keep in mind that in these examples, the results are not expressed in map units.

In [53]:
latitude = geo_gp_pc['latitude']
longitude = geo_gp_pc['longitude']
x, y, z =  generate_density_contour(longitude,latitude,bw_method=0.2)

fig_gp_kde_12, ax_gp_kde_12 = main_map(bbox_parispc)
contour_kde12 = ax_gp_kde_12.contourf(x, y, z, levels=6, cmap='Reds', alpha=0.6)

cbar = plt.colorbar(contour_kde12, ax=ax_gp_kde_12, shrink=0.7)
fig_gp_kde_12 ;

Two dimensionals KDE with an estimator bandwidth of 0.06

A smaller bandwidth synthesizes the distribution less but, conversely, adds details to the spatial distribution of GPs.

In [1]:
latitude = geo_gp_pc['latitude']
longitude = geo_gp_pc['longitude']
x, y, z =  generate_density_contour(longitude,latitude,bw_method=0.06)

fig_gp_kde_06, ax_gp_kde_06 = main_map(bbox_parispc)
contour = ax_gp_kde_06.contourf(x, y, z, levels=6, cmap='Reds', alpha=0.6)

cbar = plt.colorbar(contour, ax=ax_gp_kde_06, shrink=0.7)
fig_gp_kde_06 ;

---------------------------------------------------------------------------
NameError                                 Traceback (most recent call last)
Cell In[1], line 1
----> 1 latitude = geo_gp_pc['latitude']
      2 longitude = geo_gp_pc['longitude']
      3 x, y, z =  generate_density_contour(longitude,latitude,bw_method=0.06)

NameError: name 'geo_gp_pc' is not defined

With the help of the KDE, the administrative mesh no longer acts as a fictitious barrier to the observed phenomena, as long as the data has a level of precision that is finer than that of the mesh.

For more information about KDE, see : Silverman, B. W. (1986). Density estimation for statistics and data analysis (Vol. 26). CRC press.

Regulard grid

Another approach to circumvent the limitations addressed by the MAUP is to create regular grids within your study area.

This way, you won't be dependent on abstract administrative boundaries. However, border effects may occur (unlike with KDE).

For this, we will use H3pandas. In addition to creating hexagonal grids of various sizes with reusable IDs across different projects, H3pandas allows for performing aggregation operations within the grid.

Creating hexagonal grids with h3pandas

In [55]:
import h3pandas

def aggregate_h3_grid(points, poly, aggregation_level):
    """
    Aggregate point data into H3 hexagons and calculate density.

    Args:
        points (geopandas.GeoDataFrame): Input GeoDataFrame with point geometries.
        poly (geopandas.GeoDataFrame): Polygon GeoDataFrame for the polyfill resampling.
        aggregation_level (int): The H3 aggregation level to use.
        
    Returns:
        geopandas.GeoDataFrame: Aggregated GeoDataFrame with density calculated.

    """
    
    crs = points.crs
    
    points = points.to_crs(4326).copy()
    points = points[['geometry']]
    points["n"] = 1
    poly = poly.to_crs(4326).copy()
    poly = poly[['geometry']]

    # polyfill is used instead of geo_to_h3_aggregate to fill all the area, instead empty regions will appear
    h3 = poly.h3.polyfill_resample(aggregation_level)
    h3["n"] = h3.sjoin(points).groupby('h3_polyfill').size()
    h3["n"].fillna(0, inplace=True)
    
    h3 = h3.to_crs(crs)
    h3['dens'] = h3["n"] / h3.geometry.area
    h3['dens'] = h3['dens'] * 1000000 if crs in (2154, 3857) else h3['dens']
    
    return h3

Larger hexagonal grid : H7

In [56]:
fig_gp_h7, ax_gp_h7 = main_map(bbox_parispc)

grid_h7 = aggregate_h3_grid(geo_gp, gdf_cities, 7)

grid_h7.plot(ax=ax_gp_h7, column='dens', cmap='OrRd', scheme='FisherJenks', k=4,
              edgecolor=Colors.gray, linewidth=0.2, alpha=0.7, zorder=3,
              legend=True, legend_kwds=legend )

customize_legend(ax_gp_h7.get_legend())

ax_gp_h7.set_title("GPs density : H7", color=Colors.blue)
fig_gp_h7;

Larger hexagonal grid : H8

(long time computation)

In [57]:
%%time
fig_gp_h8, ax_gp_h8 = main_map(bbox_parispc)

grid_h8 = aggregate_h3_grid(geo_gp,gdf_cities, 8)

grid_h8.plot(ax=ax_gp_h8, column='dens', cmap='OrRd', scheme='FisherJenks', k=4,
              edgecolor=Colors.gray, linewidth=0.2, alpha=0.7, zorder=3,
              legend=True, legend_kwds=legend )

customize_legend(ax_gp_h8.get_legend())

ax_gp_h8.set_title("GPs density : H8")
fig_gp_h8;

CPU times: user 41.8 s, sys: 0 ns, total: 41.8 s
Wall time: 41.8 s

MAUP and variance

Another consequence of the MAUP is that as more data is aggregated at larger unit, the variance tends to decrease.

The data generated using H3pandas clearly illustrates this phenomenon, particularly when examining the variance in density.

Now, let's compute the variance in the density of GPs using 6 H3pandas grids.

In [58]:
var_dict = {}
for i in range(4, 10):
    d = aggregate_h3_grid(geo_gp_pc, gdf_cities, i).dens
    var_dict[f'h3_{i}'] = round(np.var(d))

keys = list(var_dict.keys())
values = list(var_dict.values())

Smaller spatial units, increased variance

Selecting an appropriate grid size is crucial to ensure it aligns well with the specific phenomenon under study.

It's essential to remember that the analysis of variance, and more broadly, covariances, plays a significant role in data analysis.

In [59]:
fig_var, ax_var = plt.subplots()
ax_var.plot(keys, values, marker='o', linestyle='-', color=Colors.red)
ax_var.set_xlabel('H3 aggregation level')
ax_var.set_ylabel('Variance')
ax_var.set_title('Smaller spatial units (H3), increased variance', color=Colors.white)

customize_axes(ax_var,fig_var)

fig_var;

Hot Spot Detection / Spatial Autocorrelation

As we've seen, the cartographic approach to interpreting a spatial phenomenon is not always straightforward: choosing the right indicator, map classification methods, issues with the Modifiable Areal Unit Problem (MAUP)...

However, some statistical tools used by geographers can help overcome these challenges. For instance, hotspot detection

This involves detecting spatial clusters of values that are higher or lower than expected.

Detecting hotspots and clusters in geography indeed warrants a full-day workshop. Today, we will only cover one method involving spatial autocorrelation :

  • The Global Moran's Index
  • The Local Moran's Index (LISA)

Global Spatial Autocorrelation : Moran's $\,I\,$ (1)

The Moran's I index helps identify whether the data is spatially clustered (values close to each other are spatially grouped), random* or if they tend to repel each other (dispersed*) : the spatial autocorrelation*

Global Moran's $I$ is calculated with the following :

\begin{equation} I = \frac{n}{W} \sum_{i=1}^{n} \sum_{j=1}^{n} w_{ij} (x_i - \bar{X}) (x_j - \bar{x}) / \sum_{i=1}^{N} (x_i - \bar{X})^2 \end{equation}

\ where \ \begin{align*} n & \text{ is the number of spatial units indexed }\\ x & \text{ is the variable of interest} \\ \bar{X} & \text{ is the mean of } x \\ w_{ij} & \text{ are spatial weights between } i \text{ and } j \\ W & \text{ is the sum of all } w_{ij} \text{ (i.e. } W = \sum_{i=1}^{N} \sum_{j=1}^{N} w_{ij}) \end{align*}

Global Spatial Autocorrelation : Moran's $\,I\,$ (2)

For each weighted values $w$ of $i$ and $j$ features, it calculates the deviation to the area mean and cross-products them. The larger the deviation from the mean, the larger the cross-product result.

$w_{ij}$ is the weighted distance matrix (binary or continuous), assessing the Spatial Lag. i.e. a weighted sum of the values observed at neighboring locations.

$I$ is standardized by the variance : it falls between -1 (dispersed) and +1 (clustered).

Moran's $\,I\,$ example : data

Let's create an example to illustrate the Moran's Index.

To do so, we will generate spatially clustered, random, and dispersed values within a grid.

In [60]:
grid_moran = grid_10km.sort_values(['latitude','longitude']).reset_index(drop=True)

np.random.seed(42)

size = len(grid_moran)
pos = np.sort(np.random.binomial(n=2, p=0.5, size=[size]))
pattern = np.array([1, 2])
neg = np.tile(pattern, size // 2)

grid_moran['positive'] = pos
grid_moran['negative'] = neg
grid_moran['random'] = np.random.randint(1, 4, size=size)

Moran's $\,I\,$ example : contiguity matrix

Let's add the contiguity matrix with a Queen metric. It will be used to assess the Spatial Lag

The library libpysal provides tools for calculating various matrices : rook, queen or continuous

Contiguity matrices are available in varying orders, with data weights usually diminishing as the order escalates

In [61]:
from libpysal.weights.contiguity import Queen
w = Queen.from_dataframe(grid_moran,use_index=True)
In [62]:
fig_matrix, ax_matrix_queen, ax_matrix_rook = main_maup(title1="Queen metric (order 1)", title2="Rook metric (order 1)", double_grid=True)

grid_10km["queen"] = [0,1,1,1,0,1,2,1,0,1,1,1,0,0,0,0]
grid_10km.plot(ax= ax_matrix_queen, column="queen", cmap='Reds', edgecolor=Colors.gray, linewidth=1)

grid_10km["rook"] = [0,0,1,0,0,1,2,1,0,0,1,0,0,0,0,0]
grid_10km.plot(ax= ax_matrix_rook, column="rook", cmap='Reds', edgecolor=Colors.gray, linewidth=1)
fig_matrix;

Moran's $\,I\,$ example : computing

esda package (Exploratory Spatial Data Analysis) is used to calculate the Moran Index and its p-value

In [63]:
from esda.moran import Moran
def moran_index(values, w_matrix, significance_level=0.01):
    """
    Calculate Moran's I and assess spatial clustering or dispersion.

    Parameters:
    values (array-like): Numeric data values.
    w_matrix (scipy.sparse matrix): Spatial weights matrix.
    significance_level (float): Significance level for p-value.

    Returns:
    tuple: Moran's I, p-value, and spatial pattern assessment result.
    The result can be one of the following:
    - "Significant clustering" if data is significantly clustered.
    - "Significant dispersion" if data is significantly dispersed.
    - "Random" if data is not significant.

    Note: A positive Moran's I indicates clustering, and a negative Moran's I indicates dispersion.
    """

    moran = Moran(values, w_matrix)
    
    moran_I = moran.I
    p_value = moran.p_norm

    # Check if p-value is below the significance level
    if p_value < significance_level:
        # Determine if the data is clustered or dispersed
        if moran_I > 0:
            result = "Significant clustering"
        elif moran_I < 0:
            result = "Significant dispersion"
        p_value_text = f"P-Value < {significance_level}"
    else:
        result = "Random"
        p_value_text = f"P-Value = {p_value:.4f}"

    # Return Moran's I, p-value, and the result
    return moran_I, p_value_text, result

Moran's $\,I\,$ example : illustration

In [64]:
import matplotlib.pyplot as plt
from matplotlib.colors import ListedColormap

def main_moran(values, cm=1 / 2.54):

    custom_colors = [Colors.blue, Colors.white, Colors.red]
    custom_cmap = ListedColormap(custom_colors)
    
    fig, axes = plt.subplots(1, 3, sharex='all', sharey='all', figsize=(25 * cm, 25 * cm))
    plt.subplots_adjust(wspace=0.1)

    for ax, title in zip(axes, moran_values.keys()):
        configure_axis(ax)
        grid_moran.plot(ax=ax, column=title, cmap=custom_cmap, edgecolor=Colors.gray, linewidth=2, zorder=0)
        w.plot(grid_moran, ax=ax,
               edge_kws=dict(color=Colors.darkgray, linestyle=':', linewidth=1, alpha=0.5),
               node_kws=dict(marker=''))
        
        moran_I, p_value, result = moran_index(grid_moran[title], w) 
        
        ax.set_title(title, color=Colors.blue)
        ax.text(0.5, -0.3, f'Moran I: {moran_I:.3f}\nP-value: {p_value}\nResult: {result}', transform=ax.transAxes, ha='center', color=Colors.blue)

    return fig, axes


moran_values = {
    'positive': moran_index(grid_moran['positive'].values, w),
    'random': moran_index(grid_moran['random'].values, w),
    'negative': moran_index(grid_moran['negative'].values, w)
}

fig_moran, axes = main_moran(moran_values)

Moran's $\,I\,$ example : GPs density H7

The Moran's $I$ is positive and statistically significant, indicating that the values are spatially clustered

In [65]:
w_h7 = Queen.from_dataframe(grid_h7,use_index=True, silence_warnings=True)
fig_gp_queens_h7, ax_gp_queens_h7 = main_map(bbox_parispc)

grid_h7.plot(ax=ax_gp_queens_h7, column='dens', cmap='OrRd', scheme='FisherJenks', k=4, edgecolor=Colors.gray, linewidth=0.2, alpha=0.7, zorder=3, legend=True, legend_kwds=legend )
customize_legend(ax_gp_queens_h7.get_legend())

w_h7.plot(grid_h7, ax=ax_gp_queens_h7, edge_kws=dict(color=Colors.darkgray, linestyle=':', linewidth=1, alpha=0.5), node_kws=dict(marker=''))

i, p, r = moran_index(grid_h7.dens,w_h7)
ax_gp_queens_h7.set_title(f"GPs density : H7. Moran's I:{i:.3f}, {p}\n\n{r}", color=Colors.blue)
fig_gp_queens_h7;

Moran's $\,I\,$ example : GPs density H8

The results remain statistically significant, despite a decrease in Moran's $I$.

In [66]:
w_h8 = Queen.from_dataframe(grid_h8,use_index=True, silence_warnings=True)
fig_gp_queens_h8, ax_gp_queens_h8 = main_map(bbox_parispc)

grid_h8.plot(ax=ax_gp_queens_h8, column='dens', cmap='OrRd', scheme='FisherJenks', k=4,
              edgecolor=Colors.gray, linewidth=0.2, alpha=0.7, zorder=3,
              legend=True, legend_kwds=legend )

customize_legend(ax_gp_queens_h8.get_legend())

w_h8.plot(grid_h8,
       ax=ax_gp_queens_h8,
       edge_kws=dict(color=Colors.darkgray, linestyle=':', linewidth=1, alpha=0.5),
       node_kws=dict(marker=''))

i, p, r = moran_index(grid_h8.dens,w_h8)
ax_gp_queens_h8.set_title(f"GPs density : H8. Moran's I:{i:.3f}, {p}\n\n{r}", color=Colors.blue)
fig_gp_queens_h8;

Local Spatial Autocorrelation : $\,LISA$

Moran's I is a metric employed to assess global spatial autocorrelation, which provides a singular value to encapsulate the spatial relationships within a particular study area. It operates under the assumption that autocorrelation is uniformly distributed across the entire geographical region being examined.

Nonetheless, it is often the case that the spatial autocorrelation is not uniform and exhibits local variations within the study area. These variations can manifest as clustered patterns in certain areas, random patterns in others, and dispersed patterns in yet another set of regions.

To address these localized patterns and relationships, the Local Indicators of Spatial Association ($LISA$) methodology is employed.

Anselin, L. (1995). Local indicators of spatial association—LISA. Geographical analysis, 27(2), 93-115.

$\,LISA\,$ formula

The LISA uses the individual cross-products of the previous Global Moran's I to evaluate if each feature is surrounded by the same local values.

\begin{equation} I_i = \frac{x_i - \bar{X}}{S^2_i} \sum_{j=1}^{n} w_{ij} (x_j - \bar{X}) \end{equation}

whith:

\begin{equation} {S^2_i} = \frac{\sum_{j=1}^{n}(x_j - \bar{X})^2}{n-1} \end{equation}

where

\begin{align*} n & \text{ is the number of spatial units} \\ x_i & \text{ is the variable of interest of } i \\ x_j & \text{ is the variable of interest of } j \\ \bar{X} & \text{ is the mean of } x \\ w_{ij} & \text{ are spatial weights between } i \text{ and } j \\ \end{align*}

$\,LISA\,$ example

Let's illustrate this concept with the standardized graph depicting the Spatial Lag of GPs density and the GPs density itself.

Given that the values have been standardized (with a mean of 0 and a standard deviation of 1), we can readily differentiate values that surpass the mean from those that fall below it. This principle holds true for both the original data and their respective spatial lags.

Consequently, we can categorize the data into four distinct groups that significantly deviate from the mean:

  • High values surrounded by high spatial lag (HH).
  • High values surrounded by low spatial lag (HL).
  • Low values surrounded by high spatial lag (LH).
  • Low values surrounded by low spatial lag (LL)

Moran Local Scatterplot

This scatterplot displays the local spatial correlation between the values of a variable in different geographic areas and the weighted average of values in neighboring areas (spatial lag).

note : There appears to be a random error in the package. The HL values are occasionally swapped with the LL values.

In [67]:
from splot.esda import moran_scatterplot, plot_local_autocorrelation
from esda.moran import Moran_Local

moran_h7 = Moran(grid_h7.dens, w_h7)
moran_loc_h7 = Moran_Local(grid_h7.dens, w_h7)

fig_moran_h7, ax_moran_h7 = moran_scatterplot(moran_loc_h7, aspect_equal=True, p=0.05)
ax_moran_h7.set_xlabel('GPs density', color=Colors.blue)
ax_moran_h7.set_ylabel('Spatial Lag of GPs density', color=Colors.blue)
ax_moran_h7.title.set_color(Colors.blue)
label_info = {
    "HH": {"color": "#e7787a", "position": (3, 4)},
    "HL": {"color": "#fcb16a", "position": (3, -1)},
    "LH": {"color": "#abd9e9", "position": (-1, 1)},
    "LL": {"color": "#2c7bb6", "position": (-1, -1)}
}
for label, info in label_info.items():
    ax_moran_h7.text(info["position"][0], info["position"][1], label, fontsize=15, c=info["color"])

fig_moran_h7;

$\,LISA\,$ : GPs density - H7 grid

splot.esda also provides tools for easily visualizing the $LISA$ outputs

Paris and Créteil exhibit significant HH densities.

Note that the analysis area has deliberately been expanded to encompass neighboring entities along the borders

In [68]:
def plot_dep(ax):
    for idx in [1, 2]:
        gdf_dep.boundary.plot(ax=ax[idx], color=Colors.darkgray, linewidth=0.35, linestyle='-', facecolor="none", zorder=5)

fig_lisa_h7, axs_lisa_h7 = plot_local_autocorrelation(moran_loc_h7, grid_h7, 'dens', p=0.05)
plot_dep(axs_lisa_h7)
fig_lisa_h7;

$\,LISA\,$ : GPs density - H8 grid

The results are similar when reducing the grid size. New hotspots emerge, such as in the vicinity of Bobigny, Levallois-Perret or Neuilly-sur-Seine

In [69]:
moran_loc_h8 = Moran_Local(grid_h8.dens, w_h8)

fig_lisa_h8, axs_lisa_h8 = plot_local_autocorrelation(moran_loc_h8, grid_h8, 'dens', p=0.05)
plot_dep(axs_lisa_h8)
fig_lisa_h8;

$\,LISA\,$ : GPs density - Paris and its outskirt

Changing the grid does not alter the overall result. The Bobigny hot spot disappears, but those in Neuilly-sur-Seine and Levallois-Perret persist. It's worth noting that the 12th arrondissement of Paris transitions to LH

In [70]:
w_city_map = Queen.from_dataframe(city_map,use_index=True, silence_warnings=True)

moran_loc_poly = Moran_Local(city_map.GP_density, w_city_map)
plot_local_autocorrelation(moran_loc_poly, city_map, 'GP_density', p=0.05);

$\,LISA\,$ : GPs density - Paris and its outskirt without administratives boundaries

When considering the surroundings of the study area, we revert to a distribution of Hot Spots similar to what was observed with H7

In [71]:
city_map_large = gdf_cities.merge(city_gp,on='insee_com',how='left')

city_map_large['area'] = city_map_large.geometry.area /1000000
city_map_large["GP_density"] = city_map_large["GPcount"] / city_map_large['area']
city_map_large['GP_density'] = city_map_large['GP_density'].fillna(0)

w_city_map_large = Queen.from_dataframe(city_map_large,use_index=True, silence_warnings=True)

moran_loc_city_large = Moran_Local(city_map_large.GP_density, w_city_map_large)

fig_lisa_city_large, axs_lisa_city_large = plot_local_autocorrelation(moran_loc_city_large, city_map_large, 'GP_density', p=0.05);
plot_dep(axs_lisa_city_large)
fig_lisa_city_large;

$\,LISA\,$ : GPs density - Ile-de-France

The ideal approach is to consider the entire Ile-de-France region, and even its borders if possible. Naturally, the average density used in the calculation of Moran's indices will change

In [72]:
gdf_cities_idf = gpd.read_file(url_cities)
gdf_cities_idf = gdf_cities_idf.to_crs(2154)
idf_map = gdf_cities_idf.merge(city_gp,on='insee_com',how='left')

idf_map['area'] = idf_map.geometry.area /1000000
idf_map["GP_density"] = idf_map["GPcount"] / idf_map['area']
idf_map['GP_density'] = idf_map['GP_density'].fillna(0)

w_idf_map = Queen.from_dataframe(idf_map,use_index=True, silence_warnings=True)

moran_loc_idf = Moran_Local(idf_map.GP_density, w_idf_map)

fig_lisa_idf, axs_lisa_idf = plot_local_autocorrelation(moran_loc_idf, idf_map, 'GP_density', p=0.05);
plot_dep(axs_lisa_idf)
fig_lisa_idf;

$\,LISA\,$ : GPs per population - Paris and its outskirt

Finally, for practical reasons, we used GP density, but it would be necessary to conduct the analyses by normalizing them with respect to the population

In [73]:
moran_loc_poly = Moran_Local(city_map.GP_pop, w_city_map)
plot_local_autocorrelation(moran_loc_poly, city_map, 'GP_pop', p=0.05);

Conclusion

Addressed points

  • Address Geocoding employing the ADDOK API and assessing geocoding accuracy
  • Constructing and visualizing a geodataframe using geopandas and matplotlib.
  • Considerations pertaining to the Modifiable Areal Unit Problem (MAUP):
    • Artificial clustering of phenomena, intricately tied to the grid structure.
    • Variance reduction with increasing grid size.
    • Partial mitigation of these issues via supplementary grids or kernel density in conjunction with the administrative grid.
  • Utilization of Global and Local Moran's Autocorrelation indicators for the detection of Hot Spots.

Unaddressed points

  • Threshold and distance functions in spatial lag
    • Consideration of metrics like average nearest neighbor distance or the concept of incremental spatial autocorrelation, as described (here)[incremental spatial autocorrelaton]
    • The importance of selecting an appropriate spatial relationship, such as contiguity, continuity, inverse distance, or inverse distance squared
  • Geographically Weighted Regression
    • Brunsdon, C., Fotheringham, A. S., & Charlton, M. E. (1996). Geographically weighted regression: a method for exploring spatial nonstationarity. Geographical analysis, 28(4), 281-298.
    • MGWR
  • Travel time calculation
    • Illustrative examples provided in the last presentation slide
  • General Practitioners per population
    • Referring to the INSEE données carroyées
  • Spatial, temporal, and space-time scan statistics
    • Overview of methodologies and tools for conducting spatial, temporal, and space-time scan statistics, including resources such as SatScan
  • Classification method for mapping
    • course content (in french)

Spatial analysis ressources

  • Geospatial Analysis - A comprehensive guide
  • CATMOG
  • ESRI Tools Reference
  • Crimestat

Some good practices (1)

  • Considering a broader area than that of your study: spatial phenomena do not always halt at borders.
  • Evaluating Administrative Grid Suitability:
    • It is a common practice to employ an administrative grid for spatial analysis; however, it is imperative to critically assess its appropriateness.
    • For example, in France, maps based on the new regional divisions may introduce geographical distortions that necessitate careful examination.
  • Presentation of results:
    • It is acceptable to present results with diverse boundaries, such as the administrative grid, gridded data, or kernel density, depending on the specific context. In some cases, discrepancies from the administrative grid may be negligible and sufficient for decision-making.

Some good practices (2)

  • Optimal Grid Granularity:
    • Whenever feasible, selecting the finest granularity of the grid is advisable before starting your study, even if it requires subsequent data reaggregation.
  • Consideration of Statistical Power:
    • Nevertheless, caution should be exercised with regard to statistical power. Finer grids lead to a reduced number of statistical units, which can potentially impact the robustness of the findings. This trade-off should be considered
  • Autocompletion Address Parser:
    • If feasible, implement an address parser with autocompletion at the front-end when users enter addresses.
    • Ideally, the autocompletion database should align with the one used by your geocoder, ensuring consistency and accuracy in the address-based data input process

Thank you for your attention
Thanks to Carto and Arkeup

Appendix: Données carroyées and Travel Times

To simplify the workshop, we solely computed GPs densities within grids.

However, in practice, it would have been essential to complement this with other approaches, such as :

  • calculating the number of GPs relative to the population (as discussed in the workshop).
  • calculating distances between the population and GPs.

An example will be provided using the IGN API and INSEE data

Données carroyées INSEE 200 meters

In [74]:
path_insee = os.path.join(data_dir,"insee_example.geojson")
gdf_insee = gpd.read_file(path_insee)
map = gdf_insee.explore(tiles="CartoDB dark_matter")
map
Out[74]:
Make this Notebook Trusted to load map: File -> Trust Notebook

Select the GPs in the area

We are selecting the GPs within a 25 meters radius around the study area

In [75]:
bbox_insee = gdf_insee.buffer(25).total_bounds
gp_example = geo_gp.clip(bbox_insee)

gp_example.explore(m=map, color='#e63946', name="GPs",)
Out[75]:
Make this Notebook Trusted to load map: File -> Trust Notebook

Preparing the data for computation

In [76]:
gdf_insee["longitude_insee"] = gdf_insee.geometry.centroid.x
gdf_insee["latitude_insee"] = gdf_insee.geometry.centroid.y
In [77]:
gp_example = gp_example.drop_duplicates(subset="result_label") # avoid API's spamming
In [78]:
gdf_cross = gdf_insee[["Groupe","Ind","latitude_insee","longitude_insee"]].merge(gp_example[["latitude","longitude"]],how='cross')
gdf_cross.head()
Out[78]:
Groupe Ind latitude_insee longitude_insee latitude longitude
0 870089 289.5 6.864278e+06 650578.211848 6.864182e+06 651001.020234
1 870089 289.5 6.864278e+06 650578.211848 6.864147e+06 650741.580695
2 870089 289.5 6.864278e+06 650578.211848 6.864192e+06 650736.535319
3 870089 289.5 6.864278e+06 650578.211848 6.864296e+06 650674.781277
4 870089 289.5 6.864278e+06 650578.211848 6.864475e+06 650645.130671

Pedestrian travel time

The calculation between the centroids of the grid cells and the general practitioners can be performed using the IGN API

In [79]:
import requests

def calculate_itinerary(start_lon, start_lat, end_lon, end_lat, url="https://wxs.ign.fr/calcul/geoportail/itineraire/rest/1.0.0/route", profile="car", crs="4326"):
    """
    Calculate a route using the IGN Geoportail itinerary service.

    Args:
        start_lon (float): The longitude of the starting point.
        start_lat (float): The latitude of the starting point.
        end_lon (float): The longitude of the destination.
        end_lat (float): The latitude of the destination.
        url (str, optional): The URL of the IGN Geoportail itinerary service. Default is the official URL.
        profile (str, optional): The profile for the route calculation, "car" or "pedestrian".
        crs (int, optional): The CRS (Coordinate Reference System) code, either 4326 or 2154.

    Returns:
        dict or None: A dictionary containing the calculated itinerary or None if an error occurs.

    Example:
        start_lon = 2.3017215728759766
        start_lat = 48.81876120037664
        end_lon = 2.324380874633789
        end_lat = 48.8287067867079
        itinerary = calculate_itinerary(start_lon, start_lat, end_lon, end_lat)
        if itinerary:
            print(itinerary)
    """

    start_coords = f"{start_lon},{start_lat}"
    end_coords = f"{end_lon},{end_lat}"

    params = {
        "resource": "bdtopo-pgr",
        "profile": profile,
        "optimization": "shortest",
        "start": start_coords,
        "end": end_coords,
        "intermediates": "",
        "getSteps": "false",
        "crs":f"EPSG:{crs}",
        "constraints": '{"constraintType":"banned","key":"wayType","operator":"=","value":"tunnel"}'
    }

    response = requests.get(url, params=params)

    if response.status_code == 200:
        itinerary = response.json()
        return itinerary
    else:
        print(f"Error {response.status_code}: Unable to calculate the itinerary.")
        return None

Speed up computing using multiprocessing

In [80]:
import os
import pickle
import multiprocessing

def calculate_itinerary_parallel(row):
    index, data = row  
    start_lon = data['longitude_insee']
    start_lat = data['latitude_insee']
    end_lon = data['longitude']
    end_lat = data['latitude']
    
    itinerary = calculate_itinerary(start_lon, start_lat, end_lon, end_lat, crs=2154, profile="pedestrian") 
    
    result = {
        'duration': itinerary.get('duration', None) if itinerary else None,
        'geometry': itinerary.get('geometry', None) if itinerary else None
    }
    
    return result

num_cores = multiprocessing.cpu_count() - 1

path_results = os.path.join(data_dir, 'results_ign.pkl')

if os.path.exists(path_results):
    with open(path_results, 'rb') as f:
        results = pickle.load(f)
else:
    from tqdm import tqdm 
    rows = list(gdf_cross.iterrows()) 
    with multiprocessing.Pool(processes=num_cores) as pool:
        results_iterator = pool.imap(calculate_itinerary_parallel, rows)
        results = list(tqdm(results_iterator, total=len(rows), desc="Calculating itineraries"))
    with open(path_results, 'wb') as f:
        pickle.dump(results, f)

Mapping the pedestrian routes

In [81]:
from shapely.geometry import shape  

geometry_list = [result['geometry'] for result in results]
geometries = [shape(geometry_dict) for geometry_dict in geometry_list]
geometry_gdf = gpd.GeoDataFrame(geometry=geometries, crs="EPSG:2154")

duration_list = [result['duration'] for result in results]
duration_list = np.round(duration_list,1)

geometry_gdf['duration'] = duration_list
geometry_gdf.explore(color='#e6394616', tiles="CartoDB dark_matter")
Out[81]:
Make this Notebook Trusted to load map: File -> Trust Notebook

Mapping the average travel times to all general practitioners

The primary goal is to illustrate the use of travel times with Python. A more in-depth study would require, for example, the creation of an indicator that takes into account supply, demand, and a distance function.

In [82]:
gdf_cross['duration'] = duration_list
durations = gdf_cross.groupby('Groupe')['duration'].mean().reset_index()
durations = np.round(durations,1)
In [83]:
gdf_insee = gdf_insee.merge(durations)
gdf_insee.explore("duration", tooltip = ['Groupe', 'Ind', 'duration'],
                  cmap="YlOrRd", tiles="CartoDB dark_matter")
Out[83]:
Make this Notebook Trusted to load map: File -> Trust Notebook

Accessibility to dialysis centers in France with spatial interaction : the 2SCFA

In [84]:
filepath = "./assets/2scfa.jpg"
html_code = f"""
<div style="display: flex; align-items: center;">
    <div style="flex: 1;"><img src="{filepath}" width="600"></div>
</div>
"""
HTML(html_code)
Out[84]: