NOPT042 Constraint programming: Tutorial 3 – Improving your model¶

Debuging¶

  • Try very small instances where you understand the solution set.
  • Unit-test constraints one by one.
  • Start with a model that is as simple as possible.
  • For advanced debuging options you can use debug, see "How to Use the Debugger" from the Picat Guide.

How to import a file¶

Use cl(instance) to compile (to bytecode instance.qi) & load the file instance.pi (anywhere in $PATH).

main =>
    cl(instance),
    puzzle(Vars),
    solve(Vars).

See also Modules (import).

Improving the model¶

It is a good practice to first create a baseline model, and then try to improve. Ways to create more efficient model include:

  • global constraints: e.g. all_different
  • symmetry breaking: if there is a symmetry in the search space, e.g. in variables or in values, we can fix one element of the orbit and thus limit the part of the space that needs to be explored
  • choosing the best solver for your model (or the best model for your solver)
  • choosing a good solver configuration (e.g. search strategy---see the next tutorial)

Example: Map coloring¶

Create a model to color the map of Australian states and territories 7 with four colors (cf. The 4-color Theorem). (We exclude the Australian Capital Territory, the Jervis Bay Territory, and the external territories. Map coloring is a special case of graph coloring, see this map.

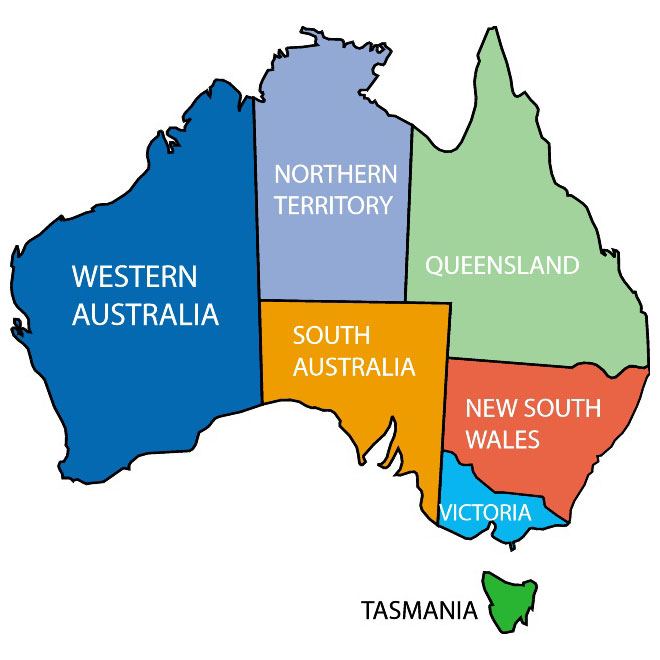
Map of Australia

Let's use the following decision variables:

Territories = [WA, NT, SA, Q, NSW, V, T]
In [1]:
!picat map-coloring/map-coloring-baseline.pi

[1,2,3,1,2,1,1]
In [2]:
!cat map-coloring/map-coloring-baseline.pi

import cp.

color_map(Territories) =>
    % variables
    Territories = [WA, NT, SA, Q, NSW, V, T],
    Territories :: 1..4,

    % constraints
    WA #!= NT,
    WA #!= SA,
    NT #!= SA,
    NT #!= Q,
    SA #!= Q,
    SA #!= NSW,
    SA #!= V,
    Q  #!= NSW,
    V  #!= NSW.


main =>
    color_map(Territories),
    solve(Territories),
    println(Territories).

How can we improve the model?

In [3]:
!picat map-coloring/map-coloring-improved.pi

Western Australia is red.
Northern Territory is green.
South Australia is blue.
Queensland is red.
New South Wales is green.
Victoria is red.
Tasmania is red.
In [4]:
!cat map-coloring/map-coloring-improved.pi

import cp.

color_map(Territories) =>
    % variables
    Territories = [WA, NT, SA, Q, NSW, V, T],
    Territories :: 1..8,

    % constraints
    Edges = [
        {WA,NT},
        {WA,SA},
        {NT,SA},
        {NT,Q},
        {SA,Q},
        {SA,NSW},
        {SA,V},
        {Q ,NSW},
        {V ,NSW}
    ],
    foreach(E in Edges)        
        E[1] #!= E[2]
    end.

% symmetry breaking constraints
precolor(Territories) =>
    WA #= 1,
    NT #= 2,
    SA #= 3.

% better output than `println(Territories)` (we could also use a map, i.e. a dictionary)
output(Territories) =>
    Color_names = ["red", "green", "blue", "yellow"],
    Territory_names = ["Western Australia", "Northern Territory", "South Australia", "Queensland", "New South Wales", "Victoria", "Tasmania"],
    foreach(I in 1..Territories.length)
        writef("%s is %s.\n", Territory_names[I], Color_names[Territories[I]])
    end.


main =>
    color_map(Territories),
    % precolor(Territories),
    solve(Territories), 
    output(Territories).

What else is wrong with this model? We always want to separate the model from the data. (See the exercise Graph-coloring below.)

Choosing a solver¶

Picat provides the following four solvers (implemented as modules):

  • cp
  • sat
  • smt
  • mip

What are the differences?

Example: Balanced diet (optimization)¶

This is (one of?) the first optimization problem for which Linear programming was used. Given a list of food items together with their nutritional values and prices, the goal is to choose a balanced diet---one that contains required minimal amounts of nutrients---while minimizing total price.

Note how we pass options to the solver: solve($[min(XSum)],Xs) The $ sign tells the solver to interpret the following as a term, rather than evaluating it as a function.

We will use the mip solver. It requires an external MIP solver. Here we use the Computational Infrastructure for Operations Research (COIN-OR)'s Cbc (branch and cut).

First, we need to install the Cbc package.

sudo apt-get install  coinor-cbc coinor-libcbc-dev

Or without root privileges:

wget https://raw.githubusercontent.com/coin-or/coinbrew/master/coinbrew
chmod u+x coinbrew
./coinbrew fetch Cbc@master
./coinbrew build Cbc
export PATH=$PATH:~/coinbrew/dist/bin
In [5]:
 !picat balanced-diet/balanced-diet.pi

'Done'
Welcome to the CBC MILP Solver 
Version: 2.10.7 
Build Date: Feb 14 2022 

command line - cbc __tmp.lp solve solu __tmp.sol (default strategy 1)

Continuous objective value is 90 - 0.01 seconds
Cgl0004I processed model has 4 rows, 4 columns (4 integer (0 of which binary)) and 14 elements
Cutoff increment increased from 1e-05 to 9.9999
Cbc0012I Integer solution of 90 found by DiveCoefficient after 0 iterations and 0 nodes (0.01 seconds)
Cbc0001I Search completed - best objective 90, took 0 iterations and 0 nodes (0.01 seconds)
Cbc0035I Maximum depth 0, 0 variables fixed on reduced cost
Cuts at root node changed objective from 90 to 90
Probing was tried 0 times and created 0 cuts of which 0 were active after adding rounds of cuts (0.000 seconds)
Gomory was tried 0 times and created 0 cuts of which 0 were active after adding rounds of cuts (0.000 seconds)
Knapsack was tried 0 times and created 0 cuts of which 0 were active after adding rounds of cuts (0.000 seconds)
Clique was tried 0 times and created 0 cuts of which 0 were active after adding rounds of cuts (0.000 seconds)
MixedIntegerRounding2 was tried 0 times and created 0 cuts of which 0 were active after adding rounds of cuts (0.000 seconds)
FlowCover was tried 0 times and created 0 cuts of which 0 were active after adding rounds of cuts (0.000 seconds)
TwoMirCuts was tried 0 times and created 0 cuts of which 0 were active after adding rounds of cuts (0.000 seconds)
ZeroHalf was tried 0 times and created 0 cuts of which 0 were active after adding rounds of cuts (0.000 seconds)

Result - Optimal solution found

Objective value:                90.00000000
Enumerated nodes:               0
Total iterations:               0
Time (CPU seconds):             0.01
Time (Wallclock seconds):       0.01

Total time (CPU seconds):       0.02   (Wallclock seconds):       0.01

{0,3,1,0}
In [6]:
!cat balanced-diet/balanced-diet.pi

/***********************************************************
  from Constraint Solving and Planning with Picat, Springer 
  by Neng-Fa Zhou, Hakan Kjellerstrand, and Jonathan Fruhman 
***********************************************************/
import mip.

main =>
  data(Prices,Limits,Nutrients),
  Len = length(Prices),
  Xs = new_array(Len),
  Xs :: 0..10,
  foreach (I in 1..Nutrients.length)
    scalar_product(Nutrients[I],Xs,#>=,Limits[I])
  end,
  scalar_product(Prices,Xs,XSum),
  solve($[min(XSum)],Xs),
  writeln(Xs).

% plain scalar product
scalar_product(A,Xs,Product) => 
  Product #= sum([A[I]*Xs[I] : I in 1..A.length]).

scalar_product(A,Xs,Rel,Product) => 
  scalar_product(A,Xs,P),
  call(Rel,P,Product).

data(Prices,Limits,Nutrition) =>
  % prices in cents for each product
  Prices = {50,20,30,80},
  % required amount for each nutrition type 
  Limits = {500,6,10,8},  

  % nutrition for each product
  Nutrition = 
    {{400,200,150,500},  % calories
     {  3,  2,  0,  0},  % chocolate
     {  2,  2,  4,  4},  % sugar
     {  2,  4,  1,  5}}. % fat

Exercises¶

Exercise: Coins grid¶

Place coins on a $31\times 31$ board such that each row and each column contain exactly 14 coins, minimize the sum of quadratic horizontal distances of all coins from the main diagonal. (Source: Tony Hurlimann, "A coin puzzle - SVOR-contest 2007")

Exercise: Sudoku¶

A traditional constraint satisfaction example: solve an $n\times n$ sudoku puzzle. Try the following simple instance (from the book):

Instance = {
    {4, _,  _, _},
    {_, 1,  _, _},
    {_, _,  _, 1},
    {_, _,  _, 2}
}.

Exercise: Minesweeper¶

Identify the positions of all mines in a given board. Try the following instance (from the book:

Instance = {
    {_,_,2,_,3,_},
    {2,_,_,_,_,_},
    {_,_,2,4,_,3},
    {1,_,3,4,_,_},
    {_,_,_,_,_,3},
    {_,3,_,3,_,_}
}.

Exercise: Magic square¶

Arrange numbers $1,2,\dots,n^2$ in a square such that every row, every column, and the two main diagonals all sum to the same quantity. How many magic squares are there for a given $n$? Allow also for a partially filled instance.

Exercise: Graph-coloring¶

  1. Write a program that solves the (directed) graph 3-coloring problem with a given number of colors and a given graph. The graph is given by a list of edges, each edge is a 2-element array. We assume that vertices of the graph are $1,\dots,n$ where $n$ is the maximum number appearing in the list.
  2. Generalize your program to graph $k$-coloring where $k$ is a positive integer given on the input.
  3. Modify your program to accept the incidence matrix (a 2D array) instead of the list of edges.
  4. Add the flag -n to output the minimum number of colors (the chromatic number) of a given graph. For example:
picat graph-coloring.pi "[{1,2},{2,3},{3,4},{4,1}]"
picat graph-coloring.pi "[{1,2},{2,3},{3,1}]" 4
picat graph-coloring.pi "{{0,1,1},{1,0,1},{1,1,0}}" 4
picat graph-coloring.pi -n "[{1,2},{2,3},{3,4},{4,1}]"