Imports

library(ggplot2)
library(dplyr)
library(tidyr)
source("../code/ebnm_bimodal.R")

Functions

Here are some helper function for simulation, fitting, and plotting.

sim = function(n0, n1, sigma_e){
  n = n0+n1
  beta = c(rep(0, n0), rep(1, n1))
  s = abs(rnorm(n, 0, sigma_e))
  betahat = rnorm(n, beta, s)
  
  return(list(betahat=betahat, s=s, beta=beta, n=n))
}


fit = function(betahat, s, beta){
  
  n = length(betahat)
  fit_res = ebnm_bimodal(betahat, s, list())
  betapm = fit_res$postmean
  df = data.frame(betahat=betahat, beta=beta, betapm=betapm, s=s, idx=1:n)  

  return(df)
}

plot_sim = function(df, title){
  
  gath_df = df %>% gather(variable, value, -idx, -s)
  p0 = ggplot(gath_df, aes(x=idx, y=value, 
                        color=factor(variable, levels=c("beta", "betahat", "betapm")))) + 
      geom_point() + 
      theme_bw() +
      labs(color="") +
      xlab("Variable") + 
      ylab("Value") +
      theme(legend.position="bottom")
  
  min_betahat = min(df$betahat)
  max_betahat = max(df$betahat)
  p1 = ggplot(df, aes(betahat, betapm, color=s)) + 
       geom_point() + viridis::scale_color_viridis() + 
       theme_bw() + 
       theme(legend.position="bottom") +
       xlim(c(min_betahat, max_betahat)) +
       ylim(c(min_betahat, max_betahat)) + 
       geom_abline() 

  p = cowplot::plot_grid(p0, p1, nrow=1) 
  title = cowplot::ggdraw() + cowplot::draw_label(title)
  print(cowplot::plot_grid(title, p, ncol=1, rel_heights=c(0.1, 1)))

}

Approach

The approach I took was to setup two grids:

1. A “positive” mixture of uniforms ash prior with mode 0 and grange from 0 to 1
2. A “negative” mixture of uniforms ash prior with mode 1 and grange from 0 to 1

I adapted code from ashr to extract the grids in ../code/ebnm_bimodal.R. Below is a sanity check that my helper function extracts the “correct” grids:

# simulate data
sim_res = sim(40, 40, .1)
betahat = sim_res$betahat
s = sim_res$s
data = ashr:::set_data(as.vector(betahat), as.vector(s), ashr:::add_etruncFUN(ashr::lik_normal()), 0)

# get grid for mode 0 (my helper function)
grid0 = get_bimodal_grid(data, 0, "+uniform")

# get grid for mode 0 (ashr)
res = ashr::ash(betahat, s, mixcompdist="+uniform", mode=0, grange=c(0, 1))
res$fitted_g$a == grid0$a

 [1] TRUE TRUE TRUE TRUE TRUE TRUE TRUE TRUE TRUE TRUE TRUE TRUE TRUE TRUE
[15] TRUE TRUE TRUE TRUE TRUE TRUE TRUE TRUE TRUE TRUE TRUE TRUE TRUE TRUE
[29] TRUE TRUE TRUE

res$fitted_g$b == grid0$b

 [1] TRUE TRUE TRUE TRUE TRUE TRUE TRUE TRUE TRUE TRUE TRUE TRUE TRUE TRUE
[15] TRUE TRUE TRUE TRUE TRUE TRUE TRUE TRUE TRUE TRUE TRUE TRUE TRUE TRUE
[29] TRUE TRUE TRUE

# get grid for mode 1 (my helper function)
grid1 = get_bimodal_grid(data, 1, "-uniform")

# get grid for mode 1 (ashr)
res = ashr::ash(betahat, s, mixcompdist="-uniform", mode=1, grange=c(0, 1))
res$fitted_g$a == grid1$a

 [1] TRUE TRUE TRUE TRUE TRUE TRUE TRUE TRUE TRUE TRUE TRUE TRUE TRUE TRUE
[15] TRUE TRUE TRUE TRUE TRUE TRUE TRUE TRUE TRUE TRUE TRUE TRUE TRUE TRUE
[29] TRUE TRUE TRUE

res$fitted_g$b == grid1$b

 [1] TRUE TRUE TRUE TRUE TRUE TRUE TRUE TRUE TRUE TRUE TRUE TRUE TRUE TRUE
[15] TRUE TRUE TRUE TRUE TRUE TRUE TRUE TRUE TRUE TRUE TRUE TRUE TRUE TRUE
[29] TRUE TRUE TRUE

It looks like the grids match the ashr implementation. I next wrote an additional helper function that estimates the prior \(g\) using the the grid of “intervals” defined above (see get_bimodal_g in ../code/ebnm_bimodal.R):

# setup bimodal grid
a = c(grid0$a, grid1$a)
b = c(grid0$b, grid1$b)

# estimate prior
ghat = get_bimodal_g(data, a, b)
idx_c = which(ghat$pi > 1e-5)
print(a[idx_c])

[1] 0.0000000 1.0000000 0.9724091

print(b[idx_c])

[1] 0 1 1

We can see for this example only a few components get weight i.e. those with mass close to 0 and 1. Finally given this \(g\) I wrote a ebnm function that computes the posterior with the fixed \(g\) (see ebnm_bimodal in ../code/ebnm_bimodal.R):

df = fit(betahat, s, sim_res$beta)
plot_sim(df, "")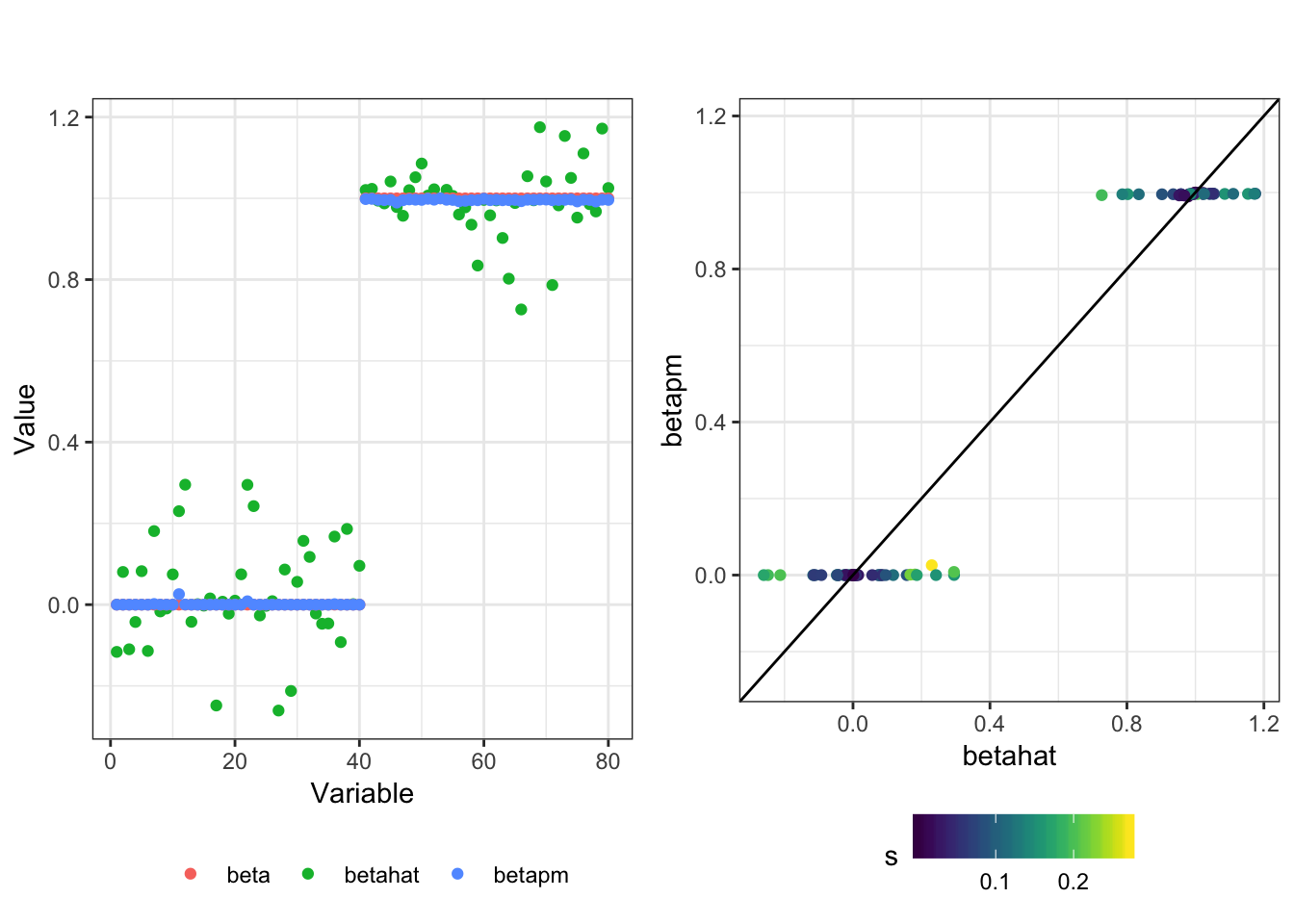

Pretty cool! Effects close to 0 are shrunk to 0 while effects close to 1 are shrunk to 1.

Simulations

Next I simulated a bunch of normal means scenarios where the true \(\beta\)s are set to 0 or 1. In each simulation I specify the number of zeros n0 the number of ones n1 and standard deviation used to simulate std. errors.

n0 = c(rep(40, 3), rep(25, 3), rep(10, 3), rep(0, 3))
n1 = c(rep(40, 3), rep(55, 3), rep(70, 3), rep(80, 3))
sigma_e = rep(c(.05, .1, .25), 4)

for(i in 1:length(n0)){
  sim_res = sim(n0[i], n1[i], sigma_e[i])
  betahat = sim_res$betahat
  s = sim_res$s
  beta = sim_res$beta
  df = fit(betahat, s, beta)
  title = paste0("n0=",n0[i], ",n1=", n1[i], ",sigma_e=", sigma_e[i])
  plot_sim(df, title)
}

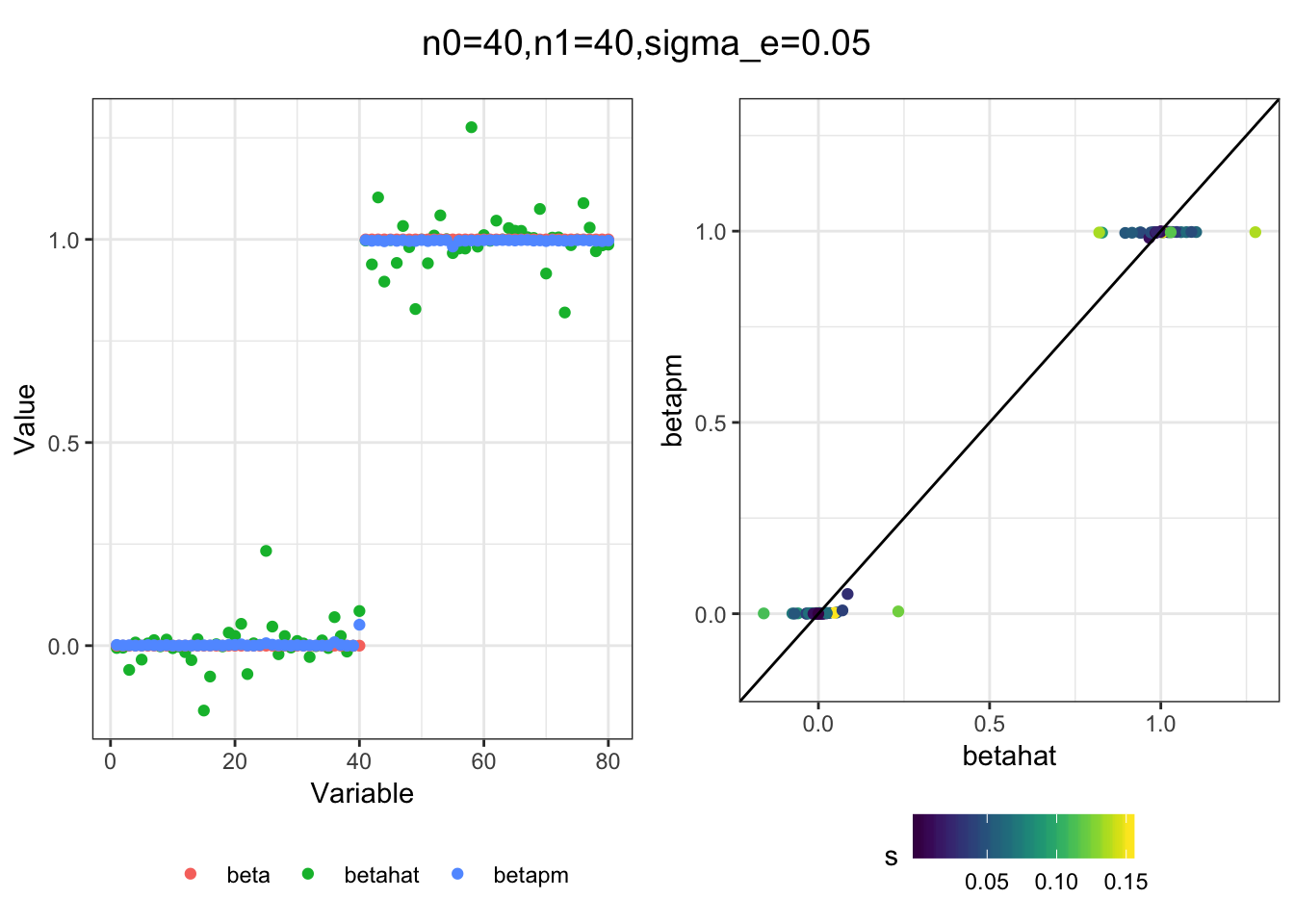
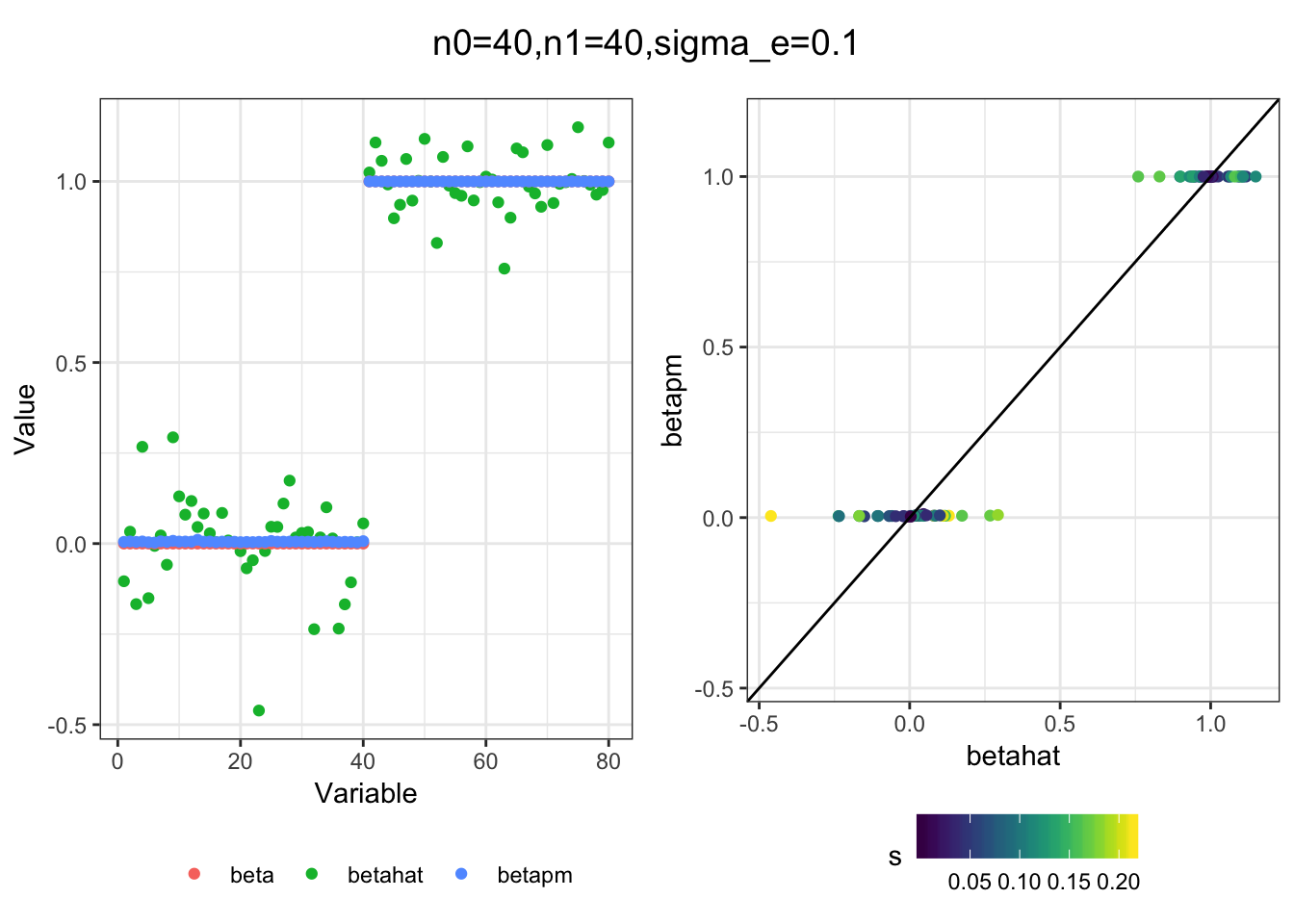
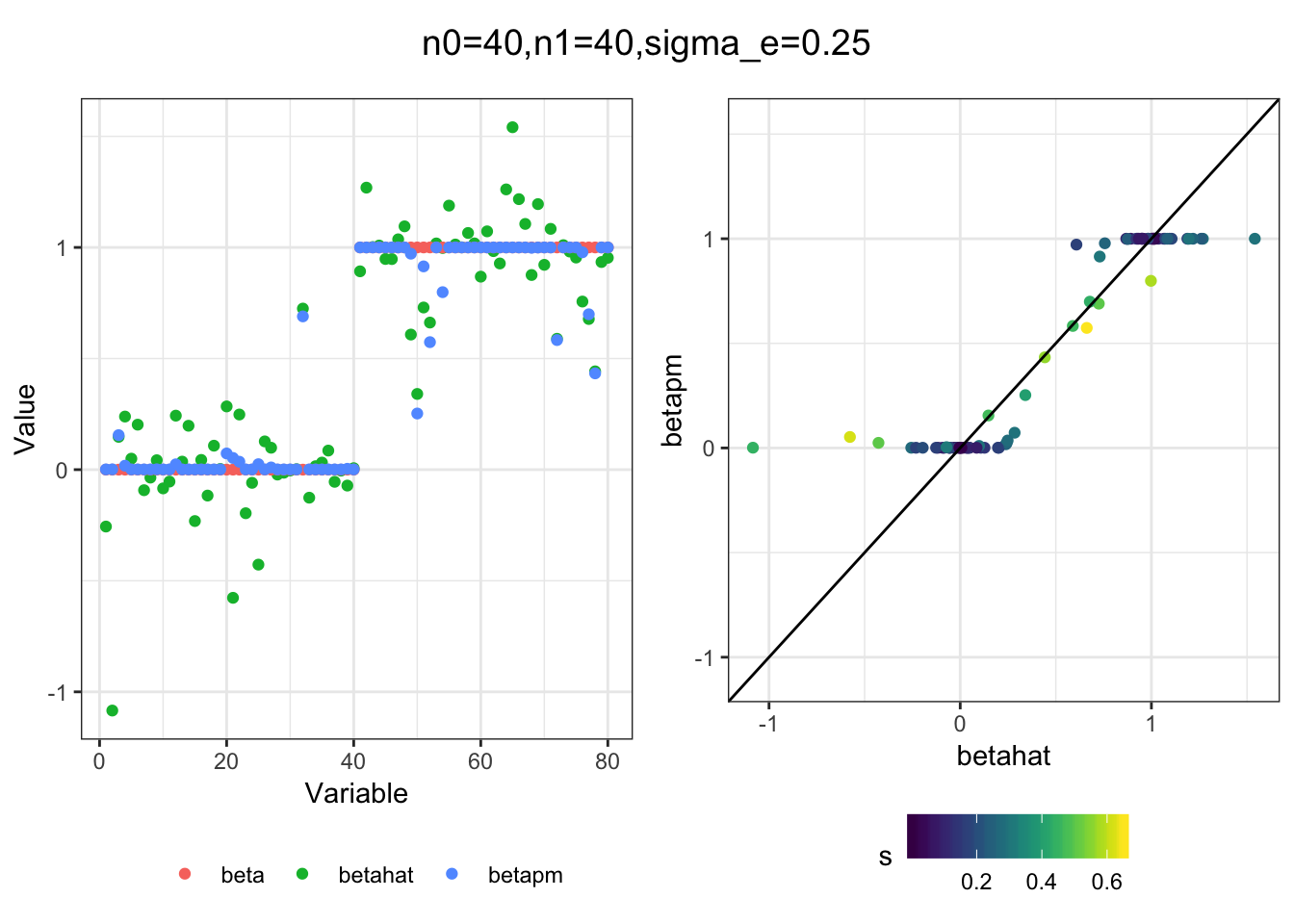
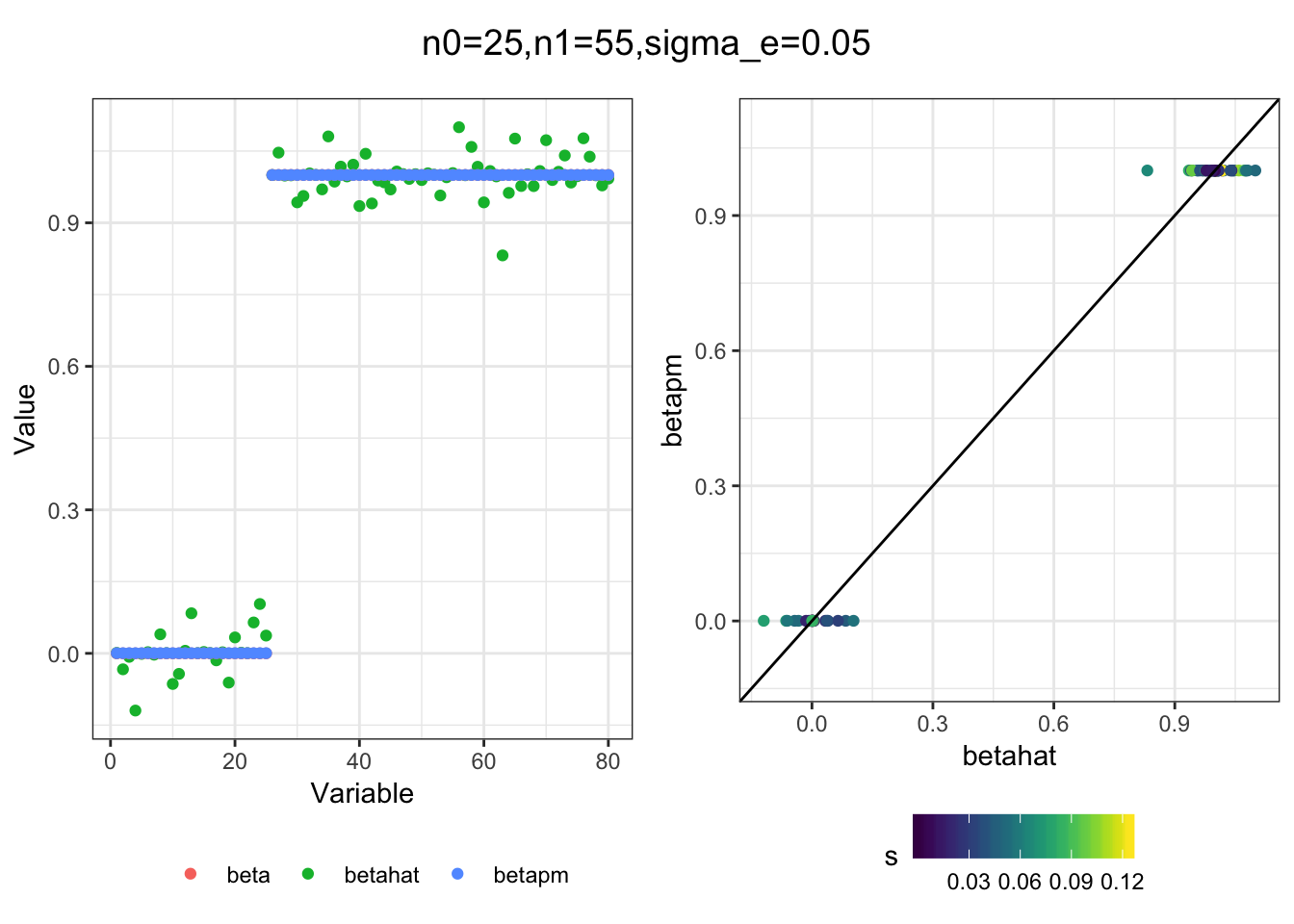
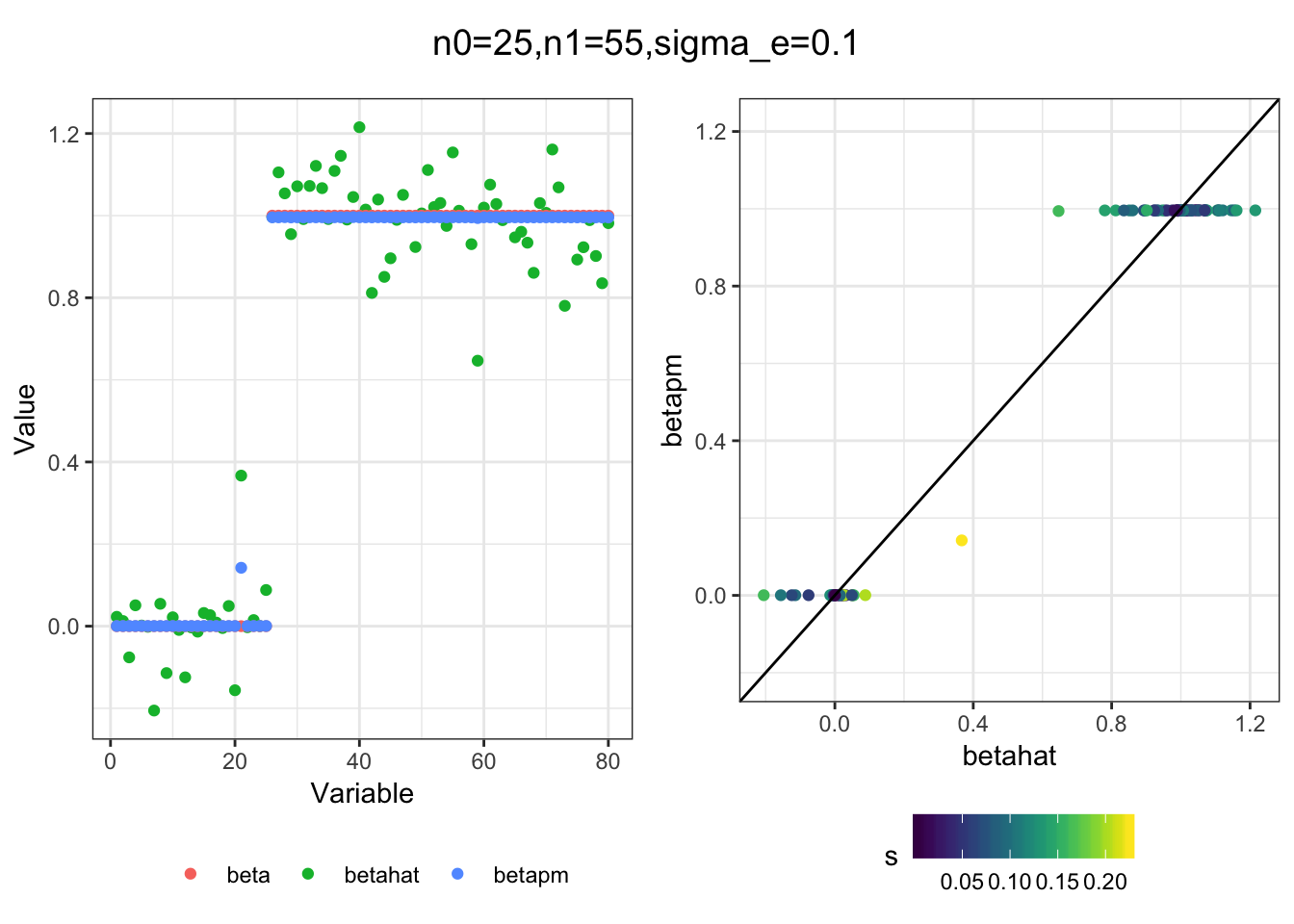
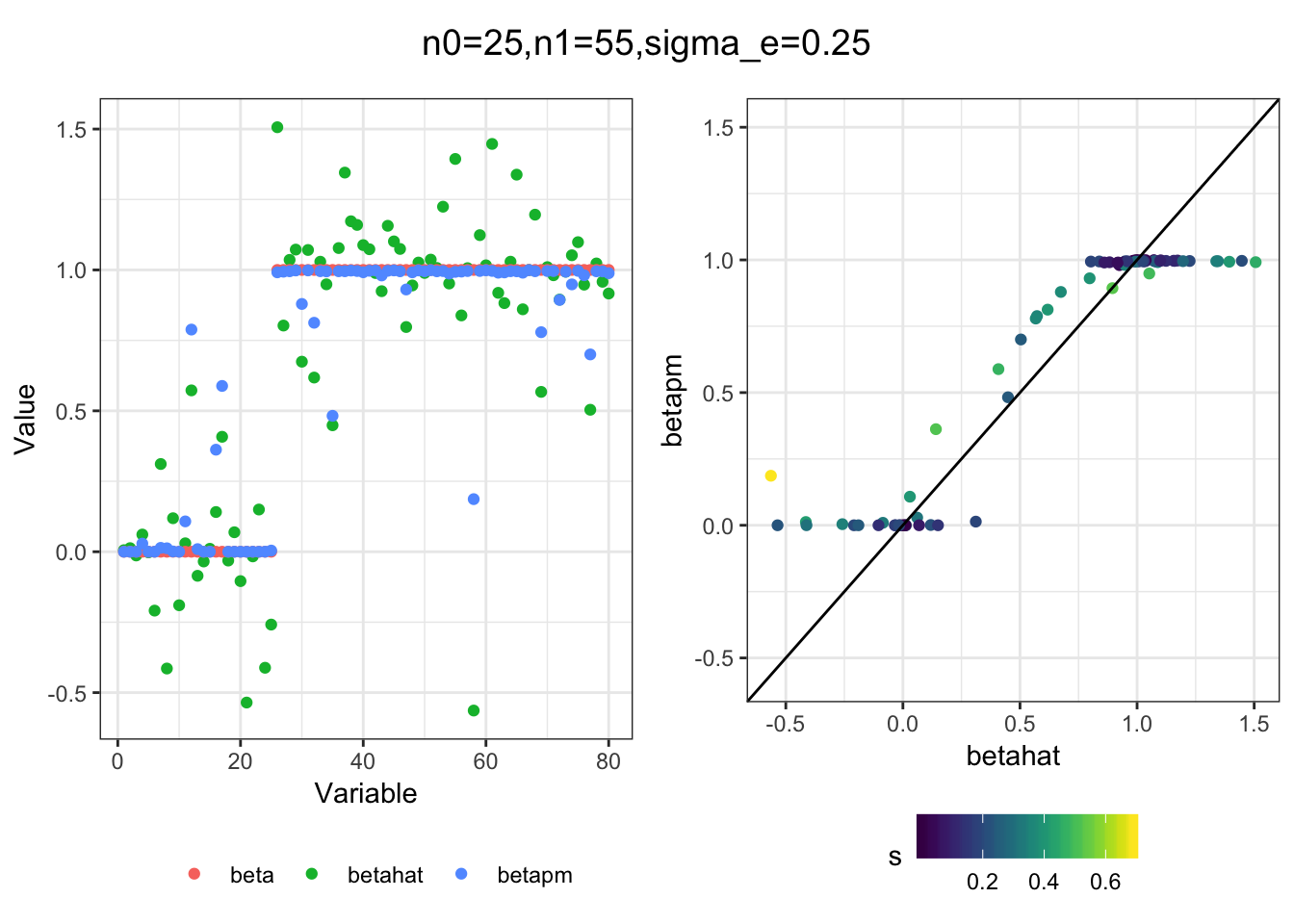
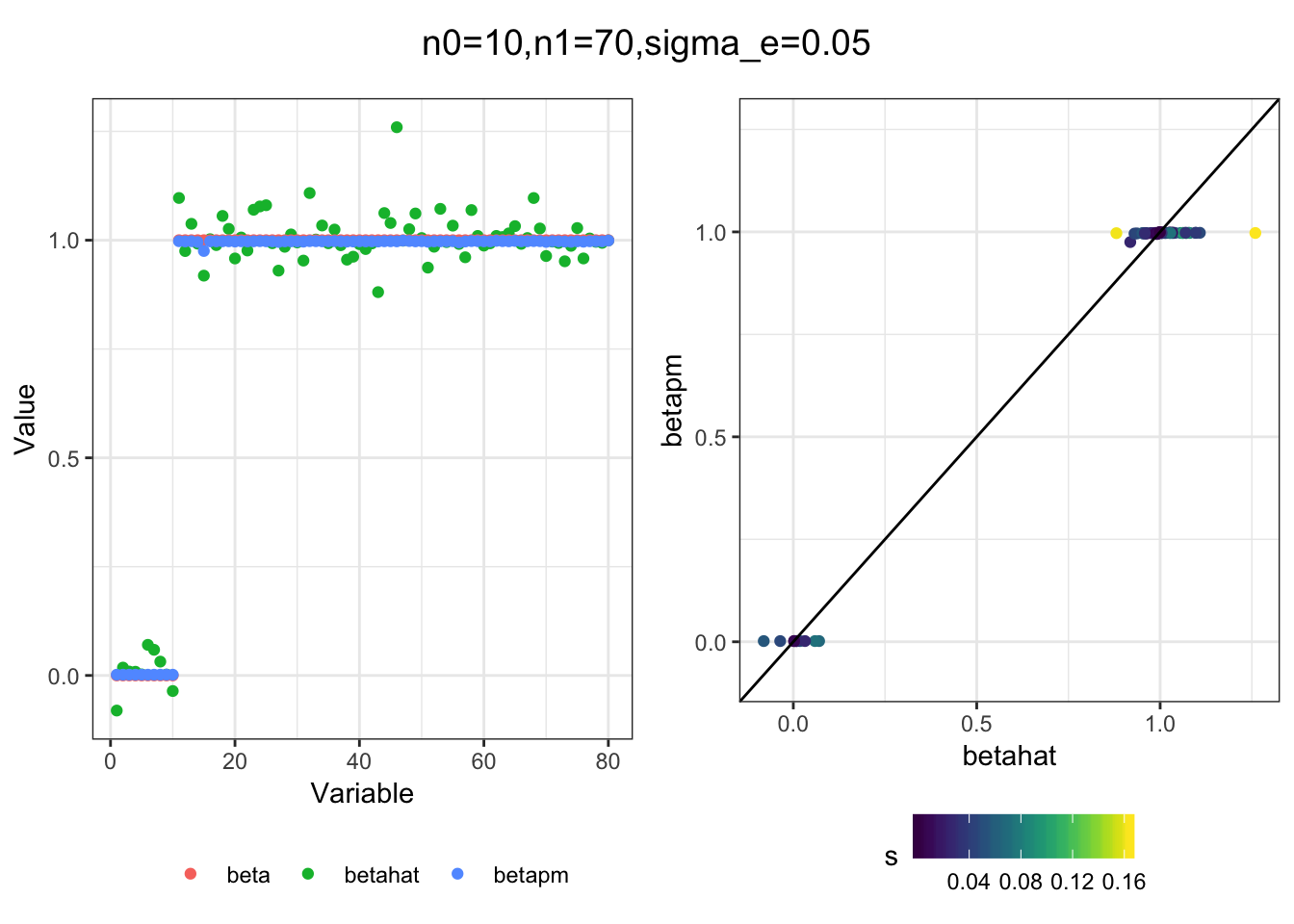
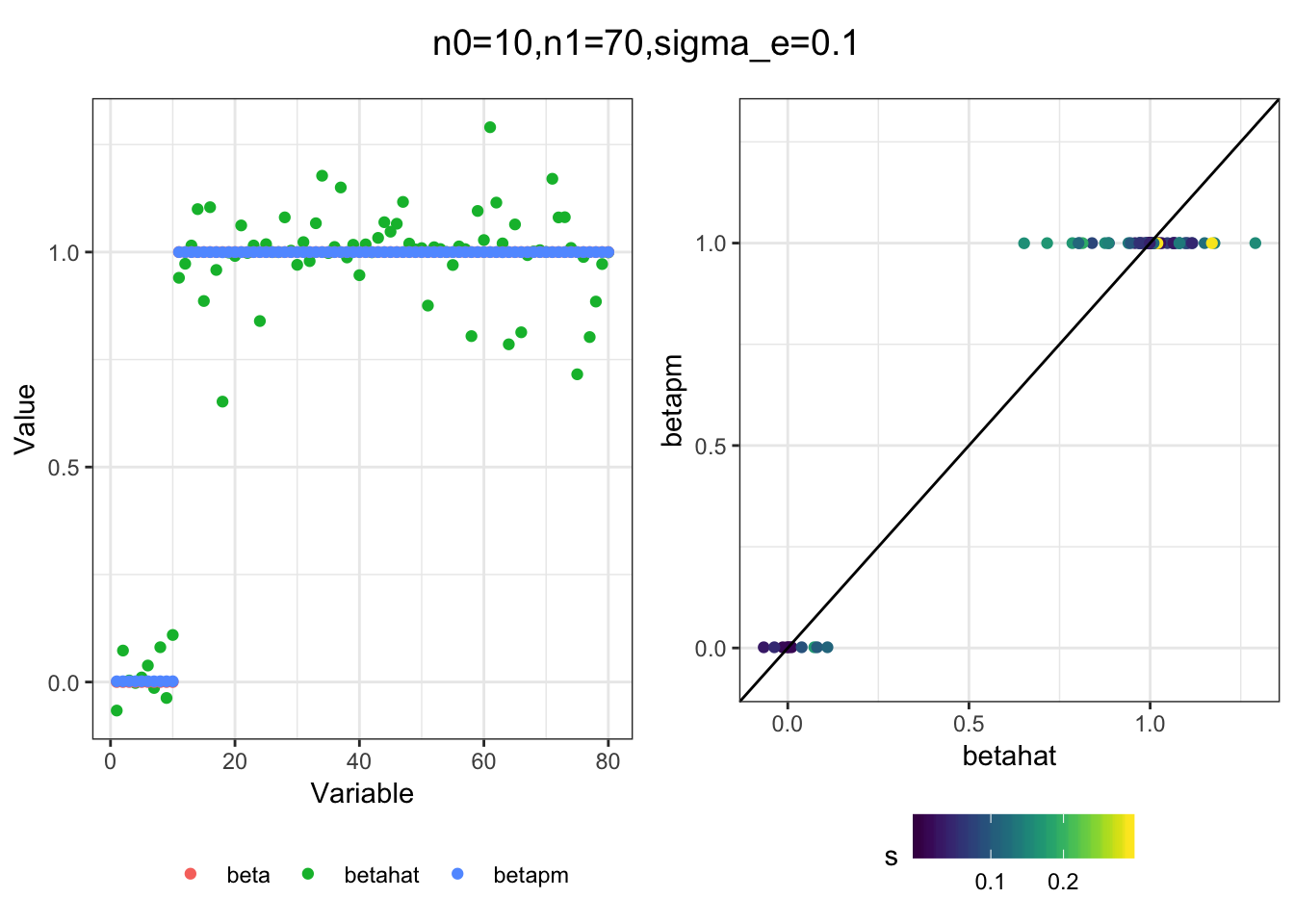
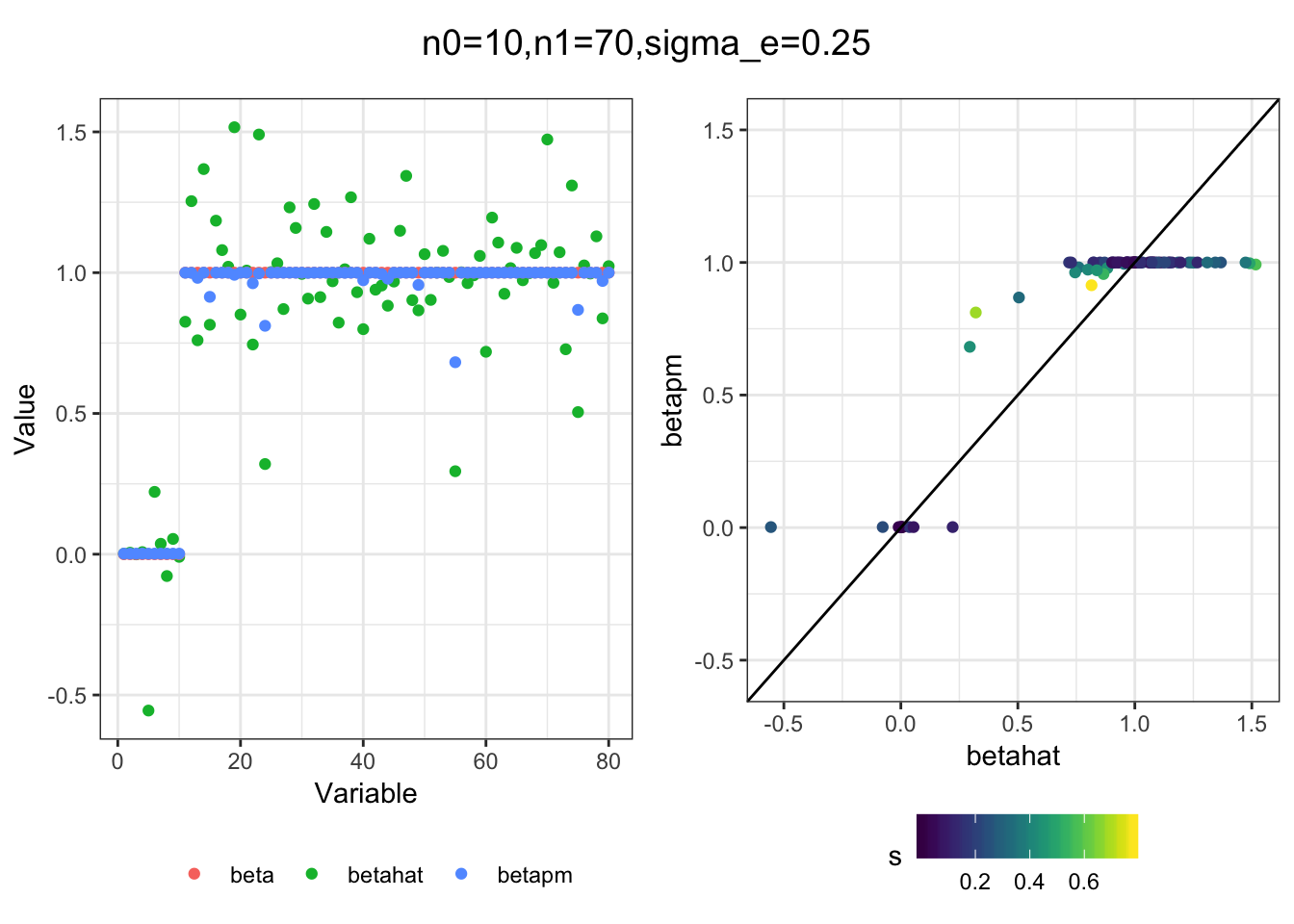
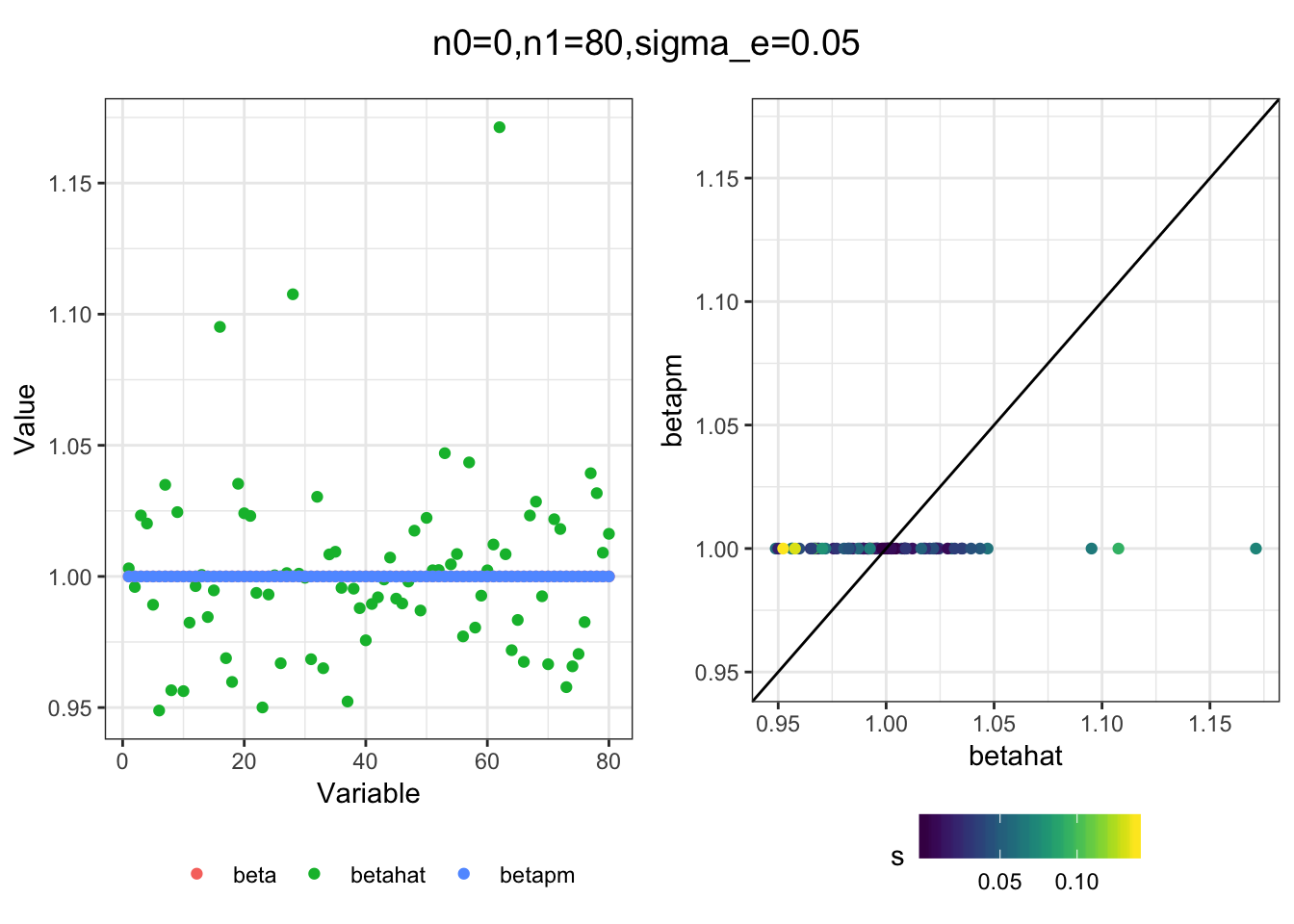
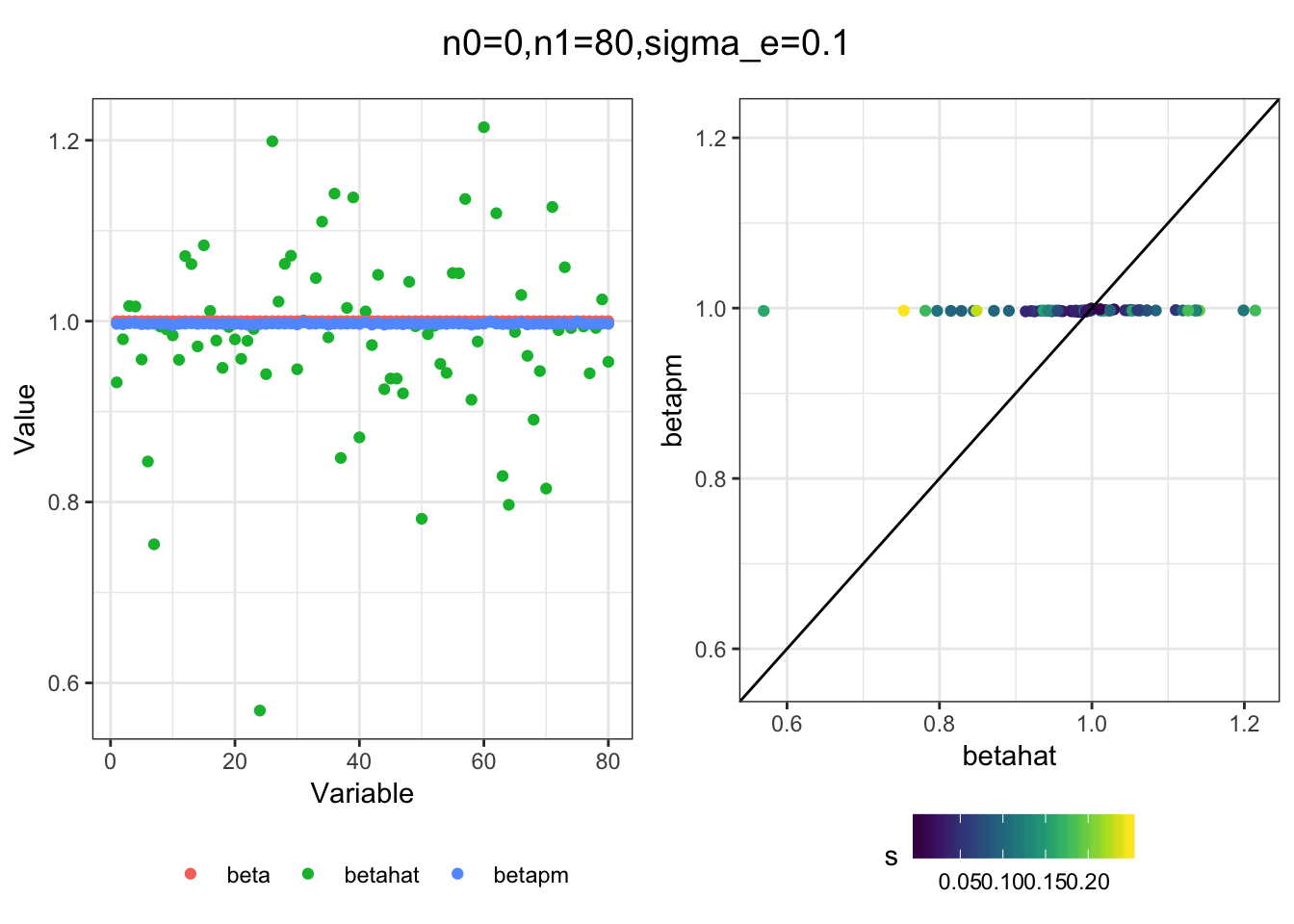
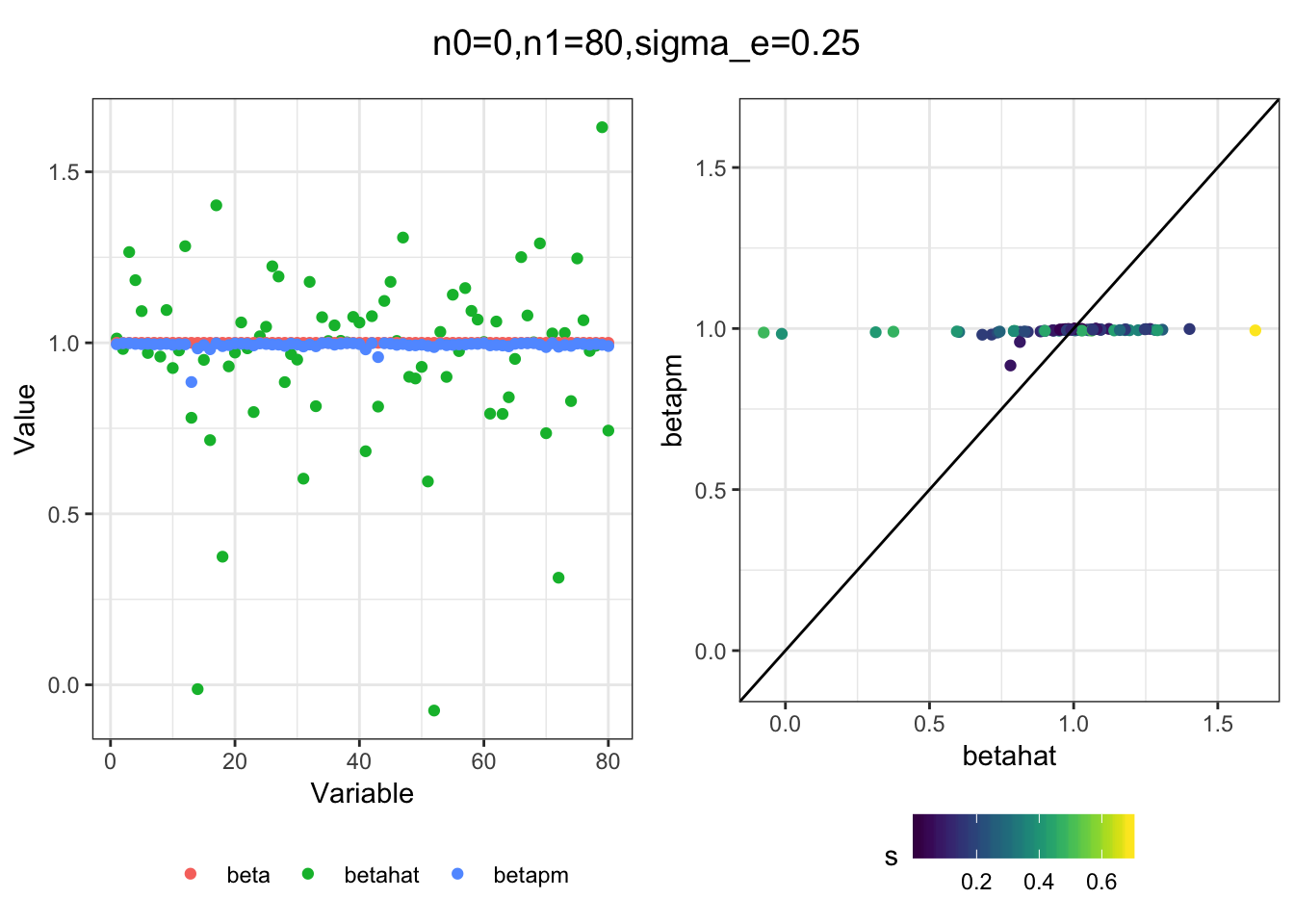
I think the idea roughly works! The most interesting scenarios to compare are when the std. errors of the estmates are high but the number of zeros and ones are different. Maybe we can define a term “bimodality” which I’m thinking is how bimodal the distribution is. When the bimodality is low (i.e. the prior distribution is closer to unimodal) the effects seem to be more correctly estimated. As we can see estimating more bimodal effects is a more difficult problem than unimodal effects.

Session information

sessionInfo()

R version 3.5.1 (2018-07-02)
Platform: x86_64-apple-darwin13.4.0 (64-bit)
Running under: macOS  10.14.2

Matrix products: default
BLAS/LAPACK: /Users/jhmarcus/miniconda3/lib/R/lib/libRblas.dylib

locale:
[1] en_US.UTF-8/en_US.UTF-8/en_US.UTF-8/C/en_US.UTF-8/en_US.UTF-8

attached base packages:
[1] stats     graphics  grDevices utils     datasets  methods   base     

other attached packages:
[1] tidyr_0.8.2   dplyr_0.8.0.1 ggplot2_3.1.0

loaded via a namespace (and not attached):
 [1] Rcpp_1.0.0        compiler_3.5.1    pillar_1.3.1     
 [4] git2r_0.23.0      plyr_1.8.4        workflowr_1.2.0  
 [7] viridis_0.5.1     iterators_1.0.10  tools_3.5.1      
[10] digest_0.6.18     viridisLite_0.3.0 evaluate_0.12    
[13] tibble_2.0.1      gtable_0.2.0      lattice_0.20-38  
[16] pkgconfig_2.0.2   rlang_0.3.1       foreach_1.4.4    
[19] Matrix_1.2-15     parallel_3.5.1    yaml_2.2.0       
[22] xfun_0.4          gridExtra_2.3     withr_2.1.2      
[25] stringr_1.4.0     knitr_1.21        fs_1.2.6         
[28] cowplot_0.9.4     rprojroot_1.3-2   grid_3.5.1       
[31] tidyselect_0.2.5  glue_1.3.0        R6_2.4.0         
[34] rmarkdown_1.11    mixsqp_0.1-115    purrr_0.3.0      
[37] ashr_2.2-37       magrittr_1.5      MASS_7.3-51.1    
[40] codetools_0.2-16  backports_1.1.3   scales_1.0.0     
[43] htmltools_0.3.6   assertthat_0.2.0  colorspace_1.4-0 
[46] labeling_0.3      stringi_1.2.4     pscl_1.5.2       
[49] doParallel_1.0.14 lazyeval_0.2.1    munsell_0.5.0    
[52] truncnorm_1.0-8   SQUAREM_2017.10-1 crayon_1.3.4