Human Origins Array Global Results

Last updated: 2019-02-24

workflowr checks: (Click a bullet for more information)

✔ R Markdown file: up-to-date

Great! Since the R Markdown file has been committed to the Git repository, you know the exact version of the code that produced these results.
✔ Environment: empty

Great job! The global environment was empty. Objects defined in the global environment can affect the analysis in your R Markdown file in unknown ways. For reproduciblity it’s best to always run the code in an empty environment.
✔ Seed: set.seed(20190211)

The command set.seed(20190211) was run prior to running the code in the R Markdown file. Setting a seed ensures that any results that rely on randomness, e.g. subsampling or permutations, are reproducible.
✔ Session information: recorded

Great job! Recording the operating system, R version, and package versions is critical for reproducibility.
✔ Repository version: 63e7173
Great! You are using Git for version control. Tracking code development and connecting the code version to the results is critical for reproducibility. The version displayed above was the version of the Git repository at the time these results were generated.

Note that you need to be careful to ensure that all relevant files for the analysis have been committed to Git prior to generating the results (you can use wflow_publish or wflow_git_commit). workflowr only checks the R Markdown file, but you know if there are other scripts or data files that it depends on. Below is the status of the Git repository when the results were generated:
```
Ignored files:
    Ignored:    .Rhistory
    Ignored:    analysis/.Rhistory
    Ignored:    output.tar.gz
    Ignored:    output/flash_backfit/
    Ignored:    output/flash_greedy/
    Ignored:    output/log/
    Ignored:    output/sim/
    Ignored:    output/softImpute/
```
Note that any generated files, e.g. HTML, png, CSS, etc., are not included in this status report because it is ok for generated content to have uncommitted changes.

Expand here to see past versions:

File	Version	Author	Date	Message
Rmd	63e7173	jhmarcus	2019-02-24	expanded upon mean variance
html	63e7173	jhmarcus	2019-02-24	expanded upon mean variance
Rmd	38b57c5	jhmarcus	2019-02-24	simplified greedy flash global analysis
html	38b57c5	jhmarcus	2019-02-24	simplified greedy flash global analysis
Rmd	403bc6b	jhmarcus	2019-02-15	added hide code blocks
html	403bc6b	jhmarcus	2019-02-15	added hide code blocks
Rmd	b4749ac	jhmarcus	2019-02-15	fixed some typos
html	b4749ac	jhmarcus	2019-02-15	fixed some typos
Rmd	7a2b6c7	jhmarcus	2019-02-15	added backfit
html	7a2b6c7	jhmarcus	2019-02-15	added backfit
Rmd	f5ef1af	jhmarcus	2019-02-15	added workflows for human origins datasets
html	f5ef1af	jhmarcus	2019-02-15	added workflows for human origins datasets
Rmd	4afc77e	jhmarcus	2019-02-15	init hoa global analysis

Imports

Lets import some needed packages:

library(ggplot2)
library(tidyr)
library(dplyr)
library(RColorBrewer)
source("../code/viz.R")

Human Origins Global (LD Pruned)

This is the full Human Origins dataset 2068 sampled from around the world. I filtered out rare variants with global minor allele frequency less than 5%, and remove any variants with a missingness level greater than 1%. I then LD pruned the SNPs using standard parameters in plink, resulting in 167178 SNPs.

Greedy

Lets first read the greedy flashier fit

flash_fit = readRDS("../output/flash_greedy/hoa_global_ld/HumanOriginsPublic2068_maf_geno_ldprune.rds")
K = ncol(flash_fit$loadings$normalized.loadings[[1]]) 
n = nrow(flash_fit$loadings$normalized.loadings[[1]])
p = nrow(flash_fit$loadings$normalized.loadings[[2]])
print(K)

[1] 21

print(n)

[1] 2068

print(p)

[1] 167178

Lets now plot the distribution of factors for each drift event

# read factors
delta_df = as.data.frame(flash_fit$loadings$normalized.loadings[[2]])
colnames(delta_df)[1:K] = 1:K 

# gather the data.frame for plotting
delta_gath_df = delta_df %>% 
                gather(K, value) %>%
                filter(K!=1)

# plot the factors
K_ = K
p_fct = ggplot(delta_gath_df, aes(x=value)) + 
        scale_fill_manual(values = getPalette(K_)) +
        geom_histogram() + 
        facet_wrap(~factor(K, levels=2:K_), scales = "free") + 
        labs(fill="K") + 
        scale_x_continuous(breaks = scales::pretty_breaks(n = 3)) +
        scale_y_continuous(breaks = scales::pretty_breaks(n = 3)) + 
        theme_bw()
p_fct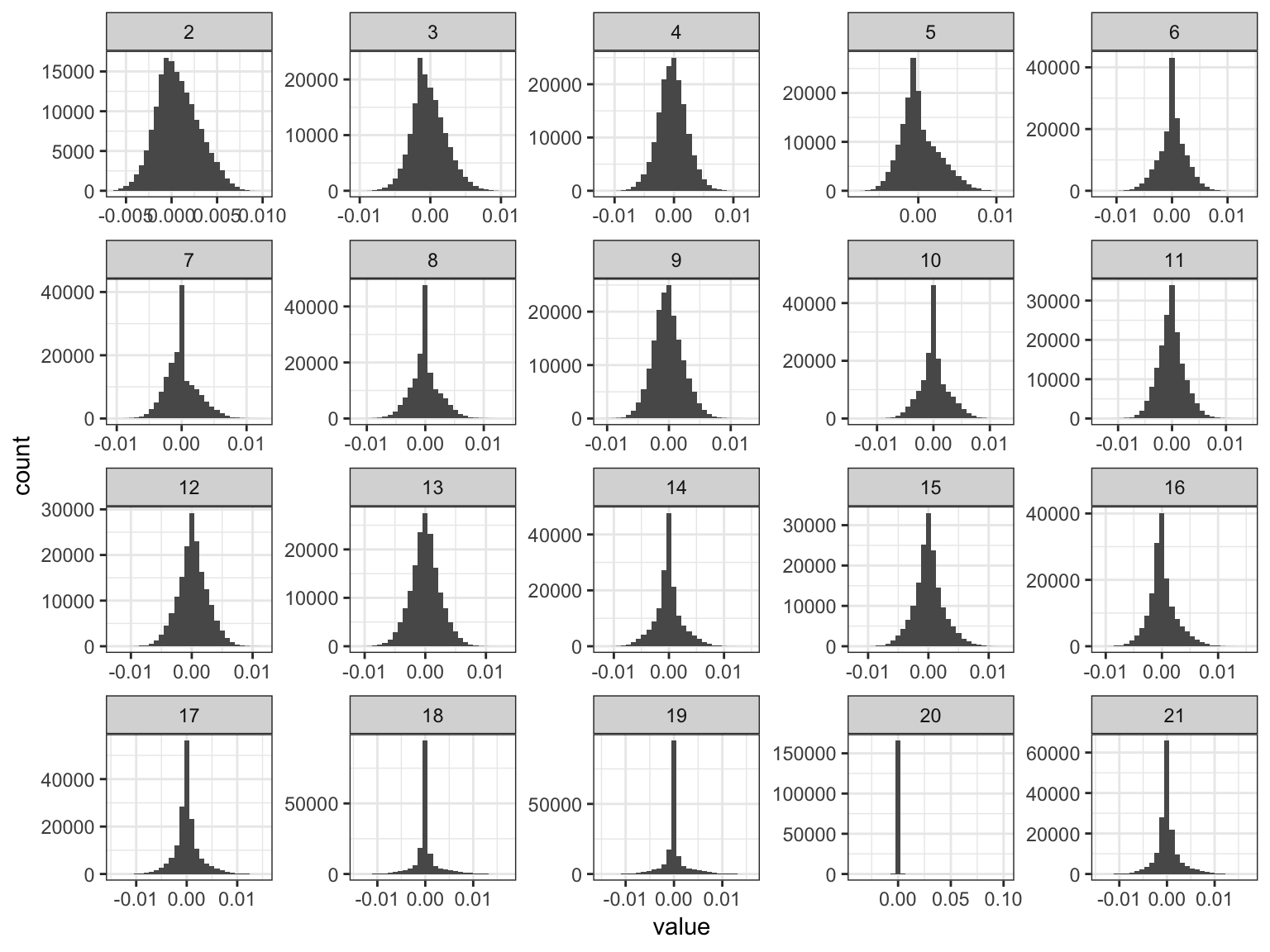

Expand here to see past versions of flash-greedy-ld-viz-factors-1.png:

Version	Author	Date
38b57c5	jhmarcus	2019-02-24
f5ef1af	jhmarcus	2019-02-15

We can see the later factors tend to get sparser but they still seem to contribute! Here is a plot of the “proportion of variance explained” of each factor:

qplot(2:K, flash_fit$pve[2:K]) + ylab("Proportion of Varaince Explained") + xlab("K") + theme_bw()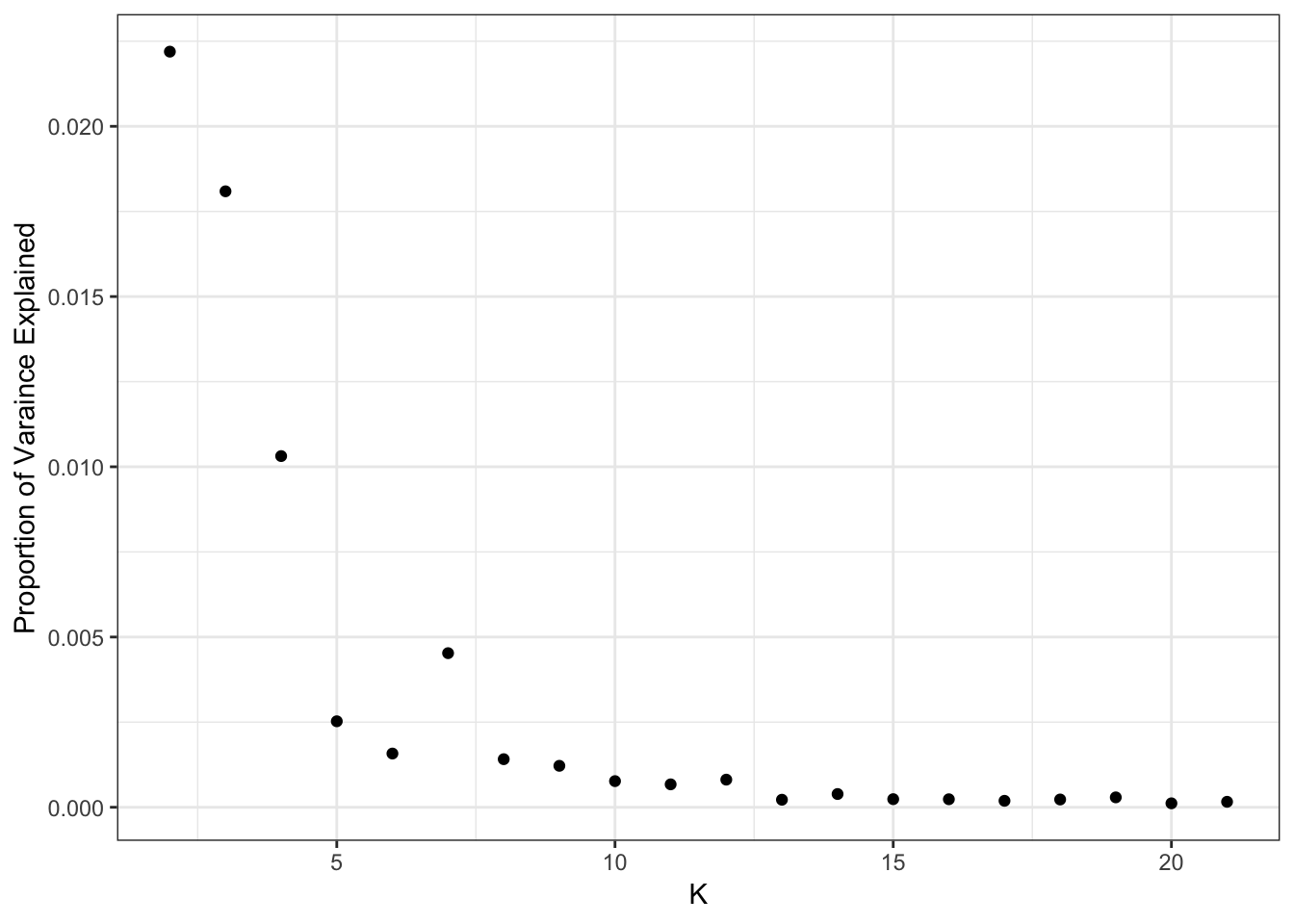

Expand here to see past versions of flash-greedy-ld-viz-pve-1.png:

Version	Author	Date
38b57c5	jhmarcus	2019-02-24

print(flash_fit$pve)

 [1] 0.4750002010 0.0221931227 0.0180913971 0.0103143286 0.0025255466
 [6] 0.0015774930 0.0045260494 0.0014121917 0.0012173854 0.0007676335
[11] 0.0006728921 0.0008111508 0.0002212648 0.0003887796 0.0002380212
[16] 0.0002352021 0.0001895606 0.0002282840 0.0002907459 0.0001156450
[21] 0.0001605612

It looks like the PVE drops off at around 11 or so? I setup the flashier run so it estimates a SNP specific precision term. Here is a histogram of fitted variances:

qplot(1/flash_fit$fit$est.tau) + xlab("Estimated Variance") + ylab("Count") + theme_bw()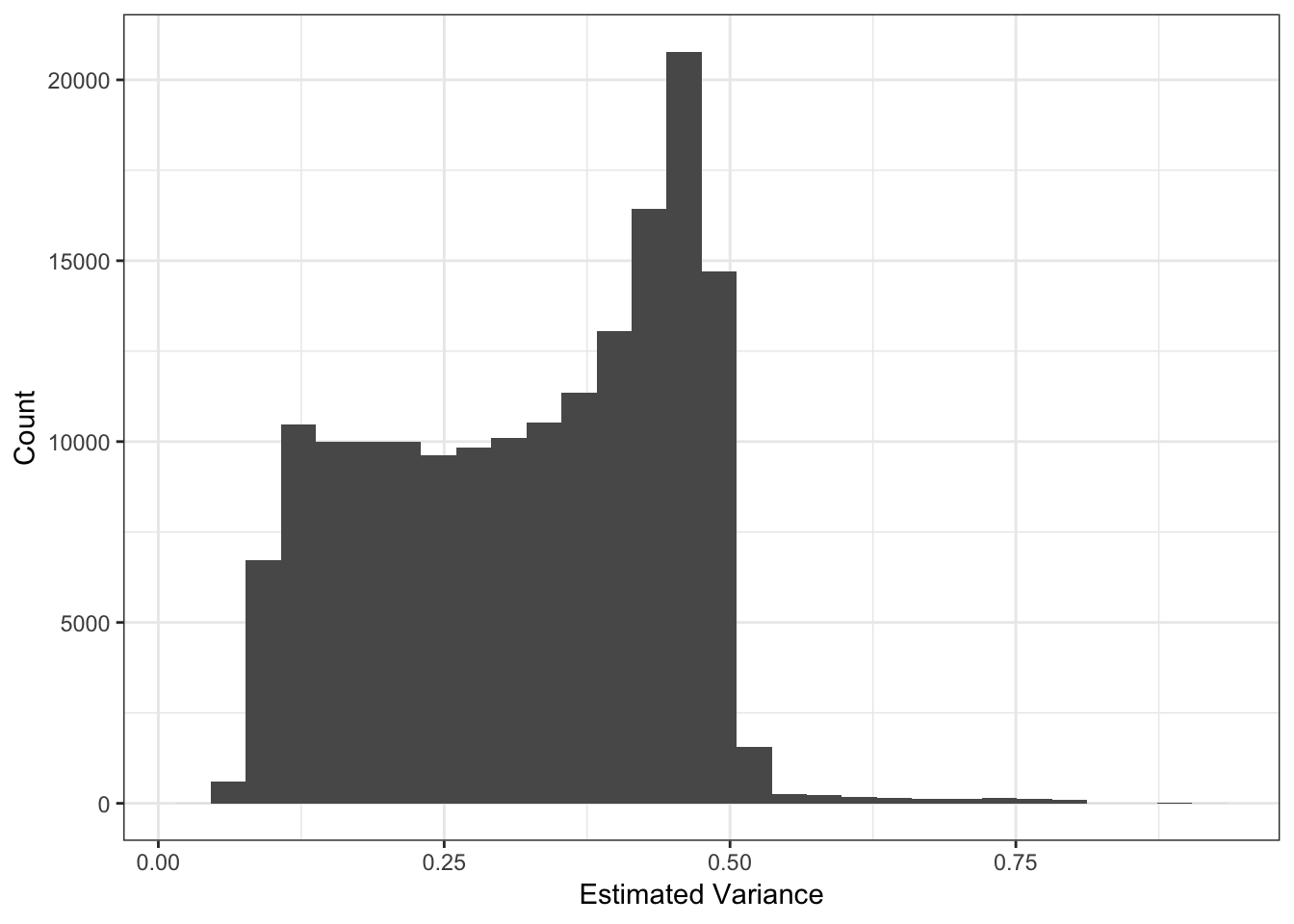

Expand here to see past versions of flash-greedy-ld-viz-var-1.png:

Version	Author	Date
38b57c5	jhmarcus	2019-02-24

Lets now look the the fitted means:

qplot(delta_df$`1`) + xlab("Estimated Mean") + ylab("Count") + theme_bw()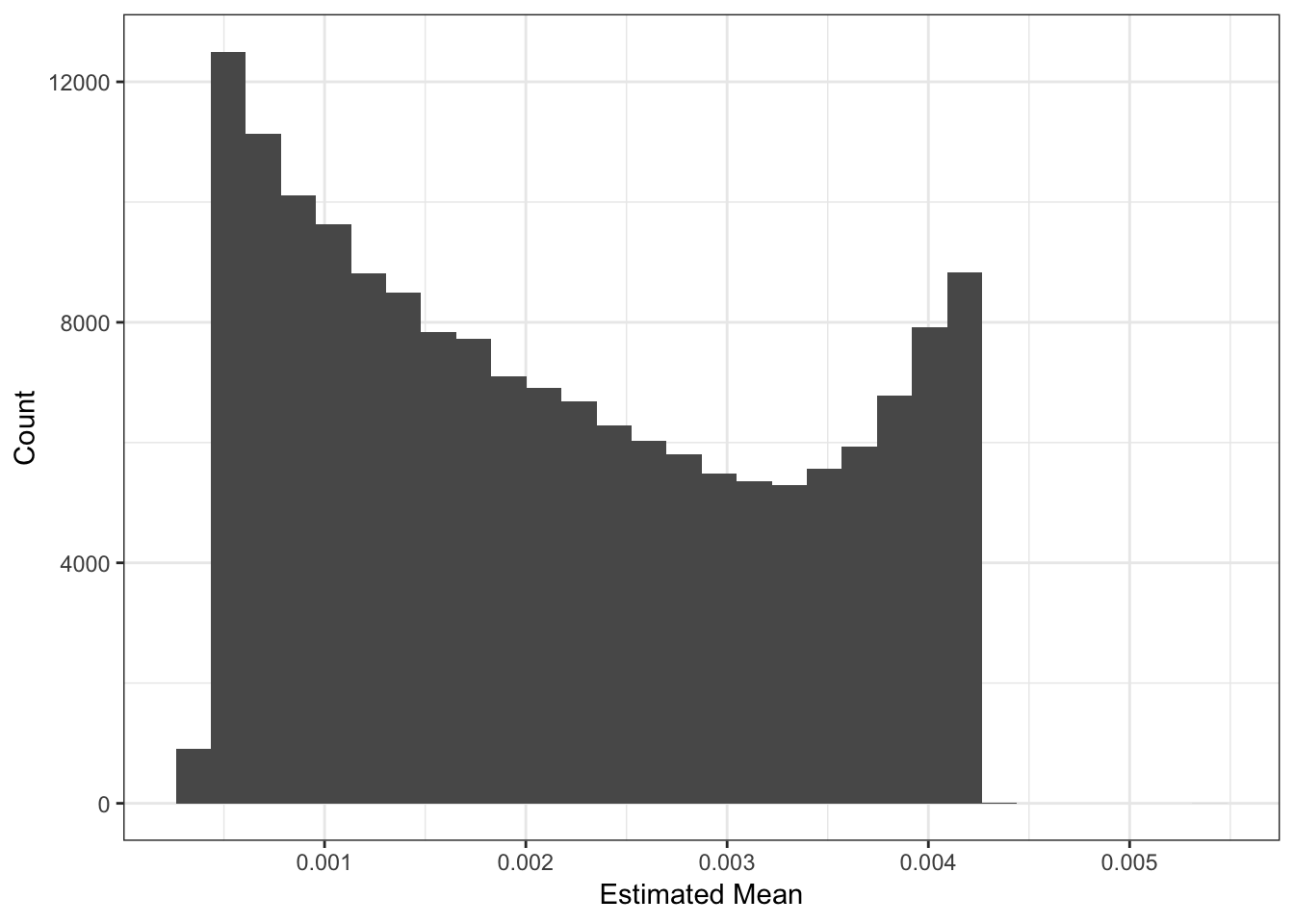

Expand here to see past versions of flash-greedy-ld-viz-mean-1.png:

Version	Author	Date
38b57c5	jhmarcus	2019-02-24

The mean seems smaller than I would have expected but thats probably because its normalized to have unit norm?! These plots looks about reasonable as each of the SNP variances should roughly be interpreted as average heterozygosity \(\approx 2p(1-p)\)? The mean term should roughly be interpreted as the mean minor allele frequency at the SNP and thus we should see a quadratic relationship with the estimated variance:

d1 = flash_fit$loadings$scale.constant[1]
p_mv = qplot(sqrt(d1) * delta_df$`1`, 1/flash_fit$fit$est.tau, alpha=.3) + 
       xlab("Rescaled Estimated Mean") + ylab("Estimated Variance") + 
       scale_alpha(guide = "none") + 
       stat_function(fun = function(x){return(2*x*(1-x))}, color="red") + 
       xlim(0, .5) + 
       theme_bw()
p_mv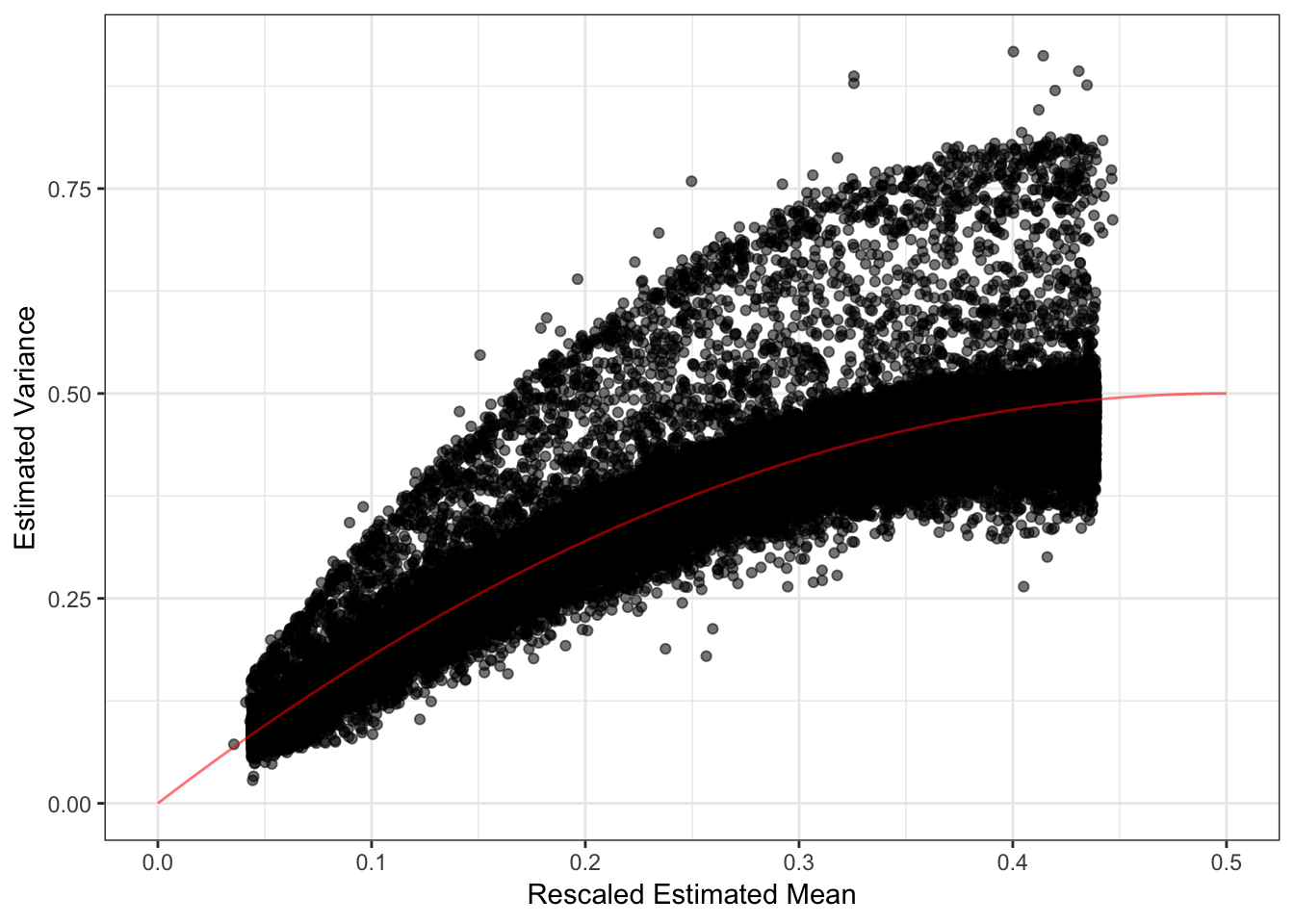

Expand here to see past versions of flash-greedy-ld-viz-mv-1.png:

Version	Author	Date
63e7173	jhmarcus	2019-02-24
38b57c5	jhmarcus	2019-02-24

I need to better understand the flashier output but it seems that when I scale the estimated mean by the square root of the output scale constant and plot this rescaled mean against the estimated variance, most of the SNPs have a mean-variance relationship expected under a simple Binomial model for the genotypes i.e. \(y_{ij} \sim Binomial(2, p_{ij})\). Though, there are indeed many SNPs that have a a much larger variance than expected under this simple “Hardy-Weinberg” model. I wonder if there is anything “special” going on with those SNPs (this is something to follow up on). Lets now take a look at the loadings. First we setup a data.frame that we can work with:

# read the meta data
meta_df = read.table("../data/meta/HumanOriginsPublic2068_maf_geno_ldprune.meta", sep=" ", header=T)

# setup loadings data.frame
l_df = as.data.frame(flash_fit$loadings$normalized.loadings[[1]])
K = ncol(l_df)
l_df$iid = as.vector(meta_df$iid) # individual ids
l_df$clst = meta_df$clst # population labels
pops = unique(l_df$clst) # all unique pop labels

# join with the meta data
l_df = l_df %>% inner_join(meta_df, on="clst")
l_df = l_df %>% arrange(region, clst) # sort by region then by population
l_df$iid = factor(l_df$iid, levels = l_df$iid) # make sure the ids are sorted
colnames(l_df)[1:K] = 1:K

head(l_df)

           1           2            3          4            5          6
1 0.02198997 0.009454832 4.485180e-06 0.02211841 3.303098e-05 0.01764253
2 0.02198997 0.009511229 4.406670e-06 0.02247997 4.952488e-05 0.01608845
3 0.02198997 0.006147078 4.086449e-06 0.02482062 2.726321e-05 0.01692735
4 0.02198997 0.009103984 4.338176e-06 0.02293795 2.797966e-05 0.01742585
5 0.02198997 0.009529573 4.394827e-06 0.02267025 3.845100e-05 0.01450389
6 0.02198997 0.009243629 4.460459e-06 0.02215776 2.795106e-05 0.01760249
            7            8            9           10           11
1 0.004374536 1.089539e-03 2.812993e-05 3.470028e-05 3.866924e-05
2 0.003241962 4.231122e-04 2.932860e-05 3.615817e-05 3.888100e-05
3 0.004951296 9.893482e-05 2.583221e-05 3.555401e-05 3.744459e-05
4 0.004661258 1.784788e-04 2.702595e-05 3.411185e-05 3.742829e-05
5 0.004437185 8.043608e-04 2.643633e-05 3.423255e-05 3.784264e-05
6 0.005064440 8.324509e-05 2.791866e-05 3.363985e-05 3.856931e-05
          12           13           14         15           16
1 0.05017069 8.140998e-05 4.952727e-05 0.08068407 7.771326e-05
2 0.04589132 8.638569e-05 5.161609e-05 0.05897009 7.994484e-05
3 0.05074213 8.358567e-05 5.114096e-05 0.08024062 7.892103e-05
4 0.05519966 7.798145e-05 4.992192e-05 0.09129734 8.299529e-05
5 0.05242051 7.961690e-05 4.865967e-05 0.09571542 8.121683e-05
6 0.05152888 8.057720e-05 5.030271e-05 0.07831456 7.913664e-05
            17           18           19           20           21
1 7.842225e-05 1.019054e-04 2.147227e-04 8.793061e-05 8.502300e-05
2 8.227041e-05 8.412758e-05 1.665734e-04 8.801740e-05 1.154576e-04
3 9.672675e-05 8.794415e-05 1.557965e-04 8.469595e-05 2.321882e-04
4 8.006631e-05 1.754711e-04 9.898022e-05 8.627449e-05 3.734673e-04
5 7.616521e-05 8.802899e-05 1.127468e-04 8.540387e-05 6.950001e-03
6 8.043370e-05 8.734172e-05 2.415143e-04 8.651963e-05 8.910156e-05
            iid     clst region country  lat lon    clst2
1 Algerian43A22 Algerian Africa Algeria 36.8   3 Algerian
2 Algerian43A21 Algerian Africa Algeria 36.8   3 Algerian
3 Algerian43A34 Algerian Africa Algeria 36.8   3 Algerian
4 Algerian43A13 Algerian Africa Algeria 36.8   3 Algerian
5 Algerian43A24 Algerian Africa Algeria 36.8   3 Algerian
6 Algerian43A32 Algerian Africa Algeria 36.8   3 Algerian

Its hard to find a color scale that can sufficiently visualize all of the loadings in a single plot. Instead I just split the loadings up into two plots (K=2,…,11) and (K=12,…,21). Lets first visualize loadings 2 through 12:

# gather the data.frame for plotting
l_gath_df = l_df %>% 
            gather(K, value, -iid, -clst, -region, -country, -lat, -lon, -clst2) %>% 
            filter(K %in% paste0(2:11))

# Africa
africa_pops = get_pops(meta_df, "Africa")
p_africa = positive_structure_plot(l_gath_df %>% filter(region == "Africa"), 
                                   africa_pops, colset="Set3", label_size=5) +
           ggtitle("Africa") + theme(plot.title = element_text(size=6))

# America
america_pops = get_pops(meta_df, "America")
p_america = positive_structure_plot(l_gath_df %>% filter(region == "America"), 
                                    america_pops, colset="Set3", label_size=5) + 
            ggtitle("America") + theme(plot.title = element_text(size=6))

# Central Asia Siberia
central_asia_siberia_pops = get_pops(meta_df, "CentralAsiaSiberia")
p_central_asia_siberia = positive_structure_plot(l_gath_df %>% filter(region == "CentralAsiaSiberia"), 
                                                 central_asia_siberia_pops, colset="Set3", label_size=5) + 
                         ggtitle("CentralAsiaSiberia") + theme(plot.title = element_text(size=6))

# East Asia
east_asia_pops = get_pops(meta_df, "EastAsia")
p_east_asia = positive_structure_plot(l_gath_df %>% filter(region == "EastAsia"), 
                                      east_asia_pops, colset="Set3", label_size=5) + 
              ggtitle("EastAsia") + theme(plot.title = element_text(size=6))

# South Asia
south_asia_pops = get_pops(meta_df, "SouthAsia")
p_south_asia= positive_structure_plot(l_gath_df %>% filter(region == "SouthAsia"),
                                      south_asia_pops, colset="Set3", label_size=5) + 
              ggtitle("SouthAsia") + theme(plot.title = element_text(size=6))

# West Eurasia
west_eurasia_pops = get_pops(meta_df, "WestEurasia")
p_west_eurasia = positive_structure_plot(l_gath_df %>% filter(region == "WestEurasia"), 
                                         west_eurasia_pops, colset="Set3", label_size=5) + 
                 ggtitle("WestEurasia") + theme(plot.title = element_text(size=6))

# Oceania
oceania_pops = get_pops(meta_df, "Oceania")
p_oceania = positive_structure_plot(l_gath_df %>% filter(region == "Oceania"), 
                                    oceania_pops, colset="Set3", label_size=5) + 
            ggtitle("Oceania") + theme(plot.title = element_text(size=6))

# Global
p = cowplot::plot_grid(p_africa, p_west_eurasia, p_central_asia_siberia, p_america, p_east_asia, p_south_asia, p_oceania, 
                       rel_heights = c(1.2, 1.3, 1, 1, 1, 1, 1.1),
                       nrow = 7, align = "v") 
p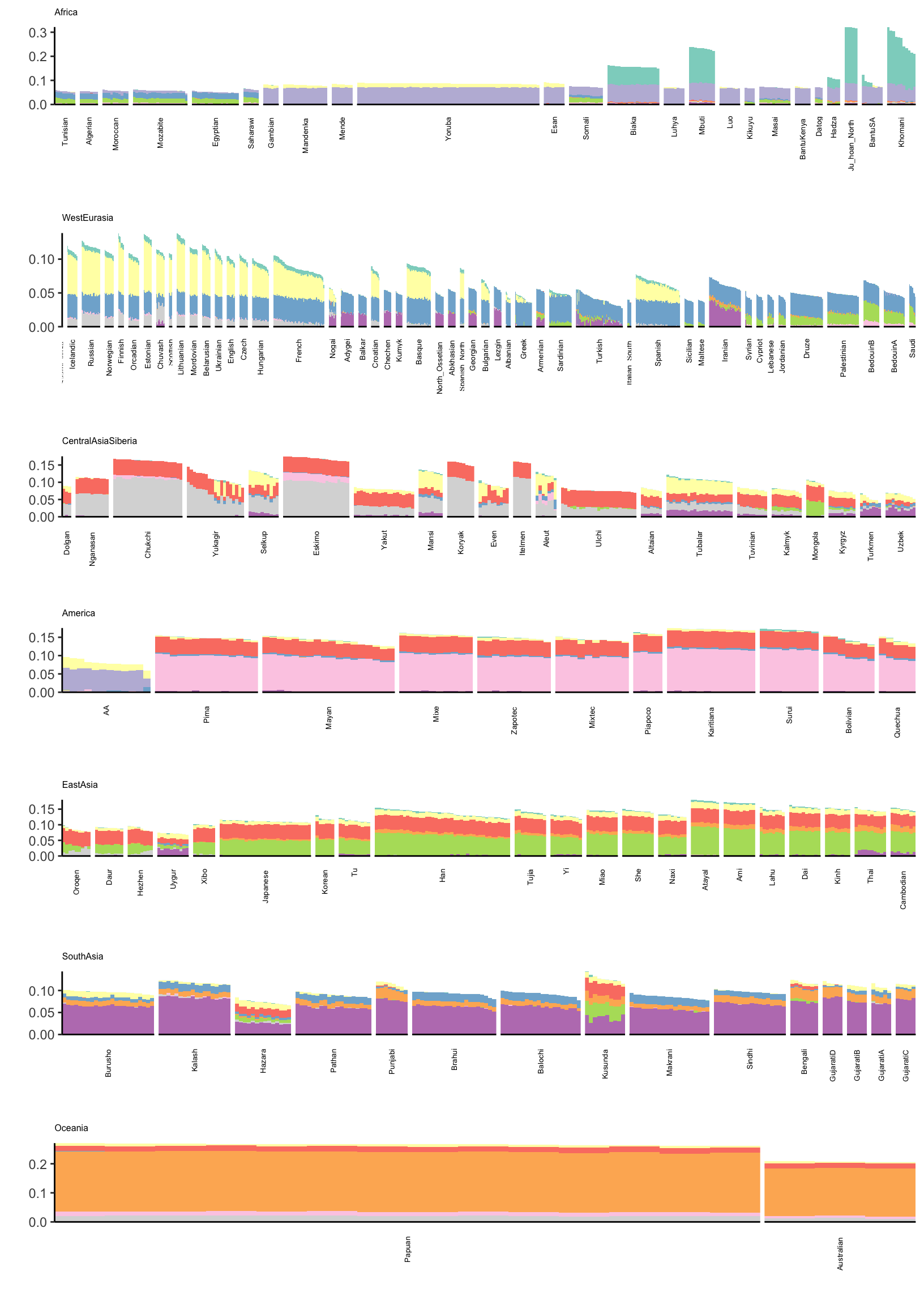

Expand here to see past versions of flash-greedy-ld-viz-loadings-2-11-1.png:

Version	Author	Date
38b57c5	jhmarcus	2019-02-24

Lets now visualize loadings 12 to 21 (be careful: there is no connection to the colors in the last plot):

# gather the data.frame for plotting
l_gath_df = l_df %>% 
            gather(K, value, -iid, -clst, -region, -country, -lat, -lon, -clst2) %>% 
            filter(K %in% paste0(12:21))

# Africa
africa_pops = get_pops(meta_df, "Africa")
p_africa = positive_structure_plot(l_gath_df %>% filter(region == "Africa"), 
                                   africa_pops, colset="Set3", label_size=5) +
           ggtitle("Africa") + theme(plot.title = element_text(size=6))

# America
america_pops = get_pops(meta_df, "America")
p_america = positive_structure_plot(l_gath_df %>% filter(region == "America"), 
                                    america_pops, colset="Set3", label_size=5) + 
            ggtitle("America") + theme(plot.title = element_text(size=6))

# Central Asia Siberia
central_asia_siberia_pops = get_pops(meta_df, "CentralAsiaSiberia")
p_central_asia_siberia = positive_structure_plot(l_gath_df %>% filter(region == "CentralAsiaSiberia"), 
                                                 central_asia_siberia_pops, colset="Set3", label_size=5) + 
                         ggtitle("CentralAsiaSiberia") + theme(plot.title = element_text(size=6))

# East Asia
east_asia_pops = get_pops(meta_df, "EastAsia")
p_east_asia = positive_structure_plot(l_gath_df %>% filter(region == "EastAsia"), 
                                      east_asia_pops, colset="Set3", label_size=5) + 
              ggtitle("EastAsia") + theme(plot.title = element_text(size=6))

# South Asia
south_asia_pops = get_pops(meta_df, "SouthAsia")
p_south_asia= positive_structure_plot(l_gath_df %>% filter(region == "SouthAsia"),
                                      south_asia_pops, colset="Set3", label_size=5) + 
              ggtitle("SouthAsia") + theme(plot.title = element_text(size=6))

# West Eurasia
west_eurasia_pops = get_pops(meta_df, "WestEurasia")
p_west_eurasia = positive_structure_plot(l_gath_df %>% filter(region == "WestEurasia"), 
                                         west_eurasia_pops, colset="Set3", label_size=5) + 
                 ggtitle("WestEurasia") + theme(plot.title = element_text(size=6))

# Oceania
oceania_pops = get_pops(meta_df, "Oceania")
p_oceania = positive_structure_plot(l_gath_df %>% filter(region == "Oceania"), 
                                    oceania_pops, colset="Set3", label_size=5) + 
            ggtitle("Oceania") + theme(plot.title = element_text(size=6))

# Global
p = cowplot::plot_grid(p_africa, p_west_eurasia, p_central_asia_siberia, p_america, p_east_asia, p_south_asia, p_oceania, 
                       rel_heights = c(1.2, 1.3, 1, 1, 1, 1, 1.1),
                       nrow = 7, align = "v") 
p

Expand here to see past versions of flash-greedy-ld-viz-loadings-12-21-1.png:

Version	Author	Date
38b57c5	jhmarcus	2019-02-24

Its kinda interesting to see that some populations have zero loading on later factors. This would be difficult to visualize see if using a single plot for all the factors.

ADMIXTURE

Lets visualize ADMIXTURE with 9 factors which should roughly align to the first plot i.e. FLASH with 2,…,11 (be careful: there is no connection to the colors in the last plot):

l_df = read.table("../output/admixture/hoa_global_ld/HumanOriginsPublic2068_maf_geno_ldprune.K9r1.Q", sep=" ", header=F)
K = ncol(l_df)

l_df$iid = as.vector(meta_df$iid) # individual ids
l_df$clst = meta_df$clst # population labels

# join with the meta data
l_df = l_df %>% inner_join(meta_df, on="clst")
l_df = l_df %>% arrange(region, clst) # sort by region then by population
l_df$iid = factor(l_df$iid, levels = l_df$iid) # make sure the ids are sorted
colnames(l_df)[1:K] = 1:K

# gather the data.frame for plotting
l_gath_df = l_df %>% 
            gather(K, value, -iid, -clst, -region, -country, -lat, -lon, -clst2)

# Africa
africa_pops = get_pops(meta_df, "Africa")
p_africa = positive_structure_plot(l_gath_df %>% filter(region == "Africa"), 
                                   africa_pops, colset="Set3", label_size=5) +
           ggtitle("Africa") + theme(plot.title = element_text(size=6))

# America
america_pops = get_pops(meta_df, "America")
p_america = positive_structure_plot(l_gath_df %>% filter(region == "America"), 
                                    america_pops, colset="Set3", label_size=5) + 
            ggtitle("America") + theme(plot.title = element_text(size=6))

# Central Asia Siberia
central_asia_siberia_pops = get_pops(meta_df, "CentralAsiaSiberia")
p_central_asia_siberia = positive_structure_plot(l_gath_df %>% filter(region == "CentralAsiaSiberia"), 
                                                 central_asia_siberia_pops, colset="Set3", label_size=5) + 
                         ggtitle("CentralAsiaSiberia") + theme(plot.title = element_text(size=6))

# East Asia
east_asia_pops = get_pops(meta_df, "EastAsia")
p_east_asia = positive_structure_plot(l_gath_df %>% filter(region == "EastAsia"), 
                                      east_asia_pops, colset="Set3", label_size=5) + 
              ggtitle("EastAsia") + theme(plot.title = element_text(size=6))

# South Asia
south_asia_pops = get_pops(meta_df, "SouthAsia")
p_south_asia= positive_structure_plot(l_gath_df %>% filter(region == "SouthAsia"),
                                      south_asia_pops, colset="Set3", label_size=5) + 
              ggtitle("SouthAsia") + theme(plot.title = element_text(size=6))

# West Eurasia
west_eurasia_pops = get_pops(meta_df, "WestEurasia")
p_west_eurasia = positive_structure_plot(l_gath_df %>% filter(region == "WestEurasia"), 
                                         west_eurasia_pops, colset="Set3", label_size=5) + 
                 ggtitle("WestEurasia") + theme(plot.title = element_text(size=6))

# Oceania
oceania_pops = get_pops(meta_df, "Oceania")
p_oceania = positive_structure_plot(l_gath_df %>% filter(region == "Oceania"), 
                                    oceania_pops, colset="Set3", label_size=5) + 
            ggtitle("Oceania") + theme(plot.title = element_text(size=6))

# Global
p = cowplot::plot_grid(p_africa, p_west_eurasia, p_central_asia_siberia, p_america, p_east_asia, p_south_asia, p_oceania, 
                       rel_heights = c(1.2, 1.3, 1, 1, 1, 1, 1.1),
                       nrow = 7, align = "v") 
p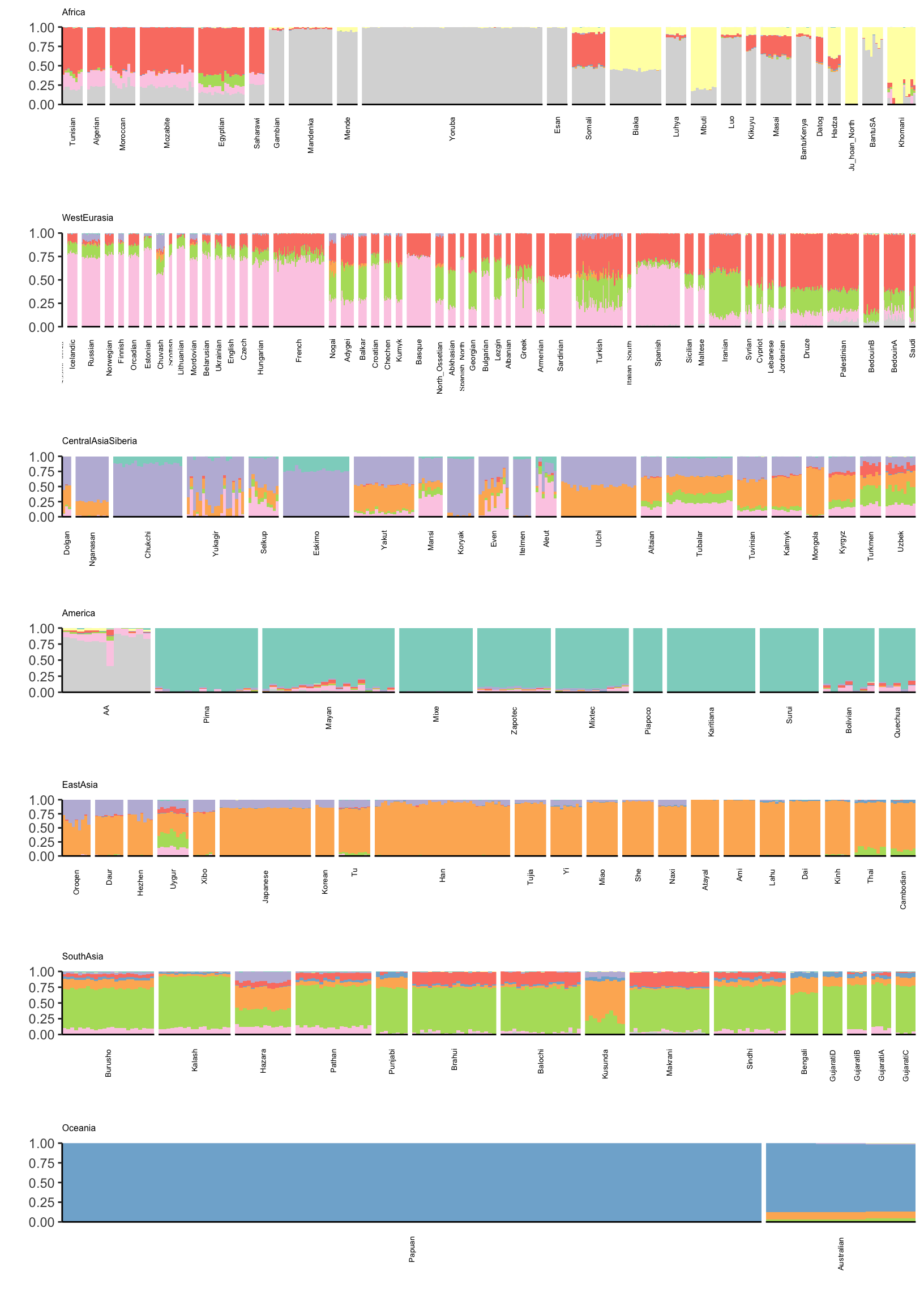

Expand here to see past versions of admixtrue-ld-viz-loadings-9-1.png:

Version	Author	Date
38b57c5	jhmarcus	2019-02-24

There is a lot that one can compare between the ADMIXTURE and FLASH results. A high level observation seems that the ADMIXTURE results look a bit more clustered i.e. the Americas and East Asia look like they are explained mostly by 1 or 2 factors whereas FLASH uses 3-4. Its hard to tell be it seems that this is true in many of the super regions … ADMIXTURE tends use fewer factors to explain population structure in each region, leading to a more clustered result?

Session information

sessionInfo()

R version 3.5.1 (2018-07-02)
Platform: x86_64-apple-darwin13.4.0 (64-bit)
Running under: macOS  10.14.2

Matrix products: default
BLAS/LAPACK: /Users/jhmarcus/miniconda3/lib/R/lib/libRblas.dylib

locale:
[1] en_US.UTF-8/en_US.UTF-8/en_US.UTF-8/C/en_US.UTF-8/en_US.UTF-8

attached base packages:
[1] stats     graphics  grDevices utils     datasets  methods   base     

other attached packages:
[1] bindrcpp_0.2.2     RColorBrewer_1.1-2 dplyr_0.7.6       
[4] tidyr_0.8.1        ggplot2_3.0.0     

loaded via a namespace (and not attached):
 [1] Rcpp_1.0.0        compiler_3.5.1    pillar_1.3.0     
 [4] git2r_0.23.0      plyr_1.8.4        workflowr_1.1.1  
 [7] bindr_0.1.1       R.methodsS3_1.7.1 R.utils_2.7.0    
[10] tools_3.5.1       digest_0.6.18     evaluate_0.12    
[13] tibble_1.4.2      gtable_0.2.0      pkgconfig_2.0.1  
[16] rlang_0.3.1       yaml_2.2.0        xfun_0.4         
[19] flashier_0.1.0    withr_2.1.2       stringr_1.3.1    
[22] knitr_1.21        cowplot_0.9.4     rprojroot_1.3-2  
[25] grid_3.5.1        tidyselect_0.2.4  glue_1.3.0       
[28] R6_2.3.0          rmarkdown_1.11    reshape2_1.4.3   
[31] purrr_0.2.5       magrittr_1.5      whisker_0.3-2    
[34] backports_1.1.2   scales_0.5.0      htmltools_0.3.6  
[37] assertthat_0.2.0  colorspace_1.3-2  labeling_0.3     
[40] stringi_1.2.4     lazyeval_0.2.1    munsell_0.5.0    
[43] crayon_1.3.4      R.oo_1.22.0

This reproducible R Markdown analysis was created with workflowr 1.1.1