bonus
Lijia Wang
2020-12-16
Last updated: 2020-12-17
Checks: 7 0
Knit directory: gacha/
This reproducible R Markdown analysis was created with workflowr (version 1.6.2). The Checks tab describes the reproducibility checks that were applied when the results were created. The Past versions tab lists the development history.
Great! Since the R Markdown file has been committed to the Git repository, you know the exact version of the code that produced these results.
Great job! The global environment was empty. Objects defined in the global environment can affect the analysis in your R Markdown file in unknown ways. For reproduciblity it’s best to always run the code in an empty environment.
The command set.seed(20201216) was run prior to running the code in the R Markdown file. Setting a seed ensures that any results that rely on randomness, e.g. subsampling or permutations, are reproducible.
Great job! Recording the operating system, R version, and package versions is critical for reproducibility.
Nice! There were no cached chunks for this analysis, so you can be confident that you successfully produced the results during this run.
Great job! Using relative paths to the files within your workflowr project makes it easier to run your code on other machines.
Great! You are using Git for version control. Tracking code development and connecting the code version to the results is critical for reproducibility.
The results in this page were generated with repository version 985204e. See the Past versions tab to see a history of the changes made to the R Markdown and HTML files.
Note that you need to be careful to ensure that all relevant files for the analysis have been committed to Git prior to generating the results (you can use wflow_publish or wflow_git_commit). workflowr only checks the R Markdown file, but you know if there are other scripts or data files that it depends on. Below is the status of the Git repository when the results were generated:
Ignored files:
Ignored: .DS_Store
Ignored: .RData
Ignored: .Rhistory
Ignored: gacha/.RData
Ignored: gacha/.Rhistory
Untracked files:
Untracked: analysis/pity.Rmd
Unstaged changes:
Modified: code/wflow_init.R
Note that any generated files, e.g. HTML, png, CSS, etc., are not included in this status report because it is ok for generated content to have uncommitted changes.
These are the previous versions of the repository in which changes were made to the R Markdown (analysis/bonus.Rmd) and HTML (docs/bonus.html) files. If you’ve configured a remote Git repository (see ?wflow_git_remote), click on the hyperlinks in the table below to view the files as they were in that past version.
| File | Version | Author | Date | Message |
|---|---|---|---|---|
| Rmd | 985204e | Lijia Wang | 2020-12-17 | appended 10-pull bonus |
| html | 2357df5 | Lijia Wang | 2020-12-17 | Build site. |
| Rmd | c90faa1 | Lijia Wang | 2020-12-17 | finished 10-pull bonus |
| html | e97114c | Lijia Wang | 2020-12-17 | Build site. |
| Rmd | 81db14e | Lijia Wang | 2020-12-17 | 10-pull bonus (WIP) |
Introduction
In this section, we will explore how making a “10-pull” instead of using single pulls changes the probability model we constructed for the generic single-pull mechanism. Most gacha games encourage 10x pulls in order to incentivize the players to purchase more in-game currency and make extra pulls than they normally would, since presumably a player only doing single pulls would stop as soon as they obtained the card they desire. Therefore, they offer various “10-pull bonuses”, where they either provide an extra free pull, or guarantee a card above a certain rarity.
We will continue to use our assumption regarding the i.i.d nature of each Bernoulli trial, and that our player would like an SSR card. However, most of these “10-pull” bonuses do not offer a guaranteed card of top rarity, but normally one above the second highest rarity. So the 10-pull bonus for our player could be an SR or an SSR card.
For most games, it is unclear the distribution in probability between the SR and SSR cards for the 10-pull bonus. We will assume that they follow the same ratio their non-bonus probabilities, only that they now add up to 1 for this bonus pull.
Probability of 1+ SSR in one 10-pull
We’re unsure about how the gacha algorithm employed in the game actually works, but I will assume that in this scenario, the first 9 pulls are still i.i.d Bernoulli trials. During the last pull, a new set of probabilities, which we will refer to as “bonus probabilities”, will be applied regardless of whether you obtained any SR/SSR cards previously. Bonus probabilities are only assigned to SR and SSR cards only, and they add up to 1.
In any 10-pull, the probability of you NOT obtaininging an SSR card can be modeled as: you did not obtain any SSR cards in the first 9 pulls AND pulled an SR card for the bonus.
For each normal trial, let the probability of pulling any SSR card be \(p\), and the probability of pulling any SR card be \(q\). For the bonus probabilities, let that for an SSR card be \(bp\), and that for an SR card be \(bq\), where \(b\) is a constant and \(bp + bq = 1\)
Pr(no SSR in first 9 & SR in bonus) = \((1-p)^9 bq\)
Therefore, the probability of PULLING at least one SSR during any 10-pull is:
\[Pr(X\geq1) = 1-(1-p)^9 bq \]
Application in F/GO
Similarly, we will use Fate/Grand Order non-event pool as an example, and our player desire a 5-star servant (Note that in Fate/Grand Order, Servants/characters have different probabilities from Craft Essence/equipments). Since we only desire a subcategory of SSR cards (characters, not equipment), we need to subdivide the overall probability into character probability \(p_c\), and equipment probability \(p_e\). Their respective bonus probabilities can be denoted as \(bp_c\) and \(bp_e\).
Probabilities:
SSR character (\(p_c\)): 1.000%
SSR equipment (\(p_e\)): 4.000%
total SSR probability (\(p\)): \(p_c + p_e = 5.000 \%\)
SR character (\(q_c\)): 3.000%
SR equipment (\(q_e\)): 12.000%
total SR probability (\(q\)): \(q_c + q_e = 15.000 \%\)
b = 5
For each 10-pull:
\[Pr(X\geq1) = 1-(1-p_c)^9 (bq + bp_e) = 1-(1-0.01)^9(5*0.15+5*0.04) = 0.132 \]
As a quick comparison, the probability of obtaining more than 1 SSR for 10 single pulls are:
\[Pr(X\geq1) = 1- Pr(X=0) = 1-e^{-np} = 1-e^{-10*0.01} = 1-0.905 = 0.095\]
Which shows that the 10-pull bonus is indeed working in our favor.
Approximation with Binomial Distribution
We will try to visualize this new probability like we did for single pulls. From our observations in the case of single pulls, the probability of obtaining 2 or more SSR character cards in 10 pulls is very small. To be precise:
\[Pr(X=2) = \frac{\lambda^2}{2!}e^{-\lambda} = \frac{(np)^2}{2!}e^{-np} = \frac{(10*0.01)^2}{2!}e^{-10*0.01} = 0.00452\]
\[Pr(X=3) = \frac{\lambda^3}{3!}e^{-\lambda} = \frac{(np)^3}{3!}e^{-np} = \frac{(10*0.01)^3}{3!}e^{-10*0.01} = 1.508 \times 10^{-4}\]
Therefore, we can approximate the probability of getting one SSR in any 10-pull to be very close to our calculated \(Pr(X\geq1)\):
\[ Pr(X\geq1) = Pr(X=1) + Pr(X=2) + \dots \] \[ Pr(X=1) = Pr(X\geq 1) - [Pr(X=2) + Pr(X=3) + \dots]\]
but as we have discussed before, \(Pr(X=2) + Pr(X=3) - \dots\) is small, therefore we can claim that:
\[[Pr(X=2) + Pr(X=3) + \dots] \approx 0\]
So \(Pr(X=1) \approx Pr(X\geq1)\) for each 10-pull.
If we regard each 10-pull as one trial, we can observe that trials are still i.i.d. Bernoulli. However, since the probablity of obtaining 1 SSR card is a lot larger (e.g. 0.132 in our calculation for F/GO) compared to the probability of obtaining 1 SSR in any single pull (e.g. 0.001 in F/GO), modeling probabilities with Poisson Distribution might not be appropriate anymore. Instead, we will use the binomial distribution:
\[ f(k,n,p) = Pr(k; n,p)=Pr(X=k) = {n \choose k}p^k(1-p)^{n-k} = \frac{n!}{k!(n-k!)}p^k(1-p)^{n-k}\]
Application in F/GO:
Similar to our example in single pulls, we plotted the probabilities of obtaining 1, 2, and 3 SSR cards in 1 to 500 pulls. Here we used the Fate/Grand Order Saint Quartz Summon Distribution Rate on an non-event banner. We define “success” as pulling a 5-star servant (character), and the probability is 1.000% (according to in-game statistics provided). Detailed probabilities are listed in the “Application in F/GO” section in “Probability of 1+ SSR in one 10-pull” section.
As we stated earlier, we will regard each 10-pull as one trial, therefore we will be looking at 50 trials (500 pulls) so our results here can be compared to our results in the single pulls example.
[1] "Number of 10-pulls that maximizes probability of 1 SSR is 7"[1] "Number of 10-pulls that maximizes probability of 2 SSR is 15"
[1] "Number of 10-pulls that maximizes probability of 3 SSR is 22"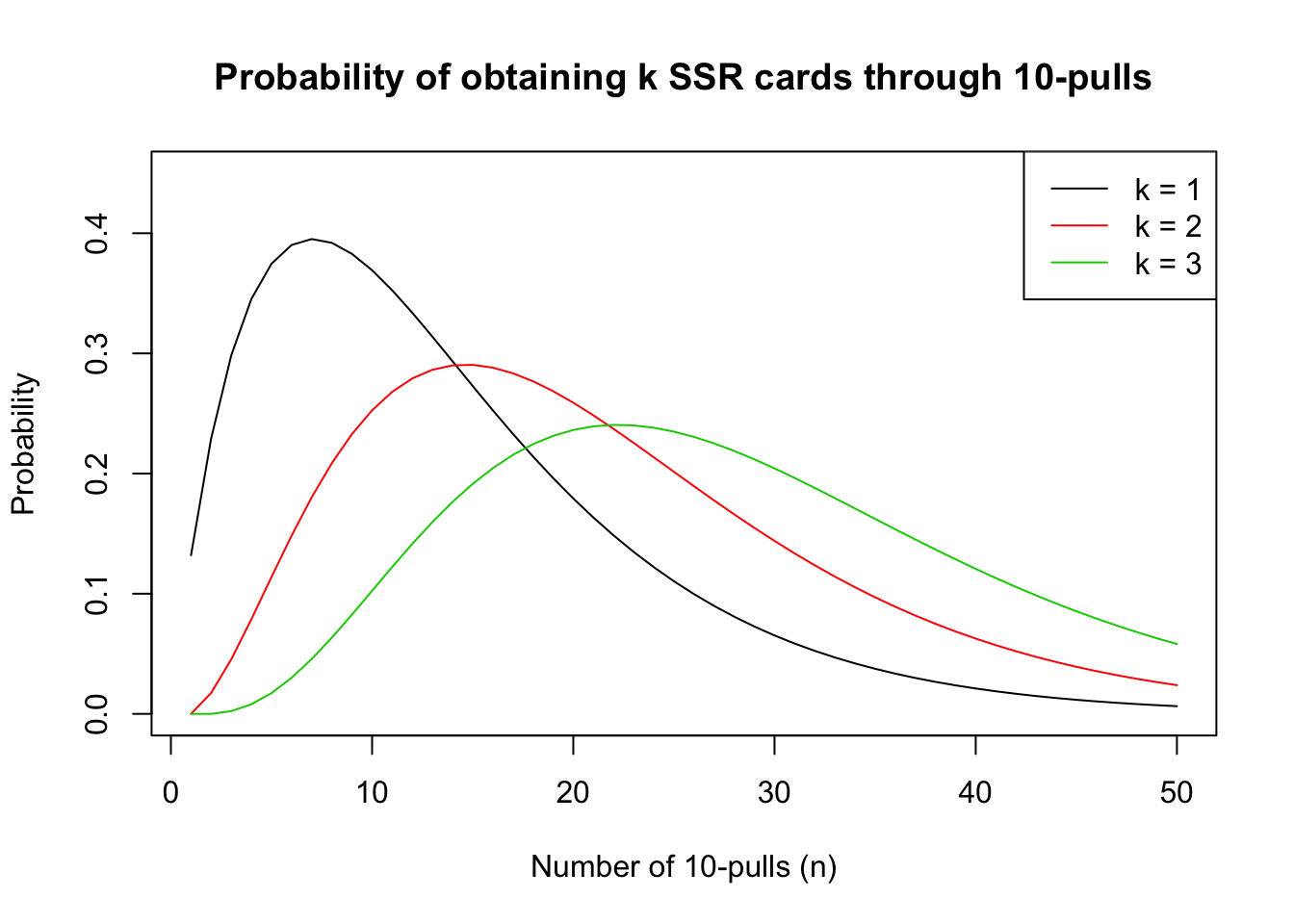
| Version | Author | Date |
|---|---|---|
| 2357df5 | Lijia Wang | 2020-12-17 |
Trials to first Success
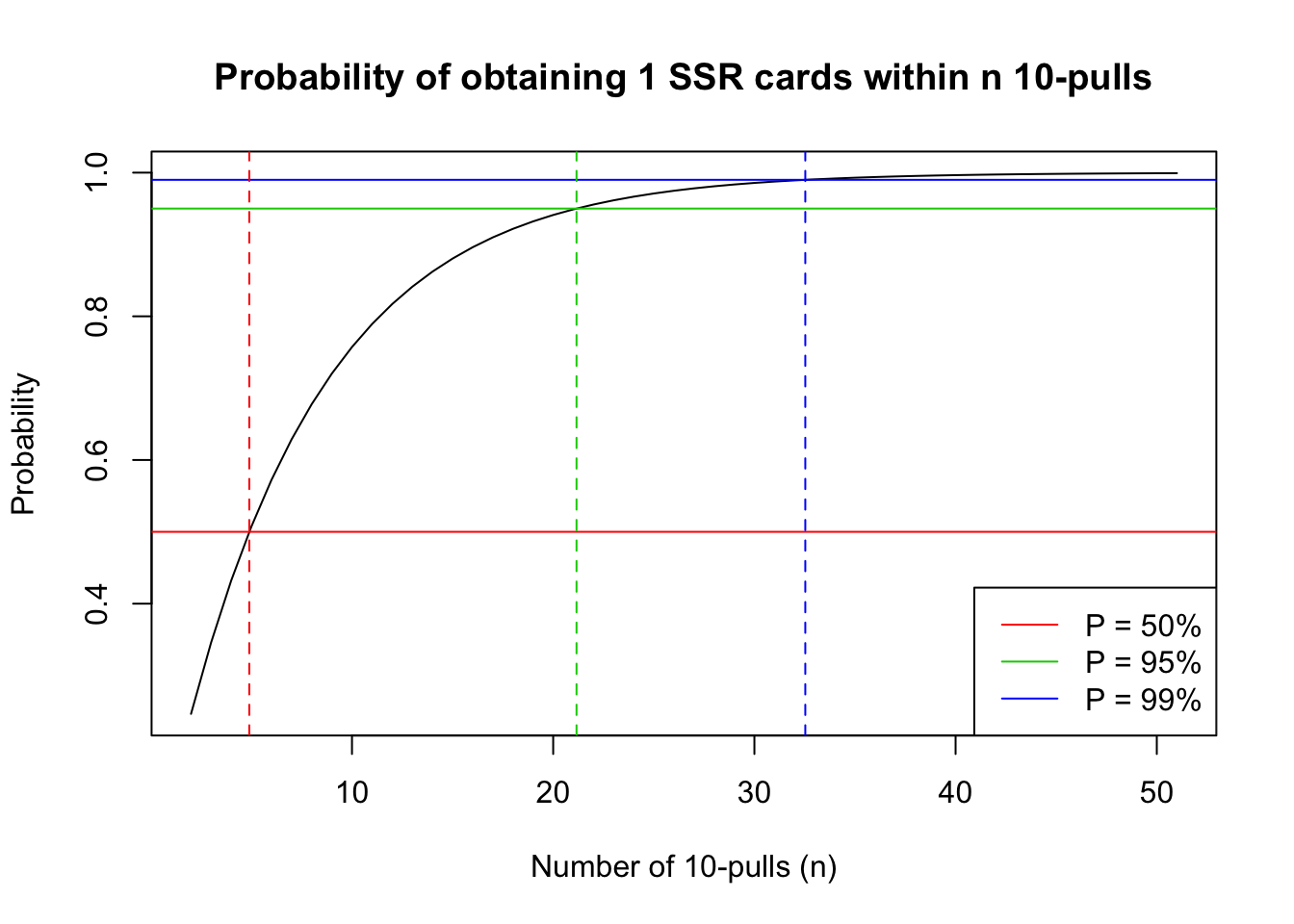
We know that our probability of pulling 1 character is maximized at 7 10-pulls, but that information itself is not all that useful. We will use the cumulative distribution function to explore at what point we will obtain a 95% chance of pulling an SSR character through 10-pulls only.
Each 10-pull is a Bernoulli Variable \(X_i\) and are independentally and identically distributed. Therefore, we can apply the geometric distribution and obtain the probability of obtaining the first success at the \(k\)-th trial:
\[ Pr(X=k) = (1-p)^{k-1}p\]
and we have the cumulative distribution function:
\[ Pr(X\leq k) = 1-(1-p)^k \]
And we would like to find the number \(k\) when \(Pr(X\leq k) \geq 0.95\), which can be easily computed given probability \(p\).
Application in F/GO
In the F/GO case, If we would like to achieve 50% chance of getting an SSR:
\[ Pr(X\leq k) = 1-(1-p)^k = 1-(1-0.132)^k = 0.50\]
\[ k = \frac{log(0.50)}{log(1-0.132)} = 4.896\]
If we would like to achieve 95% chance of getting an SSR:
\[ Pr(X\leq k) = 1-(1-p)^k = 1-(1-0.132)^k = 0.95\]
\[ k = \frac{log(0.05)}{log(1-0.132)} = 21.16\]
And for 99% chance, you would get:
\[ k = \frac{log(0.01)}{log(1-0.132)} = 32.53\]
This means if you saved up for 33 10-pulls, you are almost guaranteed to obtain an SSR character from the gacha.
Visualization
Comparison with single-pulls
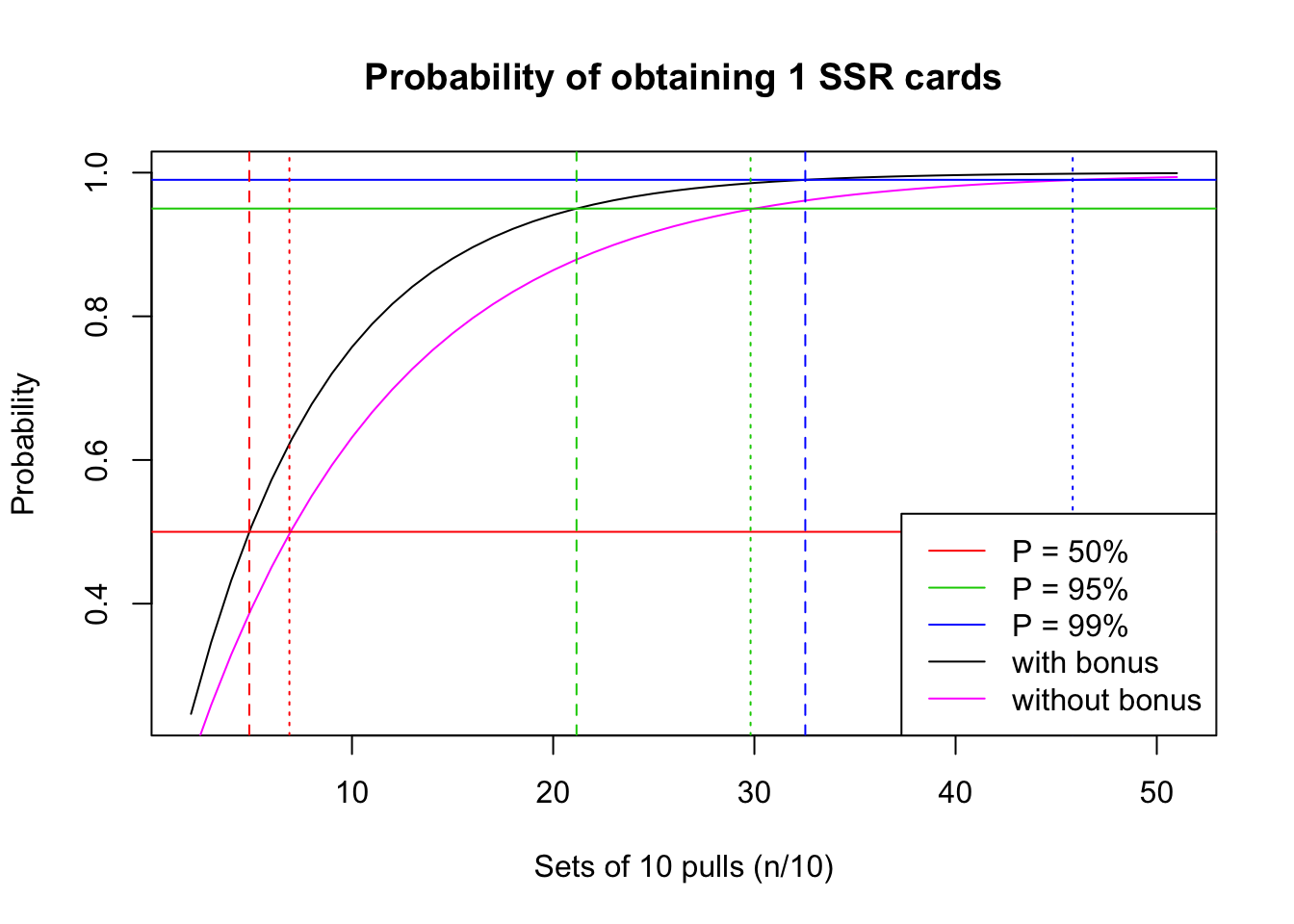
Remarks
To reiterate, the “10-pull bonus” modeled here is under the assumption that for the last pull, the SR and SSR rates are both adjusted to add up to 100% while maintaining their previous ratio. One possible that only SR rate is increased (e.g. to 99% in F/GO) and SSR rate is remains the same for the bonus pull). But in this case, if our player is still interested in only the SSR character, pulling through 10-pull or through single pulls will make no difference – the probability will be the same as pulling through single pulls only.
We are unsure as if which one of those mechanisms is actually employed by the game. If we are able to collect a large enough gacha pulls data, we might be able to figure out which model the gacha actually follows, but this is beyond the scope of this project.
R version 3.6.2 (2019-12-12)
Platform: x86_64-apple-darwin15.6.0 (64-bit)
Running under: macOS 10.16
Matrix products: default
BLAS: /Library/Frameworks/R.framework/Versions/3.6/Resources/lib/libRblas.0.dylib
LAPACK: /Library/Frameworks/R.framework/Versions/3.6/Resources/lib/libRlapack.dylib
locale:
[1] en_US.UTF-8/en_US.UTF-8/en_US.UTF-8/C/en_US.UTF-8/en_US.UTF-8
attached base packages:
[1] stats graphics grDevices utils datasets methods base
other attached packages:
[1] workflowr_1.6.2
loaded via a namespace (and not attached):
[1] Rcpp_1.0.3 rprojroot_1.3-2 digest_0.6.25 later_1.0.0
[5] R6_2.4.1 backports_1.1.5 git2r_0.26.1 magrittr_1.5
[9] evaluate_0.14 stringi_1.4.6 rlang_0.4.5 fs_1.3.2
[13] promises_1.1.0 whisker_0.4 rmarkdown_2.1 tools_3.6.2
[17] stringr_1.4.0 glue_1.3.2 httpuv_1.5.2 xfun_0.12
[21] yaml_2.2.1 compiler_3.6.2 htmltools_0.4.0 knitr_1.28