Null simulations
Belinda Phipson
01/06/2022
Last updated: 2022-06-01
Checks: 7 0
Knit directory: propeller-paper-analysis/
This reproducible R Markdown analysis was created with workflowr (version 1.7.0). The Checks tab describes the reproducibility checks that were applied when the results were created. The Past versions tab lists the development history.
Great! Since the R Markdown file has been committed to the Git repository, you know the exact version of the code that produced these results.
Great job! The global environment was empty. Objects defined in the global environment can affect the analysis in your R Markdown file in unknown ways. For reproduciblity it’s best to always run the code in an empty environment.
The command set.seed(20220531) was run prior to running
the code in the R Markdown file. Setting a seed ensures that any results
that rely on randomness, e.g. subsampling or permutations, are
reproducible.
Great job! Recording the operating system, R version, and package versions is critical for reproducibility.
Nice! There were no cached chunks for this analysis, so you can be confident that you successfully produced the results during this run.
Great job! Using relative paths to the files within your workflowr project makes it easier to run your code on other machines.
Great! You are using Git for version control. Tracking code development and connecting the code version to the results is critical for reproducibility.
The results in this page were generated with repository version 7ec7a76. See the Past versions tab to see a history of the changes made to the R Markdown and HTML files.
Note that you need to be careful to ensure that all relevant files for
the analysis have been committed to Git prior to generating the results
(you can use wflow_publish or
wflow_git_commit). workflowr only checks the R Markdown
file, but you know if there are other scripts or data files that it
depends on. Below is the status of the Git repository when the results
were generated:
Ignored files:
Ignored: .Rproj.user/
Ignored: data/cold_warm_fresh_cellinfo.txt
Ignored: data/covid.cell.annotation.meta.txt
Ignored: data/heartFYA.Rds
Ignored: data/pool_1.rds
Untracked files:
Untracked: analysis/Sims2vs20CT.Rmd
Untracked: code/SimCode.R
Untracked: code/SimCodeTrueDiff.R
Untracked: code/auroc.R
Untracked: data/CTpropsTransposed.txt
Untracked: data/CelltypeLevels.csv
Untracked: data/TypeIErrTables.Rdata
Untracked: data/appnote1cdata.rdata
Untracked: data/cellinfo.csv
Untracked: data/nullsimsVaryN_results.Rdata
Untracked: data/sampleinfo.csv
Untracked: output/Fig1ab.pdf
Untracked: output/Fig1cde.pdf
Untracked: output/example_simdata.pdf
Untracked: output/fig2d.pdf
Untracked: output/legend-fig2d.pdf
Untracked: output/typeIerrorResults.Rda
Note that any generated files, e.g. HTML, png, CSS, etc., are not included in this status report because it is ok for generated content to have uncommitted changes.
These are the previous versions of the repository in which changes were
made to the R Markdown (analysis/nullsims.Rmd) and HTML
(docs/nullsims.html) files. If you’ve configured a remote
Git repository (see ?wflow_git_remote), click on the
hyperlinks in the table below to view the files as they were in that
past version.
| File | Version | Author | Date | Message |
|---|---|---|---|---|
| Rmd | 3a453fb | bphipson | 2022-06-01 | add null simulation results |
Load the libraries
library(speckle)
library(limma)
library(edgeR)Source the simulation code:
source("./code/SimCode.R")Hierarchical model for simulating cell type proportions
I am simulating cell type proportions in a hierarchical manner.
- The total number of cells, \(n_j\), for each sample \(j\), are drawn from a negative binomial distribution with mean 5000 and dispersion 20.
- The true cell type proportions for 5 cell types are 0.01, 0.05, 0.15, 0.35, 0.45.
- The sample proportion \(p_{ij}\) for cell type \(i\) and sample \(j\) is assumed to be drawn from a Beta distribution with parameters \(\alpha\) and \(\beta\).
- The count for cell type \(i\) and sample \(j\) is then drawn from a binomial distribution with probability \(p_{ij}\) and size \(n_j\).
The Beta-Binomial model allows for biological variability to be simulated between samples. The paramaters of the Beta distribution, \(\alpha\) and \(\beta\), determine how variable the \(p_{ij}\) will be. Larger values of \(\alpha\) and \(\beta\) result in a more precise distribution centred around the true proportions, while smaller values result in a more diffuse prior. Figure @ref(fig:betadist) shows the distributions of the \(p_{ij}\) as \(\alpha\) and \(\beta\) vary.
For a given value of \(\alpha\) and \(p\), \(\beta\) can be calculated as \[\beta = \frac{\alpha (1-p)}{p}\]
p <- c(0.01, 0.05, 0.15, 0.34, 0.45)
a <- c(seq(0.1, 1, by=0.1), seq(2,10,by=2), seq(25,50,by=5), 100, 150, 200)
par(mfrow=c(1,1))
for(j in 1: length(p)){
myp <- p[j]
b = a*(1-myp)/myp
cols <- ggplotColors(length(a))
plot(density(rbeta(1000,a[length(a)],b[length(a)])),xlim=c(0,1),
main=paste("True proportion = ",myp), col="white",
xlab="", cex.axis=1.5, cex.lab=1.5)
legend("topright", legend=paste(a,round(b,2),sep=","),lty=1,col=cols, cex=0.6)
for(i in 1:length(a)){
lines(density(rbeta(1000,a[i],b[i])),xlim=c(0,1), col=cols[i])
}
abline(v=myp,lty=2,lwd=2)
lines(density(rbeta(1000,a[15],b[15])), col="dark blue", lwd=2, lty=3)
}
Density plots of simulated proportions
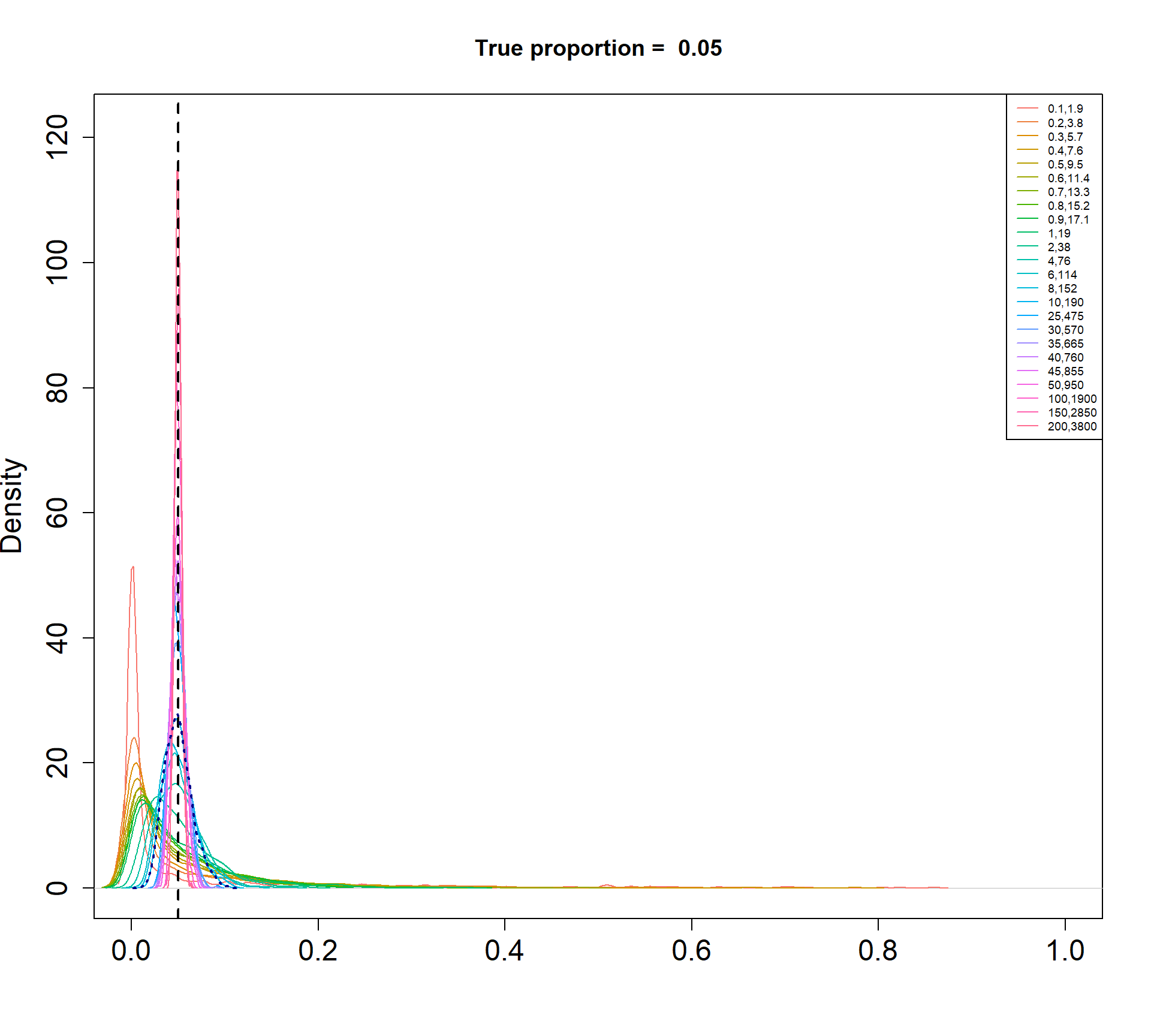
Density plots of simulated proportions
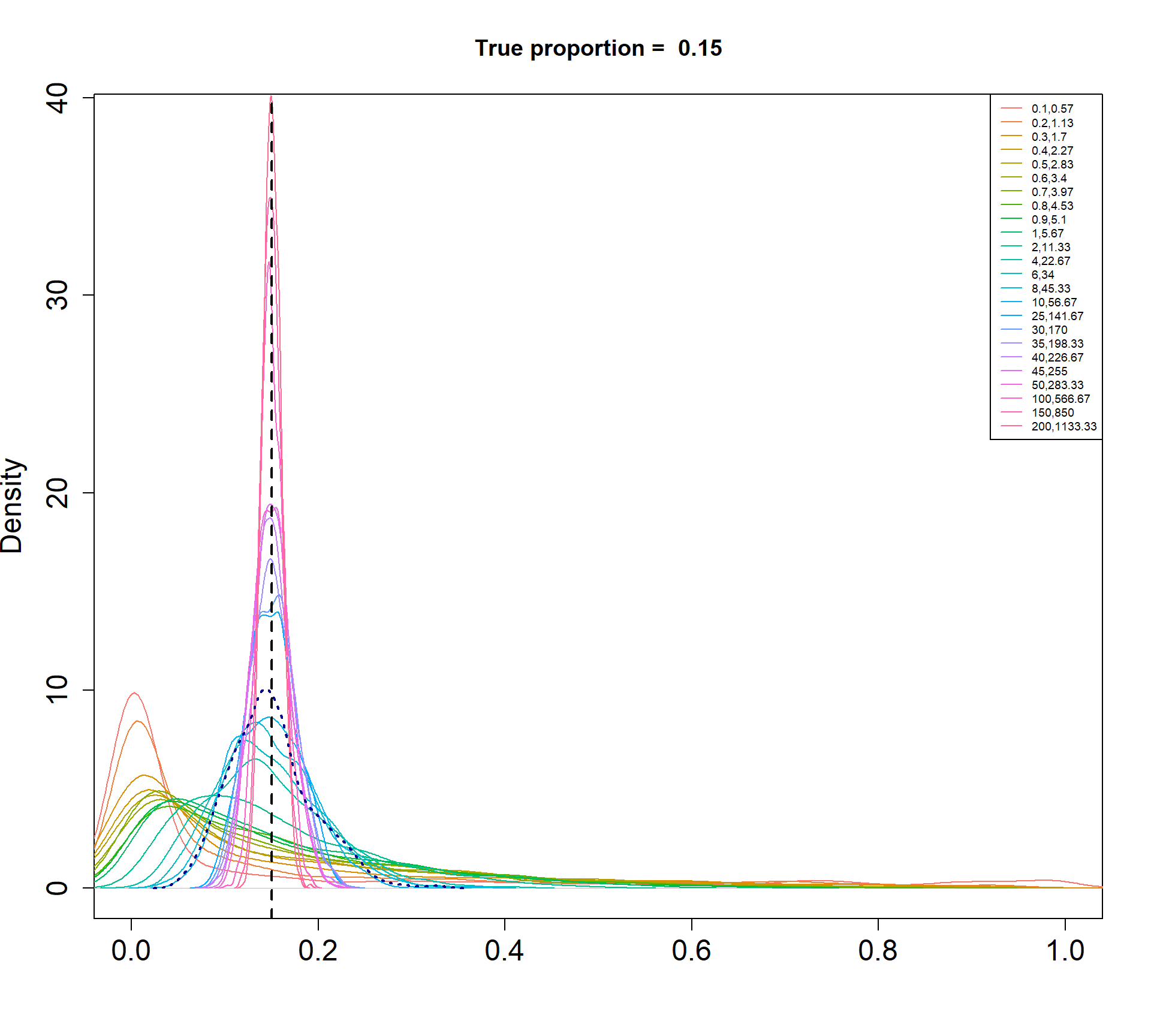
Density plots of simulated proportions
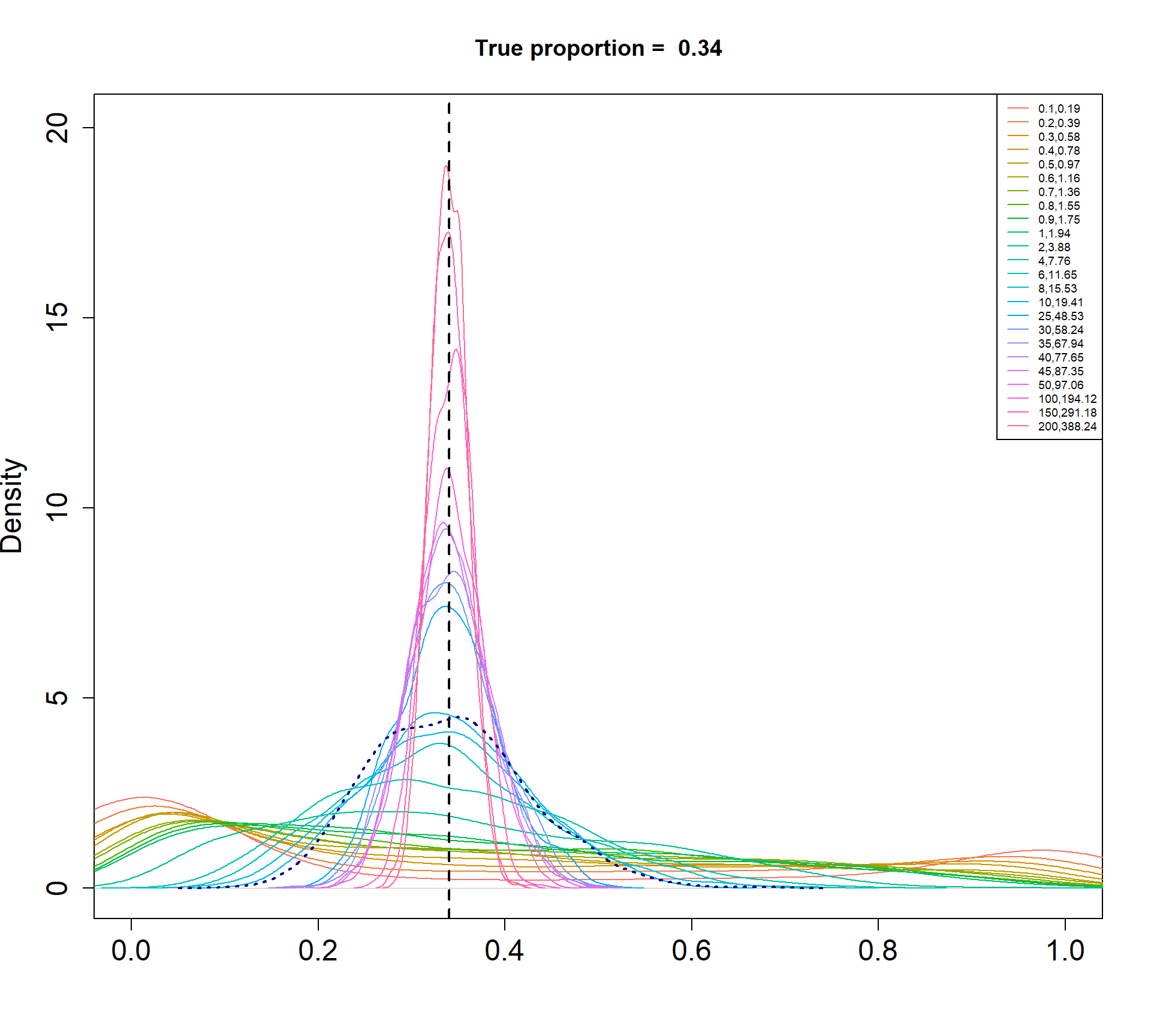
Density plots of simulated proportions
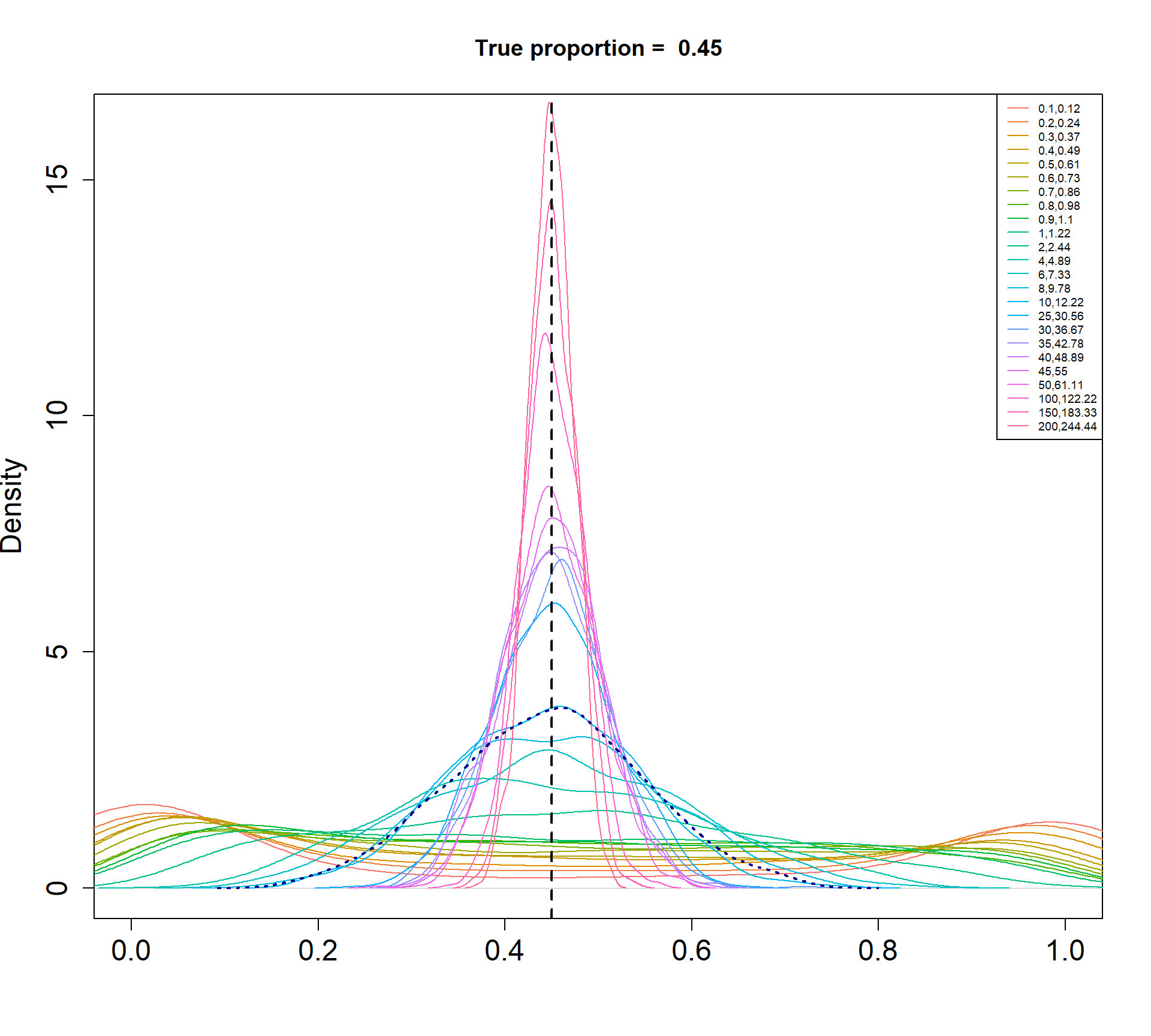
Density plots of simulated proportions
Null simulations, two groups, 5 cell types
I will generate cell type counts for five cell types, assuming two experimental groups with a sample size of n=(3,5,10,20) in each group. I will calculate p-values from the following models:
- propeller (arcsin sqrt transformation)
- propeller (logit transformation)
- chi-square test of differences in proportions
- beta-binomial model using alternative parameterisation in edgeR
- logistic binomial regression (beta-binomial with dispersion=0)
- negative binomial regression (LRT and QLF in edgeR)
- Poisson regression (negative binomial with dispersion=0)
- CODA model
Ten thousand simulation datasets will be generated. First I set up the simulation parameters and set up the objects to capture the output.
# Sim parameters
set.seed(10)
nsim <- 10000
depth <- 5000
# True cell type proportions
p <- c(0.01, 0.05, 0.15, 0.34, 0.45)
# Parameters for beta distribution
a <- 10
b <- a*(1-p)/p
# Decide on what output to keep
pval.chsq <- pval.bb <- pval.lb <- pval.nb <- pval.qlf <- pval.pois <- pval.logit <- pval.asin <-
pval.coda <- matrix(NA,nrow=length(p),ncol=nsim)Next we simulate the cell type counts and run the various statistical models for testing cell type proportion differences between the two groups. In this scenario we don’t expect to detect many statistically significant differences if a test correctly controls the type I error rate.
Sample size of 3 in each group
nsamp <- 6
for(i in 1:nsim){
#Simulate cell type counts
counts <- SimulateCellCounts(props=p,nsamp=nsamp,depth=depth,a=a,b=b)
tot.cells <- colSums(counts)
# propeller
est.props <- t(t(counts)/tot.cells)
#asin transform
trans.prop <- asin(sqrt(est.props))
#logit transform
nc <- normCounts(counts)
est.props.logit <- t(t(nc+0.5)/(colSums(nc+0.5)))
logit.prop <- log(est.props.logit/(1-est.props.logit))
grp <- rep(c(0,1), each=nsamp/2)
des <- model.matrix(~grp)
# asinsqrt transform
fit <- lmFit(trans.prop, des)
fit <- eBayes(fit, robust=TRUE)
pval.asin[,i] <- fit$p.value[,2]
# logit transform
fit.logit <- lmFit(logit.prop, des)
fit.logit <- eBayes(fit.logit, robust=TRUE)
pval.logit[,i] <- fit.logit$p.value[,2]
# Chi-square test for differences in proportions
n <- tapply(tot.cells, grp, sum)
for(h in 1:length(p)){
pval.chsq[h,i] <- prop.test(tapply(counts[h,],grp,sum),n)$p.value
}
# Beta binomial implemented in edgeR (methylation workflow)
meth.counts <- counts
unmeth.counts <- t(tot.cells - t(counts))
new.counts <- cbind(meth.counts,unmeth.counts)
sam.info <- data.frame(Sample = rep(1:nsamp,2), Group=rep(grp,2), Meth = rep(c("me","un"), each=nsamp))
design.samples <- model.matrix(~0+factor(sam.info$Sample))
colnames(design.samples) <- paste("S",1:nsamp,sep="")
design.group <- model.matrix(~0+factor(sam.info$Group))
colnames(design.group) <- c("A","B")
design.bb <- cbind(design.samples, (sam.info$Meth=="me") * design.group)
lib.size = rep(tot.cells,2)
y <- DGEList(new.counts)
y$samples$lib.size <- lib.size
y <- estimateDisp(y, design.bb, trend="none")
fit.bb <- glmFit(y, design.bb)
contr <- makeContrasts(Grp=B-A, levels=design.bb)
lrt <- glmLRT(fit.bb, contrast=contr)
pval.bb[,i] <- lrt$table$PValue
# Logistic binomial regression
fit.lb <- glmFit(y, design.bb, dispersion = 0)
lrt.lb <- glmLRT(fit.lb, contrast=contr)
pval.lb[,i] <- lrt.lb$table$PValue
# Negative binomial
y.nb <- DGEList(counts)
y.nb <- estimateDisp(y.nb, des, trend="none")
fit.nb <- glmFit(y.nb, des)
lrt.nb <- glmLRT(fit.nb, coef=2)
pval.nb[,i] <- lrt.nb$table$PValue
# Negative binomial QLF test
fit.qlf <- glmQLFit(y.nb, des, robust=TRUE, abundance.trend = FALSE)
res.qlf <- glmQLFTest(fit.qlf, coef=2)
pval.qlf[,i] <- res.qlf$table$PValue
# Poisson
fit.poi <- glmFit(y.nb, des, dispersion = 0)
lrt.poi <- glmLRT(fit.poi, coef=2)
pval.pois[,i] <- lrt.poi$table$PValue
# CODA
# Replace zero counts with 0.5 so that the geometric mean always works
if(any(counts==0)) counts[counts==0] <- 0.5
geomean <- apply(counts,2, function(x) exp(mean(log(x))))
geomean.mat <- expandAsMatrix(geomean,dim=c(nrow(counts),ncol(counts)),byrow = FALSE)
clr <- counts/geomean.mat
logratio <- log(clr)
fit.coda <- lmFit(logratio, des)
fit.coda <- eBayes(fit.coda, robust=TRUE)
pval.coda[,i] <- fit.coda$p.value[,2]
}We can look at the number of significant tests at different p-value cut-offs:
pcut <- 0.01
type1error <- matrix(NA,nrow=length(p),ncol=9)
rownames(type1error) <- rownames(counts)
colnames(type1error) <- c("chisq","logbin","pois","asin", "logit","betabin","negbin", "nbQLF","CODA")
type1error[,1]<-rowSums(pval.chsq<pcut)/nsim
type1error[,2]<-rowSums(pval.lb<pcut)/nsim
type1error[,3]<-rowSums(pval.pois<pcut)/nsim
type1error[,4]<-rowSums(pval.asin<pcut)/nsim
type1error[,5]<-rowSums(pval.logit<pcut)/nsim
type1error[,6]<-rowSums(pval.bb<pcut)/nsim
type1error[,7]<-rowSums(pval.nb<pcut)/nsim
type1error[,8]<-rowSums(pval.qlf<pcut)/nsim
type1error[,9]<-rowSums(pval.coda<pcut)/nsim
type1error chisq logbin pois asin logit betabin negbin nbQLF CODA
c0 0.3208 0.3327 0.3304 0.0010 0.0235 0.0241 0.0470 0.0307 0.0254
c1 0.6159 0.6210 0.6112 0.0077 0.0150 0.0263 0.0454 0.0275 0.0171
c2 0.7645 0.7668 0.7460 0.0254 0.0162 0.0323 0.0390 0.0233 0.0158
c3 0.7963 0.7975 0.7540 0.0394 0.0135 0.0239 0.0179 0.0093 0.0117
c4 0.8074 0.8088 0.7413 0.0357 0.0103 0.0200 0.0088 0.0046 0.0074pcut <- 0.05
type1error <- matrix(NA,nrow=length(p),ncol=9)
rownames(type1error) <- rownames(counts)
colnames(type1error) <- c("chisq","logbin","pois","asin", "logit","betabin","negbin","nbQLF","CODA")
type1error[,1]<-rowSums(pval.chsq<pcut)/nsim
type1error[,2]<-rowSums(pval.lb<pcut)/nsim
type1error[,3]<-rowSums(pval.pois<pcut)/nsim
type1error[,4]<-rowSums(pval.asin<pcut)/nsim
type1error[,5]<-rowSums(pval.logit<pcut)/nsim
type1error[,6]<-rowSums(pval.bb<pcut)/nsim
type1error[,7]<-rowSums(pval.nb<pcut)/nsim
type1error[,8]<-rowSums(pval.qlf<pcut)/nsim
type1error[,9]<-rowSums(pval.coda<pcut)/nsim
type1error chisq logbin pois asin logit betabin negbin nbQLF CODA
c0 0.4491 0.4612 0.4588 0.0111 0.0860 0.0813 0.1167 0.0956 0.0922
c1 0.7007 0.7054 0.6971 0.0413 0.0643 0.0812 0.1144 0.0917 0.0672
c2 0.8209 0.8224 0.8069 0.0871 0.0637 0.0849 0.0964 0.0757 0.0604
c3 0.8448 0.8460 0.8098 0.1076 0.0555 0.0753 0.0501 0.0421 0.0495
c4 0.8552 0.8559 0.8027 0.1041 0.0438 0.0632 0.0261 0.0220 0.0403Plot of all type I error rates for the 5 cell types:
par(mfrow=c(1,1))
par(mar=c(5,5.5,3,2))
par(mgp=c(4,1,0))
barplot(type1error,beside=TRUE,col=ggplotColors(length(p)),
ylab="Proportion sig. tests",
cex.axis = 1.5, cex.lab=1.5, cex.names = 1.35, ylim=c(0,1), las=2)
legend("topright",fill=ggplotColors(length(p)),legend=c(paste("True p=",p,sep="")), cex=1.5)
abline(h=pcut,lty=2,lwd=2)
title(c(paste("Type I error rate at alpha = 0.05, n=", nsamp/2,sep="")), cex.main=1.75)
Removing the most poorly performing methods (1-3):
par(mfrow=c(1,1))
par(mar=c(5,5.5,3,2))
par(mgp=c(4,1,0))
barplot(type1error[,4:9],beside=TRUE,col=ggplotColors(length(p)),
ylab="Proportion sig. tests",
cex.axis = 1.5, cex.lab=1.5, cex.names = 1.35, ylim=c(0,0.15), las=2)
#legend("top",fill=ggplotColors(length(b)),legend=c(paste("True p=",p,sep="")), cex=1.5)
abline(h=pcut,lty=2,lwd=2)
title(c(paste("Type I error rate at alpha = 0.05, n=", nsamp/2,sep="")), cex.main=1.75)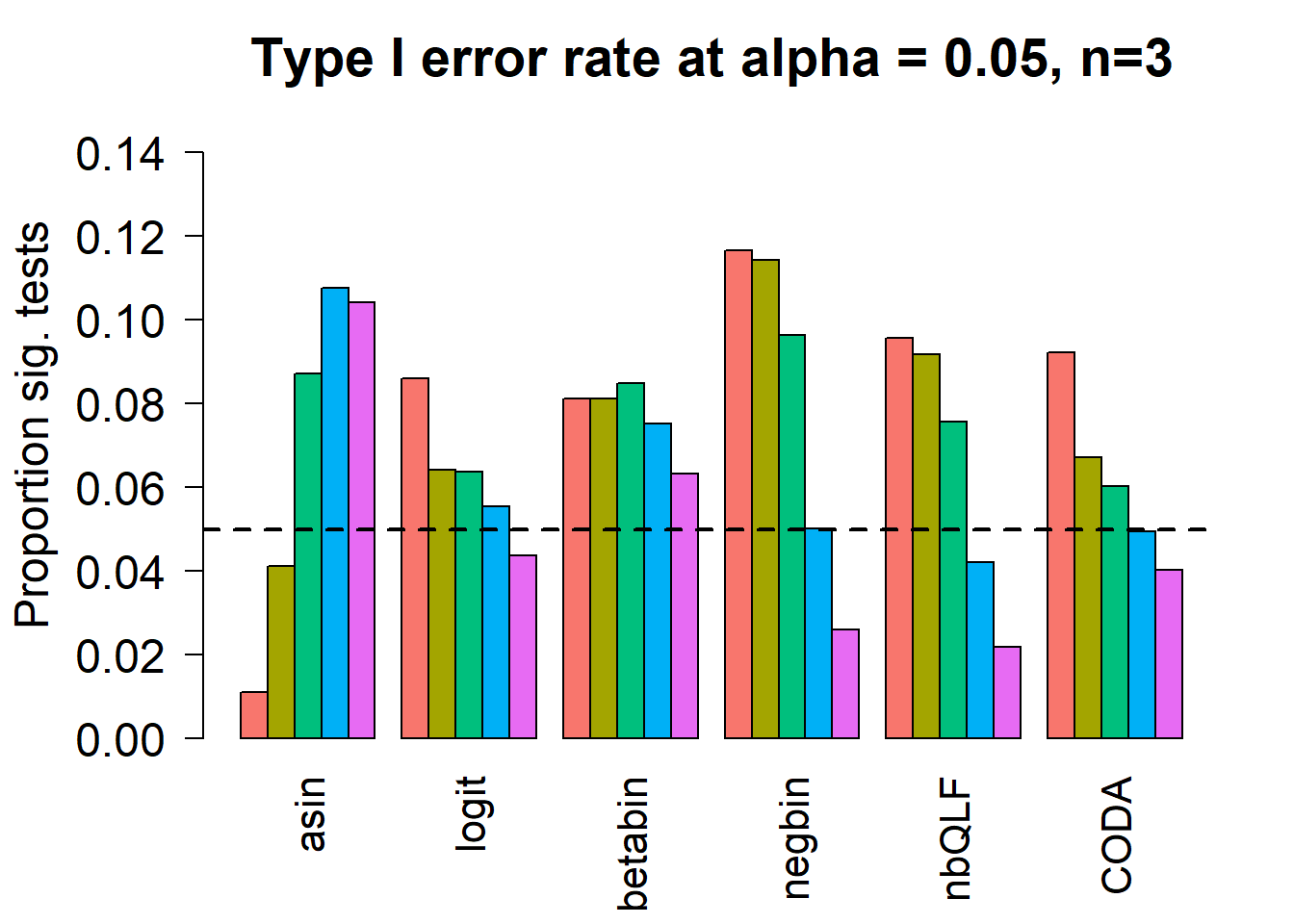
# save the type 1 error objects for n=3
type1error3 <- type1errorSample size of 5 in each group
nsamp <- 10
for(i in 1:nsim){
#Simulate cell type counts
counts <- SimulateCellCounts(props=p,nsamp=nsamp,depth=depth,a=a,b=b)
tot.cells <- colSums(counts)
# propeller
est.props <- t(t(counts)/tot.cells)
#asin transform
trans.prop <- asin(sqrt(est.props))
#logit transform
nc <- normCounts(counts)
est.props.logit <- t(t(nc+0.5)/(colSums(nc+0.5)))
logit.prop <- log(est.props.logit/(1-est.props.logit))
grp <- rep(c(0,1), each=nsamp/2)
des <- model.matrix(~grp)
# asinsqrt transform
fit <- lmFit(trans.prop, des)
fit <- eBayes(fit, robust=TRUE)
pval.asin[,i] <- fit$p.value[,2]
# logit transform
fit.logit <- lmFit(logit.prop, des)
fit.logit <- eBayes(fit.logit, robust=TRUE)
pval.logit[,i] <- fit.logit$p.value[,2]
# Chi-square test for differences in proportions
n <- tapply(tot.cells, grp, sum)
for(h in 1:length(p)){
pval.chsq[h,i] <- prop.test(tapply(counts[h,],grp,sum),n)$p.value
}
# Beta binomial implemented in edgeR (methylation workflow)
meth.counts <- counts
unmeth.counts <- t(tot.cells - t(counts))
new.counts <- cbind(meth.counts,unmeth.counts)
sam.info <- data.frame(Sample = rep(1:nsamp,2), Group=rep(grp,2), Meth = rep(c("me","un"), each=nsamp))
design.samples <- model.matrix(~0+factor(sam.info$Sample))
colnames(design.samples) <- paste("S",1:nsamp,sep="")
design.group <- model.matrix(~0+factor(sam.info$Group))
colnames(design.group) <- c("A","B")
design.bb <- cbind(design.samples, (sam.info$Meth=="me") * design.group)
lib.size = rep(tot.cells,2)
y <- DGEList(new.counts)
y$samples$lib.size <- lib.size
y <- estimateDisp(y, design.bb, trend="none")
fit.bb <- glmFit(y, design.bb)
contr <- makeContrasts(Grp=B-A, levels=design.bb)
lrt <- glmLRT(fit.bb, contrast=contr)
pval.bb[,i] <- lrt$table$PValue
# Logistic binomial regression
fit.lb <- glmFit(y, design.bb, dispersion = 0)
lrt.lb <- glmLRT(fit.lb, contrast=contr)
pval.lb[,i] <- lrt.lb$table$PValue
# Negative binomial
y.nb <- DGEList(counts)
y.nb <- estimateDisp(y.nb, des, trend="none")
fit.nb <- glmFit(y.nb, des)
lrt.nb <- glmLRT(fit.nb, coef=2)
pval.nb[,i] <- lrt.nb$table$PValue
# Negative binomial QLF test
fit.qlf <- glmQLFit(y.nb, des, robust=TRUE, abundance.trend = FALSE)
res.qlf <- glmQLFTest(fit.qlf, coef=2)
pval.qlf[,i] <- res.qlf$table$PValue
# Poisson
fit.poi <- glmFit(y.nb, des, dispersion = 0)
lrt.poi <- glmLRT(fit.poi, coef=2)
pval.pois[,i] <- lrt.poi$table$PValue
# CODA
# Replace zero counts with 0.5 so that the geometric mean always works
if(any(counts==0)) counts[counts==0] <- 0.5
geomean <- apply(counts,2, function(x) exp(mean(log(x))))
geomean.mat <- expandAsMatrix(geomean,dim=c(nrow(counts),ncol(counts)),byrow = FALSE)
clr <- counts/geomean.mat
logratio <- log(clr)
fit.coda <- lmFit(logratio, des)
fit.coda <- eBayes(fit.coda, robust=TRUE)
pval.coda[,i] <- fit.coda$p.value[,2]
}We can look at the number of significant tests at different p-value cut-offs:
pcut <- 0.01
type1error <- matrix(NA,nrow=length(p),ncol=9)
rownames(type1error) <- rownames(counts)
colnames(type1error) <- c("chisq","logbin","pois","asin", "logit","betabin","negbin", "nbQLF","CODA")
type1error[,1]<-rowSums(pval.chsq<pcut)/nsim
type1error[,2]<-rowSums(pval.lb<pcut)/nsim
type1error[,3]<-rowSums(pval.pois<pcut)/nsim
type1error[,4]<-rowSums(pval.asin<pcut)/nsim
type1error[,5]<-rowSums(pval.logit<pcut)/nsim
type1error[,6]<-rowSums(pval.bb<pcut)/nsim
type1error[,7]<-rowSums(pval.nb<pcut)/nsim
type1error[,8]<-rowSums(pval.qlf<pcut)/nsim
type1error[,9]<-rowSums(pval.coda<pcut)/nsim
type1error chisq logbin pois asin logit betabin negbin nbQLF CODA
c0 0.3220 0.3309 0.3283 0.0014 0.0203 0.0193 0.0310 0.0219 0.0199
c1 0.6382 0.6408 0.6323 0.0106 0.0162 0.0228 0.0365 0.0245 0.0170
c2 0.7586 0.7601 0.7396 0.0171 0.0129 0.0205 0.0242 0.0162 0.0149
c3 0.8012 0.8021 0.7614 0.0212 0.0097 0.0166 0.0130 0.0074 0.0076
c4 0.8095 0.8101 0.7420 0.0210 0.0086 0.0131 0.0069 0.0040 0.0061pcut <- 0.05
type1error <- matrix(NA,nrow=length(p),ncol=9)
rownames(type1error) <- rownames(counts)
colnames(type1error) <- c("chisq","logbin","pois","asin", "logit","betabin","negbin","nbQLF","CODA")
type1error[,1]<-rowSums(pval.chsq<pcut)/nsim
type1error[,2]<-rowSums(pval.lb<pcut)/nsim
type1error[,3]<-rowSums(pval.pois<pcut)/nsim
type1error[,4]<-rowSums(pval.asin<pcut)/nsim
type1error[,5]<-rowSums(pval.logit<pcut)/nsim
type1error[,6]<-rowSums(pval.bb<pcut)/nsim
type1error[,7]<-rowSums(pval.nb<pcut)/nsim
type1error[,8]<-rowSums(pval.qlf<pcut)/nsim
type1error[,9]<-rowSums(pval.coda<pcut)/nsim
type1error chisq logbin pois asin logit betabin negbin nbQLF CODA
c0 0.4501 0.4605 0.4586 0.0141 0.0738 0.0651 0.0951 0.0815 0.0791
c1 0.7238 0.7268 0.7198 0.0493 0.0662 0.0757 0.1003 0.0854 0.0693
c2 0.8142 0.8155 0.7980 0.0705 0.0579 0.0694 0.0789 0.0672 0.0585
c3 0.8473 0.8478 0.8160 0.0774 0.0466 0.0578 0.0428 0.0364 0.0433
c4 0.8552 0.8563 0.8041 0.0746 0.0389 0.0487 0.0254 0.0201 0.0348Plot of all type I error rates for the 5 cell types:
par(mfrow=c(1,1))
par(mar=c(5,5.5,3,2))
par(mgp=c(4,1,0))
barplot(type1error,beside=TRUE,col=ggplotColors(length(p)),
ylab="Proportion sig. tests",
cex.axis = 1.5, cex.lab=1.5, cex.names = 1.35, ylim=c(0,1), las=2)
legend("topright",fill=ggplotColors(length(p)),legend=c(paste("True p=",p,sep="")), cex=1.5)
abline(h=pcut,lty=2,lwd=2)
title(c(paste("Type I error rate at alpha = 0.05, n=", nsamp/2,sep="")), cex.main=1.75)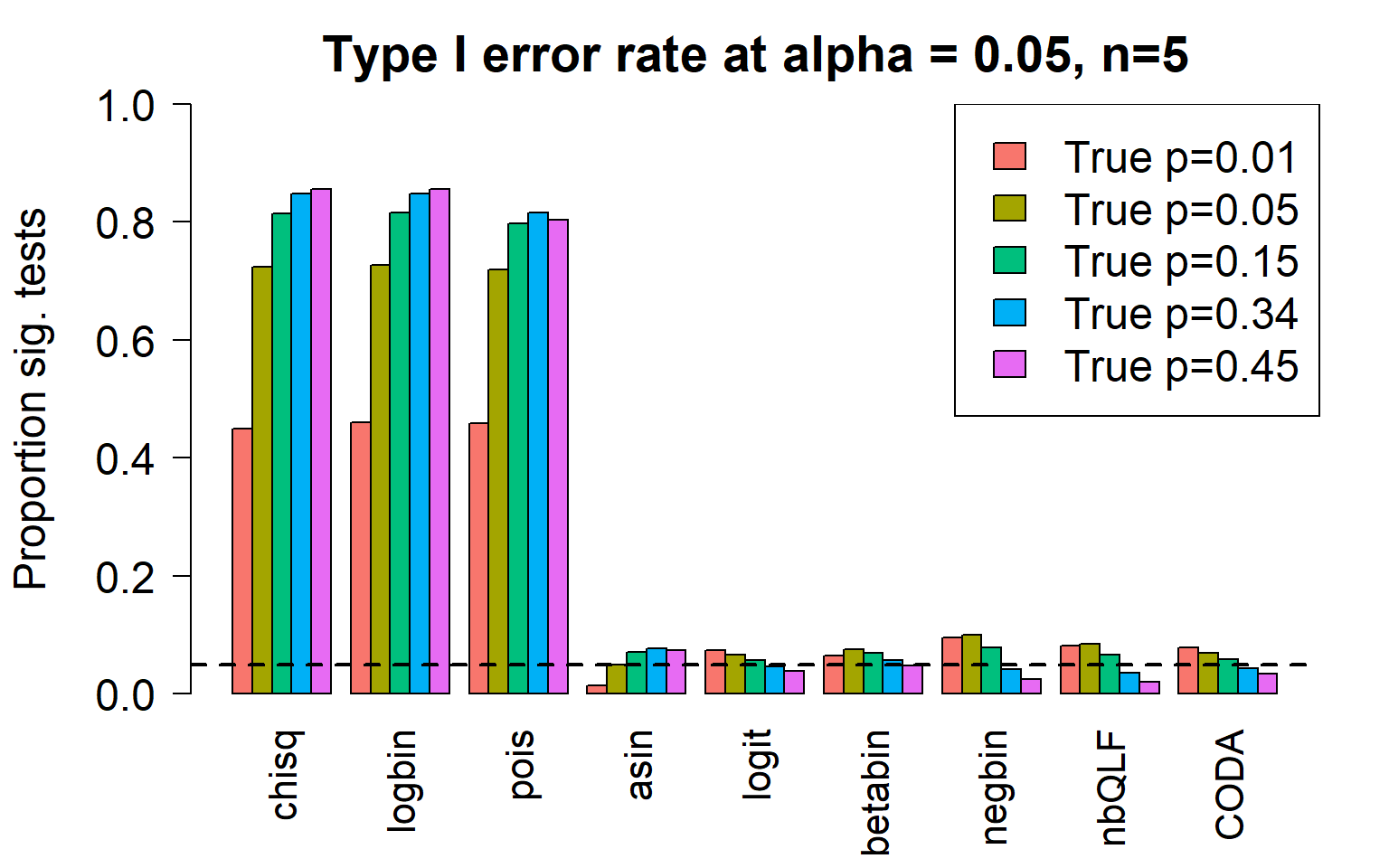
Removing the most poorly performing methods (1-3):
par(mfrow=c(1,1))
par(mar=c(5,5.5,3,2))
par(mgp=c(4,1,0))
barplot(type1error[,4:9],beside=TRUE,col=ggplotColors(length(p)),
ylab="Proportion sig. tests",
cex.axis = 1.5, cex.lab=1.5, cex.names = 1.35, ylim=c(0,0.15), las=2)
#legend("top",fill=ggplotColors(length(b)),legend=c(paste("True p=",p,sep="")), cex=1.5)
abline(h=pcut,lty=2,lwd=2)
title(c(paste("Type I error rate at alpha = 0.05, n=", nsamp/2,sep="")), cex.main=1.75)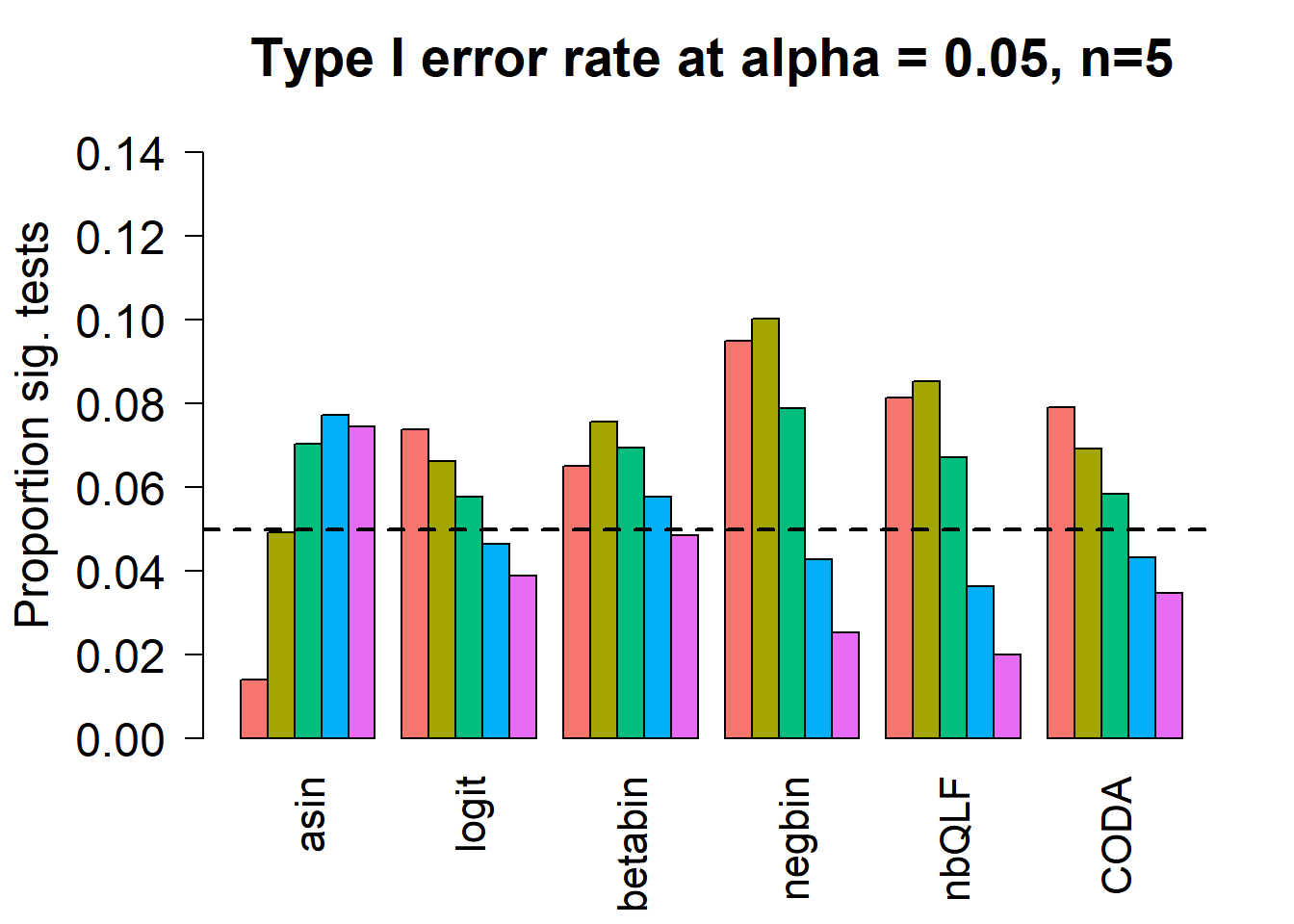
# save the type 1 error objects for n=5
type1error5 <- type1errorSample size of 10 in each group
nsamp <- 20
for(i in 1:nsim){
#Simulate cell type counts
counts <- SimulateCellCounts(props=p,nsamp=nsamp,depth=depth,a=a,b=b)
tot.cells <- colSums(counts)
# propeller
est.props <- t(t(counts)/tot.cells)
#asin transform
trans.prop <- asin(sqrt(est.props))
#logit transform
nc <- normCounts(counts)
est.props.logit <- t(t(nc+0.5)/(colSums(nc+0.5)))
logit.prop <- log(est.props.logit/(1-est.props.logit))
grp <- rep(c(0,1), each=nsamp/2)
des <- model.matrix(~grp)
# asinsqrt transform
fit <- lmFit(trans.prop, des)
fit <- eBayes(fit, robust=TRUE)
pval.asin[,i] <- fit$p.value[,2]
# logit transform
fit.logit <- lmFit(logit.prop, des)
fit.logit <- eBayes(fit.logit, robust=TRUE)
pval.logit[,i] <- fit.logit$p.value[,2]
# Chi-square test for differences in proportions
n <- tapply(tot.cells, grp, sum)
for(h in 1:length(p)){
pval.chsq[h,i] <- prop.test(tapply(counts[h,],grp,sum),n)$p.value
}
# Beta binomial implemented in edgeR (methylation workflow)
meth.counts <- counts
unmeth.counts <- t(tot.cells - t(counts))
new.counts <- cbind(meth.counts,unmeth.counts)
sam.info <- data.frame(Sample = rep(1:nsamp,2), Group=rep(grp,2), Meth = rep(c("me","un"), each=nsamp))
design.samples <- model.matrix(~0+factor(sam.info$Sample))
colnames(design.samples) <- paste("S",1:nsamp,sep="")
design.group <- model.matrix(~0+factor(sam.info$Group))
colnames(design.group) <- c("A","B")
design.bb <- cbind(design.samples, (sam.info$Meth=="me") * design.group)
lib.size = rep(tot.cells,2)
y <- DGEList(new.counts)
y$samples$lib.size <- lib.size
y <- estimateDisp(y, design.bb, trend="none")
fit.bb <- glmFit(y, design.bb)
contr <- makeContrasts(Grp=B-A, levels=design.bb)
lrt <- glmLRT(fit.bb, contrast=contr)
pval.bb[,i] <- lrt$table$PValue
# Logistic binomial regression
fit.lb <- glmFit(y, design.bb, dispersion = 0)
lrt.lb <- glmLRT(fit.lb, contrast=contr)
pval.lb[,i] <- lrt.lb$table$PValue
# Negative binomial
y.nb <- DGEList(counts)
y.nb <- estimateDisp(y.nb, des, trend="none")
fit.nb <- glmFit(y.nb, des)
lrt.nb <- glmLRT(fit.nb, coef=2)
pval.nb[,i] <- lrt.nb$table$PValue
# Negative binomial QLF test
fit.qlf <- glmQLFit(y.nb, des, robust=TRUE, abundance.trend = FALSE)
res.qlf <- glmQLFTest(fit.qlf, coef=2)
pval.qlf[,i] <- res.qlf$table$PValue
# Poisson
fit.poi <- glmFit(y.nb, des, dispersion = 0)
lrt.poi <- glmLRT(fit.poi, coef=2)
pval.pois[,i] <- lrt.poi$table$PValue
# CODA
# Replace zero counts with 0.5 so that the geometric mean always works
if(any(counts==0)) counts[counts==0] <- 0.5
geomean <- apply(counts,2, function(x) exp(mean(log(x))))
geomean.mat <- expandAsMatrix(geomean,dim=c(nrow(counts),ncol(counts)),byrow = FALSE)
clr <- counts/geomean.mat
logratio <- log(clr)
fit.coda <- lmFit(logratio, des)
fit.coda <- eBayes(fit.coda, robust=TRUE)
pval.coda[,i] <- fit.coda$p.value[,2]
}We can look at the number of significant tests at different p-value cut-offs:
pcut <- 0.01
type1error <- matrix(NA,nrow=length(p),ncol=9)
rownames(type1error) <- rownames(counts)
colnames(type1error) <- c("chisq","logbin","pois","asin", "logit","betabin","negbin", "nbQLF","CODA")
type1error[,1]<-rowSums(pval.chsq<pcut)/nsim
type1error[,2]<-rowSums(pval.lb<pcut)/nsim
type1error[,3]<-rowSums(pval.pois<pcut)/nsim
type1error[,4]<-rowSums(pval.asin<pcut)/nsim
type1error[,5]<-rowSums(pval.logit<pcut)/nsim
type1error[,6]<-rowSums(pval.bb<pcut)/nsim
type1error[,7]<-rowSums(pval.nb<pcut)/nsim
type1error[,8]<-rowSums(pval.qlf<pcut)/nsim
type1error[,9]<-rowSums(pval.coda<pcut)/nsim
type1error chisq logbin pois asin logit betabin negbin nbQLF CODA
c0 0.3309 0.3362 0.3341 0.0031 0.0187 0.0155 0.0260 0.0189 0.0198
c1 0.6276 0.6296 0.6189 0.0103 0.0133 0.0167 0.0227 0.0166 0.0132
c2 0.7628 0.7637 0.7435 0.0128 0.0104 0.0150 0.0173 0.0130 0.0116
c3 0.8029 0.8037 0.7594 0.0145 0.0080 0.0115 0.0092 0.0062 0.0074
c4 0.8039 0.8043 0.7361 0.0133 0.0055 0.0071 0.0045 0.0032 0.0055pcut <- 0.05
type1error <- matrix(NA,nrow=length(p),ncol=9)
rownames(type1error) <- rownames(counts)
colnames(type1error) <- c("chisq","logbin","pois","asin", "logit","betabin","negbin","nbQLF","CODA")
type1error[,1]<-rowSums(pval.chsq<pcut)/nsim
type1error[,2]<-rowSums(pval.lb<pcut)/nsim
type1error[,3]<-rowSums(pval.pois<pcut)/nsim
type1error[,4]<-rowSums(pval.asin<pcut)/nsim
type1error[,5]<-rowSums(pval.logit<pcut)/nsim
type1error[,6]<-rowSums(pval.bb<pcut)/nsim
type1error[,7]<-rowSums(pval.nb<pcut)/nsim
type1error[,8]<-rowSums(pval.qlf<pcut)/nsim
type1error[,9]<-rowSums(pval.coda<pcut)/nsim
type1error chisq logbin pois asin logit betabin negbin nbQLF CODA
c0 0.4589 0.4679 0.4653 0.0259 0.0769 0.0682 0.0834 0.0735 0.0787
c1 0.7129 0.7150 0.7079 0.0485 0.0562 0.0617 0.0748 0.0662 0.0592
c2 0.8178 0.8187 0.8033 0.0589 0.0520 0.0604 0.0649 0.0583 0.0566
c3 0.8482 0.8490 0.8162 0.0608 0.0458 0.0516 0.0425 0.0389 0.0406
c4 0.8473 0.8475 0.7996 0.0574 0.0362 0.0414 0.0281 0.0248 0.0297Plot of all type I error rates for the 5 cell types:
par(mfrow=c(1,1))
par(mar=c(5,5.5,3,2))
par(mgp=c(4,1,0))
barplot(type1error,beside=TRUE,col=ggplotColors(length(p)),
ylab="Proportion sig. tests",
cex.axis = 1.5, cex.lab=1.5, cex.names = 1.35, ylim=c(0,1), las=2)
legend("topright",fill=ggplotColors(length(p)),legend=c(paste("True p=",p,sep="")), cex=1.5)
abline(h=pcut,lty=2,lwd=2)
title(c(paste("Type I error rate at alpha = 0.05, n=", nsamp/2,sep="")), cex.main=1.75)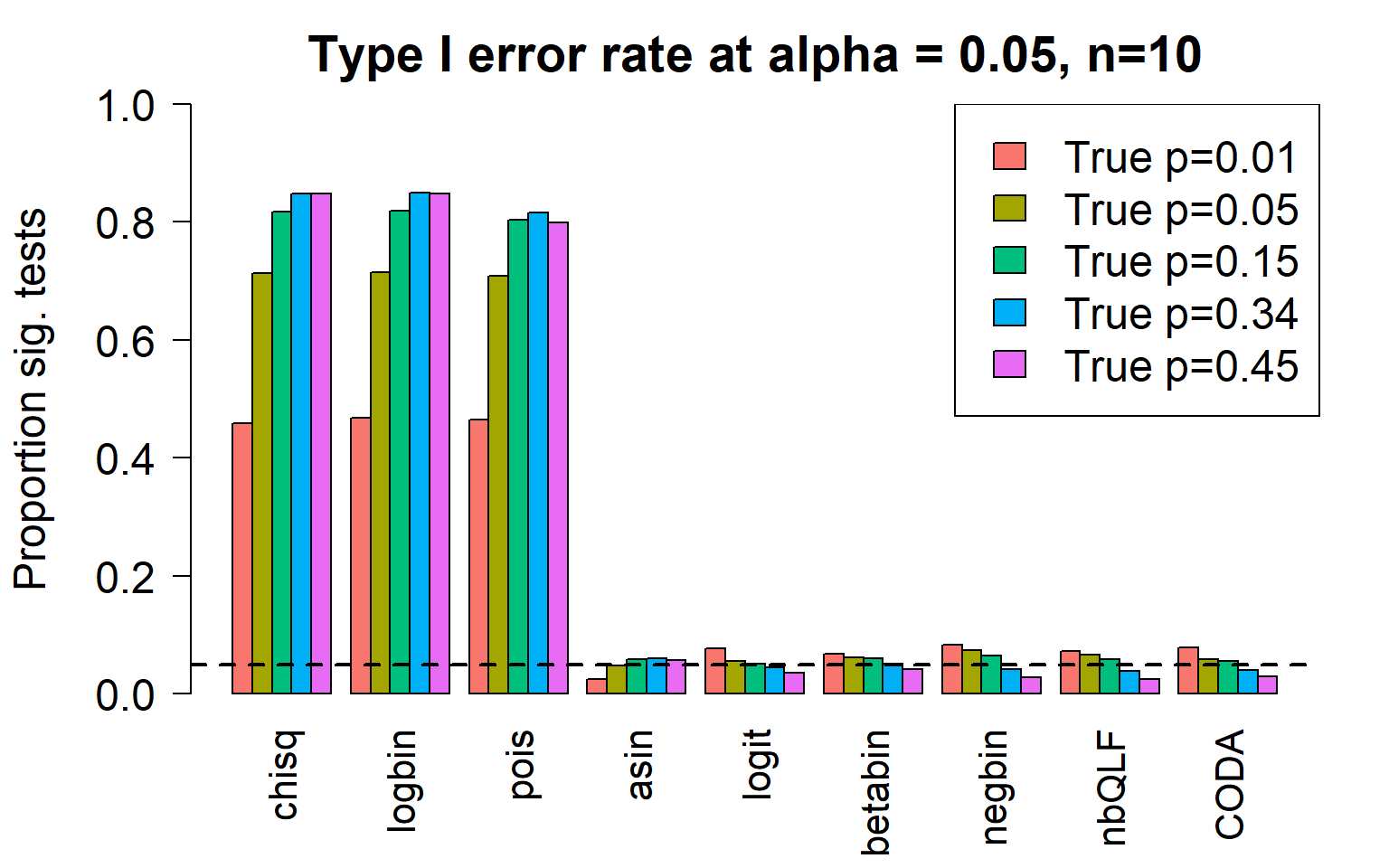
Removing the most poorly performing methods (1-3):
par(mfrow=c(1,1))
par(mar=c(5,5.5,3,2))
par(mgp=c(4,1,0))
barplot(type1error[,4:9],beside=TRUE,col=ggplotColors(length(p)),
ylab="Proportion sig. tests",
cex.axis = 1.5, cex.lab=1.5, cex.names = 1.35, ylim=c(0,0.15), las=2)
#legend("top",fill=ggplotColors(length(b)),legend=c(paste("True p=",p,sep="")), cex=1.5)
abline(h=pcut,lty=2,lwd=2)
title(c(paste("Type I error rate at alpha = 0.05, n=", nsamp/2,sep="")), cex.main=1.75)
# save the type 1 error objects for n=10
type1error10 <- type1errorSample size of 20 in each group
nsamp <- 40
for(i in 1:nsim){
#Simulate cell type counts
counts <- SimulateCellCounts(props=p,nsamp=nsamp,depth=depth,a=a,b=b)
tot.cells <- colSums(counts)
# propeller
est.props <- t(t(counts)/tot.cells)
#asin transform
trans.prop <- asin(sqrt(est.props))
#logit transform
nc <- normCounts(counts)
est.props.logit <- t(t(nc+0.5)/(colSums(nc+0.5)))
logit.prop <- log(est.props.logit/(1-est.props.logit))
grp <- rep(c(0,1), each=nsamp/2)
des <- model.matrix(~grp)
# asinsqrt transform
fit <- lmFit(trans.prop, des)
fit <- eBayes(fit, robust=TRUE)
pval.asin[,i] <- fit$p.value[,2]
# logit transform
fit.logit <- lmFit(logit.prop, des)
fit.logit <- eBayes(fit.logit, robust=TRUE)
pval.logit[,i] <- fit.logit$p.value[,2]
# Chi-square test for differences in proportions
n <- tapply(tot.cells, grp, sum)
for(h in 1:length(p)){
pval.chsq[h,i] <- prop.test(tapply(counts[h,],grp,sum),n)$p.value
}
# Beta binomial implemented in edgeR (methylation workflow)
meth.counts <- counts
unmeth.counts <- t(tot.cells - t(counts))
new.counts <- cbind(meth.counts,unmeth.counts)
sam.info <- data.frame(Sample = rep(1:nsamp,2), Group=rep(grp,2), Meth = rep(c("me","un"), each=nsamp))
design.samples <- model.matrix(~0+factor(sam.info$Sample))
colnames(design.samples) <- paste("S",1:nsamp,sep="")
design.group <- model.matrix(~0+factor(sam.info$Group))
colnames(design.group) <- c("A","B")
design.bb <- cbind(design.samples, (sam.info$Meth=="me") * design.group)
lib.size = rep(tot.cells,2)
y <- DGEList(new.counts)
y$samples$lib.size <- lib.size
y <- estimateDisp(y, design.bb, trend="none")
fit.bb <- glmFit(y, design.bb)
contr <- makeContrasts(Grp=B-A, levels=design.bb)
lrt <- glmLRT(fit.bb, contrast=contr)
pval.bb[,i] <- lrt$table$PValue
# Logistic binomial regression
fit.lb <- glmFit(y, design.bb, dispersion = 0)
lrt.lb <- glmLRT(fit.lb, contrast=contr)
pval.lb[,i] <- lrt.lb$table$PValue
# Negative binomial
y.nb <- DGEList(counts)
y.nb <- estimateDisp(y.nb, des, trend="none")
fit.nb <- glmFit(y.nb, des)
lrt.nb <- glmLRT(fit.nb, coef=2)
pval.nb[,i] <- lrt.nb$table$PValue
# Negative binomial QLF test
fit.qlf <- glmQLFit(y.nb, des, robust=TRUE, abundance.trend = FALSE)
res.qlf <- glmQLFTest(fit.qlf, coef=2)
pval.qlf[,i] <- res.qlf$table$PValue
# Poisson
fit.poi <- glmFit(y.nb, des, dispersion = 0)
lrt.poi <- glmLRT(fit.poi, coef=2)
pval.pois[,i] <- lrt.poi$table$PValue
# CODA
# Replace zero counts with 0.5 so that the geometric mean always works
if(any(counts==0)) counts[counts==0] <- 0.5
geomean <- apply(counts,2, function(x) exp(mean(log(x))))
geomean.mat <- expandAsMatrix(geomean,dim=c(nrow(counts),ncol(counts)),byrow = FALSE)
clr <- counts/geomean.mat
logratio <- log(clr)
fit.coda <- lmFit(logratio, des)
fit.coda <- eBayes(fit.coda, robust=TRUE)
pval.coda[,i] <- fit.coda$p.value[,2]
}We can look at the number of significant tests at different p-value cut-offs:
pcut <- 0.01
type1error <- matrix(NA,nrow=length(p),ncol=9)
rownames(type1error) <- rownames(counts)
colnames(type1error) <- c("chisq","logbin","pois","asin", "logit","betabin","negbin", "nbQLF","CODA")
type1error[,1]<-rowSums(pval.chsq<pcut)/nsim
type1error[,2]<-rowSums(pval.lb<pcut)/nsim
type1error[,3]<-rowSums(pval.pois<pcut)/nsim
type1error[,4]<-rowSums(pval.asin<pcut)/nsim
type1error[,5]<-rowSums(pval.logit<pcut)/nsim
type1error[,6]<-rowSums(pval.bb<pcut)/nsim
type1error[,7]<-rowSums(pval.nb<pcut)/nsim
type1error[,8]<-rowSums(pval.qlf<pcut)/nsim
type1error[,9]<-rowSums(pval.coda<pcut)/nsim
type1error chisq logbin pois asin logit betabin negbin nbQLF CODA
c0 0.3399 0.3428 0.3409 0.0055 0.0175 0.0140 0.0180 0.0142 0.0183
c1 0.6338 0.6353 0.6263 0.0082 0.0102 0.0120 0.0140 0.0102 0.0123
c2 0.7626 0.7632 0.7434 0.0126 0.0121 0.0143 0.0143 0.0114 0.0134
c3 0.8016 0.8021 0.7551 0.0121 0.0082 0.0104 0.0094 0.0073 0.0063
c4 0.8078 0.8081 0.7442 0.0133 0.0074 0.0097 0.0080 0.0062 0.0072pcut <- 0.05
type1error <- matrix(NA,nrow=length(p),ncol=9)
rownames(type1error) <- rownames(counts)
colnames(type1error) <- c("chisq","logbin","pois","asin", "logit","betabin","negbin","nbQLF","CODA")
type1error[,1]<-rowSums(pval.chsq<pcut)/nsim
type1error[,2]<-rowSums(pval.lb<pcut)/nsim
type1error[,3]<-rowSums(pval.pois<pcut)/nsim
type1error[,4]<-rowSums(pval.asin<pcut)/nsim
type1error[,5]<-rowSums(pval.logit<pcut)/nsim
type1error[,6]<-rowSums(pval.bb<pcut)/nsim
type1error[,7]<-rowSums(pval.nb<pcut)/nsim
type1error[,8]<-rowSums(pval.qlf<pcut)/nsim
type1error[,9]<-rowSums(pval.coda<pcut)/nsim
type1error chisq logbin pois asin logit betabin negbin nbQLF CODA
c0 0.4632 0.4683 0.4660 0.0372 0.0716 0.0622 0.0698 0.0628 0.0722
c1 0.7155 0.7172 0.7102 0.0472 0.0564 0.0602 0.0618 0.0565 0.0566
c2 0.8171 0.8174 0.8030 0.0596 0.0571 0.0636 0.0597 0.0568 0.0544
c3 0.8486 0.8490 0.8149 0.0551 0.0440 0.0478 0.0435 0.0410 0.0417
c4 0.8542 0.8543 0.8038 0.0568 0.0409 0.0445 0.0352 0.0322 0.0391Plot of all type I error rates for the 5 cell types:
par(mfrow=c(1,1))
par(mar=c(5,5.5,3,2))
par(mgp=c(4,1,0))
barplot(type1error,beside=TRUE,col=ggplotColors(length(p)),
ylab="Proportion sig. tests",
cex.axis = 1.5, cex.lab=1.5, cex.names = 1.35, ylim=c(0,1), las=2)
legend("topright",fill=ggplotColors(length(p)),legend=c(paste("True p=",p,sep="")), cex=1.5)
abline(h=pcut,lty=2,lwd=2)
title(c(paste("Type I error rate at alpha = 0.05, n=", nsamp/2,sep="")), cex.main=1.75)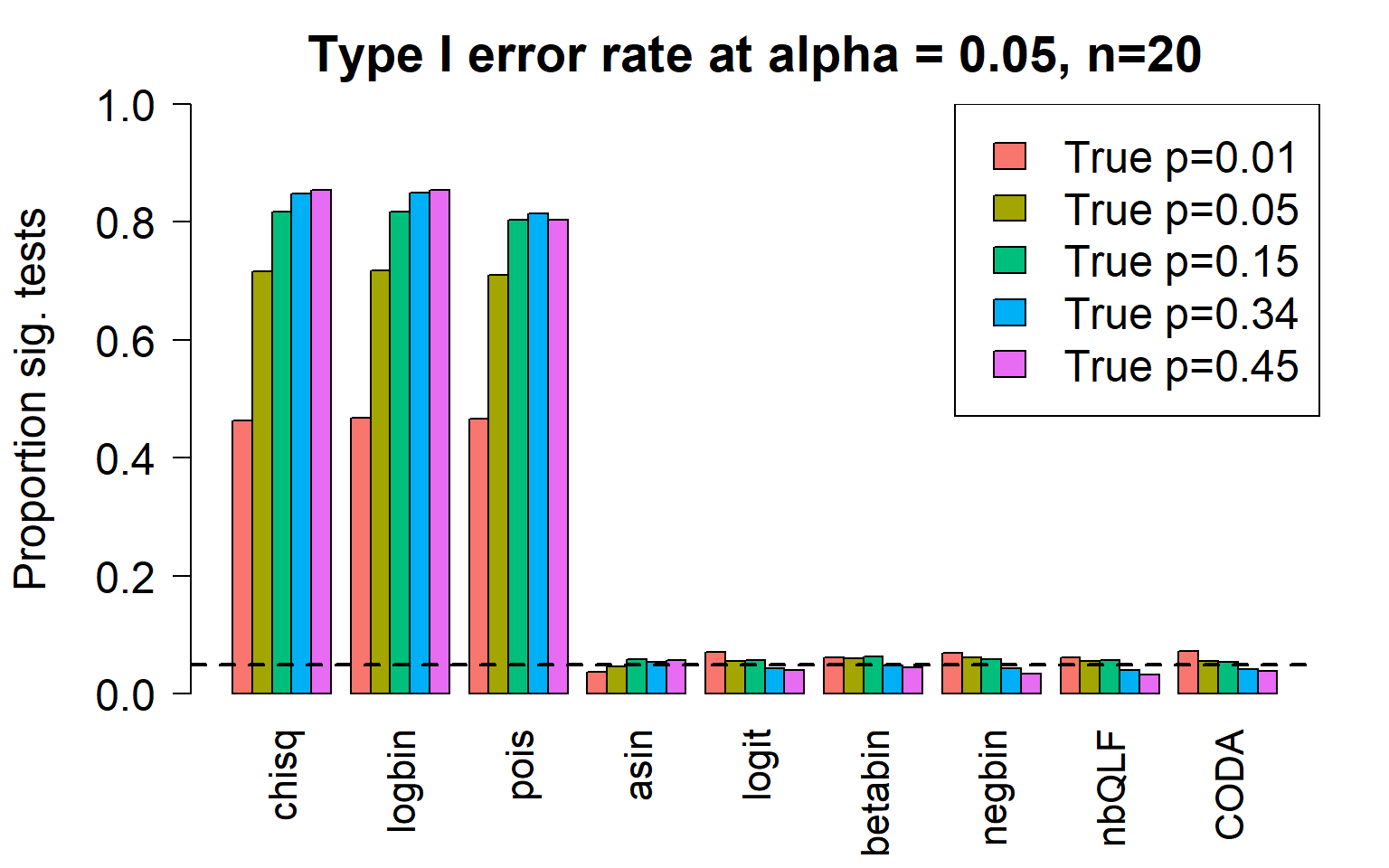
Removing the most poorly performing methods (1-3):
par(mfrow=c(1,1))
par(mar=c(5,5.5,3,2))
par(mgp=c(4,1,0))
barplot(type1error[,4:9],beside=TRUE,col=ggplotColors(length(p)),
ylab="Proportion sig. tests",
cex.axis = 1.5, cex.lab=1.5, cex.names = 1.35, ylim=c(0,0.15), las=2)
abline(h=pcut,lty=2,lwd=2)
title(c(paste("Type I error rate at alpha = 0.05, n=", nsamp/2,sep="")), cex.main=1.75)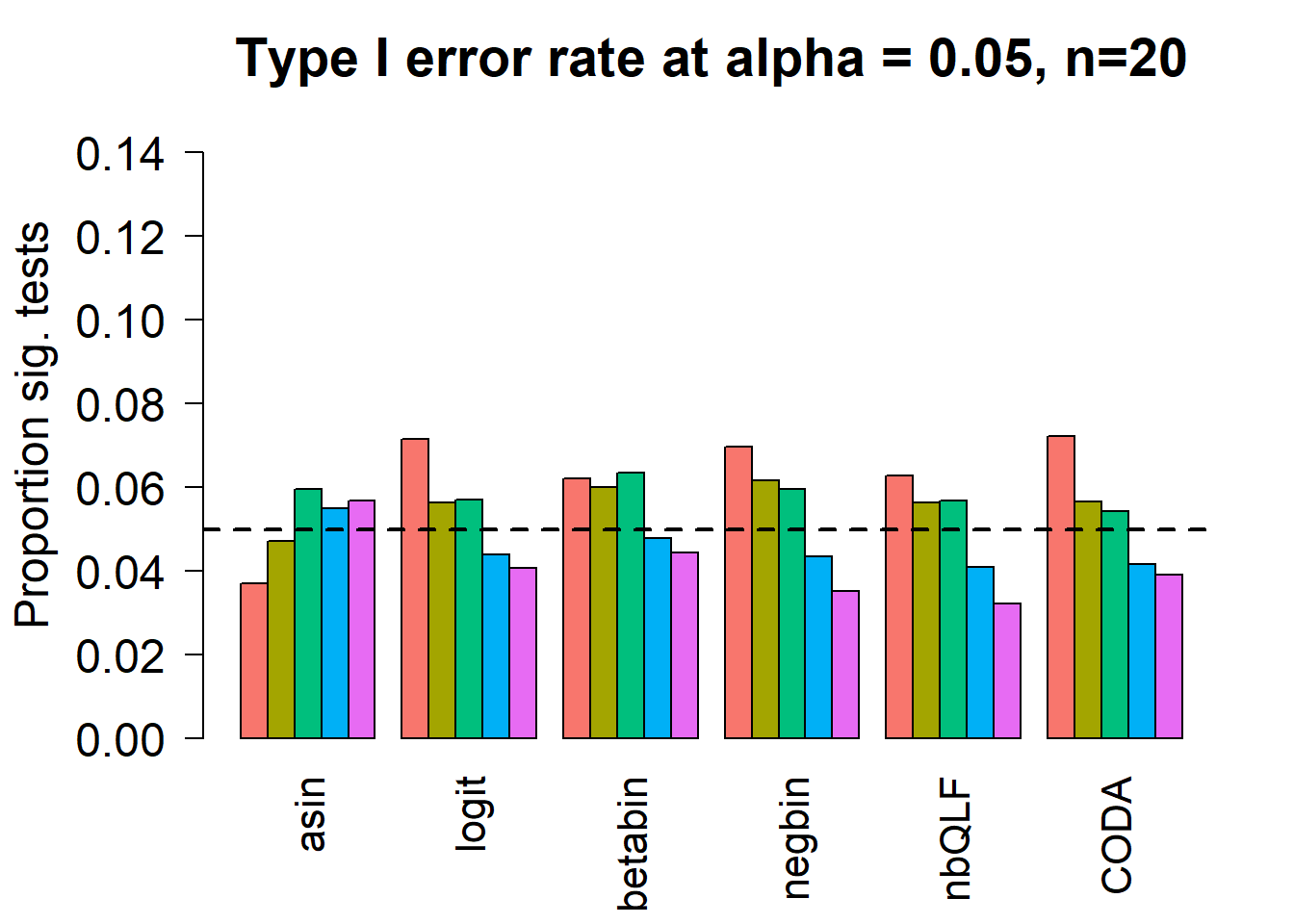
# save the type 1 error objects for n=20
type1error20 <- type1errorPlot results together across all sample sizes
par(mar=c(8,5,3,2))
par(mgp=c(3, 0.5, 0))
layout(matrix(c(1,1,1,2), 1, 4, byrow = TRUE))
#layout.show(2)
names <- c("propeller (asin)","propeller (logit)","betabin","negbin","negbinQLF","CODA")
barplot(cbind(type1error3[,4:9], type1error5[,4:9],type1error10[,4:9], type1error20[,4:9]),
beside=TRUE,col=ggplotColors(5), ylab="Proportion sig. tests",
cex.axis = 1.25, cex.lab=1.5, cex.names = 1.25, ylim=c(0,0.15),
names=rep(names,4), las=2)
title("Type I error at alpha = 0.05", cex.main=2, adj=0)
#legend("topright",fill=ggplotColors(5),legend=c(paste("True p=",p,sep="")), cex=1.2)
abline(v=36.5, lty=1, lwd=2)
abline(v=72.5, lty=1, lwd=2)
abline(v=108.5, lty=1, lwd=2)
abline(h=0.05, col="dark blue", lty=2, lwd=2)
text(20,0.14, labels = "n = 3", cex=1.5)
text(55,0.14, labels = "n = 5", cex=1.5)
text(90,0.14, labels = "n = 10", cex=1.5)
text(125,0.14, labels = "n = 20", cex=1.5)
text(0,0.055, labels = "0.05", cex=1.25, col="dark blue")
par(mar=c(0,0,0,0))
plot(1, type = "n", xlab = "", ylab = "", xaxt="n",yaxt="n", bty="n")
legend("center",fill=ggplotColors(5),legend=c(paste("True p=",p,sep="")), cex=2)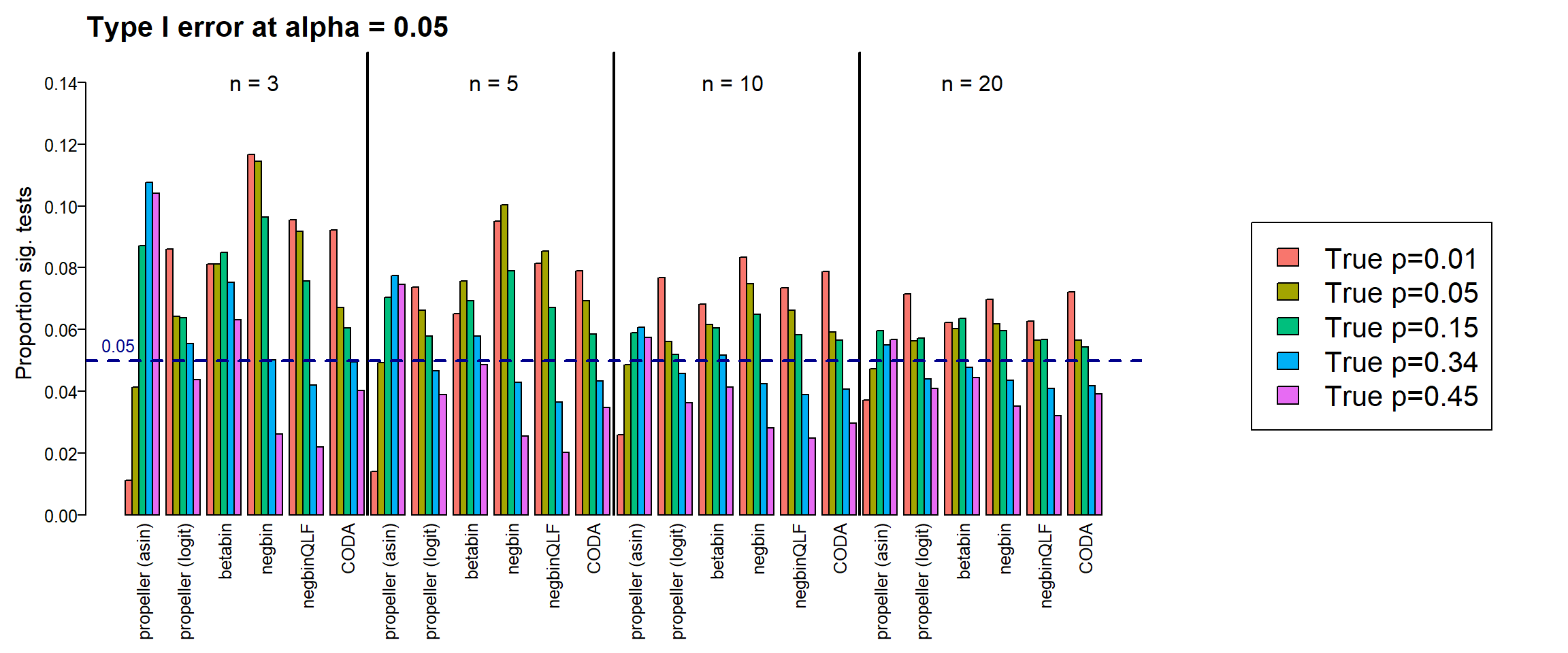
pdf(file="./output/fig2d.pdf", width=12, height=5)
par(mar=c(8,5,3,2))
par(mgp=c(3, 0.5, 0))
layout(matrix(c(1,1,1,2), 1, 4, byrow = TRUE))
#layout.show(2)
names <- c("propeller (asin)","propeller (logit)","betabin","negbin","negbinQLF","CODA")
barplot(cbind(type1error3[,4:9], type1error5[,4:9],type1error10[,4:9], type1error20[,4:9]),
beside=TRUE,col=ggplotColors(5), ylab="Proportion sig. tests",
cex.axis = 1.25, cex.lab=1.5, cex.names = 1.25, ylim=c(0,0.15),
names=rep(names,4), las=2)
title("Type I error at alpha = 0.05", cex.main=2, adj=0)
#legend("topright",fill=ggplotColors(5),legend=c(paste("True p=",p,sep="")), cex=1.2)
abline(v=36.5, lty=1, lwd=2)
abline(v=72.5, lty=1, lwd=2)
abline(v=108.5, lty=1, lwd=2)
abline(h=0.05, col="dark blue", lty=2, lwd=2)
text(20,0.14, labels = "n = 3", cex=1.5)
text(55,0.14, labels = "n = 5", cex=1.5)
text(90,0.14, labels = "n = 10", cex=1.5)
text(125,0.14, labels = "n = 20", cex=1.5)
text(0,0.055, labels = "0.05", cex=1.25, col="dark blue")
par(mar=c(0,0,0,0))
plot(1, type = "n", xlab = "", ylab = "", xaxt="n",yaxt="n", bty="n")
legend("center",fill=ggplotColors(5),legend=c(paste("True p=",p,sep="")), cex=2)
dev.off()png
2 pdf(file="./output/legend-fig2d.pdf", height = 4, width = 4)
par(mfrow=c(1,1))
par(mar=c(0,0,0,0))
plot.new()
legend("center",fill=ggplotColors(5),legend=c(paste("True p=",p,sep="")), cex=2)
dev.off()png
2 Mean-variance relationship from simulated counts
This is the mean variance relationship from one simulated dataset, n=5.
counts <- SimulateCellCounts(props=p,nsamp=10,depth=depth,a=a,b=b)
tot.cells <- colSums(counts)
est.props <- t(t(counts)/tot.cells)par(mfrow=c(1,3))
par(mar=c(5,5,3,2))
barplot(est.props, col=ggplotColors(5), names=paste("S",1:10,sep=""),
cex.names = 1.25, cex.axis = 1.5, cex.lab = 1.5, cex.main=2,
ylab = "Proportion", xlab="Sample",
main = "Cell type proportions")
plotCellTypeMeanVar(counts)
plotCellTypePropsMeanVar(counts)
pdf(file="./output/example_simdata.pdf", width=13, height=5)
par(mfrow=c(1,3))
par(mar=c(5,5,3,2))
barplot(est.props, col=ggplotColors(5), names=paste("S",1:10,sep=""),
cex.names = 1.15, cex.axis = 1.5, cex.lab = 1.5, cex.main=2,
ylab = "Proportion", xlab="Sample",
main = "a) Cell type proportions")
plotCellTypeMeanVar(counts)
plotCellTypePropsMeanVar(counts)
dev.off()png
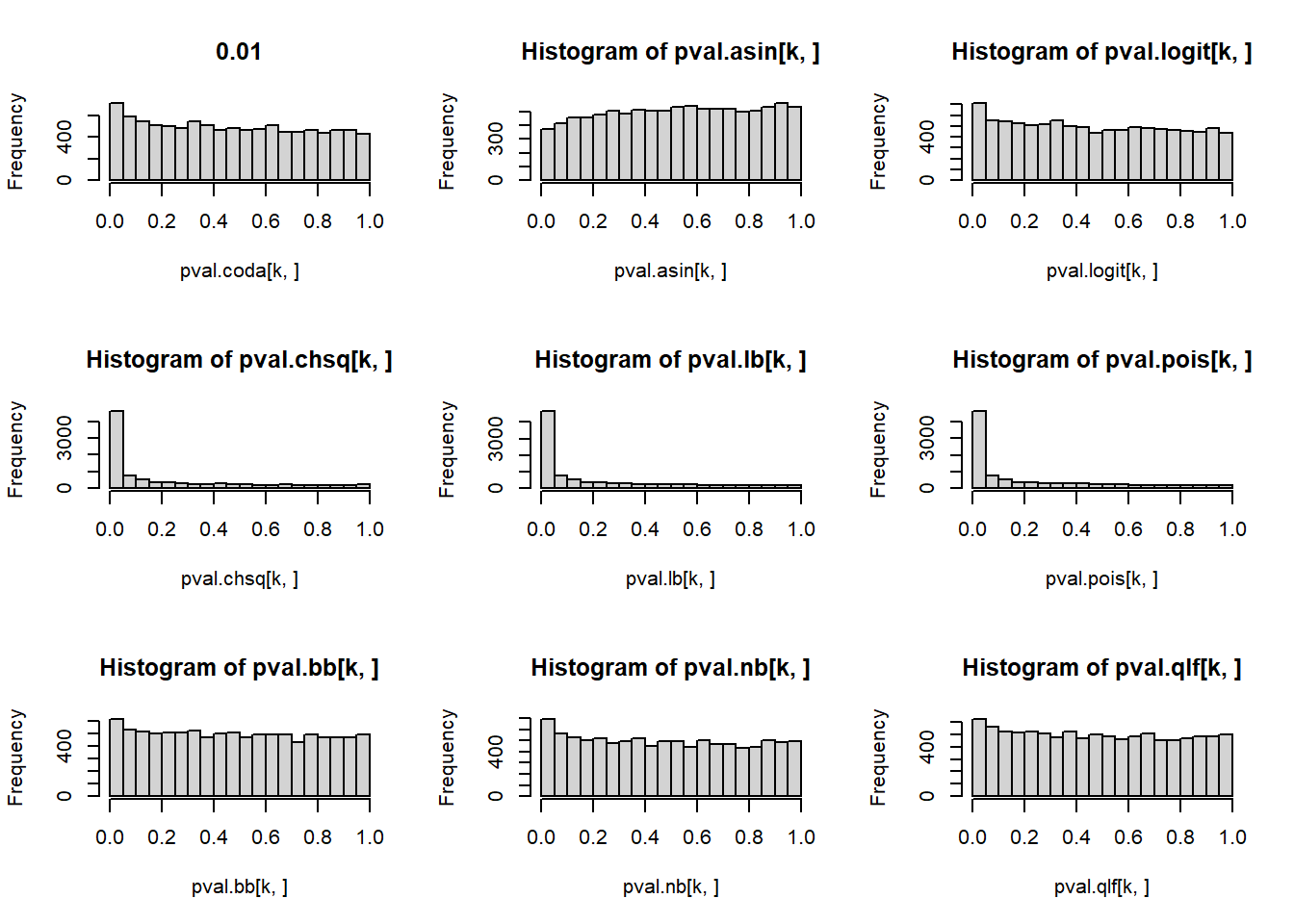
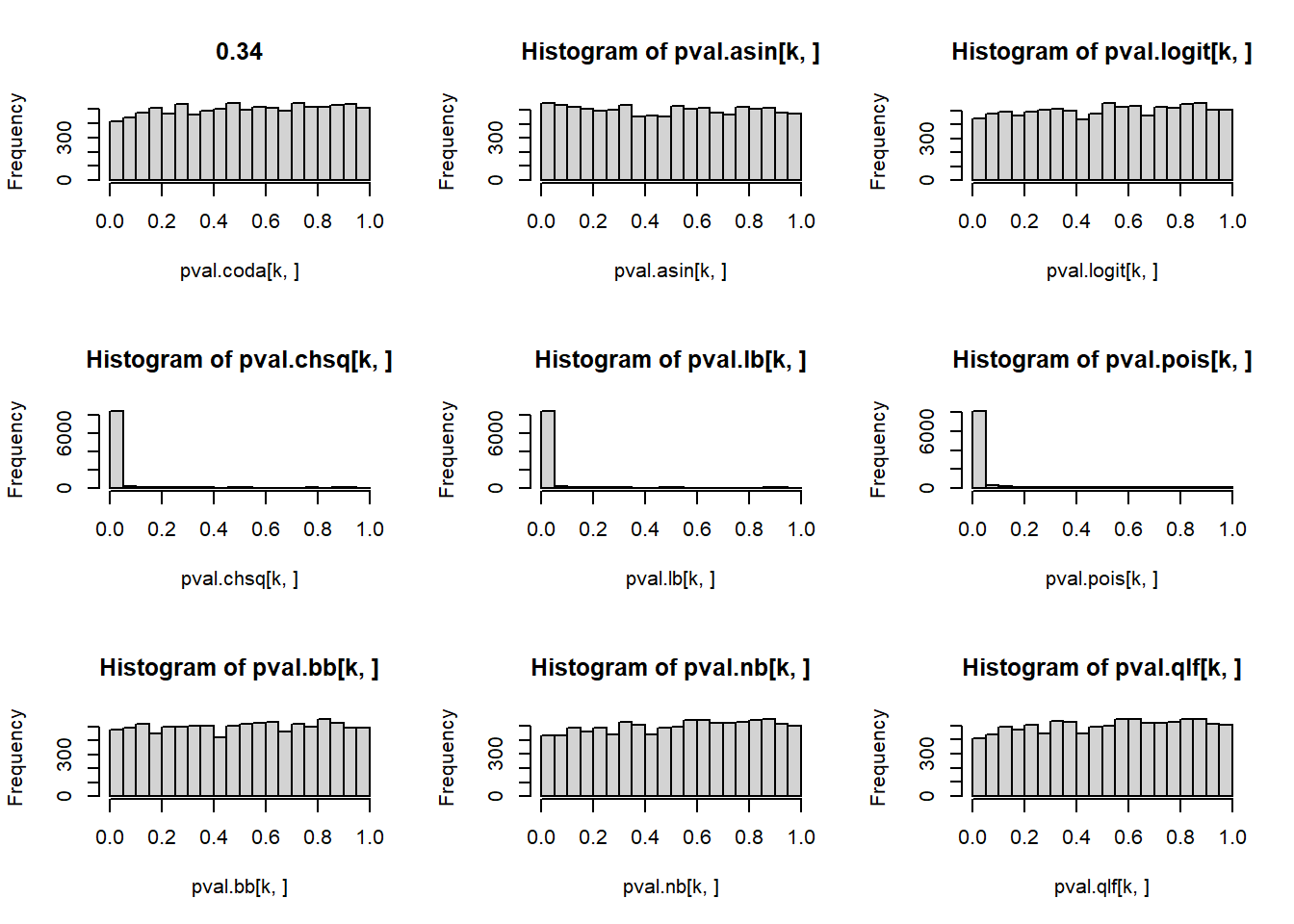
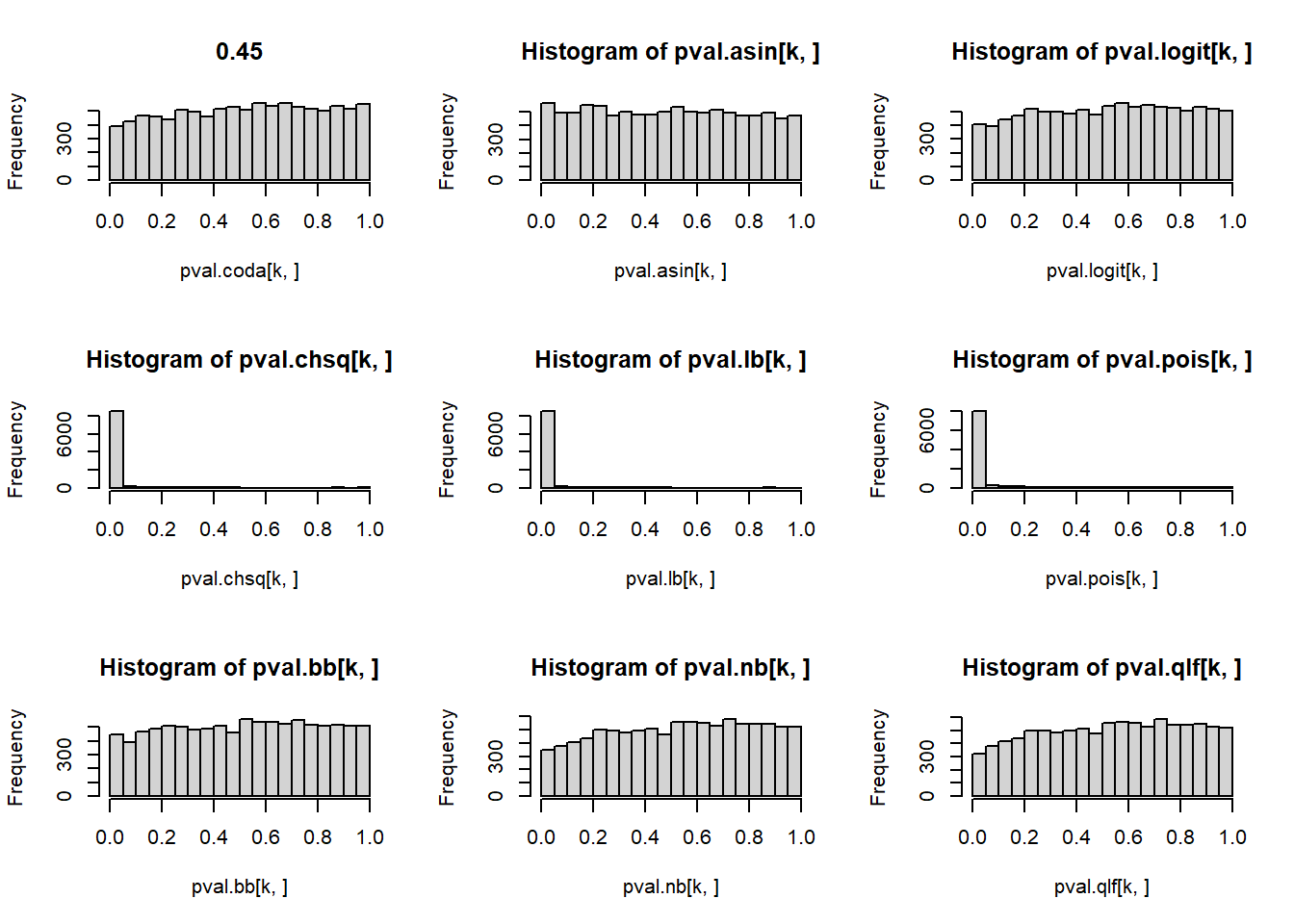
2 P-value histograms
# P-values across all cell types and simulations
par(mfrow=c(3,3))
hist(pval.coda)
hist(pval.asin)
hist(pval.logit)
hist(pval.chsq)
hist(pval.lb)
hist(pval.pois)
hist(pval.bb)
hist(pval.nb)
hist(pval.qlf)
# P-values for each cell type across simulations
par(mfrow=c(3,3))
for(k in 1:5){
hist(pval.coda[k,], main=p[k])
hist(pval.asin[k,])
hist(pval.logit[k,])
hist(pval.chsq[k,])
hist(pval.lb[k,])
hist(pval.pois[k,])
hist(pval.bb[k,])
hist(pval.nb[k,])
hist(pval.qlf[k,])
}


save(type1error3, type1error5, type1error10, type1error20,
file="./output/typeIerrorResults.Rda")
sessionInfo()R version 4.2.0 (2022-04-22 ucrt)
Platform: x86_64-w64-mingw32/x64 (64-bit)
Running under: Windows 10 x64 (build 22000)
Matrix products: default
locale:
[1] LC_COLLATE=English_United States.utf8
[2] LC_CTYPE=English_United States.utf8
[3] LC_MONETARY=English_United States.utf8
[4] LC_NUMERIC=C
[5] LC_TIME=English_United States.utf8
attached base packages:
[1] stats graphics grDevices utils datasets methods base
other attached packages:
[1] edgeR_3.38.1 limma_3.52.1 speckle_0.99.0 workflowr_1.7.0
loaded via a namespace (and not attached):
[1] plyr_1.8.7 igraph_1.3.1
[3] lazyeval_0.2.2 sp_1.4-7
[5] splines_4.2.0 BiocParallel_1.30.2
[7] listenv_0.8.0 scattermore_0.8
[9] GenomeInfoDb_1.32.2 ggplot2_3.3.6
[11] digest_0.6.29 htmltools_0.5.2
[13] fansi_1.0.3 magrittr_2.0.3
[15] memoise_2.0.1 tensor_1.5
[17] cluster_2.1.3 ROCR_1.0-11
[19] globals_0.15.0 Biostrings_2.64.0
[21] matrixStats_0.62.0 spatstat.sparse_2.1-1
[23] colorspace_2.0-3 blob_1.2.3
[25] ggrepel_0.9.1 xfun_0.31
[27] dplyr_1.0.9 callr_3.7.0
[29] crayon_1.5.1 RCurl_1.98-1.6
[31] jsonlite_1.8.0 org.Mm.eg.db_3.15.0
[33] progressr_0.10.0 spatstat.data_2.2-0
[35] survival_3.3-1 zoo_1.8-10
[37] glue_1.6.2 polyclip_1.10-0
[39] gtable_0.3.0 zlibbioc_1.42.0
[41] XVector_0.36.0 leiden_0.4.2
[43] DelayedArray_0.22.0 SingleCellExperiment_1.18.0
[45] future.apply_1.9.0 BiocGenerics_0.42.0
[47] abind_1.4-5 scales_1.2.0
[49] DBI_1.1.2 spatstat.random_2.2-0
[51] miniUI_0.1.1.1 Rcpp_1.0.8.3
[53] viridisLite_0.4.0 xtable_1.8-4
[55] reticulate_1.25 spatstat.core_2.4-4
[57] bit_4.0.4 stats4_4.2.0
[59] htmlwidgets_1.5.4 httr_1.4.3
[61] RColorBrewer_1.1-3 ellipsis_0.3.2
[63] Seurat_4.1.1 ica_1.0-2
[65] scuttle_1.6.2 pkgconfig_2.0.3
[67] uwot_0.1.11 sass_0.4.1
[69] deldir_1.0-6 locfit_1.5-9.5
[71] utf8_1.2.2 tidyselect_1.1.2
[73] rlang_1.0.2 reshape2_1.4.4
[75] later_1.3.0 AnnotationDbi_1.58.0
[77] munsell_0.5.0 tools_4.2.0
[79] cachem_1.0.6 cli_3.3.0
[81] generics_0.1.2 RSQLite_2.2.14
[83] ggridges_0.5.3 evaluate_0.15
[85] stringr_1.4.0 fastmap_1.1.0
[87] yaml_2.3.5 goftest_1.2-3
[89] org.Hs.eg.db_3.15.0 processx_3.5.3
[91] knitr_1.39 bit64_4.0.5
[93] fs_1.5.2 fitdistrplus_1.1-8
[95] purrr_0.3.4 RANN_2.6.1
[97] KEGGREST_1.36.0 sparseMatrixStats_1.8.0
[99] pbapply_1.5-0 future_1.26.1
[101] nlme_3.1-157 whisker_0.4
[103] mime_0.12 compiler_4.2.0
[105] rstudioapi_0.13 plotly_4.10.0
[107] png_0.1-7 spatstat.utils_2.3-1
[109] tibble_3.1.7 bslib_0.3.1
[111] stringi_1.7.6 highr_0.9
[113] ps_1.7.0 rgeos_0.5-9
[115] lattice_0.20-45 Matrix_1.4-1
[117] vctrs_0.4.1 pillar_1.7.0
[119] lifecycle_1.0.1 spatstat.geom_2.4-0
[121] lmtest_0.9-40 jquerylib_0.1.4
[123] RcppAnnoy_0.0.19 data.table_1.14.2
[125] cowplot_1.1.1 bitops_1.0-7
[127] irlba_2.3.5 GenomicRanges_1.48.0
[129] httpuv_1.6.5 patchwork_1.1.1
[131] R6_2.5.1 promises_1.2.0.1
[133] KernSmooth_2.23-20 gridExtra_2.3
[135] IRanges_2.30.0 parallelly_1.31.1
[137] codetools_0.2-18 MASS_7.3-57
[139] assertthat_0.2.1 SummarizedExperiment_1.26.1
[141] rprojroot_2.0.3 SeuratObject_4.1.0
[143] sctransform_0.3.3 S4Vectors_0.34.0
[145] GenomeInfoDbData_1.2.8 mgcv_1.8-40
[147] parallel_4.2.0 beachmat_2.12.0
[149] rpart_4.1.16 grid_4.2.0
[151] tidyr_1.2.0 DelayedMatrixStats_1.18.0
[153] rmarkdown_2.14 MatrixGenerics_1.8.0
[155] Rtsne_0.16 git2r_0.30.1
[157] getPass_0.2-2 Biobase_2.56.0
[159] shiny_1.7.1