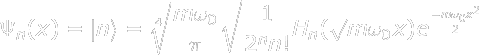Home
Harmonic Well
Position Arrowheads correspond to units of distance.
Real Axis of Wavefunction
Imaginary Axis of Wavefunction
Momentum Display Momentum Wavefunction
Play Speed(1=RealTime):
X Scaling:
Y Scaling:
Length of X Axis: 5
Mass: 3
Spring "K": 6
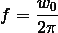
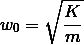
*No. of points:
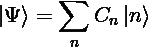
*Manually Input Coefficients:
Define Cn=f(n,t,u,w)
*Max value of n: 16
u = 1 + 0i
w = 1 + 0i
*f(n,t,u,w)=
*Needs "Apply"