A prelude to the EM algorithm
Matthew Stephens
2021-01-26
Last updated: 2021-01-26
Checks: 7 0
Knit directory: fiveMinuteStats/analysis/
This reproducible R Markdown analysis was created with workflowr (version 1.6.2). The Checks tab describes the reproducibility checks that were applied when the results were created. The Past versions tab lists the development history.
Great! Since the R Markdown file has been committed to the Git repository, you know the exact version of the code that produced these results.
Great job! The global environment was empty. Objects defined in the global environment can affect the analysis in your R Markdown file in unknown ways. For reproduciblity it’s best to always run the code in an empty environment.
The command set.seed(12345) was run prior to running the code in the R Markdown file. Setting a seed ensures that any results that rely on randomness, e.g. subsampling or permutations, are reproducible.
Great job! Recording the operating system, R version, and package versions is critical for reproducibility.
Nice! There were no cached chunks for this analysis, so you can be confident that you successfully produced the results during this run.
Great job! Using relative paths to the files within your workflowr project makes it easier to run your code on other machines.
Great! You are using Git for version control. Tracking code development and connecting the code version to the results is critical for reproducibility.
The results in this page were generated with repository version e551909. See the Past versions tab to see a history of the changes made to the R Markdown and HTML files.
Note that you need to be careful to ensure that all relevant files for the analysis have been committed to Git prior to generating the results (you can use wflow_publish or wflow_git_commit). workflowr only checks the R Markdown file, but you know if there are other scripts or data files that it depends on. Below is the status of the Git repository when the results were generated:
Ignored files:
Ignored: .Rhistory
Ignored: .Rproj.user/
Ignored: analysis/.Rhistory
Ignored: analysis/bernoulli_poisson_process_cache/
Untracked files:
Untracked: _workflowr.yml
Untracked: analysis/CI.Rmd
Untracked: analysis/gibbs_structure.Rmd
Untracked: analysis/libs/
Untracked: analysis/results.Rmd
Untracked: analysis/shiny/tester/
Unstaged changes:
Modified: analysis/LR_and_BF.Rmd
Deleted: analysis/r_simplemix_extended.Rmd
Note that any generated files, e.g. HTML, png, CSS, etc., are not included in this status report because it is ok for generated content to have uncommitted changes.
These are the previous versions of the repository in which changes were made to the R Markdown (analysis/em_algorithm_01.Rmd) and HTML (docs/em_algorithm_01.html) files. If you’ve configured a remote Git repository (see ?wflow_git_remote), click on the hyperlinks in the table below to view the files as they were in that past version.
| File | Version | Author | Date | Message |
|---|---|---|---|---|
| Rmd | e551909 | Matthew Stephens | 2021-01-26 | workflowr::wflow_publish(“em_algorithm_01.Rmd”) |
Pre-requisites
This document assumes basic familiarity with mixture models, likelihoods and Bayesian computations for the two-class problem.
Overview
The expectation-maximization algorithm, usually known as the EM algorithm, is a widely-used computational method for performing maximum likelihood method in certain models. Its attractions include that it is often simple to code and monotonic (every iteration increases the likelihood). It is also often quick to find a “reasonably good” solution, although if a very precise solution is required then it can be slow. In this document we describe the EM algorithm for a particular problem – maximum likelihood estimation of the mixture proportions – where it has a particularly simple and intuitive form. We do not give any formal derivation or explain why it works, which will require further study. The idea is to motivate you to perfom this further study.
The problem
We consider again the medical screening example from this vignette. This example involves a test for a disease that is based on measuring the concentration (\(X\)) of a protein in the blood. In normal individuals \(X\) has a Gamma distribution with mean 1 and shape 2 (so scale parameter is 0.5 as scale = mean/shape). In diseased individuals the protein becomes elevated, and \(X\) has a Gamma distribution with mean 2 and shape 2 (so scale =1).
Now consider the following question. Suppose we observe data \(x_1,\dots,x_n\) on \(n\) individuals randomly sampled from a population. How can we estimate the proportion of individuals in the population that are diseased?
Formulating via maximum likelihood
A natural approach to parameter estimation to use maximum likelihood. The first step in this approach is to write down the likelihood. To do this note that the samples are independent from the following mixture model: \[p(x | \pi) = \pi_1 \Gamma(x;0.5,2) + \pi_2 \Gamma(x; 1, 2)\] where \(\pi:=(\pi_1,\pi_2)\), with \(\pi_1\) the proportion of normal individuals, and \(\pi_2\) the proportion of diseased individuals. Note that \(\pi_1+\pi_2=1\) as these are the only possibilities, so there is only really one parameter to be estimated here.
The likelihood for \(\pi\) is: \[L(\pi) = \prod_j [\pi_1 \Gamma(x_j;0.5,2) + \pi_2 \Gamma(x_j; 1, 2)]\] and so the log-likelihood is: \[l(\pi) = \sum_j \log [\pi_1 \Gamma(x_j;0.5,2) + \pi_2 \Gamma(x_j; 1, 2)].\] The following code simulates data from the model (with true value of \(\pi_1=0.7\)) and then plots the log-likelihood:
n = 1000 # number of samples
x = rep(0,n) # to store the samples
shape = c(2,2) # shapes of the two components
scale = c(0.5,1) # scales of the two components
for(i in 1:n){
if(runif(1)<0.7)
z=1 else z=2
x[i] = rgamma(1,scale=scale[z],shape=shape[z])
}
mix_loglik = function(pi1,x){
sum(log(pi1 * dgamma(x,scale=0.5,shape=2) + (1-pi1)*dgamma(x,scale=1,shape=2)))
}
pi1_vec = seq(0,1,length=100)
loglik = rep(0,100)
for(i in 1:length(pi1_vec)){
loglik[i] = mix_loglik(pi1_vec[i],x)
}
plot(pi1_vec, loglik, type="l", main="log-likelihoood", xlab="pi_1")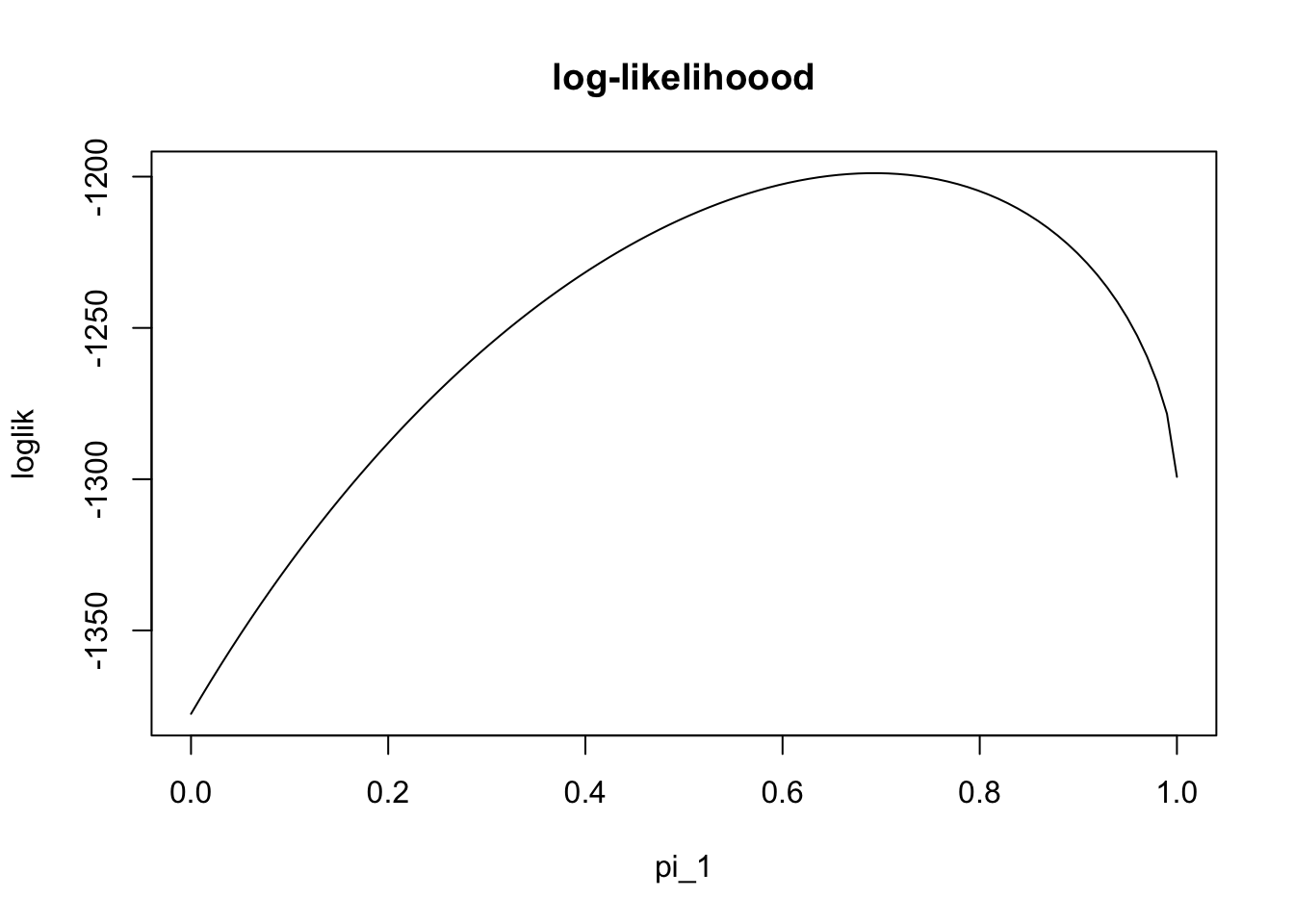
plot(pi1_vec,loglik-max(loglik), ylim=c(-10,0),type="l", main="log-likelihood (zoomed in)" , xlab="pi_1")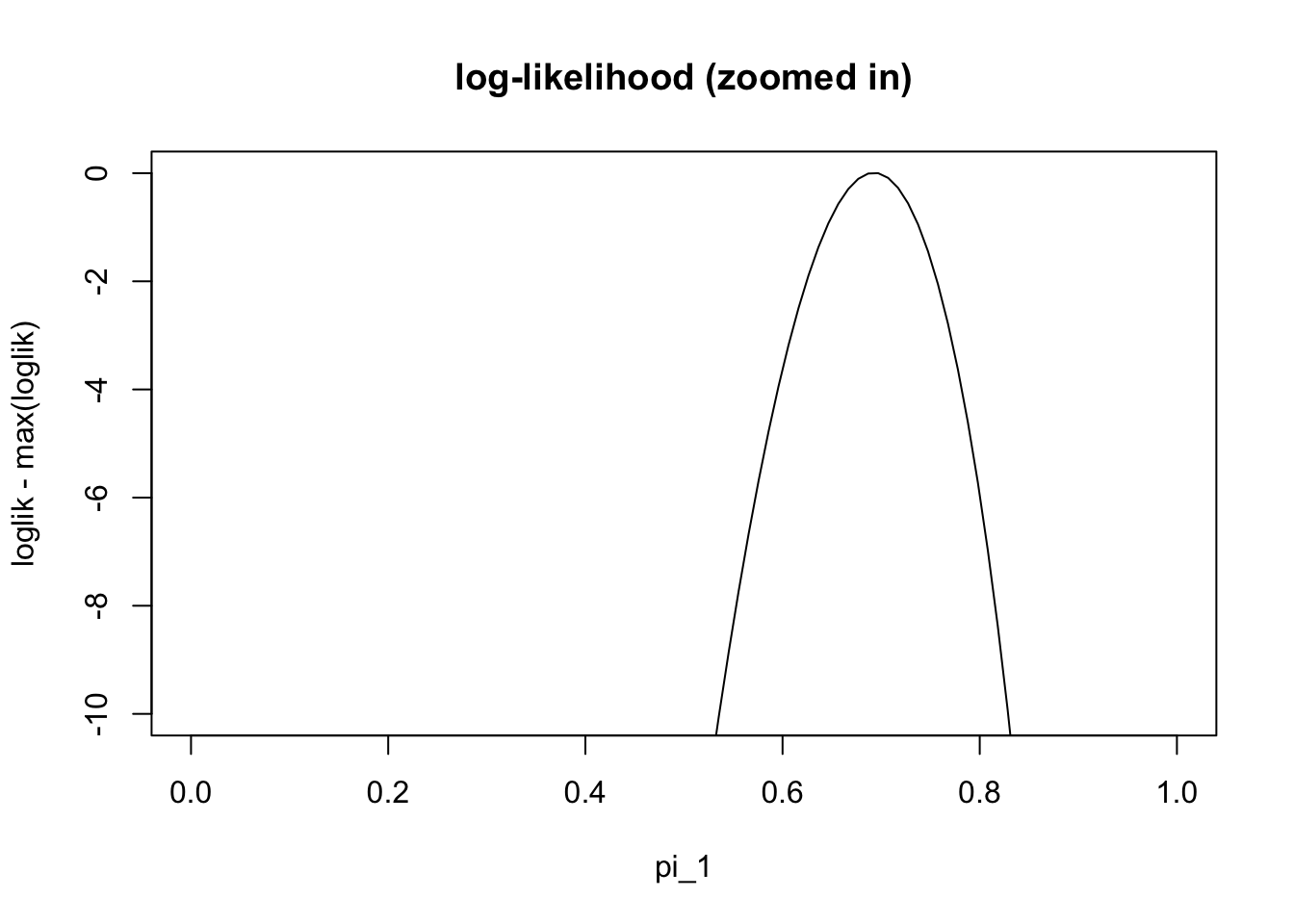
We can see from this plot that the maximum likelihood estiamte is near the true value (0.7). However, we cannot actually find the maximum easily analytically (e.g. try differentiating the log-likelihood and setting the derivative to zero). Therefore we need numerical methods. There are many numerical methods, and the EM algorithm is just one of many that could be used for this problem.
The EM algorithm
For this problem the EM algorithm has an intuitive form which we now describe. (Note this is not a derivation - it is just an intuitive heuristic argument).
For convenience introduce latent variables \(Z_i\) for each individual to indicate whether individual \(i\) is normal (\(Z_i=1\)) or diseased (\(Z_i=2\)). Of course the \(Z_i\) are unobserved.
Now note that if we knew \(\pi\) then we could easily compute the posterior probability that each individual is diseased given their test result \(X_i=x_i\). Specifically \[w_{ik}:=\Pr(Z_i = k | X_i=x_i) = \pi_k L_{ik}/ \sum_{k'} \pi_{k'} L_{ik'}\] where \(L_{ik} := p(x_i | Z_i=k)\). See Bayesian computations for the two-class problem for details.
Furthermore, if we knew these probabilities it would be natural to estimate the proportion of individuals in class \(k\) by the average of the \(w_{ik}\): \[\pi_k \approx (1/n) \sum_{i=1}^2 w_{ik}\].
So we have the following challenge: if we knew \(w\) we could estimate \(\pi\), but we need to know \(\pi\) to compute \(w\). This suggests, intuitively, an iterative procedure: repeatedly iterate between computing \(w\) and estimating \(\pi\). Here is code implementing this idea:
simple_em = function(x, pi1.init=0.5, niter = 100){
n = length(x)
pi1 = rep(0,niter+1)
pi1[1] = pi1.init
L = matrix(nrow=n,ncol=2)
L[,1] = dgamma(x,scale=0.5,shape=2)
L[,2] = dgamma(x,scale=1,shape=2)
w = matrix(nrow=n,ncol=2)
for(iter in 1:niter){
w[,1] = pi1[iter]*L[,1]
w[,2] = (1-pi1[iter])*L[,2]
for(i in 1:n){ # normalize the rows of w to sum to 1
w[i,] = w[i,]/(w[i,1]+w[i,2])
}
pi1[iter+1] = mean(w[,1])
}
return(pi1)
}
pi1.iter = simple_em(x)
plot(pi1.iter, xlab="iteration", ylab="pi1")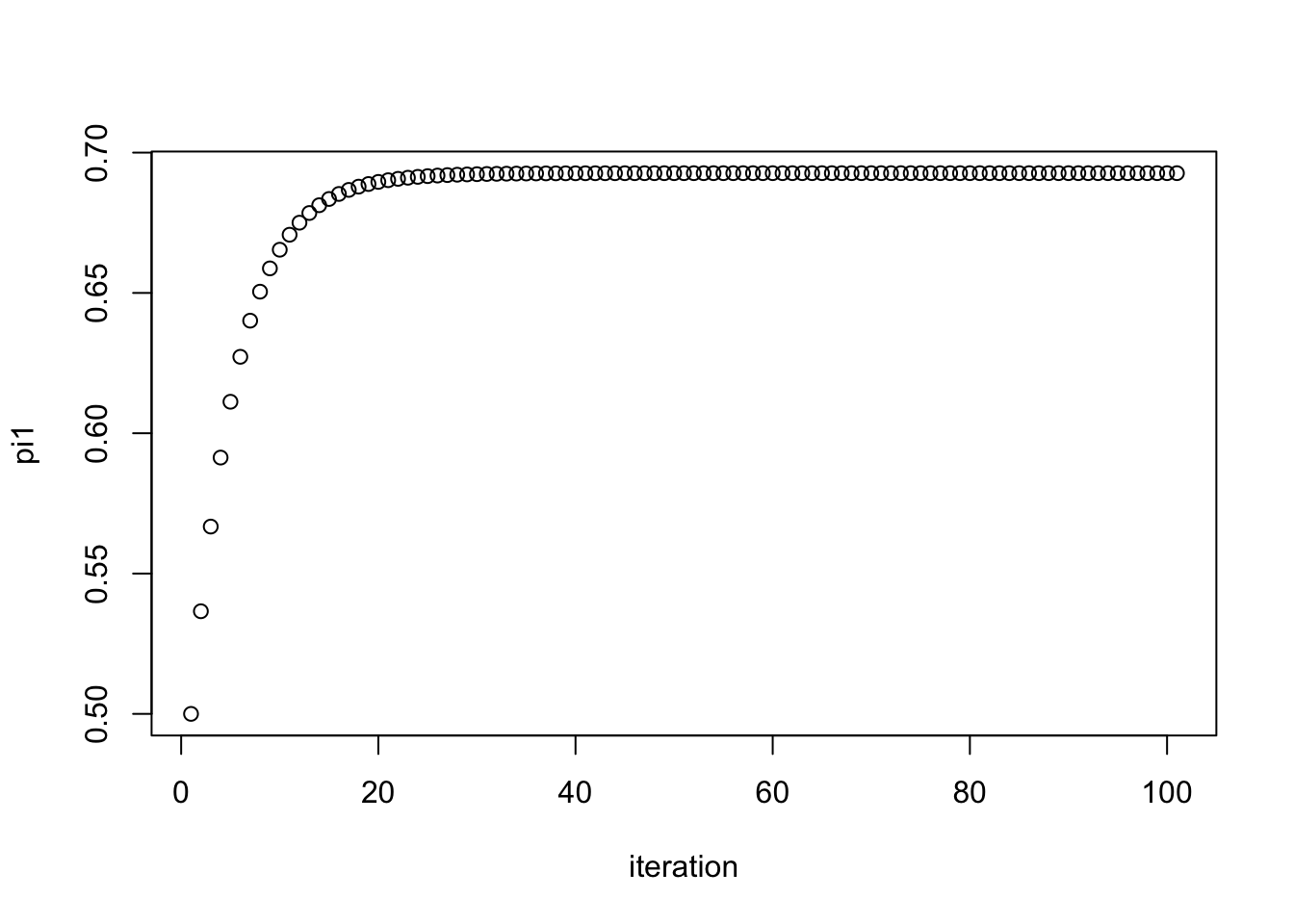
pi1.iter[101][1] 0.6926776Here we try another starting point. We see it converges to the same value.
pi1.iter = simple_em(x,pi1.init=0.9)
plot(pi1.iter, xlab="iteration", ylab="pi1")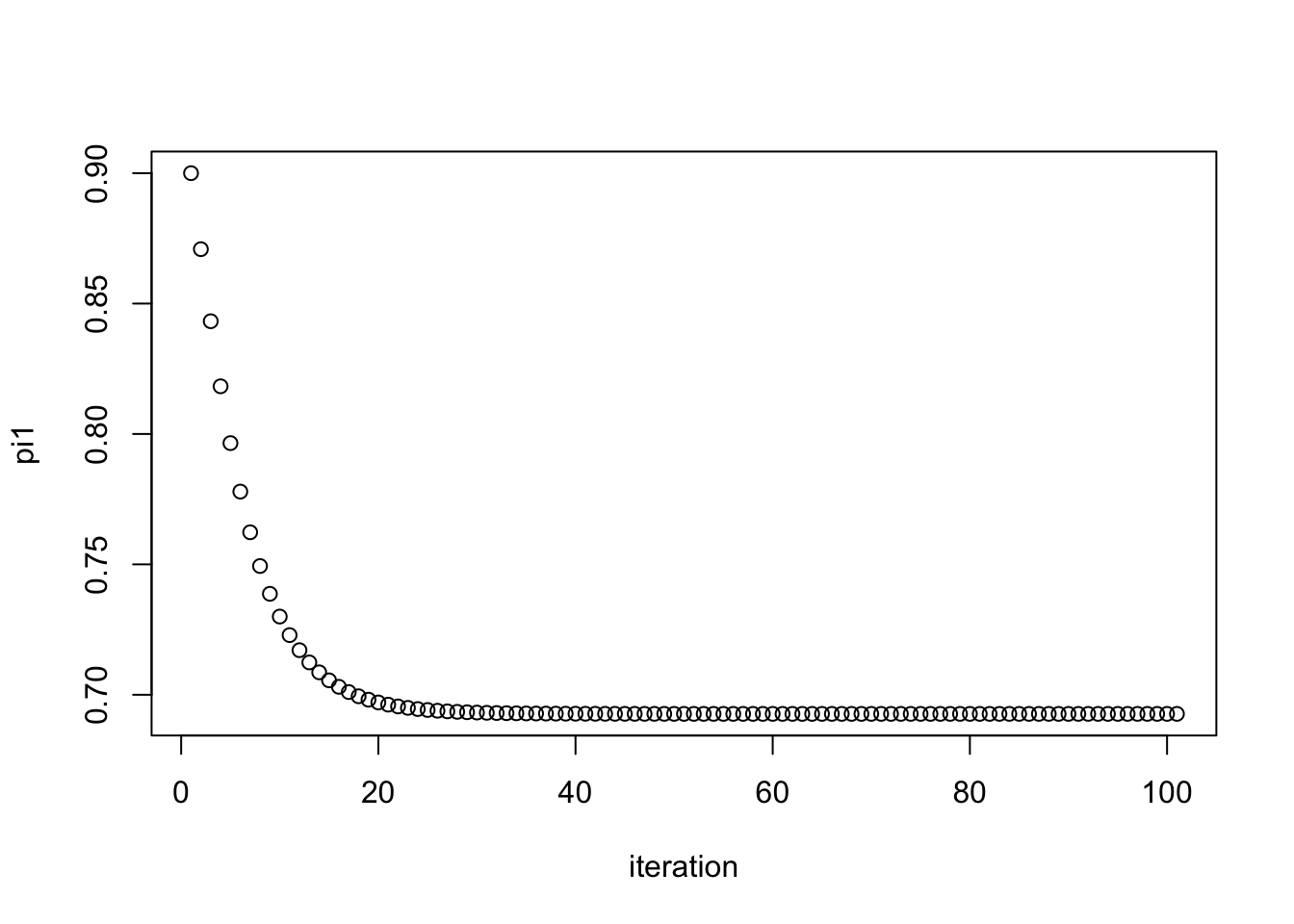
pi1.iter[101][1] 0.6926776And check that this value it converges to is the maximum likelihood estimate:
plot(pi1_vec,loglik-max(loglik), ylim=c(-10,0),type="l", main="log-likelihood (zoomed in)" , xlab="pi_1")
abline(v=pi1.iter[101])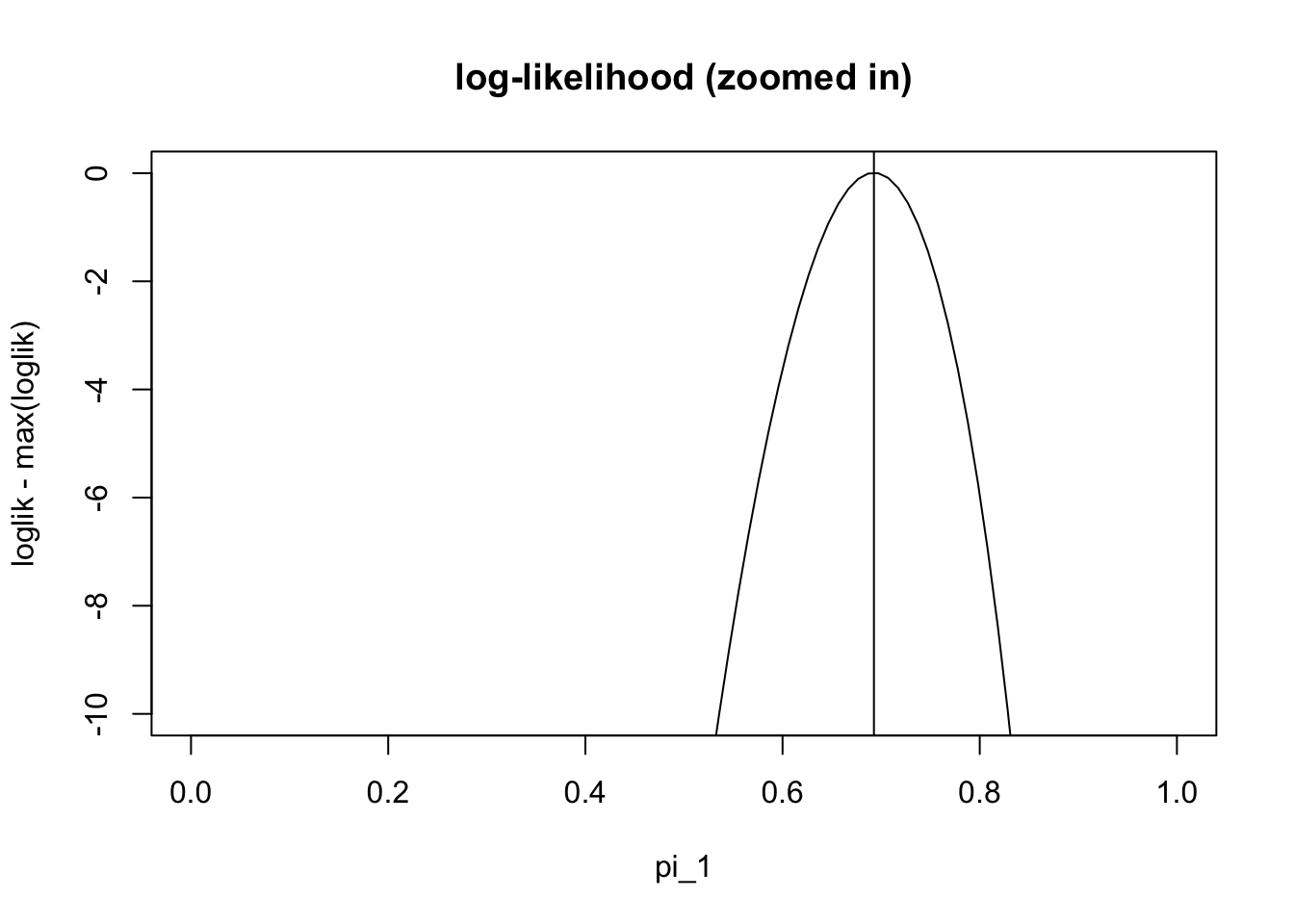
sessionInfo()R version 3.6.0 (2019-04-26)
Platform: x86_64-apple-darwin15.6.0 (64-bit)
Running under: macOS 10.16
Matrix products: default
BLAS: /Library/Frameworks/R.framework/Versions/3.6/Resources/lib/libRblas.0.dylib
LAPACK: /Library/Frameworks/R.framework/Versions/3.6/Resources/lib/libRlapack.dylib
locale:
[1] en_US.UTF-8/en_US.UTF-8/en_US.UTF-8/C/en_US.UTF-8/en_US.UTF-8
attached base packages:
[1] stats graphics grDevices utils datasets methods base
loaded via a namespace (and not attached):
[1] Rcpp_1.0.6 rstudioapi_0.11 whisker_0.4 knitr_1.29
[5] magrittr_1.5 workflowr_1.6.2 R6_2.4.1 rlang_0.4.8
[9] stringr_1.4.0 tools_3.6.0 xfun_0.16 git2r_0.27.1
[13] htmltools_0.5.0 ellipsis_0.3.1 yaml_2.2.1 digest_0.6.27
[17] rprojroot_1.3-2 tibble_3.0.4 lifecycle_0.2.0 crayon_1.3.4
[21] later_1.1.0.1 vctrs_0.3.4 fs_1.5.0 promises_1.1.1
[25] glue_1.4.2 evaluate_0.14 rmarkdown_2.3 stringi_1.4.6
[29] compiler_3.6.0 pillar_1.4.6 backports_1.1.10 httpuv_1.5.4
[33] pkgconfig_2.0.3 This site was created with R Markdown