Pre-requisites

You should know what a Bayes Factor is and what a p value is.

Overview

Sellke et al (The American Statistician; Volume 55, Issue 1, 2001) study the following question (paraphrased and shortened here).

Consider the situation in which experimental drugs D1; D2; D3; etc are to be tested. Each test will be thought of as completely independent; we simply have a series of tests so that we can explore the frequentist properties of p values. In each test, the following hypotheses are to be tested: \[H_0 : D_i \text{ has negligible effect}\] versus \[H_1 : D_i \text{ has a non-negligible effect}.\]

Suppose that one of these tests results in a p value \(\approx p\). The question we consider is: How strong is the evidence that the drug in question has a non-negligible effect?

The answer to this question has to depend on the distribution of effects under \(H_1\). However, Sellke et al derive a bound for the Bayes Factor. Specifically they show that, provided \(p<1/e\), the BF in favor of \(H_1\) is not larger than \[1/B(p) = -[e p \log(p)]^{-1}.\] (Note: the inverse comes from the fact that here we consider the BF in favor of \(H_1\), whereas Sellke et al consider the BF in favor of H_0).

Here we illustrate this result using Bayes Theorem to do calculations under a simple scenario.

Details

Let \(\theta_i\) denote the effect of drug \(D_i\). We will translate the null \(H_0\) above to mean \(\theta_i=0\). We will also make an assumption that the effects of the non-null drugs are normally distributed \(N(0,\sigma^2)\), where the value of \(\sigma\) determines how different the typical effect is from 0.

Thus we have: \[H_{0i}: \theta_i = 0\] \[H_{1i}: \theta_i \sim N(0,\sigma^2)\].

In addition we will assume that we have data (e.g. the results of a drug trial) that give us imperfect information about \(\theta\). Specifically we assume \(X_i | \theta_i \sim N(\theta_i,1)\). This implies that: \[X_i | H_{0i} \sim N(0,1)\] \[X_i | H_{1i} \sim N(0,1+\sigma^2)\]

Consequently the Bayes Factor (BF) comparing \(H_1\) vs \(H_0\) can be computed as follows:

BF= function(x,s){dnorm(x,0,sqrt(s^2+1))/dnorm(x,0,1)}

Of course the BF depends both on the data \(x\) and the choice of \(\sigma\) (here s in the code).

We can plot this BF for \(x=1.96\) (which is the value for which \(p=0.05\)):

s = seq(0,10,length=100)
plot(s,BF(1.96,s),xlab="sigma",ylab="BF at p=0.05",type="l",ylim=c(0,4))
BFbound=function(p){1/(-exp(1)*p*log(p))}
abline(h=BFbound(0.05),col=2)

Here the horizontal line shows the bound on the Bayes Factor computed by Sellke et al.

And here is the same plot for \(x=2.58\) (\(p=0.01\)):

plot(s,BF(2.58,s),xlab="sigma",ylab="BF at p=0.01",type="l",ylim=c(0,10))
abline(h=BFbound(0.01),col=2)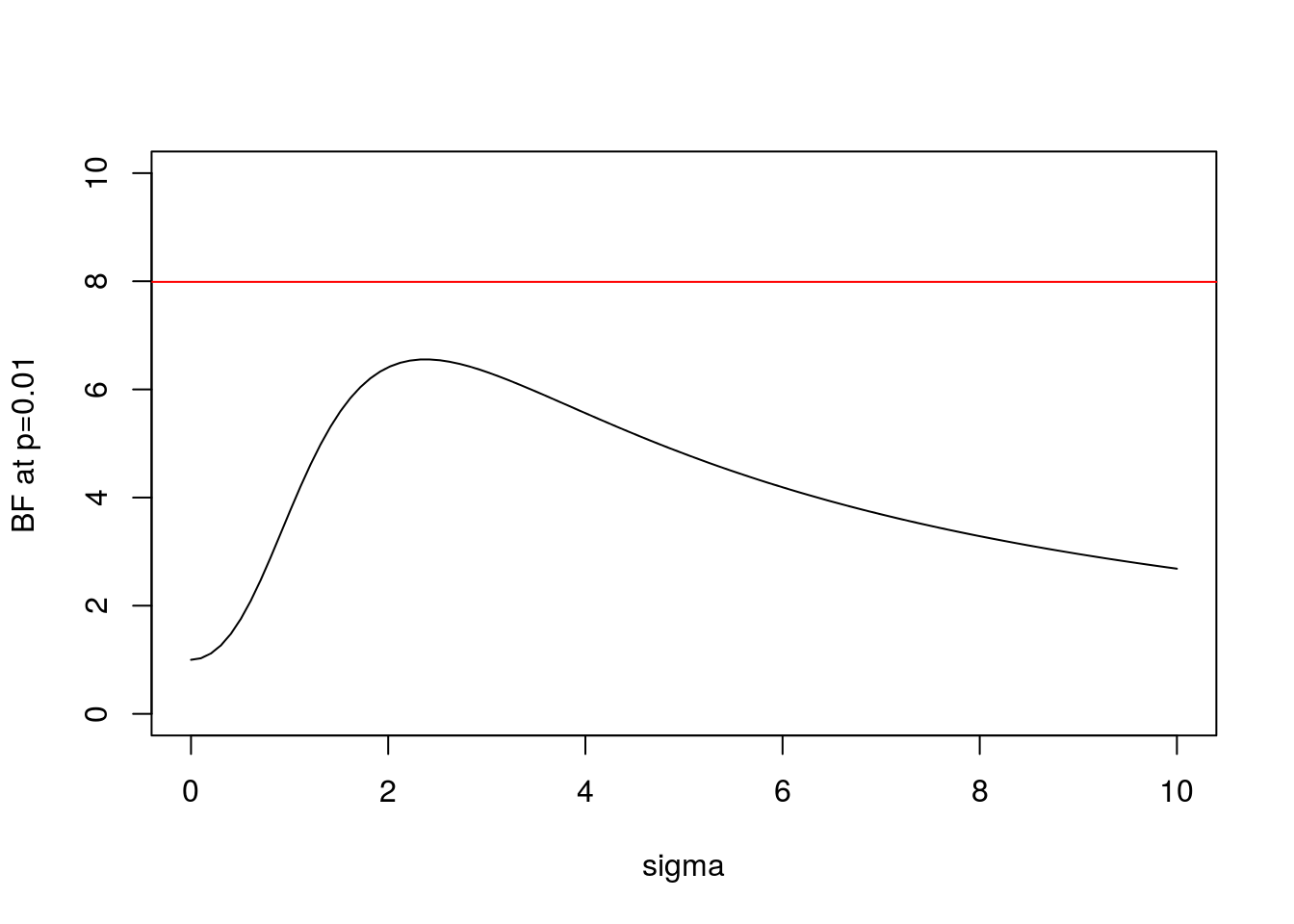

Note some key features:

• In both cases the BF is below the bound given by Sellke et al, as expected.
• As \(\sigma\) increases from 0 the BF is initially 1, rises to a maximum, and then gradually decays. This behavior, which occurs for any \(x\), perhaps helps provide intuition into why it is even possible to derive an upper bound.
• In the limit as \(\sigma \rightarrow \infty\) it is easy to show that (for any \(x\)) the BF \(\rightarrow 0\). This is an example of “Bartlett’s paradox”, and illustrates why you should not just use a “very flat” prior for \(\theta\) under \(H_1\): the Bayes Factor will depend on how flat you mean by “very flat”, and in the limit will always favor \(H_0\).

sessionInfo()

R version 3.3.2 (2016-10-31)
Platform: x86_64-pc-linux-gnu (64-bit)
Running under: Ubuntu 14.04.5 LTS

locale:
 [1] LC_CTYPE=en_US.UTF-8       LC_NUMERIC=C              
 [3] LC_TIME=en_US.UTF-8        LC_COLLATE=en_US.UTF-8    
 [5] LC_MONETARY=en_US.UTF-8    LC_MESSAGES=en_US.UTF-8   
 [7] LC_PAPER=en_US.UTF-8       LC_NAME=C                 
 [9] LC_ADDRESS=C               LC_TELEPHONE=C            
[11] LC_MEASUREMENT=en_US.UTF-8 LC_IDENTIFICATION=C       

attached base packages:
[1] stats     graphics  grDevices utils     datasets  methods   base     

other attached packages:
[1] rmarkdown_1.1

loaded via a namespace (and not attached):
 [1] magrittr_1.5    assertthat_0.1  formatR_1.4     htmltools_0.3.5
 [5] tools_3.3.2     yaml_2.1.13     tibble_1.2      Rcpp_0.12.7    
 [9] stringi_1.1.1   knitr_1.14      stringr_1.0.0   digest_0.6.9   
[13] evaluate_0.9