ebpower

Introduction

Tree structured data

Rank 1 fit
Run multiple factors

SVD initialization

Last updated: 2025-03-12

Checks: 7 0

Knit directory: misc/analysis/

This reproducible R Markdown analysis was created with workflowr (version 1.7.1). The Checks tab describes the reproducibility checks that were applied when the results were created. The Past versions tab lists the development history.

R Markdown file: up-to-date

Great! Since the R Markdown file has been committed to the Git repository, you know the exact version of the code that produced these results.

Environment: empty

Great job! The global environment was empty. Objects defined in the global environment can affect the analysis in your R Markdown file in unknown ways. For reproduciblity it’s best to always run the code in an empty environment.

Seed: set.seed(1)

The command set.seed(1) was run prior to running the code in the R Markdown file. Setting a seed ensures that any results that rely on randomness, e.g. subsampling or permutations, are reproducible.

Session information: recorded

Great job! Recording the operating system, R version, and package versions is critical for reproducibility.

Cache: none

Nice! There were no cached chunks for this analysis, so you can be confident that you successfully produced the results during this run.

File paths: relative

Great job! Using relative paths to the files within your workflowr project makes it easier to run your code on other machines.

Repository version: 6aa4dfe

Great! You are using Git for version control. Tracking code development and connecting the code version to the results is critical for reproducibility.

The results in this page were generated with repository version 6aa4dfe. See the Past versions tab to see a history of the changes made to the R Markdown and HTML files.

Note that you need to be careful to ensure that all relevant files for the analysis have been committed to Git prior to generating the results (you can use wflow_publish or wflow_git_commit). workflowr only checks the R Markdown file, but you know if there are other scripts or data files that it depends on. Below is the status of the Git repository when the results were generated:


Ignored files:
    Ignored:    .DS_Store
    Ignored:    .Rhistory
    Ignored:    .Rproj.user/
    Ignored:    analysis/.RData
    Ignored:    analysis/.Rhistory
    Ignored:    analysis/ALStruct_cache/
    Ignored:    data/.Rhistory
    Ignored:    data/methylation-data-for-matthew.rds
    Ignored:    data/pbmc/
    Ignored:    data/pbmc_purified.RData

Untracked files:
    Untracked:  .dropbox
    Untracked:  Icon
    Untracked:  analysis/GHstan.Rmd
    Untracked:  analysis/GTEX-cogaps.Rmd
    Untracked:  analysis/PACS.Rmd
    Untracked:  analysis/Rplot.png
    Untracked:  analysis/SPCAvRP.rmd
    Untracked:  analysis/abf_comparisons.Rmd
    Untracked:  analysis/admm_02.Rmd
    Untracked:  analysis/admm_03.Rmd
    Untracked:  analysis/bispca.Rmd
    Untracked:  analysis/cache/
    Untracked:  analysis/cholesky.Rmd
    Untracked:  analysis/compare-transformed-models.Rmd
    Untracked:  analysis/cormotif.Rmd
    Untracked:  analysis/cp_ash.Rmd
    Untracked:  analysis/eQTL.perm.rand.pdf
    Untracked:  analysis/eb_prepilot.Rmd
    Untracked:  analysis/eb_var.Rmd
    Untracked:  analysis/ebpmf1.Rmd
    Untracked:  analysis/ebpmf_sla_text.Rmd
    Untracked:  analysis/ebspca_sims.Rmd
    Untracked:  analysis/explore_psvd.Rmd
    Untracked:  analysis/fa_check_identify.Rmd
    Untracked:  analysis/fa_iterative.Rmd
    Untracked:  analysis/flash_cov_overlapping_groups_init.Rmd
    Untracked:  analysis/flash_test_tree.Rmd
    Untracked:  analysis/flashier_newgroups.Rmd
    Untracked:  analysis/flashier_nmf_triples.Rmd
    Untracked:  analysis/flashier_pbmc.Rmd
    Untracked:  analysis/flashier_snn_shifted_prior.Rmd
    Untracked:  analysis/greedy_ebpmf_exploration_00.Rmd
    Untracked:  analysis/ieQTL.perm.rand.pdf
    Untracked:  analysis/lasso_em_03.Rmd
    Untracked:  analysis/m6amash.Rmd
    Untracked:  analysis/mash_bhat_z.Rmd
    Untracked:  analysis/mash_ieqtl_permutations.Rmd
    Untracked:  analysis/methylation_example.Rmd
    Untracked:  analysis/mixsqp.Rmd
    Untracked:  analysis/mr.ash_lasso_init.Rmd
    Untracked:  analysis/mr.mash.test.Rmd
    Untracked:  analysis/mr_ash_modular.Rmd
    Untracked:  analysis/mr_ash_parameterization.Rmd
    Untracked:  analysis/mr_ash_ridge.Rmd
    Untracked:  analysis/mv_gaussian_message_passing.Rmd
    Untracked:  analysis/nejm.Rmd
    Untracked:  analysis/nmf_bg.Rmd
    Untracked:  analysis/nonneg_underapprox.Rmd
    Untracked:  analysis/normal_conditional_on_r2.Rmd
    Untracked:  analysis/normalize.Rmd
    Untracked:  analysis/pbmc.Rmd
    Untracked:  analysis/pca_binary_weighted.Rmd
    Untracked:  analysis/pca_l1.Rmd
    Untracked:  analysis/poisson_nmf_approx.Rmd
    Untracked:  analysis/poisson_shrink.Rmd
    Untracked:  analysis/poisson_transform.Rmd
    Untracked:  analysis/qrnotes.txt
    Untracked:  analysis/ridge_iterative_02.Rmd
    Untracked:  analysis/ridge_iterative_splitting.Rmd
    Untracked:  analysis/samps/
    Untracked:  analysis/sc_bimodal.Rmd
    Untracked:  analysis/shrinkage_comparisons_changepoints.Rmd
    Untracked:  analysis/susie_cov.Rmd
    Untracked:  analysis/susie_en.Rmd
    Untracked:  analysis/susie_z_investigate.Rmd
    Untracked:  analysis/svd-timing.Rmd
    Untracked:  analysis/temp.RDS
    Untracked:  analysis/temp.Rmd
    Untracked:  analysis/test-figure/
    Untracked:  analysis/test.Rmd
    Untracked:  analysis/test.Rpres
    Untracked:  analysis/test.md
    Untracked:  analysis/test_qr.R
    Untracked:  analysis/test_sparse.Rmd
    Untracked:  analysis/tree_dist_top_eigenvector.Rmd
    Untracked:  analysis/z.txt
    Untracked:  code/multivariate_testfuncs.R
    Untracked:  code/rqb.hacked.R
    Untracked:  data/4matthew/
    Untracked:  data/4matthew2/
    Untracked:  data/E-MTAB-2805.processed.1/
    Untracked:  data/ENSG00000156738.Sim_Y2.RDS
    Untracked:  data/GDS5363_full.soft.gz
    Untracked:  data/GSE41265_allGenesTPM.txt
    Untracked:  data/Muscle_Skeletal.ACTN3.pm1Mb.RDS
    Untracked:  data/P.rds
    Untracked:  data/Thyroid.FMO2.pm1Mb.RDS
    Untracked:  data/bmass.HaemgenRBC2016.MAF01.Vs2.MergedDataSources.200kRanSubset.ChrBPMAFMarkerZScores.vs1.txt.gz
    Untracked:  data/bmass.HaemgenRBC2016.Vs2.NewSNPs.ZScores.hclust.vs1.txt
    Untracked:  data/bmass.HaemgenRBC2016.Vs2.PreviousSNPs.ZScores.hclust.vs1.txt
    Untracked:  data/eb_prepilot/
    Untracked:  data/finemap_data/fmo2.sim/b.txt
    Untracked:  data/finemap_data/fmo2.sim/dap_out.txt
    Untracked:  data/finemap_data/fmo2.sim/dap_out2.txt
    Untracked:  data/finemap_data/fmo2.sim/dap_out2_snp.txt
    Untracked:  data/finemap_data/fmo2.sim/dap_out_snp.txt
    Untracked:  data/finemap_data/fmo2.sim/data
    Untracked:  data/finemap_data/fmo2.sim/fmo2.sim.config
    Untracked:  data/finemap_data/fmo2.sim/fmo2.sim.k
    Untracked:  data/finemap_data/fmo2.sim/fmo2.sim.k4.config
    Untracked:  data/finemap_data/fmo2.sim/fmo2.sim.k4.snp
    Untracked:  data/finemap_data/fmo2.sim/fmo2.sim.ld
    Untracked:  data/finemap_data/fmo2.sim/fmo2.sim.snp
    Untracked:  data/finemap_data/fmo2.sim/fmo2.sim.z
    Untracked:  data/finemap_data/fmo2.sim/pos.txt
    Untracked:  data/logm.csv
    Untracked:  data/m.cd.RDS
    Untracked:  data/m.cdu.old.RDS
    Untracked:  data/m.new.cd.RDS
    Untracked:  data/m.old.cd.RDS
    Untracked:  data/mainbib.bib.old
    Untracked:  data/mat.csv
    Untracked:  data/mat.txt
    Untracked:  data/mat_new.csv
    Untracked:  data/matrix_lik.rds
    Untracked:  data/paintor_data/
    Untracked:  data/running_data_chris.csv
    Untracked:  data/running_data_matthew.csv
    Untracked:  data/temp.txt
    Untracked:  data/y.txt
    Untracked:  data/y_f.txt
    Untracked:  data/zscore_jointLCLs_m6AQTLs_susie_eQTLpruned.rds
    Untracked:  data/zscore_jointLCLs_random.rds
    Untracked:  explore_udi.R
    Untracked:  output/fit.k10.rds
    Untracked:  output/fit.nn.pbmc.purified.rds
    Untracked:  output/fit.nn.rds
    Untracked:  output/fit.nn.s.001.rds
    Untracked:  output/fit.nn.s.01.rds
    Untracked:  output/fit.nn.s.1.rds
    Untracked:  output/fit.nn.s.10.rds
    Untracked:  output/fit.snn.s.001.rds
    Untracked:  output/fit.snn.s.01.nninit.rds
    Untracked:  output/fit.snn.s.01.rds
    Untracked:  output/fit.varbvs.RDS
    Untracked:  output/fit2.nn.pbmc.purified.rds
    Untracked:  output/glmnet.fit.RDS
    Untracked:  output/snn07.txt
    Untracked:  output/snn34.txt
    Untracked:  output/test.bv.txt
    Untracked:  output/test.gamma.txt
    Untracked:  output/test.hyp.txt
    Untracked:  output/test.log.txt
    Untracked:  output/test.param.txt
    Untracked:  output/test2.bv.txt
    Untracked:  output/test2.gamma.txt
    Untracked:  output/test2.hyp.txt
    Untracked:  output/test2.log.txt
    Untracked:  output/test2.param.txt
    Untracked:  output/test3.bv.txt
    Untracked:  output/test3.gamma.txt
    Untracked:  output/test3.hyp.txt
    Untracked:  output/test3.log.txt
    Untracked:  output/test3.param.txt
    Untracked:  output/test4.bv.txt
    Untracked:  output/test4.gamma.txt
    Untracked:  output/test4.hyp.txt
    Untracked:  output/test4.log.txt
    Untracked:  output/test4.param.txt
    Untracked:  output/test5.bv.txt
    Untracked:  output/test5.gamma.txt
    Untracked:  output/test5.hyp.txt
    Untracked:  output/test5.log.txt
    Untracked:  output/test5.param.txt

Unstaged changes:
    Modified:   .gitignore
    Modified:   analysis/flashier_log1p.Rmd
    Modified:   analysis/flashier_sla_text.Rmd
    Modified:   analysis/logistic_z_scores.Rmd
    Modified:   analysis/mr_ash_pen.Rmd
    Modified:   analysis/nmu_em.Rmd
    Modified:   analysis/susie_flash.Rmd
    Modified:   misc.Rproj

Note that any generated files, e.g. HTML, png, CSS, etc., are not included in this status report because it is ok for generated content to have uncommitted changes.

These are the previous versions of the repository in which changes were made to the R Markdown (analysis/ebpower.Rmd) and HTML (docs/ebpower.html) files. If you’ve configured a remote Git repository (see ?wflow_git_remote), click on the hyperlinks in the table below to view the files as they were in that past version.

File	Version	Author	Date	Message
Rmd	6aa4dfe	Matthew Stephens	2025-03-12	workflowr::wflow_publish("analysis/ebpower.Rmd")

library("ebnm")

Introduction

I want to implement an EB version of the power update for a symmetric data matrix S. I haven’t implemented an update to the residual error yet

# model is  S \sim VDV' + E with eb prior on V
eb_power_update = function(S,v,d,ebnm_fn){
  K = ncol(v)
  sigma2=mean((S-v %*% diag(d,nrow=length(d)) %*% t(v))^2)
  
  for(k in 1:K){
    U = v[,-k,drop=FALSE]
    D = diag(d[-k],nrow=length(d[-k]))
    
    newv = (S %*% v[,k,drop=FALSE] - U %*% D %*% t(U) %*% v[,k,drop=FALSE] )
    if(!all(newv==0)){
      fit.ebnm = ebnm_fn(newv,sigma2)        
      newv = fit.ebnm$posterior$mean
      if(!all(newv==0)){
        newv = newv/sqrt(sum(newv^2 + fit.ebnm$posterior$sd^2))
      } 
    }
    v[,k] = newv
    d[k] = t(v[,k]) %*% S %*% v[,k] - t(v[,k]) %*% U %*% D %*% t(U) %*% v[,k] 
  }
  return(list(v=v,d=d))
}

#helper function
compute_sqerr = function(S,fit){
  sum((S-fit$v %*% diag(fit$d,nrow=length(fit$d)) %*% t(fit$v))^2)
}

# a random initialization
random_init = function(S,K){
  n = nrow(S)
  v = matrix(nrow=n,ncol=K)
  for(k in 1:K){
    v[,k] = pmax(cbind(rnorm(n)),0) # initialize v
    v[,k] = v[,k]/sum(v[,k]^2)
  }
  d = rep(1e-8,K)
  return(list(v=v,d=d))
}

Tree structured data

Simulate some data from a tree structure.

set.seed(1)
n = 40
x = cbind(c(rep(1,n),rep(0,n)), c(rep(0,n),rep(1,n)), c(rep(1,n/2),rep(0,3*n/2)), c(rep(0,n/2), rep(1,n/2), rep(0,n)), c(rep(0,n),rep(1,n/2),rep(0,n/2)), c(rep(0,3*n/2),rep(1,n/2)))
E = matrix(0.1*rexp(2*n*2*n),nrow=2*n)
E = E+t(E) #symmetric errors
A = x %*% t(x) + E
image(A)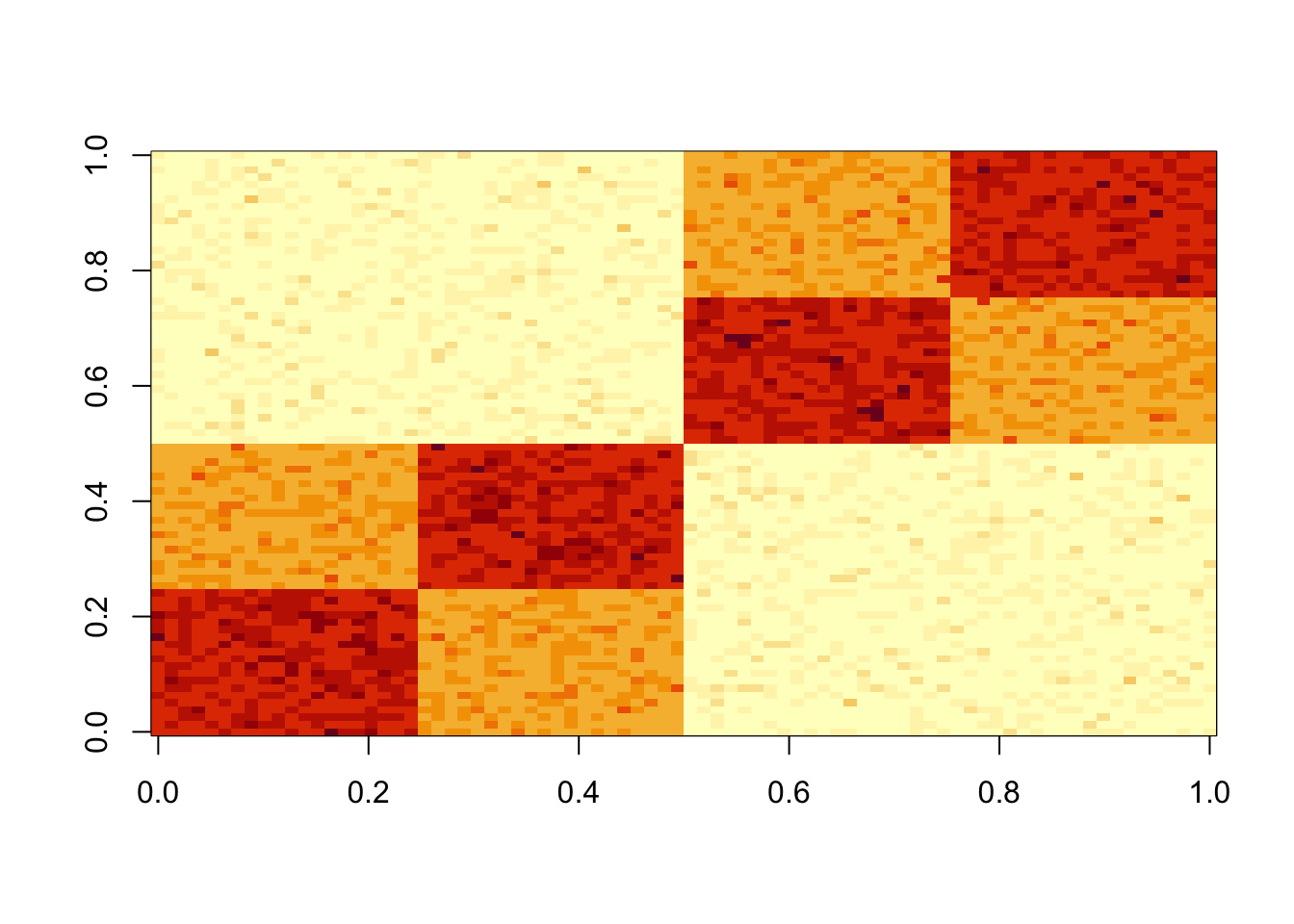

Rank 1 fit

Here I fit a single factor with point exponential prior. It finds the solution where everything is approximately equal.This is also the leading eigenvector of A.

set.seed(1)
fit = random_init(A,1)

err = rep(0,10)
err[1] = compute_sqerr(A,fit)
for(i in 2:100){
  fit = eb_power_update(A,fit$v,fit$d,ebnm_point_exponential)
  err[i] = compute_sqerr(A,fit)
}
plot(err)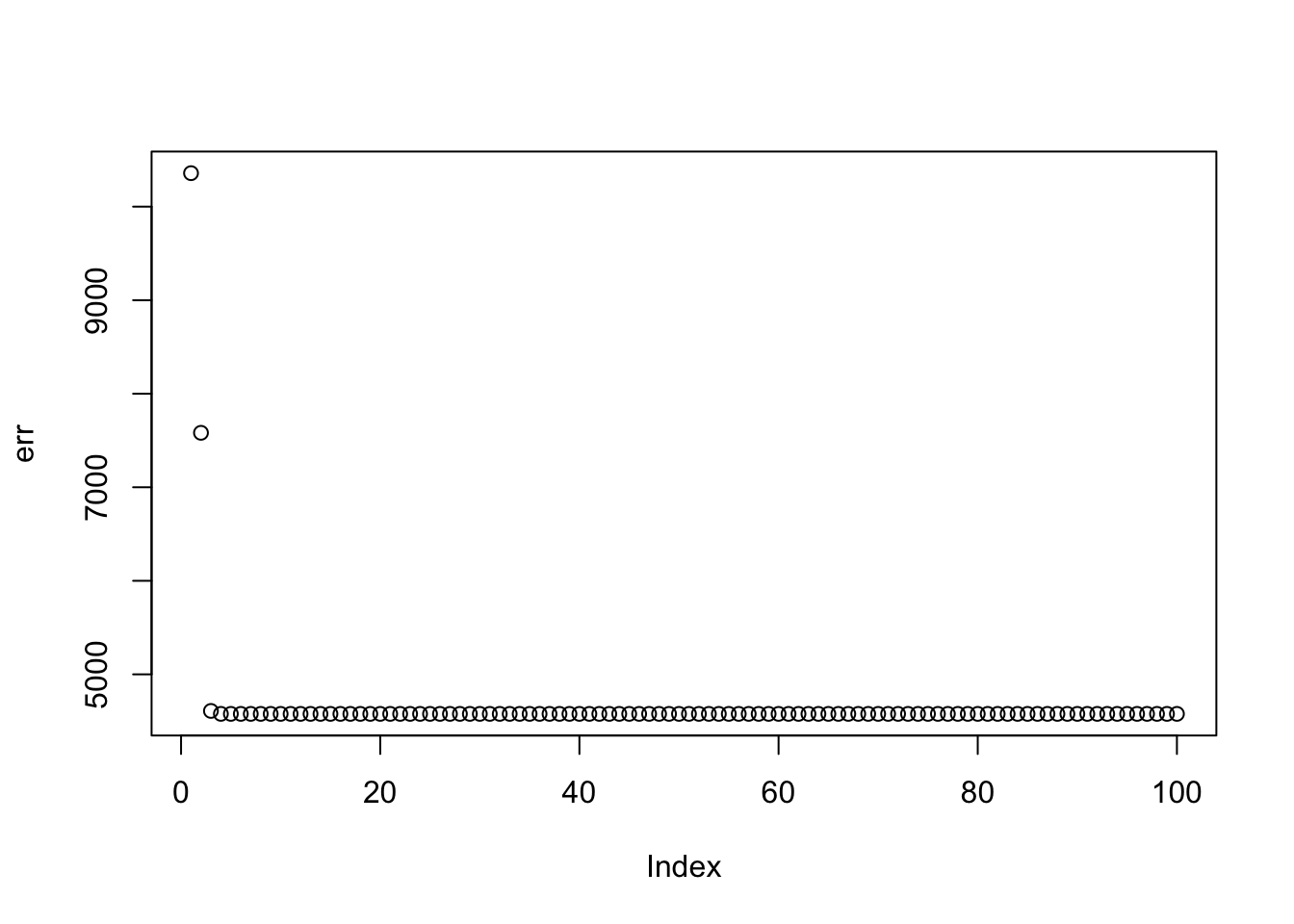

plot(fit$v[,1],svd(A)$v[,1])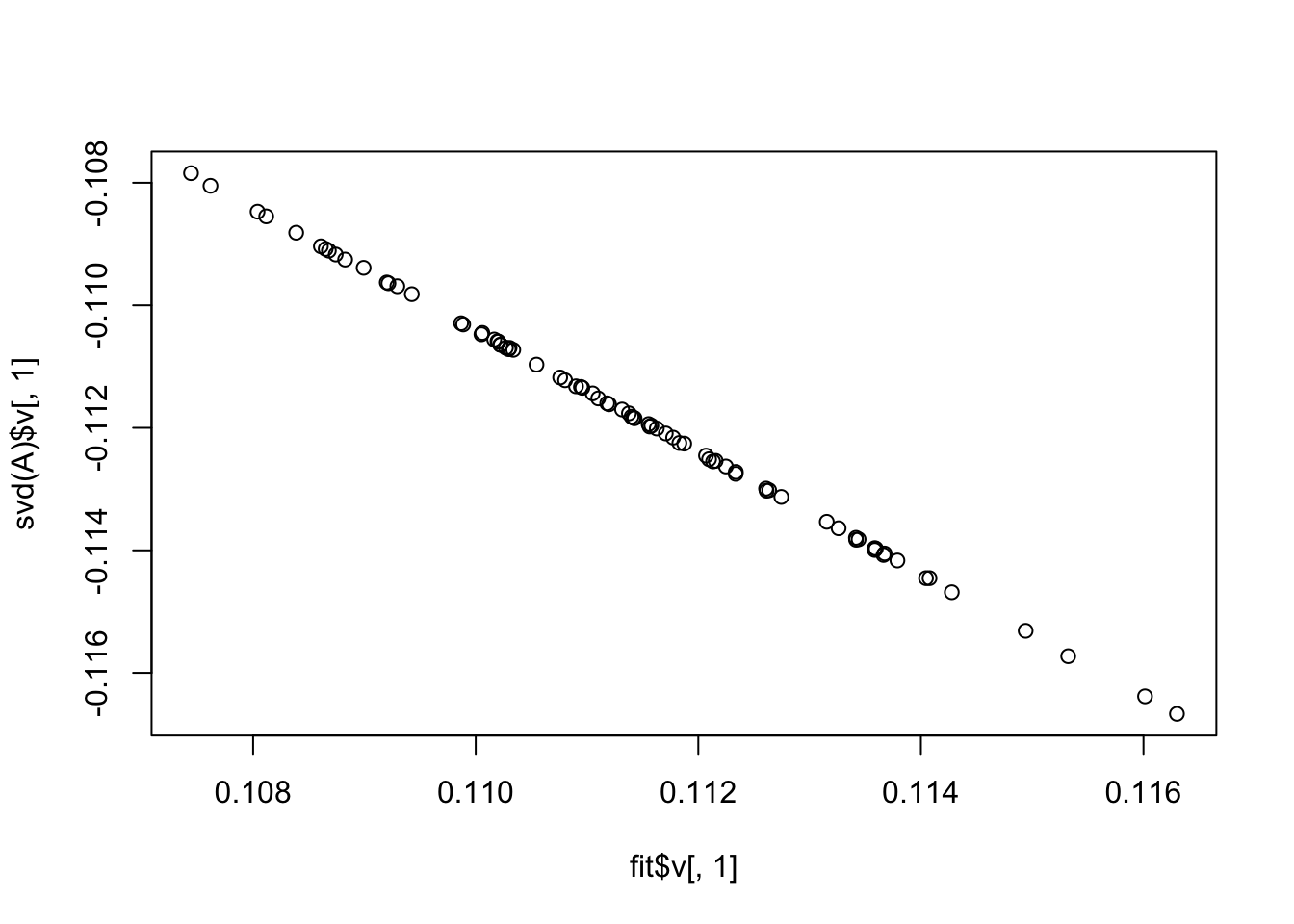

plot(fit$v)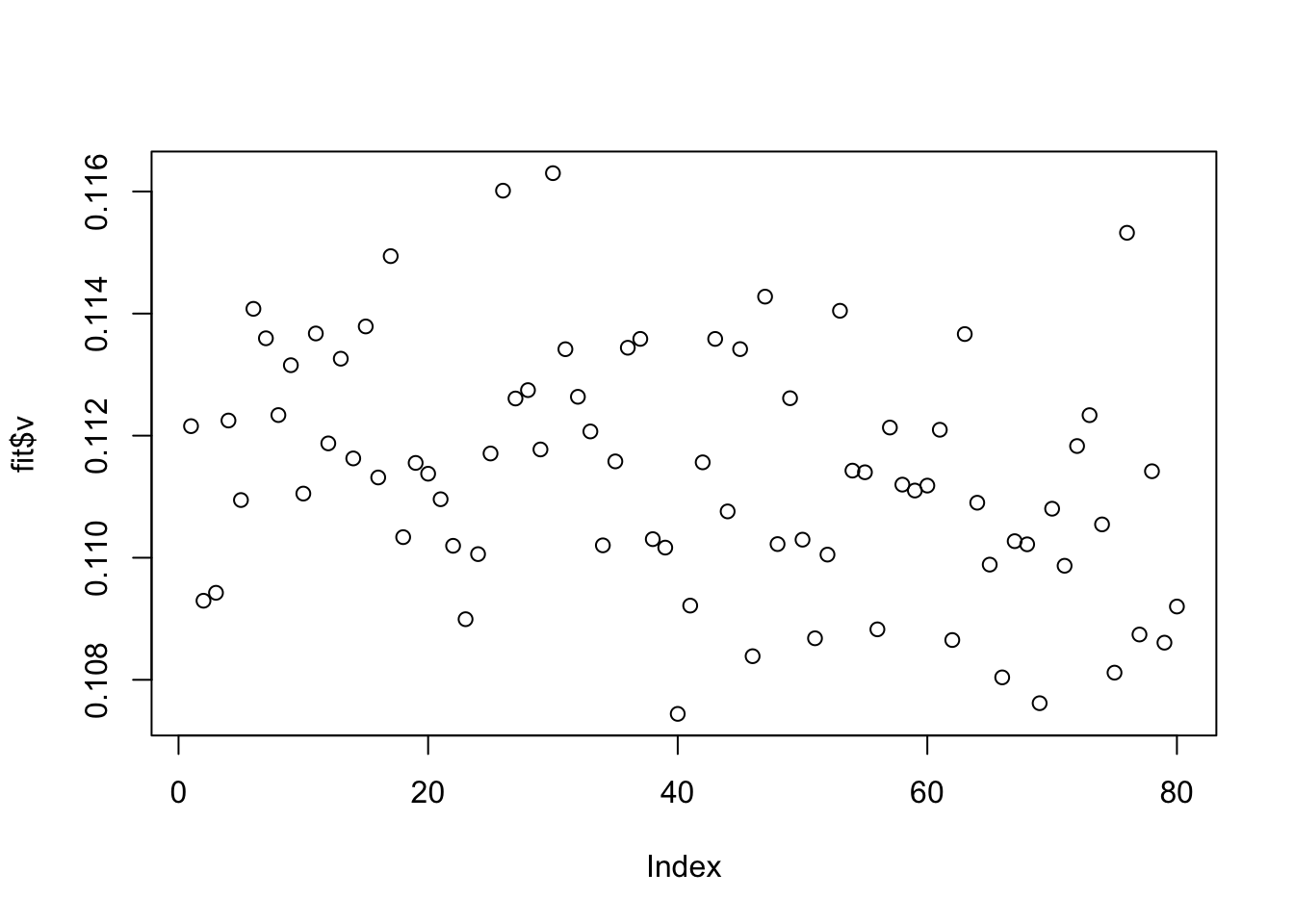

Interestingly the point-Laplace prior zeros everything out. This indicates the need to be a bit careful about initialization (maybe particularly for sigma2).

set.seed(1)
fit = random_init(A,1)

err = rep(0,10)
err[1] = compute_sqerr(A,fit)
for(i in 2:100){
  fit = eb_power_update(A,fit$v,fit$d,ebnm_point_laplace)
  err[i] = compute_sqerr(A,fit)
}
plot(fit$v[,1],svd(A)$v[,1])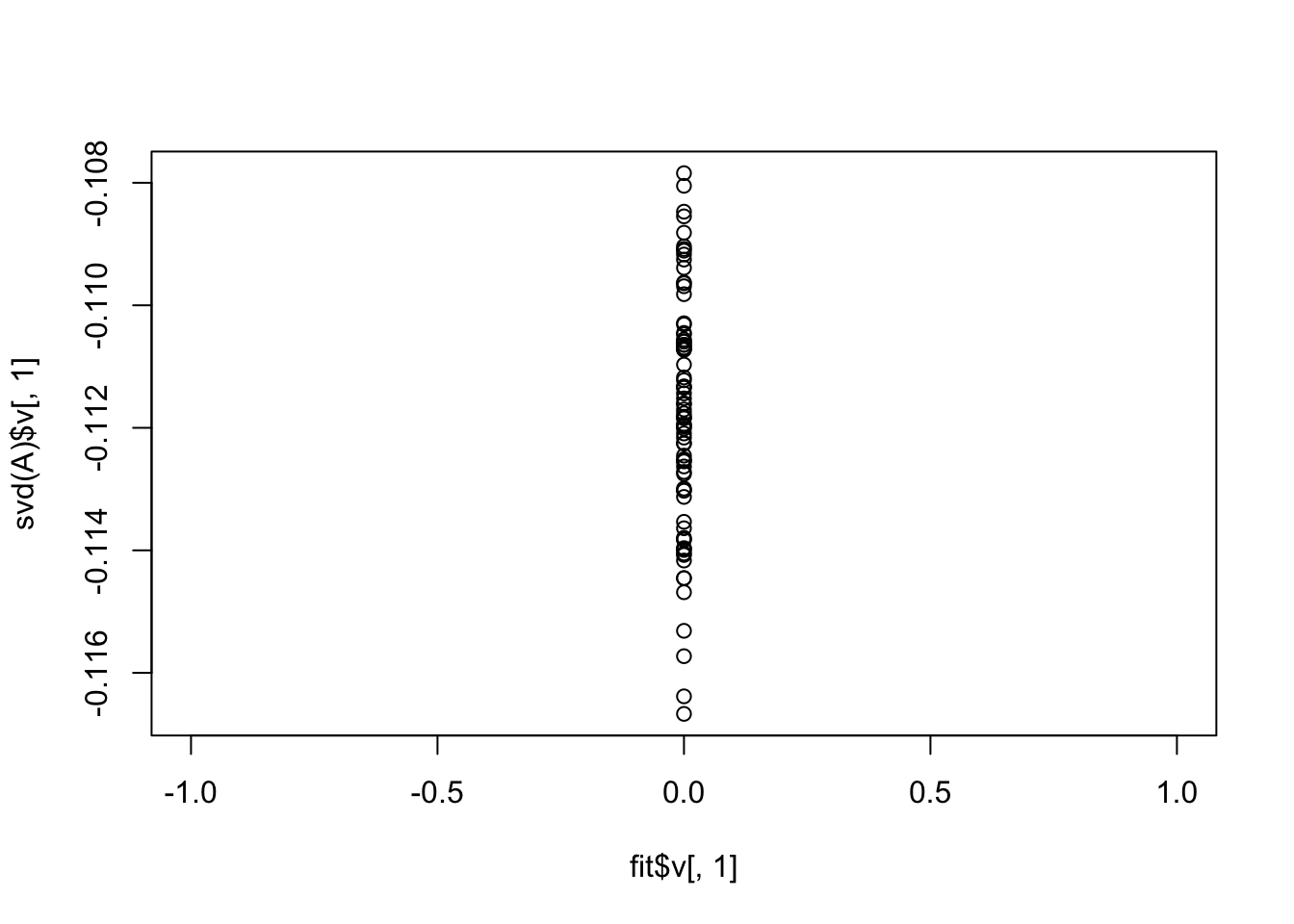

plot(fit$v)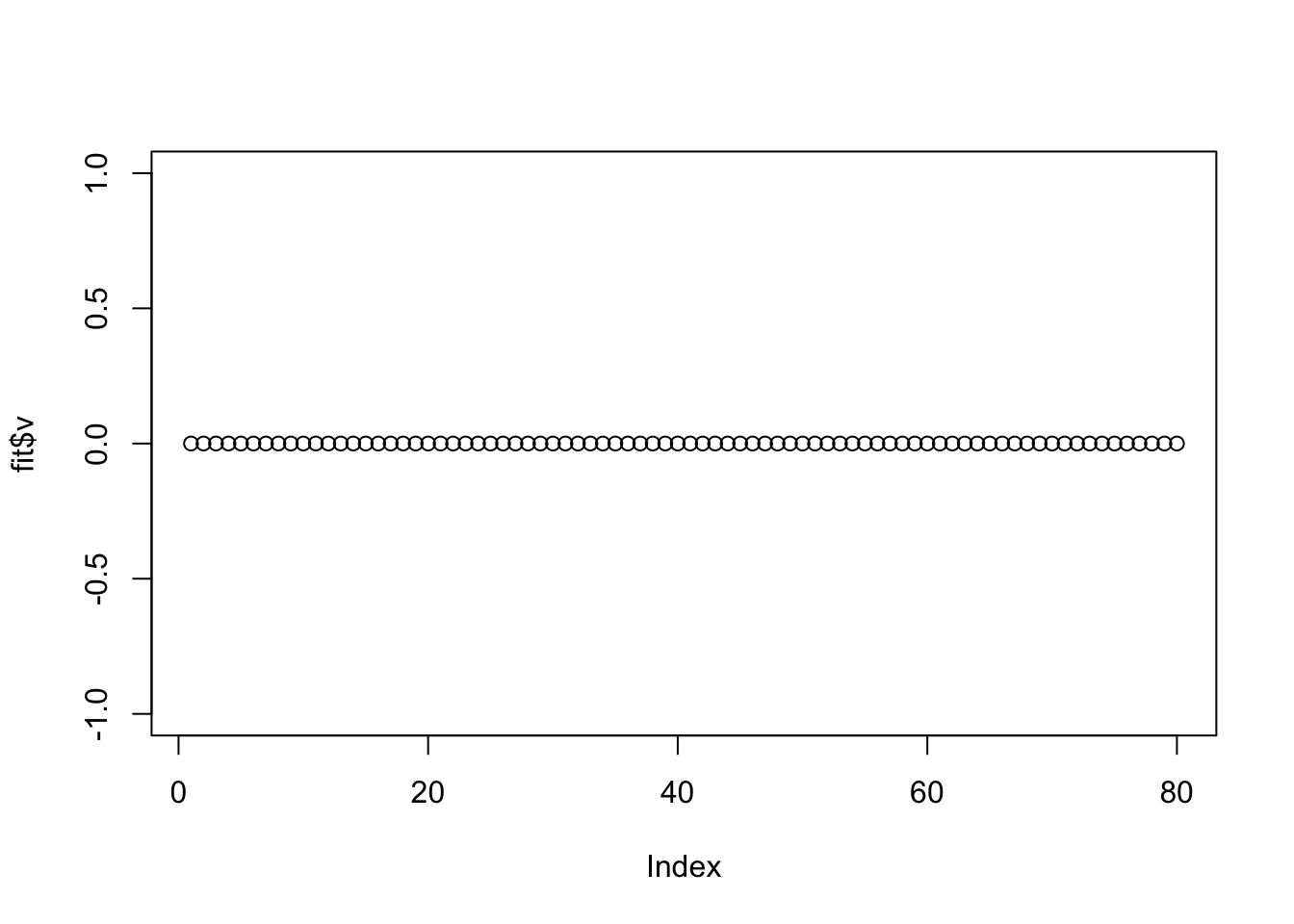

Run multiple factors

Here I run with $K=9$ . It finds a rank 4 solution, zeroing out the other 5. One can compare this with non-negative without the EB approach here.

set.seed(2)
fit = random_init(A,9)
err = rep(0,10)
err[1] = sum((A-fit$v %*% diag(fit$d) %*% t(fit$v))^2)
for(i in 2:100){
  fit = eb_power_update(A,fit$v,fit$d,ebnm_point_exponential)
  err[i] = sum((A-fit$v %*% diag(fit$d) %*% t(fit$v))^2)
}
plot(err)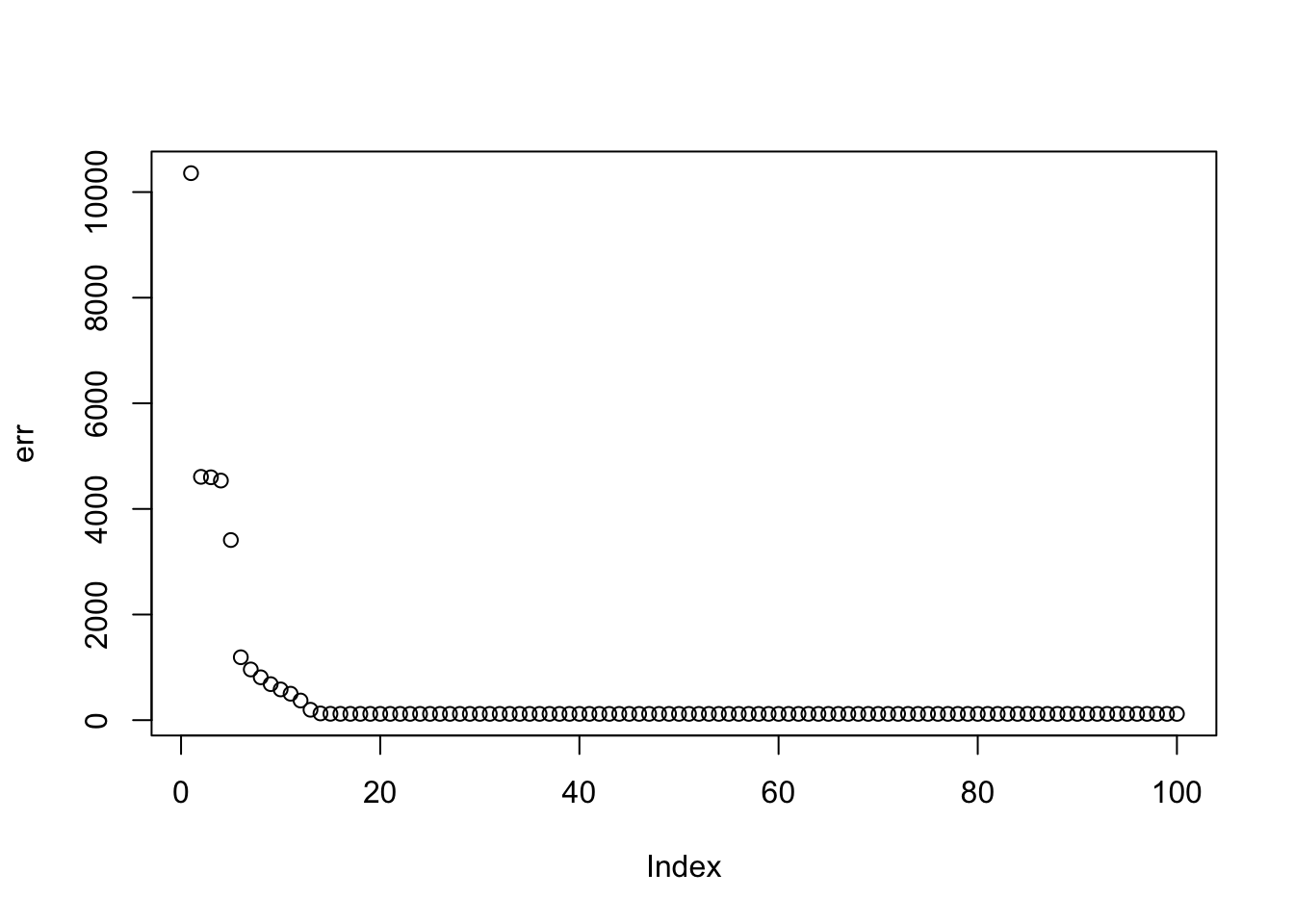

par(mfcol=c(3,3),mai=rep(0.3,4))
for(i in 1:9){plot(fit$v[,i],main=paste0(fit$d[i]))}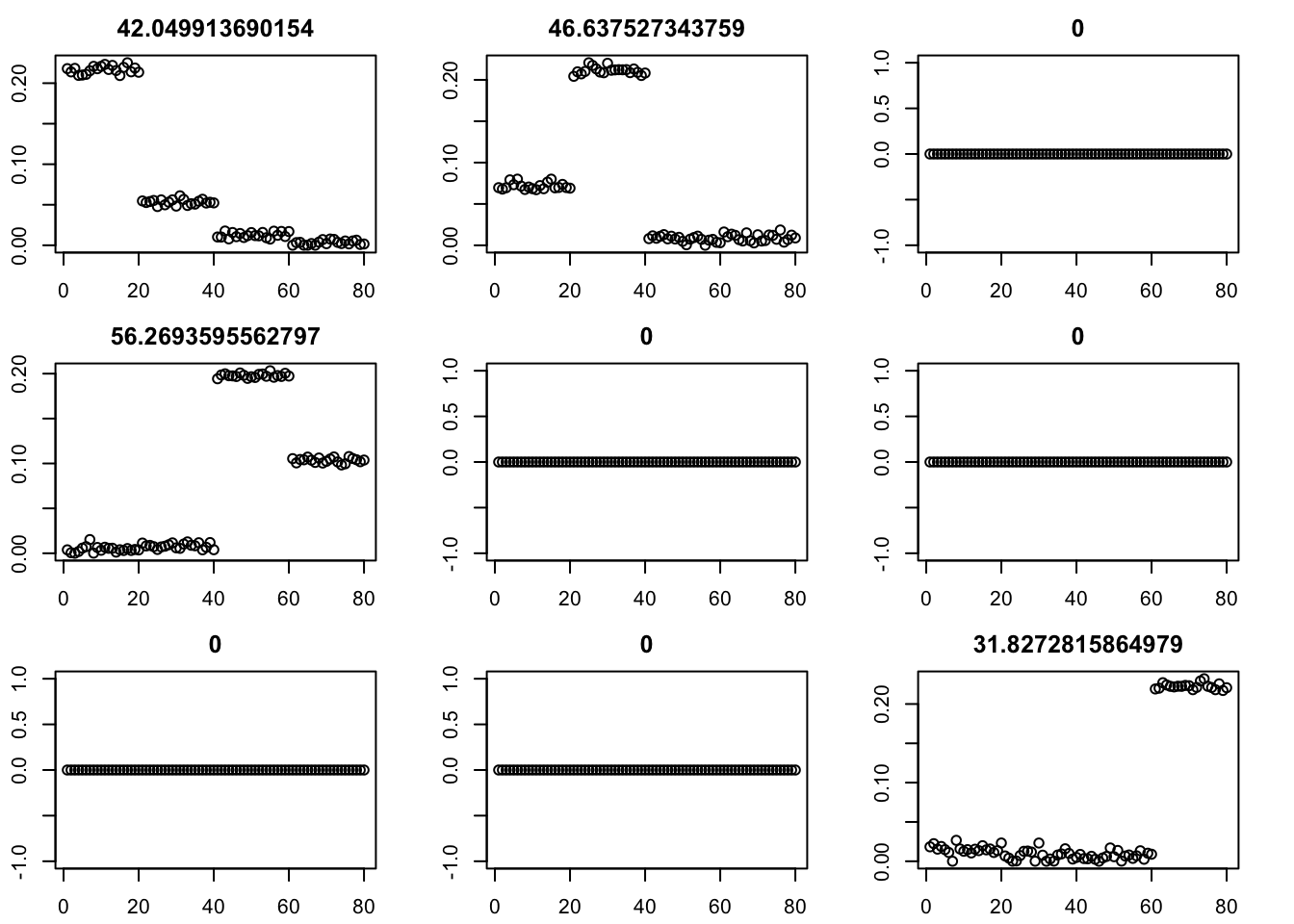

Here I try the generalized binary prior. So far I’m finding this does not work well, especially if started from random starting point. I debugged and found that what happens is that initially all the v are quite non-negative, bounded away from 0. So the gb prior puts all its weight on the non-null normal component and does not shrink anything. (Is it worth using a laplace for the non-null component?) The point exponential does not have that problem - it shrinks the smallest values towards 0, and eventually gets to a point where everything is 0.

set.seed(2)
fit = random_init(A,9)
err = rep(0,10)
err[1] = sum((A-fit$v %*% diag(fit$d) %*% t(fit$v))^2)
 
for(i in 2:10){
  fit = eb_power_update(A,fit$v,fit$d,ebnm_generalized_binary)
  err[i] = sum((A-fit$v %*% diag(fit$d) %*% t(fit$v))^2)
}
plot(err)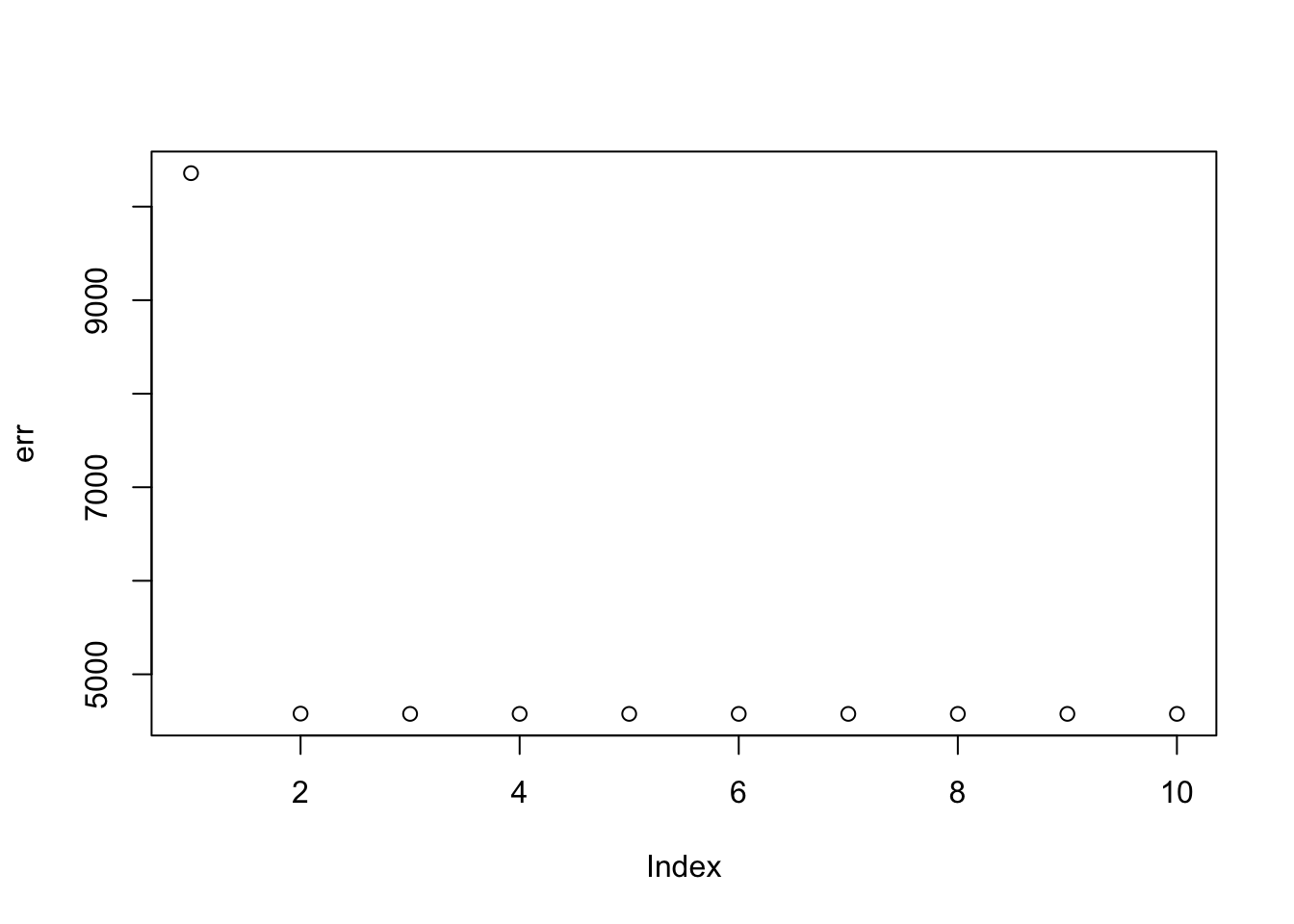

par(mfcol=c(3,3),mai=rep(0.3,4))
for(i in 1:9){plot(fit$v[,i],main=paste0(fit$d[i]))}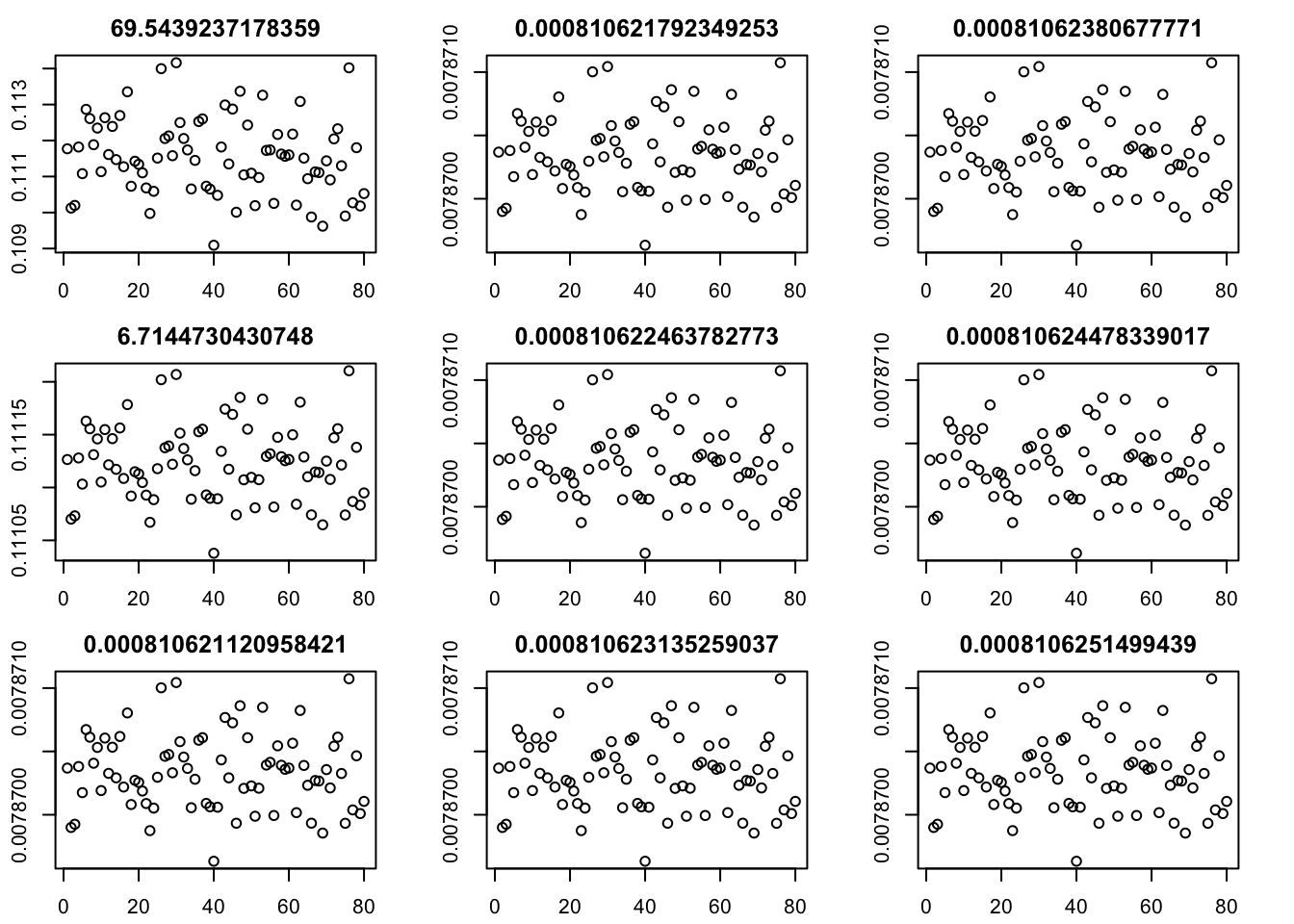

I should try with a fixed GB prior? I want to force the shrinkage towards 0… Here we try initializing GB with point-exponential.

set.seed(2)
fit = random_init(A,9)

err = rep(0,10)
err[1] = compute_sqerr(A,fit)
 
for(i in 2:50){
  fit = eb_power_update(A,fit$v,fit$d,ebnm_point_exponential)
  err[i] = compute_sqerr(A,fit)
}
par(mfcol=c(3,3),mai=rep(0.3,4))
for(i in 1:9){plot(fit$v[,i],main=paste0(fit$d[i]))}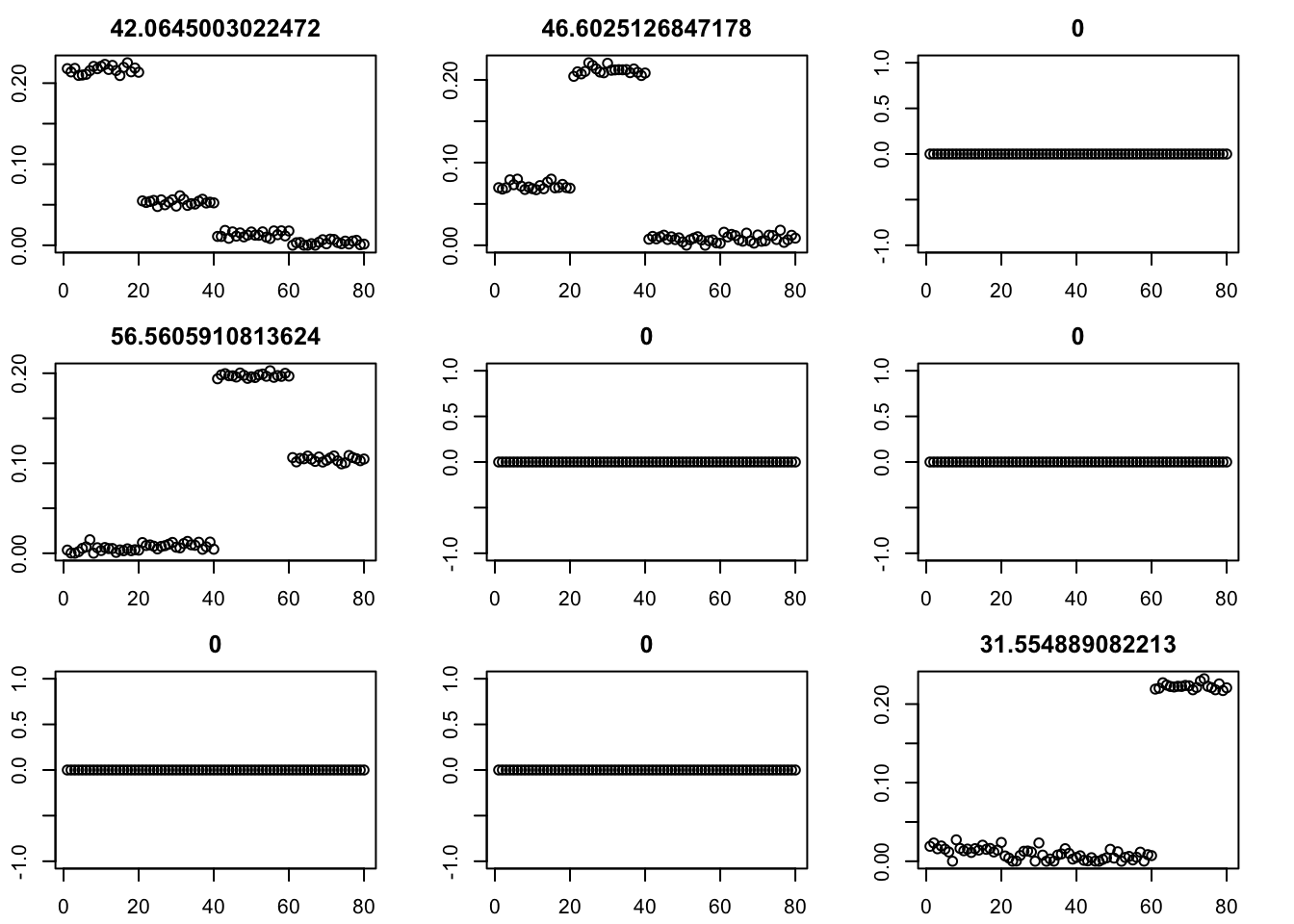

err

 [1] 10358.0063  4607.3557  4598.9735  4537.0254  3410.6696  1191.1974
 [7]   959.9479   811.3587   682.0467   581.9783   500.5249   371.6257
[13]   196.7067   127.1278   120.6584   119.9063   119.6007   119.4296
[19]   119.3242   119.2502   119.1947   119.1548   119.1264   119.1049
[25]   119.0875   119.0733   119.0618   119.0524   119.0446   119.0379
[31]   119.0322   119.0272   119.0227   119.0185   119.0144   119.0105
[37]   119.0068   119.0034   119.0003   118.9974   118.9947   118.9923
[43]   118.9902   118.9883   118.9866   118.9851   118.9838   118.9825
[49]   118.9814   118.9803

fit$d = rep(1e-8,9)
for(i in 2:50){
  fit = eb_power_update(A,fit$v,fit$d,ebnm_generalized_binary)
  err[i] = compute_sqerr(A,fit)
}
par(mfcol=c(3,3),mai=rep(0.3,4))
for(i in 1:9){plot(fit$v[,i],main=paste0(fit$d[i]))}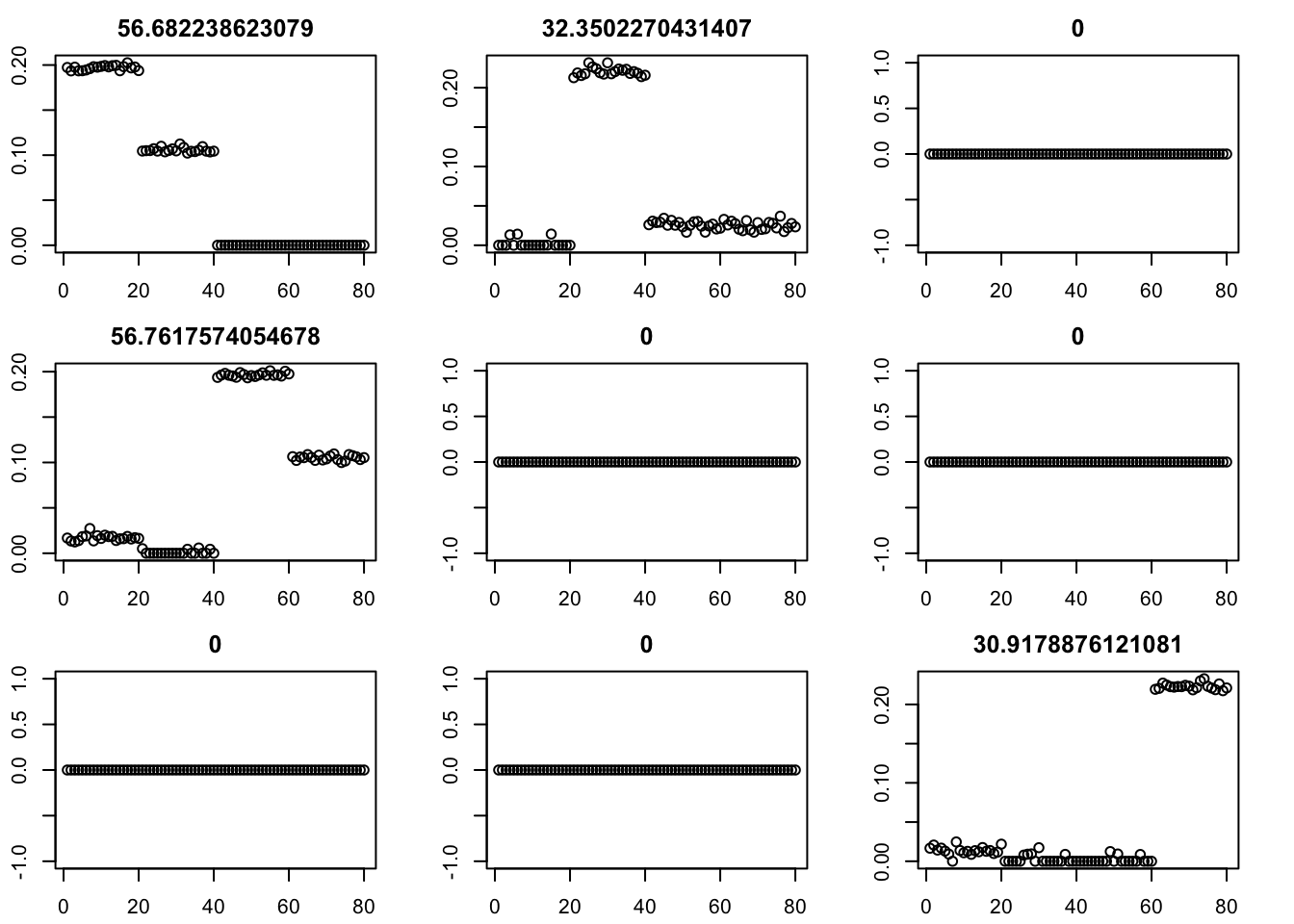

err

 [1] 10358.0063   997.5409   864.8641   744.9060   633.3875   567.5381
 [7]   534.0768   506.6033   438.9509   294.1267   201.6841   150.2595
[13]   129.7993   124.1713   122.6030   121.8072   121.4878   121.3150
[19]   121.1241   121.0973   121.0897   121.0870   121.0856   121.0848
[25]   121.0843   121.0839   121.0836   121.0834   121.0832   121.0831
[31]   121.0830   121.0830   121.0829   121.0829   121.0829   121.0828
[37]   121.0828   121.0828   121.0828   121.0828   121.0828   121.0828
[43]   121.0828   121.0828   121.0828   121.0828   121.0828   121.0828
[49]   121.0828   121.0828

sum(E^2) # compare with "true" error

[1] 388.104

SVD initialization

I’m going to try initializing with SVD, then running point-laplace, then running GB (similar to GBCD strategy). Interestingly, initializing at SVD with d set to the svd-based value leads point-laplace to a solution with negative d values (not shown) so here I initialize d to be very small and let it learn the non-zero values more gradually.

set.seed(2)
A.svd = svd(A)

fit = list(v=A.svd$u[,1:4],d=rep(1e-8,4)) #init d to be very small

err = rep(0,10)
err[1] = compute_sqerr(A,fit)
 
for(i in 2:100){
  fit = eb_power_update(A,fit$v,fit$d,ebnm_point_laplace)
  err[i] = compute_sqerr(A,fit)
}
par(mfcol=c(3,3),mai=rep(0.3,4))
for(i in 1:4){plot(fit$v[,i],main=paste0(fit$d[i]))}
err

  [1] 10358.0063   736.7750   120.5348   118.9666   118.9591   118.9599
  [7]   118.9606   118.9609   118.9607   118.9601   118.9596   118.9593
 [13]   118.9590   118.9589   118.9588   118.9587   118.9586   118.9586
 [19]   118.9586   118.9587   118.9588   118.9590   118.9592   118.9593
 [25]   118.9595   118.9597   118.9598   118.9600   118.9601   118.9602
 [31]   118.9603   118.9604   118.9605   118.9605   118.9606   118.9606
 [37]   118.9607   118.9607   118.9608   118.9608   118.9608   118.9608
 [43]   118.9609   118.9609   118.9609   118.9609   118.9609   118.9609
 [49]   118.9610   118.9610   118.9610   118.9610   118.9610   118.9610
 [55]   118.9610   118.9610   118.9610   118.9610   118.9610   118.9611
 [61]   118.9611   118.9611   118.9611   118.9611   118.9611   118.9611
 [67]   118.9611   118.9611   118.9611   118.9611   118.9611   118.9611
 [73]   118.9611   118.9611   118.9611   118.9611   118.9611   118.9611
 [79]   118.9611   118.9611   118.9611   118.9611   118.9611   118.9611
 [85]   118.9611   118.9611   118.9611   118.9611   118.9611   118.9611
 [91]   118.9611   118.9611   118.9611   118.9611   118.9611   118.9612
 [97]   118.9612   118.9612   118.9612   118.9612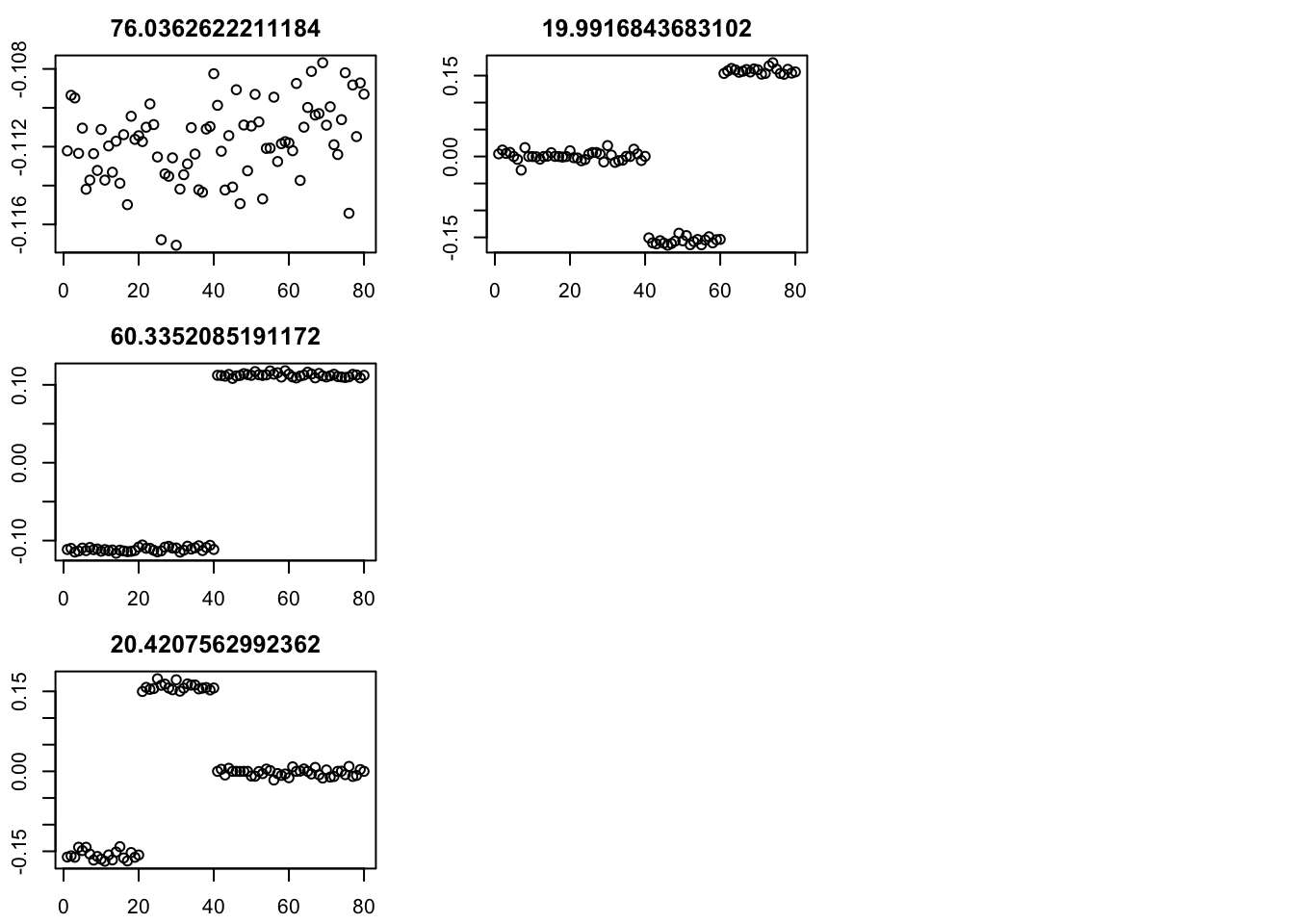

split_v = function(v){
  v = cbind(pmax(v,0),pmax(-v,0))
}

fit$v = split_v(fit$v)
fit$d= rep(fit$d/2,2)

for(i in 2:100){
  fit = eb_power_update(A,fit$v,fit$d,ebnm_point_exponential)
  err[i] = compute_sqerr(A,fit)
}

for(i in 2:50){
  fit = eb_power_update(A,fit$v,fit$d,ebnm_generalized_binary)
  err[i] = compute_sqerr(A,fit)
}
par(mfcol=c(3,3),mai=rep(0.3,4))
for(i in 1:4){plot(fit$v[,i],main=paste0(fit$d[i]))}
err

  [1] 10358.0063   108.6040   108.5842   108.5771   108.6587   108.7029
  [7]   108.6780   108.7333   108.8173   108.7955   108.8543   108.8530
 [13]   108.8317   108.8515   108.8325   108.8746   108.8902   108.8967
 [19]   108.8792   108.8969   108.8839   108.8752   108.8795   108.9067
 [25]   108.9010   108.8965   108.8927   108.8894   108.8865   108.8841
 [31]   108.8819   108.8801   108.8785   108.8772   108.8761   108.8751
 [37]   108.8743   108.8736   108.8731   108.8726   108.8722   108.8719
 [43]   108.8717   108.8715   108.8714   108.8713   108.8712   108.8712
 [49]   108.8712   108.8712   109.8584   109.7571   109.6662   109.5818
 [55]   109.5042   109.4326   109.3657   109.3023   109.2416   109.1830
 [61]   109.1271   109.0745   109.0247   108.9786   108.9351   108.8937
 [67]   108.8547   108.8164   108.7790   108.7436   108.7096   108.6770
 [73]   108.6449   108.6124   108.5800   108.5484   108.5179   108.4888
 [79]   108.4612   108.4348   108.4094   108.3848   108.3607   108.3368
 [85]   108.3133   108.2901   108.2669   108.2428   108.2191   108.1958
 [91]   108.1730   108.1506   108.1284   108.1068   108.0863   108.0665
 [97]   108.0473   108.0286   108.0101   107.9917

sum(E^2) # co

[1] 388.104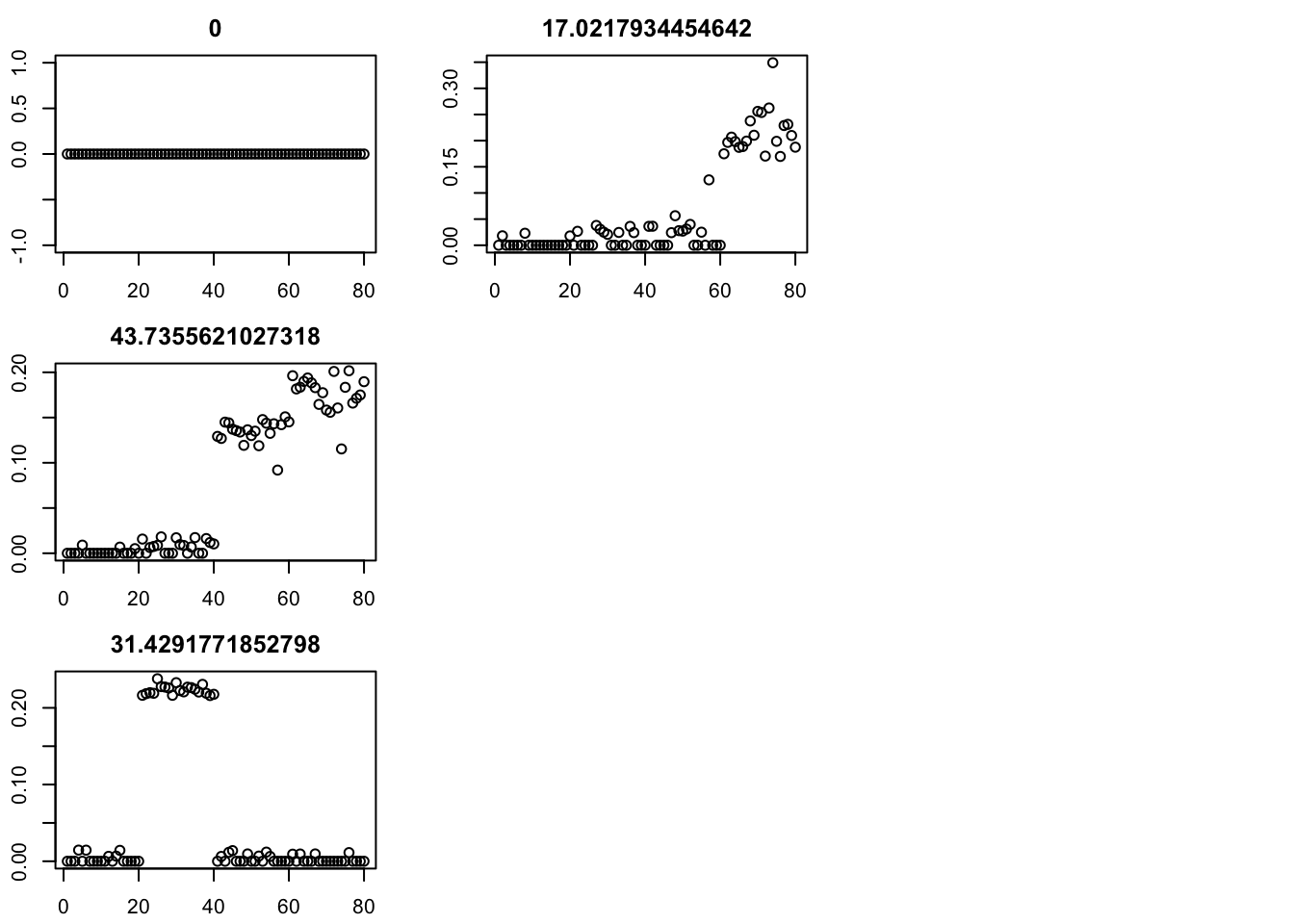

sessionInfo()

R version 4.4.2 (2024-10-31)
Platform: aarch64-apple-darwin20
Running under: macOS Sequoia 15.3.1

Matrix products: default
BLAS:   /Library/Frameworks/R.framework/Versions/4.4-arm64/Resources/lib/libRblas.0.dylib 
LAPACK: /Library/Frameworks/R.framework/Versions/4.4-arm64/Resources/lib/libRlapack.dylib;  LAPACK version 3.12.0

locale:
[1] en_US.UTF-8/en_US.UTF-8/en_US.UTF-8/C/en_US.UTF-8/en_US.UTF-8

time zone: America/Chicago
tzcode source: internal

attached base packages:
[1] stats     graphics  grDevices utils     datasets  methods   base     

other attached packages:
[1] ebnm_1.1-2

loaded via a namespace (and not attached):
 [1] sass_0.4.9        generics_0.1.3    ashr_2.2-63       stringi_1.8.4    
 [5] lattice_0.22-6    digest_0.6.37     magrittr_2.0.3    evaluate_1.0.3   
 [9] grid_4.4.2        fastmap_1.2.0     rprojroot_2.0.4   workflowr_1.7.1  
[13] jsonlite_1.8.9    Matrix_1.7-2      whisker_0.4.1     mixsqp_0.3-54    
[17] promises_1.3.2    scales_1.3.0      truncnorm_1.0-9   invgamma_1.1     
[21] jquerylib_0.1.4   cli_3.6.3         rlang_1.1.5       deconvolveR_1.2-1
[25] munsell_0.5.1     splines_4.4.2     cachem_1.1.0      yaml_2.3.10      
[29] tools_4.4.2       SQUAREM_2021.1    dplyr_1.1.4       colorspace_2.1-1 
[33] ggplot2_3.5.1     httpuv_1.6.15     vctrs_0.6.5       R6_2.5.1         
[37] lifecycle_1.0.4   git2r_0.35.0      stringr_1.5.1     fs_1.6.5         
[41] trust_0.1-8       irlba_2.3.5.1     pkgconfig_2.0.3   pillar_1.10.1    
[45] bslib_0.9.0       later_1.4.1       gtable_0.3.6      glue_1.8.0       
[49] Rcpp_1.0.14       xfun_0.50         tibble_3.2.1      tidyselect_1.2.1 
[53] rstudioapi_0.17.1 knitr_1.49        htmltools_0.5.8.1 rmarkdown_2.29   
[57] compiler_4.4.2    horseshoe_0.2.0