flashier_log1p
Matthew Stephens
2023-10-21
Last updated: 2023-11-06
Checks: 7 0
Knit directory: misc/analysis/
This reproducible R Markdown analysis was created with workflowr (version 1.7.0). The Checks tab describes the reproducibility checks that were applied when the results were created. The Past versions tab lists the development history.
Great! Since the R Markdown file has been committed to the Git repository, you know the exact version of the code that produced these results.
Great job! The global environment was empty. Objects defined in the global environment can affect the analysis in your R Markdown file in unknown ways. For reproduciblity it’s best to always run the code in an empty environment.
The command set.seed(1) was run prior to running the
code in the R Markdown file. Setting a seed ensures that any results
that rely on randomness, e.g. subsampling or permutations, are
reproducible.
Great job! Recording the operating system, R version, and package versions is critical for reproducibility.
Nice! There were no cached chunks for this analysis, so you can be confident that you successfully produced the results during this run.
Great job! Using relative paths to the files within your workflowr project makes it easier to run your code on other machines.
Great! You are using Git for version control. Tracking code development and connecting the code version to the results is critical for reproducibility.
The results in this page were generated with repository version 7f572ae. See the Past versions tab to see a history of the changes made to the R Markdown and HTML files.
Note that you need to be careful to ensure that all relevant files for
the analysis have been committed to Git prior to generating the results
(you can use wflow_publish or
wflow_git_commit). workflowr only checks the R Markdown
file, but you know if there are other scripts or data files that it
depends on. Below is the status of the Git repository when the results
were generated:
Ignored files:
Ignored: .DS_Store
Ignored: .Rhistory
Ignored: .Rproj.user/
Ignored: analysis/.RData
Ignored: analysis/.Rhistory
Ignored: analysis/ALStruct_cache/
Ignored: data/.Rhistory
Ignored: data/methylation-data-for-matthew.rds
Ignored: data/pbmc/
Untracked files:
Untracked: .dropbox
Untracked: Icon
Untracked: analysis/GHstan.Rmd
Untracked: analysis/GTEX-cogaps.Rmd
Untracked: analysis/PACS.Rmd
Untracked: analysis/Rplot.png
Untracked: analysis/SPCAvRP.rmd
Untracked: analysis/admm_02.Rmd
Untracked: analysis/admm_03.Rmd
Untracked: analysis/cholesky.Rmd
Untracked: analysis/compare-transformed-models.Rmd
Untracked: analysis/cormotif.Rmd
Untracked: analysis/cp_ash.Rmd
Untracked: analysis/eQTL.perm.rand.pdf
Untracked: analysis/eb_prepilot.Rmd
Untracked: analysis/eb_var.Rmd
Untracked: analysis/ebpmf1.Rmd
Untracked: analysis/ebpmf_sla_text.Rmd
Untracked: analysis/ebspca_sims.Rmd
Untracked: analysis/explore_psvd.Rmd
Untracked: analysis/fa_check_identify.Rmd
Untracked: analysis/fa_iterative.Rmd
Untracked: analysis/flash_test_tree.Rmd
Untracked: analysis/flash_tree.Rmd
Untracked: analysis/flashier_newgroups.Rmd
Untracked: analysis/greedy_ebpmf_exploration_00.Rmd
Untracked: analysis/ieQTL.perm.rand.pdf
Untracked: analysis/lasso_em_03.Rmd
Untracked: analysis/m6amash.Rmd
Untracked: analysis/mash_bhat_z.Rmd
Untracked: analysis/mash_ieqtl_permutations.Rmd
Untracked: analysis/methylation_example.Rmd
Untracked: analysis/mixsqp.Rmd
Untracked: analysis/mr.ash_lasso_init.Rmd
Untracked: analysis/mr.mash.test.Rmd
Untracked: analysis/mr_ash_modular.Rmd
Untracked: analysis/mr_ash_parameterization.Rmd
Untracked: analysis/mr_ash_ridge.Rmd
Untracked: analysis/mv_gaussian_message_passing.Rmd
Untracked: analysis/nejm.Rmd
Untracked: analysis/nmf_bg.Rmd
Untracked: analysis/normal_conditional_on_r2.Rmd
Untracked: analysis/normalize.Rmd
Untracked: analysis/pbmc.Rmd
Untracked: analysis/pca_binary_weighted.Rmd
Untracked: analysis/pca_l1.Rmd
Untracked: analysis/poisson_nmf_approx.Rmd
Untracked: analysis/poisson_shrink.Rmd
Untracked: analysis/poisson_transform.Rmd
Untracked: analysis/pseudodata.Rmd
Untracked: analysis/qrnotes.txt
Untracked: analysis/ridge_iterative_02.Rmd
Untracked: analysis/ridge_iterative_splitting.Rmd
Untracked: analysis/samps/
Untracked: analysis/sc_bimodal.Rmd
Untracked: analysis/shrinkage_comparisons_changepoints.Rmd
Untracked: analysis/susie_en.Rmd
Untracked: analysis/susie_z_investigate.Rmd
Untracked: analysis/svd-timing.Rmd
Untracked: analysis/temp.RDS
Untracked: analysis/temp.Rmd
Untracked: analysis/test-figure/
Untracked: analysis/test.Rmd
Untracked: analysis/test.Rpres
Untracked: analysis/test.md
Untracked: analysis/test_qr.R
Untracked: analysis/test_sparse.Rmd
Untracked: analysis/tree_dist_top_eigenvector.Rmd
Untracked: analysis/z.txt
Untracked: code/multivariate_testfuncs.R
Untracked: code/rqb.hacked.R
Untracked: data/4matthew/
Untracked: data/4matthew2/
Untracked: data/E-MTAB-2805.processed.1/
Untracked: data/ENSG00000156738.Sim_Y2.RDS
Untracked: data/GDS5363_full.soft.gz
Untracked: data/GSE41265_allGenesTPM.txt
Untracked: data/Muscle_Skeletal.ACTN3.pm1Mb.RDS
Untracked: data/Thyroid.FMO2.pm1Mb.RDS
Untracked: data/bmass.HaemgenRBC2016.MAF01.Vs2.MergedDataSources.200kRanSubset.ChrBPMAFMarkerZScores.vs1.txt.gz
Untracked: data/bmass.HaemgenRBC2016.Vs2.NewSNPs.ZScores.hclust.vs1.txt
Untracked: data/bmass.HaemgenRBC2016.Vs2.PreviousSNPs.ZScores.hclust.vs1.txt
Untracked: data/eb_prepilot/
Untracked: data/finemap_data/fmo2.sim/b.txt
Untracked: data/finemap_data/fmo2.sim/dap_out.txt
Untracked: data/finemap_data/fmo2.sim/dap_out2.txt
Untracked: data/finemap_data/fmo2.sim/dap_out2_snp.txt
Untracked: data/finemap_data/fmo2.sim/dap_out_snp.txt
Untracked: data/finemap_data/fmo2.sim/data
Untracked: data/finemap_data/fmo2.sim/fmo2.sim.config
Untracked: data/finemap_data/fmo2.sim/fmo2.sim.k
Untracked: data/finemap_data/fmo2.sim/fmo2.sim.k4.config
Untracked: data/finemap_data/fmo2.sim/fmo2.sim.k4.snp
Untracked: data/finemap_data/fmo2.sim/fmo2.sim.ld
Untracked: data/finemap_data/fmo2.sim/fmo2.sim.snp
Untracked: data/finemap_data/fmo2.sim/fmo2.sim.z
Untracked: data/finemap_data/fmo2.sim/pos.txt
Untracked: data/logm.csv
Untracked: data/m.cd.RDS
Untracked: data/m.cdu.old.RDS
Untracked: data/m.new.cd.RDS
Untracked: data/m.old.cd.RDS
Untracked: data/mainbib.bib.old
Untracked: data/mat.csv
Untracked: data/mat.txt
Untracked: data/mat_new.csv
Untracked: data/matrix_lik.rds
Untracked: data/paintor_data/
Untracked: data/running_data_chris.csv
Untracked: data/running_data_matthew.csv
Untracked: data/temp.txt
Untracked: data/y.txt
Untracked: data/y_f.txt
Untracked: data/zscore_jointLCLs_m6AQTLs_susie_eQTLpruned.rds
Untracked: data/zscore_jointLCLs_random.rds
Untracked: explore_udi.R
Untracked: output/fit.k10.rds
Untracked: output/fit.varbvs.RDS
Untracked: output/glmnet.fit.RDS
Untracked: output/test.bv.txt
Untracked: output/test.gamma.txt
Untracked: output/test.hyp.txt
Untracked: output/test.log.txt
Untracked: output/test.param.txt
Untracked: output/test2.bv.txt
Untracked: output/test2.gamma.txt
Untracked: output/test2.hyp.txt
Untracked: output/test2.log.txt
Untracked: output/test2.param.txt
Untracked: output/test3.bv.txt
Untracked: output/test3.gamma.txt
Untracked: output/test3.hyp.txt
Untracked: output/test3.log.txt
Untracked: output/test3.param.txt
Untracked: output/test4.bv.txt
Untracked: output/test4.gamma.txt
Untracked: output/test4.hyp.txt
Untracked: output/test4.log.txt
Untracked: output/test4.param.txt
Untracked: output/test5.bv.txt
Untracked: output/test5.gamma.txt
Untracked: output/test5.hyp.txt
Untracked: output/test5.log.txt
Untracked: output/test5.param.txt
Unstaged changes:
Modified: .gitignore
Modified: analysis/flashier_sla_text.Rmd
Modified: analysis/mr_ash_pen.Rmd
Modified: analysis/susie_flash.Rmd
Note that any generated files, e.g. HTML, png, CSS, etc., are not included in this status report because it is ok for generated content to have uncommitted changes.
These are the previous versions of the repository in which changes were
made to the R Markdown (analysis/flashier_log1p.Rmd) and
HTML (docs/flashier_log1p.html) files. If you’ve configured
a remote Git repository (see ?wflow_git_remote), click on
the hyperlinks in the table below to view the files as they were in that
past version.
| File | Version | Author | Date | Message |
|---|---|---|---|---|
| Rmd | 7f572ae | Matthew Stephens | 2023-11-06 | workflowr::wflow_publish("flashier_log1p.Rmd") |
| html | 342338e | Matthew Stephens | 2023-10-21 | Build site. |
| Rmd | 38c2d39 | Matthew Stephens | 2023-10-21 | wflow_publish("flashier_log1p.Rmd") |
library(flashier)Loading required package: ebnmLoading required package: magrittrLoading required package: ggplot2Introduction
When applied to (log1p-transformed) Poisson data, flashier often overestimates the rank (too many factors). However this is usually in simulations where the underlying low-rank structure is the log-mean (or maybe the mean). In practice we don’t know if the low-rank structure is in the log mean or some other function of the mean - for example, in the log1p(mean). Motivated by this, I look at how (nonnegative) flashier behaves on log1p transformed data when the underlying log1p(mu) is itself low rank with non-negative factors.
log1p mean and variance
I want to start by studying the mean and variance of log(1+X)
By Taylor series of \(f(x) = log(1+x)\) we have \[\log(1+X) \approx \log(1+\mu) + (X-\mu)f'(\mu) + 0.5 (X-\mu)^2 f''(\mu)\] so \[E(\log(1+X)) = \log(1+\mu) - 0.5 \mu/(1+\mu)^2\] For small \(\mu\) this is approximately \(\mu/2\) and for large \(\mu\) it is \(\log(1+\mu)\).
Rearranging the above gives \[(log(1+X) - log(1+\mu))^2 \approx (X-\mu)^2 f'(\mu)^2\] so \[var(log(1+X)) \approx \mu/(1+\mu)^2.\]
We can check the accuracy by simulation. It matches pretty well. Also, I note that the standard deviation is not that variable for mu in the range exp(-5) to exp(3). (a factor of just under 10 variation in standard deviation, so not entirely negligible, but it could be worse). This might suggest we might get away without taking account of variation in standard error, which is practically very convenient.
mm = exp(seq(-5,3,length=9))
m = v =mm
for(i in 1:length(mm)){
x = rpois(100000,mm[i])
m[i] = mean(log(1+x))
v[i] = var(log(1+x))
}
plot(mm,m)
lines(mm, log(1+mm) - 0.5*mm/(1+mm)^2 )
| Version | Author | Date |
|---|---|---|
| 342338e | Matthew Stephens | 2023-10-21 |
plot(mm,sqrt(v))
lines(mm, sqrt(mm)/(1+mm))
abline(v=1)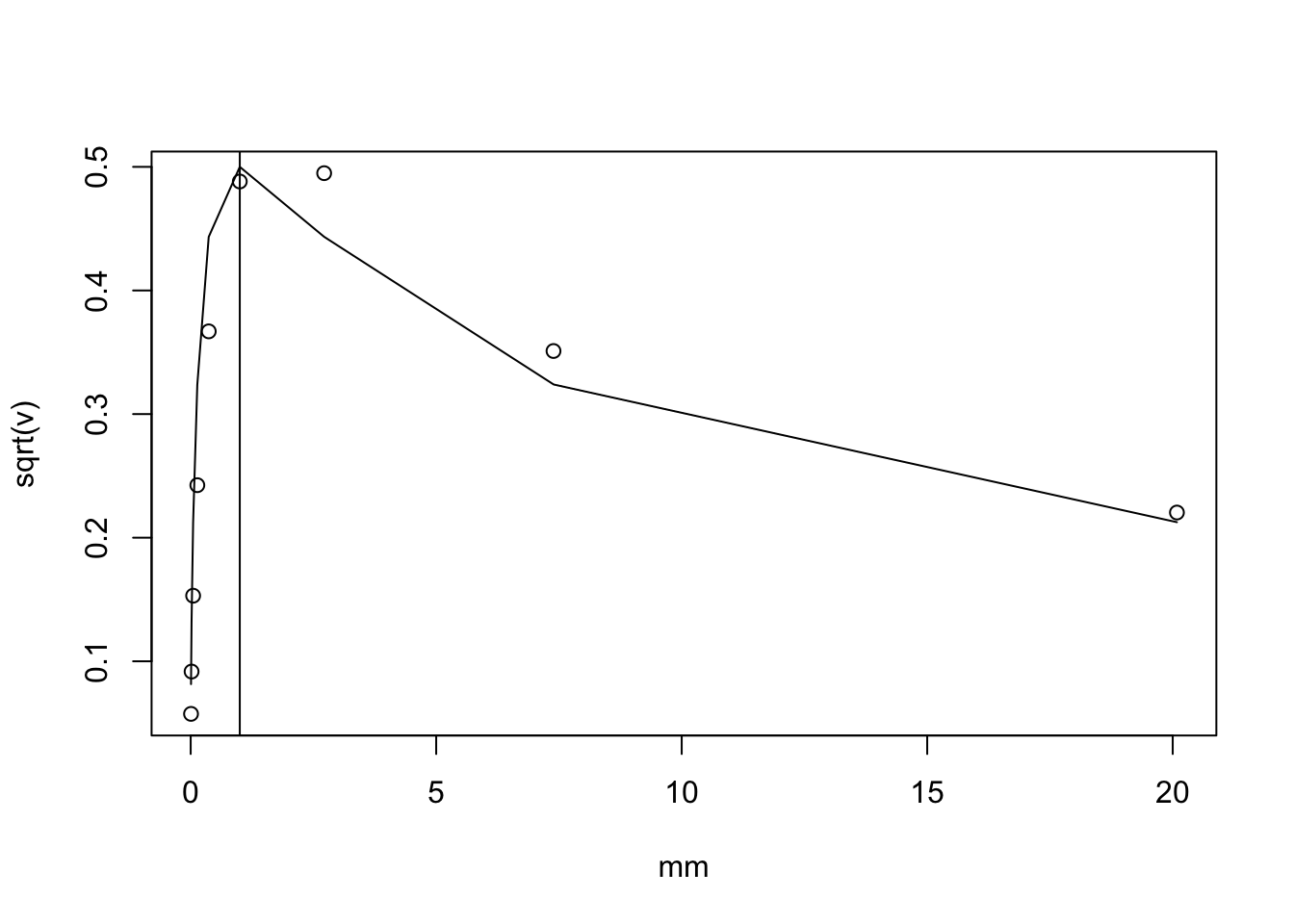
| Version | Author | Date |
|---|---|---|
| 342338e | Matthew Stephens | 2023-10-21 |
log(c+X)
We can extend this to \(log(c+X)\). By Taylor series we have: \[E(log(c+X)) = log(c+\mu) - 0.5 \mu/(c+\mu)^2\] and \[Var(log(c+X)) \approx \mu/(c+\mu)^2.\]
c=0.1
mm = exp(seq(-5,3,length=9))
mc = vc =mm
for(i in 1:length(mm)){
x = rpois(100000,mm[i])
mc[i] = mean(log(c+x))
vc[i] = var(log(c+x))
}
plot(mm, log(c+mm) - 0.5*mm/(c+mm)^2,type="l" )
points(mm,mc)
| Version | Author | Date |
|---|---|---|
| 342338e | Matthew Stephens | 2023-10-21 |
plot(mm,sqrt(vc))
lines(mm, sqrt(mm)/(c+mm))
| Version | Author | Date |
|---|---|---|
| 342338e | Matthew Stephens | 2023-10-21 |
Interesting that (unless I made a mistake) the mean is quite off for small mu and the variance is also off. I need to understand this better. However, I do note again that the standard deviation doesn’t vary too much with mm.
log(1+cX)
Here I instead extend this to \(log(1+cX)\) (which is sparse). By Taylor series we have: \[E(log(1+cX)) = log(1+c\mu) - 0.5 c^2 \mu /(1+c\mu)^2\] and \[Var(log(c+X)) \approx \mu c^2/(1+c\mu)^2.\]
c=10
mm = exp(seq(-5,3,length=9))
mc = vc =mm
for(i in 1:length(mm)){
x = rpois(100000,mm[i])
mc[i] = mean(log(1+c*x))
vc[i] = var(log(1+c*x))
}
plot(mm, log(1+c*mm) - 0.5*c^2 * mm/(1+c*mm)^2,type="l" )
points(mm,mc)
| Version | Author | Date |
|---|---|---|
| 342338e | Matthew Stephens | 2023-10-21 |
plot(mm,sqrt(vc))
lines(mm, c *sqrt(mm)/(1+c*mm))
Simple simulation
I do a simple simulation where \(log(1+\mu) =LF'\) where \(L\) and \(F\) are non-negative and \(LF'\) is rank 4..
set.seed(1)
n= 1000
p = 200
K = 4
LL = matrix(runif(n*K),nrow=n)
FF = matrix(runif(p*K),nrow=p)
mu = matrix(exp(LL %*% t(FF))-1,ncol=p, nrow=n)
X= matrix(rpois(n*p,mu), ncol=p, nrow=n)
hist(mu)
mean(X>0)[1] 0.744955Try flashier
fit.nn.1 = flash(log(X+1),ebnm_fn = ebnm_point_exponential,var_type=2,backfit=TRUE)Adding factor 1 to flash object...
Adding factor 2 to flash object...
Adding factor 3 to flash object...
Adding factor 4 to flash object...
Adding factor 5 to flash object...
Adding factor 6 to flash object...
Adding factor 7 to flash object...
Factor doesn't significantly increase objective and won't be added.
Wrapping up...
Done.
Backfitting 6 factors (tolerance: 2.98e-03)...
Difference between iterations is within 1.0e+02...
Difference between iterations is within 1.0e+01...
--Estimate of factor 6 is numerically zero!
--Estimate of factor 6 is numerically zero!
--Estimate of factor 4 is numerically zero!
Difference between iterations is within 1.0e+00...
Difference between iterations is within 1.0e-01...
Wrapping up...
Done.
Nullchecking 6 factors...
One factor is identically zero.
Wrapping up...
Removed one factor.
Done.The greedy approach fits 6 factors, but the backfitting ends up with 5 factors. And one of the factors is capturing a single row.
plot(fit.nn.1$F_pm[,4])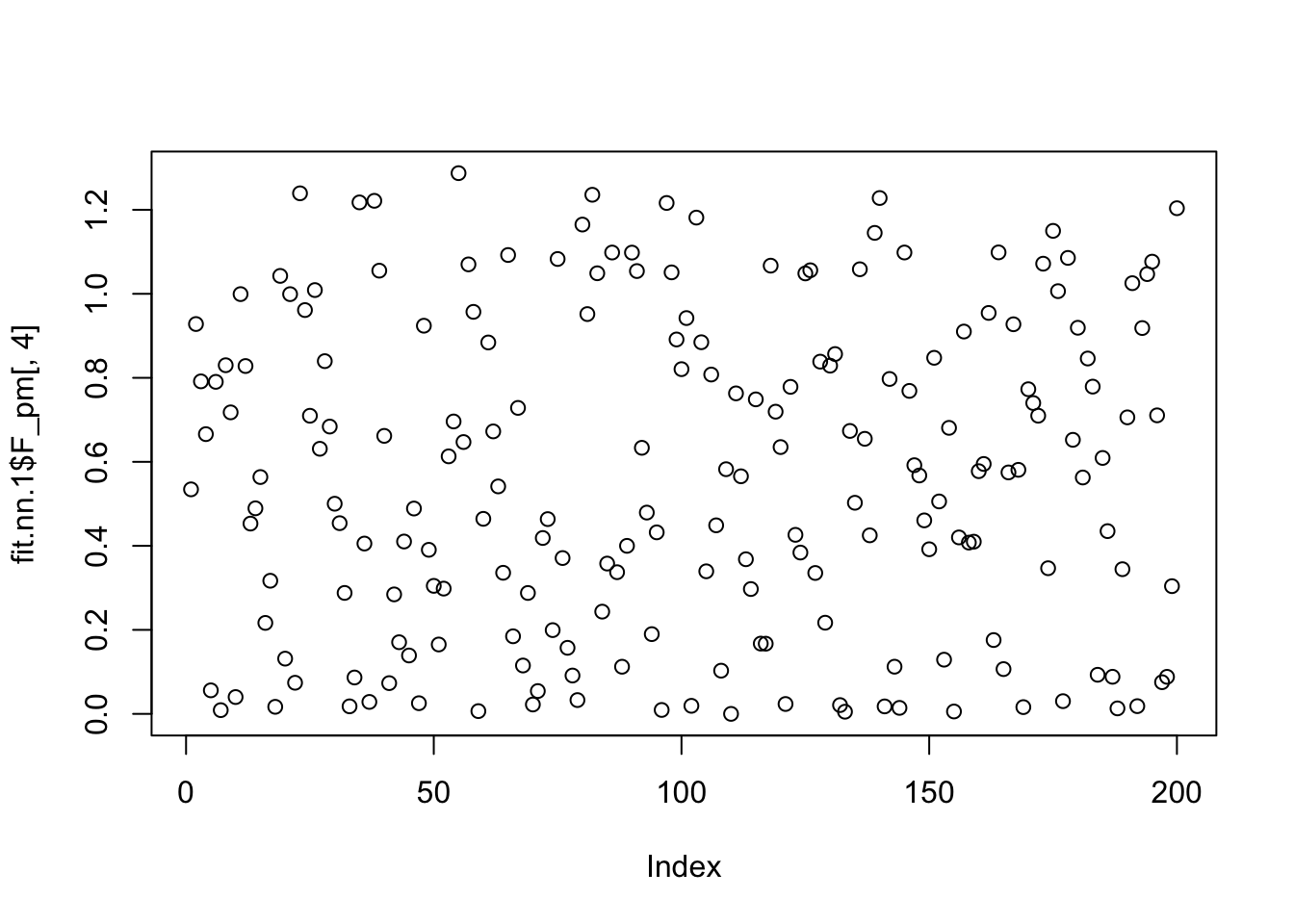
which.max(fit.nn.1$F_pm[,4])[1] 55plot(fit.nn.1$L_pm[,4])
plot(X[,54])
fit.nn.1$flash_fit$tau[54][1] 4.274929So it seems the extra factor here is due to flash converging to a solution that picks out one column, and sets its variance close to 0 (tau is very big). And the null check does not work because the flash objective goes to infinity as tau goes to infinity with a perfect fit to the column. We could probably avoid this by setting a minimum tau somehow (or regularizing it).
After experimenting I found that S=0.5 fixed it (but smaller values of S do not).
fit.nn.1 = flash(log(X+1),ebnm_fn = ebnm_point_exponential,var_type=2,backfit=TRUE, S=0.5)Adding factor 1 to flash object...
Adding factor 2 to flash object...
Adding factor 3 to flash object...
Adding factor 4 to flash object...
Adding factor 5 to flash object...
Factor doesn't significantly increase objective and won't be added.
Wrapping up...
Done.
Backfitting 4 factors (tolerance: 2.98e-03)...
Difference between iterations is within 1.0e+02...
Difference between iterations is within 1.0e+01...
Difference between iterations is within 1.0e+00...
Difference between iterations is within 1.0e-01...
Difference between iterations is within 1.0e-02...
Wrapping up...
Done.
Nullchecking 4 factors...
Done.We need more investigation, but maybe flash can do OK with estimating the rank if the true log(1+mu) is low rank and we fix the issue with outlying factors capturing a single column.
sessionInfo()R version 4.2.1 (2022-06-23)
Platform: x86_64-apple-darwin17.0 (64-bit)
Running under: macOS Big Sur ... 10.16
Matrix products: default
BLAS: /Library/Frameworks/R.framework/Versions/4.2/Resources/lib/libRblas.0.dylib
LAPACK: /Library/Frameworks/R.framework/Versions/4.2/Resources/lib/libRlapack.dylib
locale:
[1] en_US.UTF-8/en_US.UTF-8/en_US.UTF-8/C/en_US.UTF-8/en_US.UTF-8
attached base packages:
[1] stats graphics grDevices utils datasets methods base
other attached packages:
[1] flashier_1.0.0 ggplot2_3.4.3 magrittr_2.0.3 ebnm_1.0-55
loaded via a namespace (and not attached):
[1] Rcpp_1.0.11 horseshoe_0.2.0 invgamma_1.1 lattice_0.20-45
[5] tidyr_1.3.0 rprojroot_2.0.3 digest_0.6.33 utf8_1.2.3
[9] truncnorm_1.0-9 R6_2.5.1 evaluate_0.22 highr_0.10
[13] pillar_1.9.0 rlang_1.1.1 rstudioapi_0.14 irlba_2.3.5.1
[17] whisker_0.4.1 jquerylib_0.1.4 Matrix_1.5-3 rmarkdown_2.20
[21] splines_4.2.1 stringr_1.5.0 munsell_0.5.0 mixsqp_0.3-48
[25] compiler_4.2.1 httpuv_1.6.9 xfun_0.37 pkgconfig_2.0.3
[29] SQUAREM_2021.1 htmltools_0.5.4 tidyselect_1.2.0 tibble_3.2.1
[33] workflowr_1.7.0 fansi_1.0.5 dplyr_1.1.3 withr_2.5.1
[37] later_1.3.0 grid_4.2.1 jsonlite_1.8.7 gtable_0.3.4
[41] lifecycle_1.0.3 git2r_0.31.0 scales_1.2.1 cli_3.6.1
[45] stringi_1.7.12 cachem_1.0.7 fs_1.6.3 promises_1.2.0.1
[49] bslib_0.4.2 generics_0.1.3 vctrs_0.6.4 trust_0.1-8
[53] tools_4.2.1 glue_1.6.2 softImpute_1.4-1 purrr_1.0.2
[57] parallel_4.2.1 fastmap_1.1.1 yaml_2.3.7 colorspace_2.1-0
[61] ashr_2.2-63 deconvolveR_1.2-1 knitr_1.42 sass_0.4.5