EB Flash, n=p=1
Matthew Stephens
2017-06-14
Last updated: 2017-06-15
Code version: 9a49441
Background
I was interested in whether we can try to differentiate the flash likelihood at the “null” (\(g_l=g_f=0\)).
Let n=p=1. And Y (1 by 1 matrix) be given by factor model \[Y = lf + e\] where \(l,f \sim N(0,s^2)\) and \(e \sim N(0,1)\).
Integrating out \(l\) and \(f\) yields a likelihood for \(s\): \[L(s) = \int p(Y| l, f) p(l) p(f) dl df \]
My question is what is the derivative of the likelihood (or log likelihood) with respect to \(s\). Particularly what is it at \(s=0\) (which is the 0-factor model)?
If we define \(h\) to be the log-likelihood for \(l,f\) \[h(l,f) = \log p(Y|l,f)\] then is easy to show that
\[d^2h/dl^2 = f^2/s^2\] and \[d^2h/dldf = -(Y-2lf)\]
so at \(l=f=0\) the hessian is the matrix with 0 on diagonal and \(-Y\) on off-diagonal. This matrix has eigenvalues \(\pm Y\).
This suggests that the posterior distribution of \((l,f)\) will be approximated by a multivariate normal with inverse covariance matrix with \(1/s^2\) on diagonal and \(Y\) on off-diagonal. Let’s try with s=0.1.
l = rnorm(100000,0,0.1)
f = rnorm(100000,0,0.1)
y = 2
Lik = dnorm((y-l*f),0,1)
ss = sample(1:100000,prob=Lik,replace=TRUE)
plot(l[ss],f[ss])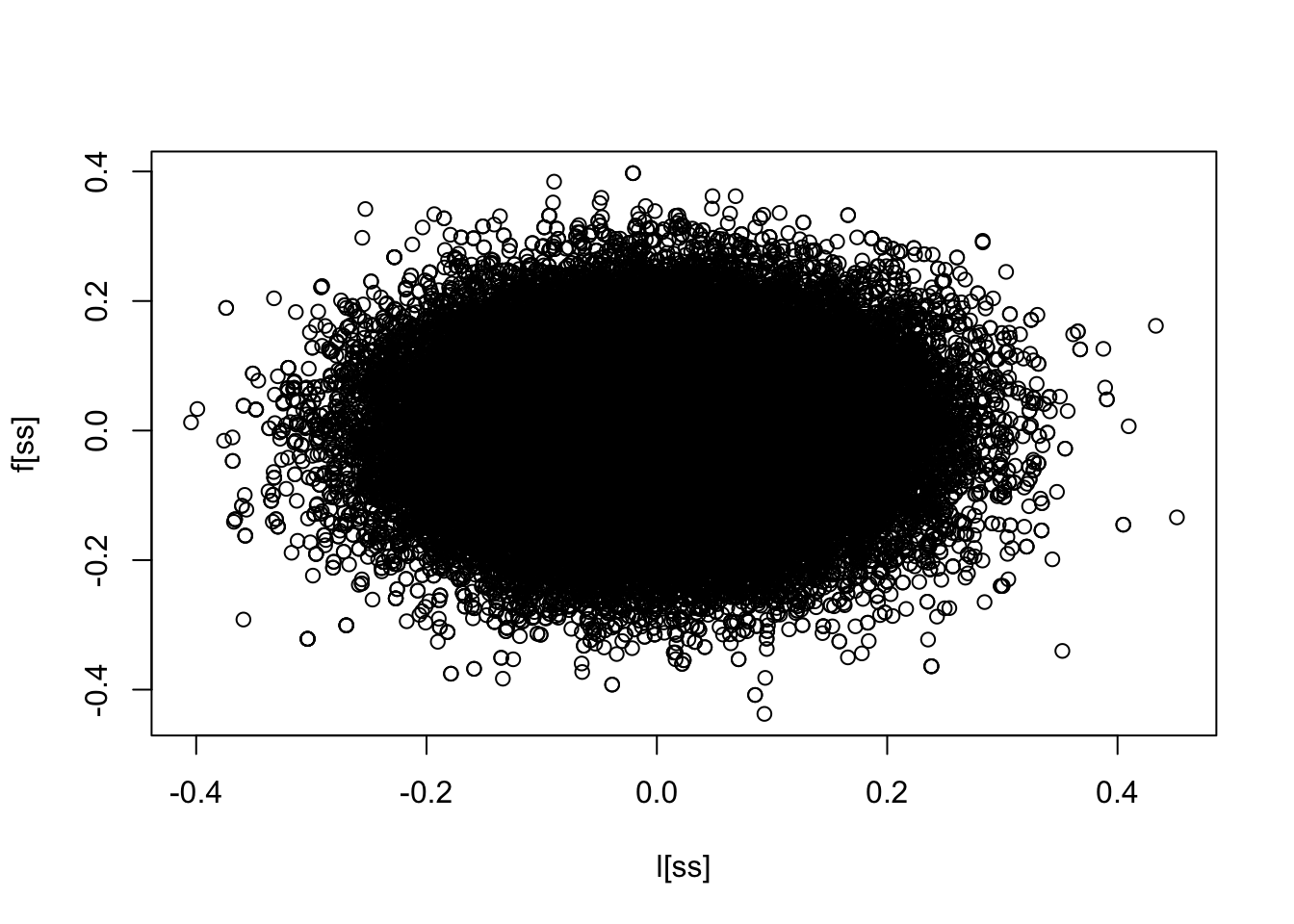
So we see the problem - indeed the posterior is approximated by this, but it looks just like the prior… So the ratio of the posterior to the prior will be 1.
Session information
sessionInfo()R version 3.3.2 (2016-10-31)
Platform: x86_64-apple-darwin13.4.0 (64-bit)
Running under: OS X El Capitan 10.11.6
locale:
[1] en_US.UTF-8/en_US.UTF-8/en_US.UTF-8/C/en_US.UTF-8/en_US.UTF-8
attached base packages:
[1] stats graphics grDevices utils datasets methods base
loaded via a namespace (and not attached):
[1] Rcpp_0.12.11 rstudioapi_0.6 knitr_1.15.1
[4] magrittr_1.5 workflowr_0.4.0 MASS_7.3-47
[7] doParallel_1.0.10 pscl_1.4.9 SQUAREM_2016.8-2
[10] lattice_0.20-35 foreach_1.4.3 ashr_2.1-19
[13] stringr_1.2.0 tools_3.3.2 parallel_3.3.2
[16] grid_3.3.2 git2r_0.18.0 htmltools_0.3.6
[19] iterators_1.0.8 yaml_2.1.14 rprojroot_1.2
[22] digest_0.6.12 Matrix_1.2-10 codetools_0.2-15
[25] evaluate_0.10 rmarkdown_1.5 stringi_1.1.5
[28] backports_1.0.5 truncnorm_1.0-7 This R Markdown site was created with workflowr