Test ash npmle with n big
Matthew Stephens
2017-06-02
Last updated: 2017-06-03
Code version: b5a4b44
Background
The NPMLE for the EB normal means problem is a discrete distribution. For n=1000 I’ve found it is “quite” discrete, with just a few masses. What happens for larger n?
set.seed(1)
library("ashr")
bhat = rnorm(100000,0,2)
grid = seq(from = min(bhat),to = max(bhat),length = 100)
k = length(grid)
b.ash.npmle = ash(bhat,1,g = unimix(pi = rep(1/(k-1),(k-1)),a = grid[-k],b = grid[-1]),method = "shrink")
plot(grid[-1],get_fitted_g(b.ash.npmle)$pi)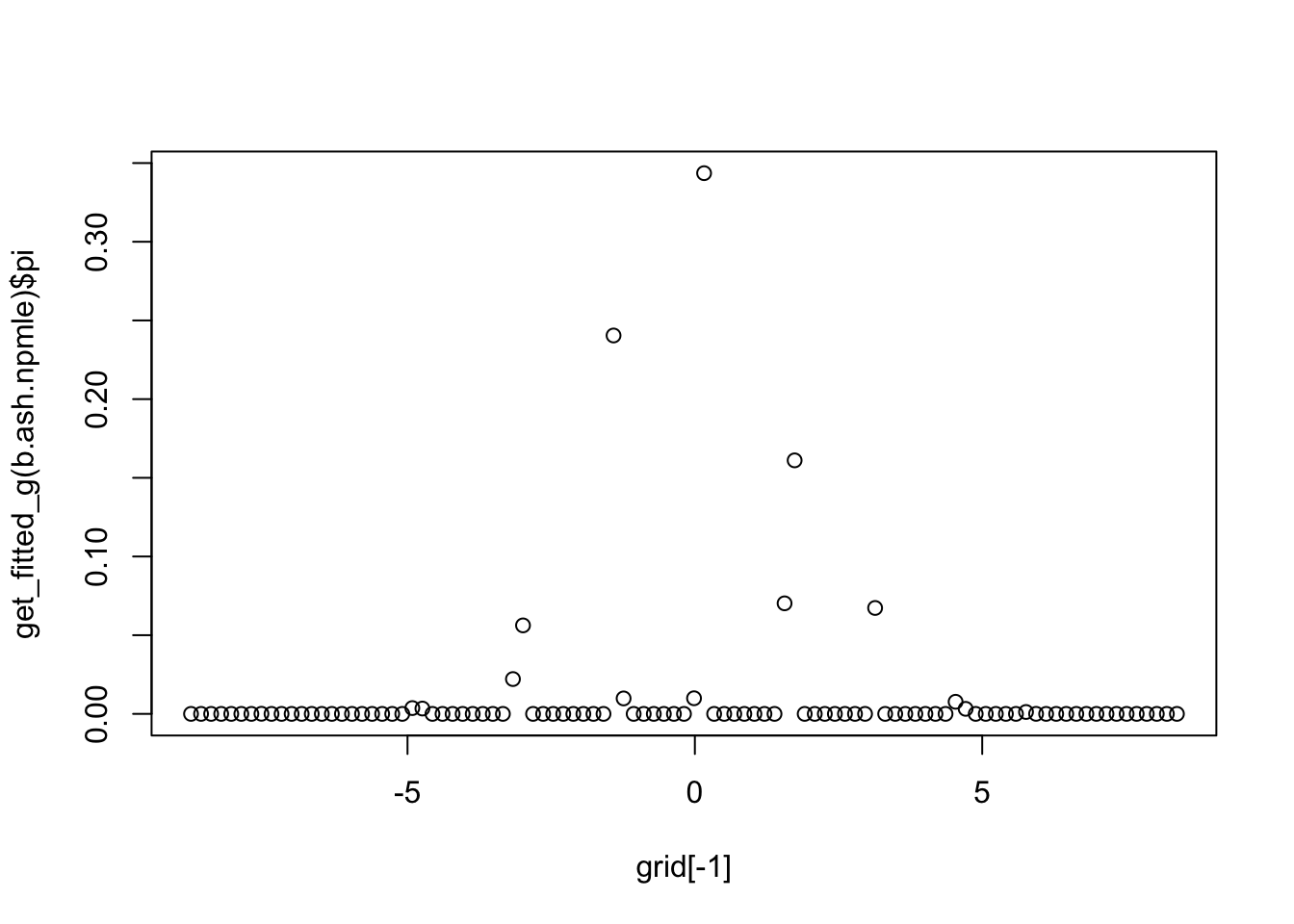
b.ash.npmle$loglik[1] -210981.2sum(dnorm(bhat,0,2,log=TRUE))[1] -210987.5Session information
sessionInfo()R version 3.3.2 (2016-10-31)
Platform: x86_64-apple-darwin13.4.0 (64-bit)
Running under: OS X El Capitan 10.11.6
locale:
[1] en_US.UTF-8/en_US.UTF-8/en_US.UTF-8/C/en_US.UTF-8/en_US.UTF-8
attached base packages:
[1] stats graphics grDevices utils datasets methods base
other attached packages:
[1] ashr_2.1-19
loaded via a namespace (and not attached):
[1] Rcpp_0.12.11 knitr_1.15.1 magrittr_1.5
[4] workflowr_0.4.0 REBayes_0.73 MASS_7.3-47
[7] doParallel_1.0.10 pscl_1.4.9 SQUAREM_2016.8-2
[10] lattice_0.20-35 foreach_1.4.3 stringr_1.2.0
[13] tools_3.3.2 parallel_3.3.2 grid_3.3.2
[16] git2r_0.18.0 htmltools_0.3.6 iterators_1.0.8
[19] assertthat_0.2.0 yaml_2.1.14 rprojroot_1.2
[22] digest_0.6.12 Matrix_1.2-10 codetools_0.2-15
[25] rsconnect_0.7 evaluate_0.10 rmarkdown_1.5
[28] stringi_1.1.5 Rmosek_7.1.2 backports_1.0.5
[31] truncnorm_1.0-7 This R Markdown site was created with workflowr