Mean and variance functions used to simulate Gaussian data
Zhengrong Xing, Peter Carbonetto and Matthew Stephens
Last updated: 2018-12-04
workflowr checks: (Click a bullet for more information)-
✔ R Markdown file: up-to-date
Great! Since the R Markdown file has been committed to the Git repository, you know the exact version of the code that produced these results.
-
✔ Environment: empty
Great job! The global environment was empty. Objects defined in the global environment can affect the analysis in your R Markdown file in unknown ways. For reproduciblity it’s best to always run the code in an empty environment.
-
✔ Seed:
set.seed(1)The command
set.seed(1)was run prior to running the code in the R Markdown file. Setting a seed ensures that any results that rely on randomness, e.g. subsampling or permutations, are reproducible. -
✔ Session information: recorded
Great job! Recording the operating system, R version, and package versions is critical for reproducibility.
-
Great! You are using Git for version control. Tracking code development and connecting the code version to the results is critical for reproducibility. The version displayed above was the version of the Git repository at the time these results were generated.✔ Repository version: 1bddd73
Note that you need to be careful to ensure that all relevant files for the analysis have been committed to Git prior to generating the results (you can usewflow_publishorwflow_git_commit). workflowr only checks the R Markdown file, but you know if there are other scripts or data files that it depends on. Below is the status of the Git repository when the results were generated:
Note that any generated files, e.g. HTML, png, CSS, etc., are not included in this status report because it is ok for generated content to have uncommitted changes.Ignored files: Ignored: dsc/code/Wavelab850/MEXSource/CPAnalysis.mexmac Ignored: dsc/code/Wavelab850/MEXSource/DownDyadHi.mexmac Ignored: dsc/code/Wavelab850/MEXSource/DownDyadLo.mexmac Ignored: dsc/code/Wavelab850/MEXSource/FAIPT.mexmac Ignored: dsc/code/Wavelab850/MEXSource/FCPSynthesis.mexmac Ignored: dsc/code/Wavelab850/MEXSource/FMIPT.mexmac Ignored: dsc/code/Wavelab850/MEXSource/FWPSynthesis.mexmac Ignored: dsc/code/Wavelab850/MEXSource/FWT2_PO.mexmac Ignored: dsc/code/Wavelab850/MEXSource/FWT_PBS.mexmac Ignored: dsc/code/Wavelab850/MEXSource/FWT_PO.mexmac Ignored: dsc/code/Wavelab850/MEXSource/FWT_TI.mexmac Ignored: dsc/code/Wavelab850/MEXSource/IAIPT.mexmac Ignored: dsc/code/Wavelab850/MEXSource/IMIPT.mexmac Ignored: dsc/code/Wavelab850/MEXSource/IWT2_PO.mexmac Ignored: dsc/code/Wavelab850/MEXSource/IWT_PBS.mexmac Ignored: dsc/code/Wavelab850/MEXSource/IWT_PO.mexmac Ignored: dsc/code/Wavelab850/MEXSource/IWT_TI.mexmac Ignored: dsc/code/Wavelab850/MEXSource/LMIRefineSeq.mexmac Ignored: dsc/code/Wavelab850/MEXSource/MedRefineSeq.mexmac Ignored: dsc/code/Wavelab850/MEXSource/UpDyadHi.mexmac Ignored: dsc/code/Wavelab850/MEXSource/UpDyadLo.mexmac Ignored: dsc/code/Wavelab850/MEXSource/WPAnalysis.mexmac Ignored: dsc/code/Wavelab850/MEXSource/dct_ii.mexmac Ignored: dsc/code/Wavelab850/MEXSource/dct_iii.mexmac Ignored: dsc/code/Wavelab850/MEXSource/dct_iv.mexmac Ignored: dsc/code/Wavelab850/MEXSource/dst_ii.mexmac Ignored: dsc/code/Wavelab850/MEXSource/dst_iii.mexmac Untracked files: Untracked: analysis/.#gaussian_signals.Rmd
Expand here to see past versions:
| File | Version | Author | Date | Message |
|---|---|---|---|---|
| Rmd | 1bddd73 | Peter Carbonetto | 2018-12-04 | wflow_publish(“gaussian_signals.Rmd”) |
| html | dc4c6cd | Peter Carbonetto | 2018-12-04 | I now have plots of all the mean functions in gaussian_signals.Rmd. |
| Rmd | a8b9722 | Peter Carbonetto | 2018-12-04 | wflow_publish(“gaussian_signals.Rmd”) |
| Rmd | 2ab6ac0 | Peter Carbonetto | 2018-12-04 | wflow_publish(“gaussian_signals.Rmd”) |
| Rmd | ee71f27 | Peter Carbonetto | 2018-12-04 | Made a few small adjustments to the text in the “gaussianmeanest” analysis. |
Set up environment
Load the ggplot2 and cowplot packages, and the functions definining the mean and variances used to simulate the data.
library(ggplot2)
library(cowplot)
source("../code/signals.R")Generate the ground-truth signals
Here, n specifies the length of the signals.
n = 1024
t = 1:n/nSome code.
mu.s = spike.f(t)More code.
pos = c(0.1, 0.13, 0.15, 0.23, 0.25, 0.4, 0.44, 0.65, 0.76, 0.78, 0.81)
hgt = 2.97/5 * c(4, 5, 3, 4, 5, 4.2, 2.1, 4.3, 3.1, 5.1, 4.2)
wth = c(0.005, 0.005, 0.006, 0.01, 0.01, 0.03, 0.01, 0.01, 0.005, 0.008, 0.005)
mu.b = rep(0, n)
for (j in 1:length(pos))
mu.b = mu.b + hgt[j]/((1 + (abs(t - pos[j])/wth[j]))^4)
mu.dop = dop.f(t)
mu.dop = 3/(max(mu.dop) - min(mu.dop)) * (mu.dop - min(mu.dop))
mu.dop.var = 10 * dop.f(t)
mu.dop.var = mu.dop.var - min(mu.dop.var)
sig = ((2 * t + 0.5) * (t <= 0.15)) +
((-12 * (t - 0.15) + 0.8) * (t > 0.15 & t <= 0.2)) +
0.2 * (t > 0.2 & t <= 0.5) +
((6 * (t - 0.5) + 0.2) * (t > 0.5 & t <= 0.6)) +
((-10 * (t - 0.6) + 0.8) * (t > 0.6 & t <= 0.65)) +
((-0.5 * (t - 0.65) + 0.3) * (t > 0.65 & t <= 0.85)) +
((2 * (t - 0.85) + 0.2) * (t > 0.85))
mu.ang = 3/5 * ((5/(max(sig) - min(sig))) * sig - 1.6) - 0.0419569
heavi = 4 * sin(4 * pi * t) - sign(t - 0.3) - sign(0.72 - t)
mu.hs = heavi/sqrt(var(heavi)) * 1 * 2.99/3.366185
mu.hs = mu.hs - min(mu.hs)
pos = c(0.1, 0.13, 0.15, 0.23, 0.25, 0.4, 0.44, 0.65, 0.76, 0.78, 0.81)
hgt = 2.88/5 * c(4, (-5), 3, (-4), 5, (-4.2), 2.1, 4.3, (-3.1), 2.1, (-4.2))
mu.blk = rep(0, n)
for (j in 1:length(pos))
mu.blk = mu.blk + (1 + sign(t - pos[j])) * (hgt[j]/2)
mu.cblk = mu.blk
mu.cblk[mu.cblk < 0] = 0Define the Blip mean function.
mu.blip = (0.32 + 0.6 * t +
0.3 * exp(-100 * (t - 0.3)^2)) * (t >= 0 & t <= 0.8) +
(-0.28 + 0.6 * t + 0.3 * exp(-100 * (t - 1.3)^2)) * (t > 0.8 & t <= 1)Define the Corner mean function.
mu.cor = 623.87 * t^3 * (1 - 2 * t) * (t >= 0 & t <= 0.5) +
187.161 * (0.125 - t^3) * t^4 * (t > 0.5 & t <= 0.8) +
3708.470441 * (t - 1)^3 * (t > 0.8 & t <= 1)
mu.cor = (0.6/(max(mu.cor) - min(mu.cor))) * mu.cor
mu.cor = mu.cor - min(mu.cor) + 0.2Define the rest of the mean functions.
mu.sp = (1 + mu.s)/5
mu.bump = (1 + mu.b)/5
mu.blk = 0.2 + 0.6 * (mu.blk - min(mu.blk))/max(mu.blk - min(mu.blk))
mu.ang = (1 + mu.ang)/5
mu.dop = (1 + mu.dop)/5Define the variance functions.
var1 = rep(1, n)
var2 = (1e-02 + 4 * (exp(-550 * (t - 0.2)^2) +
exp(-200 * (t - 0.5)^2) +
exp(-950 * (t - 0.8)^2)))
var3 = (1e-02 + 2 * mu.dop.var)
var4 = 1e-02 + mu.b
var5 = 1e-02 + 1 * (mu.cblk - min(mu.cblk))/max(mu.cblk)
var1 = var1/2
var2 = var2/max(var2)
var3 = var3/max(var3)
var4 = var4/max(var4)
var5 = var5/max(var5)Plot the signal means
These plots show each of the mean functions used to generate the simulated data sets.
plot_grid(qplot(t,mu.sp, geom="line",xlab="",ylab="",main="Spikes (sp)"),
qplot(t,mu.bump,geom="line",xlab="",ylab="",main="Bumps (bump)"),
qplot(t,mu.blk, geom="line",xlab="",ylab="",main="Blocks (blk)"),
qplot(t,mu.ang, geom="line",xlab="",ylab="",main="Angles (ang)"),
qplot(t,mu.dop, geom="line",xlab="",ylab="",main="Doppler (dop)"),
qplot(t,mu.blip,geom="line",xlab="",ylab="",main="Blip (blip)"),
qplot(t,mu.cor, geom="line",xlab="",ylab="",main="Corner (cor)"),
nrow = 4,ncol = 2)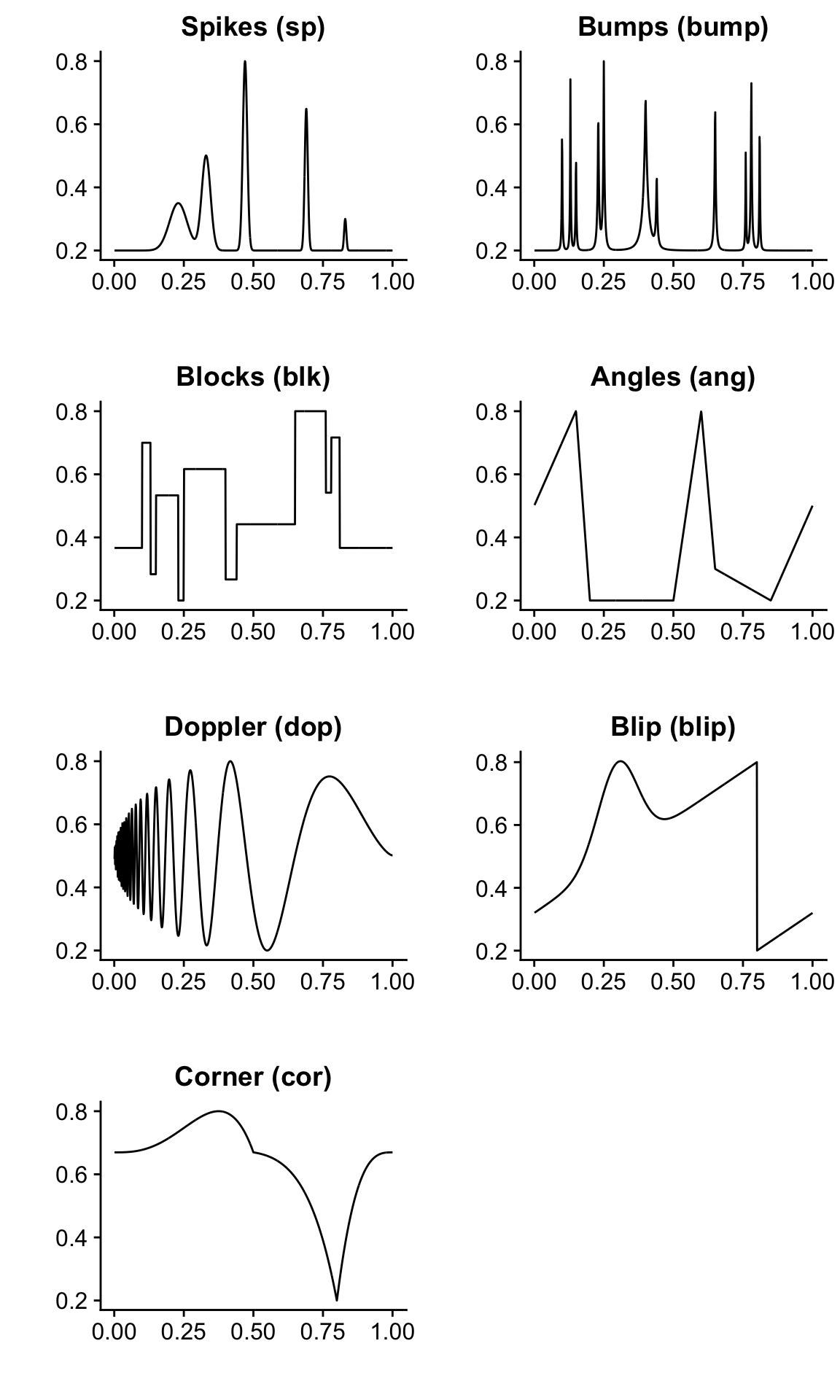
Expand here to see past versions of plot-mean-functions-1.png:
| Version | Author | Date |
|---|---|---|
| dc4c6cd | Peter Carbonetto | 2018-12-04 |
Plot the signal variances
These are rescaled in the simulations to achieve the desired signal-to-noise ratios (see the paper for a more detailed explanation).
plot(t,var1,xlab = "",ylab = "",ylim = c(0,1),type = "l",
main = "Constant variance function")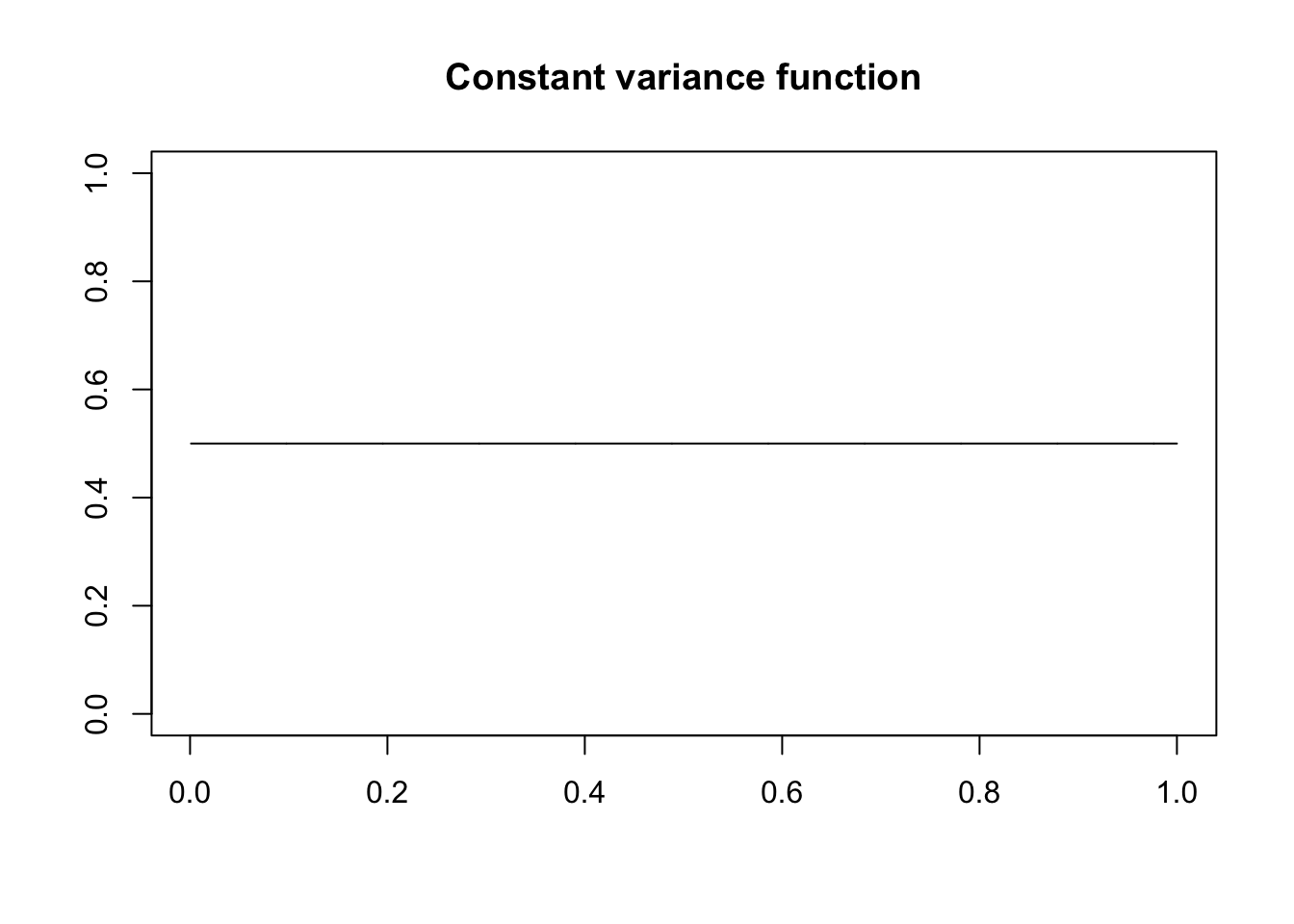
plot(t,var2,xlab = "",ylab = "",type = "l",
main = "Triple exponential variance function")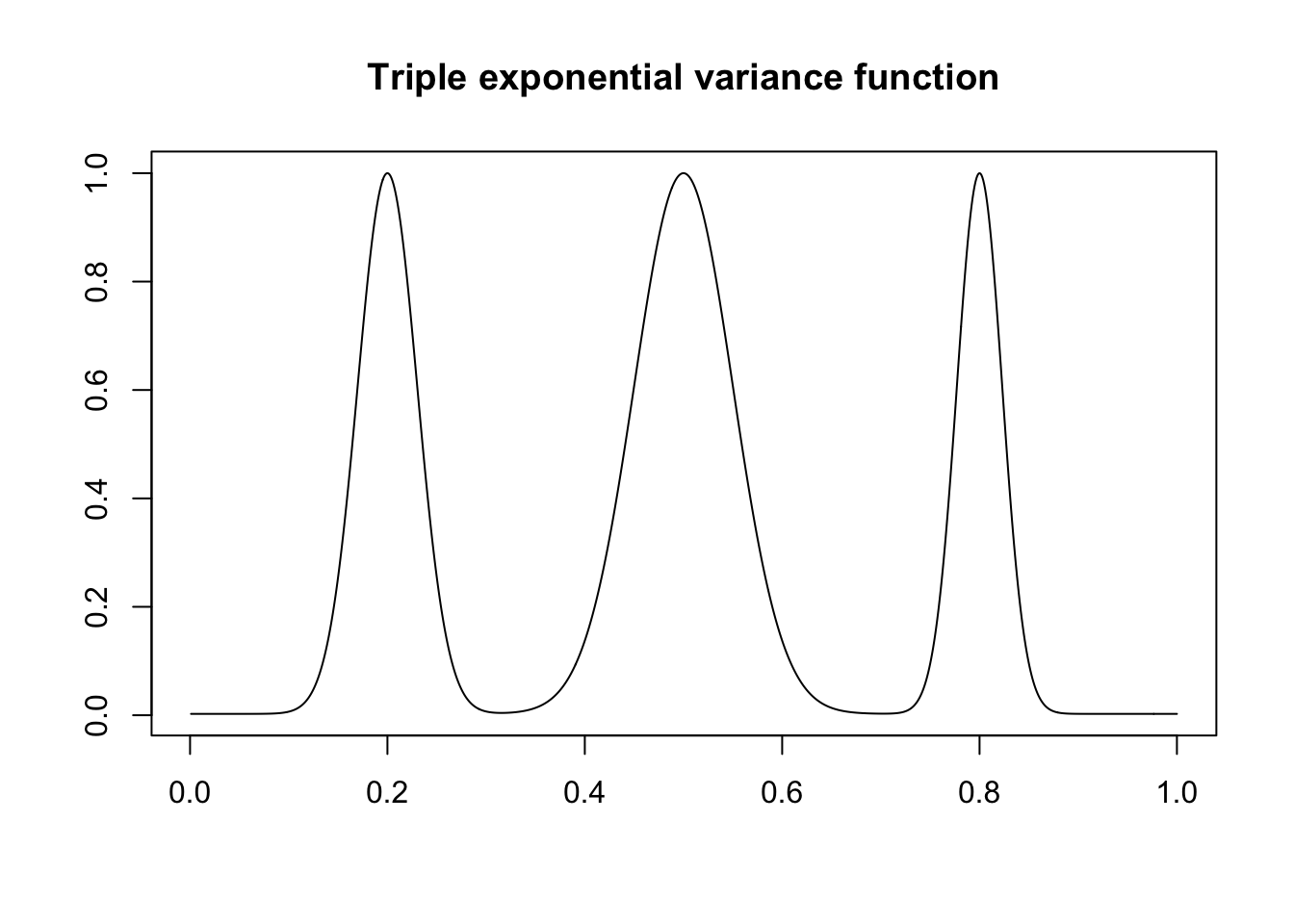
plot(t,var3,xlab = "",ylab = "",type = "l",main = "Doppler variance function")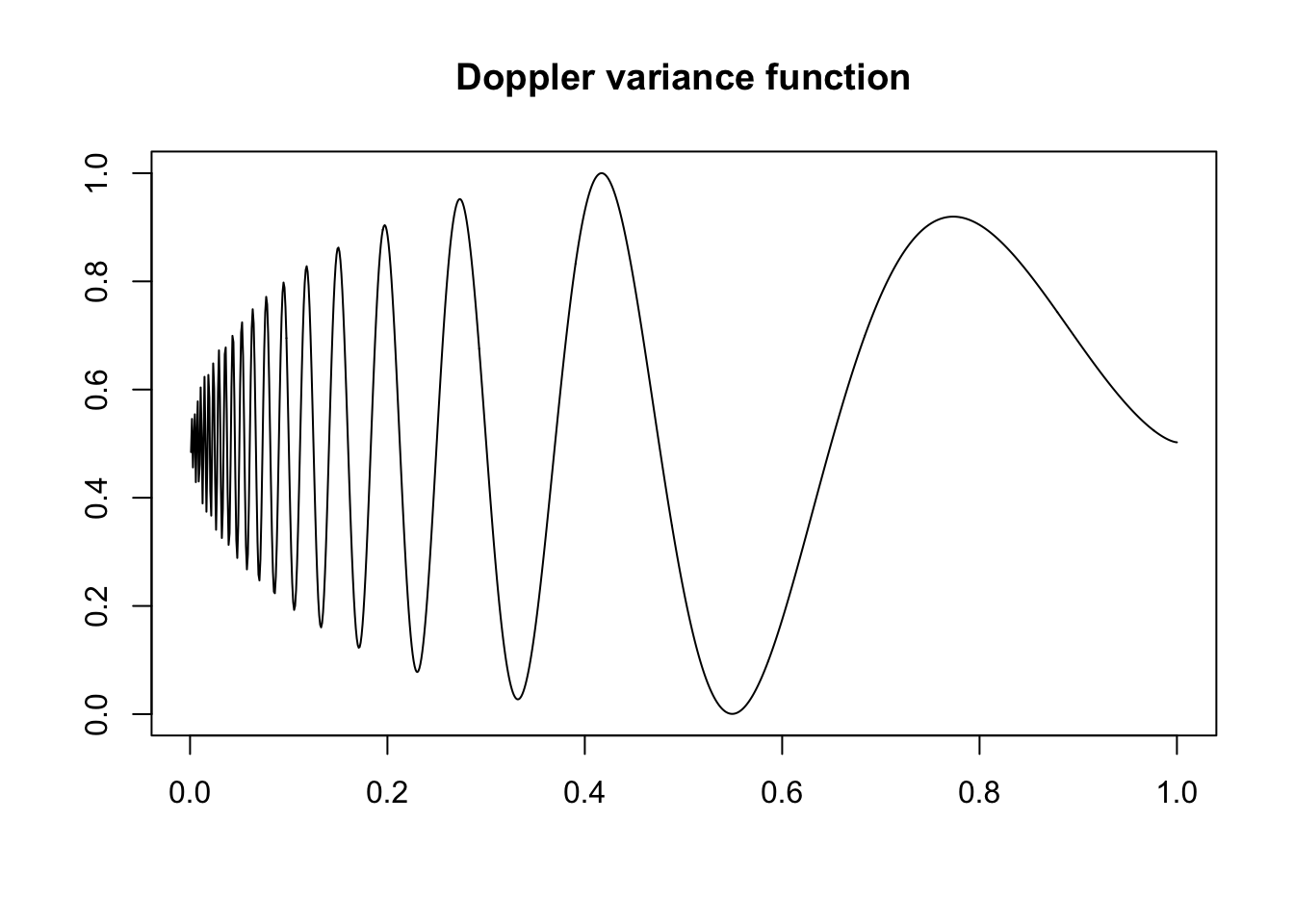
plot(t,var4,xlab = "",ylab = "",type = "l",main = "Bumps variance function")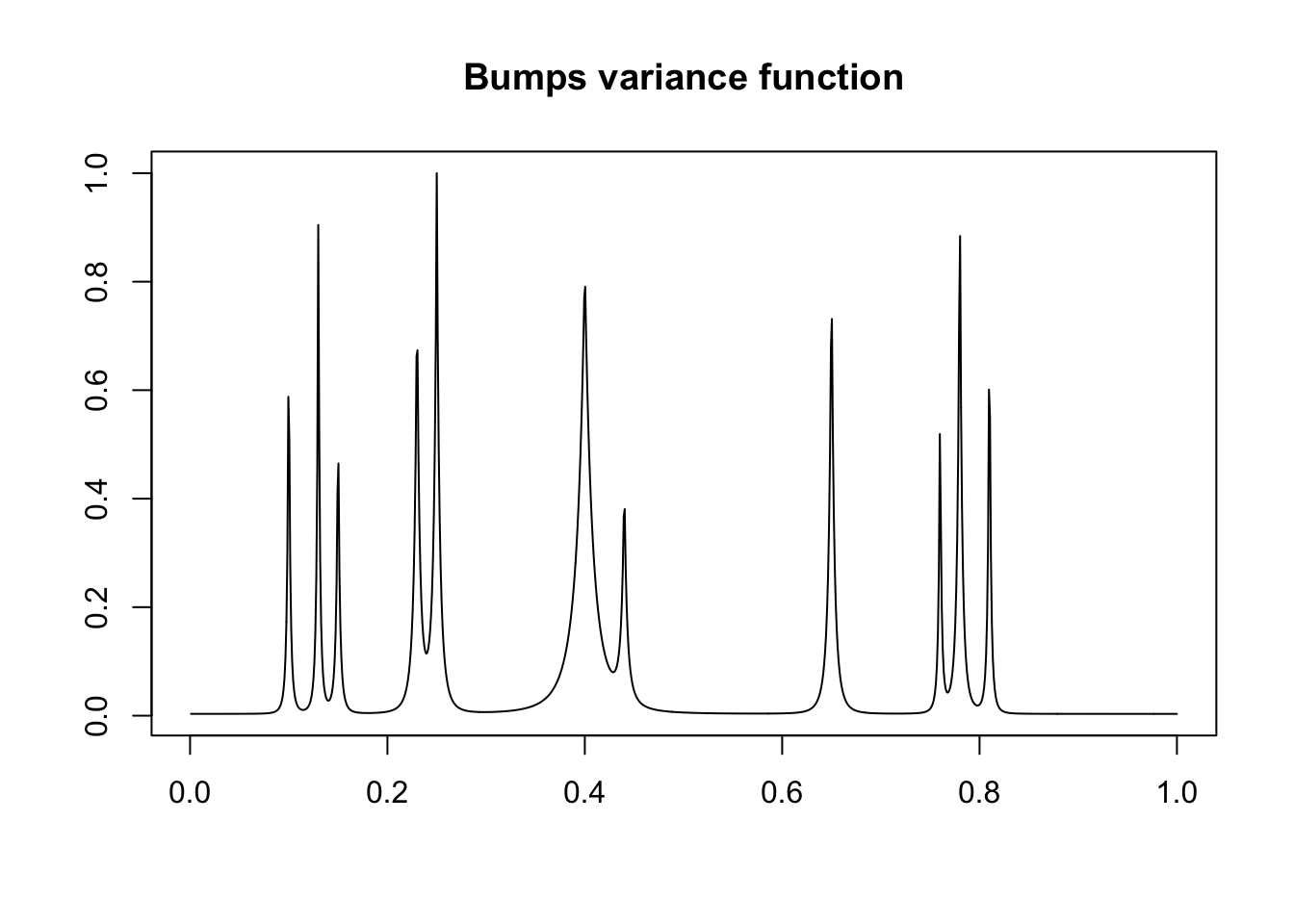
plot(t,var5,xlab = "",ylab = "",type = "l",main = "Clipped variance function")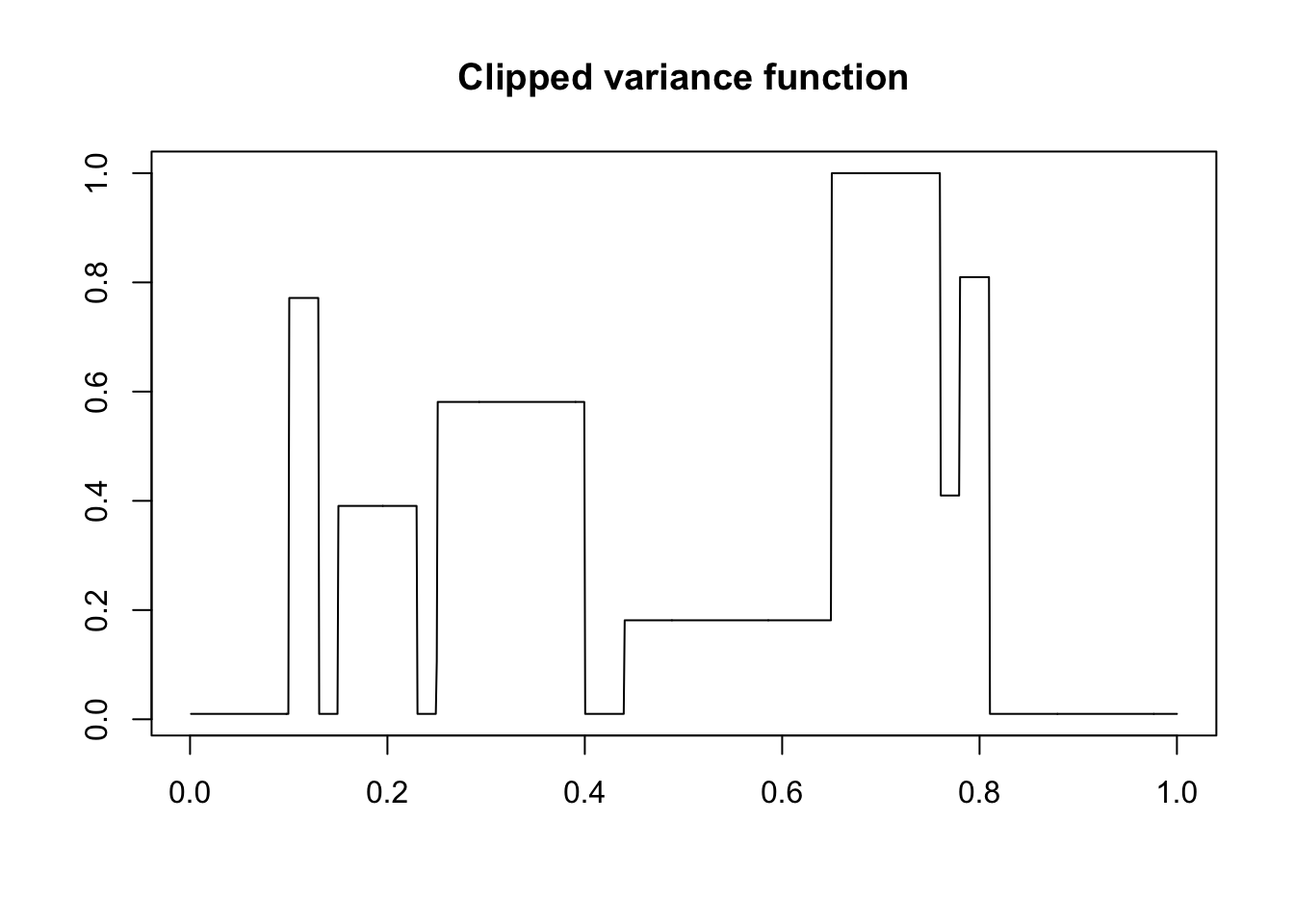
Session information
sessionInfo()R version 3.4.3 (2017-11-30)
Platform: x86_64-apple-darwin15.6.0 (64-bit)
Running under: macOS High Sierra 10.13.6
Matrix products: default
BLAS: /Library/Frameworks/R.framework/Versions/3.4/Resources/lib/libRblas.0.dylib
LAPACK: /Library/Frameworks/R.framework/Versions/3.4/Resources/lib/libRlapack.dylib
locale:
[1] en_US.UTF-8/en_US.UTF-8/en_US.UTF-8/C/en_US.UTF-8/en_US.UTF-8
attached base packages:
[1] stats graphics grDevices utils datasets methods base
other attached packages:
[1] cowplot_0.9.3 ggplot2_3.1.0
loaded via a namespace (and not attached):
[1] Rcpp_1.0.0 compiler_3.4.3 pillar_1.2.1
[4] git2r_0.23.0 plyr_1.8.4 workflowr_1.1.1
[7] bindr_0.1.1 R.methodsS3_1.7.1 R.utils_2.6.0
[10] tools_3.4.3 digest_0.6.17 evaluate_0.11
[13] tibble_1.4.2 gtable_0.2.0 pkgconfig_2.0.2
[16] rlang_0.2.2 yaml_2.2.0 bindrcpp_0.2.2
[19] withr_2.1.2 stringr_1.3.1 dplyr_0.7.6
[22] knitr_1.20 rprojroot_1.3-2 grid_3.4.3
[25] tidyselect_0.2.4 glue_1.3.0 R6_2.2.2
[28] rmarkdown_1.10 purrr_0.2.5 magrittr_1.5
[31] whisker_0.3-2 backports_1.1.2 scales_0.5.0
[34] htmltools_0.3.6 assertthat_0.2.0 colorspace_1.4-0
[37] labeling_0.3 stringi_1.2.4 lazyeval_0.2.1
[40] munsell_0.4.3 R.oo_1.21.0 This reproducible R Markdown analysis was created with workflowr 1.1.1