Last updated: 2021-07-04

Checks: 7 0

Knit directory: 2021/

This reproducible R Markdown analysis was created with workflowr (version 1.6.2). The Checks tab describes the reproducibility checks that were applied when the results were created. The Past versions tab lists the development history.

R Markdown file: up-to-date

Great! Since the R Markdown file has been committed to the Git repository, you know the exact version of the code that produced these results.

Environment: empty

Great job! The global environment was empty. Objects defined in the global environment can affect the analysis in your R Markdown file in unknown ways. For reproduciblity it’s best to always run the code in an empty environment.

Seed: set.seed(20210412)

The command set.seed(20210412) was run prior to running the code in the R Markdown file. Setting a seed ensures that any results that rely on randomness, e.g. subsampling or permutations, are reproducible.

Session information: recorded

Great job! Recording the operating system, R version, and package versions is critical for reproducibility.

Cache: none

Nice! There were no cached chunks for this analysis, so you can be confident that you successfully produced the results during this run.

File paths: relative

Great job! Using relative paths to the files within your workflowr project makes it easier to run your code on other machines.

Repository version: f42c33c

Great! You are using Git for version control. Tracking code development and connecting the code version to the results is critical for reproducibility.

The results in this page were generated with repository version f42c33c. See the Past versions tab to see a history of the changes made to the R Markdown and HTML files.

Note that you need to be careful to ensure that all relevant files for the analysis have been committed to Git prior to generating the results (you can use wflow_publish or wflow_git_commit). workflowr only checks the R Markdown file, but you know if there are other scripts or data files that it depends on. Below is the status of the Git repository when the results were generated:


Ignored files:
    Ignored:    .Rhistory
    Ignored:    .Rproj.user/

Untracked files:
    Untracked:  Curso_Bioestadistica_MTripp_cuatriII.docx
    Untracked:  Curso_Bioestadistica_MTripp_cuatriII.pdf
    Untracked:  Diapositivas/
    Untracked:  Prueba_markdown.Rmd
    Untracked:  Prueba_markdown.pdf
    Untracked:  README.html
    Untracked:  Resources/
    Untracked:  Tarea_Tstudent.Rmd
    Untracked:  Tarea_Tstudent.docx
    Untracked:  Tarea_Tstudent.html
    Untracked:  Tarea_Tstudent.pdf
    Untracked:  analysis/images/
    Untracked:  code/tarea_macrograd.R
    Untracked:  data/CS_subset.csv
    Untracked:  data/Consumo_oxigeno_wide.csv
    Untracked:  data/Darwin_esp.csv
    Untracked:  data/Data_enzimas_Experimento1.txt
    Untracked:  data/Data_enzimas_Experimento2.txt
    Untracked:  data/Data_enzimas_Experimento3.txt
    Untracked:  data/Data_enzimas_Experimento4.txt
    Untracked:  data/DownloadFestival(No Outlier).dat
    Untracked:  data/Festival.csv
    Untracked:  data/LungCapData.txt
    Untracked:  data/LungCapDataEsp.csv
    Untracked:  data/RExam.dat
    Untracked:  data/Rexamendat.csv
    Untracked:  data/Tabla1_Muestreo.txt
    Untracked:  data/Transcriptome_Anotacion.csv
    Untracked:  data/Transcriptome_DGE.csv
    Untracked:  data/Vinogradov_2004_Titanic.tab
    Untracked:  data/Vinogradov_2004_Titanic.tab.csv
    Untracked:  data/data_tukey.txt
    Untracked:  data/datasets_Pokemon.csv
    Untracked:  data/datasets_Pokemon.xls
    Untracked:  data/exp_macrogard_growth.tab
    Untracked:  data/exp_macrogard_rna-dna.tab
    Untracked:  data/fertilizantes_luz.csv
    Untracked:  data/macrogard_crecimiento.csv
    Untracked:  data/penguins_size.csv
    Untracked:  data/pokemon_extended.csv
    Untracked:  output/Plot_all_penguins.pdf
    Untracked:  output/Plot_all_penguins.tiff
    Untracked:  output/graficos/

Unstaged changes:
    Modified:   analysis/_site.yml

Note that any generated files, e.g. HTML, png, CSS, etc., are not included in this status report because it is ok for generated content to have uncommitted changes.

These are the previous versions of the repository in which changes were made to the R Markdown (analysis/Clase6_Supuestos.Rmd) and HTML (docs/Clase6_Supuestos.html) files. If you’ve configured a remote Git repository (see ?wflow_git_remote), click on the hyperlinks in the table below to view the files as they were in that past version.

File	Version	Author	Date	Message
html	392444f	Miguel Tripp	2021-07-04	Build site.
html	c188ae8	Miguel Tripp	2021-06-29	Build site.
html	1136768	Miguel Tripp	2021-06-28	Build site.
html	a33d4bb	Miguel Tripp	2021-06-23	Build site.
html	209299f	Miguel Tripp	2021-06-21	Build site.
html	d025507	Miguel Tripp	2021-06-17	Build site.
html	fb9e91e	Miguel Tripp	2021-06-16	Build site.
html	c5dfe6a	Miguel Tripp	2021-06-14	Build site.
html	2352c47	Miguel Tripp	2021-06-12	Build site.
html	99c3644	Miguel Tripp	2021-06-05	Build site.
html	fbd7857	Miguel Tripp	2021-06-05	Build site.
html	87a646f	Miguel Tripp	2021-06-02	Build site.
html	47a7147	Miguel Tripp	2021-05-31	Build site.
Rmd	3b99032	Miguel Tripp	2021-05-31	Publish the initial files for myproject
html	95c661f	Miguel Tripp	2021-05-31	Build site.
Rmd	d2189e1	Miguel Tripp	2021-05-31	Publish the initial files for myproject
html	34660de	Miguel Tripp	2021-05-24	Build site.
Rmd	458bf8f	Miguel Tripp	2021-05-24	Publish the initial files for myproject
html	da04854	Miguel Tripp	2021-05-24	Build site.
html	3321935	Miguel Tripp	2021-05-24	Build site.
Rmd	4233f46	Miguel Tripp	2021-05-24	Publish the initial files for myproject

1 Introduction

Muchos de los estadisticos que se abordan en el curso son pruebas paramétricas las cuales se basan en una distribución normal, es decir, que las muestras se hayan obtenido de una población distribución normal (Gausiana), por lo tanto, resulta de imortancía confirmar dicho supuesto antes de decidir que prueba estadistica es apropiada.

La mayoria de las pruebas paramétricas basadas en la distribución normal tienen cuatro supuestos que deben de cumplirse para que la prueba sea precisa:

Datos distribuidos normalmente: La interpretación de la mayoria de la pruebas estadisticas requiere del supuesto de que los datos fueron colectados de una población que sigue una distribución normal simetrica en el centro (la media).

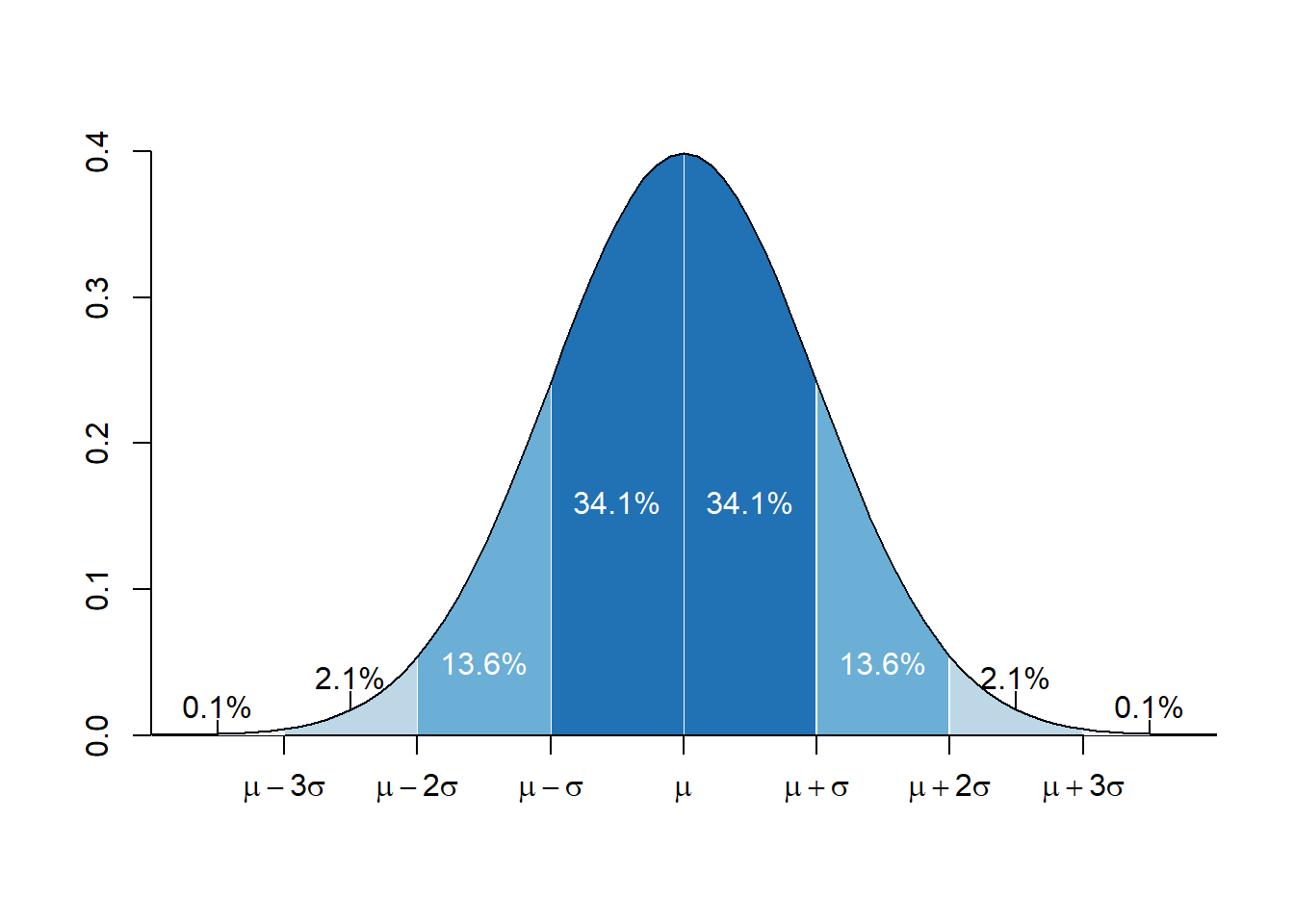
Figura: WikiCommons

Homogeneidad de varianzas: El supuesto de homogeneidad de varianzas, también conocido como supuesto de homocedasticidad, implica que las varianzas deben de ser iguales en los datos. En diseños que implican una prueba entre varios grupos o tratamientos, este supuesto implica que cada uno de estos grupos viene de una población con la misma varianza. En diseños de correlación, este supuesto implica que la varianza de una variable debe mantenerse estable en todos los niveles de la otra variable

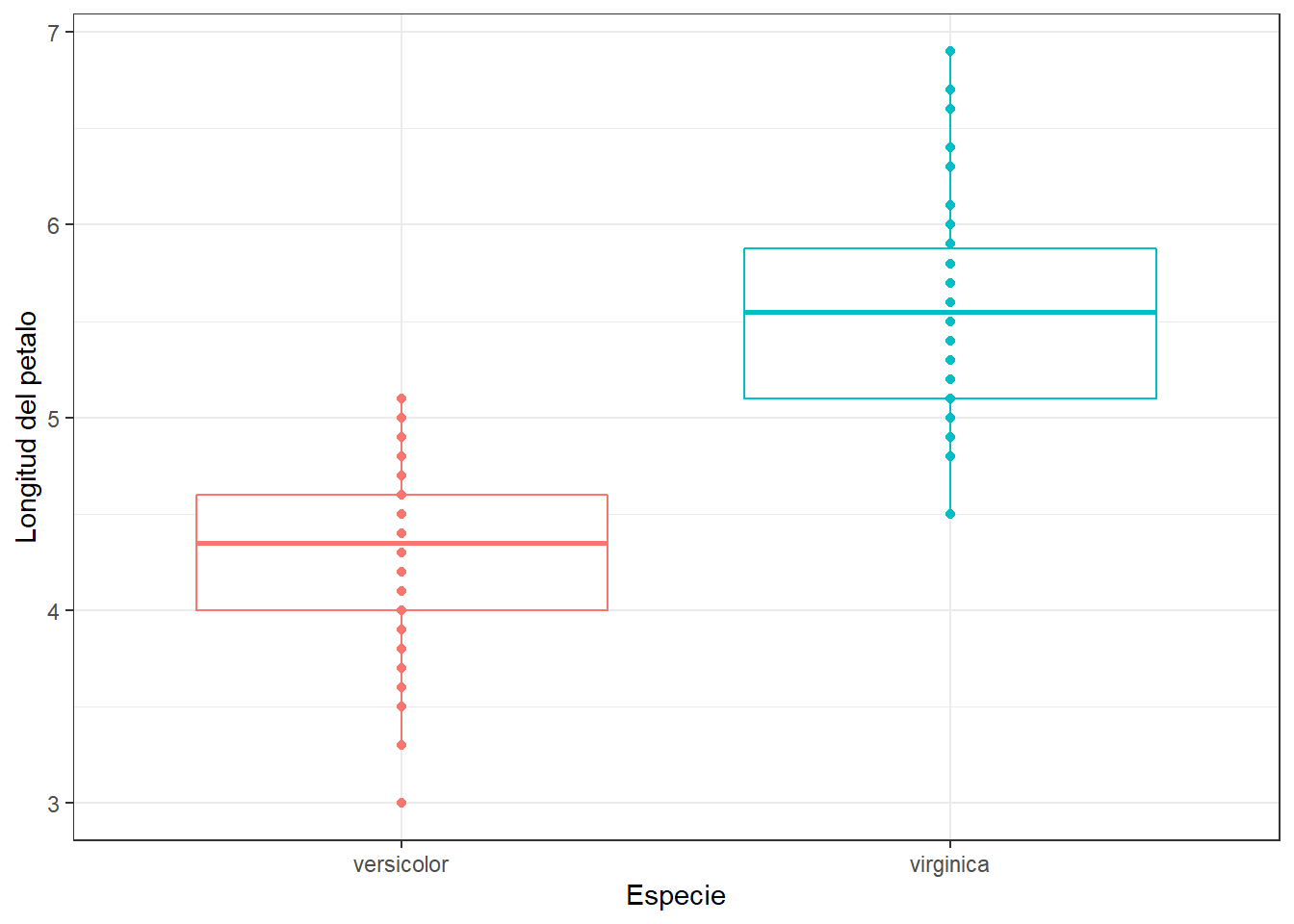
Independencia de los datos: Este supuesto va a depender del tipo de análisis que vayamos a realizar. En ciertos casos, este supuesto implica que las observaciones de cada individuo de un grupo experimental no afecta las observaciones de los otros individuos

2 Comprobar la normalidad de los datos

2.1 Histogramas y distribución normal

Con una cantidad de datos de la muestra suficientemente grande (n>30) la violación del supuesto de la normalidad no debería causar mayores problemas. Esto implica que podemos ignorar la distribución de los datos y usar pruebas paramétricas si estamos tratando con muestras de gran tamaño.

El teorema del límite central nos dice que sin importar el tipo de distribución que tengan las cosas, la distribución de la muestra tiende a ser normal si ésta es lo suficientemente grande (n>30).

Una de las formas en que podemos visualizar la distribución de los datos es mediante la generación de histogramas de frecuencia.

El histograma y el gráfico de densidad son herramientas muy útiles porque sirven para mostrar la distribución, la simetría, el sesgo, variabilidad, moda, mediana y observaciones atípicas de un conjunto de datos. Para explorar la normalidad de un conjunto de datos lo que se busca es que el histograma o gráfico de densidad presenten un patrón más o menos simétrico.

2.1.1 Asimetría y curtosis

La asimetría es el grado en que los datos no son simétricos. El hecho de que el valor de la asimetría sea 0, positivo o negativo, revela información sobre la forma de los datos. *A medida que los datos se vuelven más simétricos, el valor de su asimetría se acerca a cero. A medida que los valores se alejen del cero, es mas factible que los datos no tengan una distribución normal.
Valores positivos de asimetria indican que hay muchos valores bajos en la distribución, mientras que una asimetria negativa indican que hay un exceso de valores altos

null device 
          1

La curtosis indica la manera en que las colas de una distribución difieren de la distribución normal.
Los datos que siguen una distribución normal perfectamente tienen un valor de curtosis de 0. Los datos distribuidos normalmente establecen la línea de base para la curtosis. Una curtosis de la muestra que se desvía significativamente de 0 puede indicar que los datos no están distribuidos normalmente.
Una distribución con un valor positivo de curtosis indica que la distribución tiene colas más pesadas que la distribución normal.
Una distribución con un valor negativo de curtosis indica que la distribución tiene colas más livianas que la distribución normal

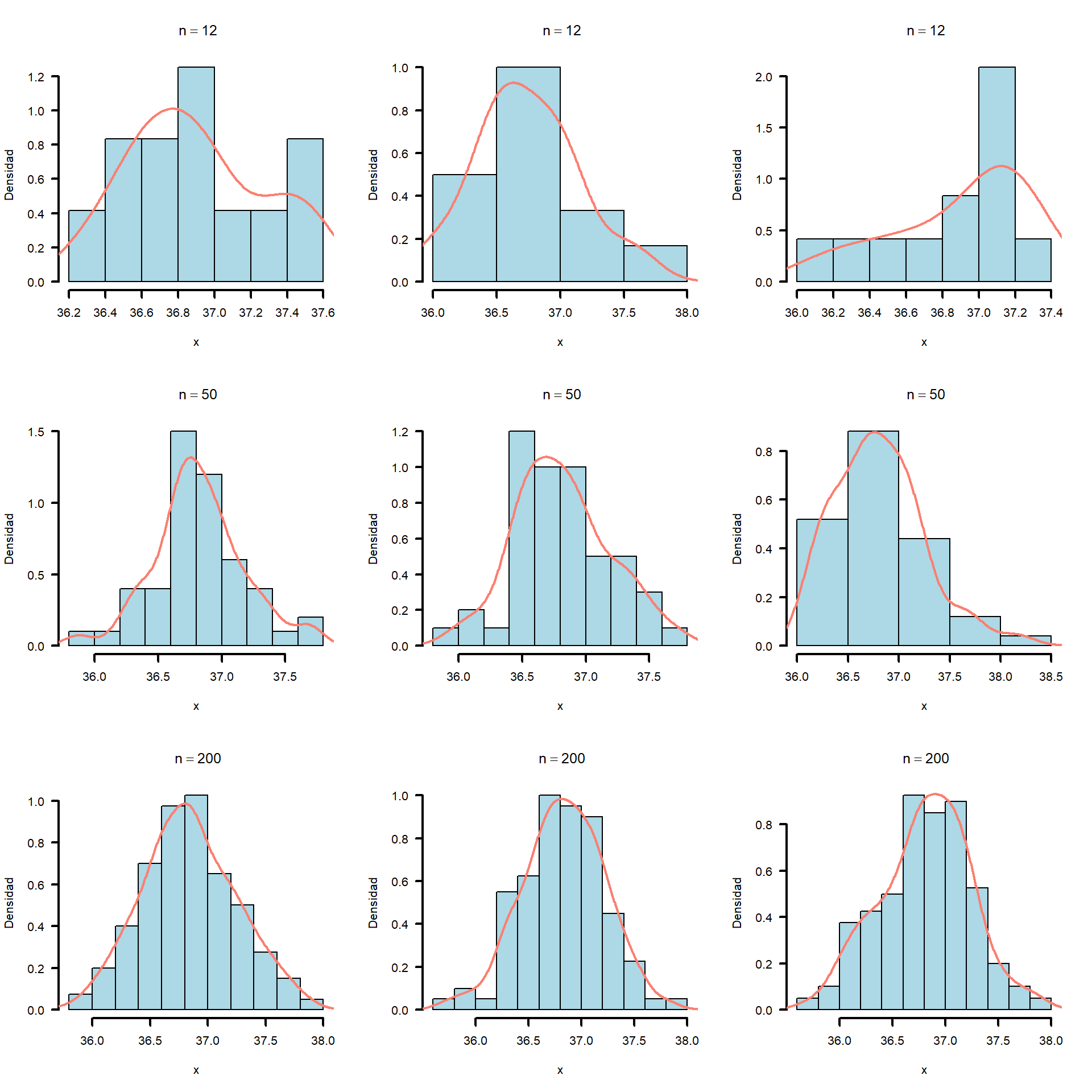
2.1.2 Las distribuciones normales no siempre lucen normales

Las siguientes gráficas muestran la distribución de frecuencias de valores esogidos al asar de una distribución normal con una media = 36.77 y una desviación estandar de 0.40. La variación entre gráfico y gráfico es simplemente el resultado de la variación aleatoria durante el muestreo.

2.1.3 Gráficos Cuantil-Cuantil (Q-Q plot)

Un gráfico Cuantil-Cuantil permite observar cuan cerca está la distribución de un conjunto de datos a alguna distribución ideal ó comparar la distribución de dos conjuntos de datos.
Los diagramas cuantil-cuantil normales se construyen trazando los cuantiles de una variable numérica respecto de los cuantiles de una distribución normal. Esto significa que cada valor es comaparado con valor esperado si siguiera una distribucón normal.
Si las distribuciones de los cuantiles comparados son idénticas, los puntos del diagrama formarán una línea recta de 45 grados. Cuanto más lejos se desvíen los puntos del diagrama de una línea recta, menos similares serán las distribuciones comparadas.

Generar un gráfico Q-Q con R base

set.seed(123)

datos_norm <- rnorm(n = 100, mean = 0, sd = 1)

hist(datos_norm, breaks = 12)

qqnorm(datos_norm)
qqline(datos_norm)

Con ggplot

ggplot()+
  geom_histogram(aes(datos_norm), col = "grey75", fill = "white", bins = 12)

ggplot()+
  geom_qq(aes(sample = datos_norm))+
  geom_qq_line(aes(sample = datos_norm))

Los gráficos Q-Q tambien nos permiten inspeccionar la distribución de los datos. Los datos que muestren una asimetria positiva o negativa tambien se veran reflejados en la desviación de los puntos de los valores obsverados con respecto a la distribución teórica.

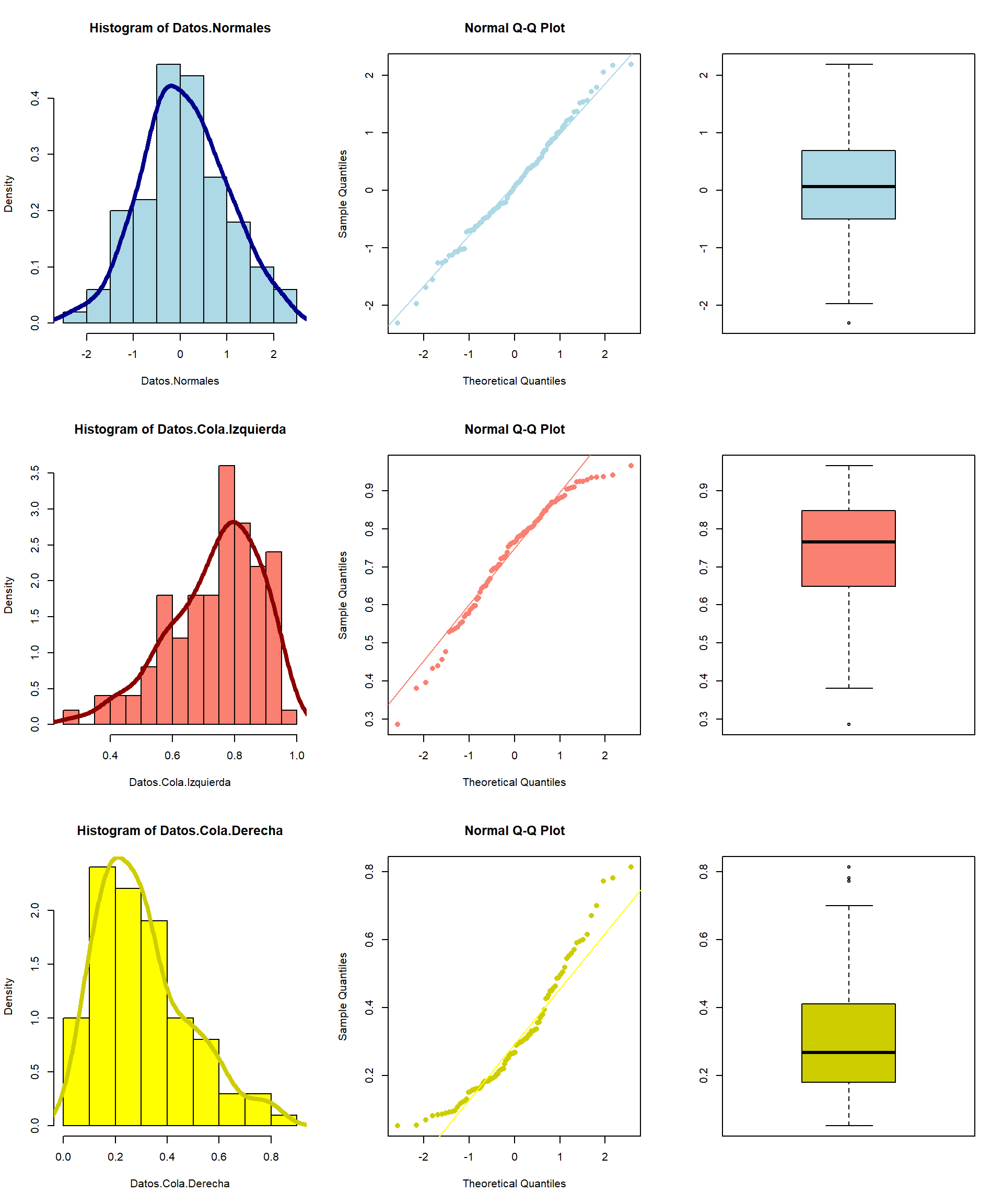
null device 
          1

¿Por qué la distribución normal es central en la teoría estadistca? La distribución normal o Gaussiana juega un papel central en la estadística debido a la relación matemática conocida como el teorema del límite central. Este dice que si tu muestra es lo suficientemente grande, la distribución de las medias se aproximará a la distribución Gaussiana, aún si la población no es Gaussiana. Debido a que la mayoria de las pruebas estadisticas (como la t de Student o el análisis de varianzas) se centran solamente en las diferencias entre las medias, la teoría del limite central explica porque estas pruebas funcionan aún cuando la población no es Gaussiana.

3 Evaluando la normalidad

Para evaluar el supuesto de normalidad, vamos a usar un set de datos obtenidos de un festival de música en el Reino Unido, en el cual se evaluó la higiene de los participantes durante los tres dias del festival utilizando una técnica estandarizada con un valor entre 4 (huele a rosas durante el rocio de la mañana) y 0 (huele a cuerpo putrefacto escondido en el traseso de un zorillo)(Andy Field)

festival_url <- "https://raw.githubusercontent.com/trippv/Miguel_Tripp/master/Festival.csv"

festival <- read_csv(festival_url)

head(festival)

# A tibble: 6 x 5
  numero genero  dia1  dia2  dia3
   <dbl> <chr>  <dbl> <dbl> <dbl>
1   2111 Hombre  2.64  1.35  1.61
2   2229 Mujer   0.97  1.41  0.29
3   2338 Hombre  0.84 NA    NA   
4   2384 Mujer   3.03 NA    NA   
5   2401 Mujer   0.88  0.08 NA   
6   2405 Hombre  0.85 NA    NA

Dibujamos el histograma con los valores de densidad

d1 <- ggplot(data = festival, aes(x = dia1))+
  geom_histogram(aes(y = ..density..), color = "black", fill = "white")+
  labs(x = "valores de higiene en dia 1", y = "Densidad")+
  stat_function(fun = dnorm, args = list(mean = mean(festival$dia1, na.rm = TRUE),
                                                                 sd = sd(festival$dia1, na.rm = TRUE)
                                                     ))
d1

`stat_bin()` using `bins = 30`. Pick better value with `binwidth`.

La figura sugiere que los datos siguen una distribución normal. Ahora si gráficamos un QQplot

d1_qq <- ggplot(data = festival, aes(sample = dia1))+
  geom_qq()+
  geom_qq_line()

d1_qq

Los datos se ajustan bastante a la diagonal.

Para explorar mas a fondo la distribución de los datos, es posible utilizar la funcion describe() dentro del paquete psych o la función stat.desc() del paquete pastecs.

recuerda que para instalar un paquete debes usar la función install.package()

psych::describe(festival$dia1)

   vars   n mean   sd median trimmed mad  min  max range skew kurtosis   se
X1    1 810 1.77 0.69   1.79    1.77 0.7 0.02 3.69  3.67    0    -0.42 0.02

alternativamente:

#indicamos norm = T para desplegar estadisticos de normalidad
pastecs::stat.desc(festival$dia1, basic = FALSE, norm = TRUE)  %>% 
  round(3)

      median         mean      SE.mean CI.mean.0.95          var      std.dev 
       1.790        1.771        0.024        0.048        0.481        0.694 
    coef.var     skewness     skew.2SE     kurtosis     kurt.2SE   normtest.W 
       0.392       -0.004       -0.026       -0.422       -1.228        0.996 
  normtest.p 
       0.032

Ejercicio 1: Usando ggplot y patchwork grafica el histograma de frecuencia con la distribución normal y los qqplots para cada unos de los dias del festival. Incluye el análisis con pastecs para cada grupo

library(patchwork)

#1. definir los histogramas
d1 <- ggplot(data = festival, aes(x = dia1))+
  geom_histogram(aes(y = ..density..), color = "black", fill = "white")+
  labs(x = "valores de higiene en dia 1", y = "Densidad")+
  stat_function(fun = dnorm, args = list(mean = mean(festival$dia1, na.rm = TRUE),
                                                                 sd = sd(festival$dia1, na.rm = TRUE)
                                                     ))

d2 <- ggplot(data = festival, aes(x = dia2))+
  geom_histogram(aes(y = ..density..), color = "black", fill = "white")+
  labs(x = "valores de higiene en dia 2", y = "Densidad")+
  stat_function(fun = dnorm, args = list(mean = mean(festival$dia3, na.rm = TRUE),
                                                                 sd = sd(festival$dia3, na.rm = TRUE)
                                                     ))


d3 <- ggplot(data = festival, aes(x = dia3))+
  geom_histogram(aes(y = ..density..), color = "black", fill = "white")+
  labs(x = "valores de higiene en dia 2", y = "Densidad")+
  stat_function(fun = dnorm, args = list(mean = mean(festival$dia3, na.rm = TRUE),
                                                                 sd = sd(festival$dia3, na.rm = TRUE)
                                                                                             ))

# definir los qq 
d2_qq <- ggplot(data = festival, aes(sample = dia2))+
  geom_qq()+
  geom_qq_line()

d3_qq <- ggplot(data = festival, aes(sample = dia3))+
  geom_qq()+
  geom_qq_line()


# combinar con pathchwor
(d1 + d1_qq) / (d2 + d2_qq) / (d3 + d3_qq)

pastec_res <- pastecs::stat.desc(festival[, c("dia1", "dia2","dia3")], basic = TRUE, norm = TRUE) %>% 
  round(., 3)

Los gráficos, asi como los valores de asimetría y curtosis sugieren que la higiene de los asistentes del festival se deteriora notablemente con el paso de los días.

4 Probando la distribución normal

Otra forma de evaluar el supuesto de normalidad de los datos es mediante una prueba que nos indique si la distribución de los datos se desvia de una distribución normal.

4.1 Prueba de Shapiro-Wilk

Como el resto de tests que analizan la normalidad, se considera como hipótesis nula que los datos sí proceden de una distribución normal, la hipótesis alternativa que no lo hacen.

El valor p de estos test indica la probabilidad de obtener una distribución como la observada si los datos realmente proceden de una población con una distribución normal.

Sin embargo, es importante tomar que cuenta que esta prueba tiene sus limitaciones, ya que con tamaños de muestra grandes es fácil tener valores singificativos de pequeñas desviaciones de la normalidad, por lo que una prueba significativa no necesariamente nos indica si la desviación de la normalidad es lo suficientemente grande como para sesgar los resultados de una prueba estadística.

La prueba de Shapiro-Wilk esta incluida dentro de los resultados de stat.desc() pero tambien es posible aplicarla usando la función shapiro.test()

# Prueba shapiro dia1
shapiro.test(festival$dia1)


    Shapiro-Wilk normality test

data:  festival$dia1
W = 0.99592, p-value = 0.03198

# Prueba shapiro dia2
shapiro.test(festival$dia2)


    Shapiro-Wilk normality test

data:  festival$dia2
W = 0.90832, p-value = 1.282e-11

# Prueba shapiro dia3
shapiro.test(festival$dia3)


    Shapiro-Wilk normality test

data:  festival$dia3
W = 0.90775, p-value = 3.804e-07

4.2 Prueba de Kolmogorov-Smirnov

Este test se emplea para contrastar normalidad cuando el tamaño de la muestra es relativamente grande (>50 [30]).

Es importante cnsiderar que la prueba de Kolmogorov-Smirnov asume que se conocen la media y varianza poblacional, lo que en la mayoría de los casos no es posible. Esto hace que el test sea muy conservador y poco potente. Para solventar este problema se desarrolló una modificación del Kolmogorov-Smirnov conocida como test Lilliefors. El test Lilliefors asume que la media y varianza son desconocidas, estando especialmente desarrollado para testar la normalidad.

ks.test(festival$dia1, y = "pnorm", mean=mean(festival$dia1), sd=sd(festival$dia1))

Warning in ks.test(festival$dia1, y = "pnorm", mean = mean(festival$dia1), :
ties should not be present for the Kolmogorov-Smirnov test


    One-sample Kolmogorov-Smirnov test

data:  festival$dia1
D = 0.029298, p-value = 0.4902
alternative hypothesis: two-sided

Para poder usar la prueba de Lilliefors es necesario instalar el paquete nortest

#install.packages("nortest")
nortest::lillie.test(festival$dia1)


    Lilliefors (Kolmogorov-Smirnov) normality test

data:  festival$dia1
D = 0.029298, p-value = 0.09694

5 Homogeneidad de varianzas (Homocedasticidad)

El supuesto de homogeneidad de varianzas, también conocido como supuesto de homocedasticidad, considera que la varianza es constante (no varía) en los diferentes niveles de un factor, es decir, entre diferentes grupos.

Existen diferentes test que permiten evaluar la distribución de la varianza. Todos ellos consideran como hipótesis nula que la varianza es igual entre los grupos y como hipótesis alternativa que no lo es. La diferencia entre ellos es el estadístico de centralidad que utilizan.

5.0.1 Prueba de Levene

La prueba de Levene es una prueba simple que trabaja realizando una ANOVA de una via sobre los valores de desvicación; es decir, la diferecia absoluta entre cada valor y la media del grupo del que viene.

Para utilizar esta prueba es necesario instalar el paquete car y usar la funcion leveneTest()

La prueba LeveneTest se caracteriza ademas por permitir elegir entre diferentes estadísticos de centralidad :mediana (por defecto), media, media truncada. Esto es importante a la hora de contrastar la homocedasticidad dependiendo de si los grupos se distribuyen de forma normal o no.

Nota: es importante considerar que necesitamos valores agrupados.

Para este ejercicio, trabajaremos los datos Rexamendat los cuales contienen los resultados de un examen de R conducido en dos universidades

Aplicamos la prueba de Levene sobre los valores del examen y aritmetica (numeracy)

Rexam_url <- "https://raw.githubusercontent.com/trippv/Miguel_Tripp/master/Rexamendat.csv"
Rexam <- read_csv(Rexam_url)


-- Column specification --------------------------------------------------------
cols(
  examen = col_double(),
  habilidades = col_double(),
  lectura = col_double(),
  aritmetica = col_double(),
  uni = col_character()
)

#convertir la uni a factor
Rexam$uni <- as.factor(Rexam$uni)

# graficas

ggplot(Rexam, aes(x = examen))+
  geom_histogram(col = "grey65", fill = "white")+
  labs(title = "histograma de frecuencia para examen de R por universidad")+
  facet_grid(uni ~ .)

`stat_bin()` using `bins = 30`. Pick better value with `binwidth`.

shapiro.test(Rexam$examen[Rexam$uni == "Universidad Duncetown"])


    Shapiro-Wilk normality test

data:  Rexam$examen[Rexam$uni == "Universidad Duncetown"]
W = 0.97217, p-value = 0.2829

ggplot(Rexam, aes(x = aritmetica))+
  geom_histogram(col = "grey65", fill = "white")+
  labs(title = "histograma de frecuencia para examen de aritmentica por universidad")+
  facet_grid(uni ~ .)

`stat_bin()` using `bins = 30`. Pick better value with `binwidth`.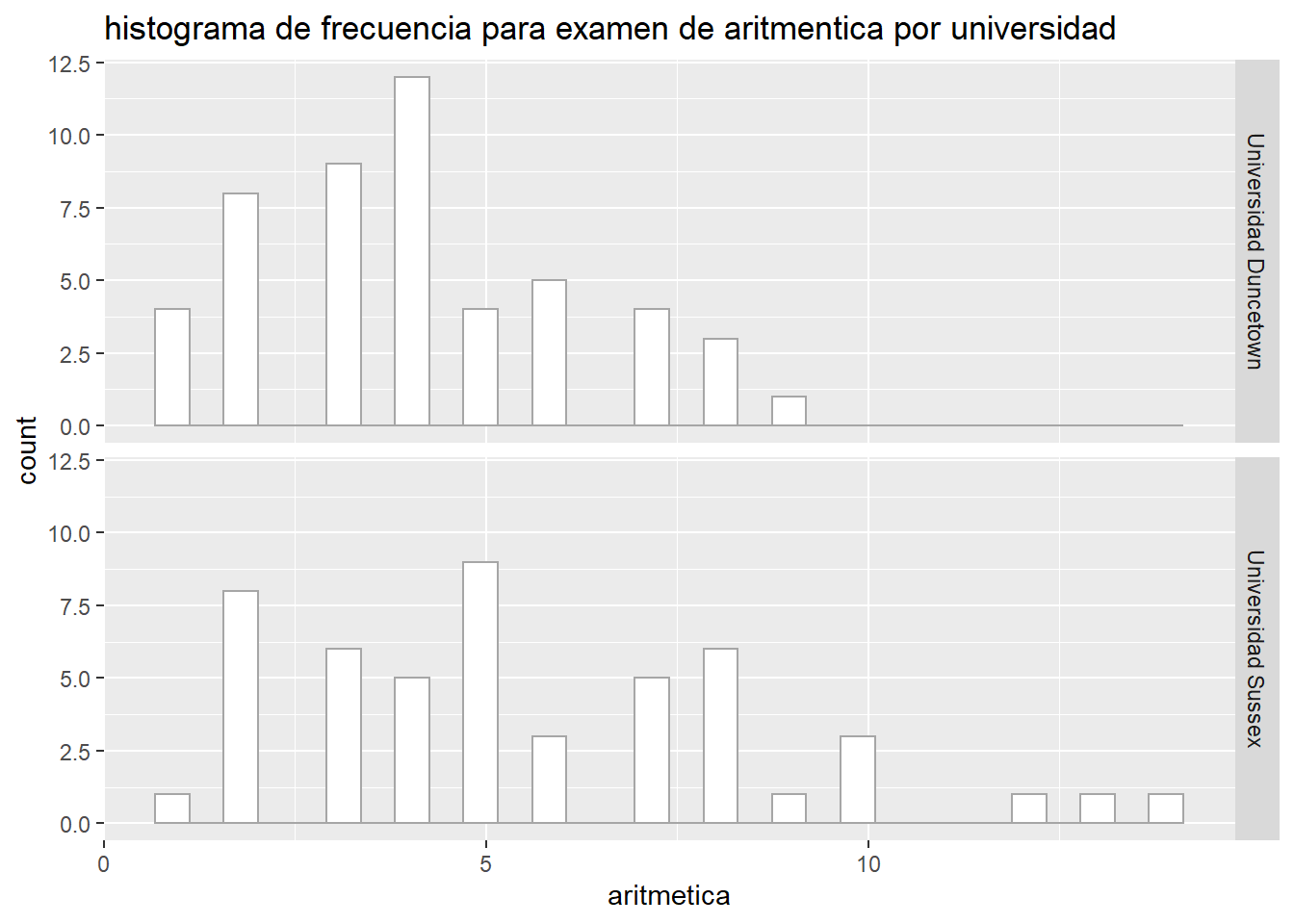

shapiro.test(Rexam$examen[Rexam$uni == "Universidad Sussex"])


    Shapiro-Wilk normality test

data:  Rexam$examen[Rexam$uni == "Universidad Sussex"]
W = 0.98371, p-value = 0.7151

Para realizar la prueba de Levene ejecutamos la función leveneTest()

car::leveneTest(Rexam$examen, Rexam$uni)

Levene's Test for Homogeneity of Variance (center = median)
      Df F value Pr(>F)
group  1  2.0886 0.1516
      98

#alternativamente se puede ejecutar de la forma
car::leveneTest(Rexam$examen ~ Rexam$uni)

Levene's Test for Homogeneity of Variance (center = median)
      Df F value Pr(>F)
group  1  2.0886 0.1516
      98

car::leveneTest(Rexam$aritmetica, Rexam$uni)

Levene's Test for Homogeneity of Variance (center = median)
      Df F value  Pr(>F)  
group  1   5.366 0.02262 *
      98                  
---
Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

Los resultados de la prueba se denotan con la letra F y en este caso hay dos tipos de grados de libertad (grupo y total). Por tanto se puede expresar en la forma F(gl1, gl2) = valor.

De manera que podemos decir que para los resultados de la prueba de R, las varianzas fueron similares en ambas universidades con F(1,98) = 2.09; P > 0.05 pero para los resultados de aritmentica, las varianzas fueron significativamente diferentes entre los grupos F(1,98) = 5.37; P = 0.023

5.1 Prueba F (razón de varianzas)

Es muy potente, detecta diferencias muy sutiles, pero es muy sensible a violaciones de la normalidad de las poblaciones. Por esta razón, no es un test recomendable si no se tiene mucha certeza de que las poblaciones se distribuyen de forma normal.

El F-test estudia el cociente de varianzas \(\sigma_2^{2} / \sigma_1^{2}\), que en caso de que sean iguales, toma el valor 1.

Dentro de R, esta prueba se ejecuta con la función var.test()

# Prueba de varianzas para examen R
var.test(Rexam$examen ~ Rexam$uni)


    F test to compare two variances

data:  Rexam$examen by Rexam$uni
F = 1.5217, num df = 49, denom df = 49, p-value = 0.1452
alternative hypothesis: true ratio of variances is not equal to 1
95 percent confidence interval:
 0.863548 2.681583
sample estimates:
ratio of variances 
          1.521734

# Prueba de varianzas para aritmentica
var.test(Rexam$aritmetica ~ Rexam$uni)


    F test to compare two variances

data:  Rexam$aritmetica by Rexam$uni
F = 0.45281, num df = 49, denom df = 49, p-value = 0.006446
alternative hypothesis: true ratio of variances is not equal to 1
95 percent confidence interval:
 0.2569592 0.7979376
sample estimates:
ratio of variances 
         0.4528106

5.1.1 Prueba de Bartlett

Permite contrastar la igualdad de varianza en 2 o más poblaciones sin necesidad de que el tamaño de los grupos sea el mismo. Es más sensible que el test de Levene a la falta de normalidad, pero si se está seguro de que los datos provienen de una distribución normal, es la mejor opción.Se ejecuta con la función bartlett.test()

#Prueba para examen R
bartlett.test(Rexam$examen ~ Rexam$uni)


    Bartlett test of homogeneity of variances

data:  Rexam$examen by Rexam$uni
Bartlett's K-squared = 2.122, df = 1, p-value = 0.1452

#Prueba para aritmética
bartlett.test(Rexam$aritmetica ~ Rexam$uni)


    Bartlett test of homogeneity of variances

data:  Rexam$aritmetica by Rexam$uni
Bartlett's K-squared = 7.4206, df = 1, p-value = 0.006448

5.1.2 Test de Fligner-Killeen

Se trata de un test no paramétrico que compara las varianzas basándose en la mediana. Es también una alternativa cuando no se cumple la condición de normalidad en las muestras.

Se ejecuta con la función fligner.test()

#Prueba para examen R
fligner.test(Rexam$examen ~ Rexam$uni)


    Fligner-Killeen test of homogeneity of variances

data:  Rexam$examen by Rexam$uni
Fligner-Killeen:med chi-squared = 2.1791, df = 1, p-value = 0.1399

#Prueba para aritmética
fligner.test(Rexam$aritmetica ~ Rexam$uni)


    Fligner-Killeen test of homogeneity of variances

data:  Rexam$aritmetica by Rexam$uni
Fligner-Killeen:med chi-squared = 4.8469, df = 1, p-value = 0.0277

En conclusión: Si se tiene seguridad de que las muestras a comparar proceden de poblaciones que siguen una distribución normal, son recomendables el F-test y el test de Bartlet, pareciendo ser el segundo más recomendable ya que el primero es muy potente pero extremadamente sensible a desviaciones de la normal. Si no se tiene la seguridad de que las poblaciones de origen son normales, se recomiendan el test de Leven utilizando la mediana o el test no paramétrico Fligner-Killeen que también se basa en la mediana.

6 Pruebas de supuestos con `rstatixs()`

rstatixs es un aquete que permite realizar las pruebas de normalizadad y varianza en un formato pipe-friendly

library(rstatix)


Attaching package: 'rstatix'

The following object is masked from 'package:stats':

    filter

# Obtner el resumen de una variable o variables
Rexam %>% 
  group_by(uni) %>% 
  get_summary_stats(examen, type = "common")

# A tibble: 2 x 11
  uni            variable     n   min   max median   iqr  mean    sd    se    ci
  <fct>          <chr>    <dbl> <dbl> <dbl>  <dbl> <dbl> <dbl> <dbl> <dbl> <dbl>
1 Universidad D~ examen      50    15    66     38  16.5  40.2  12.6  1.78  3.58
2 Universidad S~ examen      50    56    99     75  12    76.0  10.2  1.44  2.9

# Prueba de shapiro de una variable
Rexam %>% 
  shapiro_test(examen)

# A tibble: 1 x 3
  variable statistic       p
  <chr>        <dbl>   <dbl>
1 examen       0.961 0.00499

# Prueba de Shapiro por grupo
Rexam %>% 
  group_by(uni) %>% 
  shapiro_test(examen)

# A tibble: 2 x 4
  uni                   variable statistic     p
  <fct>                 <chr>        <dbl> <dbl>
1 Universidad Duncetown examen       0.972 0.283
2 Universidad Sussex    examen       0.984 0.715

# Prueba de Levene por grupo

Rexam %>% 
  levene_test(examen ~ uni)

# A tibble: 1 x 4
    df1   df2 statistic     p
  <int> <int>     <dbl> <dbl>
1     1    98      2.09 0.152

Ejercicio 2: Utiliza la base de datos de pingüinos, evalua si los valores de la longitud de la aleta (flipper_length_mm) entre cada especie cumplen los supuestos normalidad y homogeneidad de varianzas. Utiliza métodos gráficos y pruebas estadísticas

penguins <- read_csv("data/penguins_size.csv")

penguins <- penguins %>% 
  select(species, island, flipper_length_mm) %>% 
  filter(complete.cases(flipper_length_mm))

ggplot(penguins, aes(x = flipper_length_mm)) +
  geom_histogram()+
 facet_wrap(~species)


ggplot(penguins, aes(sample = flipper_length_mm)) +
  geom_qq()+
  geom_qq_line()+
  facet_wrap(~species)


# Prueba de normalidad

# Todo el set
penguins %>% 
  shapiro_test(flipper_length_mm)

# Por especie
penguins %>% 
  group_by(species) %>% 
  shapiro_test(flipper_length_mm)



# Prueba de homogeneidad de varianzas

penguins %>% 
  levene_test(flipper_length_mm ~ species)


# Visualización por medio de boxlot

p1 <- penguins %>% 
  ggplot(., aes(x = species, y = flipper_length_mm, color = species))+
  geom_point(position = position_jitter(width = 0.2))+
  geom_boxplot(alpha = 0.4)+
  theme(legend.position = "none")


p2 <- penguins %>% 
  ggplot(., aes(x = flipper_length_mm, fill = species))+
  geom_density(alpha = 0.4)+
  coord_flip()+
  theme(legend.position = "none",
        axis.title.y = element_blank(),
        axis.text.y = element_blank())
  

library(patchwork)

p1 + p2 + plot_layout(ncol = 2, widths = c(4,1))

sessionInfo()

R version 4.0.5 (2021-03-31)
Platform: x86_64-w64-mingw32/x64 (64-bit)
Running under: Windows 10 x64 (build 19041)

Matrix products: default

locale:
[1] LC_COLLATE=English_United States.1252 
[2] LC_CTYPE=English_United States.1252   
[3] LC_MONETARY=English_United States.1252
[4] LC_NUMERIC=C                          
[5] LC_TIME=English_United States.1252    

attached base packages:
[1] stats     graphics  grDevices utils     datasets  methods   base     

other attached packages:
 [1] rstatix_0.7.0   patchwork_1.1.1 forcats_0.5.1   stringr_1.4.0  
 [5] dplyr_1.0.5     purrr_0.3.4     readr_1.4.0     tidyr_1.1.3    
 [9] tibble_3.0.4    ggplot2_3.3.3   tidyverse_1.3.1 workflowr_1.6.2

loaded via a namespace (and not attached):
 [1] nlme_3.1-152      fs_1.5.0          lubridate_1.7.10  httr_1.4.2       
 [5] rprojroot_2.0.2   tools_4.0.5       backports_1.2.1   utf8_1.2.1       
 [9] R6_2.5.0          nortest_1.0-4     DBI_1.1.0         colorspace_2.0-0 
[13] withr_2.4.2       tidyselect_1.1.1  mnormt_2.0.2      curl_4.3         
[17] compiler_4.0.5    git2r_0.27.1      cli_2.5.0         rvest_1.0.0      
[21] pastecs_1.3.21    xml2_1.3.2        labeling_0.4.2    scales_1.1.1     
[25] psych_2.0.12      digest_0.6.27     foreign_0.8-81    rmarkdown_2.6    
[29] rio_0.5.16        pkgconfig_2.0.3   htmltools_0.5.1.1 dbplyr_2.1.1     
[33] highr_0.8         rlang_0.4.11      readxl_1.3.1      rstudioapi_0.13  
[37] farver_2.0.3      generics_0.1.0    jsonlite_1.7.2    zip_2.1.1        
[41] car_3.0-10        magrittr_2.0.1    Rcpp_1.0.5        munsell_0.5.0    
[45] fansi_0.4.2       abind_1.4-5       lifecycle_1.0.0   stringi_1.5.3    
[49] whisker_0.4       yaml_2.2.1        carData_3.0-4     grid_4.0.5       
[53] parallel_4.0.5    promises_1.1.1    crayon_1.4.1      lattice_0.20-41  
[57] haven_2.3.1       hms_1.0.0         tmvnsim_1.0-2     knitr_1.30       
[61] ps_1.5.0          pillar_1.6.0      boot_1.3-27       reprex_2.0.0     
[65] glue_1.4.2        evaluate_0.14     data.table_1.13.6 modelr_0.1.8     
[69] vctrs_0.3.8       httpuv_1.5.4      cellranger_1.1.0  gtable_0.3.0     
[73] assertthat_0.2.1  xfun_0.23         openxlsx_4.2.3    broom_0.7.6      
[77] later_1.1.0.1     ellipsis_0.3.1

Clase 6: Supuestos

Miguel Tripp

2021-05-18

1 Introduction

2 Comprobar la normalidad de los datos

2.1 Histogramas y distribución normal

2.1.1 Asimetría y curtosis

2.1.2 Las distribuciones normales no siempre lucen normales

2.1.3 Gráficos Cuantil-Cuantil (Q-Q plot)

3 Evaluando la normalidad

4 Probando la distribución normal

4.1 Prueba de Shapiro-Wilk

4.2 Prueba de Kolmogorov-Smirnov

5 Homogeneidad de varianzas (Homocedasticidad)

5.0.1 Prueba de Levene

5.1 Prueba F (razón de varianzas)

5.1.1 Prueba de Bartlett

5.1.2 Test de Fligner-Killeen

6 Pruebas de supuestos con `rstatixs()`

Clase 6: Supuestos

Miguel Tripp

2021-05-18

1 Introduction

2 Comprobar la normalidad de los datos

2.1 Histogramas y distribución normal

2.1.1 Asimetría y curtosis

2.1.2 Las distribuciones normales no siempre lucen normales

2.1.3 Gráficos Cuantil-Cuantil (Q-Q plot)

3 Evaluando la normalidad

4 Probando la distribución normal

4.1 Prueba de Shapiro-Wilk

4.2 Prueba de Kolmogorov-Smirnov

5 Homogeneidad de varianzas (Homocedasticidad)

5.0.1 Prueba de Levene

5.1 Prueba F (razón de varianzas)

5.1.1 Prueba de Bartlett

5.1.2 Test de Fligner-Killeen

6 Pruebas de supuestos con rstatixs()

6 Pruebas de supuestos con `rstatixs()`