An ASH approach to finding structure in count data

Introduction

Let’s say that we’re interested in finding structure in a matrix of counts \(Y\). The usual approach is to set \(X = \log(Y + \alpha)\) for some pseudocount \(\alpha > 0\) and then look for low-rank structure in \(X\).

Here I propose a different method that uses ashr to shrink the counts \(Y_{ij}\).

Model for the data-generating process

One can consider the individual counts \(Y_{ij}\) as Poisson random variables with (unknown) rate parameters \(\lambda_{ij}\). And in fact, it’s structure in \(\Lambda\) that we’re primarily interested in, not structure in \(Y\).

The simplest model is that \[ \Lambda = \exp(LF'), \] but in most applications one wouldn’t expect the matrix of log-rates to be low-rank. A more useful model puts \[ \Lambda = \exp(LF' + E), \] where \(E_{ij} \sim N(0, \sigma_{ij}^2)\) (with some structure in the matrix of variances \(\Sigma\)).

Fitting \(LF'\) using ASH and FLASH

I propose a three-step approach to estimating \(LF'\):

1. Since we’re really interested in \(\Lambda\) (not \(Y\)), I propose that we first estimate \(\Lambda\) using ashr. The ASH model is \[ Y_{ij} \sim \text{Poisson}(\lambda_{ij});\ \lambda_{ij} \sim g, \] where \(g\) is a unimodal prior to be estimated. (One can also run ashr separately on each row or column of \(Y\) to get row-wise or column-wise priors.) Conveniently, ashr directly gives estimates for posterior means \(\mathbb{E} (\lambda_{ij})\) and posterior variances \(\text{Var}(\lambda_{ij})\).

2. Transform the ASH estimates using the approximations \[ X_{ij} := \mathbb{E} (\log \lambda_{ij}) \approx \log \mathbb{E}(\lambda_{ij}) - \frac{\text{Var}(\lambda_{ij})}{2(\mathbb{E}(\lambda_{ij}))^2}\] and \[ S_{ij}^2 := \text{Var} (\log \lambda_{ij}) \approx \frac{\text{Var}(\lambda_{ij})}{(\mathbb{E}(\lambda_{ij}))^2} \] (Importantly, the posterior means are all non-zero so that one can directly take logarithms. No pseudo-counts are needed.)

3. Run FLASH on the data \((X, S)\) with the additional variance in \(E\) specified as a “noisy” variance structure. In other words, the FLASH model is \[ X_{ij} = LF' + E^{(1)} + E^{(2)} \] where \(E_{ij}^{(1)} \sim N(0, S_{ij}^2)\) (with the \(S_{ij}\)s fixed) and \(E_{ij}^{(2)} \sim N(0, 1 / \tau_{ij})\) (with the \(\tau_{ij}\)s to be estimated). (And, as usual, there are priors on each column of \(L\) and \(F\).) The variance structure in \(E^{(2)}\) matches the assumed noise structure in \(\log (\Lambda)\).

Example

To illustrate the approach, I consider a very simple example with a low-intensity baseline and a block of higher intensity:

set.seed(666)
n <- 120
p <- 160

log.lambda <- (-1 + outer(c(2 * abs(rnorm(0.25 * n)), rep(0, 0.75 * n)),
                          c(abs(rnorm(0.25 * p)), rep(0, 0.75 * p)))
               + 0.5 * rnorm(n * p))
Y <- matrix(rpois(n * p, exp(log.lambda)), n, p)

# Define some variables to make analysis easier.
hi.rows <- rep(FALSE, n)
hi.rows[1:(n / 4)] <- TRUE
hi.cols <- rep(FALSE, p)
hi.cols[1:(p / 4)] <- TRUE

# Show heatmap.
image(x = 1:n, y = 1:p, z = log.lambda, xlab = "x index", ylab = "y index")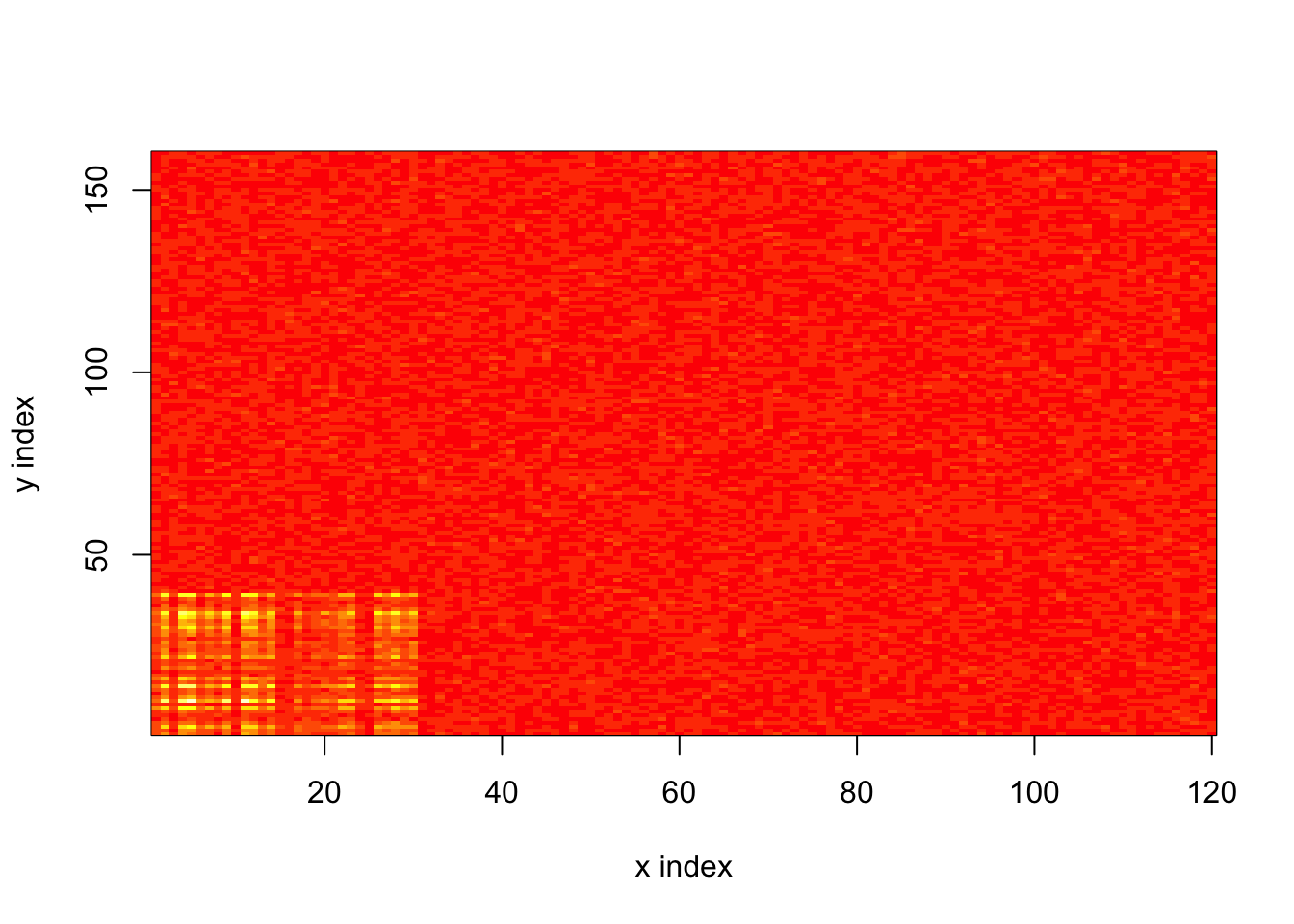

Expand here to see past versions of simY-1.png:

Version	Author	Date
38224ab	Jason Willwerscheid	2019-02-13

The usual approach would run FLASH as follows.

# Use my own branch due to bug in stephens999/master.
devtools::load_all("~/Github/ashr")

Loading ashr

devtools::load_all("~/Github/flashier")

Loading flashier

fl.log1p <- flashier(log1p(Y), var.type = 0,
                     greedy.Kmax = 10, verbose = 1)

Initializing flash object...
Adding factor 1 to flash object...
Adding factor 2 to flash object...
Adding factor 3 to flash object...
Factor doesn't increase objective and won't be added.
Nullchecking 2 factors...
Wrapping up...
Done.

My proposed approach is the following.

# 1. Get ASH estimates for lambda (posterior means and SDs).
Y.ash <- ashr::ash(betahat = rep(0, n * p), sebetahat = 1, 
                   lik = ashr::lik_pois(as.vector(Y)), mode = 0,
                   method = "shrink")
pm <- Y.ash$result$PosteriorMean
psd <- Y.ash$result$PosteriorSD

# 2. Transform to log scale.
X <- matrix(log(pm) - psd^2 / pm^2, n, p)
S <- matrix(psd / pm, n, p)

# 3. Run FLASH.
fl.ash <- flashier(X, S = S, var.type = 0, 
                   greedy.Kmax = 10, verbose = 1)

Initializing flash object...
Adding factor 1 to flash object...
Adding factor 2 to flash object...
Adding factor 3 to flash object...
Factor doesn't increase objective and won't be added.
Nullchecking 2 factors...
Wrapping up...
Done.

For comparison, I also run ashr separately on each column of \(Y\).

colwise.pm <- array(0, dim = dim(Y))
colwise.psd <- array(0, dim = dim(Y))
for (i in 1:p) {
  # For a fair comparison, I use the same grid that was selected by Y.ash.
  col.ash <- ashr::ash(betahat = rep(0, n), sebetahat = 1, 
                       lik = ashr::lik_pois(Y[, i]), mode = 0,
                       method = "shrink", mixsd = Y.ash$fitted_g$b)
  colwise.pm[, i] <- col.ash$result$PosteriorMean
  colwise.psd[, i] <- col.ash$result$PosteriorSD
}

colw.X <- log(colwise.pm) - colwise.psd^2 / colwise.pm^2
colw.S <- colwise.psd / colwise.pm

fl.colw <- flashier(colw.X, S = colw.S, var.type = 0, 
                    greedy.Kmax = 10, verbose = 1)

Initializing flash object...
Adding factor 1 to flash object...
Adding factor 2 to flash object...
Adding factor 3 to flash object...
Adding factor 4 to flash object...
Factor doesn't increase objective and won't be added.
Nullchecking 3 factors...
Wrapping up...
Done.

(Note that three factors are fit here. The third is loaded on a small number of columns and accounts for a very small proportion of total variance. Such factors are frequently found when using Gaussian methods on Poisson data.)

I calculate the root mean-squared error and the mean shrinkage obtained using each method. I calculate separately for large \(\lambda_{ij}\), small \(\lambda_{ij}\) in columns where all values are small, and small \(\lambda_{ij}\) in columns where some values are large.

get.res <- function(fl, log1p) {
  preds <- flashier:::lowrank.expand(get.EF(fl$fit))
  # "De-bias" the log1p method by transforming everything to the log1p scale.
  true.vals <- log(exp(log.lambda) + 1)
  if (!log1p)
    preds <- log(exp(preds) + 1)
  
  hi.resid <- preds[hi.rows, hi.cols] - true.vals[hi.rows, hi.cols]
  lo.resid <- preds[, !hi.cols] - true.vals[, !hi.cols]
  mix.resid <- preds[!hi.rows, hi.cols] - true.vals[!hi.rows, hi.cols]
  
  res <- list(rmse.hi = sqrt(mean((hi.resid)^2)),
              rmse.lo = sqrt(mean((lo.resid)^2)),
              rmse.mix = sqrt(mean((mix.resid)^2)),
              shrnk.hi = -mean(hi.resid),
              shrnk.lo = -mean(lo.resid),
              shrnk.mix = -mean(mix.resid))
  res <- lapply(res, round, 2)
  
  return(res)
}

res <- data.frame(cbind(get.res(fl.log1p, TRUE), 
                        get.res(fl.ash, FALSE), 
                        get.res(fl.colw, FALSE)))
var.names <- c("RMSE (lg vals)", 
               "RMSE (sm vals)", 
               "RMSE (sm vals in lg cols)", 
               "Mean shrinkage (lg vals)",
               "Mean shrinkage (sm vals)", 
               "Mean shrinkage (sm vals in lg cols)")
meth.names <- c("log1p", "ASH", "col-wise ASH")
row.names(res) <- var.names
colnames(res) <- meth.names

knitr::kable(res, digits = 2)

	log1p	ASH	col-wise ASH
RMSE (lg vals)	0.33	0.45	0.39
RMSE (sm vals)	0.18	0.17	0.17
RMSE (sm vals in lg cols)	0.18	0.17	0.19
Mean shrinkage (lg vals)	0.11	0.26	0.21
Mean shrinkage (sm vals)	0.09	0.08	0.07
Mean shrinkage (sm vals in lg cols)	0.08	0.09	0.1

Although the usual log1p method does best in terms of RMSE, the new methods do better in shrinking larger rates, which might be advantageous for FDR control. Another possible advantage of the new methods is that they give estimates on the log scale and are thus easy to interpret. The log1p approach can return negative fitted values, which must be thresholded to zero after the fact.

Session information

sessionInfo()

R version 3.4.3 (2017-11-30)
Platform: x86_64-apple-darwin15.6.0 (64-bit)
Running under: macOS High Sierra 10.13.6

Matrix products: default
BLAS: /Library/Frameworks/R.framework/Versions/3.4/Resources/lib/libRblas.0.dylib
LAPACK: /Library/Frameworks/R.framework/Versions/3.4/Resources/lib/libRlapack.dylib

locale:
[1] en_US.UTF-8/en_US.UTF-8/en_US.UTF-8/C/en_US.UTF-8/en_US.UTF-8

attached base packages:
[1] stats     graphics  grDevices utils     datasets  methods   base     

other attached packages:
[1] flashier_0.1.0 ashr_2.2-29   

loaded via a namespace (and not attached):
 [1] Rcpp_1.0.0          highr_0.7           compiler_3.4.3     
 [4] git2r_0.21.0        workflowr_1.0.1     R.methodsS3_1.7.1  
 [7] R.utils_2.6.0       iterators_1.0.10    tools_3.4.3        
[10] testthat_2.0.1      digest_0.6.18       etrunct_0.1        
[13] evaluate_0.12       memoise_1.1.0       lattice_0.20-35    
[16] rlang_0.3.0.1       Matrix_1.2-14       foreach_1.4.4      
[19] commonmark_1.4      yaml_2.2.0          parallel_3.4.3     
[22] ebnm_0.1-17         xfun_0.4            withr_2.1.2.9000   
[25] stringr_1.3.1       roxygen2_6.0.1.9000 xml2_1.2.0         
[28] knitr_1.21.6        devtools_1.13.4     rprojroot_1.3-2    
[31] grid_3.4.3          R6_2.3.0            rmarkdown_1.11     
[34] mixsqp_0.1-97       magrittr_1.5        whisker_0.3-2      
[37] backports_1.1.2     codetools_0.2-15    htmltools_0.3.6    
[40] MASS_7.3-48         assertthat_0.2.0    stringi_1.2.4      
[43] doParallel_1.0.14   pscl_1.5.2          truncnorm_1.0-8    
[46] SQUAREM_2017.10-1   R.oo_1.21.0