Last updated: 2018-07-16

workflowr checks: (Click a bullet for more information)

  • ✔ R Markdown file: up-to-date

    Great! Since the R Markdown file has been committed to the Git repository, you know the exact version of the code that produced these results.

  • ✔ Environment: empty

    Great job! The global environment was empty. Objects defined in the global environment can affect the analysis in your R Markdown file in unknown ways. For reproduciblity it’s best to always run the code in an empty environment.

  • ✔ Seed: set.seed(20180714)

    The command set.seed(20180714) was run prior to running the code in the R Markdown file. Setting a seed ensures that any results that rely on randomness, e.g. subsampling or permutations, are reproducible.

  • ✔ Session information: recorded

    Great job! Recording the operating system, R version, and package versions is critical for reproducibility.

  • ✔ Repository version: 055d572

    Great! You are using Git for version control. Tracking code development and connecting the code version to the results is critical for reproducibility. The version displayed above was the version of the Git repository at the time these results were generated.

    Note that you need to be careful to ensure that all relevant files for the analysis have been committed to Git prior to generating the results (you can use wflow_publish or wflow_git_commit). workflowr only checks the R Markdown file, but you know if there are other scripts or data files that it depends on. Below is the status of the Git repository when the results were generated: 
    
Ignored files:
    Ignored:    .DS_Store
    Ignored:    .Rhistory
    Ignored:    .Rproj.user/
    Ignored:    docs/.DS_Store
    Ignored:    docs/figure/.DS_Store
    Note that any generated files, e.g. HTML, png, CSS, etc., are not included in this status report because it is ok for generated content to have uncommitted changes.
Expand here to see past versions:
    File Version Author Date Message
    Rmd 055d572 Jason Willwerscheid 2018-07-16 wflow_publish(“analysis/objective.Rmd”)
    html 7db12a1 Jason Willwerscheid 2018-07-16 Build site.
    Rmd 87a47fd Jason Willwerscheid 2018-07-16 wflow_publish(“analysis/objective.Rmd”, republish = T)
    html c7b5ab1 Jason Willwerscheid 2018-07-15 Build site.
    Rmd 8258811 Jason Willwerscheid 2018-07-15 wflow_publish(“analysis/objective.Rmd”)
    html 0b30bef Jason Willwerscheid 2018-07-15 Build site.
    Rmd db11cbb Jason Willwerscheid 2018-07-15 wflow_publish(“analysis/objective.Rmd”)

Introduction

Here I begin to look into why the FLASH objective function can decrease after an iteration.

Illustration of problem

I’m using the “strong” tests from the MASH paper GTEx dataset. The first problem appears when fitting the fourth factor. Notice that in the final iteration, the objective decreases by a very small amount and a warning is displayed.

# devtools::install_github("stephenslab/flashr", ref="trackObj")
devtools::load_all("/Users/willwerscheid/GitHub/flashr")
Loading flashr
# devtools::install_github("stephenslab/ebnm")
devtools::load_all("/Users/willwerscheid/GitHub/ebnm")
Loading ebnm
gtex <- readRDS(gzcon(url("https://github.com/stephenslab/gtexresults/blob/master/data/MatrixEQTLSumStats.Portable.Z.rds?raw=TRUE")))
strong <- gtex$strong.z
res <- flash_add_greedy(strong, Kmax=3, verbose=FALSE)
fitting factor/loading 1
fitting factor/loading 2
fitting factor/loading 3
res <- flash_add_greedy(strong, f_init=res$f, Kmax=1, verbose=TRUE)
fitting factor/loading 1
Objective:-1298710.64322328
Objective:-1297543.71231454
Objective:-1297377.02562144
Objective:-1297291.11358246
Objective:-1297239.23330907
Objective:-1297207.28393276
Objective:-1297187.26387941
Objective:-1297174.44135814
Objective:-1297166.02132697
Objective:-1297160.35163403
Objective:-1297156.46023221
Objective:-1297153.76860079
Objective:-1297151.90730432
Objective:-1297150.62250311
Objective:-1297149.73767208
Objective:-1297149.13102524
Objective:-1297148.71858473
Objective:-1297148.44214222
Objective:-1297148.26107547
Objective:-1297148.14684887
Objective:-1297148.07930637
Objective:-1297148.04415067
Objective:-1297148.0312139
Objective:-1297148.033256
Warning in r1_opt(flash_get_Rk(data, f, k), flash_get_R2k(data, f, k), f
$EL[, : An iteration decreased the objective. This happens occasionally,
perhaps due to numeric reasons. You could ignore this warning, but you
might like to check out https://github.com/stephenslab/flashr/issues/26 for
more details.
performing nullcheck
objective from deleting factor:-1301896.87271162
objective from keeping factor:-1297148.033256
nullcheck complete, objective:-1297148.033256

Analysis

A more granular tracking of the objective function reveals a larger problem. Recall that there are three steps in each iteration: updating the precision matrix, updating the factors (via the prior \(g_f\)), and updating the loadings (via \(g_l\)). Plotting the objective after each step rather than each iteration reveals a sawtooth pattern. (See branch trackObj, file r1_opt.R for the code used to obtain these results.)

obj_data <- as.vector(rbind(res$obj[[1]]$after_tau,
                            res$obj[[1]]$after_f,
                            res$obj[[1]]$after_l))
max_obj <- max(obj_data)
obj_data <- obj_data - max_obj
iter <- 1:length(obj_data) / 3

plt_xlab = "Iteration"
plt_ylab = "Diff. from maximum obj."
plot(iter, obj_data, type='l', xlab=plt_xlab, ylab=plt_ylab)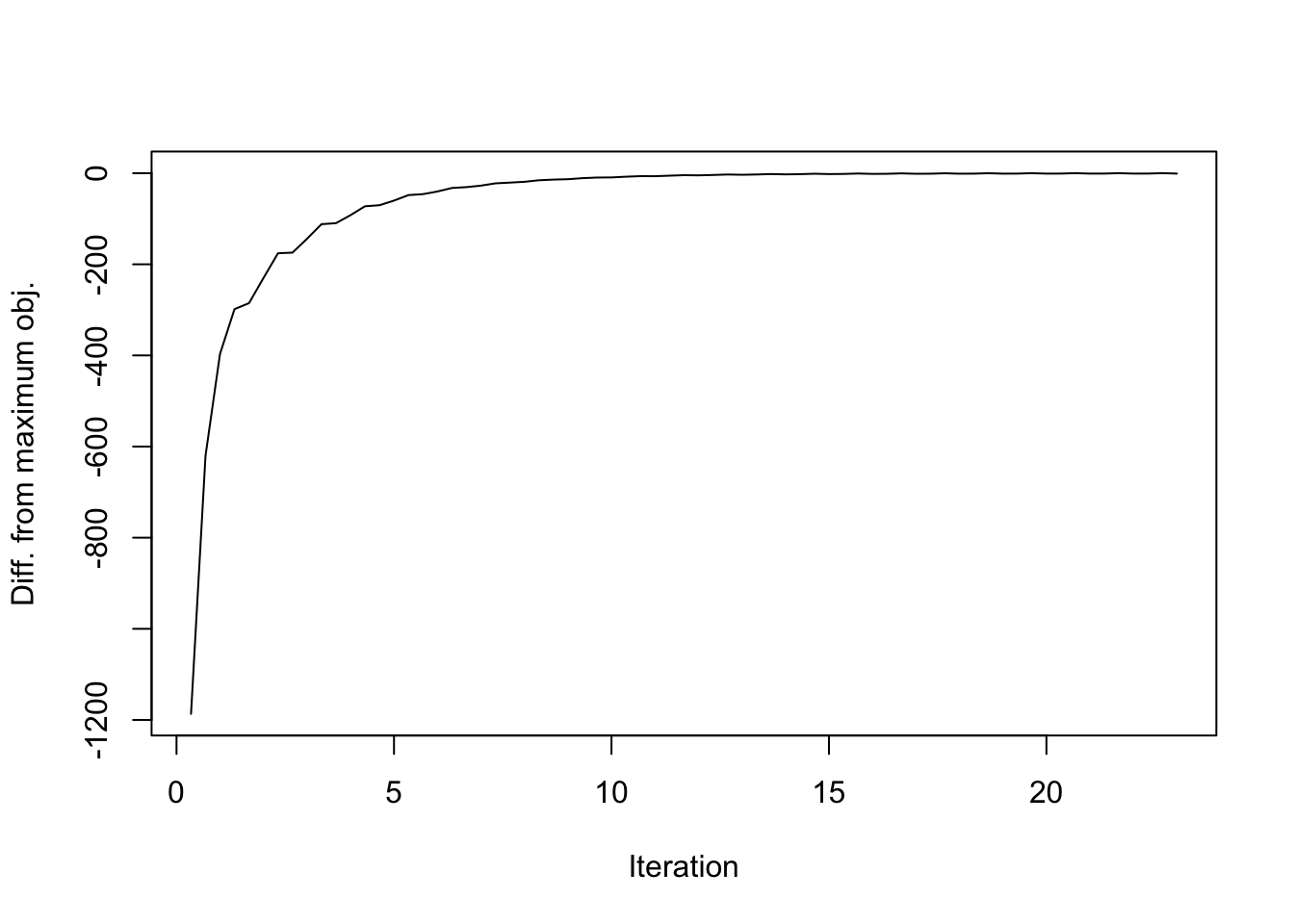

Expand here to see past versions of plot-1.png:
Version Author Date
7db12a1 Jason Willwerscheid 2018-07-16
0b30bef Jason Willwerscheid 2018-07-15

Discarding the first 8 iterations in order to zoom in on the problem area:

obj_data <- obj_data[-(1:24)]
iter <- iter[-(1:24)]
plt_colors <- c("indianred1", "indianred3", "indianred4")
plt_pch <- c(16, 17, 15)

plot(iter, obj_data, col=plt_colors, pch=plt_pch,
     xlab=plt_xlab, ylab=plt_ylab)
legend("bottomright", c("after tau", "after f", "after l"),
       col=plt_colors, pch=plt_pch)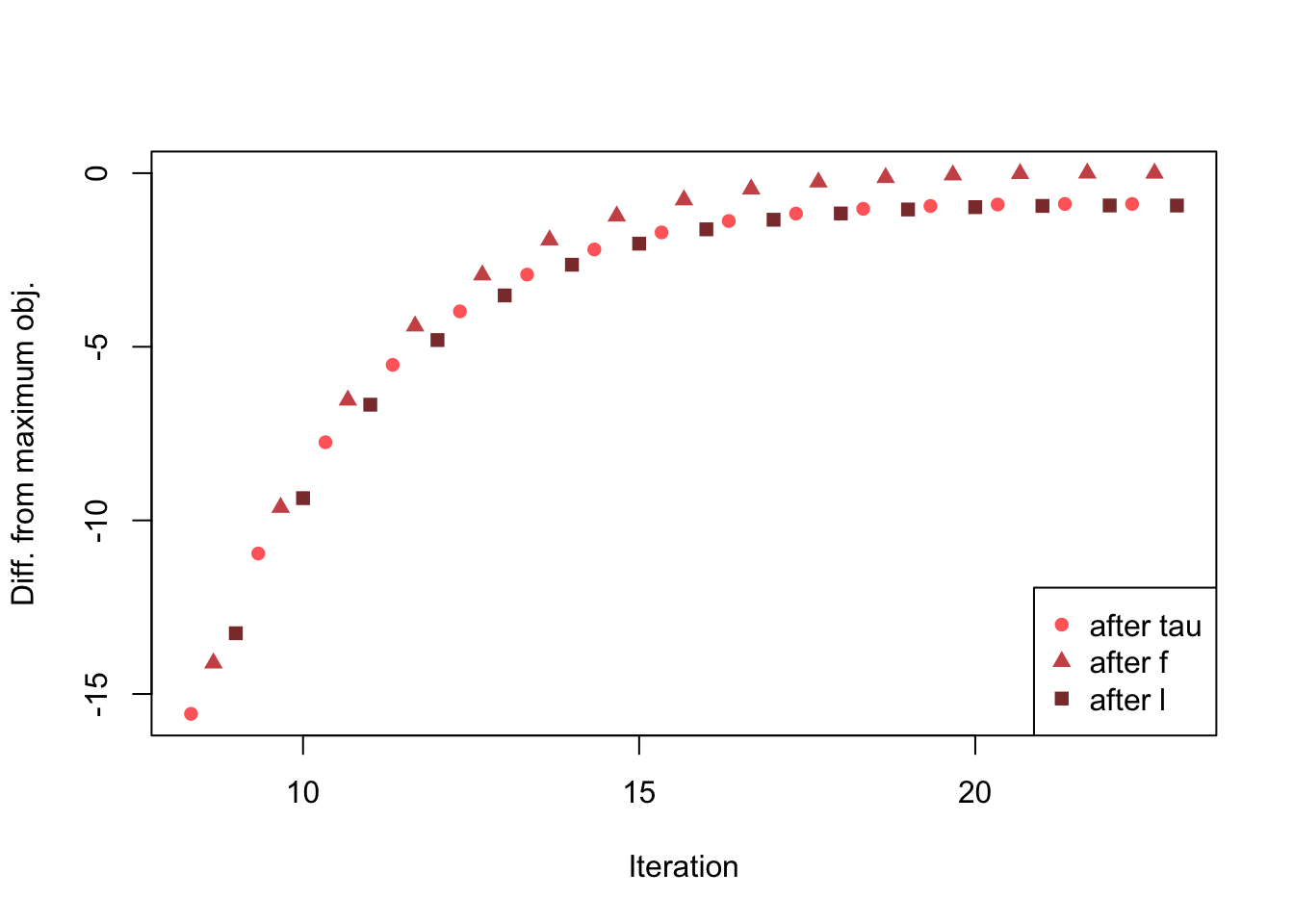

Expand here to see past versions of plot2-1.png:
Version Author Date
7db12a1 Jason Willwerscheid 2018-07-16
0b30bef Jason Willwerscheid 2018-07-15

I backtrack to just before the “bad” update.

res2 <- flash_add_greedy(strong, Kmax=4, stopAtObj=-1297148.032)
fitting factor/loading 1
fitting factor/loading 2
fitting factor/loading 3
fitting factor/loading 4
flash_get_objective(strong, res2$f) - flash_get_objective(strong, res$f)
[1] 0.002265139

So at this point, the objective is indeed better than for the flash object attained above. The component parts of the objective are:

fl <- res2$f
data <- flash_set_data(strong)
k <- 4

KL_l <- fl$KL_l[[k]]
KL_f <- fl$KL_f[[k]]
loglik <- flashr:::e_loglik(data, fl)
list(KL_l = KL_l, KL_f = KL_f, loglik = loglik)
$KL_l
[1] -8324.404

$KL_f
[1] -128.9907

$loglik
[1] -1227371

First I update the precision (I follow the code in r1_opt). Only the “loglik” component is affected by this update:

init_fl = fl
init_KL_l = KL_l
init_KL_f = KL_f
init_loglik = loglik

R2 = flashr:::flash_get_R2(data, fl)
fl$tau = flashr:::compute_precision(R2, data$missing, 
                                    "by_column", data$S)
flashr:::e_loglik(data, fl) - init_loglik
[1] 0.04306088

So the overall objective indeed increases. Now I update the loadings (FLASH updates factors first, but the order of updates is not supposed to affect the monotonicity of the objective function).

s2 = 1/(fl$EF2[, k] %*% t(fl$tau))
s = sqrt(s2)
Rk = flashr:::flash_get_Rk(data, fl, k)
x = fl$EF[, k] %*% t(Rk * fl$tau) * s2
ebnm_l = flashr:::ebnm_pn(x, s, list())
KL_l = (ebnm_l$penloglik 
        - flashr:::NM_posterior_e_loglik(x, s, ebnm_l$postmean,
                                         ebnm_l$postmean2))

fl$EL[, k] = ebnm_l$postmean
fl$EL2[, k] = ebnm_l$postmean2
fl$gl[[k]] = ebnm_l$fitted_g
fl$KL_l[[k]] = KL_l
flash_get_objective(data, fl) - flash_get_objective(data, init_fl)
[1] -0.1154427

So the objective has in fact gotten worse. And tightening the control parameters or changing the initialization for the ebnm function does not help matters. For example:

s2 = 1/(fl$EF2[, k] %*% t(fl$tau))
s = sqrt(s2)
Rk = flashr:::flash_get_Rk(data, fl, k)
x = fl$EF[, k] %*% t(Rk * fl$tau) * s2
ebnm_l = flashr:::ebnm_pn(x, s, list(g=list(a=100),
                                     control=list(factr=100)))
KL_l = (ebnm_l$penloglik 
        - flashr:::NM_posterior_e_loglik(x, s, ebnm_l$postmean,
                                         ebnm_l$postmean2))

fl$EL[, k] = ebnm_l$postmean
fl$EL2[, k] = ebnm_l$postmean2
fl$gl[[k]] = ebnm_l$fitted_g
fl$KL_l[[k]] = KL_l
flash_get_objective(data, fl) - flash_get_objective(data, init_fl)
[1] -0.1154426

Conclusions and questions

The decrease appears too large to be explained by numerical error. Indeed, it would be very surprising to me if EL and EL2 could only be trusted to five digits or so (as would have to be the case to produce errors of the above magnitude).

More seriously, the sawtooth pattern depicted above points to a more regular feature of the optimization. Indeed, it appears that all of the triangles (objectives after updating factors) are biased upwards and all of the squares (objectives after updating loadings) are biased slightly downwards.

The theory appears to be sound, so what is going on here?

Session information

sessionInfo()
R version 3.4.3 (2017-11-30)
Platform: x86_64-apple-darwin15.6.0 (64-bit)
Running under: macOS Sierra 10.12.6

Matrix products: default
BLAS: /Library/Frameworks/R.framework/Versions/3.4/Resources/lib/libRblas.0.dylib
LAPACK: /Library/Frameworks/R.framework/Versions/3.4/Resources/lib/libRlapack.dylib

locale:
[1] en_US.UTF-8/en_US.UTF-8/en_US.UTF-8/C/en_US.UTF-8/en_US.UTF-8

attached base packages:
[1] stats     graphics  grDevices utils     datasets  methods   base     

other attached packages:
[1] ebnm_0.1-12   flashr_0.5-12

loaded via a namespace (and not attached):
 [1] Rcpp_0.12.17        pillar_1.2.1        plyr_1.8.4         
 [4] compiler_3.4.3      git2r_0.21.0        workflowr_1.0.1    
 [7] R.methodsS3_1.7.1   R.utils_2.6.0       iterators_1.0.9    
[10] tools_3.4.3         testthat_2.0.0      digest_0.6.15      
[13] tibble_1.4.2        evaluate_0.10.1     memoise_1.1.0      
[16] gtable_0.2.0        lattice_0.20-35     rlang_0.2.0        
[19] Matrix_1.2-12       foreach_1.4.4       commonmark_1.4     
[22] yaml_2.1.17         parallel_3.4.3      withr_2.1.1.9000   
[25] stringr_1.3.0       roxygen2_6.0.1.9000 xml2_1.2.0         
[28] knitr_1.20          devtools_1.13.4     rprojroot_1.3-2    
[31] grid_3.4.3          R6_2.2.2            rmarkdown_1.8      
[34] ggplot2_2.2.1       ashr_2.2-10         magrittr_1.5       
[37] whisker_0.3-2       backports_1.1.2     scales_0.5.0       
[40] codetools_0.2-15    htmltools_0.3.6     MASS_7.3-48        
[43] assertthat_0.2.0    softImpute_1.4      colorspace_1.3-2   
[46] stringi_1.1.6       lazyeval_0.2.1      munsell_0.4.3      
[49] doParallel_1.0.11   pscl_1.5.2          truncnorm_1.0-8    
[52] SQUAREM_2017.10-1   R.oo_1.21.0

This reproducible R Markdown analysis was created with workflowr 1.0.1