Quality of ashr Grid Approximations

Scale mixtures of normals

Let \(\mathcal{G}\) be the family of all scale mixtures of normals and let \(\hat{g} \in \mathcal{G}\) be the MLE solution to the EBNM problem. In ashr, we approximate \(\mathcal{G}\) by the family of finite mixtures of normals \[ \pi_1 \mathcal{N}(0, \sigma_1^2) + \ldots + \pi_K \mathcal{N}(0, \sigma_K^2), \] where the grid \(\{ \sigma_1^2, \ldots, \sigma_K^2 \}\) is fixed in advance. Let \(\tilde{\mathcal{G}}\) be this restricted family and let \(\hat{\tilde{g}} \in \tilde{\mathcal{G}}\) be the restricted MLE solution (as given by ashr).

The quality of the grid can be measured by the per-observation difference in log likelihood \[ \frac{1}{n} \sum_{i = 1}^n \left( \log p(x_i \mid s_i, \hat{g}) - \log p(x_i \mid s_i, \hat{\tilde{g}}) \right) \]

Assume that all standard errors \(s_i\) are identical to \(s\). Then the likelihood \(p(x_i \mid s_i, \hat{g})\) is \[ h(x_i) := \int \mathcal{N}(x_i; 0, \tau^2 + s^2) df(\tau), \] where \(f\) is the mixing density of \(\hat{g}\), and \(p(x_i \mid s_i, \hat{\tilde{g}})\) is \[ \tilde{h}(x_i) := \pi_1 \mathcal{N}(x_i; 0, \sigma_1^2 + s^2) + \ldots + \pi_K \mathcal{N}(x_i; 0, \sigma_K^2 + s^2) \]

Next, assume that the population distribution of the \(x_i\)s is truly \(h\), so that the expected value of the per-observation difference in log likelihood is the KL-divergence between \(h\) and \(\tilde{h}\) \[ \text{KL}(h \mid\mid \tilde{h}) = \mathbb{E}_h \log \frac{h(x)}{\tilde{h}(x)} \]

Finally, to simplify analysis, assume that \(h\) is a finite mixture of normals \[ h(x_i) = \rho_1 \mathcal{N}(x_i; 0, \tau_1^2 + s^2) + \ldots + \rho_L \mathcal{N}(x_i; 0, \tau_L^2 + s^2) \] (Note, however, that \(\hat{g}\) can be approximated arbitrary well by a finite mixture!)

Now, for each \(1 \le \ell \le L\), let \(\sigma_{k(\ell)}^2\) be the largest \(\sigma_k^2\) such that \(\sigma_k^2 \le \tau_\ell^2\), so that \(\sigma_{k(\ell) + 1}^2\) is the smallest \(\sigma_k^2\) such that \(\tau_\ell^2 < \sigma_k^2\). In other words, if \(\sigma_1^2, \ldots, \sigma_K^2\) divides the positive real line into segments, then \(\tau_\ell^2\) is on the segment \(\left[\sigma_{k(\ell)}^2, \sigma_{k(\ell) + 1}^2\right)\). (I assume that \(\sigma_1^2\) has been chosen sufficiently small and \(\sigma_K^2\) sufficiently large.) Now approximate each mixture component of \(h\) by a mixture of two normals: \[ \tilde{\tilde{h}} := \rho_1 \left( \omega_1 \mathcal{N}(0, \sigma_{k(1)}^2 + s^2) + (1 - \omega_1) \mathcal{N}(0, \sigma_{k(1) + 1}^2 + s^2) \right) + \ldots + \rho_L \left( \omega_L \mathcal{N}(0, \sigma_{k(L)}^2 + s^2) + (1 - \omega_L) \mathcal{N}(0, \sigma_{k(L) + 1}^2 + s^2) \right), \] where \(\omega_1, \ldots, \omega_L\) remains to be determined.

Since \(\tilde{\tilde{h}}\) is on the ashr grid and \(\tilde{h}\) is the maximum likelihood estimate on the ashr grid, it must be true that \[ \text{KL}(h \mid\mid \tilde{h}) \le \text{KL}(h \mid\mid \tilde{\tilde{h}}) \] for any choice of \(\omega_1, \ldots, \omega_L\). Further (see section 6 here), \[ \begin{aligned} \text{KL}(h \mid\mid \tilde{\tilde{h}}) &\le \sum_\ell \rho_\ell \left( \text{KL} \left(\mathcal{N}(0, \tau_\ell^2 + s^2) \mid\mid \omega_\ell \mathcal{N}(0, \sigma_{k(\ell)}^2 + s^2) + (1 - \omega_\ell) \mathcal{N}(0, \sigma_{k(\ell) + 1}^2 + s^2) \right) \right) \\ &\le \max_\ell \text{KL}\left(\mathcal{N}(0, \tau_\ell^2 + s^2) \mid\mid \omega_\ell \mathcal{N}(0, \sigma_{k(\ell)}^2 + s^2) + (1 - \omega_\ell) \mathcal{N}(0, \sigma_{k(\ell) + 1}^2 + s^2) \right)\\ &\le \max_{k,\ \sigma_k \le \tau \le \sigma_{k + 1}} \text{KL}\left(\mathcal{N}(0, \tau^2 + s^2) \mid\mid \omega \mathcal{N}(0, \sigma_k^2 + s^2) + (1 - \omega) \mathcal{N}(0, \sigma_{k + 1}^2 + s^2) \right) \end{aligned} \] Next, since KL-divergence is invariant to scaling, if we set the grid so that the ratio \[ m_k := \frac{\sigma_{k + 1}^2 + s^2}{\sigma_k^2 + s^2} \] is identical to \(m\) for all \(1 \le k \le K - 1\), then we can conclude that \[ \text{KL}(h \mid\mid \tilde{h}) \le \max_{1 \le a \le m} \text{KL} (\mathcal{N}(0, a) \mid\mid \omega \mathcal{N}(0, 1) + (1 - \omega) \mathcal{N}(0, m))\] Since this is true for all \(0 \le \omega \le 1\), we can get an upper bound for the per-observation difference in likelihood (given the assumptions listed above) by solving the minimax problem \[ \text{KL}(h \mid\mid \tilde{h}) \le \max_{1 \le a \le m} \min_\omega \text{KL} (\mathcal{N}(0, a) \mid\mid \omega \mathcal{N}(0, 1) + (1 - \omega) \mathcal{N}(0, m)) \] I use importance sampling to approximate the KL-divergence. The current ashr default \(m = \sqrt{2}\) gives:

log_add <- function(x, y) {
  C <- pmax(x, y)
  x <- x - C
  y <- y - C
  return(log(exp(x) + exp(y)) + C)
}

# To "sample" from different a, sample once and then scale depending on a. This method ensures a
#   smooth optimization objective.
smn_KLdiv <- function(a, omega, m, samp) {
  samp <- samp * sqrt(a)
  h_llik <- mean(dnorm(samp, sd = sqrt(a), log = TRUE))
  llik1 <- log(omega) + dnorm(samp, sd = 1, log = TRUE)
  llik2 <- log(1 - omega) + dnorm(samp, sd = sqrt(m), log = TRUE)
  htilde_llik <- mean(log_add(llik1, llik2))
  return(h_llik - htilde_llik)
}

min_smnKLdiv <- function(a, m, samp) {
  optres <- optimize(function(omega) smn_KLdiv(a, omega, m, samp), interval = c(0, 1), maximum = FALSE)
  return(optres$objective)
}

ub_smnKLdiv <- function(m, samp) {
  optres <- optimize(function(a) min_smnKLdiv(a, m, samp), interval = c(1, m), maximum = TRUE)
  return(optres$objective)
}

set.seed(666)
sampsize <- 1000000
samp <- rnorm(sampsize)

default_ub <- ub_smnKLdiv(sqrt(2), samp)
default_ub

#> [1] 0.0001525892

Thus ashr will give an approximation that’s within one log likelihood unit of the exact solution for problems as large as \(n = 6000\) or so. (Note, however, that ashr spaces the \(\sigma_k^2\)s equally rather than \(\sigma_k^2 + s^2\), as would be more efficient. When \(s = 1\) and \(m = \sqrt{2}\), for example, it’s best to use the grid \(\{0, \sqrt{2} - 1, 1, 2\sqrt{2} - 1, 3, \ldots\}\).)

To get a sense of how tight the upper bound is, we can sample \(a \sim \text{Unif}\left[1, m\right]\) to get an “expected” KL-divergence.

m <- sqrt(2)

set.seed(666)
a <- runif(1000, min = 1, max = m)

# Use a smaller sample here.
sampsize <- 50000
samp <- rnorm(sampsize)

default_ev <- mean(sapply(a, function(a) min_smnKLdiv(a, m, samp)))
default_ev

#> [1] 3.857677e-05

So the above upper bound can be expected to be reasonably tight.

For larger problems or to obtain better approximations, a denser grid can be used. I show upper bounds and expected values for a range of \(m\) (the code was run in advance):

smn_res <- readRDS("./output/ashr_grid/smn_res.rds")
smn_res <- as_tibble(smn_res)

df <- gather(smn_res, "metric", "KLdiv", -m) %>%
  filter(KLdiv > 0) %>%
  mutate(metric = ifelse(metric == "ub", "bound", "expected"))

ggplot(df, aes(x = m, y = KLdiv, color = metric)) + 
  geom_line() +
  scale_y_log10() +
  labs(x = "grid multiplier", y = "KL divergence", color = "")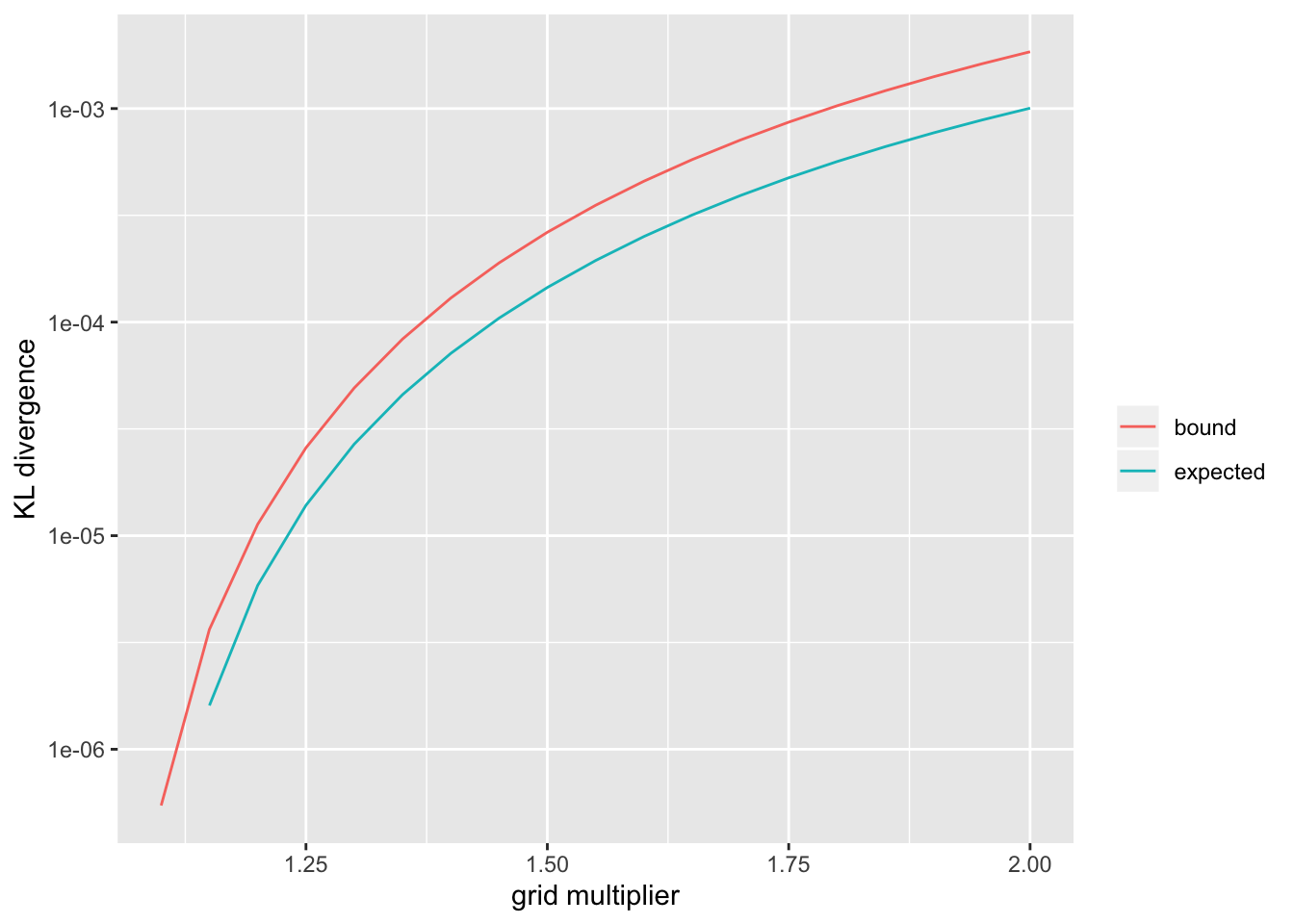

Symmetric unimodal priors

Now let \(\mathcal{G}\) be the family of symmetric priors that are unimodal at zero. ashr approximates \(\mathcal{G}\) by the family of finite mixtures of uniforms \[ \pi_1 \text{Unif}\left[-a_1, a_1\right] + \ldots + \pi_K \text{Unif}\left[-a_K, a_K\right], \] where the grid \(\{ a_1, \ldots, a_K \}\) is fixed in advance.

Let all notation be similar to the above, and let \[\text{UN}(a, s^2)\] denote the convolution of a uniform distribution on \(\left[-a, a\right]\) with \(\mathcal{N}(0, s^2)\) noise. Then, by an identical argument to the above, \[ \text{KL}(h \mid\mid \tilde{h}) \le \max_{k,\ a_k \le a \le a_{k + 1}} \min_\omega \text{KL}\left(\text{UN}(a, s^2) \mid\mid \omega \text{UN}(a_k, s^2) + (1 - \omega) \text{UN}(a_{k + 1}, s^2) \right) \]

Unlike for scale mixtures of normals, however, a scaling argument can’t reduce this to a single minimax problem, and it’s not immediately clear how the grid should be spaced. To get an idea of what an optimal grid should look like, I set \(s = 1\), choose a target KL-divergence, and then iteratively construct the grid:

log_minus <- function(x, y) {
  C <- pmax(x, y)
  x <- x - C
  y <- y - C
  return(log(exp(x) - exp(y)) + C)
}

llik_UN <- function(a, samp) {
  llik1 <- pnorm(a, mean = samp, log.p = TRUE)
  llik2 <- pnorm(-a, mean = samp, log.p = TRUE)
  return(log_minus(llik1, llik2) - log(2 * a))
}

UN_KLdiv <- function(a, omega, aleft, aright, unif_samp, norm_samp) {
  samp <- a * unif_samp + norm_samp
  h_llik <- mean(llik_UN(a, samp))
  llik1 <- log(omega) + llik_UN(aleft, samp)
  llik2 <- log(1 - omega) + llik_UN(aright, samp)
  htilde_llik <- mean(log_add(llik1, llik2))
  return(h_llik - htilde_llik)
}

min_symmKLdiv <- function(a, aleft, aright, unif_samp, norm_samp) {
  optres <- optimize(function(omega) UN_KLdiv(a, omega, aleft, aright, unif_samp, norm_samp), 
                     interval = c(0, 1), maximum = FALSE)
  return(optres$objective)
}

ub_symmKLdiv <- function(aleft, aright, unif_samp, norm_samp) {
  optres <- optimize(function(a) min_symmKLdiv(a, aleft, aright, unif_samp, norm_samp), 
                     interval = c(aleft, aright), maximum = TRUE)
  return(optres$objective)
}

find_next_gridpt <- function(aleft, targetKL, unif_samp, norm_samp, max_space) {
  uniroot_fn <- function(aright) {ub_symmKLdiv(aleft, aright, unif_samp, norm_samp) - targetKL}
  optres <- uniroot(uniroot_fn, c(aleft + 1e-6, aleft + max_space))
  return(optres$root)
}

build_grid <- function(targetKL, unif_samp, norm_samp, len = 30L) {
  i <- 1
  startpt <- 1e-6
  cat("Gridpoint", i, ":", startpt, "\n")
  i <- 2
  nextpt <- find_next_gridpt(startpt, targetKL, unif_samp, norm_samp, max_space = 10)
  grid <- c(startpt, nextpt)
  cat("Gridpoint", i, ":", max(grid), "\n")
  last_ratio <- 2 * nextpt
  for (i in 3:len) {
    nextpt <- find_next_gridpt(max(grid), targetKL, unif_samp, norm_samp, max(grid) * last_ratio)
    last_ratio <- nextpt / max(grid)
    grid <- c(grid, nextpt)
    cat("Gridpoint", i, ":", max(grid), "\n")
  }
  return(grid)
}

# The sample size again needs to be relatively small.
sampsize <- 50000
unif_samp <- runif(sampsize, min = -1, max = 1)
norm_samp <- rnorm(sampsize)

grid <- build_grid(targetKL = default_ub, unif_samp, norm_samp, len = 3L)

#> Gridpoint 1 : 1e-06 
#> Gridpoint 2 : 1.31824 
#> Gridpoint 3 : 1.993085

Since the problem is slow to solve, I’ve only added three grid points here as an illustration. In code run in advance, I’ve built ashr grids for various KL-divergence targets. They appear as follows:

symm_res <- readRDS("./output/ashr_grid/symm_ub_res.rds")

df <- symm_res %>%
  mutate(KL = as.factor(KL)) %>%
  mutate(KL = fct_relevel(KL, rev))

ggplot(df, aes(x = idx, y = grid, color = as.factor(KL))) + 
  geom_point() +
  labs(x = "index (k)", y = "grid point location (a_k)", color = "KL-divergence")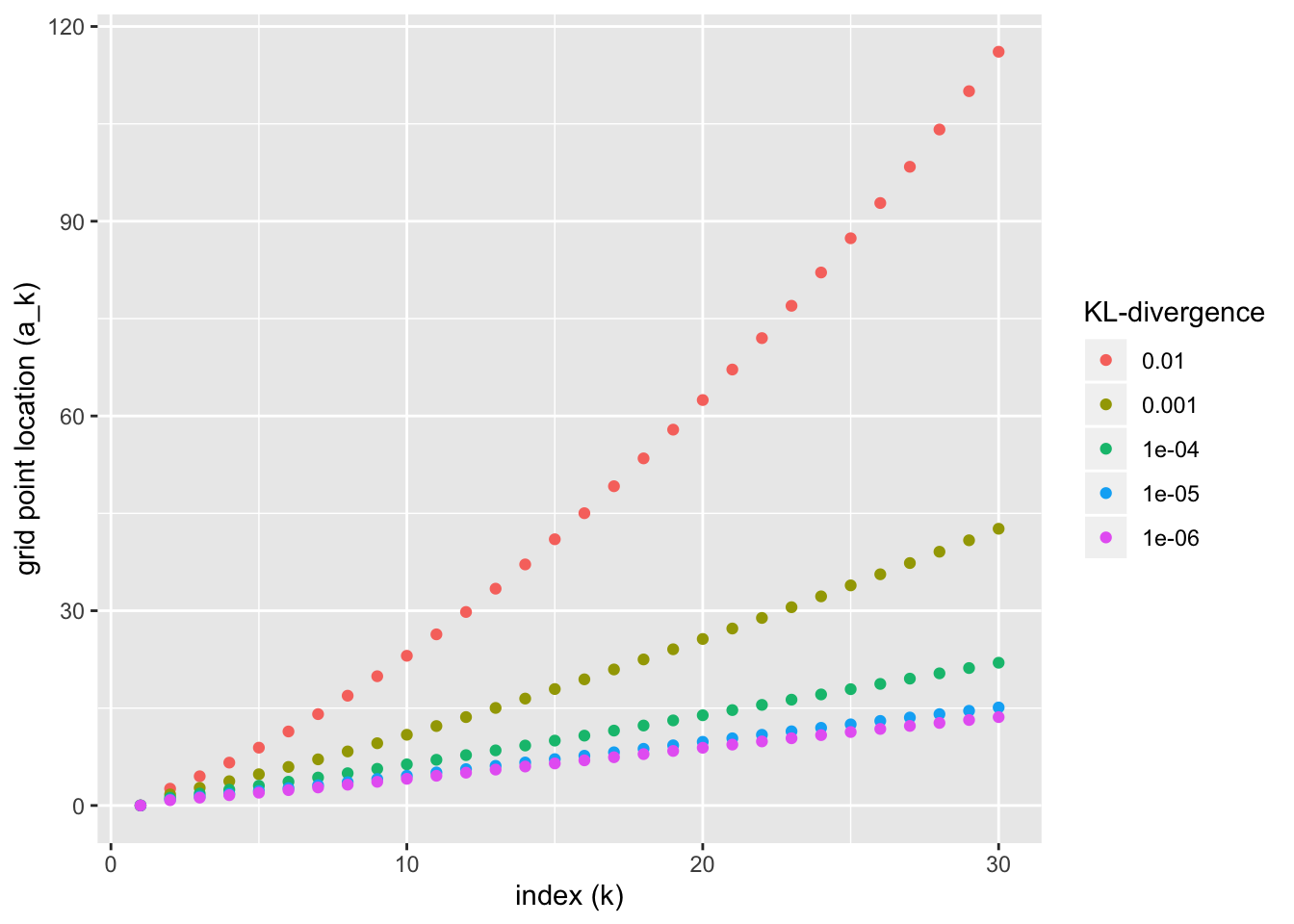

What happens as \(k \to \infty\)? Intuitively, as \(a\) becomes very large, we can ignore the additive noise and just look at the KL-divergence between uniforms: \[\begin{aligned} \text{KL}\left(\text{Unif}\left[-a, a\right] \mid\mid \omega \text{Unif}\left[-a_k, a_k \right] + (1 - \omega) \text{Unif}\left[-a_{k + 1}, a_{k + 1}\right] \right) &= -\frac{a_k}{a} \log \frac{\frac{\omega}{2a_k} + \frac{1 - \omega}{2a_{k + 1}}}{\frac{1}{2a}} - \frac{a - a_k}{a} \log \frac{\frac{1 - \omega}{2a_{k + 1}}}{\frac{1}{2a}} \\ &= -\frac{a_k}{a} \log \left(\frac{\omega a_{k + 1}}{(1 - \omega)a_k} + 1\right) - \log \frac{a(1 - \omega)}{a_{k + 1}} \end{aligned}\] This is minimized over \(0 \le \omega \le 1\) by setting \[ \omega = \frac{a_k(a_{k + 1} - a)}{a(a_{k + 1} - a_k)} \] so that \[ \begin{aligned} \min_\omega \text{KL}\left(\text{Unif}\left[-a, a\right] \mid\mid \omega \text{Unif}\left[-a_k, a_k \right] + (1 - \omega) \text{Unif}\left[-a_{k + 1}, a_{k + 1}\right] \right) &= \frac{a - a_k}{a} \log \frac{a_{k + 1} - a_k}{a - a_k} \\ &\approx \frac{a - a_k}{a_k} \log \frac{a_{k + 1} - a_k}{a - a_k} \end{aligned} \] The function \(x \log x\) is minimized at \(x = \frac{1}{e}\), so \[ \max_a \min_\omega \text{KL}\left(\text{Unif}\left[-a, a\right] \mid\mid \omega \text{Unif}\left[-a_k, a_k \right] + (1 - \omega) \text{Unif}\left[-a_{k + 1}, a_{k + 1}\right] \right) \approx \frac{a_{k + 1} - a_k}{ea_k} \] Given \(a_k\) and a desired target KL-divergence \(\kappa\), then, we should set \[ a_{k + 1} = (1 + \kappa e)a_k\] That is, the spacing between grid points grows exponentially as \(k \to \infty\), but for most reasonable values of \(\kappa\) it grows so slowly that it will essentially look linear.

To check these calculations, I set \(a_k = 100000\) and \(\kappa = .001\) and I calculate \(a_{k + 1}\) using the above code:

nextpt <- find_next_gridpt(aleft = 100000, targetKL = 1e-3, unif_samp, norm_samp, max_space = 500)
cat(" Next grid point:", nextpt, "\n",
    "Estimated rate of growth as k goes to infinity:", 1 + exp(1)*1e-3)

#>  Next grid point: 100295.9 
#>  Estimated rate of growth as k goes to infinity: 1.002718

Session information

sessionInfo()

#> R version 3.5.3 (2019-03-11)
#> Platform: x86_64-apple-darwin15.6.0 (64-bit)
#> Running under: macOS Mojave 10.14.6
#> 
#> Matrix products: default
#> BLAS: /Library/Frameworks/R.framework/Versions/3.5/Resources/lib/libRblas.0.dylib
#> LAPACK: /Library/Frameworks/R.framework/Versions/3.5/Resources/lib/libRlapack.dylib
#> 
#> locale:
#> [1] en_US.UTF-8/en_US.UTF-8/en_US.UTF-8/C/en_US.UTF-8/en_US.UTF-8
#> 
#> attached base packages:
#> [1] stats     graphics  grDevices utils     datasets  methods   base     
#> 
#> other attached packages:
#> [1] forcats_0.4.0   stringr_1.4.0   dplyr_0.8.0.1   purrr_0.3.2    
#> [5] readr_1.3.1     tidyr_0.8.3     tibble_2.1.1    ggplot2_3.2.0  
#> [9] tidyverse_1.2.1
#> 
#> loaded via a namespace (and not attached):
#>  [1] Rcpp_1.0.4.6     cellranger_1.1.0 pillar_1.3.1     compiler_3.5.3  
#>  [5] git2r_0.25.2     workflowr_1.2.0  tools_3.5.3      digest_0.6.18   
#>  [9] lubridate_1.7.4  jsonlite_1.6     evaluate_0.13    nlme_3.1-137    
#> [13] gtable_0.3.0     lattice_0.20-38  pkgconfig_2.0.2  rlang_0.4.2     
#> [17] cli_1.1.0        rstudioapi_0.10  yaml_2.2.0       haven_2.1.1     
#> [21] xfun_0.6         withr_2.1.2      xml2_1.2.0       httr_1.4.0      
#> [25] knitr_1.22       hms_0.4.2        generics_0.0.2   fs_1.2.7        
#> [29] rprojroot_1.3-2  grid_3.5.3       tidyselect_0.2.5 glue_1.3.1      
#> [33] R6_2.4.0         readxl_1.3.1     rmarkdown_1.12   modelr_0.1.5    
#> [37] magrittr_1.5     whisker_0.3-2    backports_1.1.3  scales_1.0.0    
#> [41] htmltools_0.3.6  rvest_0.3.4      assertthat_0.2.1 colorspace_1.4-1
#> [45] labeling_0.3     stringi_1.4.3    lazyeval_0.2.2   munsell_0.5.0   
#> [49] broom_0.5.1      crayon_1.3.4