Single cell differential expression analysis
Dongyue Xie
2019-12-27
Last updated: 2020-01-16
Checks: 7 0
Knit directory: misc/
This reproducible R Markdown analysis was created with workflowr (version 1.5.0). The Checks tab describes the reproducibility checks that were applied when the results were created. The Past versions tab lists the development history.
Great! Since the R Markdown file has been committed to the Git repository, you know the exact version of the code that produced these results.
Great job! The global environment was empty. Objects defined in the global environment can affect the analysis in your R Markdown file in unknown ways. For reproduciblity it’s best to always run the code in an empty environment.
The command set.seed(20191122) was run prior to running the code in the R Markdown file. Setting a seed ensures that any results that rely on randomness, e.g. subsampling or permutations, are reproducible.
Great job! Recording the operating system, R version, and package versions is critical for reproducibility.
Nice! There were no cached chunks for this analysis, so you can be confident that you successfully produced the results during this run.
Great job! Using relative paths to the files within your workflowr project makes it easier to run your code on other machines.
Great! You are using Git for version control. Tracking code development and connecting the code version to the results is critical for reproducibility. The version displayed above was the version of the Git repository at the time these results were generated.
Note that you need to be careful to ensure that all relevant files for the analysis have been committed to Git prior to generating the results (you can use wflow_publish or wflow_git_commit). workflowr only checks the R Markdown file, but you know if there are other scripts or data files that it depends on. Below is the status of the Git repository when the results were generated:
Ignored files:
Ignored: .Rhistory
Ignored: .Rproj.user/
Untracked files:
Untracked: analysis/pbmcdata.Rmd
Note that any generated files, e.g. HTML, png, CSS, etc., are not included in this status report because it is ok for generated content to have uncommitted changes.
These are the previous versions of the R Markdown and HTML files. If you’ve configured a remote Git repository (see ?wflow_git_remote), click on the hyperlinks in the table below to view them.
| File | Version | Author | Date | Message |
|---|---|---|---|---|
| Rmd | 9f38415 | Dongyue Xie | 2020-01-16 | wflow_publish(“analysis/scde.Rmd”) |
| html | 6332585 | Dongyue Xie | 2020-01-06 | Build site. |
| Rmd | 7808f0c | Dongyue Xie | 2020-01-06 | wflow_publish(“analysis/scde.Rmd”) |
| html | 42c073c | Dongyue Xie | 2020-01-06 | Build site. |
| Rmd | fb35a52 | Dongyue Xie | 2020-01-06 | wflow_publish(“analysis/scde.Rmd”) |
Introduction
Two review papers on single cell differential expression analysis I found: Wang et al, and Sonenson and Robinson.
One review paper on RNA-seq bulk data differential expression analysis: Sonenson and Delorenzi.
Single cell RNA seq datasets: conquer
What are UMI data sets?, Full length vs UMI
The data object contains: TPM, counts, length-scaled TPMs, the average length of the transcripts expressed in each sample for each gene.
Task:
- Whether we need to RUV? Apply some single cell DE method like MAST, D3E, scDD, SCDE, DEsngle etc, maybe also try methods for RNA seq data like edgeR, Deseq2, voomlimma.
– in paper Sonenson and Robinson(2018), the did an experiment on null datasets and found that for unfiltered data sets, many methods struggled to correctly control the type I error.
– DE methods performance depend heavily on whether filtering out low expressed genes / how to filter out low expressed genes.
If need to RUV, how does current methods like SVA and MOUTHWASH work?
If current method does not work, why? How to improve?
For this GSE45719 datasets: mouse, total 291 cells, among which 50 cells are 16-cell stage blastomere and 50 cells are Mid blastocyst cell (92-94h post-fertilization).
To create NULL datasets, we can use only 16-cell stage cells and randomly partition the cells into two groups.
NULL sc-dataset DE
library(ggplot2)
suppressPackageStartupMessages(library(SummarizedExperiment))
suppressPackageStartupMessages(library(MultiAssayExperiment))
datax<- readRDS("~/Downloads/GSE45719.rds")
datax_gene = experiments(datax)[["gene"]]
#head(assays(datax_gene)[["count"]])
cell16_idx = 1:50
cell16_readcounts = (assays(datax_gene)[["count"]])[,1:50]
#filter out genes that are not expressed
cell16_reads = cell16_readcounts[rowSums(cell16_readcounts)!=0,]
cell16=cell16_reads
dim(cell16)[1] 27517 50sum(cell16==0)/prod(dim(cell16))[1] 0.5125835#
# task 1
# randomly partition the data into 2 groups, then simply use a two sample t test
# first partition
set.seed(12345)
group1_idx = sample(1:ncol(cell16),ncol(cell16)/2)
group1 = cell16[,group1_idx]
group2 = cell16[,-group1_idx]
## for each gene, run a two-sample t test
p_values1 = c()
for(i in 1:nrow(cell16)){
p_values1[i] = t.test(log(group1[i,]+1),log(group2[i,]+1),alternative='two.sided')$p.value
}
hist(p_values1,breaks = 15)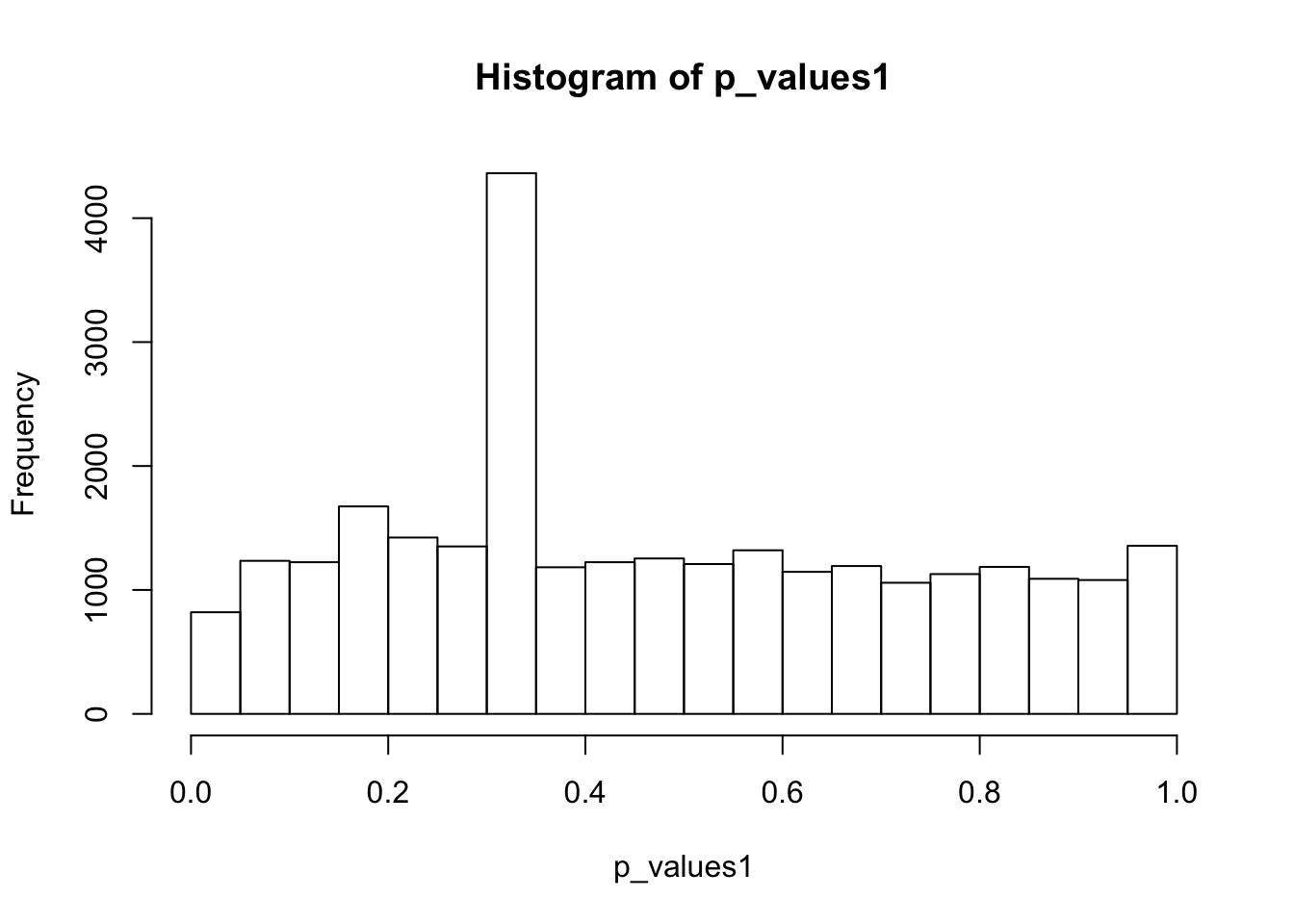
| Version | Author | Date |
|---|---|---|
| 42c073c | Dongyue Xie | 2020-01-06 |
summary(p_values1) Min. 1st Qu. Median Mean 3rd Qu. Max.
0.0003268 0.2681154 0.4197380 0.4742346 0.7012693 1.0000000 A lot of p-values are around 0.3-0.35. Take a look at gene 12:
as.numeric(cell16[12,group1_idx]) [1] 0 0 0 0 0 0 0 1 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0as.numeric(cell16[12,-group1_idx]) [1] 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0t.test(log(cell16[12,group1_idx]+1),log(cell16[12,-group1_idx]+1),alternative = 'two.sided')$p.value[1] 0.3272869Only one cell has non-zero read counts among two groups. To apply two-sample t-test, we should try to avoid this situation. So choose the top 1000 expressed genes:
#Choose the top 1000 expressed genes
top_expressed_genes = (order(rowSums(cell16_reads),decreasing = TRUE))[1:1000]
cell16 = cell16_reads[top_expressed_genes,]
dim(cell16)[1] 1000 50sum(cell16==0)/prod(dim(cell16))[1] 0.00876#
# task 1
# randomly partition the data into 2 groups, then simply use a two sample t test
# first partition
set.seed(12345)
group1_idx = sample(1:ncol(cell16),ncol(cell16)/2)
group1 = cell16[,group1_idx]
group2 = cell16[,-group1_idx]
## for each gene, run a two-sample t test
p_values1 = c()
for(i in 1:nrow(cell16)){
p_values1[i] = t.test(log(group1[i,]+1),log(group2[i,]+1),alternative='two.sided')$p.value
}
ks.test(p_values1,'punif',0,1)
One-sample Kolmogorov-Smirnov test
data: p_values1
D = 0.13088, p-value = 2.665e-15
alternative hypothesis: two-sidedhist(p_values1,breaks = 15)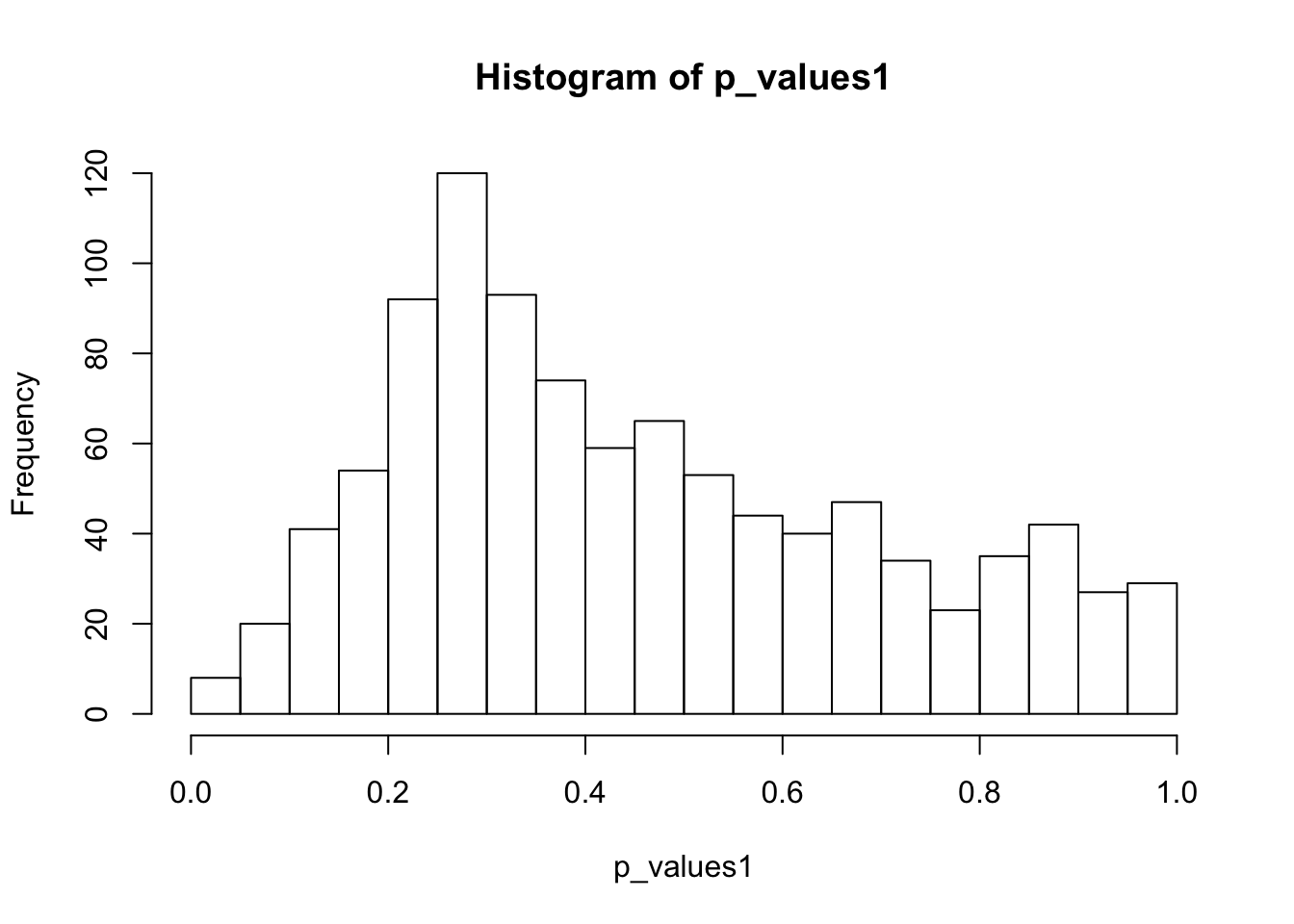
| Version | Author | Date |
|---|---|---|
| 42c073c | Dongyue Xie | 2020-01-06 |
# second partition
group1_idx = sample(1:ncol(cell16),ncol(cell16)/2)
group1 = cell16[,group1_idx]
group2 = cell16[,-group1_idx]
## for each gene, run a two-sample t test
p_values1 = c()
for(i in 1:nrow(cell16)){
p_values1[i] = t.test(log(group1[i,]+1),log(group2[i,]+1),alternative='two.sided')$p.value
}
ks.test(p_values1,'punif',0,1)
One-sample Kolmogorov-Smirnov test
data: p_values1
D = 0.10674, p-value = 2.535e-10
alternative hypothesis: two-sidedhist(p_values1,breaks = 15)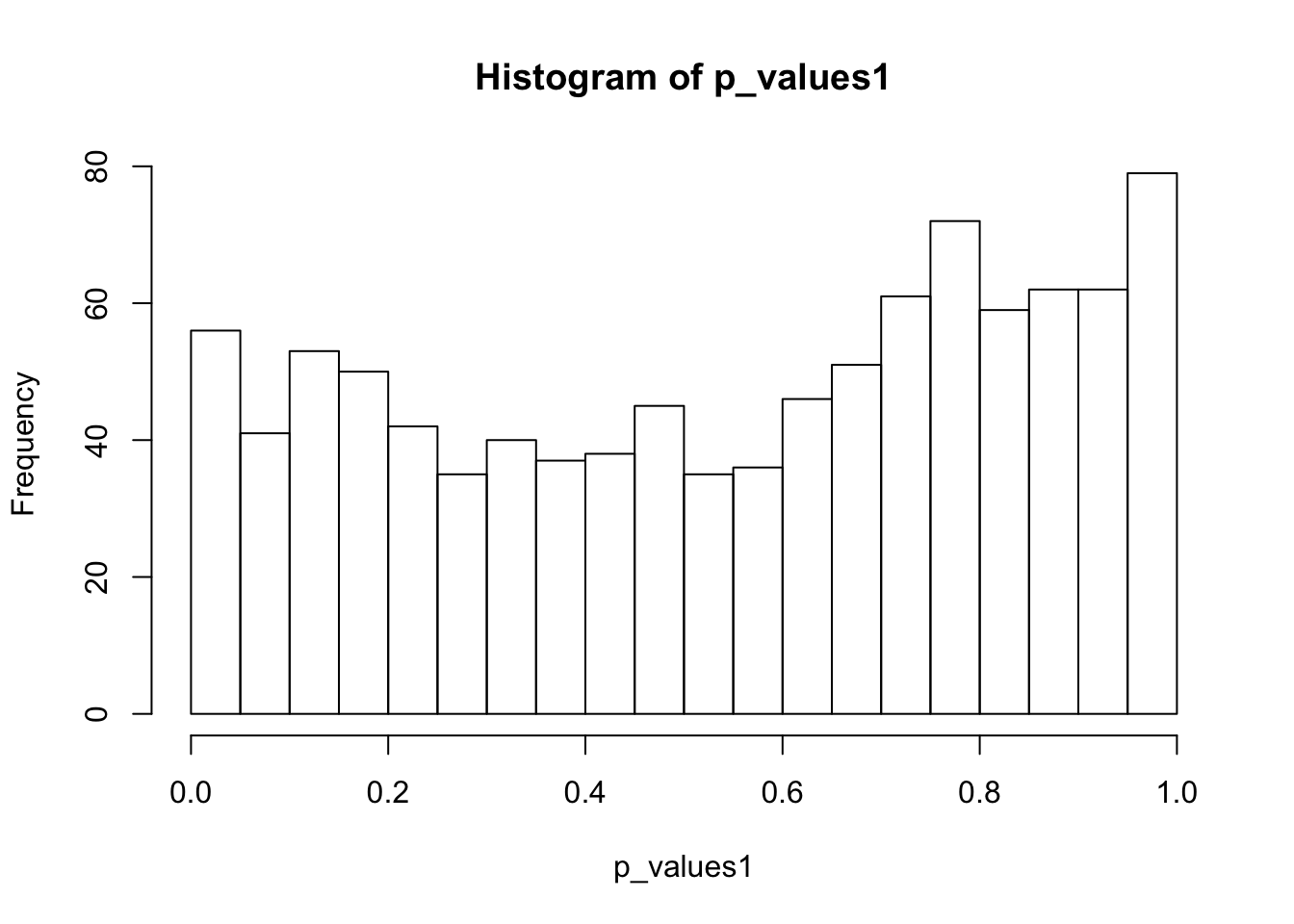
| Version | Author | Date |
|---|---|---|
| 42c073c | Dongyue Xie | 2020-01-06 |
# third partition
group1_idx = sample(1:ncol(cell16),ncol(cell16)/2)
group1 = cell16[,group1_idx]
group2 = cell16[,-group1_idx]
## for each gene, run a two-sample t test
p_values1 = c()
for(i in 1:nrow(cell16)){
p_values1[i] = t.test(log(group1[i,]+1),log(group2[i,]+1),alternative='two.sided')$p.value
}
ks.test(p_values1,'punif',0,1)
One-sample Kolmogorov-Smirnov test
data: p_values1
D = 0.093565, p-value = 4.977e-08
alternative hypothesis: two-sidedhist(p_values1,breaks = 15)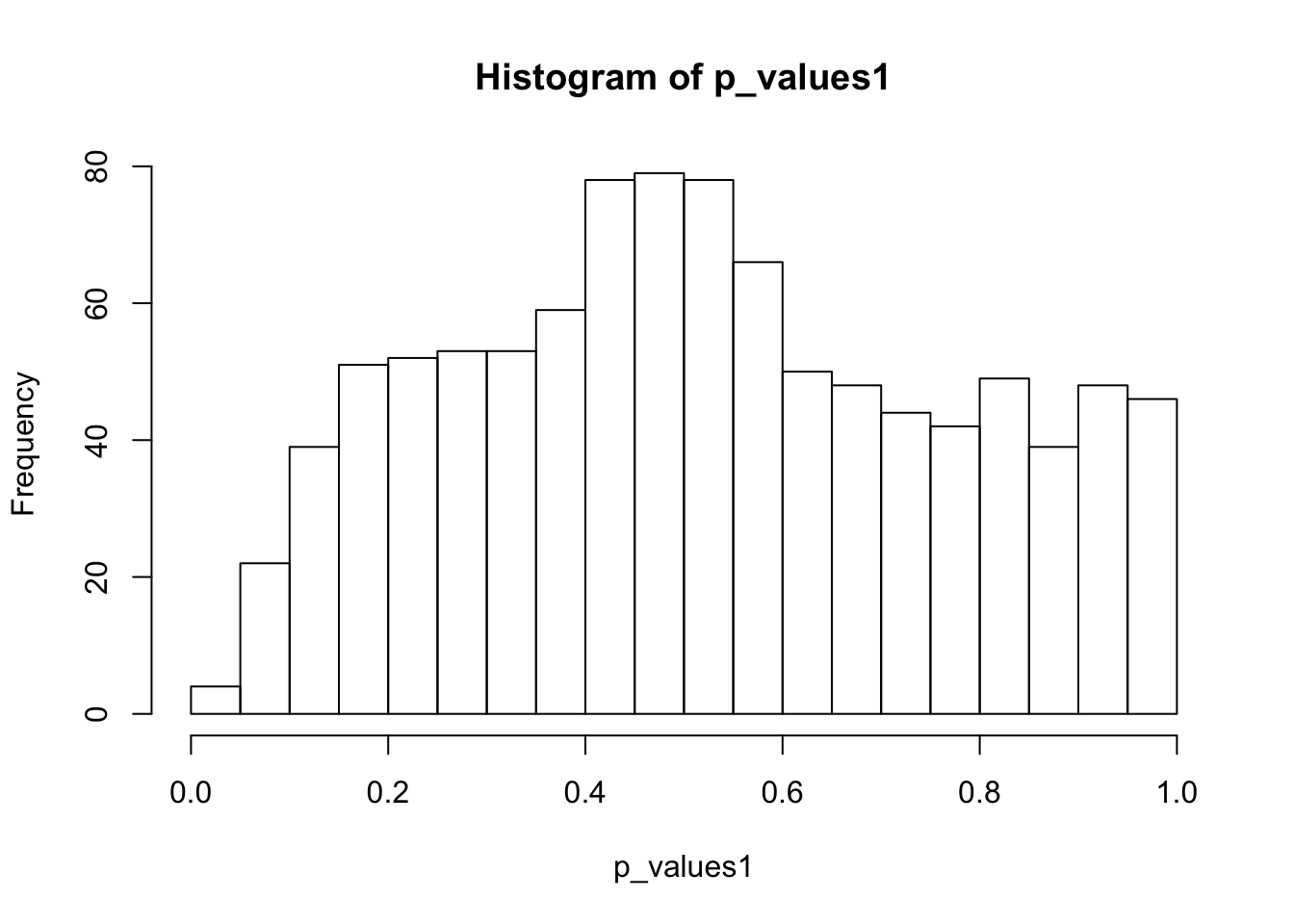
| Version | Author | Date |
|---|---|---|
| 42c073c | Dongyue Xie | 2020-01-06 |
Try ROTS
set.seed(12345)
group1_idx = sample(1:ncol(cell16),ncol(cell16)/2)
group1 = cell16[,group1_idx]
group2 = cell16[,-group1_idx]
group_indicator = rep(0,ncol(cell16))
group_indicator[group1_idx] = 1
library(edgeR)
tmm = calcNormFactors(cell16,method='TMM')
cell16norm = cpm(cell16,tmm)
library(ROTS)
ROTS_results = ROTS(data = cell16norm, groups = group_indicator , B = 100 , K = 500 , seed = 1234)
summary(ROTS_results, fdr = 0.05)ROTS results:
Number of resamplings: 100
a1: 0
a2: 1
Top list size: 90
Reproducibility value: 0.2438889
Z-score: 1.346383
1 rows satisfy the condition.
Row ROTS-statistic pvalue FDR
ENSMUSG00000108980.1 430 3.193407 0.001605 0hist(ROTS_results$pvalue,breaks = 15)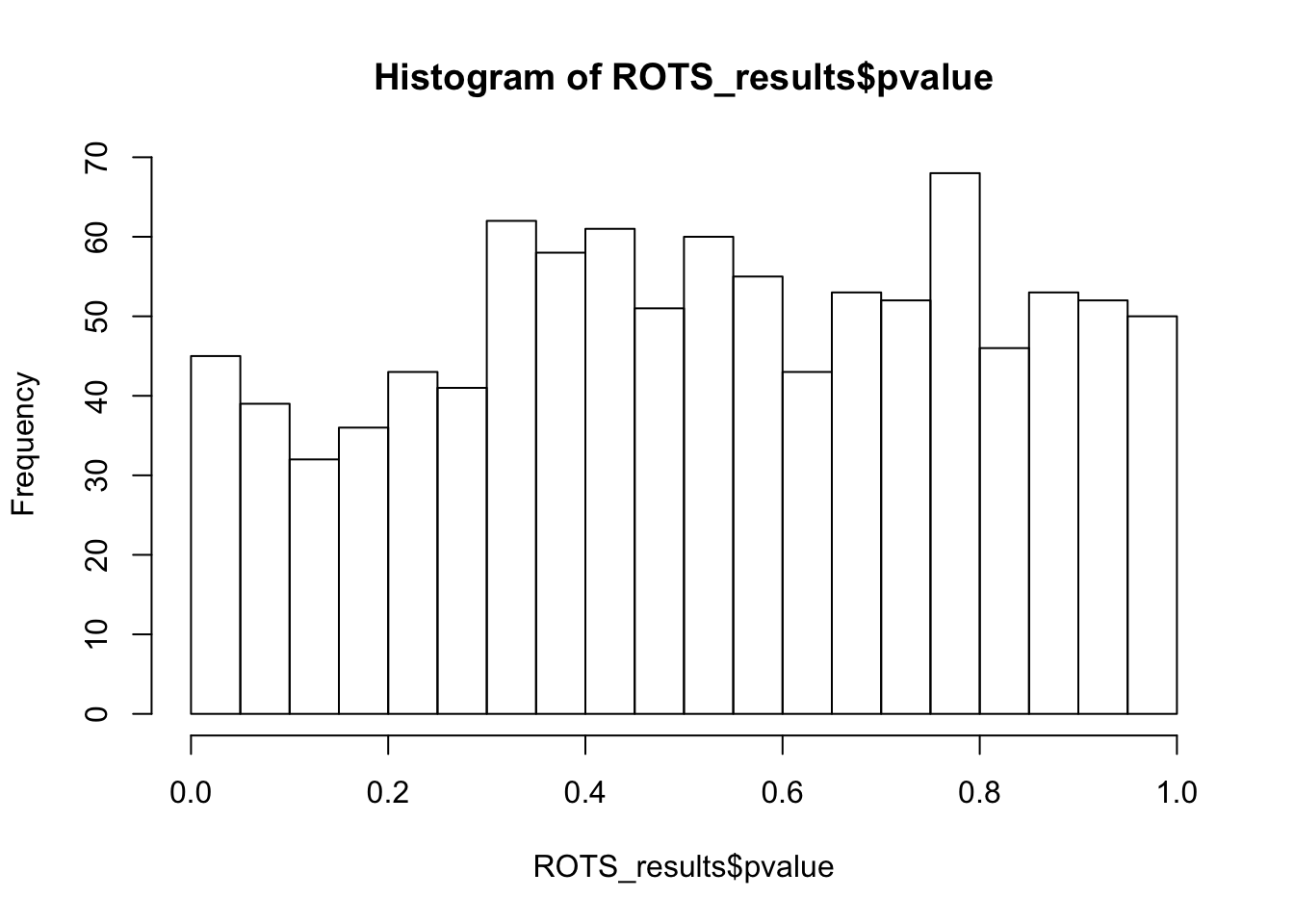
ks.test(ROTS_results$pvalue,'punif',0,1)
One-sample Kolmogorov-Smirnov test
data: ROTS_results$pvalue
D = 0.064455, p-value = 0.0004926
alternative hypothesis: two-sidedSummary - NULL
If not accounting for 0’s in scData, then the null distribution of p-values is certainly not uniform. Mainly because two-sample t test is not applicable.
If removing genes with two many 0’s, then the p-value distributions deviate from uniform.
RUV methods for RNA-seq
First apply on NULL data then add signals to genes using Poisson thinning.
library(vicar)
set.seed(12345)
group1_idx = sample(1:ncol(cell16),ncol(cell16)/2)
group1 = cell16[,group1_idx]
group2 = cell16[,-group1_idx]
group_indicator = rep(0,ncol(cell16))
group_indicator[group1_idx] = 1
X = model.matrix(~group_indicator)
Y = t(cell16)
num_sv <- sva::num.sv(dat = t(Y), mod = X, method = "be")
num_sv_l <- sva::num.sv(dat = t(Y), mod = X, method = "leek")
num_sv[1] 4num_sv_l[1] 48Two approaches give very different number of surrogate variables! Try to use 4 SVs in the following analysis.
mout = mouthwash(Y,X,k=num_sv,cov_of_interest = 2,include_intercept = FALSE)Running mouthwash on 50 x 2 matrix X and 50 x 1000 matrix Y.
- Computing independent basis using QR decomposition.
- Computation took 0.016 seconds.
- Running additional preprocessing steps.
- Computation took 0 seconds.
- Running second step of mouthwash:
+ Estimating model parameters using EM.
+ Computation took 2.484 seconds.
+ Generating adaptive shrinkage (ash) output.
+ Computation took 0.245 seconds.
- Second step took 3.519 seconds.
- Estimating additional hidden confounders.
- Computation took 0.014 seconds.mout$pi0[1] 0.9922996library(cate)
#library(leapp)
cate_cate <- cate::cate.fit(X.primary = X[, 2, drop = FALSE], X.nuis = X[, -2, drop = FALSE],
Y = Y, r = num_sv, adj.method = "rr")
# this method is vey slow!
#leapp_leapp <- leapp::leapp(data = t(Y), pred.prim = X[, 2, drop = FALSE],
# pred.covar = X[, -2, drop = FALSE], num.fac = num_sv)
sva_sva <- sva::sva(dat = t(Y), mod = X, mod0 = X[, -2, drop = FALSE], n.sv = num_sv)Number of significant surrogate variables is: 4
Iteration (out of 5 ):1 2 3 4 5 X.sva <- cbind(X, sva_sva$sv)
lmout <- limma::lmFit(object = t(Y), design = X.sva)
eout <- limma::eBayes(lmout)
svaout <- list()
svaout$betahat <- lmout$coefficients[, 2]
svaout$sebetahat <- lmout$stdev.unscaled[, 2] * sqrt(eout$s2.post)
svaout$pvalues <- eout$p.value[, 2]
hist(svaout$pvalues,breaks=15)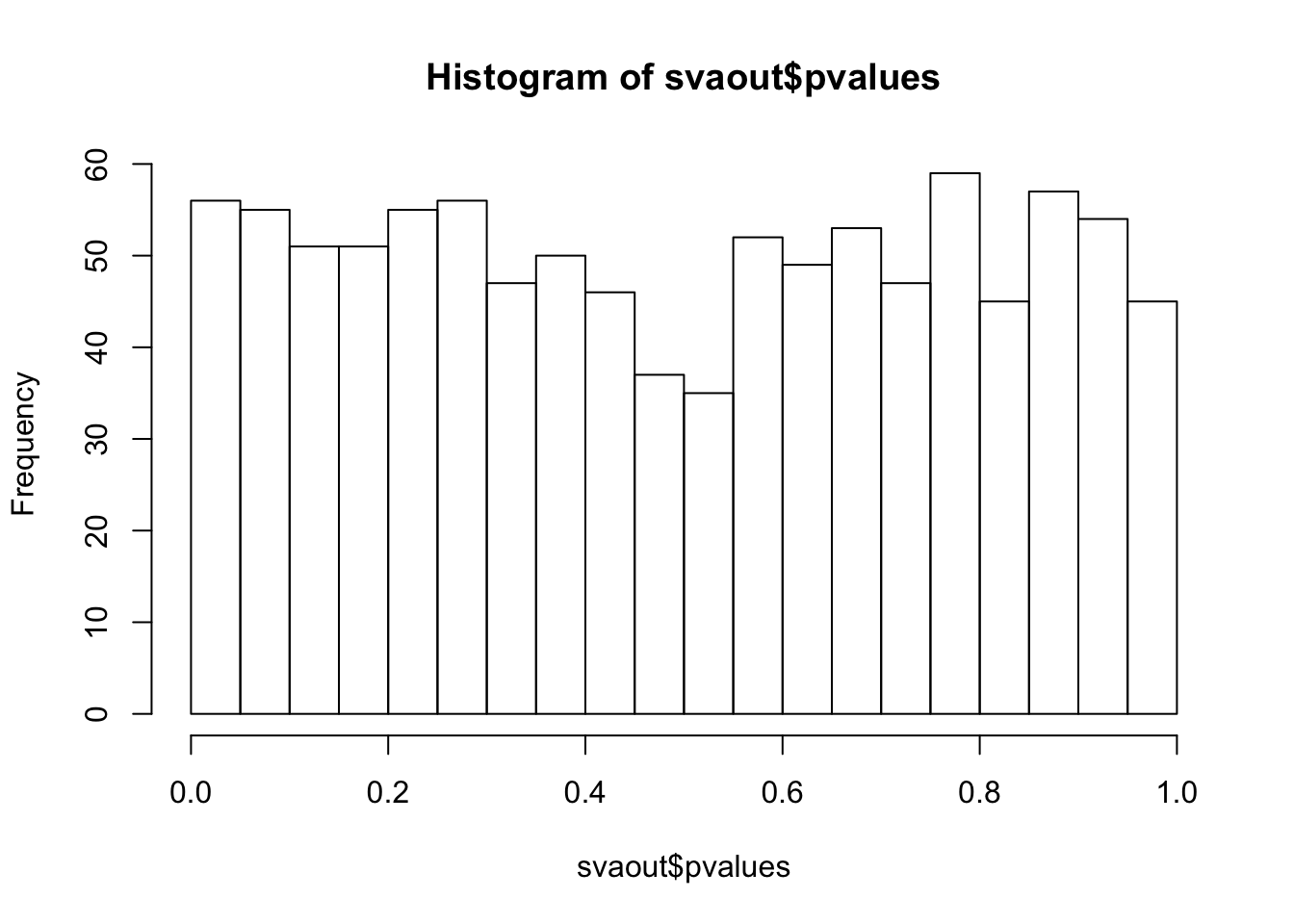
| Version | Author | Date |
|---|---|---|
| 42c073c | Dongyue Xie | 2020-01-06 |
ks.test(svaout$pvalues,'punif',0,1)
One-sample Kolmogorov-Smirnov test
data: svaout$pvalues
D = 0.032173, p-value = 0.2518
alternative hypothesis: two-sidedhist(cate_cate$beta.p.value,breaks = 15)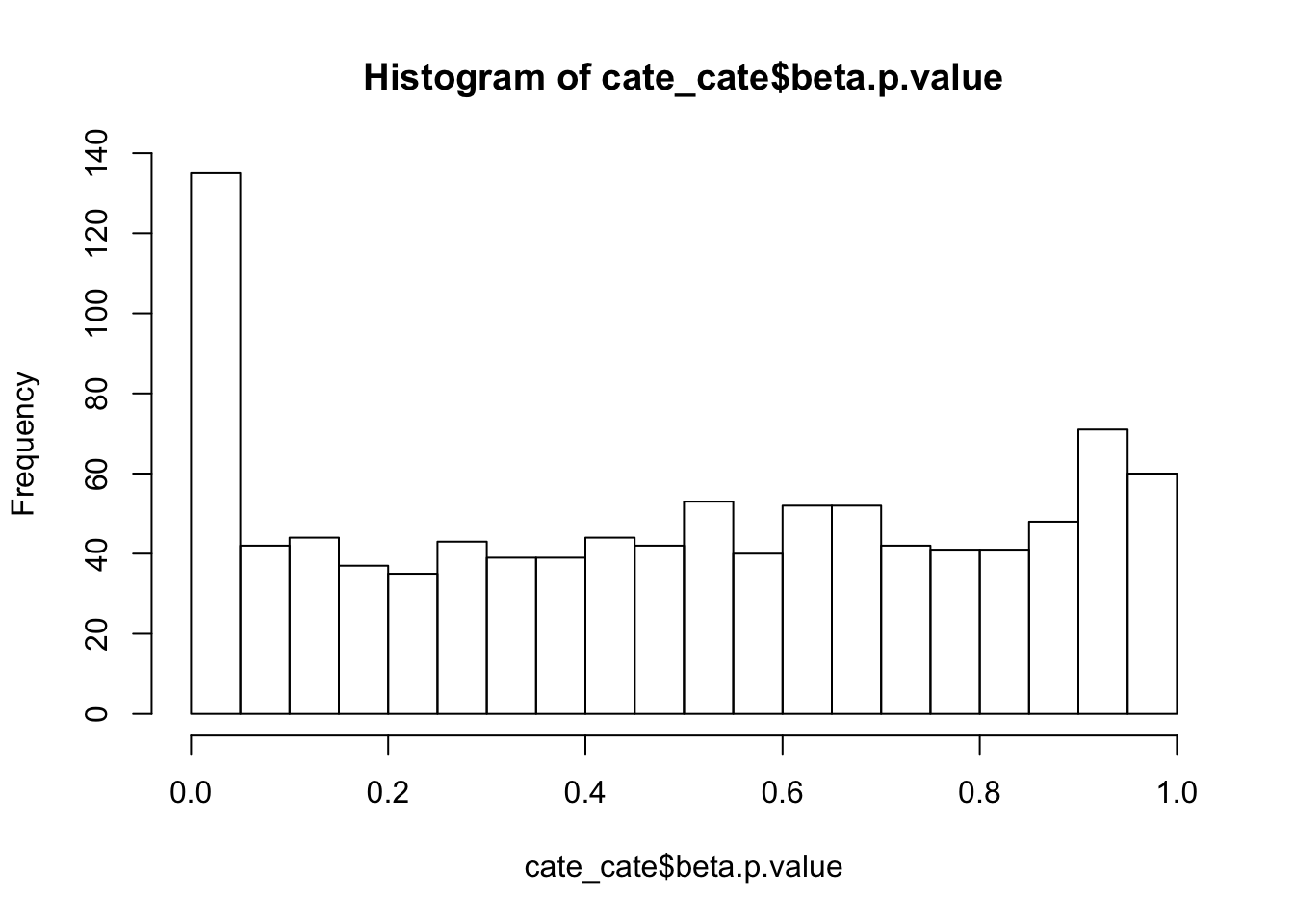
| Version | Author | Date |
|---|---|---|
| 42c073c | Dongyue Xie | 2020-01-06 |
ks.test(cate_cate$beta.p.value,'punif',0,1)
One-sample Kolmogorov-Smirnov test
data: cate_cate$beta.p.value
D = 0.085223, p-value = 9.83e-07
alternative hypothesis: two-sidedAdd some signal to the NULL dataset.
library(seqgendiff)
#tt = thin_diff(round(cell16), design_fixed = X[,2,drop=FALSE])
set.seed(12345)
thinout = thin_2group(round(cell16),0.9,signal_fun = stats::rexp,signal_params = list(rate=0.5))
#check null groups
group1 = cell16[,which(thinout$designmat==1)]
group2 = cell16[,which(thinout$designmat==0)]
## for each gene, run a two-sample t test
p_values1 = c()
for(i in 1:nrow(cell16)){
p_values1[i] = t.test(group1[i,],group2[i,],alternative='two.sided')$p.value
}
ks.test(p_values1,'punif',0,1)
One-sample Kolmogorov-Smirnov test
data: p_values1
D = 0.1421, p-value < 2.2e-16
alternative hypothesis: two-sidedhist(p_values1,breaks = 15)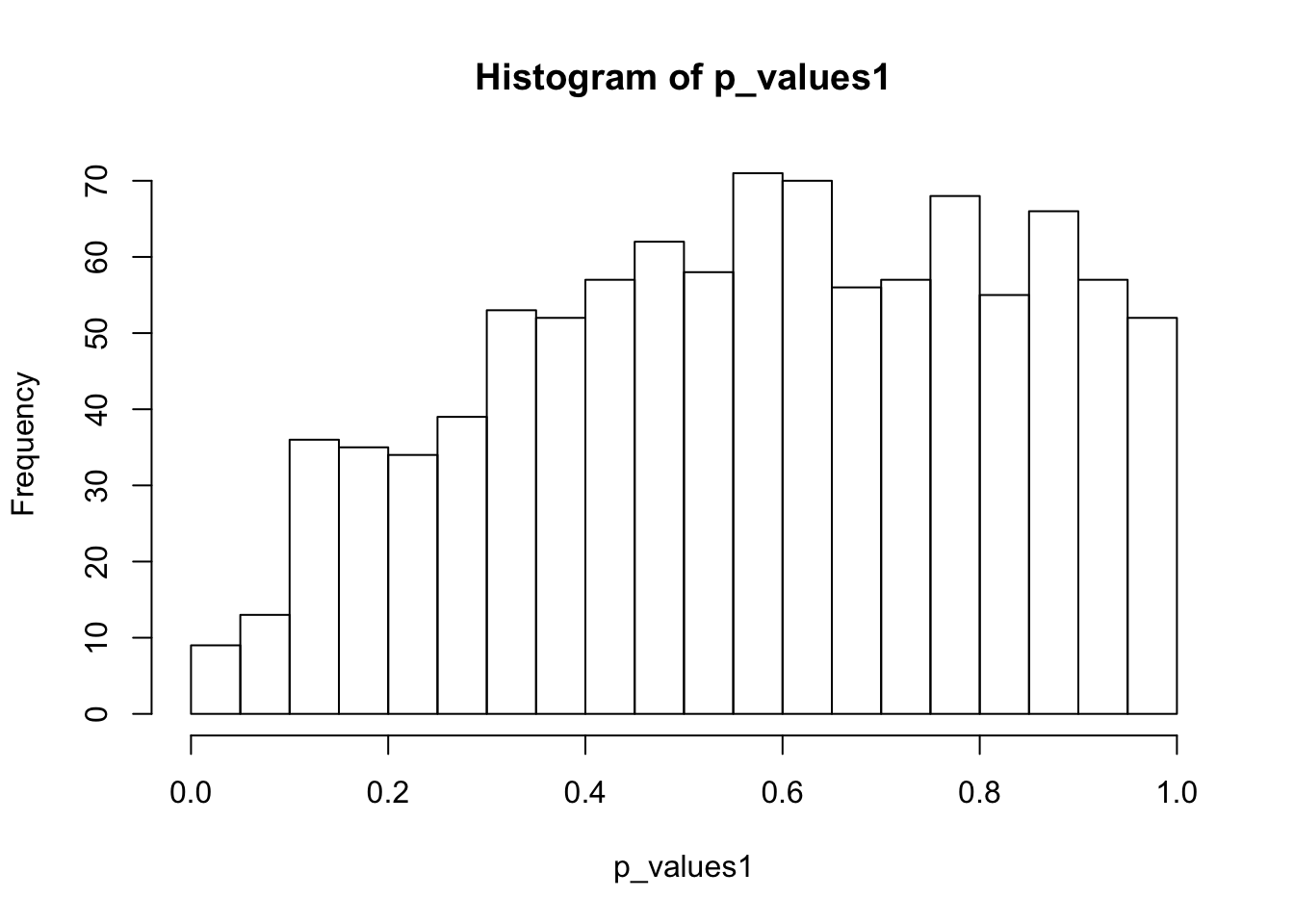
Y = t(thinout$mat)
X = model.matrix(~thinout$designmat)
num_sv <- sva::num.sv(dat = t(Y), mod = X, method = "be")
num_sv_l <- sva::num.sv(dat = t(Y), mod = X, method = "leek")
num_sv[1] 4num_sv_l[1] 48mean(abs(thinout$coef) < 10^-6)[1] 0.9mout = mouthwash(Y,X,k=num_sv,cov_of_interest = 2,include_intercept = FALSE)Running mouthwash on 50 x 2 matrix X and 50 x 1000 matrix Y.
- Computing independent basis using QR decomposition.
- Computation took 0.011 seconds.
- Running additional preprocessing steps.
- Computation took 0.001 seconds.
- Running second step of mouthwash:
+ Estimating model parameters using EM.
+ Computation took 2.466 seconds.
+ Generating adaptive shrinkage (ash) output.
+ Computation took 0.111 seconds.
- Second step took 3.337 seconds.
- Estimating additional hidden confounders.
- Computation took 0.019 seconds.mout$pi0[1] 0.806857bout <- backwash(Y = Y, X = X, k = num_sv, cov_of_interest = 2, include_intercept = FALSE) - Computing independent basis using QR decomposition.
- Computation took 0.016 seconds.
- Running additional preprocessing steps.
- Computation took 0 seconds.
- Running second step of backwash:
+ Initializing parameters for EM algorithm.
+ Computation took 0.196 seconds.
+ Running one round of parameter updates.
+ Computation took 0.028 seconds.
+ Estimating model parameters using EM.
+ Computation took 9.428 seconds.
+ Generating posterior statistics.
+ Computation took 0.003 seconds.
- Second step took 11.253 seconds.
- Generating final backwash outputs.
- Computation took 0.013 seconds.bout$pi0[1] 0.8127092cate_cate = cate::cate.fit(X.primary = X[, 2, drop = FALSE], X.nuis = X[, -2, drop = FALSE],
Y = Y, r = num_sv, adj.method = "rr")
sva_sva <- sva::sva(dat = t(Y), mod = X, mod0 = X[, -2, drop = FALSE], n.sv = num_sv)Number of significant surrogate variables is: 4
Iteration (out of 5 ):1 2 3 4 5 X.sva <- cbind(X, sva_sva$sv)
lmout <- limma::lmFit(object = t(Y), design = X.sva)
eout <- limma::eBayes(lmout)
svaout <- list()
svaout$betahat <- lmout$coefficients[, 2]
svaout$sebetahat <- lmout$stdev.unscaled[, 2] * sqrt(eout$s2.post)
svaout$pvalues <- eout$p.value[, 2]
which_null = c(1*(abs(thinout$coef) < 10^-6))
# plot ROC curve
roc_out <- list(
pROC::roc(response = which_null, predictor = c(mout$result$lfdr)),
pROC::roc(response = which_null, predictor = c(bout$result$lfdr)),
pROC::roc(response = which_null, predictor = c(cate_cate$beta.p.value)),
pROC::roc(response = which_null, predictor = c(svaout$pvalues)))
name_vec <- c("MOUTHWASH", 'BACKWASH',"CATErr", "SVA")
names(roc_out) <- name_vec
sout <- lapply(roc_out, function(x) { data.frame(TPR = x$sensitivities, FPR = 1 - x$specificities)})
for (index in 1:length(sout)) {
sout[[index]]$Method <- name_vec[index]
}
longdat <- do.call(rbind, sout)
shortdat <- dplyr::filter(longdat, Method == "MOUTHWASH" | Method == "BACKWASH" |
Method == "CATErr" | Method == "SVA" | Method == "LEAPP")
ggplot(data = shortdat, mapping = aes(x = FPR, y = TPR, col = Method)) +
geom_path() + theme_bw() + ggtitle("ROC Curves")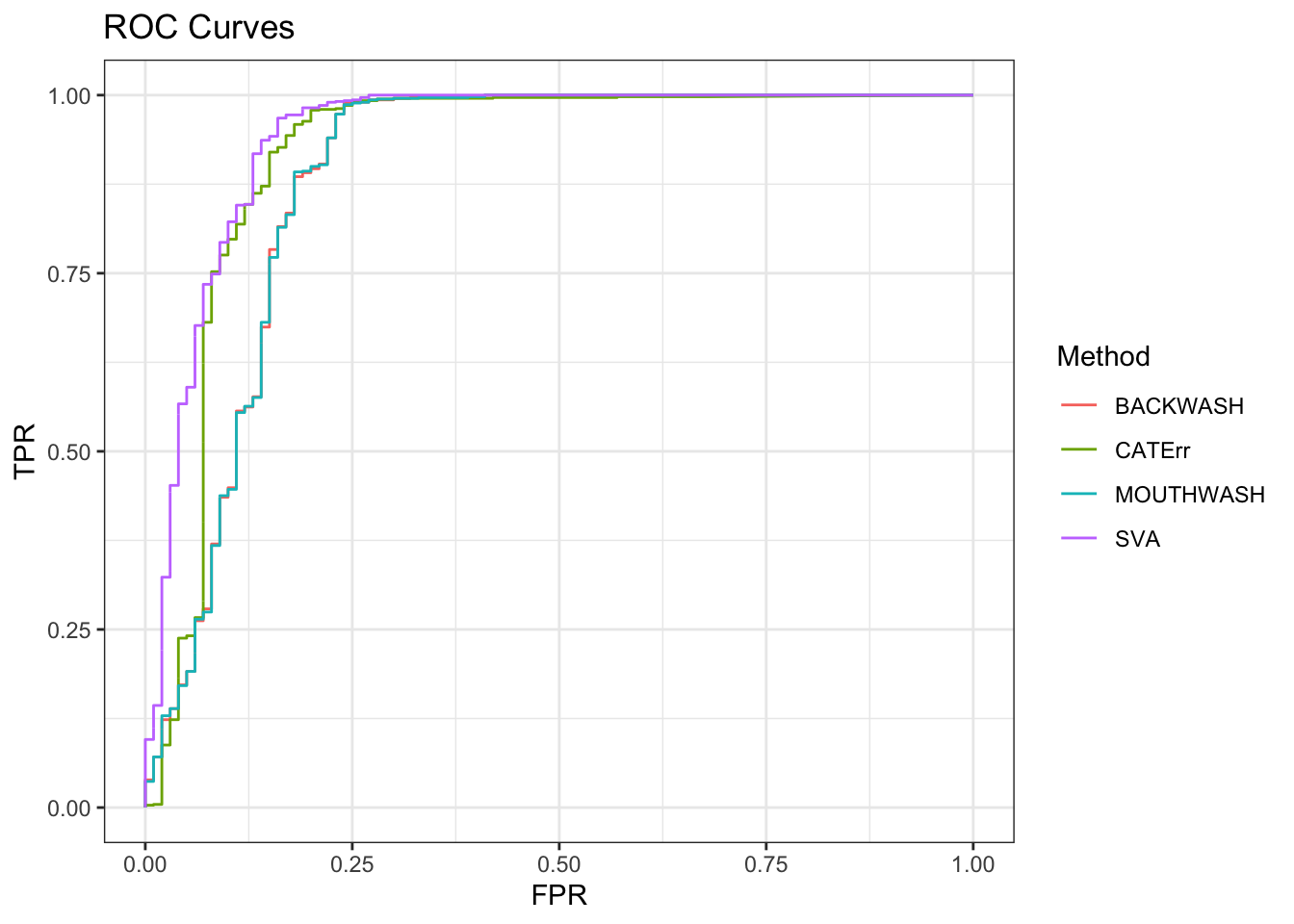
auc_vec <- sapply(roc_out, FUN = function(x) { x$auc })
knitr::kable(sort(auc_vec, decreasing = TRUE), col.names = "AUC", digits = 3)| AUC | |
|---|---|
| SVA | 0.943 |
| CATErr | 0.918 |
| BACKWASH | 0.887 |
| MOUTHWASH | 0.887 |
# estimate pi0
method_list <- list()
method_list$CATErr <- list()
method_list$CATErr$betahat <- c(cate_cate$beta)
method_list$CATErr$sebetahat <- c(sqrt(cate_cate$beta.cov.row * c(cate_cate$beta.cov.col)) / sqrt(nrow(X)))
method_list$SVA <- list()
method_list$SVA$betahat <- c(svaout$betahat)
method_list$SVA$sebetahat <- c(svaout$sebetahat)
ashfit <- lapply(method_list, FUN = function(x) { ashr::ash(x$betahat, x$sebetahat)})
api0 <- sapply(ashfit, FUN = ashr::get_pi0)
api0 <- c(api0, MOUTHWASH = mout$pi0)
api0 <- c(api0, BACKWASH = bout$pi0)
knitr::kable(sort(api0, decreasing = TRUE), col.names = "Estimate of Pi0")| E | stimate of Pi0 |
|---|---|
| BACKWASH | 0.8127092 |
| SVA | 0.8126893 |
| MOUTHWASH | 0.8068570 |
| CATErr | 0.4149302 |
Weaker signal: rexp(,rate=1)
set.seed(12345)
thinout = thin_2group(round(cell16),0.9,signal_fun = stats::rexp,signal_params = list(rate=1))
Y = t(thinout$mat)
X = model.matrix(~thinout$designmat)
mout = mouthwash(Y,X,k=num_sv,cov_of_interest = 2,include_intercept = FALSE)Running mouthwash on 50 x 2 matrix X and 50 x 1000 matrix Y.
- Computing independent basis using QR decomposition.
- Computation took 0.011 seconds.
- Running additional preprocessing steps.
- Computation took 0 seconds.
- Running second step of mouthwash:
+ Estimating model parameters using EM.
+ Computation took 5.716 seconds.
+ Generating adaptive shrinkage (ash) output.
+ Computation took 0.114 seconds.
- Second step took 6.782 seconds.
- Estimating additional hidden confounders.
- Computation took 0.019 seconds.mout$pi0[1] 0.8178142bout <- backwash(Y = Y, X = X, k = num_sv, cov_of_interest = 2, include_intercept = FALSE) - Computing independent basis using QR decomposition.
- Computation took 0.016 seconds.
- Running additional preprocessing steps.
- Computation took 0 seconds.
- Running second step of backwash:
+ Initializing parameters for EM algorithm.
+ Computation took 0.211 seconds.
+ Running one round of parameter updates.
+ Computation took 0.028 seconds.
+ Estimating model parameters using EM.
+ Computation took 8.434 seconds.
+ Generating posterior statistics.
+ Computation took 0.003 seconds.
- Second step took 10.756 seconds.
- Generating final backwash outputs.
- Computation took 0.013 seconds.bout$pi0[1] 0.8210579cate_cate = cate::cate.fit(X.primary = X[, 2, drop = FALSE], X.nuis = X[, -2, drop = FALSE],
Y = Y, r = num_sv, adj.method = "rr")
sva_sva <- sva::sva(dat = t(Y), mod = X, mod0 = X[, -2, drop = FALSE], n.sv = num_sv)Number of significant surrogate variables is: 4
Iteration (out of 5 ):1 2 3 4 5 X.sva <- cbind(X, sva_sva$sv)
lmout <- limma::lmFit(object = t(Y), design = X.sva)
eout <- limma::eBayes(lmout)
svaout <- list()
svaout$betahat <- lmout$coefficients[, 2]
svaout$sebetahat <- lmout$stdev.unscaled[, 2] * sqrt(eout$s2.post)
svaout$pvalues <- eout$p.value[, 2]
which_null = c(1*(abs(thinout$coef) < 10^-6))
roc_out <- list(
pROC::roc(response = which_null, predictor = c(mout$result$lfdr)),
pROC::roc(response = which_null, predictor = c(bout$result$lfdr)),
pROC::roc(response = which_null, predictor = c(cate_cate$beta.p.value)),
pROC::roc(response = which_null, predictor = c(svaout$pvalues)))
name_vec <- c("MOUTHWASH", 'BACKWASH',"CATErr", "SVA")
names(roc_out) <- name_vec
sout <- lapply(roc_out, function(x) { data.frame(TPR = x$sensitivities, FPR = 1 - x$specificities)})
for (index in 1:length(sout)) {
sout[[index]]$Method <- name_vec[index]
}
longdat <- do.call(rbind, sout)
shortdat <- dplyr::filter(longdat, Method == "MOUTHWASH" | Method == "BACKWASH" |
Method == "CATErr" | Method == "SVA" | Method == "LEAPP")
ggplot(data = shortdat, mapping = aes(x = FPR, y = TPR, col = Method)) +
geom_path() + theme_bw() + ggtitle("ROC Curves")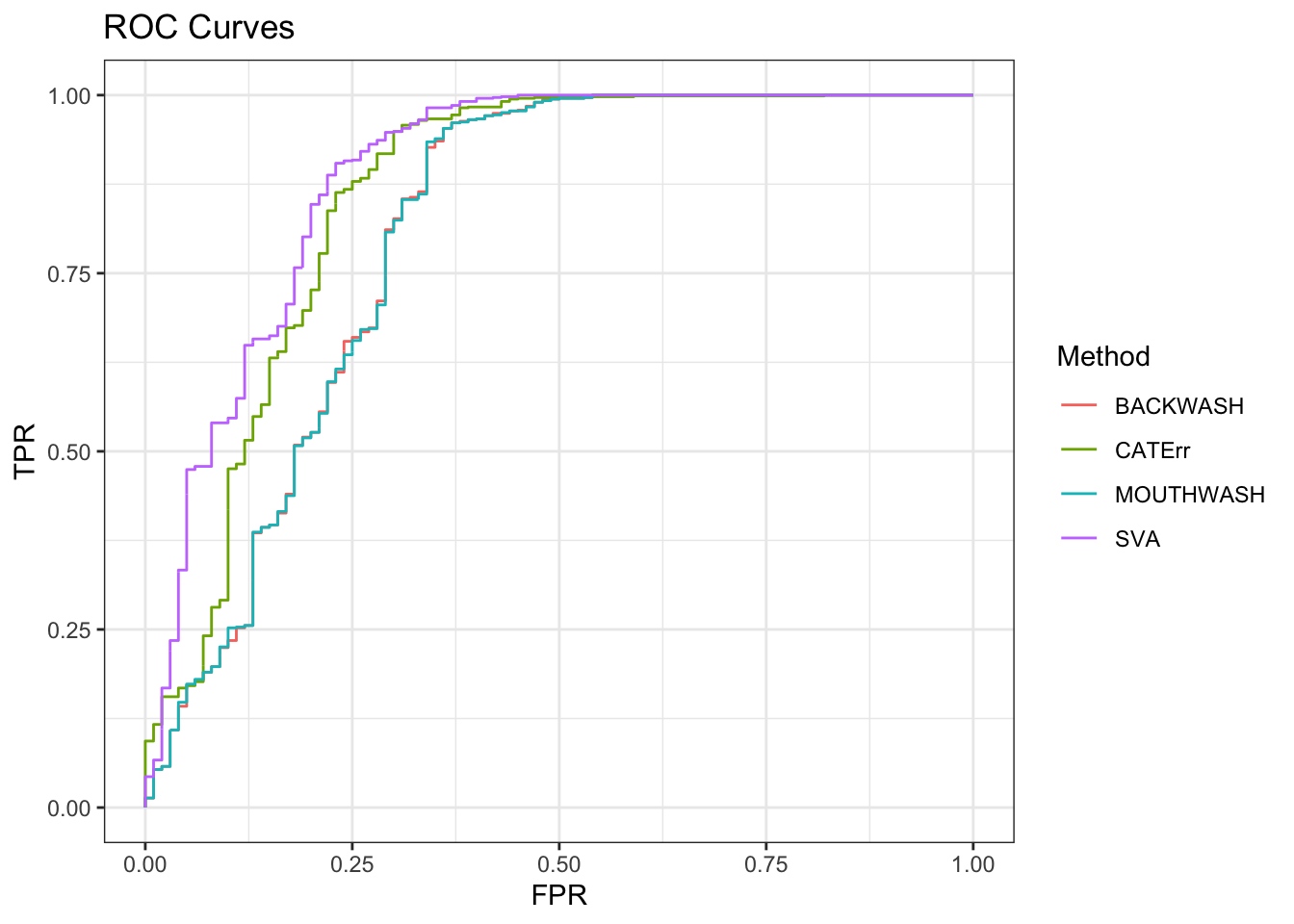
auc_vec <- sapply(roc_out, FUN = function(x) { x$auc })
knitr::kable(sort(auc_vec, decreasing = TRUE), col.names = "AUC", digits = 3)| AUC | |
|---|---|
| SVA | 0.888 |
| CATErr | 0.859 |
| BACKWASH | 0.805 |
| MOUTHWASH | 0.805 |
method_list <- list()
method_list$CATErr <- list()
method_list$CATErr$betahat <- c(cate_cate$beta)
method_list$CATErr$sebetahat <- c(sqrt(cate_cate$beta.cov.row * c(cate_cate$beta.cov.col)) / sqrt(nrow(X)))
method_list$SVA <- list()
method_list$SVA$betahat <- c(svaout$betahat)
method_list$SVA$sebetahat <- c(svaout$sebetahat)
ashfit <- lapply(method_list, FUN = function(x) { ashr::ash(x$betahat, x$sebetahat)})
api0 <- sapply(ashfit, FUN = ashr::get_pi0)
api0 <- c(api0, MOUTHWASH = mout$pi0)
api0 <- c(api0, BACKWASH = bout$pi0)
knitr::kable(sort(api0, decreasing = TRUE), col.names = "Estimate of Pi0")| E | stimate of Pi0 |
|---|---|
| SVA | 0.8212793 |
| BACKWASH | 0.8210579 |
| MOUTHWASH | 0.8178142 |
| CATErr | 0.4781507 |
Stronger signal: rexp(,rate = 0.2)
set.seed(12345)
thinout = thin_2group(round(cell16),0.9,signal_fun = stats::rexp,signal_params = list(rate=0.2))
Y = t(thinout$mat)
X = model.matrix(~thinout$designmat)
mean(abs(thinout$coef) < 10^-6)[1] 0.9mout = mouthwash(Y,X,k=num_sv,cov_of_interest = 2,include_intercept = FALSE)Running mouthwash on 50 x 2 matrix X and 50 x 1000 matrix Y.
- Computing independent basis using QR decomposition.
- Computation took 0.011 seconds.
- Running additional preprocessing steps.
- Computation took 0.001 seconds.
- Running second step of mouthwash:
+ Estimating model parameters using EM.
+ Computation took 2.282 seconds.
+ Generating adaptive shrinkage (ash) output.
+ Computation took 0.113 seconds.
- Second step took 3.246 seconds.
- Estimating additional hidden confounders.
- Computation took 0.02 seconds.mout$pi0[1] 0.7604766bout <- backwash(Y = Y, X = X, k = num_sv, cov_of_interest = 2, include_intercept = FALSE) - Computing independent basis using QR decomposition.
- Computation took 0.016 seconds.
- Running additional preprocessing steps.
- Computation took 0.001 seconds.
- Running second step of backwash:
+ Initializing parameters for EM algorithm.
+ Computation took 0.172 seconds.
+ Running one round of parameter updates.
+ Computation took 0.026 seconds.
+ Estimating model parameters using EM.
+ Computation took 19.815 seconds.
+ Generating posterior statistics.
+ Computation took 0.003 seconds.
- Second step took 21.587 seconds.
- Generating final backwash outputs.
- Computation took 0.013 seconds.bout$pi0[1] 0.8159548cate_cate = cate::cate.fit(X.primary = X[, 2, drop = FALSE], X.nuis = X[, -2, drop = FALSE],
Y = Y, r = num_sv, adj.method = "rr")
sva_sva <- sva::sva(dat = t(Y), mod = X, mod0 = X[, -2, drop = FALSE], n.sv = num_sv)Number of significant surrogate variables is: 4
Iteration (out of 5 ):1 2 3 4 5 X.sva <- cbind(X, sva_sva$sv)
lmout <- limma::lmFit(object = t(Y), design = X.sva)
eout <- limma::eBayes(lmout)
svaout <- list()
svaout$betahat <- lmout$coefficients[, 2]
svaout$sebetahat <- lmout$stdev.unscaled[, 2] * sqrt(eout$s2.post)
svaout$pvalues <- eout$p.value[, 2]
which_null = c(1*(abs(thinout$coef) < 10^-6))
roc_out <- list(
pROC::roc(response = which_null, predictor = c(mout$result$lfdr)),
pROC::roc(response = which_null, predictor = c(bout$result$lfdr)),
pROC::roc(response = which_null, predictor = c(cate_cate$beta.p.value)),
pROC::roc(response = which_null, predictor = c(svaout$pvalues)))
name_vec <- c("MOUTHWASH", 'BACKWASH',"CATErr", "SVA")
names(roc_out) <- name_vec
sout <- lapply(roc_out, function(x) { data.frame(TPR = x$sensitivities, FPR = 1 - x$specificities)})
for (index in 1:length(sout)) {
sout[[index]]$Method <- name_vec[index]
}
longdat <- do.call(rbind, sout)
shortdat <- dplyr::filter(longdat, Method == "MOUTHWASH" | Method == "BACKWASH" |
Method == "CATErr" | Method == "SVA" | Method == "LEAPP")
ggplot(data = shortdat, mapping = aes(x = FPR, y = TPR, col = Method)) +
geom_path() + theme_bw() + ggtitle("ROC Curves")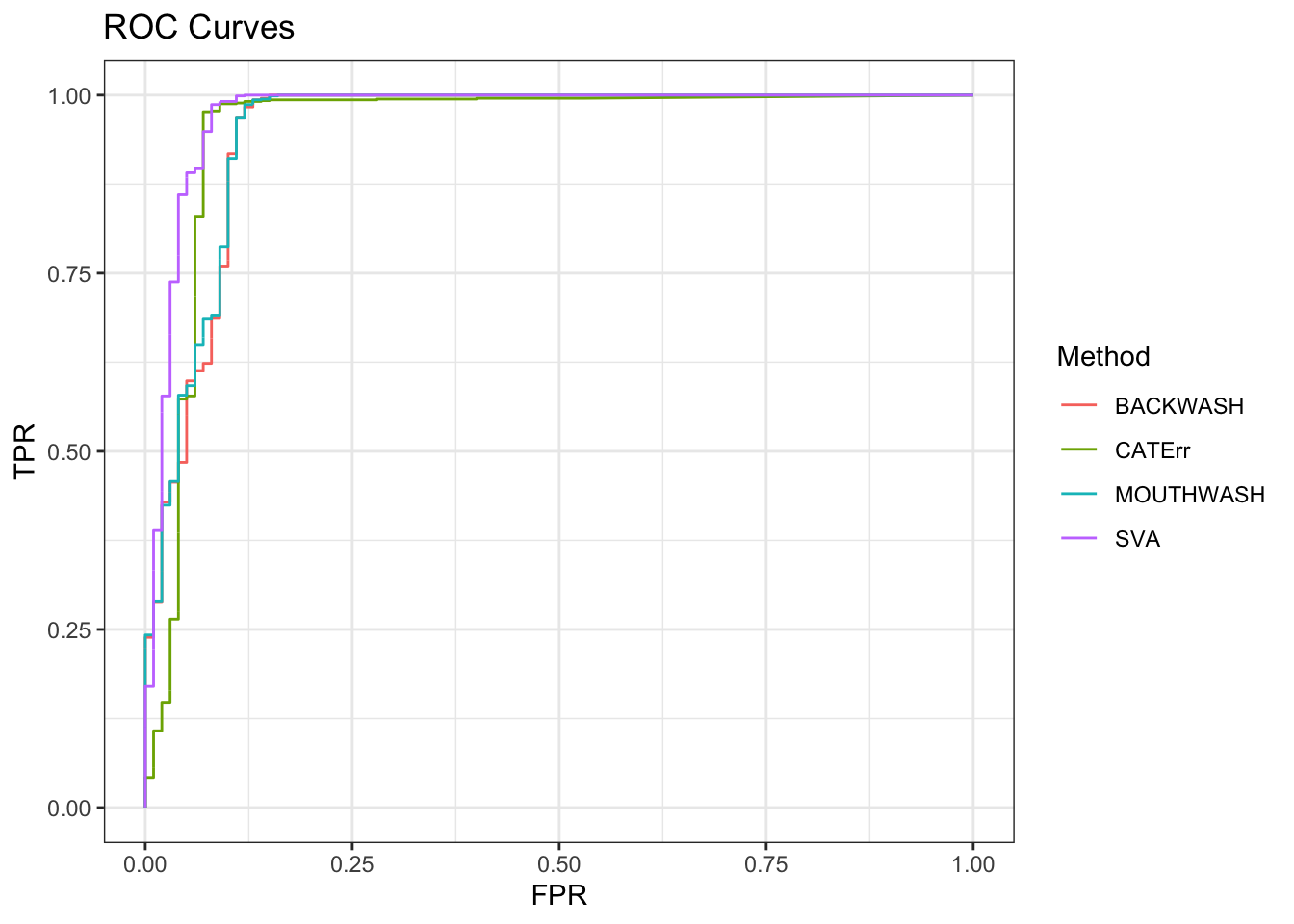
auc_vec <- sapply(roc_out, FUN = function(x) { x$auc })
knitr::kable(sort(auc_vec, decreasing = TRUE), col.names = "AUC", digits = 3)| AUC | |
|---|---|
| SVA | 0.974 |
| MOUTHWASH | 0.953 |
| CATErr | 0.951 |
| BACKWASH | 0.950 |
method_list <- list()
method_list$CATErr <- list()
method_list$CATErr$betahat <- c(cate_cate$beta)
method_list$CATErr$sebetahat <- c(sqrt(cate_cate$beta.cov.row * c(cate_cate$beta.cov.col)) / sqrt(nrow(X)))
method_list$SVA <- list()
method_list$SVA$betahat <- c(svaout$betahat)
method_list$SVA$sebetahat <- c(svaout$sebetahat)
ashfit <- lapply(method_list, FUN = function(x) { ashr::ash(x$betahat, x$sebetahat)})
api0 <- sapply(ashfit, FUN = ashr::get_pi0)
api0 <- c(api0, MOUTHWASH = mout$pi0)
api0 <- c(api0, BACKWASH = bout$pi0)
knitr::kable(sort(api0, decreasing = TRUE), col.names = "Estimate of Pi0")| E | stimate of Pi0 |
|---|---|
| SVA | 0.8503571 |
| BACKWASH | 0.8159548 |
| MOUTHWASH | 0.7604766 |
| CATErr | 0.5565965 |
Summary - RUV
Applying SVA on NULL data gives uniformly distributed p-values. Cate with robust regression didn’t make p-values uniformly distributed but considerabley more small p-values. MOUTHWASH outputs \(\hat\pi_0\) very close to 1.
Adding signals to NULL dataset.
What i didnn’t look at: two many 0’s in the dataset.
sessionInfo()R version 3.6.1 (2019-07-05)
Platform: x86_64-apple-darwin15.6.0 (64-bit)
Running under: macOS High Sierra 10.13.6
Matrix products: default
BLAS: /Library/Frameworks/R.framework/Versions/3.6/Resources/lib/libRblas.0.dylib
LAPACK: /Library/Frameworks/R.framework/Versions/3.6/Resources/lib/libRlapack.dylib
locale:
[1] en_US.UTF-8/en_US.UTF-8/en_US.UTF-8/C/en_US.UTF-8/en_US.UTF-8
attached base packages:
[1] parallel stats4 stats graphics grDevices utils datasets
[8] methods base
other attached packages:
[1] seqgendiff_1.1.1 cate_1.1
[3] vicar_0.1-10 ROTS_1.12.0
[5] edgeR_3.26.8 limma_3.40.6
[7] MultiAssayExperiment_1.10.4 SummarizedExperiment_1.14.1
[9] DelayedArray_0.10.0 BiocParallel_1.18.1
[11] matrixStats_0.55.0 Biobase_2.44.0
[13] GenomicRanges_1.36.1 GenomeInfoDb_1.20.0
[15] IRanges_2.18.3 S4Vectors_0.22.1
[17] BiocGenerics_0.30.0 ggplot2_3.2.1
loaded via a namespace (and not attached):
[1] svd_0.5 nlme_3.1-141 bitops_1.0-6
[4] fs_1.3.1 bit64_0.9-7 doParallel_1.0.15
[7] rprojroot_1.3-2 tools_3.6.1 backports_1.1.5
[10] R6_2.4.0 DBI_1.0.0 lazyeval_0.2.2
[13] mgcv_1.8-29 colorspace_1.4-1 withr_2.1.2
[16] gridExtra_2.3 tidyselect_0.2.5 bit_1.1-14
[19] compiler_3.6.1 git2r_0.26.1 labeling_0.3
[22] scales_1.0.0 SQUAREM_2017.10-1 genefilter_1.66.0
[25] mixsqp_0.1-97 esaBcv_1.2.1 stringr_1.4.0
[28] digest_0.6.21 rmarkdown_1.16 XVector_0.24.0
[31] pscl_1.5.2 pkgconfig_2.0.3 htmltools_0.4.0
[34] highr_0.8 ruv_0.9.7.1 rlang_0.4.0
[37] RSQLite_2.1.2 leapp_1.2 dplyr_0.8.3
[40] RCurl_1.95-4.12 magrittr_1.5 GenomeInfoDbData_1.2.1
[43] Matrix_1.2-17 Rcpp_1.0.2 munsell_0.5.0
[46] pROC_1.15.3 stringi_1.4.3 whisker_0.4
[49] yaml_2.2.0 MASS_7.3-51.4 zlibbioc_1.30.0
[52] plyr_1.8.4 grid_3.6.1 blob_1.2.0
[55] promises_1.1.0 crayon_1.3.4 lattice_0.20-38
[58] splines_3.6.1 annotate_1.62.0 locfit_1.5-9.1
[61] zeallot_0.1.0 knitr_1.25 pillar_1.4.2
[64] corpcor_1.6.9 codetools_0.2-16 XML_3.98-1.20
[67] glue_1.3.1 evaluate_0.14 vctrs_0.2.0
[70] httpuv_1.5.2 foreach_1.4.7 gtable_0.3.0
[73] purrr_0.3.2 assertthat_0.2.1 ashr_2.2-38
[76] xfun_0.10 xtable_1.8-4 later_1.0.0
[79] survival_2.44-1.1 truncnorm_1.0-8 tibble_2.1.3
[82] iterators_1.0.12 AnnotationDbi_1.46.1 memoise_1.1.0
[85] workflowr_1.5.0 sva_3.32.1