1 Institute of Laboratory Medicine, Clinical Chemistry and Molecular Diagnostics, University Hospital Leipzig, Paul-List-Str. 13-15, D-04103 Leipzig, Germany.
2 Section of Hepatology, Department of Gastroenterology and Rheumatology, University Hospital Leipzig, Liebigstr. 20, D-04103 Leipzig, Germany.
3 Department of Visceral, Transplantation, Vascular and Thoracic Surgery, University Hospital of Leipzig, Liebigstr. 20, D-04103 Leipzig, Germany.
4 Anesthesiology and Intensive Care Medicine, University Hospital Greifswald, Ferdinand-Sauerbruch-Str., D-17475 Greifswald, Germany.
5 Institute of Laboratory Medicine, Microbiology and Clinical Pathobiochemistry, University Hospital OWL, Hospital Lippe, Röntgenstr. 18, D-32756 Detmold, Germany.

✉ Correspondence: Sebastian Gibb <>

Last updated: 2022-08-09

Checks: 7 0

Knit directory: ampel-leipzig-meld/

This reproducible R Markdown analysis was created with workflowr (version 1.7.0). The Checks tab describes the reproducibility checks that were applied when the results were created. The Past versions tab lists the development history.

R Markdown file: up-to-date

Great! Since the R Markdown file has been committed to the Git repository, you know the exact version of the code that produced these results.

Environment: empty

Great job! The global environment was empty. Objects defined in the global environment can affect the analysis in your R Markdown file in unknown ways. For reproduciblity it’s best to always run the code in an empty environment.

Seed: set.seed(20210604)

The command set.seed(20210604) was run prior to running the code in the R Markdown file. Setting a seed ensures that any results that rely on randomness, e.g. subsampling or permutations, are reproducible.

Session information: recorded

Great job! Recording the operating system, R version, and package versions is critical for reproducibility.

Cache: none

Nice! There were no cached chunks for this analysis, so you can be confident that you successfully produced the results during this run.

File paths: relative

Great job! Using relative paths to the files within your workflowr project makes it easier to run your code on other machines.

Repository version: 1222747

Great! You are using Git for version control. Tracking code development and connecting the code version to the results is critical for reproducibility.

The results in this page were generated with repository version 1222747. See the Past versions tab to see a history of the changes made to the R Markdown and HTML files.

Note that you need to be careful to ensure that all relevant files for the analysis have been committed to Git prior to generating the results (you can use wflow_publish or wflow_git_commit). workflowr only checks the R Markdown file, but you know if there are other scripts or data files that it depends on. Below is the status of the Git repository when the results were generated: 


Ignored files:
    Ignored:    TODO
    Ignored:    _targets/
    Ignored:    analysis/article.md
    Ignored:    container/
    Ignored:    logs/
    Ignored:    scripts/R.sh

Untracked files:
    Untracked:  submission/

Note that any generated files, e.g. HTML, png, CSS, etc., are not included in this status report because it is ok for generated content to have uncommitted changes.

These are the previous versions of the repository in which changes were made to the R Markdown (analysis/article.Rmd) and HTML (docs/article.html) files. If you’ve configured a remote Git repository (see ?wflow_git_remote), click on the hyperlinks in the table below to view the files as they were in that past version.

File Version Author Date Message
Rmd 1222747 Sebastian Gibb 2022-08-09 fix: add dash between machine-learning
html afaab45 Sebastian Gibb 2022-08-09 chore: rebuild site
Rmd 288ec2a Sebastian Gibb 2022-08-09 refactor: add TB’s COI
html 1403bda Sebastian Gibb 2022-08-09 chore: rebuild site
Rmd 34c63ff Sebastian Gibb 2022-08-09 fix: add Thorsten’s new affiliation
Rmd 849ca09 Sebastian Gibb 2022-08-09 refactor: add additional co-author
Rmd 84aeda1 Sebastian Gibb 2022-08-09 refactor: integrate Berend’s suggestions
Rmd f766011 Sebastian Gibb 2022-08-09 refactor: change title
html 68ef9aa Sebastian Gibb 2022-07-22 chore: rebuild site
Rmd e6cf8a2 Sebastian Gibb 2022-07-22 refactor: apply proofreading suggestions
html 83e3c7a Sebastian Gibb 2022-07-19 chore: rebuild site
Rmd 4756fb7 Sebastian Gibb 2022-07-19 feat: extend figure captions
Rmd 112a4fe Sebastian Gibb 2022-07-19 fix: labm requires vs.
Rmd 2155e58 Sebastian Gibb 2022-07-19 refactor: create png and pdf just for non-html output
Rmd c775a67 Sebastian Gibb 2022-07-19 refactor: replace DiagrammeR CONSORT diagram by consort
Rmd 2af46fe Sebastian Gibb 2022-07-18 fix: typo
html f86c368 Sebastian Gibb 2022-07-18 chore: rebuild site
Rmd d332cbe Sebastian Gibb 2022-07-18 refactor: labm requires upper case litre
Rmd 4a757df Sebastian Gibb 2022-07-18 refactor: move data and software availability section
Rmd 5435d48 Sebastian Gibb 2022-07-18 refactor: reorder keywords
html 65d58c4 Sebastian Gibb 2022-07-18 chore: rebuild site
Rmd 0ac4a67 Sebastian Gibb 2022-07-18 refactor: restruct headings
Rmd b881188 Sebastian Gibb 2022-07-18 refactor: labm requires down style title
Rmd a0f1d2e Sebastian Gibb 2022-07-18 feat: generate png and pdfs for each plot
Rmd 9d4a890 Sebastian Gibb 2022-07-18 feat: use 1200 dpi as required by labm for word output
Rmd 93871a1 Sebastian Gibb 2022-07-18 feat: add author contributions and competing interests section
Rmd 3cd9643 Sebastian Gibb 2022-07-18 chore: add additional authors
Rmd abae68a Sebastian Gibb 2022-07-18 refactor: drop IQR for median MELD score in limitations
Rmd e81cbe1 Sebastian Gibb 2022-07-18 feat: add vancouver csl
Rmd 057248f Sebastian Gibb 2022-07-18 refactor: replace gaertner2022 by sealock2022
Rmd 024a0e0 Sebastian Gibb 2022-07-17 refactor: integrate Thorsten’s review comments
html 653f778 Sebastian Gibb 2022-07-08 chore: rebuild site
Rmd e976109 Sebastian Gibb 2022-07-08 feat: add machine learning to keywords
Rmd fab4e55 Sebastian Gibb 2022-07-08 fix: change center to Leipzig
html dcd9153 Sebastian Gibb 2022-07-03 chore: rebuild site
Rmd 048c9bb Sebastian Gibb 2022-07-03 feat: round spearman correlation to 2 digits
Rmd 6c15d1c Sebastian Gibb 2022-07-03 refactor: integrate Bernd’s suggestions
Rmd 464175f Sebastian Gibb 2022-07-03 fix: cystatin c
html 9da49ce Sebastian Gibb 2022-06-19 chore: rebuild site
Rmd 3968729 Sebastian Gibb 2022-06-19 feat: cite ameld with zenodo doi
html fb43d01 Sebastian Gibb 2022-06-19 chore: rebuild site
Rmd abe89ed Sebastian Gibb 2022-06-19 fix: cite zlog with zenodo doi
Rmd a10ff91 Sebastian Gibb 2022-06-16 fix: don’t echo code chunks
html ebe29cf Sebastian Gibb 2022-06-16 chore: rebuild site
Rmd 43a6574 Sebastian Gibb 2022-06-16 feat: further work on the manuscript
html 8035219 Sebastian Gibb 2022-06-15 chore: rebuild site
Rmd 19d9fed Sebastian Gibb 2022-06-15 feat: further work on the manuscript
html d3e9462 Sebastian Gibb 2022-06-06 chore: rebuild site
Rmd 3181fbe Sebastian Gibb 2022-06-06 refactor: suppress warning for table1
html b20484a Sebastian Gibb 2022-06-06 chore: rebuild site
Rmd 01f934b Sebastian Gibb 2022-06-06 feat: add first discussion draft
Rmd 13ac21e Sebastian Gibb 2022-06-06 feat: add docx export
html 983ec69 Sebastian Gibb 2022-03-17 chore: rebuild site
Rmd 85ff071 Sebastian Gibb 2022-03-15 fix: co2eq calculation
Rmd 839f920 Sebastian Gibb 2022-03-11 fix: cite timeROC package
Rmd 4a51c7d Sebastian Gibb 2022-03-11 feat: add co2eq estimation
Rmd c5d6267 Sebastian Gibb 2022-03-10 feat: describe model development in methods section
Rmd 74483a5 Sebastian Gibb 2022-02-10 chore: remove comments
Rmd 09c3fab Sebastian Gibb 2022-02-10 refactor: switch to grid search
html 373e7d8 Sebastian Gibb 2021-10-20 chore: rebuild site
Rmd 8b3ba9c Sebastian Gibb 2021-10-19 feat: cite gtsummary
Rmd 28ad932 Sebastian Gibb 2021-10-19 feat: describe zlog in more detail
html df8964f Sebastian Gibb 2021-10-15 chore: rebuild site
Rmd 2697ead Sebastian Gibb 2021-10-15 fix: remove missing cross reference
Rmd eeca976 Sebastian Gibb 2021-10-15 feat: add ml method part
html c66640c Sebastian Gibb 2021-09-14 feat: first nnet tests
html afa48d9 Sebastian Gibb 2021-08-07 chore: rebuild site
Rmd d32f7b3 Sebastian Gibb 2021-08-07 fix: gtsummary compact theme
Rmd ebf878b Sebastian Gibb 2021-08-07 fix: observed vs expected mortality table
Rmd 4ec3d40 Sebastian Gibb 2021-08-04 feat: add table 1 and table observed vs expected mortality
Rmd e41dd8c Sebastian Gibb 2021-08-03 feat: add flowchart and discussion notes
Rmd 523c286 Sebastian Gibb 2021-08-02 refactor: use bookdown::html_document2 instead of workflowr::wflow_html to allow crossreferences
html 3aab3e1 Sebastian Gibb 2021-08-01 chore: rebuild site
Rmd 91bfbd2 Sebastian Gibb 2021-08-01 feat: add first article draft with pandoc filters

1 Introduction

Liver cirrhosis is the terminal result of the fibrotic remodeling of liver tissue due to chronic damage. This end-stage of liver disease is usually irreversible, and the only available therapy is liver transplantation. However, the shortage of grafts for transplantation from deceased donors requires risk stratification and precise and fair allocation rules. The allocation of liver transplantation in most countries is based on disease severity determined by the model of end-stage liver disease (MELD) (Malinchoc et al. 2000; Wiesner et al. 2003; Organ Procurement and Transplantation Network 2021). The MELD score estimates patients’ 3-month mortality risk based on laboratory results, namely bilirubin, creatinine, and the international normalized ratio (INR). The MELD score has been extended by the sodium level (MELD-Na score) because this was found to be an important additional risk factor in liver cirrhosis (Kim et al. 2008; Organ Procurement and Transplantation Network 2021). The MELD was initially developed to predict the survival of patients undergoing transjugular intrahepatic portosystemic shunts. It was subsequently revalidated to predict mortality risk in patients awaiting a liver transplantation. Although the MELD score should be an objective allocation score, creatinine and INR are highly dependent on the laboratory methods used (Trotter et al. 2004; Cholongitas et al. 2007). In addition women are disadvantaged (Sealock et al. 2022). Patients with identical disease states can have very different MELD scores and thus receive different priority levels on the liver transplantation waiting list. Furthermore, for acute-on-chronic liver failure, for example, the MELD score often underestimates the mortality risk (Hernaez et al. 2020).

There have been some attempts to use the data extracted from more than 300,000 electronic medical records from two hospitals in the United States to improve the MELD score (Kartoun et al. 2017). The derived MELD-Plus7 and MELD-Plus9 risk scores add albumin, white blood cell count, total cholesterol, age, and length of stay to the MELD-Na variables. Despite their published prediction improvement, the MELD-Plus scores are not yet used for transplant allocation.

As shown by the MELD-Plus risk scores, better predictive scores often need more variables and are more complicated. To reduce the risk of overlooking or incorrectly calculating and interpreting the results, clinical decision support systems may be used and could improve patient safety. The research project on digital laboratory medicine (AMPEL) develops a clinical decision support system based on laboratory diagnostics that should support clinical practitioners in interpreting laboratory results and taking the necessary medical interventions (Eckelt et al. 2020).

This study aims to find clinical and laboratory values that improve on the risk stratification for liver transplantation of the classical MELD, MELD-Na, and MELD-Plus scores and that might be implemented as part of the AMPEL clinical decision support system.

2 Material and methods

2.1 Study population

In a retrospective cohort study we followed 778 consecutive patients, who were recruited during the evaluation process for liver transplantation at University Hospital Leipzig from November 2012 to June 2015. For each patient, we recorded 44 variables, including age, sex, etiology of liver disease, complications as listed in Table 3.1, and 25 laboratory measurements.

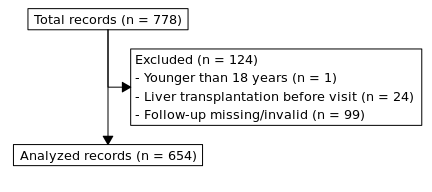
Flowchart showing inclusion and exclusion of records.

Figure 2.1: Flowchart showing inclusion and exclusion of records.

Version Author Date
68ef9aa Sebastian Gibb 2022-07-22
83e3c7a Sebastian Gibb 2022-07-19

We excluded 124 patients from our analysis (Figure 2.1). One was younger than 18 years, 24 had had a liver transplant before and in 99 cases the follow-up data were missing or invalid.

The Ethics Committee at the Leipzig University Faculty of Medicine approved the retrospective usage of the data for our study (reference number: 039/14ff).

2.2 MELD scores

MELD and MELD-Na were calculated as described in Organ Procurement and Transplantation Network (2021) using the following formulas: \(MELD = 10 * (0.957 \ln(creatinine [mg/dL]) + 0.378 \ln(bilirubin [mg/dL]) + 1.120 * \ln(INR) + 0.643)\), Creatinine, bilirubin and INR values lower than 1.0 mg/dL were set to 1.0 mg/dL. The maximum allowed creatinine was 4.0 mg/dL. If the patients received dialysis, creatinine was set to 4.0 mg/dL. For MELD-Na, MELD was calculated as above and recalculated if greater than 11 using: \(MELD\text{-}Na = MELD_i + 1.32 * (137 - Na [mmol/L]) - (0.033 * MELD_i * (137 - Na [mmol/L]))\)

Serum sodium values lower than 125 mmol/L or higher than 137 mmol/L were set to 125 mmol/L and 137 mmol/L, respectively.

The MELD-Plus7 risk score was calculated as described in Kartoun et al. (2017): \[ \begin{aligned} L = 8.53499496 &+ \\ 2.59679650 &* \log_{10}(1 + creatinine [mg/dL]) + \\ 2.06503238 &* \log_{10}(1 + bilirubin [mg/dL]) + \\ 2.99724802 &* \log_{10}(1 + INR) - \\ 6.47834101 &* \log_{10}(1 + sodium [mmol/L]) - \\ 6.34990436 &* \log_{10}(1 + albumin [g/L]) + \\ 1.92811726 &* \log_{10}(1 + wbc [th/cumm]) + \\ 0.04070442 &* age [years] \end{aligned} \]

\[MELD\text{-}Plus = \frac{\exp(L)}{1 + \exp(L)}\]

The MELD-Plus9 score was ignored because the length of stay information was not available for our cohort, and the model itself was not superior to MELD-Plus7 in its original publication (Kartoun et al. 2017).

2.3 Data processing and machine learning

All data processing, statistical, and machine-learning analyses were performed using R version 4.2.0 (R Core Team 2022). Prior to the analyses, all laboratory values were zlog transformed to approximate a normal distribution as described in Hoffmann et al. (2017) and implemented in Gibb (2021).

\[ z = (\log(x) - \frac{\log(LL) + \log(UL)}{2}) * \frac{3.92}{\log(UL) - \log(LL)} \]

where \(LL\) and \(UL\) are the lower and upper age-, and sex-related reference limits of the corresponding laboratory diagnostic, respectively. Missing laboratory measurements were replaced with a zlog value of zero. In a similar manner, where information about complications or comorbidities was missing, we treated them as not present.

We compared 13 different statistical and machine-learning algorithms using the mlr3 framework (Lang et al. 2019, 2022; Sonabend et al. 2021; Sonabend, Kiraly, and Lang 2022). The algorithms used were designed for analysis of survival data: Cox proportional hazards regression model (Cox 1972; Terry M. Therneau and Patricia M. Grambsch 2000; Therneau 2022); penalized regressions, namely, two different implementations of the lasso (least absolute shrinkage and selection operator) regression (Tibshirani 1997; Simon et al. 2011; Friedman et al. 2022; J. J. Goeman 2010; J. Goeman et al. 2022), two different implementations of the ridge regression (Simon et al. 2011; Friedman et al. 2022; J. J. Goeman 2010; J. Goeman et al. 2022), and the elastic net regression (Simon et al. 2011; Friedman et al. 2022); two different random forest implementations (Wright and Ziegler 2017; Wright, Wager, and Probst 2021; H. Ishwaran et al. 2008; Hemant Ishwaran and Kogalur 2020); extreme gradient boosting (T. Chen and Guestrin 2016; Tianqi Chen et al. 2022); two different support vector machines (Belle et al. 2011; Fouodo 2018); ;nd two neural networks (Katzman et al. 2018; Kvamme, Borgan, and Scheel 2019; Sonabend 2022).

We used nested resampling to avoid feature- and model-selection-bias to obtain reliable metrics to choose the best model. We thus applied a 5-fold inner and 3-fold outer cross-validation that was repeated 10 times. We searched the hyperparameter space using a grid search with a resolution of 10. The models were evaluated using the concordance index, which is a measure of rank correlation between predicted and observed events (Harrell 1982). Subsequently, we selected the model with the highest median concordance index. If multiple models were comparable, we chose the simpler (more penalized) one.

After selecting the final model, we trained and validated it as described in Harrell, Lee, and Mark (1996). Briefly, we developed our model using a 3-fold cross-validation that was repeated 10 times and finally predicted survival at 90 days. The predictions were sorted and grouped into equal-sized intervals so that there were 50 patients in each interval. For each group, the mean survival probability and the difference to the Kaplan-Meier estimate was calculated. The same procedure was repeated for 200 bootstrap samples. Subsequently, the differences between predicted survival and Kaplan-Meier estimates of the bootstrap samples were averaged and added to the original model difference to obtain a bias-corrected estimate between predicted and observed survival.

The final model was compared against the MELD, MELD-Na, and MELD-Plus7 scores using the area under the time-dependent receiver operating characteristic curve (AUROC) based on the nonparametric inverse probability of censoring weighting estimator (IPCW) Paul Blanche (2019). Testing was applied as described in P. Blanche, Dartigues, and Jacqmin-Gadda (2013). A \(p < 0.05\) was considered a statistically significant difference.

Summary tables were built using the gtsummary package (Sjoberg et al. 2021, 2022).

3 Results

3.1 Baseline characteristics

Table 3.1: Baseline characteristics.
Values are given as median (lower quartile, upper quartile) or n (percent).
AIH, autoimmune hepatitis; ALAT, alanine aminotransferase; ALF, acute liver failure; ASAT, aspartate aminotransferase; CLI, chronic liver insufficiency; GIB, gastrointestinal bleeding; HBV, hepatitis B virus; HCV, hepatitis C virus; IL-6, interleukin 6; INR, international normalized ratio; LTx, liver transplantation; NASH, non-alcoholic steatohepatitis; PBC, primary biliary cirrhosis; PSC, primary sclerosing cholangitis; SBP, spontaneous bacterial peritonitis
Characteristic Female, N = 240 Male, N = 414 Overall, N = 654
General
Follow-up time [days] 181 (17, 411) 198 (54, 378) 191 (38, 384)
Age 56 (51, 64) 58 (52, 63) 58 (52, 64)
LTx 20 (8.3%) 40 (9.7%) 60 (9.2%)
Laboratory measurements
Total bilirubin [µmol/L] 21 (10, 49) 26 (14, 51) 24 (13, 50)
Cystatin C [mg/L] 1.31 (1.04, 1.80) 1.32 (1.08, 1.76) 1.32 (1.07, 1.79)
(Missing) 2 5 7
Creatinine [µmol/L] 73 (58, 91) 85 (71, 110) 80 (65, 104)
INR 1.20 (1.06, 1.50) 1.22 (1.10, 1.44) 1.21 (1.09, 1.46)
(Missing) 1 1 2
Sodium [mmol/L] 138.8 (135.4, 141.0) 138.0 (135.0, 140.1) 138.1 (135.2, 140.4)
(Missing) 5 4 9
WBC [exp 9/L] 6.7 (4.7, 8.8) 6.2 (4.6, 7.8) 6.3 (4.7, 8.3)
(Missing) 10 13 23
IL-6 [pg/mL] 10 (5, 36) 14 (6, 47) 13 (6, 42)
(Missing) 27 29 56
Albumin [g/L] 41 (35, 46) 38 (33, 43) 39 (34, 45)
(Missing) 2 4 6
Total protein [g/L] 71 (63, 76) 71 (65, 76) 71 (65, 76)
(Missing) 2 4 6
Cholesterine [mmol/L] 4.64 (3.41, 5.56) 4.28 (3.34, 5.15) 4.40 (3.34, 5.31)
ALAT [µkat/L] 0.29 (0.21, 0.42) 0.36 (0.23, 0.56) 0.33 (0.22, 0.48)
(Missing) 2 8 10
ASAT [µkat/L] 0.68 (0.49, 1.05) 0.81 (0.61, 1.23) 0.77 (0.55, 1.16)
(Missing) 3 5 8
MELD
MELD score 10 (7, 18) 12 (9, 17) 11 (8, 17)
(Missing) 2 1 3
MELD Category
[6,9] 111 (47%) 146 (35%) 257 (39%)
[10,20) 80 (34%) 196 (47%) 276 (42%)
[20,30) 30 (13%) 50 (12%) 80 (12%)
[30,40) 12 (5.0%) 14 (3.4%) 26 (4.0%)
[40,52) 5 (2.1%) 7 (1.7%) 12 (1.8%)
(Missing) 2 1 3
MELD-Na score 10 (7, 19) 12 (9, 20) 11 (8, 20)
(Missing) 5 4 9
Entities
Cirrhosis 203 (85%) 391 (94%) 594 (91%)
(Missing) 1 0 1
ALF 6 (2.5%) 2 (0.5%) 8 (1.2%)
CLI 30 (12%) 21 (5.1%) 51 (7.8%)
Etiology (more than 1 per patient possible)
Ethyltoxic 114 (48%) 297 (72%) 411 (63%)
HBV 4 (1.7%) 16 (3.9%) 20 (3.1%)
HCV 17 (7.1%) 28 (6.8%) 45 (6.9%)
AIH 22 (9.2%) 9 (2.2%) 31 (4.7%)
PBC 17 (7.1%) 0 (0%) 17 (2.6%)
PSC 5 (2.1%) 11 (2.7%) 16 (2.4%)
NASH 17 (7.1%) 31 (7.5%) 48 (7.3%)
Cryptogenic 36 (15%) 32 (7.7%) 68 (10%)
Complications (more than 1 per patient possible)
Dialysis 14 (5.9%) 19 (4.6%) 33 (5.1%)
(Missing) 1 1 2
GIB 58 (24%) 104 (25%) 162 (25%)
HCC 18 (7.5%) 103 (25%) 121 (19%)
SBP 31 (13%) 60 (15%) 91 (14%)
(Missing) 0 1 1
Mortality
Within 7 days 16 (7.2%) 18 (4.5%) 34 (5.5%)
Within 30 days 25 (12%) 31 (8.1%) 56 (9.4%)
Within 90 days 32 (16%) 49 (13%) 81 (14%)
Within 365 days 39 (20%) 61 (18%) 100 (18%)

In this study, we analyzed a cohort of 654 patients evaluated for liver transplantation (Tab. 3.1). Of these, 414 (63%) were men. The median (IQR) follow-up times was 191 (38, 384) days. Within the follow-up time, 60 (9.2%) patients received a liver transplant and were censored for the analysis beyond this time point. The median (IQR) age of the cohort was 58 (52, 64) years.

Most of the patients presented with cirrhosis (594 (91%)). The remaining patients had acute liver failure (8 (1.2%)) or chronic liver insufficiency (51 (7.8%)). At evaluation time, the median (IQR) MELD and MELD-Na scores were 11 (8, 17) and 11 (8, 20), respectively. Within 90 days, 81 (14%) patients had died. In nearly two thirds of all patients (411 (63%)), alcohol was the main cause of their end-stage liver disease. The remaining patients had viral infections - hepatitis B (20 (3.1%)) or C (45 (6.9%)) - autoimmune autoimmune (31 (4.7%)), primary sclerosing cirrhosis (16 (2.4%)), primary biliary cirrhosis (17 (2.6%)), unknown causes (non-alcoholic steatohepatitis (48 (7.3%)), or cryptogenic hepatitis (68 (10%))). The most common complications among all patients were gastrointestinal bleedings in 162 (25%) patients, followed by hepatocellular carcinoma (HCC) in 121 (19%) and spontaneous bacterial peritonitis (SBP) in 91 (14%) patients. Just 33 (5.1%) patients required renal dialysis.

3.2 MELD scores

According to Wiesner et al. (2003), we divided our cohort into 5 MELD-score risk categories, with 257, 276, 80, 26, and 12 patients, respectively. As shown in Table 3.2, our observed 90-day mortality was 1.4 to 2.9 times higher than the predicted one. Only in the group with the lowest MELD scores was the mortality much lower.

Table 3.2: Observed vs. MELD-expected 90-day mortality. MELD mortality values are taken from Wiesner et al. (2003). All patients censored before day 90 are ignored for the calculation of the MELD-expected deaths. SMR, Standardized mortality ratio = observed deaths/expected deaths.
MELD category Observed deaths (n) Expected deaths (n) Standardized mortality ratio (SMR) Observed mortality (%) Expected mortality (%)
[6,9] 1 4.0 0.3 0.5 1.9
[10,20) 21 13.0 1.6 8.9 6.0
[20,30) 34 11.6 2.9 51.0 19.6
[30,40) 18 10.0 1.8 92.8 52.6
[40,52) 6 4.3 1.4 100.0 71.3

3.3 AMPEL MELD

The penalized regression and random forest models resulted in a similar high median performance in the benchmark process. In favour of simpler models, we chose a lasso-based approach for the final model development. The classical Cox model, the data and computational intense algorithms extreme gradient boosting, the support vector machines and the neural networks yielded a worse performance.

Table 3.3: Model coefficients
Coefficient
IL-6 0.193
Total protein -0.081
INR 0.067
Cholinesterase -0.037
Cystatin C 0.026
Direct bilirubin 0.010

The resulting AMPEL model of end-stage liver disease (AMELD) uses 6 predictors. Besides the classical MELD variables INR and (direct) bilirubin, the lasso regression selected cystatin C over creatinine, as well as IL-6, total protein, and cholinesterase.

Table 3.4: Underlying survival function; S0: baseline survival estimate
t [days] 2 7 30 90 180 365
S0 (t) 0.9967 0.9912 0.9816 0.9661 0.9546 0.9489

The 90-day survival estimate of a given patient can be calculated as shown in (3.1).

\[\begin{align} S &= S_{0,90}^{\exp{LP}} \\ &= 0.9661 ^{\exp{( 0.1929 * zlog(\text{IL-6})-0.0805 * zlog(\text{Total protein})+0.0667 * zlog(\text{INR})-0.0368 * zlog(\text{Cholinesterase})+0.026 * zlog(\text{Cystatin C})+0.0098 * zlog(\text{Direct bilirubin}) )}} \tag{3.1} \end{align} \]

where \(S_{0}\) is the baseline survival estimate from 3.4 and \(LP\) is the linear predictor of the coefficients in 3.3.

3.4 Model comparison

Receiver operating characteristic (ROC) curve. Area under the time-dependent ROC curve (AUC) based on the nonparametric inverse probability of censoring weighting estimate (IPCW) for AMELD, MELD, MELD-Na, and MELD-Plus7, as described in [@blanche2013].

Figure 3.1: Receiver operating characteristic (ROC) curve. Area under the time-dependent ROC curve (AUC) based on the nonparametric inverse probability of censoring weighting estimate (IPCW) for AMELD, MELD, MELD-Na, and MELD-Plus7, as described in (P. Blanche, Dartigues, and Jacqmin-Gadda 2013).

Version Author Date
65d58c4 Sebastian Gibb 2022-07-18
ebe29cf Sebastian Gibb 2022-06-16
8035219 Sebastian Gibb 2022-06-15
Table 3.5: Test comparison between AUCROC for MELD-Na and AMELD according to P. Blanche, Dartigues, and Jacqmin-Gadda (2013) at day 2, 7, 30, 90, 180, 365.\(p\)-values are shown as non-adjusted and adjusted for multiple testing.
t=2 t=7 t=30 t=90 t=180 t=365
Non-adjusted \(p\)-values 0.27 0.15 0.33 0.03 0.02 0.33
Adjusted \(p\)-values 0.75 0.52 0.84 0.15 0.08 0.84

AMELD offers the best AUROC (0.961) of all competitors. However, after correction for multiple testing, the difference against the second-best model, MELD-Na (AUROC: 0.936), is not statistical significant (\(p = 0.15\)) (see Table 3.5 for complete comparison).

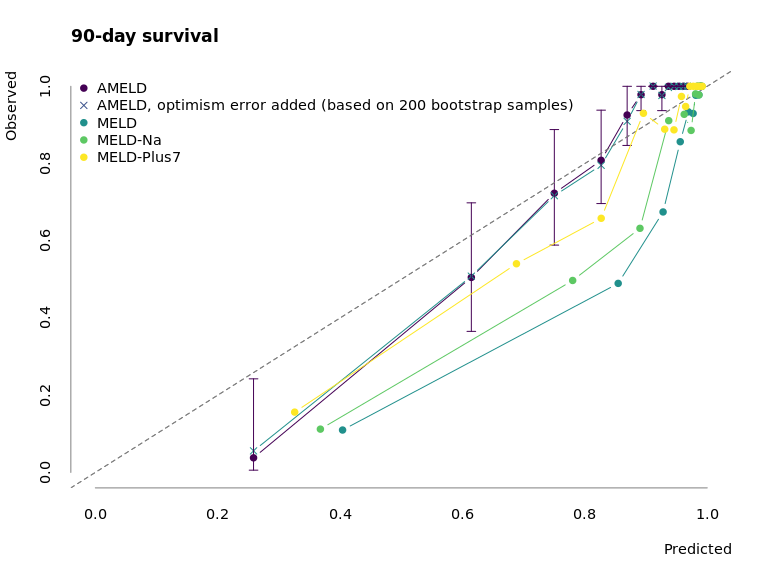
Calibration of AMELD in comparison to MELD, MELD-Na, and MELD-Plus7. The points mark the mean predicted survival of 50 patients per interval against their observed mean survival. The error bars correspond to the 95% confidence interval of the survival estimate.

Figure 3.2: Calibration of AMELD in comparison to MELD, MELD-Na, and MELD-Plus7. The points mark the mean predicted survival of 50 patients per interval against their observed mean survival. The error bars correspond to the 95% confidence interval of the survival estimate.

Version Author Date
83e3c7a Sebastian Gibb 2022-07-19
65d58c4 Sebastian Gibb 2022-07-18
ebe29cf Sebastian Gibb 2022-06-16
8035219 Sebastian Gibb 2022-06-15

Fig. 3.2 depicts the calibration curve for AMELD and the competing MELD scores. While the prediction for low-risk patients is similar to other scores, AMELD predicts the medium-risk patients more accurately.

4 Discussion

In this retrospective analysis of 654 consecutive patients who were recruited during the evaluation process for liver transplantation at University Hospital Leipzig, we developed a new model to predict 90-day survival probability. Our new model, AMELD, outperforms the MELD-Na score and the recently published MELD-Plus7 risk score.

Although the Organ Procurement and Transplantation Network recommends the use of MELD-Na over MELD, the sodium does not add any information to the score. Neither in the bootstrap selection nor in the variable importance of a random forest model does the sodium gain any important weight (in bootstrap selection rank 18 of 42 and in a random forest variable importance rank 20 of 42, see ??, ??). In addition, sodium levels can be affected by diuretic therapy, and the discrimination performance of MELD-Na has already been shown by Kartoun et al. (2017) to be insignificantly different from the classical MELD. Consequently it is not a component of our model.

It has been shown that women receive median lower scores in MELD-Na and therefore are less likely to receive an urgent listing for liver transplantation (Sealock et al. 2022). To address sexual differences, in laboratory measurements we applied the zlog transformation (Hoffmann et al. 2017) in our study. This transformation also yields comparable laboratory measurements across different clinical laboratories and methods, as well as reducing the influence of age- and sex-related differences, which could improve the objectivity of the allocation process. The already nearly normal scaled zlog-transformed laboratory measurements allow us to avoid the sample-dependent scaling prior to model development. Both should increase the external applicability of our approach.

Our model, AMELD, uses 6 predictors. Three of these - INR, (direct) bilirubin, and cystatin C - are identical or similar to the laboratory measurements utilized in the classical MELD. The direct bilirubin selected by our approach and the total bilirubin in MELD are highly correlated (Spearman correlation: 0.96) and therefore interchangeable.

In our feature selection process, cystatin C was chosen instead of creatinine. This is in line with recent studies that show a better prediction of mortality for cystatin C in unselected and critically ill patients (Helmersson-Karlqvist, Ärnlöv, and Larsson 2016; Helmersson-Karlqvist et al. 2021).

Furthermore AMELD, extends MELD by the additional synthesis parameters total protein and cholinesterase, and most importantly the inflammatory marker IL-6.

The latter is an example where results from machine-learning can aid in finding clinically meaningful patterns and guide further research. Systemic inflammatory response syndrome is an independent risk factor for poor outcomes in patients with cirrhosis (Thabut et al. 2007). However, neither MELD nor MELD-Na took inflammation into account. By contrast, IL-6 is the most important variable in our model. Even if IL-6 is excluded, the algorithms select CRP as one of the most important variables, which highlights the important role of inflammation in the prognosis of patients with end-stage liver disease. We and other researchers have already shown that adding inflammatory markers, namely IL-6 or CRP, to the classical MELD score increases the accuracy of the 90-day mortality prediction (Remmler et al. 2017; Cervoni et al. 2016).

Besides laboratory measurements, we investigated 17 other items of clinical data, but none were chosen in our model-selection process. Kartoun et al. (2017) also used the lasso approach and did not select any clinical data. In retrospective analyses in particular, the clinical data are often not detailed enough to provide valuable information.

In our benchmark of 13 different machine-learning algorithms we have seen that the more complex algorithms, such as boosting, support vector machines, and neural networks, perform worse than simpler ones. This may be due to additive effects that favor regression models or due to our relatively small sample size. It has been shown that in machine-learning more than 200 events per predictor variable are required to achieve good prediction performance (Ploeg, Austin, and Steyerberg 2014).

4.1 Limitations

Our study has several limitations. Principally, it is a single-center, retrospective analysis lacking an external validation cohort. The data were collected during the evaluation process for liver transplantation at University Hospital Leipzig. There was no controlled follow-up process. We excluded all patients who had already undergone liver transplantation, which could artificially lower the disease severity of the cohort. Furthermore, most of our patients suffered from ethyltoxic liver cirrhosis (63%), which may limited the transfer to other etiologies.

With a median MELD score of 11, our cohort was healthier than those in previous studies that reported a score of 14-15 (Kim et al. 2008; Kartoun et al. 2017). However, the 90-day mortality rate of 81 (14%) was comparable to the mortality rates seen in earlier studies ranging from 6% to 30% (Malinchoc et al. 2000; Kim et al. 2008; Kartoun et al. 2017). Although our cohort was healthier, with a medium mortality rate, the classical MELD score underestimates the observed mortality by 1.4 to 2.9 times. Unfortunately, our sample size was low in the high-risk patient category, resulting in a poor but better than MELD-based prediction performance by our AMELD for very ill patients.

5 Conclusion

In conclusion, we have developed a new model to predict the 90-day survival of patients during the evaluation process for liver transplantation. Our model, AMELD, extends the classical MELD predictors INR, (direct) bilirubin, and cystatin C (instead of creatinine) by using the synthesis parameters total protein and cholinesterase and, most importantly, the inflammatory marker IL-6. Using these six laboratory measurements, AMELD outperforms the established MELD-Na and the recently published MELD-Plus7 risk scores. For wider adoption, a prospective multi-center study for model recalibration and validation is needed.

5.1 Acknowledgments

We thank the whole AMPEL team for their support, Stefan Kemnitz for his technical support regarding the use of the high-performance computing (HPC) cluster at the University of Greifswald and Bernd Klaus for helpful discussions about survival analysis and proofreading the manuscript.

The calculations were conducted using the HPC cluster at University of Greifswald. In 2018, the average carbon efficiency of the German power grid was 0.471 kgCO2eq/kWh (Icha, Lauf, and Kuhs 2021). A single run of the complete calculation pipeline took roughly 96 hours of computation on an Intel(R) Xeon(R) E5-2650 v4 and Intel(R) Xeon(R) Gold 6240 CPU (thermal design power: 105 and 150 W). The total estimated emissions were at least 6.77 kgCO2eq (ignoring development, test runs, etc.). This is equivalent to 44 km driven by an average car (Allekotte et al. 2021).

5.2 Research funding

The study was supported by the AMPEL project (www.ampel.care). This project is co-financed through public funds according to the budget decided by the Saxon State Parliament under RL eHealthSax 2017/18 grant number 100331796. The funder provided support in the form of salaries for author SG but did not have any additional role in the study design, data collection and analysis, decision to publish, or preparation of the manuscript.

5.3 Author contributions

Funding was acquired by TK. The study was conceptualized by SG and TK. The data were acquired by TK. The data were analyzed and processed by SG. Visualization was produced by SG. The original drafts of the manuscript were written by SG and TK. Drafts were edited and reviewed by SG, TB, AH, DS, BI, and TK. The project was supervised by TK. All authors have accepted responsibility for the entire content of this manuscript and have approved its submission.

5.4 Competing interests

TB recieved grants or research support from Abbvie, BMS, Gilead, MSD/Merck, Humedics, Intercept, Merz, Norgine, Novartis, Orphalan, Sequana Medical. TB received honoraria or consultation fees/advisory board from Abbvie, Alexion, Bayer, Gilead, GSK, Eisai, Enyo Pharma, Falk Foundation, HepaRegeniX GmbH, Humedics, Intercept, Ipsen, Janssen, MSD/Merck, Novartis, Orphalan, Roche, Sequana Medical, SIRTEX, SOBI, and Shionogi TB participated in a company sponsored speaker’s bureau for Abbvie, Alexion, Bayer, Gilead, Eisai, Intercept, Ipsen, Janssen, MedUpdate GmbH, MSD/Merck, Novartis, Orphalan, Sequana Medica, SIRTEX, and SOBI. All other authors state no conflict of interest.

5.6 Ethical approval

Research involving human subjects complied with all relevant national regulations and institutional policies, as well as the tenets of the Helsinki Declaration (as revised in 2013), and was approved by the Ethics Committee at the Leipzig University Faculty of Medicine (reference number: 039/14ff).

5.7 Data and software availability

The complete code and reproducible analysis can be found at https://ampel-leipzig.github.io/ampel-leipzig-meld/. In addition, all data are available in the ameld R package (Gibb 2022) at https://github.com/ampel-leipzig/ameld DOI for further investigation.

6 References

Allekotte, M., F. Bergk, K. Biemann, C. Deregowski, W. Knörr, H.-J. Althaus, D. Sutter, and T. Bergmann. 2021. “Ökologische Bewertung von Verkehrsarten.” 3716581060. Umweltbundesamt. https://www.umweltbundesamt.de/sites/default/files/medien/479/publikationen/texte_156-2020_oekologische_bewertung_von_verkehrsarten_0.pdf.
Belle, V. Van, K. Pelckmans, S. Van Huffel, and J. A. K. Suykens. 2011. “Support Vector Methods for Survival Analysis: A Comparison Between Ranking and Regression Approaches.” Artif Intell Med 53 (2): 107–18. https://doi.org/10.1016/j.artmed.2011.06.006.
Blanche, Paul. 2019. timeROC: Time-Dependent ROC Curve and AUC for Censored Survival Data. https://CRAN.R-project.org/package=timeROC.
Blanche, P., J.-F. Dartigues, and H. Jacqmin-Gadda. 2013. “Estimating and Comparing Time-Dependent Areas Under Receiver Operating Characteristic Curves for Censored Event Times with Competing Risks.” Stat Med 32 (30): 5381–97. https://doi.org/10.1002/sim.5958.
Cervoni, J.-P., À. Amorós, R. Bañares, J. L. Montero, G. Soriano, D. Weil, R. Moreau, M. Pavesi, T. Thévenot, and V. Di Martino. 2016. “Prognostic Value of c-Reactive Protein in Cirrhosis.” Eur J Gastroenterol Hepatol 28 (9): 1028–34. https://doi.org/10.1097/meg.0000000000000676.
Chen, T., and C. Guestrin. 2016. “XGBoost: A Scalable Tree Boosting System.” Proceedings of the 22nd ACM SIGKDD International Conference on Knowledge Discovery and Data Mining, August, 785–94. https://doi.org/10.1145/2939672.2939785.
Chen, Tianqi, Tong He, Michael Benesty, Vadim Khotilovich, Yuan Tang, Hyunsu Cho, Kailong Chen, et al. 2022. Xgboost: Extreme Gradient Boosting. https://github.com/dmlc/xgboost.
Cholongitas, E., L. Marelli, A. Kerry, M. Senzolo, D. W. Goodier, D. Nair, M. Thomas, D. Patch, and A. K. Burroughs. 2007. “Different Methods of Creatinine Measurement Significantly Affect MELD Scores.” Liver Transpl 13 (4): 523–29. https://doi.org/10.1002/lt.20994.
Cox, D. R. 1972. “Regression Models and Life-Tables.” J R Stat Soc, Series B 34 (2): 187–202. https://doi.org/10.1111/j.2517-6161.1972.tb00899.x.
Eckelt, F., J. Remmler, T. Kister, M. Wernsdorfer, H. Richter, M. Federbusch, M. Adler, et al. 2020. “Verbesserte Patientensicherheit Durch “Clinical Decision Support Systems” in Der Labormedizin.” Der Internist 61 (5): 452–59. https://doi.org/10.1007/s00108-020-00775-3.
Fouodo, Cesaire J. K. 2018. Survivalsvm: Survival Support Vector Analysis. https://github.com/imbs-hl/survivalsvm.
Friedman, Jerome, Trevor Hastie, Rob Tibshirani, Balasubramanian Narasimhan, Kenneth Tay, Noah Simon, and James Yang. 2022. Glmnet: Lasso and Elastic-Net Regularized Generalized Linear Models. https://CRAN.R-project.org/package=glmnet.
Gibb, Sebastian. 2021. zlog: Z(log) Transformation for Laboratory Measurements. https://doi.org/10.5281/zenodo.4727117.
———. 2022. Data and Model of End-Stage Liver Disease Used in the AMPEL Project. https://doi.org/10.5281/zenodo.6666018.
Goeman, J. J. 2010. “L1 Penalized Estimation in the Cox Proportional Hazards Model.” Biometrical Journal, no. 52, 1: –14.
Goeman, Jelle, Rosa Meijer, Nimisha Chaturvedi, and Matthew Lueder. 2022. Penalized: L1 (Lasso and Fused Lasso) and L2 (Ridge) Penalized Estimation in GLMs and in the Cox Model. https://CRAN.R-project.org/package=penalized.
Harrell, F. E. 1982. “Evaluating the Yield of Medical Tests.” JAMA 247 (18): 2543. https://doi.org/10.1001/jama.1982.03320430047030.
Harrell, F. E., K. L. Lee, and D. B. Mark. 1996. “Multivariable Prognostic Models: Issues in Developing Models, Evaluating Assumptions and Adequacy, and Measuring and Reducing Errors.” Stat Med 15 (4): 361–87. https://doi.org/10.1002/(sici)1097-0258(19960229)15:4<361::aid-sim168>3.0.co;2-4.
Helmersson-Karlqvist, J., J. Ärnlöv, and A. Larsson. 2016. “Cystatin c-Based Glomerular Filtration Rate Associates More Closely with Mortality Than Creatinine-Based or Combined Glomerular Filtration Rate Equations in Unselected Patients.” Eur J Prev Cardiol 23 (15): 1649–57. https://doi.org/10.1177/2047487316642086.
Helmersson-Karlqvist, J., M. Lipcsey, J. Ärnlöv, M. Bell, B. Ravn, A. Dardashti, and A. Larsson. 2021. “Cystatin c Predicts Long Term Mortality Better Than Creatinine in a Nationwide Study of Intensive Care Patients.” Sci Rep 11 (1). https://doi.org/10.1038/s41598-021-85370-8.
Hernaez, R., Y. Liu, J. R. Kramer, A. Rana, H. B. El-Serag, and F. Kanwal. 2020. “Model for End-Stage Liver Disease-Sodium Underestimates 90-Day Mortality Risk in Patients with Acute-on-Chronic Liver Failure.” J Hepatol 73 (6): 1425–33. https://doi.org/10.1016/j.jhep.2020.06.005.
Hoffmann, G., F. Klawonn, R. Lichtinghagen, and M. Orth. 2017. “Der Zlog-Wert Als Basis Für Die Standardisierung von Laborwerten.” LaboratoriumsMedizin 41 (1): 23–32. https://doi.org/10.1515/labmed-2016-0087.
Icha, P., T. Lauf, and G. Kuhs. 2021. “Entwicklung Der Spezifischen Kohlendioxid-Emissionen Des Deutschen Strommix in Den Jahren 1990 - 2020.” 7. Climate Change. Vol. 45. Umweltbundesamt. https://www.umweltbundesamt.de/sites/default/files/medien/5750/publikationen/2021-05-26_cc-45-2021_strommix_2021_0.pdf.
Ishwaran, Hemant, and Udaya B. Kogalur. 2020. randomForestSRC: Fast Unified Random Forests for Survival, Regression, and Classification (RF-SRC). https://CRAN.R-project.org/package=randomForestSRC.
Ishwaran, H., U. B. Kogalur, E. H. Blackstone, and M. S. Lauer. 2008. “Random Survival Forests.” Ann. Appl. Statist. 2 (3): 841–60. http://arXiv.org/abs/0811.1645v1.
Kartoun, U., K. E. Corey, T. G. Simon, H. Zheng, R. Aggarwal, K. Ng, and S. Y. Shaw. 2017. “The MELD-Plus: A Generalizable Prediction Risk Score in Cirrhosis.” PLOS ONE 12 (10): e0186301. https://doi.org/10.1371/journal.pone.0186301.
Katzman, J. L., U. Shaham, A. Cloninger, J. Bates, T. Jiang, and Y. Kluger. 2018. “DeepSurv: Personalized Treatment Recommender System Using a Cox Proportional Hazards Deep Neural Network.” BMC Med Res Methodol 18 (1): 24. https://doi.org/10.1186/s12874-018-0482-1.
Kim, W. R., S. W. Biggins, W. K. Kremers, R. H. Wiesner, P. S. Kamath, J. T. Benson, E. Edwards, and T. M. Therneau. 2008. “Hyponatremia and Mortality Among Patients on the Liver-Transplant Waiting List.” N Engl J Med 359 (10): 1018–26. https://doi.org/10.1056/NEJMoa0801209.
Kvamme, H., Ø. Borgan, and I. Scheel. 2019. “Time-to-Event Prediction with Neural Networks and Cox Regression.” J Mach Learn Res 20 (129): 1–30.
Lang, Michel, Martin Binder, Jakob Richter, Patrick Schratz, Florian Pfisterer, Stefan Coors, Quay Au, Giuseppe Casalicchio, Lars Kotthoff, and Bernd Bischl. 2019. “mlr3: A Modern Object-Oriented Machine Learning Framework in R.” Journal of Open Source Software, December. https://doi.org/10.21105/joss.01903.
Lang, Michel, Bernd Bischl, Jakob Richter, Patrick Schratz, and Martin Binder. 2022. Mlr3: Machine Learning in r - Next Generation. https://CRAN.R-project.org/package=mlr3.
Malinchoc, M., P. S. Kamath, F. D. Gordon, C. J. Peine, J. Rank, and P. C. J. Borg. 2000. “A Model to Predict Poor Survival in Patients Undergoing Transjugular Intrahepatic Portosystemic Shunts.” Hepatology 31 (4): 864–71. https://doi.org/10.1053/he.2000.5852.
Organ Procurement and Transplantation Network. 2021. “Policies.” 2021. https://optn.transplant.hrsa.gov/media/1200/optn_policies.pdf.
Ploeg, T. van der, P. C. Austin, and E. W. Steyerberg. 2014. “Modern Modelling Techniques Are Data Hungry: A Simulation Study for Predicting Dichotomous Endpoints.” BMC Med Res Methodol 14 (1). https://doi.org/10.1186/1471-2288-14-137.
R Core Team. 2022. R: A Language and Environment for Statistical Computing. Vienna, Austria: R Foundation for Statistical Computing. https://www.R-project.org/.
Remmler, J., C. Schneider, T. Treuner-Kaueroff, M. Bartels, D. Seehofer, M. Scholz, T. Berg, and T. Kaiser. 2017. “Increased Level of Interleukin 6 Associates with Increased 90-Day and 1-Year Mortality in Patients with End-Stage Liver Disease.” Clin Gastroenterol Hepatol 16 (5): 730–37. https://doi.org/10.1016/j.cgh.2017.09.017.
Sealock, J. M., I. A. Ziogas, Z. Zhao, F. Ye, S. P. Alexopoulos, L. Matsuoka, G. Chen, and L. K. Davis. 2022. “Proposing a Sex-Adjusted Sodium-Adjusted MELD Score for Liver Transplant Allocation.” JAMA Surg 157 (7): 618. https://doi.org/10.1001/jamasurg.2022.1548.
Simon, Noah, Jerome Friedman, Trevor Hastie, and Rob Tibshirani. 2011. “Regularization Paths for Cox’s Proportional Hazards Model via Coordinate Descent.” Journal of Statistical Software 39 (5): 1–13. https://doi.org/10.18637/jss.v039.i05.
Sjoberg, Daniel D., Michael Curry, Joseph Larmarange, Jessica Lavery, Karissa Whiting, and Emily C. Zabor. 2022. Gtsummary: Presentation-Ready Data Summary and Analytic Result Tables. https://CRAN.R-project.org/package=gtsummary.
Sjoberg, Daniel D., Karissa Whiting, Michael Curry, Jessica A. Lavery, and Joseph Larmarange. 2021. “Reproducible Summary Tables with the Gtsummary Package.” The R Journal 13: 570–80. https://doi.org/10.32614/RJ-2021-053.
Sonabend, Raphael. 2022. Survivalmodels: Models for Survival Analysis. https://github.com/RaphaelS1/survivalmodels/.
Sonabend, Raphael, Franz Kiraly, and Michel Lang. 2022. Mlr3proba: Probabilistic Supervised Learning for Mlr3.
Sonabend, Raphael, Franz J Király, Andreas Bender, Bernd Bischl, and Michel Lang. 2021. “Mlr3proba: An r Package for Machine Learning in Survival Analysis.” Bioinformatics, February. https://doi.org/10.1093/bioinformatics/btab039.
Terry M. Therneau, and Patricia M. Grambsch. 2000. Modeling Survival Data: Extending the Cox Model. New York: Springer.
Thabut, D., J. Massard, A. Gangloff, N. Carbonell, C. Francoz, E. Nguyen-Khac, C. Duhamel, D. Lebrec, T. Poynard, and R. Moreau. 2007. “Model for End-Stage Liver Disease Score and Systemic Inflammatory Response Are Major Prognostic Factors in Patients with Cirrhosis and Acute Functional Renal Failure.” Hepatology 46 (6): 1872–82. https://doi.org/10.1002/hep.21920.
Therneau, Terry M. 2022. Survival: Survival Analysis. https://github.com/therneau/survival.
Tibshirani, R. 1997. “The Lasso Method for Variable Selection in the Cox Model.” Stat Med 16 (4): 385–95. https://doi.org/10.1002/(sici)1097-0258(19970228)16:4<385::aid-sim380>3.0.co;2-3.
Trotter, J. F., B. Brimhall, R. Arjal, and C. Phillips. 2004. “Specific Laboratory Methodologies Achieve Higher Model for Endstage Liver Disease (MELD) Scores for Patients Listed for Liver Transplantation.” Liver Transpl 10 (8): 995–1000. https://doi.org/10.1002/lt.20195.
Wiesner, R., E. Edwards, R. Freeman, A. Harper, R. Kim, P. Kamath, W. Kremers, et al. 2003. “Model for End-Stage Liver Disease (MELD) and Allocation of Donor Livers.” Gastroenterology 124 (1): 91–96. https://doi.org/10.1053/gast.2003.50016.
Wright, Marvin N., Stefan Wager, and Philipp Probst. 2021. Ranger: A Fast Implementation of Random Forests. https://github.com/imbs-hl/ranger.
Wright, Marvin N., and Andreas Ziegler. 2017. “ranger: A Fast Implementation of Random Forests for High Dimensional Data in C++ and R.” Journal of Statistical Software 77 (1): 1–17. https://doi.org/10.18637/jss.v077.i01. 

sessionInfo()
R version 4.2.0 (2022-04-22)
Platform: x86_64-unknown-linux-gnu (64-bit)

Matrix products: default
BLAS/LAPACK: /gnu/store/ras6dprsw3wm3swk23jjp8ww5dwxj333-openblas-0.3.18/lib/libopenblasp-r0.3.18.so

locale:
 [1] LC_CTYPE=en_US.UTF-8       LC_NUMERIC=C              
 [3] LC_TIME=en_US.UTF-8        LC_COLLATE=en_US.UTF-8    
 [5] LC_MONETARY=en_US.UTF-8    LC_MESSAGES=en_US.UTF-8   
 [7] LC_PAPER=en_US.UTF-8       LC_NAME=C                 
 [9] LC_ADDRESS=C               LC_TELEPHONE=C            
[11] LC_MEASUREMENT=en_US.UTF-8 LC_IDENTIFICATION=C       

attached base packages:
[1] grid      stats     graphics  grDevices utils     datasets  methods  
[8] base     

other attached packages:
 [1] gtsummary_1.6.0   consort_1.0.1     timeROC_0.4       ameld_0.0.26     
 [5] survival_3.3-1    glmnet_4.1-4      Matrix_1.4-1      viridis_0.6.2    
 [9] viridisLite_0.4.0 mlr3viz_0.5.9     ggplot2_3.3.6     targets_0.12.1   

loaded via a namespace (and not attached):
 [1] fs_1.5.2                 bbotk_0.5.3              rprojroot_2.0.3         
 [4] mlr3pipelines_0.4.1      mlr3proba_0.4.11         numDeriv_2016.8-1.1     
 [7] tools_4.2.0              backports_1.4.1          bslib_0.3.1             
[10] utf8_1.2.2               R6_2.5.1                 mlr3_0.13.3             
[13] colorspace_2.0-3         withr_2.5.0              mlr3misc_0.10.0         
[16] tidyselect_1.1.2         gridExtra_2.3            processx_3.5.3          
[19] compiler_4.2.0           git2r_0.30.1             cli_3.3.0               
[22] ooplah_0.2.0             gt_0.6.0                 lgr_0.4.3               
[25] bookdown_0.26            sass_0.4.1               scales_1.2.0            
[28] checkmate_2.1.0          mvtnorm_1.1-3            pec_2022.05.04          
[31] callr_3.7.0              palmerpenguins_0.1.0     commonmark_1.8.0        
[34] mlr3tuning_0.13.1        stringr_1.4.0            digest_0.6.29           
[37] mlr3extralearners_0.5.37 rmarkdown_2.14           param6_0.2.4            
[40] paradox_0.9.0            set6_0.2.4               pkgconfig_2.0.3         
[43] htmltools_0.5.2          parallelly_1.31.1        highr_0.9               
[46] fastmap_1.1.0            rlang_1.0.2              shape_1.4.6             
[49] jquerylib_0.1.4          generics_0.1.2           jsonlite_1.8.0          
[52] dplyr_1.0.9              magrittr_2.0.3           Rcpp_1.0.8.3            
[55] munsell_0.5.0            fansi_1.0.3              lifecycle_1.0.1         
[58] stringi_1.7.6            whisker_0.4              yaml_2.3.5              
[61] parallel_4.2.0           dictionar6_0.1.3         listenv_0.8.0           
[64] promises_1.2.0.1         crayon_1.5.1             lattice_0.20-45         
[67] splines_4.2.0            knitr_1.39               ps_1.7.0                
[70] pillar_1.7.0             timereg_2.0.2            igraph_1.3.1            
[73] uuid_1.1-0               base64url_1.4            future.apply_1.9.0      
[76] codetools_0.2-18         glue_1.6.2               evaluate_0.15           
[79] broom.helpers_1.7.0      data.table_1.14.2        vctrs_0.4.1             
[82] httpuv_1.6.5             foreach_1.5.2            distr6_1.6.9            
[85] tidyr_1.2.0              gtable_0.3.0             purrr_0.3.4             
[88] future_1.26.1            xfun_0.31                prodlim_2019.11.13      
[91] later_1.3.0              tibble_3.1.7             iterators_1.0.14        
[94] workflowr_1.7.0          lava_1.6.10              globals_0.15.0          
[97] ellipsis_0.3.2