Introduction to MESuSiE
Boran Gao
2022-05-30
Last updated: 2022-11-08
Checks: 1 1
Knit directory: meSuSie_Analysis/
This reproducible R Markdown analysis was created with workflowr (version 1.7.0). The Checks tab describes the reproducibility checks that were applied when the results were created. The Past versions tab lists the development history.
The R Markdown file has unstaged changes. To know which version of
the R Markdown file created these results, you’ll want to first commit
it to the Git repo. If you’re still working on the analysis, you can
ignore this warning. When you’re finished, you can run
wflow_publish to commit the R Markdown file and build the
HTML.
Great! You are using Git for version control. Tracking code development and connecting the code version to the results is critical for reproducibility.
The results in this page were generated with repository version 21891c3. See the Past versions tab to see a history of the changes made to the R Markdown and HTML files.
Note that you need to be careful to ensure that all relevant files for
the analysis have been committed to Git prior to generating the results
(you can use wflow_publish or
wflow_git_commit). workflowr only checks the R Markdown
file, but you know if there are other scripts or data files that it
depends on. Below is the status of the Git repository when the results
were generated:
Unstaged changes:
Modified: analysis/_site.yml
Modified: analysis/about.Rmd
Modified: analysis/index.Rmd
Note that any generated files, e.g. HTML, png, CSS, etc., are not included in this status report because it is ok for generated content to have uncommitted changes.
These are the previous versions of the repository in which changes were
made to the R Markdown (analysis/index.Rmd) and HTML
(docs/index.html) files. If you’ve configured a remote Git
repository (see ?wflow_git_remote), click on the hyperlinks
in the table below to view the files as they were in that past version.
| File | Version | Author | Date | Message |
|---|---|---|---|---|
| Rmd | e369d34 | borangao | 2022-05-31 | wflow_git_commit(all = TRUE) |
| html | e369d34 | borangao | 2022-05-31 | wflow_git_commit(all = TRUE) |
| html | d41b59e | borangao | 2022-05-30 | Build site. |
| html | 8a1d176 | borangao | 2022-05-30 | Build site. |
| html | 8aa902e | borangao | 2022-05-30 | Build site. |
| Rmd | a1828a2 | borangao | 2022-05-30 | Start workflowr project. |
Introduction to MESuSiE
MESuSiE is a multiple ancestry extension of Sum of Single Effect model for GWAS fine-mapping. MESuSiE assumes that the causal SNPs are shared across ancestries, thought differ in effect size due to allele heterogeneity, and hence the power of analysis increases by jointly modelling the effect across ancestries. By leveraging the independent effect assumption of SuSie, MESuSiE models the correlation structure of the effect sizes of causal SNPs across ancestries, and therefore further improve the power of causal SNP detection.
MESuSiE Overview
MESuSiE relies on GWAS summary statistics from multiple ancestries, properly accounts for the LD structure of the focal genomic region in multiple ancestries, and explicitly models both shared and ancestry-specific causal signals to accommodate causal effect size similarity as well as heterogeneity across ancestries. MESuSiE outputs posterior inclusion probability of variant being shared or ancestry-specific causal variants.
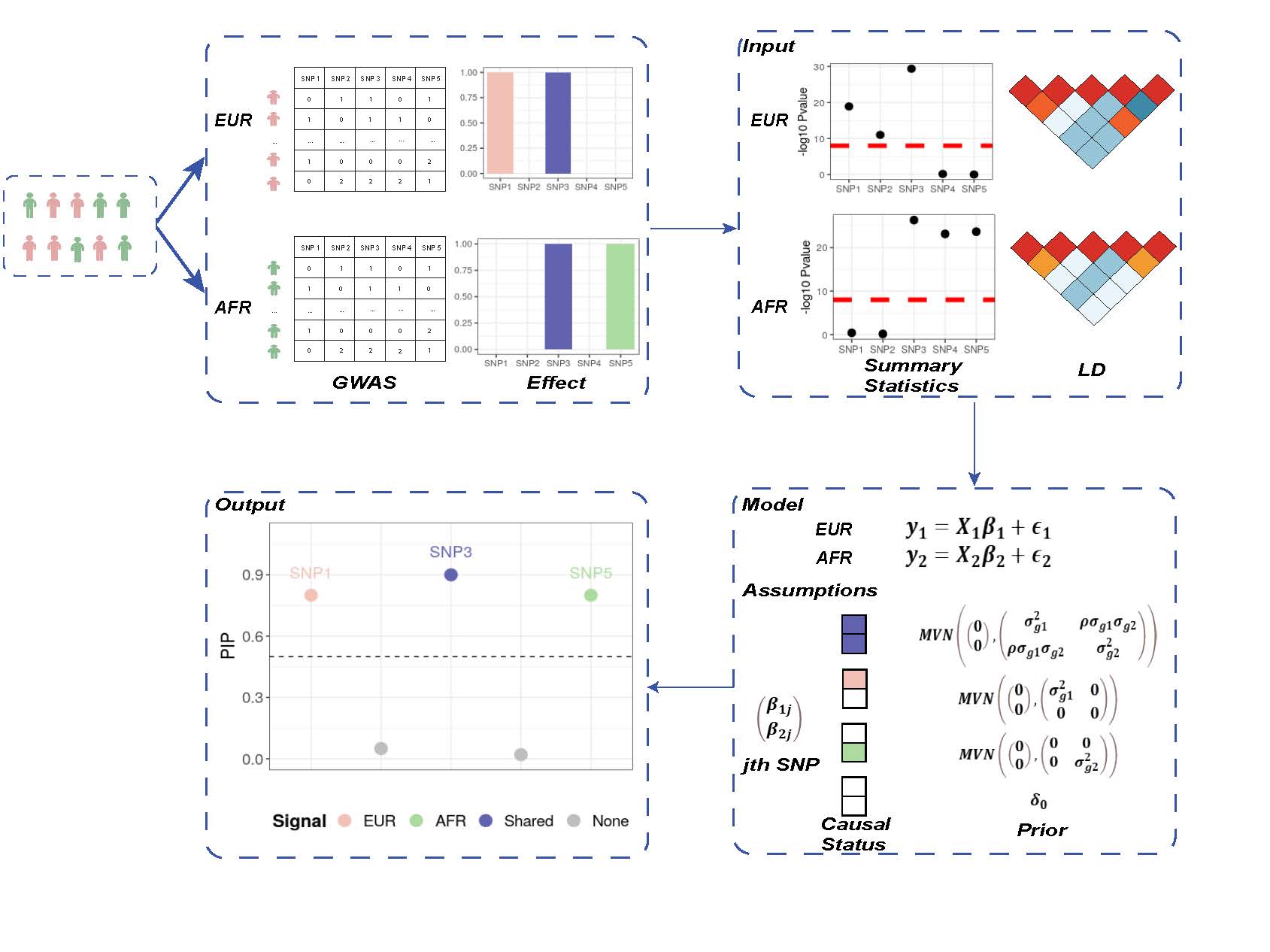
MESuSiE Model
MESuSiE builds upon the sum of single effect model, and extend the normal assumption on the effec size of causal SNP to multivariate normal, and thus capture the correlation across ancestries. fashion: \[ \left(\begin{matrix}{y}_\mathbf{1}\\{y}_\mathbf{2}\\\end{matrix}\right)=\left[\begin{matrix}{X}_\mathbf{1}&0\\0&{X}_\mathbf{2}\\\end{matrix}\right]\ast\left(\begin{matrix}{b}_\mathbf{1}\\{b}_\mathbf{2}\\\end{matrix}\right)+\left(\begin{matrix}{\epsilon}_\mathbf{1}\\{\epsilon}_\mathbf{2}\\\end{matrix}\right), \] In the above equation, \(y_1,y_2\) are standardized phenotype for each ancestry, \(X_1,X_2\) are centered genotype matrices, \(b_1,b_2\) are sum of the single effect models which are in the form, \[ \left(\begin{matrix}{b}_\mathbf{1}\\{b}_\mathbf{2}\\\end{matrix}\right) = \sum_l \gamma_l\bigotimes \left(z_l\cdot\left(\begin{matrix}{\beta}_\mathbf{1l}\\{\beta}_\mathbf{2l}\\\end{matrix}\right) \right) \] which represents the summation of the single effects.