Report

Objectives and the research question

While this research was inspired by the CinC/Physionet Challenge 2015, its purpose is not to beat the state-of-the-art on that challenge, but to identify, on streaming data, abnormal hearth electric patterns, specifically those which are life-threatening, using low CPU and low memory requirements in order to be able to generalize the use of such information on lower-end devices, outside the ICU, as ward devices, home devices, and wearable devices.

The main question is: can we accomplish this objective using a minimalist approach (low CPU, low memory) while maintaining robustness?

Principles

This research is being conducted using the Research Compendium principles¹:

1. Stick with the convention of your peers;
2. Keep data, methods, and output separated;
3. Specify your computational environment as clearly as you can.

Data management follows the FAIR principle (findable, accessible, interoperable, reusable)². Concerning these principles, the dataset was converted from Matlab’s format to CSV format, allowing more interoperability. Additionally, all the project, including the dataset, is in conformity with the Codemeta Project³.

Materials and methods

Softwares

Pipeline management

All process steps are managed using the R package targets⁴, from data extraction to the final report. An example of a pipeline visualization created with targets is shown in Fig. 1. This package helps to record the random seeds (allowing reproducibility), changes in some part of the code (or dependencies), and then run only the branches that need to be updated and several other features to keep a reproducible workflow avoiding unnecessary repetitions.

Figure 1: Figure 1 - Example of pipeline visualization using targets. From left to right we see ‘Stems’ (steps that do not create branches) and ‘Patterns’ (that contains two or more branches) and the flow of the information. The green color means that the step is up to date to the current code and dependencies.

Reports management

The report is available on the main webpage⁵, allowing inspection of previous versions managed by the R package workflowr⁶. This package complements the targets package by taking care of the versioning of every report. It is like a Log Book that keeps track of every important milestone of the project while summarizing the computational environment where it was run. Fig. 2 shows only a fraction of the generated website, where we can see that this version passed the required checks (the system is up-to-date, no caches, session information was recorded, and others), and we see a table of previous versions.

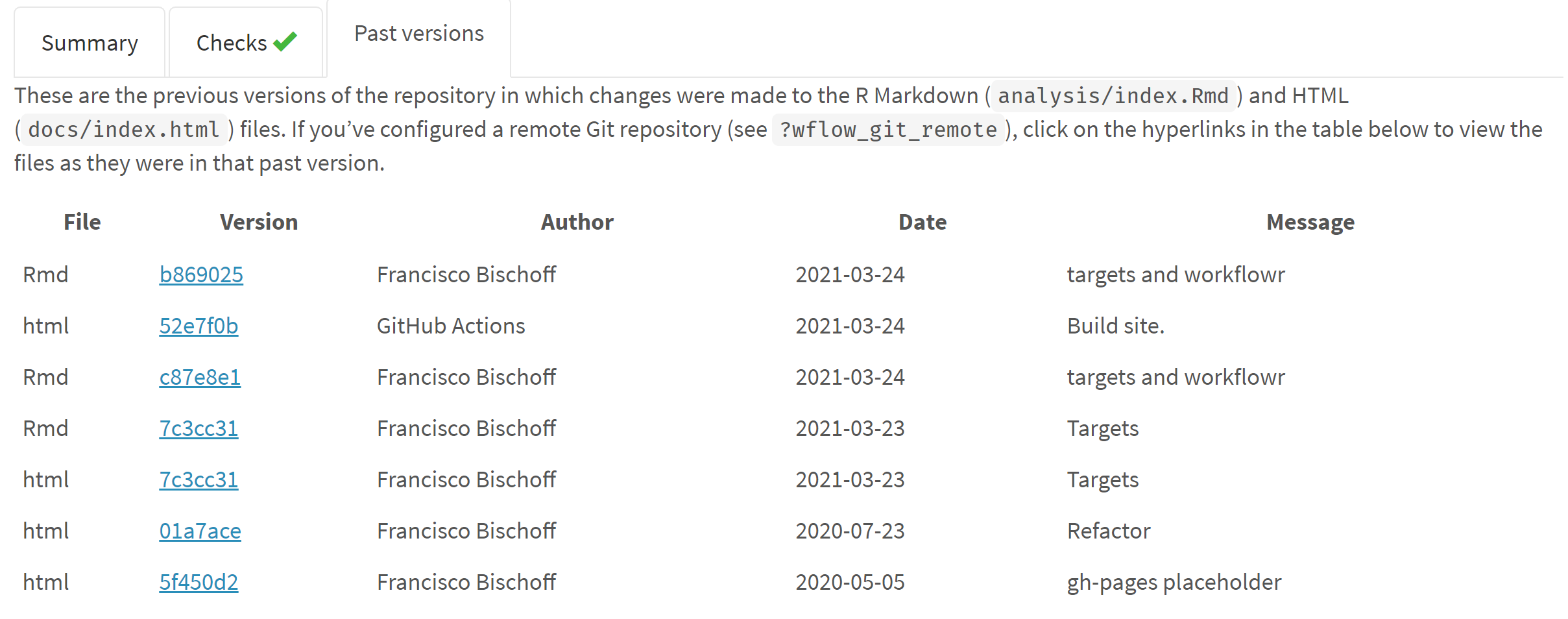
Figure 2: Figure 2 - Fraction of the website generated by workflowr. On top we see that this version passed all checks, and in the middle we see a table referring to the previous versions of the report.

Modeling and parameter tuning

The well-known package used for data science in R is the caret (short for Classification And REgression Training)⁷. Nevertheless, the author of caret recognizes several limitations of his (great) package and is now in charge of developing the tidymodels⁸ collection. For sure, there are other available frameworks and opinions⁹. Notwithstanding, this project will follow the tidymodels road. Three significant arguments 1) constantly improving and constantly being re-checked for bugs; large community contribution; 2) allows to plug in a custom modeling algorithm that, in this case, will be the one needed for developing this work; 3) caret is not in active development.

Continuous integration

Meanwhile, the project pipeline has been set up on GitHub, Inc.¹⁰, leveraging Github Actions¹¹ for the Continuous Integration lifecycle. The repository is available at¹⁰, and the resulting report is available at⁵. This thesis’s roadmap and tasks status are also publicly available on Zenhub¹².

Developed software

Matrix Profile

Matrix Profile (MP)¹³ is a state-of-the-art^14,15 time series analysis technique that, once computed, allows us to derive frameworks to all sorts of tasks, as motif discovery, anomaly detection, regime change detection, and others¹³.

Before MP, time series analysis relied on the distance matrix (DM), a matrix that stores all the distances between two time series (or itself, in the case of a Self-Join). This was very power-consuming, and several pruning and dimensionality reduction methods were researched¹⁶.

For brevity, let’s just understand that the MP and the companion Profile Index (PI) are two vectors that hold one floating-point value and one integer value, respectively, regarding the original time series: (1) the similarity distance between that point on time (let’s call these points “indexes”) and its first nearest-neighbor (1-NN), (2) The index where this 1-NN is located. The original paper has more detailed information¹³. It is computed using a rolling window, but instead of creating a whole DM, only the minimum values and the index of these minima are stored (in the MP and PI, respectively). We can have an idea of the relationship of both on Fig. 3.

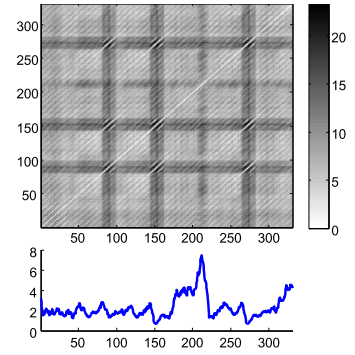
Figure 3: Figure 3 - A distance matrix (top), and a matrix profile (bottom). The matrix profile stores only the minimum values of the distance matrix.

This research has already yielded two R packages concerning the MP algorithms from UCR¹⁷. The first package is called tsmp, and a paper has also been published in the R Journal¹⁸ (Journal Impact Factor™, 2020 of 3.984). The second package is called matrixprofiler and enhances the first one, using low-level language to improve computational speed. The author has also joined the Matrix Profile Foundation as a co-founder with contributors from Python and Go languages^19,20.

This implementation in R is being used for computing the MP and MP-based algorithms of this thesis.

The data

The current dataset used is the CinC/Physionet Challenge 2015 public dataset, modified to include only the actual data and the header files in order to be read by the pipeline and is hosted by Zenodo²¹ under the same license as Physionet.

The dataset is composed of 750 patients with at least five minutes records. All signals have been resampled (using anti-alias filters) to 12 bit, 250 Hz, FIR band-pass (0.05 to 40Hz), and mains notch filters applied to remove noise. Pacemaker and other artifacts are still present on the ECG²². Furthermore, this dataset contains at least two ECG derivations and one or more variables like arterial blood pressure, photoplethysmograph readings, and respiration movements.

The events we seek to identify are the life-threatening arrhythmias as defined by Physionet in Table 1.

Table 1: Table 1 - Definition of the five alarm types used in CinC/Physionet Challenge 2015.

Alarm	Definition
Asystole	No QRS for at least 4 seconds
Extreme Bradycardia	Heart rate lower than 40 bpm for 5 consecutive beats
Extreme Tachycardia	Heart rate higher than 140 bpm for 17 consecutive beats
Ventricular Tachycardia	5 or more ventricular beats with heart rate higher than 100 bpm
Ventricular Flutter/Fibrillation	Fibrillatory, flutter, or oscillatory waveform for at least 4 seconds

The fifth minute is precisely where the alarm has been triggered on the original recording set. To meet the ANSI/AAMI EC13 Cardiac Monitor Standards²³, the onset of the event is within 10 seconds of the alarm (i.e., between 4:50 and 5:00 of the record). That doesn’t mean that there have been no other arrhythmias before.

For comparison, on Table 2 we collected the score of the five best participants of the challenge^24–28.

Table 2: Table 2 - Challenge Results on real-time data. The scores were multiplied by 100.

Score	Authors
81.39	Filip Plesinger, Petr Klimes, Josef Halamek, Pavel Jurak
79.44	Vignesh Kalidas
79.02	Paula Couto, Ruben Ramalho, Rui Rodrigues
76.11	Sibylle Fallet, Sasan Yazdani, Jean-Marc Vesin
75.55	Christoph Hoog Antink, Steffen Leonhardt

The Equation used on this challenge to compute the score of the algorithms is in the Equation \(\eqref{score}\). This Equation is the accuracy formula, with the penalization of the false negatives. The reasoning pointed out by the authors²² is the clinical impact of existing an actual life-threatening event that was considered unimportant. Accuracy is known to be misleading when there is a high class imbalance²⁹.

\[ Score = \frac{TP+TN}{TP+TN+FP+5*FN} \tag{1} \label{score} \]

Assuming that this is a finite dataset, the pathologic cases (1) \(\lim_{TP \to \infty}\) (whenever there is an event, it is positive) or (2) \(\lim_{TN \to \infty}\) (whenever there is an event, it is false), cannot happen. This dataset has 292 True alarms and 458 False alarms. Experimentally, this equation yields:

• 0.24 if all guesses are on False class
• 0.28 if random guesses
• 0.39 if all guesses are on True class
• 0.45 if no false positives plus random on True class
• 0.69 if no false negatives plus random on False class

This small experiment (knowing the data in advance) shows that “a single line of code and a few minutes of effort”³⁰ algorithm could achieve at most a score of 0.39 in this challenge (the last two lines, the algorithm must be very good on one class).

Nevertheless, this Equation will only be helpful to allow us to compare the results of this thesis with other algorithms.

Work structure

Project start

The project started with a literature survey on the databases Scopus, PubMed, Web of Science, and Google Scholar with the following query (the syntax was adapted for each database):

TITLE-ABS-KEY ( algorithm OR ‘point of care’ OR ‘signal processing’ OR ‘computer assisted’ OR ‘support vector machine’ OR ‘decision support system’ OR ’neural network’ OR ‘automatic interpretation’ OR ‘machine learning’) AND TITLE-ABS-KEY ( electrocardiography OR cardiography OR ‘electrocardiographic tracing’ OR ecg OR electrocardiogram OR cardiogram ) AND TITLE-ABS-KEY ( ‘Intensive care unit’ OR ‘cardiologic care unit’ OR ‘intensive care center’ OR ‘cardiologic care center’ )

The inclusion and exclusion criteria were defined as in Table 3.

Table 3: Table 3 - Literature review criteria.

Inclusion criteria	Exclusion criteria
ECG automatic interpretation	Manual interpretation
ECG anomaly detection	Publication older than ten years
ECG context change detection	Do not attempt to identify life-threatening arrhythmias, namely asystole, extreme bradycardia, extreme tachycardia, ventricular tachycardia, and ventricular flutter/fibrillation
Online Stream ECG analysis	No performance measurements reported
Specific diagnosis (like a flutter, hyperkalemia, etc.)

The survey is being conducted with peer review; all articles on full-text phase were obtained and assessed for the extraction phase, except 5 articles that were not available. Due to external factors, the survey is currently stalled in the Data Extraction phase.

Fig. 4 shows the flow diagram of the resulting screening using PRISMA format.

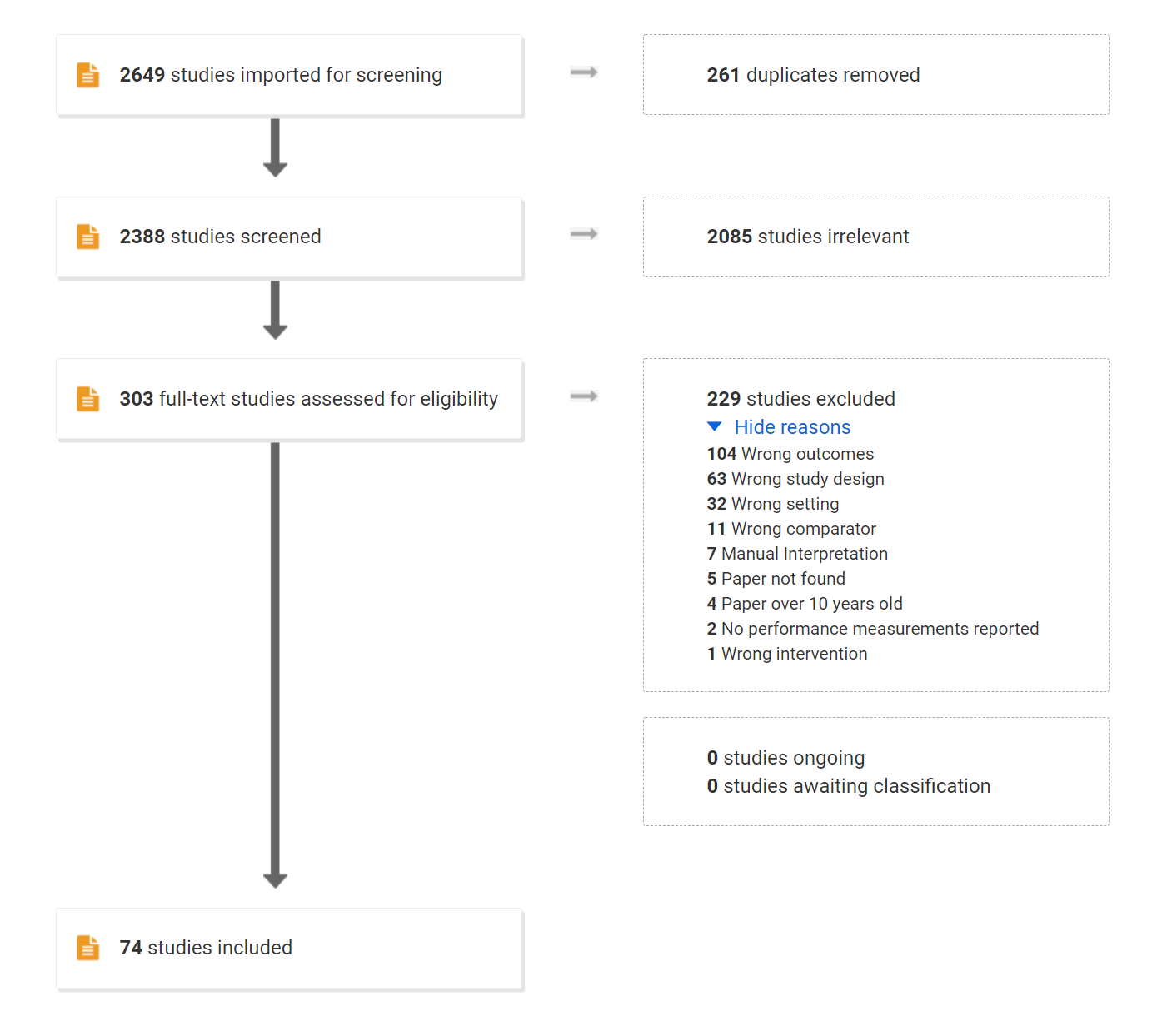
Figure 4: Figure 2 - Flowchart of the literature survey.

The peer review is being conducted by the author of this thesis and another colleague, Dr. Andrew Van Benschoten, from the Matrix Profile Foundation¹⁹.

Table. 4 shows the Inter-rater Reliability (IRR) of the screening phases, using Cohen’s \(\kappa\) statistic. The bottom line shows the estimated accuracy after correcting possible confounders³¹.

Table 4 - Inter-rater Reliability on the literature survey process.

		Title-Abstract (2388 articles)			Full-Review (303 articles)
		Reviewer #2			Reviewer #2
		Include	Exclude		Include	Exclude
Reviewer #1	Include	185	381		63	58
	Exclude	129	1693		13	169
Cohen’s omnibus \(\kappa\)		0.30			0.48
Maximum possible \(\kappa\)		0.66			0.67
Std Err for \(\kappa\)		0.02			0.05
Observed Agreement		79%			77%
Random Agreement		69%			55%
Agreement corrected with KappaAcc		82%			85%

The purpose of using Cohen’s \(\kappa\) in such a review is to allow us to gauge the agreement of both reviewers on the task of selecting the articles according to the goal of the survey. The most naive way to verify this would be simply to measure the overall agreement (the number of articles included and excluded by both, divided by the total number of articles). Nevertheless, this would not take into account the agreement we could expect purely by chance.

However, the \(\kappa\) statistic must be assessed carefully. This topic is beyond the scope of this work therefore it will be explained briefly.

While it is widely used, the \(\kappa\) statistic is well criticized. The direct interpretation of its value depends on several assumptions that are often violated. (1) It is assumed that both reviewers have the same level of experience; (2) The “codes” (include, exclude) are identified with same accuracy; (3) The “codes” prevalences are the same; (4) There is no reviewer bias towards one of the choices^32,33.

In addition, the number of “codes” affects the relation between the value of \(\kappa\) and the actual agreement between the reviewers. For example, given equiprobable “codes” and reviewers who are 85% accurate, the value of \(\kappa\) are 0.49, 0.60, 0.66, and 0.69 when number of codes is 2, 3, 5, and 10, respectively^33,34.

To take into account these limitations, the agreement between reviewers was calculated using the KappaAcc³¹ from Professor Emeritus Roger Bakeman, Georgia State University, which computes the estimated accuracy of simulated reviewers.

RAW data

To better understand the data acquisition, it has been acquired a Single Lead Heart Rate Monitor breakout from Sparkfun™³⁵ using the AD8232³⁶ microchip from Analog Devices Inc., compatible with Arduino^®37, for an in-house experiment (Fig. 5).

Figure 5: Figure 5 - Single Lead Heart Rate Monitor

The output gives us a RAW signal, as shown in Fig. 6.

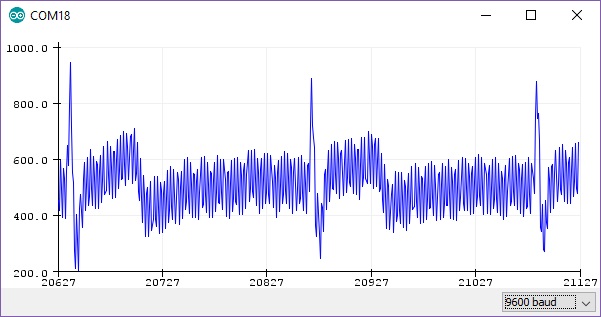
Figure 6: Figure 6 - RAW output from Arduino at ~300hz

After applying the same settings as the Physionet database (collecting the data at 500hz, resample to 250hz, pass-filter, and notch filter), the signal is much better, as shown in Fig. 7.

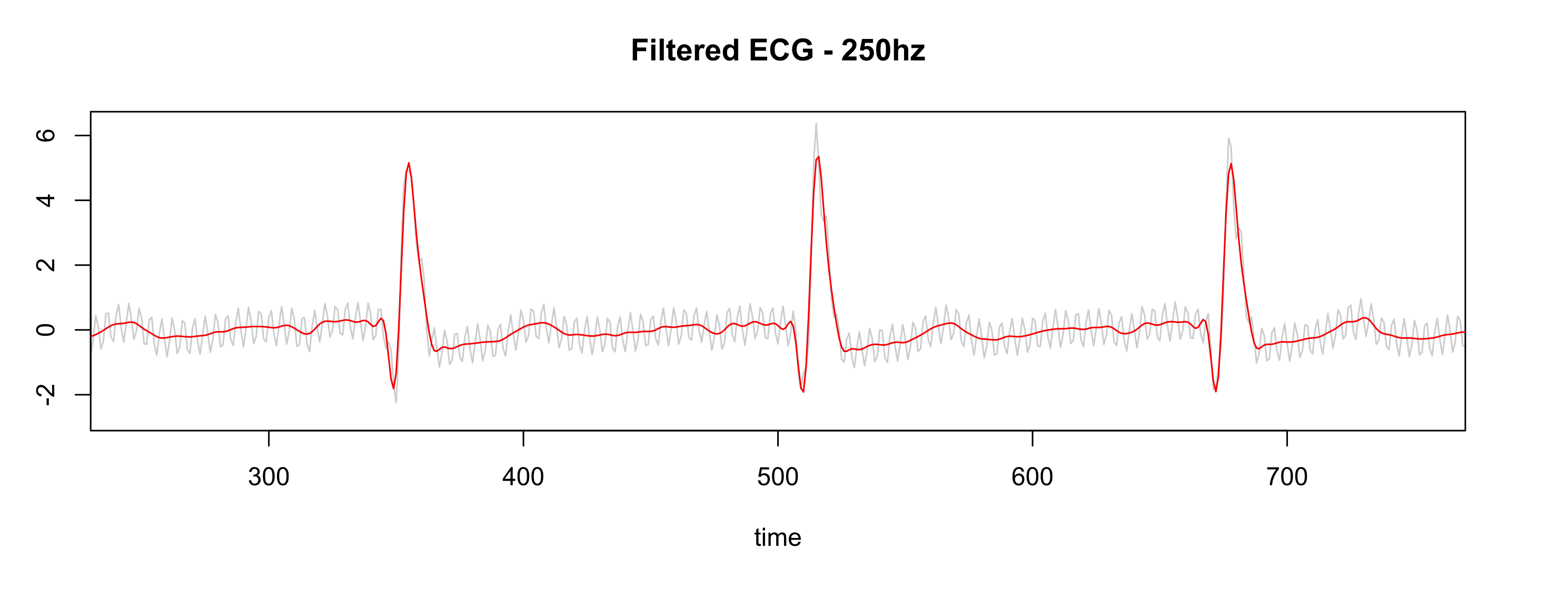
Figure 7: Figure 7 - Gray is RAW, Red is filtered

Preparing the data

Usually, data obtained by sensors needs to be “cleaned” for proper evaluation. That is different from the initial filtering process where the purpose is to enhance the signal. Here we are dealing with artifacts, disconnected cables, wandering baselines and others.

Several SQIs (Signal Quality Indexes) are used in the literature³⁸, some trivial measures as kurtosis, skewness, median local noise level, other more complex as pcaSQI (the ratio of the sum of the five largest eigenvalues associated with the principal components over the sum of all eigenvalues obtained by principal component analysis applied to the time aligned ECG segments in the window). An assessment of several different methods to estimate electrocardiogram signal quality can was performed by Del Rio, et al³⁹.

By experimentation (yet to be validated), a simple formula gives us the “complexity” of the signal and correlates well with the noisy data is shown in Equation \(\eqref{complex}\)⁴⁰.

\[ \sqrt{\sum_{i=1}^w((x_{i+1}-x_i)^2)}, \quad \text{where}\; w \; \text{is the window size} \tag{2} \label{complex} \]

Fig. 8 shows some SQIs and their relation with the data.

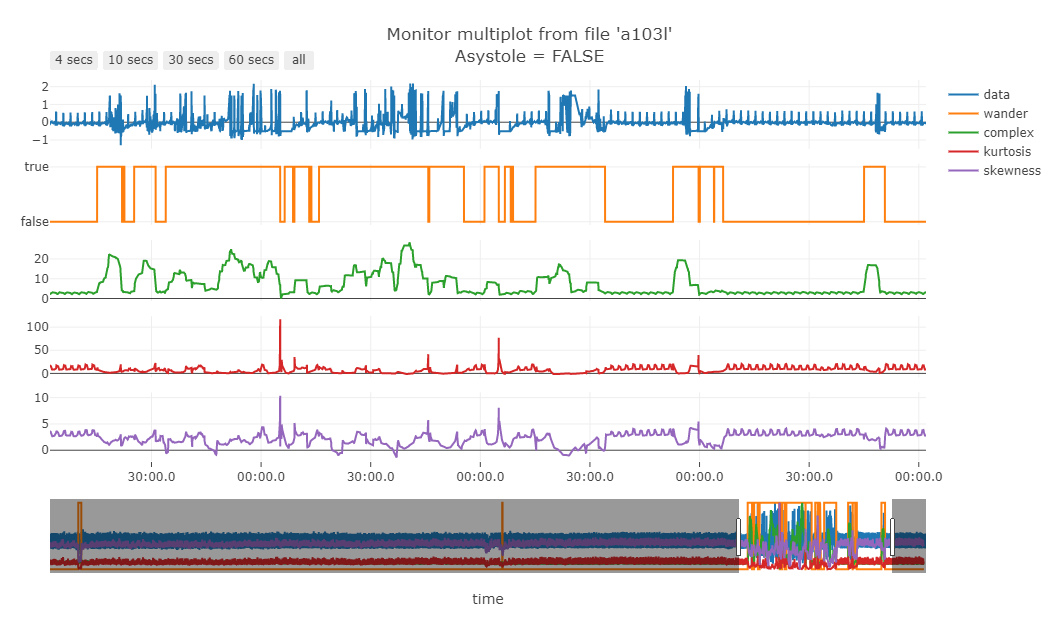
Figure 8: Figure 8 - Green line is the “complexity” of the signal

Fig. 9 shows that noisy data (probably patient muscle movements) are marked with a blue point and thus are ignored by the algorithm.

Figure 9: Figure 9 - Noisy data marked by the “complexity” filter

Although this step of “cleaning” the data is often used, this step will also be tested if it is really necessary, and the performance with and without “cleaning” will be reported.

Detecting regime changes

The regime change approach will be using the Arc Counts concept, used on the FLUSS (Fast Low-cost Unipotent Semantic Segmentation) algorithm, as explained by Gharghabi, et al.,⁴¹.

The FLUSS (and FLOSS, the online version) algorithm is built on top of the Matrix Profile (MP)¹³, described on section 1. Recalling that the MP and the companion Profile Index (PI) are two vectors holding information about the 1-NN. One can imagine several “arcs” starting from one “index” to another. This algorithm is based on the assumption that between two regimes, the most similar shape (its nearest neighbor) is located on “the same side”, so the number of “arcs” decreases when there is a change in the regime and increases again. As show on Fig. 10. This drop on the Arc Counts is a signal that a change in the shape of the signal has happened.

Figure 10: Figure 10 - FLUSS algorithm, using arc counts.

The choice of the FLOSS algorithm (the online version of FLUSS) is founded on the following arguments:

• Domain Agnosticism: the algorithm makes no assumptions about the data as opposed to most available algorithms to date.
• Streaming: the algorithm can provide real-time information.
• Real-World Data Suitability: the objective is not to explain all the data. Therefore, areas marked as “don’t know” areas are acceptable.
• FLOSS is not: a change point detection algorithm⁴². The interest here is changes in the shapes of a sequence of measurements.

Other algorithms we can cite are based on Hidden Markov Models (HMM) that require at least two parameters to be set by domain experts: cardinality and dimensionality reduction. The most attractive alternative could be the Autoplait⁴³, which is also domain agnostic and parameter-free. It segments the time series using Minimum Description Length (MDL) and recursively tests if the region is best modeled by one or two HMM. However, Autoplait is designed for batch operation, not streaming, and also requires discrete data. FLOSS was demonstrated to be superior in several datasets in its original paper. In addition, FLOSS is robust to several changes in data like downsampling, bit depth reduction, baseline wandering, noise, smoothing, and even deleting 3% of the data and filling with simple interpolation. Finally, the most important, the algorithm is light and suitable for low-power devices.

In the MP domain, it is worth also mentioning another possible algorithm: the Time Series Snippets⁴⁴, based on MPdist⁴⁵. The MPdist measures the distance between two sequences, considering how many similar sub-sequences they share, no matter the matching order. It proved to be a useful measure (not a metric) for meaningfully clustering similar sequences. Time Series Snippets exploits MPdist properties to summarize a dataset extracting the \(k\) sequences representing most of the data. The final result seems to be an alternative for detecting regime changes, but it is not. The purpose of this algorithm is to find which pattern(s) explains most of the dataset. Also, it is not suitable for streaming data. Lastly, MPdist is quite expensive compared to the trivial Euclidean distance.

The regime change detection will be evaluated following the criteria explained in section 1.

Classification of the new regime

The next step towards the objective of this work is to verify if the new regime detected by the previous step is indeed a life-threatening pattern that we should trigger the alarm.

First, let’s dismiss some apparent solutions: (1) Clustering. It is well understood that we cannot cluster time series subsequences meaningfully with any distance measure or with any algorithm⁴⁶. The main argument is that in a meaningful algorithm, the output depends on the input, and this has been proven to not happen in time series subsequence clustering⁴⁶. (2) Anomaly detection. In this work, we are not looking for surprises but for patterns that are known to be life-threatening. (3) Forecasting. We may be tempted to make predictions, but this clearly is not the idea here.

The method of choice is classification. The simplest algorithm could be a TRUE/FALSE binary classification. Nevertheless, the five life-threatening patterns have well-defined characteristics that may seem more plausible to classify the new regime using some kind of ensemble of binary classifiers or a “six-class” classifier (the sixth class being the FALSE class).

Since the model doesn’t know which life-threatening pattern will be present in the regime (or if it will be a FALSE case), the model will need to check for all five TRUE cases, and if none of these cases are identified, it will classify the regime as FALSE.

To avoid exceeding processor capacity, an initial set of shapelets⁴⁷ can be sufficient to build the TRUE/FALSE classifier. And to build such a set of shapelets, leveraging on the MP, we will use the Contrast Profile⁴⁸.

The Contrast Profile (CP) looks for patterns that are at the same time very similar to its neighbors in class A while is very different from the nearest neighbor from class B. In other words, this means that such a pattern represents well class A and may be taken as a “signature” of that class.

In this case, we need to compute two MP, one self-join MP using the positive class \(MP^{(++)}\) (the class that has the signature we want to find) and one AB-join MP using the positive and negative classes \(MP^{(+-)}\). Then we subtract the first \(MP^{(++)}\) from the last \(MP^{(+-)}\), resulting in the \(CP\). The high values on \(CP\) are the locations for the signature candidates we look for (the author of CP calls these segments Plato’s).

Due to the nature of this approach, the MP’s (containing values in Euclidean Distance) are truncated for values above \(\sqrt{2w}\), where \(w\) is the window size. This is because values above this threshold are negatively correlated in the Pearson Correlation space. Finally, we normalize the values by \(\sqrt{2w}\). The formula \(\eqref{contrast}\) synthesizes this computation.

\[ CP_w = \frac{MP_{w}^{(+-)} - MP_{w}^{(++)}}{\sqrt{2w}} \quad \text{where}\; w \; \text{is the window size} \tag{3} \label{contrast} \]

For a more complete understanding of the process, Fig. 11 shows a practical example from the original article⁴⁸.

Figure 11: Figure 11 - Top to bottom: two weakly-labeled snippets of a larger time series. T(-) contains only normal beats. T(+) also contains PVC (premature ventricular contractions). Next, two Matrix Profiles with window size 91; AB-join is in red and self-join in blue. Bottom, the Contrast Profile showing the highest location.

After extracting candidates for each class signature, a classification algorithm will be fitted and evaluated using the criteria explained on section 1.

Summary of the methodology

To summarize the steps taken on this thesis to accomplish the main objective, Figs. 12, 13 and 14 show the overview of the processes involved.

First, let us introduce the concept of Nested Resampling⁴⁹. It is known that when increasing model complexity, overfitting on the training set becomes more likely to happen⁵⁰. This is an issue that this work has to countermeasure as many steps require parameter tuning, even for almost parameter-free algorithms, like the MP.

The rule that must be followed is simple: do not evaluate a model on the same resampling split used to perform its own parameter tuning. Using simple cross-validation, the information about the test set “leaks” into the evaluation, leading to overfitting/overtuning, and gives us an optimistic biased estimate of the performance. Bernd Bischl, 2012⁴⁹ describes more deeply these factors and also provides us with a countermeasure for that: (1) from preprocessing the data to model selection use the training set; (2) the test set should be touched once, on the evaluation step; (3) repeat. This guarantees that a “new” separated data is only used after the model is trained/tuned.

Fig. 15 shows us this principle. The steps (1) and (2) described above are part of the Outer resampling, which in each loop splits the data into two sets: the training set and the test set. The training set is then used in the Inner resampling where, for example, the usual cross-validation may be used (creating an Analysis set and an Assessment set to avoid terminology conflict), and the best model/parameters are selected. Then, this best model is evaluated against the unseen test set created for this resampling.

The resulting (aggregated) performance of all outer samples gives us a more honest estimative of the expected performance on new data.

Figure 12: Figure 15 - Nested resampling. The full dataset is resampled several times (outer resampling), so each branch has its own Test set (yellow). On each branch, the Training set is used as if it were a full dataset, being resampled again (inner resampling); here, the Assessment set (blue) is used to test the learning model and tune parameters. The best model is finally evaluated on its own Test set.

After the understanding of the Nested Resampling⁴⁹, the following flowcharts can be better interpreted. Fig. 12 starts with the “Full Dataset” that contains all time series from the dataset described in section 1. Each time series represents one file from the database and represents one patient.

The regime change detection will use subsampling (bootstrapping can lead to substantial bias toward more complex models) in the Outer resampling and cross-validation in the Inner resampling. How the evaluation will be performed and why the use of cross-validation will be explained in section 1.

Figure 13: Figure 12 - Pipeline for regime change detection. The full dataset (containing several patients) is divided into a Training set and a Test set. The Training set is then resampled in an Analysis set and an Assessment set. The former is used for training/parameter tuning and the latter for assessing the result. The best parameters are then used for evaluation on the Test set. This may be repeated several times.

Fig. 13 shows the processes for training the classification model. First, the last ten seconds of each time series will be identified (the event occurs in this segment). Then the dataset will be grouped by class (type of event) and TRUE/FALSE (alarm), so the Outer/Inner resampling will produce a Training/Analysis set and Test/Assessment set with similar frequency to the full dataset.

The next step will be to extract shapelet candidates using the Contrast Profile and train the classifier.

This pipeline will use subsampling (for the same reason above) in the Outer resampling and cross-validation in the Inner resampling. How the evaluation will be performed and why the use of cross-validation will be explained in section 1.

Figure 14: Figure 13 - Pipeline for alarm classification. The full dataset (containing several patients) is grouped by class and by TRUE/FALSE alarm. This grouping allows resampling to keep a similar frequency of classes and TRUE/FALSE of the full dataset. Then the full dataset is divided on a Training set and a Test set. The Training set is then resampled in an Analysis set and an Assessment set. The former is used for extracting shapelets, training the model and parameter tuning; the latter for assessing the performance of the model. Finally, the best model is evaluated on the Test set. This may be repeated several times.

Finally, Fig. 14 shows how the final model will be used on the field. In a streaming scenario, the data will be collected and processed in real-time to maintain an up to date Matrix Profile. The FLOSS algorithm will be looking for a regime change. When a regime change is detected, a sample of this new regime will be presented to the trained classifier that will evaluate if this new regime is a life-threatening condition or not.

Figure 15: Pipeline of the final process. The streaming data, coming from one patient, is processed to create its Matrix Profile. Then, the FLOSS algorithm is computed for detecting a regime change. When a new regime is detected, a sample of this new regime is analysed by the model and a decision is made. If the new regime is life-threatening, the alarm will be fired.

Evaluation of the algorithms

The subsampling method used on both algorithms, regime change, and classification, will be the Cross-Validation, as the learning task will be in batches.

Other options dismissed⁴⁹:

• Leave-One-Out Cross-Validation: has better properties for regression than for classification. It has a high variance as an estimator of the mean loss. It also is asymptotically inconsistent and tends to select too complex models. It is demonstrated empirically that 10-fold CV is often superior.

• Bootstrapping: while it has low variance, it may be optimistic-biased on more complex models. Also, its resampling method with replacement can leak information into the assessment set.

• Subsampling: is like bootstrapping, but without replacement. The only argument for not choosing it is that we make sure all the data is used for analysis and assessment with Cross-Validation.

Regime change

A detailed discussion about the evaluation process of segmentation algorithms is made by the FLUSS/FLOSS author⁴¹. Previous researches have used precision/recall or derived measures for performance. The main issue is how to assume that the algorithm was correct? Is this a miss if the ground truth says the change occurred at location 10,000, and the algorithm detects a change at location 10,001?

As pointed out by the author, several independent researchers have suggested a temporal tolerance, that solves one issue but has a hard time penalizing any tiny miss beyond this tolerance.

The second issue is an over-penalization of an algorithm in which most of the detections are good, but just one (or a few) is poor.

The author proposes the solution depicted in Fig. 16. It gives 0 as the best score and 1 as the worst. The function sums the distances between the ground truth locations and the locations suggested by the algorithm. The sum is then divided by the length of the time series to normalize the range to [0, 1].

The goal is to minimize this score.

Figure 16: Figure 16 - Regime change evaluation. The top line illustrates the ground truth, and the bottom line the locations reported by the algorithm. Note that multiple proposed locations can be mapped to a single ground truth point.

Classification

As described in section 1, the model for classification will use a set of shapelets to identify if we have a TRUE (life-threatening) regime or a FALSE (non-life-threatening) regime.

Although the implementation of the final process will be using streaming data, the classification algorithm will work in batches because it will not be applied on every single data point but on samples that are extracted when a regime change is detected. During the training phase, the data is also analyzed in batches.

One important factor we must consider is that, in real-world, the majority of regime changes will be FALSE (i.e., not life-threatening). Thus, a performance measure that is robust to class imbalance is needed if we want to assess the model after it was trained on the field.

It is well known that the Accuracy measure is not reliable for unbalanced data^29,51 as it returns optimistic results for a classifier on the majority class. A description of common measures used on classification is available^29,52. Here we will focus on three candidate measures that can be used: F-score (well discussed on⁵²), Matthew’s Correlation Coefficient (MCC)⁵³ and \(\kappa_m\) statistic⁵⁴.

The F-score (let’s abbreviate to F₁ as this is the more common setting) is widely used on information retrieval, where the classes are usually classified as “relevant” and “irrelevant”, and combines the recall (also known as sensitivity) and the precision (the positive predicted value). Recall assess how well the algorithm retrieves relevant examples among the (usually few) relevant items in the dataset. In contrast, precision assesses the proportion of indeed relevant items which are contained in the retrieved examples. It ranges from [0, 1]. It completely ignores the irrelevant items that were not retrieved (usually, this set contains many items). In classification tasks, its main weakness is not evaluating the True Negatives. If the proportion of a random classifier gets towards the TRUE class (increasing the False Positives significantly), this score actually gets better, thus not suitable to our case. The F₁ score is defined on Equation \(\eqref{score}\).

\[ F_1 score = \frac{2 \cdot TP}{2 \cdot TP + FP + FN} = 2 \cdot \frac{precision \cdot recall}{precision + recall} \tag{4} \label{fscore} \]

The MCC is a good alternative to the F₁ when we do care about the True negatives (both were considered to “provide more realistic estimates of real-world model performance”⁵⁵). It is a method to compute the Pearson product-moment correlation coefficient⁵⁶ between the actual and predicted values. It ranges from [-1, 1]. The MCC is the only binary classification rate that only gives a high score if the binary classifier correctly classified the majority of the positive and negative instances⁵². One may argue that Cohen’s \(\kappa\) has the same behavior. Still, there are two main differences (1) MCC is undefined in the case of a majority voter. At the same time, Cohen’s \(\kappa\) doesn’t discriminate this case from the random classifier (\(\kappa\) is zero for both cases). (2) It is proven that in a special case when the classifier is increasing the False Negatives, Cohen’s \(\kappa\) doesn’t get worse as expected, MCC doesn’t have this issue⁵⁶. MCC is defined on equation \(\eqref{mccval}\).

\[ MCC = \frac{TP \cdot TN - FP \cdot FN}{\sqrt{(TP + FP) \cdot (TP + FN) \cdot (TN + FP) \cdot (TN + FN)}} \tag{5} \label{mccval} \]

The \(\kappa_m\) statistic⁵⁴ is a measure that considers not the random classifier but the majority voter (a classifier that only votes on the larger class). It was introduced by Bifet et al.⁵⁴ for being used in online settings, where the class balance may change over time. It is defined on Equation \(\eqref{kappam}\), where \(p_0\) is the observed accuracy, and \(p_m\) is the accuracy of the majority voter. Theoretically, the score ranges from (\(-\infty\), 1]. Still, in practice, you see negative numbers if the classifier performs worse than the majority voter and positive numbers if performing better than the majority number until the maximum of 1 when the classifier is optimal.

\[ \kappa_m = \frac{p_0 - p_m}{1 - p_m} \tag{6} \label{kappam} \]

In the inner resampling (model training/tuning), the classification will be binary, and in our case, we know that the data is slightly unbalanced (60% false alarms). For this step, the metric for model selection will be the MCC. Nevertheless, during the optimization process, the algorithm will seek to minimize the False Negative Rate (\(FNR = \frac{FN}{TP+FN}\)), and between ties, the smaller FNR wins.

In the outer resampling, the MCC and \(\kappa_m\) of all winning models will aggregate and report using the median and interquartile range.

For different classifiers, we will use Wilcoxon’s signed-rank test for comparing their performances. This method is known to have low Type I and Type II errors in this kind of comparison⁵⁴.

Full model (streaming setting)

For the final assessment, the best and the average model of the previous pipelines will be assembled and tested using the whole original dataset.

The algorithm will be tested in each of the five life-threatening events split individually in order to evaluate its strengths and weakness.

For more transparency, the whole confusion matrix will be reported, as well as the MCC, \(\kappa_m\), and the FLOSS evaluation.

Current results

Regime change detection

The current status of the regime change detection pipeline is the implementation of the resampling strategies and evaluation to start the parameter tuning. An example of the current implementation is shown on Fig. 17.

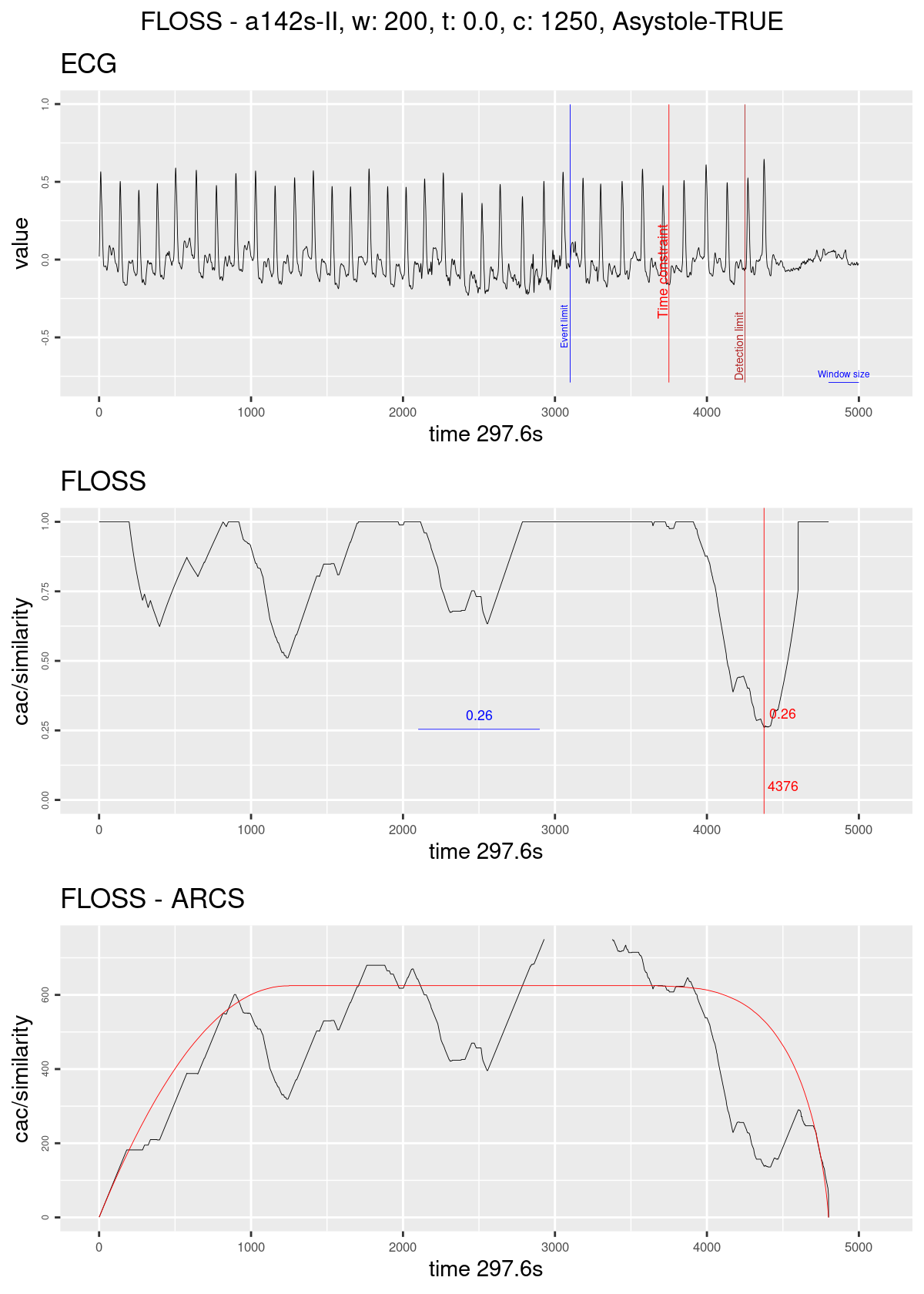
Figure 17: Figure 17 - Regime change detection example. The graph on top shows the ECG streaming; the blue line marks the ten seconds before the original alarm was fired; the red line marks the time constraint of 1250; the dark red line marks the limit for taking a decision in this case of Asystole the blue horizontal line represents the size of the sliding window. The graph on the middle shows the Arc counts as seen by the algorithm (with the corrected distribution); the red line marks the current minimum value and its index; the blue horizontal line shows the minimum value seen until then. The graph on the bottom shows the computed Arc counts (raw), and the red line is the theoretical distribution used for correction.

Classification

The current status on the classification pipeline is the implementation of the shapelets extraction using the Contrast Profile.

An example of candidates for ventricular tachycardia is presented in Fig. 18.

Figure 18: Figure 18 - Shapelet candidates for Ventricular Tachycardia.

Feasibility trial

A side-project called “false.alarm.io” has been derived from this work (an unfortunate mix of “false.alarm” and “PlatformIO”⁵⁷, the IDE chosen to interface the panoply of embedded systems we can experiment with). The current results of this side-project are very enlightening and show that the final algorithm can indeed be used in small hardware. Further data will be available in the future.

A brief mentioning, linking back to the objectives of this work, an initial trial was done using an ESP32 MCU (Fig. 19) in order to be sure if such a small device can handle the task.

Figure 19: Figure 19 - ESP32 MCU

Current results show that such device has enough computation power to handle the task in real-time using just one of its two microprocessors. The main limitation seen in advance is the on-chip SRAM that must be well managed.

Scientific contributions

Matrix Profile

Since the first paper that presented this new concept¹³, many investigations have been made to speed its computation. It is notable how all computations are not dependent on the rolling window size as previous works not using Matrix Profile. Aside from this, we can see that the first STAMP¹³ algorithm has the time complexity of \(O(n^2log{n})\) while STOMP⁵⁸ \(O(n^2)\) (a significant improvement), but STOMP lacks the “any-time” property. Later SCRIMP⁵⁹ solves this problem keeping the same time complexity of \(O(n^2)\). Here we are in the “exact” algorithms domain, and we will not extend the scope for conciseness.

The main issue with the algorithms above is the dependency on a fast Fourier transform (FFT) library. FFT has been extensively optimized and architecture/CPU bounded to exploit the most of speed. Also, padding data to some power of 2 happens to increase the algorithm’s efficiency. We can argue that time complexity doesn’t mean “faster” when we can exploit low-level instructions. In our case, using FFT in a low-power device is overkilling. For example, a quick search over the internet gives us a hint that computing FFT on 4096 data in an ESP32 takes about 21ms (~47 computations in 1 second). This means ~79 seconds for computing all FFT’s (~3797) required for STAMP using a window of 300. Currently, we can compute a full matrix of 5k data in about 9 seconds in an ESP32 MCU (Fig. 19), and keep updating it as fast as 1 min of data (at 250hz) in just 6 seconds.

Recent works using exact algorithms are using an unpublished algorithm called MPX, which computes the Matrix Profile using cross-correlation methods ending up faster and is easily portable.

On computing the Matrix Profile: the contribution of this work on this area is adding the Online capability to MPX, which means we can update the Matrix Profile as new data comes in.

On extending the Matrix Profile: the contribution of this work on this area is the use of an unexplored constraint that we could apply on building the Matrix Profile we are calling Similarity Threshold (ST). The original work outputs the similarity values in Euclidean Distance (ED) values, while MPX naturally outputs the Pearson’s correlation coefficients (CC) values. Both ED and CC are interchangeable using the Equation \(\eqref{edcc}\). However, we may argue that it is easier to compare values that do not depend on the window size during an exploratory phase. MPX happens to naturally return values in CC, saving a few more computation time. The ST is an interesting factor that we can use, especially when detecting pattern changes during time. The FLOSS algorithm relies on counting references between indexes in the time series. ST can help remove “noise” from these references since only similar patterns above a certain threshold are referenced, and changes have more impact on these counts. The best ST threshold is still to be determined.

\[ CC = 1 - \frac{ED}{(2 \times WindowSize)} \tag{7} \label{edcc} \]

Regime change detection

In the original paper, in chapter 3.5, the authors of FLOSS wisely introduce the temporal constraint, which improves the sensitivity of regime change detection on situations where a regime may alternate in short periods.

Nevertheless, the authors declare the correction curve typically used on the algorithm as “simply a uniform distribution”, but this is not an accurate statement. The Arc Counts of newly incoming data is truncated by the same amount of temporal constraint. This prevents detecting a regime change in the last 10 seconds completely, as this thesis requires.

The main contribution of this work in this area is overcoming this issue by computing the theoretical distribution using the temporal constraint parameters beforehand. as shown in Fig. 20. That gives us enough data to evaluate a regime change accurately utilizing a minimum of \(2 \times WindowSize\) datapoints.

Figure 20: Figure 20 - 1D-IAC distributions for earlier temporal constraint (on Matrix Profile)

Scientific outcomes

This research has already yielded two R packages concerning the MP algorithms from UCR¹⁷. The first package is called tsmp, and a paper was also published in the R Journal¹⁸ (Journal Impact Factor™, 2020 of 3.984). The second package is called matrixprofiler and enhances the first one, using low-level language to improve computational speed. The author has also joined the Matrix Profile Foundation is a co-founder with contributors from Python and Go languages^19,20. The benchmarks of the R implementation are available online⁶⁰.

Additionally to the above publication and the publication of the ongoing literature survey, two articles about this thesis subject will be published. The first regards the application of the FLOSS algorithm on real-time ECG showing its potential on using on low-power devices. The second is regarding the use of combined shapelets for relevant ECG patterns identification.

Expected results and outcomes

In the end, this thesis will provide a framework for identifying life-threatening conditions using biological streaming data on devices with low CPU and low memory specifications. We expect to achieve a high-quality model on identifying these pathological conditions maintaining their robustness in the presence of noise and artifacts seen on real-world applications.

1.

Research compendium. Published 2019. Accessed April 8, 2021. https://research-compendium.science

2.

Wilkinson MD, Dumontier M, Aalbersberg IjJ, et al. The FAIR Guiding Principles for scientific data management and stewardship. Scientific Data. 2016;3(1). doi:10.1038/sdata.2016.18

3.

The CodeMeta project. Published 2017. Accessed January 10, 2022. https://codemeta.github.io/

4.

Landau W, Landau W, Warkentin MT, et al. Ropensci/Targets, Dynamic Function-Oriented ’Make’-Like Declarative Workflows. Zenodo; 2021. doi:10.5281/ZENODO.4062936

5.

Franzbischoff/false.alarm: Reproducible reports. Published 2021. Accessed April 8, 2021. https://franzbischoff.github.io/false.alarm

6.

Blischak JD, Carbonetto P, Stephens M. Creating and sharing reproducible research code the workflowr way [version 1; peer review: 3 approved]. F1000Research. 2019;8(1749). doi:10.12688/f1000research.20843.1

7.

Kuhn M. Building predictive models in r using the caret package. Journal of Statistical Software, Articles. 2008;28(5):1-26. doi:10.18637/jss.v028.i05

8.

Kuhn M, Wickham H. Tidymodels: A Collection of Packages for Modeling and Machine Learning Using Tidyverse Principles.; 2020. https://www.tidymodels.org

9.

Thompson J. On not using tidymodels. Published October 2020. Accessed January 5, 2022. https://staffblogs.le.ac.uk/teachingr/2020/10/05/on-not-using-tidymodels/

10.

Bischoff F. GitHub false.alarm repository. Accessed July 14, 2021. https://github.com/franzbischoff/false.alarm

11.

GitHub Actions. Accessed July 14, 2021. https://github.com/features/actions

12.

Zenhub roadmap. Accessed January 27, 2022. https://app.zenhub.com/workspaces/phd-thesis-5eb2ce34f5f30b3aed0a35af/roadmap

13.

Yeh C-CM, Zhu Y, Ulanova L, et al. Matrix profile i: All pairs similarity joins for time series: A unifying view that includes motifs, discords and shapelets. In: 2016 IEEE 16th International Conference on Data Mining (ICDM). IEEE; 2016:1317-1322. doi:10.1109/ICDM.2016.0179

14.

De Paepe D, Vanden Hautte S, Steenwinckel B, et al. A generalized matrix profile framework with support for contextual series analysis. Engineering Applications of Artificial Intelligence. 2020;90(January):103487. doi:10.1016/j.engappai.2020.103487

15.

Feremans L, Vercruyssen V, Cule B, Meert W, Goethals B. Pattern-Based Anomaly Detection in Mixed-Type Time Series. In: Lecture Notes in Computer Science (Including Subseries Lecture Notes in Artificial Intelligence and Lecture Notes in Bioinformatics). Vol 11906 LNAI.; 2020:240-256. doi:10.1007/978-3-030-46150-8_15

16.

Lin J, Keogh E, Wei L, Lonardi S. Experiencing SAX: A novel symbolic representation of time series. Data Mining and Knowledge Discovery. 2007;15(2):107-144. doi:10.1007/s10618-007-0064-z

17.

UCR Matrix Profile Page. Accessed January 27, 2022. https://www.cs.ucr.edu/~eamonn/MatrixProfile.html

18.

Bischoff F, Rodrigues PP. tsmp: An R Package for Time Series with Matrix Profile. The R Journal. 2020;12(1):76-86. doi:10.32614/RJ-2020-021

19.

Matrix Profile Foundation. Accessed January 27, 2022. https://matrixprofile.org/

20.

Van Benschoten A, Ouyang A, Bischoff F, Marrs T. MPA: A novel cross-language API for time series analysis. Journal of Open Source Software. 2020;5(49):2179. doi:10.21105/joss.02179

21.

Reducing False Arrhythmia Alarms in the ICU - The PhysioNet Computing in Cardiology Challenge 2015. Published online March 24, 2021. doi:10.5281/zenodo.4634013

22.

Clifford GD, Silva I, Moody B, et al. The PhysioNet/computing in cardiology challenge 2015: Reducing false arrhythmia alarms in the ICU. In: Computing in Cardiology.; 2015. doi:10.1109/cic.2015.7408639

23.

Association for the Advancement of Medical Instrumentation. Cardiac monitors, heart rate meters, and alarms. Association for the Advancement of Medical Instrumentation; 2002.

24.

Plesinger F, Klimes P, Halamek J, Jurak P. False alarms in intensive care unit monitors: Detection of life-threatening arrhythmias using elementary algebra, descriptive statistics and fuzzy logic. In: IEEE; 2015. doi:10.1109/cic.2015.7408641

25.

Kalidas V, Tamil LS. Enhancing accuracy of arrhythmia classification by combining logical and machine learning techniques. In: IEEE; 2015. doi:10.1109/cic.2015.7411015

26.

Couto P, Ramalho R, Rodrigues R. Suppression of false arrhythmia alarms using ECG and pulsatile waveforms. In: IEEE; 2015. doi:10.1109/cic.2015.7411019

27.

Fallet S, Yazdani S, Vesin J-M. A multimodal approach to reduce false arrhythmia alarms in the intensive care unit. In: IEEE; 2015. doi:10.1109/cic.2015.7408640

28.

Hoog Antink C, Leonhardt S. Reducing false arrhythmia alarms using robust interval estimation and machine learning. In: IEEE; 2015. doi:10.1109/cic.2015.7408642

29.

Akosa JS. Predictive accuracy: A misleading performance measure for highly imbalanced data. SAS Global Forum. 2017;942:1-12.

30.

Wu R, Keogh E. Current Time Series Anomaly Detection Benchmarks are Flawed and are Creating the Illusion of Progress. IEEE Transactions on Knowledge and Data Engineering. Published online September 2021. doi:10.1109/TKDE.2021.3112126

31.

Bakeman R, Quera V. Sequential Analysis and Observational Methods for the Behavioral Sciences. Cambridge University Press; 2011:1-183. doi:10.1017/CBO9781139017343

32.

Sim J, Wright CC. The Kappa Statistic in Reliability Studies: Use, Interpretation, and Sample Size Requirements. Physical Therapy. 2005;85(3):257-268. doi:10.1093/ptj/85.3.257

33.

Bakeman R, McArthur D, Quera V, Robinson BF. Detecting sequential patterns and determining their reliability with fallible observers. Psychological Methods. 1997;2(4):357-370. doi:10.1037/1082-989X.2.4.357

34.

Morgan S. Research Methodology and Statistical Methods.; 2019:300.

35.

SparkFun Electronics. AD8232 single lead heart rate monitor. Published 2014. Accessed July 14, 2021. https://www.sparkfun.com/products/12650

36.

Analog Devices. AD8232 Single-Lead, Heart Rate Monitor Front End. Published online 2014. Accessed July 14, 2021. https://www.analog.com/media/en/technical-documentation/data-sheets/ad8232.pdf

37.

Arduino. Arduino. Published 2008. Accessed July 14, 2021. https://www.arduino.cc/

38.

Eerikainen LM, Vanschoren J, Rooijakkers MJ, Vullings R, Aarts RM. Decreasing the false alarm rate of arrhythmias in intensive care using a machine learning approach. In: IEEE; 2015. doi:10.1109/cic.2015.7408644

39.

Del Rio BAS, Lopetegi T, Romero I. Assessment of different methods to estimate electrocardiogram signal quality. Computing in Cardiology. 2011;38:609-612.

40.

Batista GEAPA, Keogh EJ, Tataw OM, Souza VMA de. CID: an efficient complexity-invariant distance for time series. Data Mining and Knowledge Discovery. 2014;28(3):634-669. doi:10.1007/s10618-013-0312-3

41.

Gharghabi S, Yeh C-CM, Ding Y, et al. Domain agnostic online semantic segmentation for multi-dimensional time series. Data Mining and Knowledge Discovery. 2018;33(1):96-130. doi:10.1007/s10618-018-0589-3

42.

Aminikhanghahi S, Cook DJ. A survey of methods for time series change point detection. Knowledge and Information Systems. 2016;51(2):339-367. doi:10.1007/s10115-016-0987-z

43.

Matsubara Y, Sakurai Y, Faloutsos C. AutoPlait: Automatic mining of co-evolving time sequences. Proceedings of the ACM SIGMOD International Conference on Management of Data. Published online 2014:193-204. doi:10.1145/2588555.2588556

44.

Imani S, Madrid F, Ding W, Crouter S, Keogh E. Matrix profile XIII : Time series snippets : A new primitive for time series data mining. In: 2018 IEEE International Conference on Data Mining (ICDM).; 2018.

45.

Gharghabi S, Imani S, Bagnall A, Darvishzadeh A, Keogh E. Matrix profile XII: MPdist: A novel time series distance measure to allow data mining in more challenging scenarios. In: IEEE; 2018:965-970. doi:10.1109/ICDM.2018.00119

46.

Keogh E, Lin J. Clustering of time-series subsequences is meaningless: implications for previous and future research. Knowledge and Information Systems. 2005;8(2):154-177. doi:10.1007/s10115-004-0172-7

47.

Rakthanmanon T, Keogh E. Fast shapelets: A scalable algorithm for discovering time series shapelets. In: Proceedings of the 2013 SIAM International Conference on Data Mining. Society for Industrial; Applied Mathematics; 2013:668-676. doi:10.1137/1.9781611972832.74

48.

Mercer R, Alaee S, Abdoli A, Singh S, Murillo A, Keogh E. Matrix profile XXIII: Contrast profile: A novel time series primitive that allows real world classification. In: ICDM 2021. IEEE; 2021:10.

49.

Bischl B, Mersmann O, Trautmann H, Weihs C. Resampling Methods for Meta-Model Validation with Recommendations for Evolutionary Computation. Evolutionary Computation. 2012;20(2):249-275. doi:10.1162/EVCO_a_00069

50.

Hastie T, Tibshirani R, Friedman J. The Elements of Statistical Learning: Data Mining, Inference, and Prediction. Springer; 2009. doi:10.1007/978-0-387-84858-7

51.

Bekkar M, Djemaa HK, Alitouche TA. Evaluation Measures for Models Assessment over Imbalanced Data Sets. Journal of Information Engineering and Applications. 2013;3(10):27-38. http://www.iiste.org/Journals/index.php/JIEA/article/view/7633

52.

Chicco D, Jurman G. The advantages of the Matthews correlation coefficient (MCC) over F1 score and accuracy in binary classification evaluation. BMC Genomics. 2020;21(1):6. doi:10.1186/s12864-019-6413-7

53.

Matthews BW. Comparison of the predicted and observed secondary structure of T4 phage lysozyme. Biochimica et Biophysica Acta (BBA) - Protein Structure. 1975;405(2):442-451. doi:10.1016/0005-2795(75)90109-9

54.

Bifet A, de Francisci Morales G, Read J, Holmes G, Pfahringer B. Efficient Online Evaluation of Big Data Stream Classifiers. In: Proceedings of the 21th ACM SIGKDD International Conference on Knowledge Discovery and Data Mining. Vol 2015-Augus. ACM; 2015:59-68. doi:10.1145/2783258.2783372

55.

Dubey A, Tarar S. Evaluation of approximate rank-order clustering using matthews correlation coefficient. International Journal of Engineering and Advanced Technology. 2018;8(2):106-113.

56.

Delgado R, Tibau X-A. Why Cohen’s Kappa should be avoided as performance measure in classification. Gu Q, ed. PLOS ONE. 2019;14(9):e0222916. doi:10.1371/journal.pone.0222916

57.

PlatformIO, a professional collaborative platform for embedded development. Accessed January 5, 2022. https://platformio.org/

58.

Zhu Y, Zimmerman Z, Senobari NS, et al. 2016 IEEE 16th international conference on data mining (ICDM). In: IEEE; 2016. doi:10.1109/icdm.2016.0085

59.

Zhu Y, Yeh C-CM, Zimmerman Z, Kamgar K, Keogh E. 2018 IEEE international conference on data mining (ICDM). In: IEEE; 2018. doi:10.1109/icdm.2018.00099

60.

Bischoff F. RPubs - MatrixProfileR - benchmarks. Published 2021. Accessed January 12, 2022. https://rpubs.com/franzbischoff/matrixprofiler