Response time correction of Contros HydroC pCO2 data
Jens Daniel Müller
16 March, 2020
Last updated: 2020-03-16
Checks: 7 0
Knit directory: BloomSail/
This reproducible R Markdown analysis was created with workflowr (version 1.6.0). The Checks tab describes the reproducibility checks that were applied when the results were created. The Past versions tab lists the development history.
Great! Since the R Markdown file has been committed to the Git repository, you know the exact version of the code that produced these results.
Great job! The global environment was empty. Objects defined in the global environment can affect the analysis in your R Markdown file in unknown ways. For reproduciblity it’s best to always run the code in an empty environment.
The command set.seed(20191021) was run prior to running the code in the R Markdown file. Setting a seed ensures that any results that rely on randomness, e.g. subsampling or permutations, are reproducible.
Great job! Recording the operating system, R version, and package versions is critical for reproducibility.
Nice! There were no cached chunks for this analysis, so you can be confident that you successfully produced the results during this run.
Great job! Using relative paths to the files within your workflowr project makes it easier to run your code on other machines.
Great! You are using Git for version control. Tracking code development and connecting the code version to the results is critical for reproducibility. The version displayed above was the version of the Git repository at the time these results were generated.
Note that you need to be careful to ensure that all relevant files for the analysis have been committed to Git prior to generating the results (you can use wflow_publish or wflow_git_commit). workflowr only checks the R Markdown file, but you know if there are other scripts or data files that it depends on. Below is the status of the Git repository when the results were generated:
Ignored files:
Ignored: .Rhistory
Ignored: .Rproj.user/
Ignored: data/Maps/
Ignored: data/Ostergarnsholm/
Ignored: data/TinaV/
Ignored: data/_merged_data_files/
Ignored: data/_summarized_data_files/
Note that any generated files, e.g. HTML, png, CSS, etc., are not included in this status report because it is ok for generated content to have uncommitted changes.
There are no past versions. Publish this analysis with wflow_publish() to start tracking its development.
library(tidyverse)
library(seacarb)
library(data.table)
library(broom)
library(lubridate)
library(tibbletime)
library(patchwork)1 Sensitivity considerations
A change in DIC of 1 µmol kg-1 corresponds to a change in pCO2 of around 1 µatm, in the Central Baltic Sea at a pCO2 of around 100 µatm (summertime conditions).
df <- data.frame(cbind(
(c(1720)),
(c(7))))
Tem <- seq(5,25,5)
pCO2<-seq(50,500,20)
df<-merge(df, Tem)
names(df) <- c("AT", "S", "Tem")
df<-merge(df, pCO2)
names(df) <- c("AT", "S", "Tem", "pCO2")
df<-data.table(df)
df$AT<-df$AT*1e-6
df$DIC<-carb(flag=24, var1=df$pCO2, var2=df$AT, S=df$S, T=df$Tem, k1k2="m10", kf="dg", pHscale="T")[,16]
df$pCO2.corr<-carb(flag=15, var1=df$AT, var2=df$DIC, S=df$S, T=df$Tem, k1k2="m10", kf="dg", pHscale="T")[,9]
df$pCO2.2<-df$pCO2.corr + 25
df$DIC.2<-carb(flag=24, var1=df$pCO2.2, var2=df$AT, S=df$S, T=df$Tem, k1k2="m10", kf="dg", pHscale="T")[,16]
df$ratio<-(df$pCO2.2-df$pCO2.corr)/(df$DIC.2*1e6-df$DIC*1e6)
df %>%
ggplot(aes(pCO2, ratio, col=as.factor(Tem)))+
geom_line()+
scale_color_viridis_d(option = "C",name="Tem [°C]")+
labs(x=expression(pCO[2]~(µatm)), y=expression(Delta~pCO[2]~"/"~Delta~DIC~(µatm~µmol^{-1}~kg)))+
scale_y_continuous(limits = c(0,8), breaks = seq(0,10,1))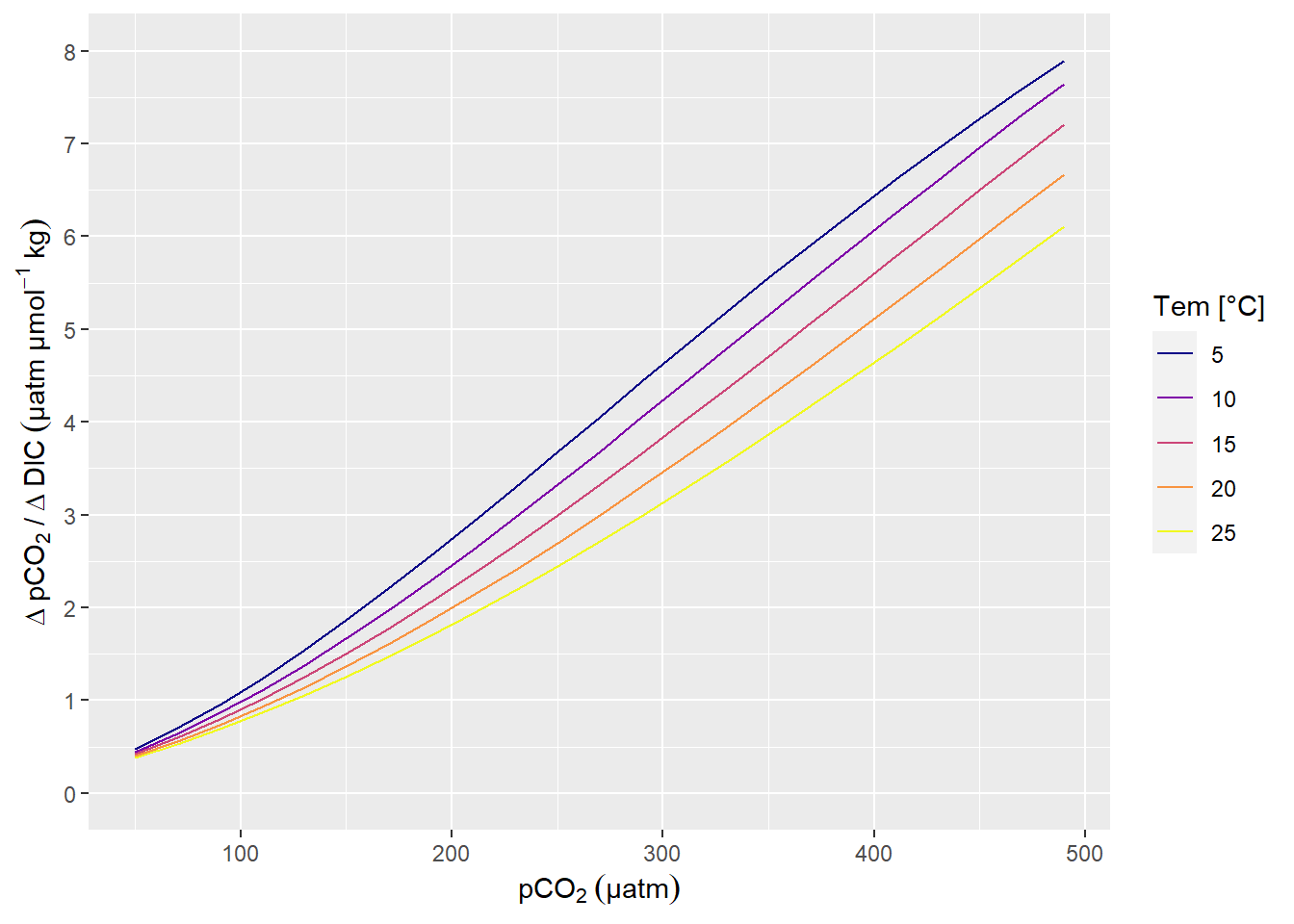
pCO2 sensitivity to changes in DIC.
rm(df, Tem, pCO2)2 Response time determination
2.1 HydroC sensor settings
The sensor was first run with a low power pump (1W). Later - and for most parts of the expedition - with a stronger (8W) pump. Pumps were switched between recordings (data file: SD_datafile_20180718_170417CO2-0618-001.txt):
- 2018-07-17;13:08:34
- 2018-07-17;13:08:35
Logging frequency for all measurement modes (Measure, Zero, Flush) was increased in two steps, It was:
10 sec for all recordings including SD_datafile_20180714_073641CO2-0618-001.txt
2 sec after change in SD_datafile_20180717_121052CO2-0618-001.txt at:
- 2018-07-14;07:52:02
- 2018-07-14;07:52:12
- 2018-07-14;07:52:14
1 sec after change in SD_datafile_20180718_170417CO2-0618-001 at:
- 2018-07-17;12:27:25
- 2018-07-17;12:27:27
- 2018-07-17;12:27:28
2.2 Model fitting
Response times were determined by fitting a nonlinear least-squares model with the nls function as described here by Douglas Watson.
- Flush period length: variable
- Flush period restricted to equilibration phase, avoiding initial gas mixing effects occuring at the start of each Flush period
- only completed Flush periods (duration > 500 sec) included
df <- read_csv(here::here("data/_merged_data_files",
"BloomSail_CTD_HydroC.csv"),
col_types = cols(ID = col_character(),
pCO2_analog = col_double(),
pCO2 = col_double(),
Zero = col_factor(),
Flush = col_factor(),
Zero_ID = col_integer(),
deployment = col_integer(),
duration = col_double(),
mixing = col_character()))
df <- df %>%
select(date_time, ID, dep, tem, Flush, pCO2, Zero_ID, duration, mixing)
df <- df %>%
filter(Flush == 1, mixing == "equilibration")
df <- df %>%
group_by(Zero_ID) %>%
mutate(duration = duration- min(duration),
max_duration = max(duration)) %>%
ungroup() %>%
filter(max_duration >= 500) %>%
select(-max_duration)An example plot for a nls model fitted to pCO2 observations during a Flush phase is shown below.
i <- unique(df$Zero_ID)[30]
df_ID <- df %>%
filter(Zero_ID == i, duration <= 300)
fit <-
df_ID %>%
nls(pCO2 ~ SSasymp(duration, yf, y0, log_alpha), data = .)
tau <- as.numeric(exp(-tidy(fit)[3,2]))
pCO2_end <- as.numeric(tidy(fit)[1,2])
pCO2_start <- as.numeric(tidy(fit)[2,2])
dpCO2 = pCO2_end - pCO2_start
mean_abs_resid <- mean(abs(resid(fit)))
augment(fit) %>%
ggplot(aes(duration, pCO2))+
geom_point()+
geom_line(aes(y = .fitted))+
geom_vline(xintercept = tau)+
geom_hline(yintercept = pCO2_start + 0.63 *(dpCO2))+
labs(y=expression(pCO[2]~(µatm)), x="Duration of Flush period (s)")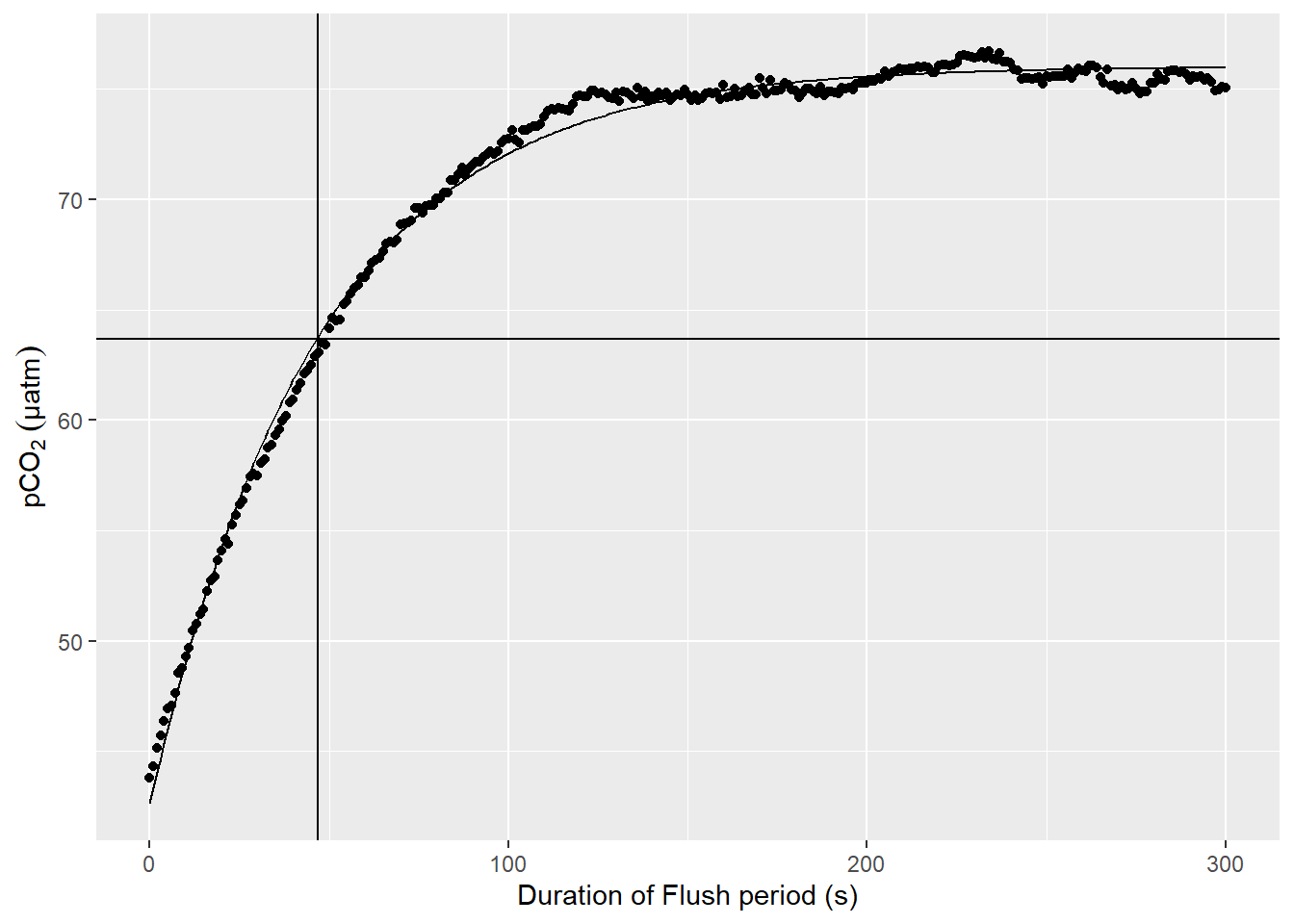
Example response time determination by non-linear least squares fit to the pCO2 recovery signal after zeroing. The vertical line indicates the determined response time tau. The horizontal line indicates 63% of the difference between start and final fitted pCO2.
rm(df_ID, fit, i, tau, dpCO2, pCO2_end, pCO2_start, mean_abs_resid)duration_intervals <- seq(150,500,50)As there was some speculation about the dependence of determined response times (\(\tau\)) on the chosen duration of the fit interval, the response time \(\tau\) was determined for all zeroings and for total durations of:
150, 200, 250, 300, 350, 400, 450, 500 secs
pdf(file=here::here("output/Plots/response_time",
"RT_determination_pCO2_flushperiods_nls.pdf"), onefile = TRUE, width = 7, height = 4)
for (i in unique(df$Zero_ID)) {
for (max_duration in duration_intervals) {
df_ID <- df %>%
filter(Zero_ID == i, duration <= max_duration)
fit <-
try(
df_ID %>%
nls(pCO2 ~ SSasymp(duration, yf, y0, log_alpha), data = .),
TRUE)
if (class(fit) == "nls"){
tau <- as.numeric(exp(-tidy(fit)[3,2]))
pCO2_end <- as.numeric(tidy(fit)[1,2])
pCO2_start <- as.numeric(tidy(fit)[2,2])
dpCO2 = pCO2_end - pCO2_start
mean_abs_resid <- mean(abs(resid(fit))/pCO2_end)*100
temp <- as_tibble(bind_cols(Zero_ID = i,
duration = max_duration,
date_time = mean(df_ID$date_time),
dep = mean(df_ID$dep),
tem = mean(df_ID$tem),
pCO2 = pCO2_end,
tau = tau,
resid = mean_abs_resid))
if (exists("tau_df")){tau_df <- bind_rows(tau_df, temp)}
else {tau_df <- temp}
if (mean_abs_resid > 1){warn <- "orange"}
else {warn <- "black"}
print(
augment(fit) %>%
ggplot(aes(duration, pCO2))+
geom_point(col = warn)+
geom_line(aes(y = .fitted))+
geom_vline(xintercept = tau)+
geom_hline(yintercept = pCO2_start + 0.63 *(dpCO2))+
labs(y=expression(pCO[2]~(µatm)), x="Duration of Flush period (s)",
title = paste("Zero_ID: ", i,
"Tau: ", round(tau,1),
"Mean absolute residual (%): ", round(mean_abs_resid, 2)))+
xlim(0,600)
)
}
else {
temp <- as_tibble(bind_cols(Zero_ID = i,
duration = max_duration,
date_time = mean(df_ID$date_time),
dep = mean(df_ID$dep),
tem = mean(df_ID$tem),
pCO2 = pCO2_end,
tau = NaN,
resid = NaN))
if (exists("tau_df")){tau_df <- bind_rows(tau_df, temp)}
else {tau_df <- temp}
print(
df_ID %>%
ggplot(aes(duration, pCO2))+
geom_point(col="red")+
labs(y=expression(pCO[2]~(µatm)), x="Duration of Flush period (s)",
title = paste("Zero_ID: ", i,
"nls model failed"))+
xlim(0,600)
)
}
}
}
dev.off()
rm(df_ID, fit, i, tau, dpCO2, pCO2_end, pCO2_start, temp, max_duration, mean_abs_resid, warn)
tau_df %>%
write_csv(here::here("data/_summarized_data_files", "Tina_V_HydroC_response_times_all.csv"))
rm(tau_df, df)A pdf with plots of all individual response time fits can be accessed here. In this pdf, response time fits that exceed the residual criterion (Mean absolute residual >1% of final pCO2) are printed in orange. Data from flush periods without succesful fit are printed red.
tau_df <- read_csv(here::here("data/_summarized_data_files", "Tina_V_HydroC_response_times_all.csv"))
# define periods of different pumps used
max_Zero_ID <- max(unique(tau_df[tau_df$date_time < ymd_hms("2018-07-17;13:08:34"),]$Zero_ID))
tau_df <- tau_df %>%
mutate(pump_power = if_else(Zero_ID <= max_Zero_ID, "1W", "8W"))
# define subsetting parameters
resid_limit <- 1
# subset determined tau values by residual threshold
tau_resid <- tau_df %>%
group_by(Zero_ID) %>%
mutate(resid_max = max(resid, na.rm = TRUE)) %>%
filter(resid_max < resid_limit) %>%
select(-resid_max) %>%
ungroup()
tau_resid_out <- tau_df %>%
group_by(Zero_ID) %>%
mutate(resid_max = max(resid, na.rm = TRUE)) %>%
filter(resid_max > resid_limit) %>%
select(-resid_max) %>%
ungroup()
# Flush periods where model failure occured
tau_df %>%
filter(is.na(resid)) %>%
group_by(Zero_ID) %>%
summarise(n()) %>%
ungroup()
# Flush periods removed due to residual criterion
tau_resid_out %>%
group_by(Zero_ID) %>%
summarise(n()) %>%
ungroup()
# mean tau of first RT determination
tau_resid %>%
filter(Zero_ID == 2) %>%
summarise(tau = mean(tau))
# mean tau of all RT determinations before pump switch, except first
tau_resid %>%
filter(Zero_ID != 2, Zero_ID <= 20) %>%
summarise(tau = mean(tau))
tau_resid <- tau_resid %>%
filter(Zero_ID != 2)
# calculate some metrics for the subsetting
n_Zero_IDs <- tau_df %>%
group_by(Zero_ID) %>%
n_groups()
n_duration_intervals <- length(duration_intervals)
n_tau_max <- n_Zero_IDs * length(duration_intervals)
n_tau_total <- nrow(tau_df %>% filter(!is.na(resid)))
n_tau_resid <- nrow(tau_resid)
rm(df)2.3 Outcome
2.3.1 General considerations
Estimated \(\tau\) values were only taken into account when stable environmental pCO2 levels were present. Absence of stable environmental pCO2 was assumed when the mean absolute fit residual was above 1 % of the final equilibrium pCO2. If one model fit (irrespective the chosen fit interval length) of a particular flush period did not match that criterion, the flush period was ignored entirely. Usually, fits with higher duration did not meet this criterion. For some unexplained reason the first \(\tau\) determination resulted in values about twice as high as all other flush periods and was therefore removed as an outlier.
Metrics to characterize the fitting procedure include the number of:
- Flush periods: 75
- Duration intervals: 8
- Exercised response time fits: 600
- Succesful response times determinations: 576 (96)%
- \(\tau\)’s after removing groups of fits with high absolute fit residual: 408 (68 %)
It should be noted that all failed model fits occured in flush periods where the residual criterion was not meet by at least one other fit (i.e. fitting only failed under unstable conditions).
tau_df %>%
ggplot(aes(resid))+
geom_histogram()+
facet_wrap(~duration, labeller = label_both)+
geom_vline(xintercept = resid_limit)+
labs(x=expression(Mean~absolute~residuals~("%"~of~equilibrium~pCO[2])))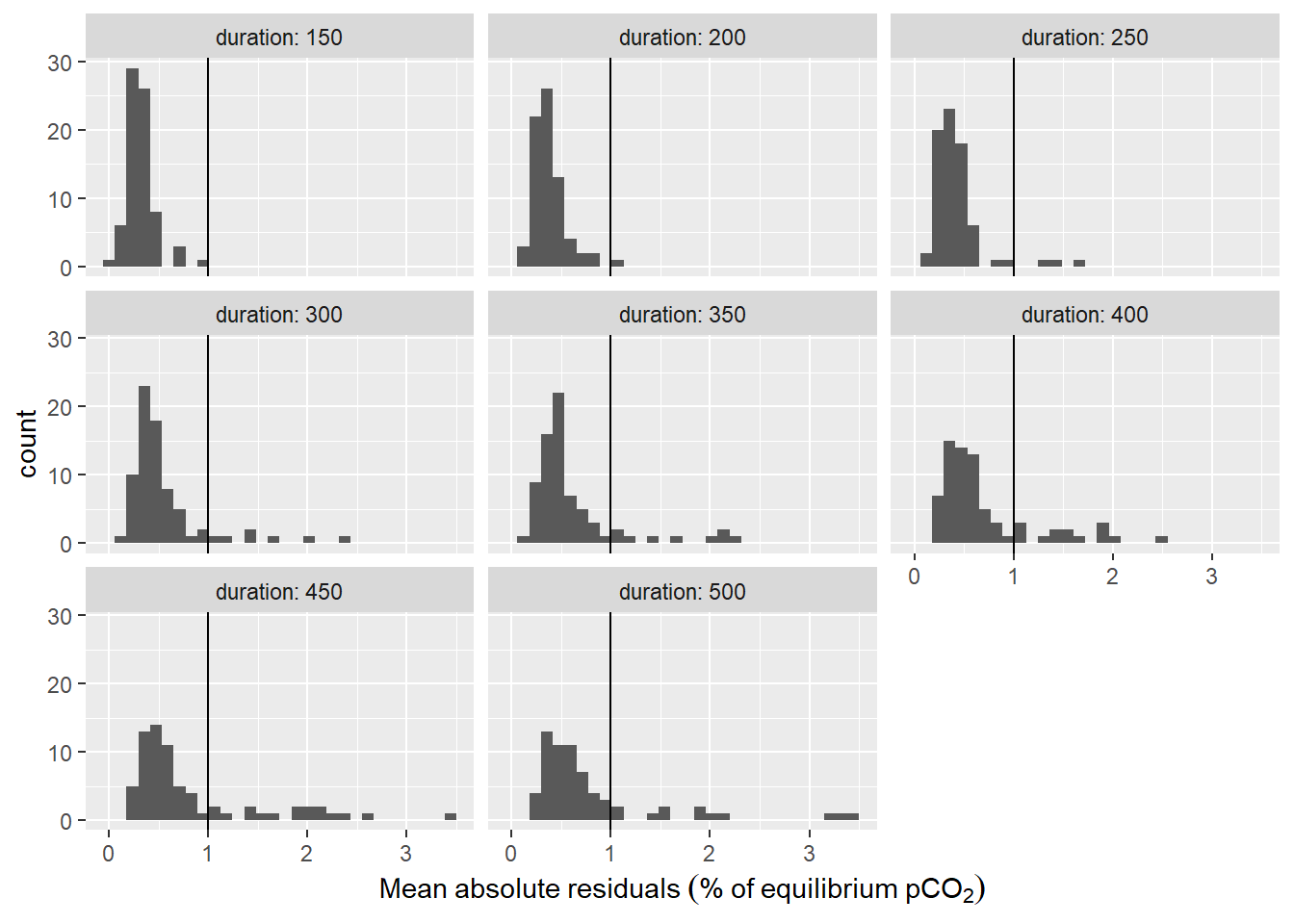
Histogram of residuals from fit displayed for the investigate durations of the fit interval. Vertical line represents the chosen threshold.
tau_resid %>%
ggplot(aes(date_time, tau, col=dep, shape=pump_power))+
geom_point()+
scale_color_viridis_c(name="Depth (m)")+
labs(y="Tau (sec)", x="Date")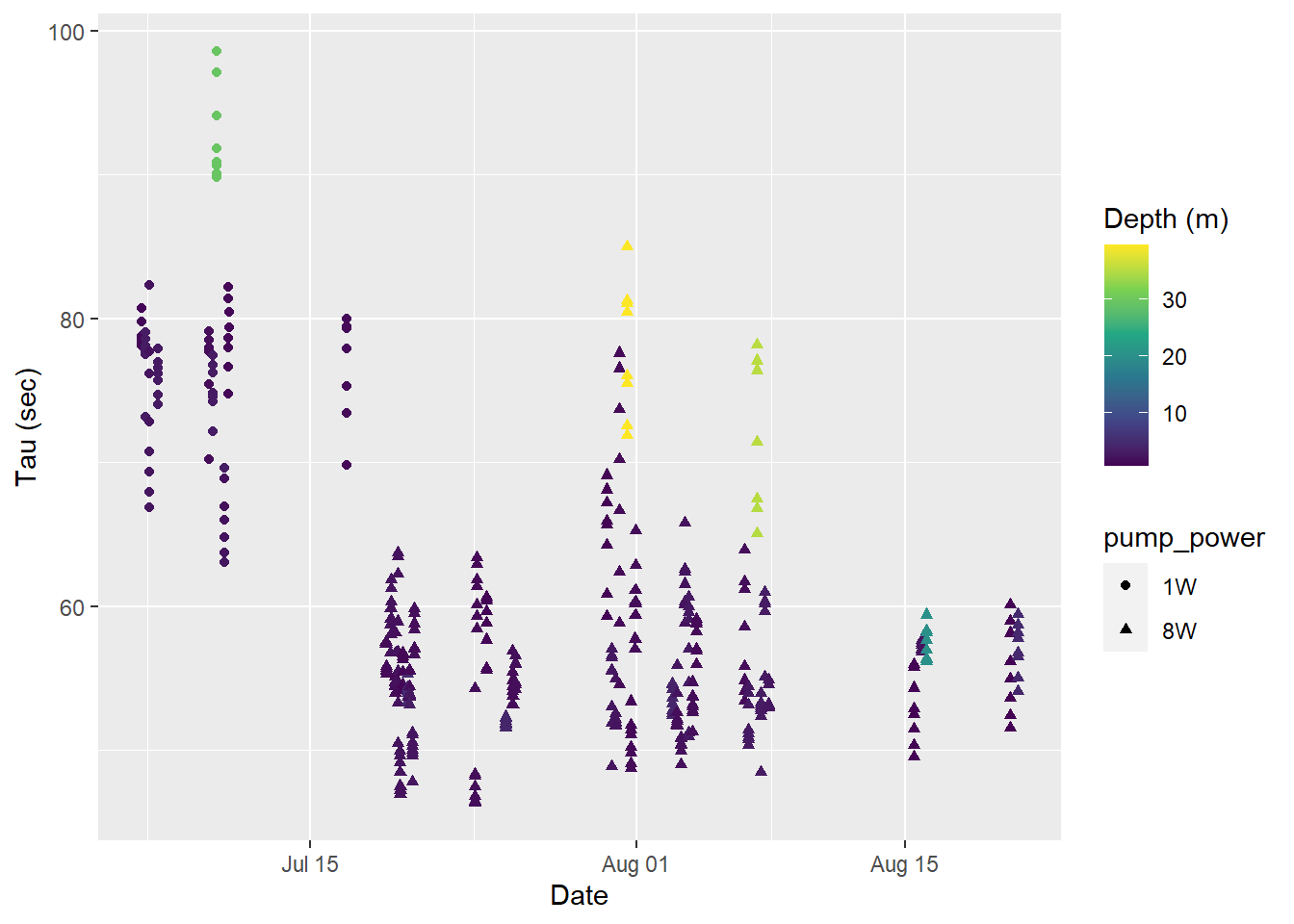
Tau for all Zeroings with color representing water depth.
2.3.2 Fit interval length
No clear dependence of \(\tau\) on the length of the flushing period was found.
tau_resid %>%
group_by(Zero_ID) %>%
mutate(d_tau = tau - mean(tau)) %>%
ggplot(aes(duration, d_tau))+
geom_hline(yintercept = 0)+
geom_smooth()+
geom_point()+
facet_wrap(~Zero_ID, ncol = 4, labeller = label_both)+
labs(x="Duration (sec)", y="Deviation from mean tau (sec)")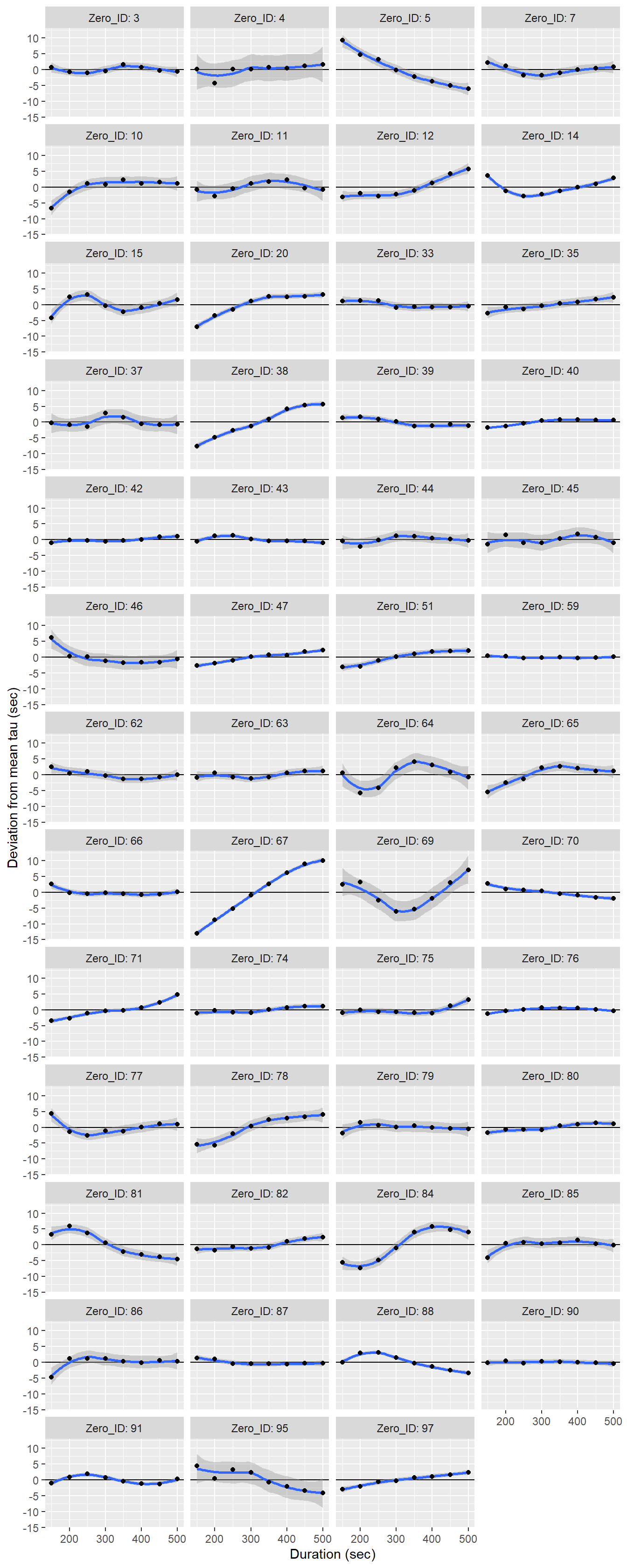
Determined tau values as a function of the fit interval duration, displayed individually for each flush period.
tau_resid %>%
group_by(Zero_ID) %>%
mutate(d_tau = tau - mean(tau)) %>%
ggplot(aes(duration, d_tau, group=duration))+
geom_violin()+
geom_point()+
labs(x="Duration (sec)", y="Deviation from mean tau (sec)")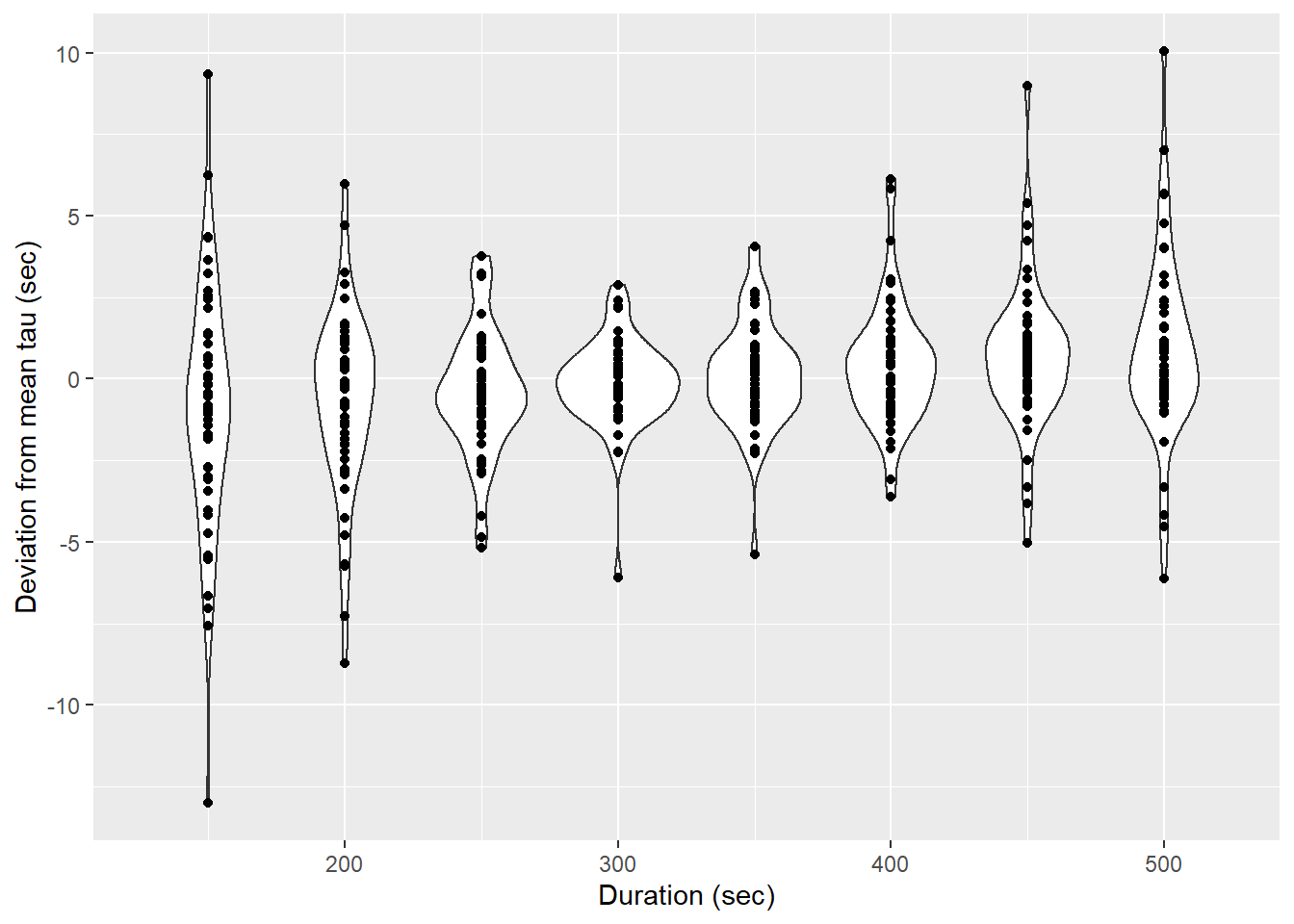
Determined tau values as a function of the fit interval duration, pooled for all flush period.
2.3.3 Temperature dependence
A temperature dependence of determined response times \(\tau\) was found, with similar slopes but different intercepts for both pumps used.
tau_resid %>%
#filter(duration > 200, duration < 400) %>%
ggplot(aes(tem, tau, col=dep))+
geom_smooth(method = "lm")+
geom_point()+
scale_color_viridis_c(name="Depth (m)")+
labs(y="Tau (sec)", x="Temperature (deg C)")+
facet_wrap(~pump_power, labeller = label_both)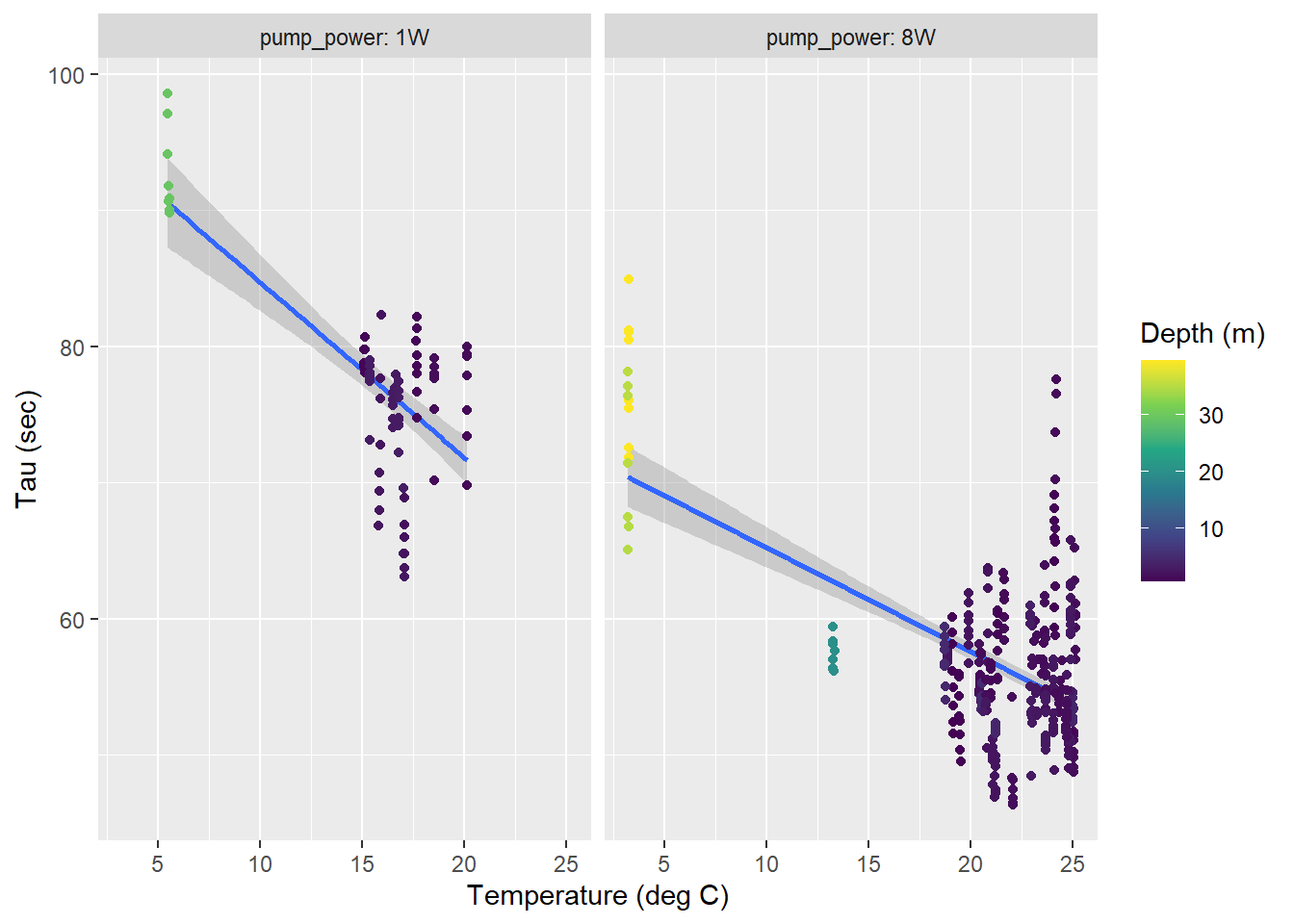
Tau as a function of temperature for all zeroings determined with low power (left) and strong (right) pump. Color represents the water depth.
For the response times determined near the surface (<10m, restricted temperature range), no clear temperature dependence of \(\tau\) was detected.
tau_resid %>%
filter(dep < 10) %>%
ggplot(aes(tem, tau, col=dep))+
geom_smooth(method = "lm")+
geom_point()+
scale_color_viridis_c(name="Depth (m)")+
labs(y="Tau (sec)", x="Temperature (deg C)")+
facet_wrap(~pump_power, labeller = label_both)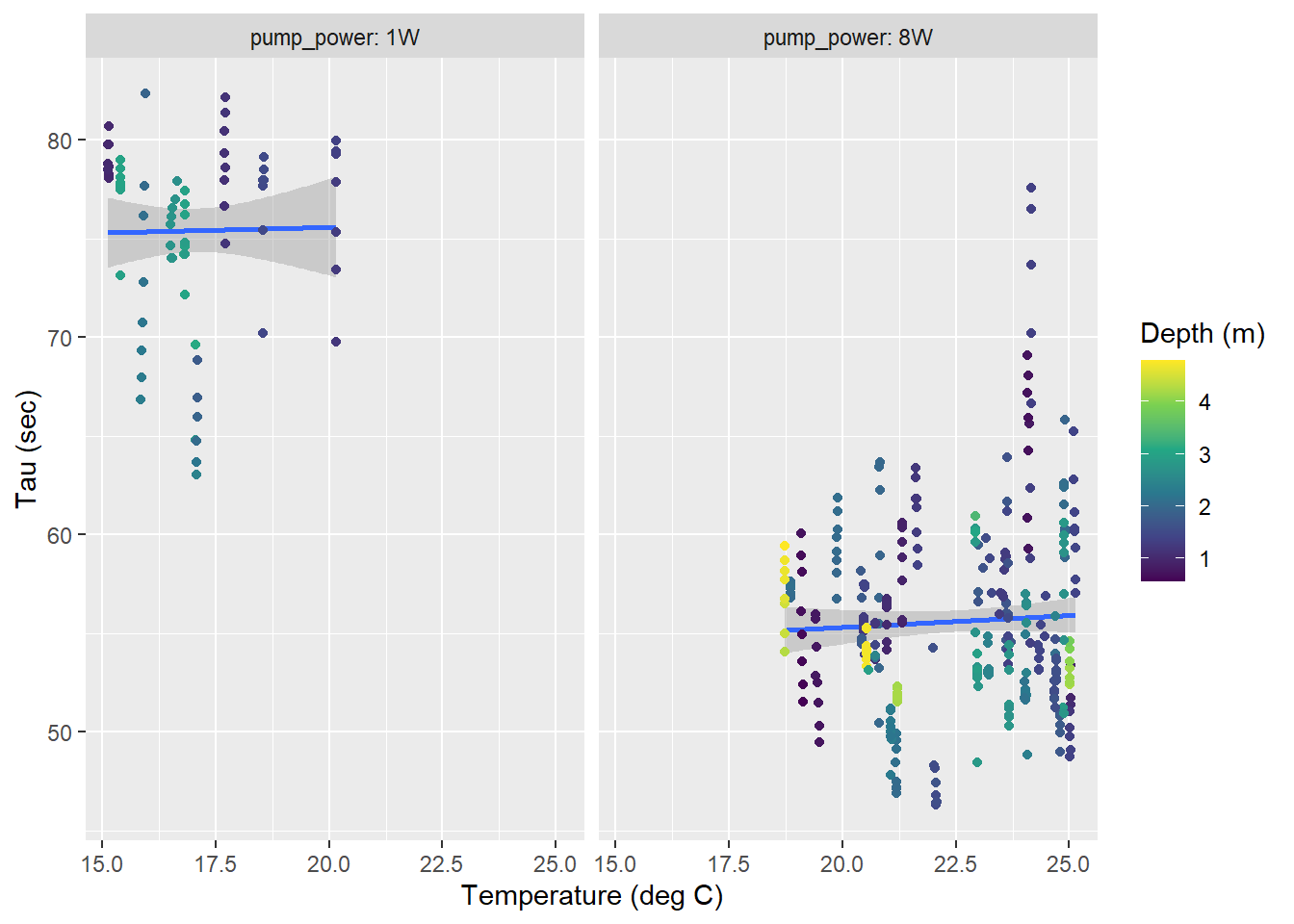
Surface tau (<10m) as a function of temperature for all zeroings determined with low power (left) and strong (right) pump. Color represents the water depth.
2.4 Final tau
Finally, the mean response times are:
RT_mean <- tau_resid %>%
group_by(pump_power) %>%
summarise(tau = mean(tau))
RT_mean# A tibble: 2 x 2
pump_power tau
<chr> <dbl>
1 1W 77.2
2 8W 56.6But we can also fit response times as a function of water temperature:
RT_fit <- tau_resid %>%
group_by(pump_power) %>%
do(fit = lm(tau ~ tem, data = .)) %>%
tidy(fit) %>%
select(pump_power, term, estimate) %>%
spread(term, estimate)
RT_fit# A tibble: 2 x 3
# Groups: pump_power [2]
pump_power `(Intercept)` tem
<chr> <dbl> <dbl>
1 1W 97.6 -1.29
2 8W 72.9 -0.763RT_fit %>% write_csv(here::here("data/_summarized_data_files", "Tina_V_HydroC_RT_fit.csv"))
rm(list=setdiff(ls(), c("tau_resid", "RT_mean", "RT_fit")))Both response time estimated (constant mean vs T-dependent) will be applied to correct the recorded pCO2 profiles.
3 Response time correction
3.1 Data preparation
Following tasks were performed to prepare data for the response time correction:
- Select only profiles
- Assign deployment periods with 1W- and 8W- pump
df <- read_csv(here::here("data/_merged_data_files",
"BloomSail_CTD_HydroC.csv"),
col_types = cols(ID = col_character(),
pCO2_analog = col_double(),
pCO2 = col_double(),
Zero = col_factor(),
Flush = col_factor(),
Zero_ID = col_integer(),
deployment = col_integer(),
duration = col_double(),
mixing = col_character()))
# extract relevant parts
df <- df %>%
select(date_time, ID, type, station, dep, sal, tem, Zero, Flush, pCO2, deployment, Zero_ID)
df <- df %>%
filter(type == "P")
df <- df %>%
group_by(ID, station) %>%
mutate(duration = as.numeric(date_time - min(date_time)),
pump_power = if_else(date_time < ymd_hms("2018-07-17;13:08:34"), "1W", "8W")) %>%
arrange(date_time)- Include manually derived meta-information about the profiling status
# Load profile meta data
meta <- read_csv(here::here("Data/_summarized_data_files",
"Tina_V_Sensor_meta.csv"),
col_types = cols(ID = col_character()))
# Merge data and meta information
df <- full_join(df, meta)
rm(meta)
# creating descriptive variables ------------------------------------------
df <- df %>%
mutate(phase = "standby",
phase = if_else(duration >= start & duration < down & !is.na(down) & !is.na(start), "down", phase),
phase = if_else(duration >= down & duration < lift & !is.na(lift) & !is.na(down ), "low", phase),
phase = if_else(duration >= lift & duration < up & !is.na(up ) & !is.na(lift ), "mid", phase),
phase = if_else(duration >= up & duration < end & !is.na(end ) & !is.na(up ), "up", phase))
df <- df %>%
select(-c(start, down, lift, up, end, comment))
df <- df %>%
filter(Zero == 0, Flush == 0)- Subset reference pCO2 recordings at the end of equilibration periods executed at constant depth
df_equi <- df %>%
filter(phase %in% c("mid")) %>%
group_by(ID, station) %>%
top_n(5, row_number()) %>%
summarise(date_time = mean(date_time),
duration = mean(duration),
pCO2 = mean(pCO2, na.rm = TRUE),
dep = mean(dep, na.rm = TRUE)) %>%
ungroup()
df_equi %>%
write_csv(here::here("data/_merged_data_files",
"BloomSail_CTD_HydroC_reference_pCO2.csv"))cast_dep <- df %>%
pivot_longer(c(dep, pCO2), names_to = "parameter", values_to = "value")
cast_dep_equi <- df_equi %>%
pivot_longer(c(dep, pCO2), names_to = "parameter", values_to = "value")
max_duration <- round(max(cast_dep$duration)/1000,0)*1000
i_ID <- "180730"
i_station <- "P01"
cast_dep_equi_sub <- cast_dep_equi %>%
filter(ID == i_ID,
station == i_station)
cast_dep %>%
filter(ID == i_ID,
station == i_station) %>%
ggplot(aes(duration, value, col=phase))+
geom_point(size=0.5)+
geom_point(data = cast_dep_equi_sub, aes(duration, value), col="black")+
scale_y_reverse()+
scale_x_continuous(breaks = seq(0,6000,500))+
labs(title = str_c("Date: ",i_ID," | Station: ",i_station))+
facet_grid(parameter~., scales = "free_y")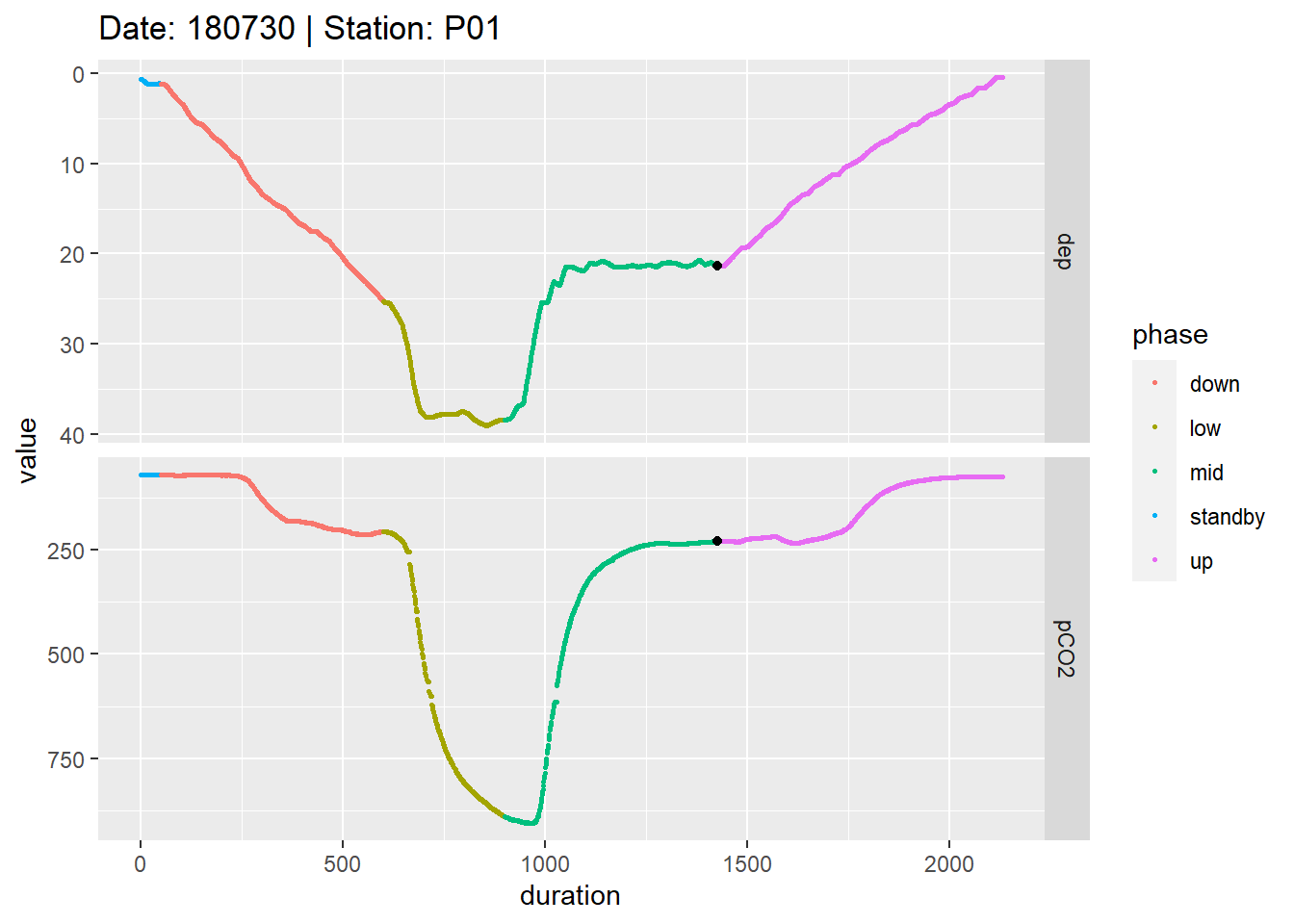
Example timeseries of profiling depth and pCO2. Colors represent manually assigned profiling phases. The black points represent reference data collected at the end of the mid equilibration period.
rm(cast_dep, cast_dep_equi, cast_dep_equi_sub, i_station, i_ID, max_duration)A pdf with all timeseries plots of profiling depth and pCO2 can be accessed here.
cast_dep <- df %>%
pivot_longer(c(dep, pCO2), names_to = "parameter", values_to = "value")
cast_dep_equi <- df_equi %>%
pivot_longer(c(dep, pCO2), names_to = "parameter", values_to = "value")
max_duration <- round(max(cast_dep$duration)/1000,0)*1000
pdf(file=here::here("output/Plots/response_time",
"RT_exploration_depth-pCO2_timeseries.pdf"), onefile = TRUE, width = 7, height = 4)
for(i_ID in unique(cast_dep$ID)){
for(i_station in unique(cast_dep$station)){
if (nrow(cast_dep %>% filter(ID == i_ID, station == i_station)) > 0){
cast_dep_equi_sub <- cast_dep_equi %>%
filter(ID == i_ID,
station == i_station)
print(
cast_dep %>%
filter(ID == i_ID,
station == i_station) %>%
ggplot(aes(duration, value, col=phase))+
geom_point(size=0.5)+
geom_point(data = cast_dep_equi_sub, aes(duration, value), col="black")+
scale_y_reverse()+
scale_x_continuous(breaks = seq(0,6000,500))+
labs(title = str_c("Date: ",i_ID," | Station: ",i_station))+
facet_grid(parameter~., scales = "free_y")+
theme_bw()
)
}
}
}
dev.off()
rm(cast_dep, cast_dep_equi, cast_dep_equi_sub, i_station, i_ID, max_duration)cast_dep <- df %>%
pivot_longer(c(dep, pCO2), names_to = "parameter", values_to = "value")
pdf(file=here::here("output/Plots/response_time",
"RT_exploration_depth-pCO2_timeseries_raw.pdf"), onefile = TRUE, width = 7, height = 4)
for(i_ID in unique(cast_dep$ID)){
for(i_station in unique(cast_dep$station)){
if (nrow(cast_dep %>% filter(ID == i_ID, station == i_station)) > 0){
print(
cast_dep %>%
filter(ID == i_ID,
station == i_station) %>%
ggplot(aes(duration, value))+
geom_point(size=0.5)+
scale_y_reverse()+
scale_x_continuous(breaks = seq(0,6000,100))+
labs(title = str_c("Date: ",i_ID," | Station: ",i_station))+
facet_grid(parameter~., scales = "free_y")+
theme_bw()
)
}
}
}
dev.off()
rm(cast_dep, i_station, i_ID)3.2 Reponse time correction
The executed response time correction featured the following aspects:
- Correction according to Bittig et al. (2018, supplement)
- RT: Constant mean vs. T-dependent response times applied (both independently quantified for 1W- and 8W-pump)
- tau_factor: Factor ranging from 0.8 - 1.6 applied to determined tau values
- Post-smoothing: 30 sec running mean (eg across 15 observations at 2 sec measurement frequency)
# Response time correction approach after Bittig --------------------------
RT_corr <- function(c1, c0, dt, tau) {
( 1 / ( 2* (( 1+(2*tau/dt) )^(-1) ))) * (c1 - (1-(2* (( 1+(2*tau/dt) )^(-1) ))) * c0)
}
# Assign mean response time (tau) values ----------------------------------------------
df_mean <- full_join(df, RT_mean)
df_mean <- df_mean %>%
mutate(RT = "constant")
# Assign T-dependent response time (tau) values ----------------------------------------------
RT_fit <- RT_fit %>%
rename(tau_intercept = `(Intercept)`, tau_slope=tem)
df_fit <- full_join(df, RT_fit)
df_fit <- df_fit %>%
mutate(tau = tau_intercept + tau_slope *tem,
RT = "T-dependent") %>%
select(-tau_intercept, -tau_slope)
df_fit <- df_fit %>%
mutate(RT = "T-dependent")
# Merge data sets with constand and T-dependent tau
df <- bind_rows(df_fit, df_mean)
rm(df_fit, df_mean)
# p1 <- df %>%
# ggplot(aes(tau, dep, col=pump_power))+
# geom_point()+
# scale_y_reverse()
#
# p2 <- df %>%
# ggplot(aes(tem, dep, col=pump_power))+
# geom_point()+
# scale_y_reverse()
#
# p1 | p2
#
# rm(p1, p2)
# Prepare data set for RT correction --------------------------------------
df <- df %>%
group_by(RT) %>%
arrange(date_time) %>%
mutate(dt = as.numeric(as.character(date_time - lag(date_time)))) %>%
ungroup()
# measurement frequency
freq <- df %>%
filter(dt < 13) %>%
group_by(ID) %>%
summarise(dt_mean = round(mean(dt, na.rm = TRUE),0))
df <- full_join(df, freq)
# tau factors
df <- expand_grid(df, tau_factor = seq(0.8, 1.6, 0.2))
df <- df %>%
mutate(tau_test = tau*tau_factor)
# Apply RT correction to entire data set
for(i_ID in unique(df$ID)){
#i_ID <- "180716"
freq_sub <- freq %>% filter(ID == i_ID) %>% pull(dt_mean)
window <- 30 / freq_sub
rolling_mean <- rollify(~mean(.x, na.rm = TRUE), window = window)
df_sub <- df %>%
filter(ID == i_ID) %>%
group_by(station, RT, tau_factor) %>%
mutate(pCO2_RT = RT_corr(pCO2, lag(pCO2), dt, tau_test),
pCO2_RT = if_else(pCO2_RT %in% c(Inf, -Inf), NaN, pCO2_RT),
window = window,
pCO2_RT_mean = rolling_mean(pCO2_RT)
#pCO2_RT_median = rolling_median(pCO2_RT)
) %>%
ungroup()
# time shift RT corrected data
shift <- as.integer(as.character(window/2))
df_sub <- df_sub %>%
group_by(station, RT, tau_factor) %>%
mutate(pCO2_RT_mean = lead(pCO2_RT_mean, shift)) %>%
ungroup()
if (exists("df_corr")){df_corr <- bind_rows(df_corr, df_sub)}
else{df_corr <- df_sub}
rm(df_sub, freq_sub, rolling_mean, shift, window)
}
df <- df_corr
rm(RT_corr, i_ID, freq, df_corr)
df %>%
write_csv(here::here("data/_merged_data_files",
"BloomSail_CTD_HydroC_profiles_RT.csv"))
rm(df)df <-
read_csv(here::here("data/_merged_data_files",
"BloomSail_CTD_HydroC_profiles_RT.csv"),
col_types = cols(ID = col_character(),
pCO2 = col_double(),
Zero = col_factor(),
Flush = col_factor(),
p_type = col_factor(),
Zero_ID = col_integer(),
deployment = col_integer(),
duration = col_double()))
i_ID <- "180730"
i_station <- "P01"
equi_cast <- df_equi %>%
filter(ID == i_ID,
station == i_station)
df %>%
filter(ID == i_ID,
station == i_station,
phase %in% c("up", "down")) %>%
ggplot()+
geom_path(aes(pCO2, dep, linetype = phase, col="raw"))+
geom_path(aes(pCO2_RT_mean, dep, linetype = phase, col="corrected"))+
geom_point(data = equi_cast, aes(pCO2, dep))+
scale_y_reverse()+
scale_color_brewer(palette = "Set1", name="")+
labs(y="Depth [m]", x=expression(pCO[2]~(µatm)),
title = str_c("Date: ",i_ID," | Station: ",i_station))+
facet_grid(tau_factor~RT, labeller = label_both)
Example plot of response time corrected and raw pCO2 profiles. Panels highlight the effect of constant vs T-dependent tau estimates (columns) and the optimization by applying a constant factor (rows).
rm(equi_cast)A pdf with all timeseries plots of profiling depth and pCO2 can be accessed here
pdf(file=here::here("output/Plots/response_time",
"RT_correction_pCO2_profiles.pdf"), onefile = TRUE, width = 7, height = 11)
for(i_ID in unique(df$ID)){
for(i_station in unique(df$station)){
if (nrow(df %>% filter(ID == i_ID, station == i_station)) > 0){
equi_cast <- df_equi %>%
filter(ID == i_ID,
station == i_station)
print(
df %>%
filter(ID == i_ID,
station == i_station,
phase %in% c("up", "down")) %>%
ggplot()+
geom_path(aes(pCO2, dep, linetype = phase, col="raw"))+
geom_path(aes(pCO2_RT_mean, dep, linetype = phase, col="corrected"))+
geom_point(data = equi_cast, aes(pCO2, dep))+
scale_y_reverse()+
scale_color_brewer(palette = "Set1", name="")+
labs(y="Depth [m]", title = str_c("Date: ",i_ID," | Station: ",i_station))+
theme_bw()+
facet_grid(tau_factor~RT, labeller = label_both)
)
}
}
}
dev.off()
rm(equi_cast)4 Diagnosis
In the following, the success of the response time correction is assessed through the offset between the downcast and:
- Upcast
- pCO2 reference value (recorded after equilibration period during upcast)
The offset comparison requires to discretize the depth recording. Depth intervals of 1m were chosen.
First, we analyse all profiles individually. Later we’ll merge the information across profiles and come up with a single metric to quantive the quality of the response time correction
4.1 Down- vs upcast
# pCO2 offset up - down cast
RT_diff <- df %>%
filter(phase %in% c("down", "up")) %>%
mutate(dep_int = as.numeric(as.character( cut(dep, seq(0,40,1), seq(0.5,39.5,1)))),
tau_factor = as.factor(tau_factor)) %>%
select(ID, station, RT, tau_factor, p_type, dep_int, phase, pCO2, pCO2_RT_mean) %>%
group_by(ID, station, RT, tau_factor, p_type, dep_int, phase) %>%
summarise_all("mean", na.rm = TRUE) %>%
ungroup() %>%
pivot_longer(cols = c(pCO2, pCO2_RT_mean), names_to = "correction") %>%
pivot_wider(names_from = phase, values_from = value) %>%
mutate(d_pCO2 = up - down,
mean_pCO2 = (down + up)/2,
d_pCO2_rel = 100 * d_pCO2 / mean_pCO2)
# descritize depth recordings of equilibrated pCO2 values
df_equi_int <- df_equi %>%
mutate(dep_int = as.numeric(as.character( cut(dep, seq(0,40,1), seq(0.5,39.5,1))))) %>%
select(ID, station, dep_int, pCO2_equi=pCO2)
RT_diff %>%
write_csv(here::here("data/_merged_data_files",
"BloomSail_CTD_HydroC_profiles_RT_cast-offset.csv"))
df_equi_int %>%
write_csv(here::here("data/_merged_data_files",
"BloomSail_CTD_HydroC_reference_pCO2_int.csv"))RT_diff <-
read_csv(here::here("data/_merged_data_files",
"BloomSail_CTD_HydroC_profiles_RT_cast-offset.csv"),
col_types = cols(ID = col_character()))
df_equi_int <-
read_csv(here::here("data/_merged_data_files",
"BloomSail_CTD_HydroC_reference_pCO2_int.csv"),
col_types = cols(ID = col_character()))
i_ID <- "180730"
i_station <- "P01"
df_equi_int_sub <- df_equi_int %>%
filter(ID == i_ID,
station == i_station)
RT_diff %>%
filter(ID == i_ID,
station == i_station) %>%
arrange(dep_int) %>%
ggplot()+
geom_path(aes(down, dep_int, col=correction, linetype="down"))+
geom_path(aes(up, dep_int, col=correction, linetype ="up"))+
geom_point(data = df_equi_int_sub, aes(pCO2_equi, dep_int))+
scale_y_reverse(breaks=seq(0,40,2))+
scale_linetype(name="cast")+
scale_color_brewer(palette = "Set1", direction = -1)+
labs(y="Depth [m]", x=expression(pCO[2]~(µatm)),
title = str_c("Date: ",i_ID," | Station: ",i_station))+
facet_grid(tau_factor~RT, labeller = label_both)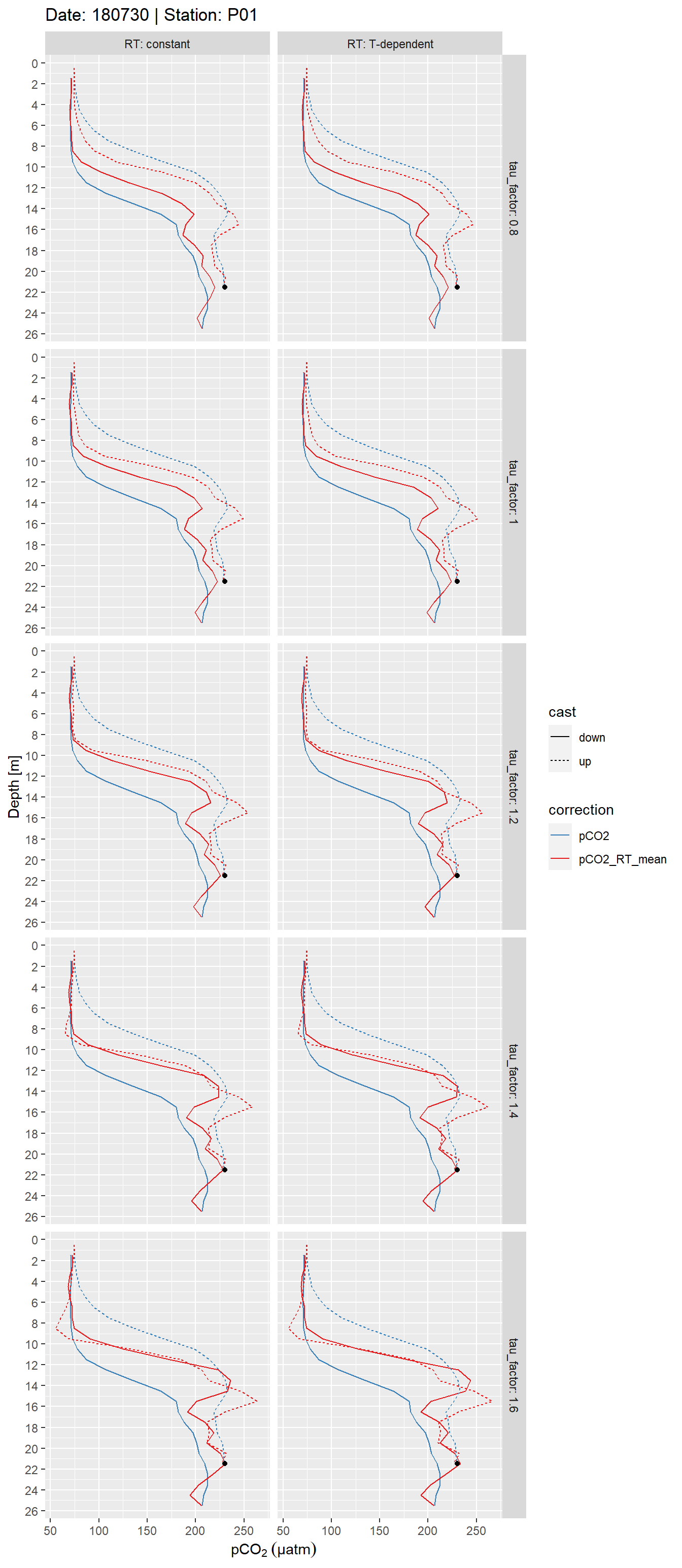
Example plot of discretized, response time corrected and raw pCO2 profiles. Panels highlight the effect of constant vs T-dependent tau estimates (columns) and the optimization by applying a constant factor (rows). The black point indicates the reference pCO2 value.
rm(df_equi_int_sub)A pdf with all discretized pCO2 profiles can be assessed here
pdf(file=here::here("output/Plots/response_time",
"RT_correction_pCO2_profiles_discrete.pdf"), onefile = TRUE, width = 7, height = 11)
for(i_ID in unique(RT_diff$ID)){
for(i_station in unique(RT_diff$station)){
if (nrow(RT_diff %>% filter(ID == i_ID, station == i_station)) > 0){
df_equi_int_sub <- df_equi_int %>%
filter(ID == i_ID,
station == i_station)
print(
RT_diff %>%
filter(ID == i_ID,
station == i_station) %>%
arrange(dep_int) %>%
ggplot()+
geom_path(aes(down, dep_int, col=correction, linetype="down"))+
geom_path(aes(up, dep_int, col=correction, linetype ="up"))+
geom_point(data = df_equi_int_sub, aes(pCO2_equi, dep_int))+
scale_y_reverse(breaks=seq(0,40,2))+
scale_linetype(name="cast")+
scale_color_brewer(palette = "Set1", direction = -1)+
labs(y="Depth [m]", title = str_c("Date: ",i_ID," | Station: ",i_station))+
theme_bw()+
facet_grid(tau_factor~RT, labeller = label_both)
)
rm(df_equi_int_sub)
}
}
}
dev.off()i_ID <- "180730"
i_station <- "P01"
RT_diff %>%
filter(ID == i_ID,
station == i_station,
correction == "pCO2_RT_mean") %>%
arrange(dep_int) %>%
ggplot(aes(d_pCO2, dep_int, col=as.factor(tau_factor)))+
geom_path()+
geom_point()+
scale_y_reverse(breaks=seq(0,40,2))+
scale_color_discrete(name="tau factor")+
labs(x=expression(Delta~pCO[2]~(µatm)), y="Depth [m]", title = str_c("Date: ",i_ID," | Station: ",i_station))+
geom_vline(xintercept = 0)+
geom_vline(xintercept = c(-10,10), col="red")+
facet_wrap(~RT, labeller = label_both)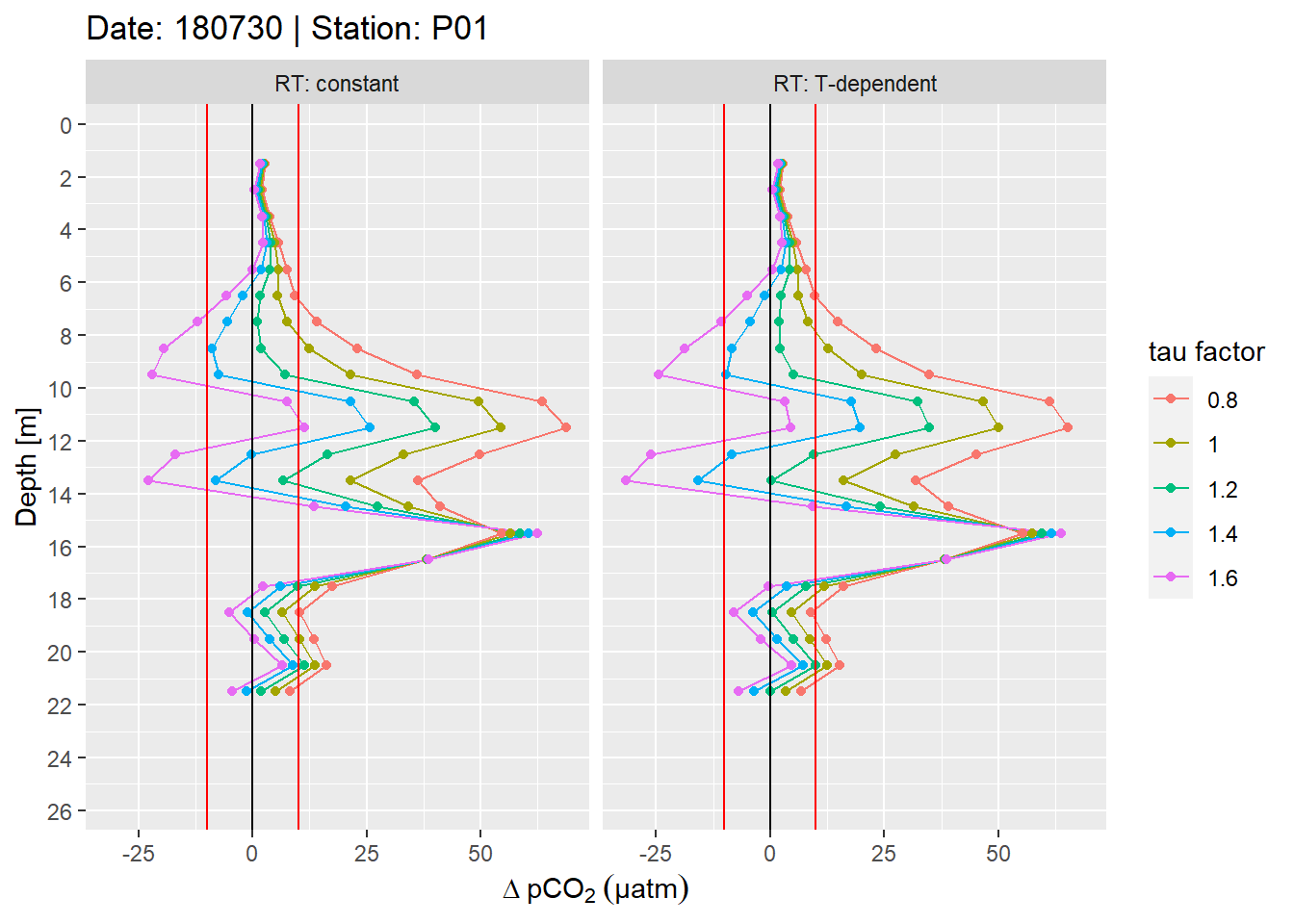
Example plot of absolute pCO2 offset profiles. Panels highlight the effect of constant vs T-dependent tau estimates. Colour indicates the optimization by applying a constant factor to tau. Vertical red lines mark an arbitray 10 µatm pCO2 threshold.
pdf(file=here::here("output/Plots/response_time",
"RT_correction_delta_pCO2_absolute_profiles_discrete.pdf"), onefile = TRUE, width = 7, height = 7)
for(i_ID in unique(RT_diff$ID)){
for(i_station in unique(RT_diff$station)){
if (nrow(RT_diff %>% filter(ID == i_ID, station == i_station)) > 0){
print(
RT_diff %>%
filter(ID == i_ID,
station == i_station,
correction == "pCO2_RT_mean") %>%
arrange(dep_int) %>%
ggplot(aes(d_pCO2, dep_int, col=as.factor(tau_factor)))+
geom_path()+
geom_point()+
scale_y_reverse(breaks=seq(0,40,2))+
scale_color_discrete(name="tau factor")+
labs(x = "delta pCO2 [µatm]", y="Depth [m]", title = str_c("Date: ",i_ID," | Station: ",i_station))+
geom_vline(xintercept = 0)+
geom_vline(xintercept = c(-10,10), col="red")+
theme_bw()+
facet_wrap(~RT, labeller = label_both)
)
}
}
}
dev.off()A pdf with all absolute pCO2 offset profiles can be assessed here.
i_ID <- "180730"
i_station <- "P01"
RT_diff %>%
filter(ID == i_ID,
station == i_station,
correction == "pCO2_RT_mean") %>%
arrange(dep_int) %>%
ggplot(aes(d_pCO2_rel, dep_int, col=as.factor(tau_factor)))+
geom_path()+
geom_point()+
scale_y_reverse(breaks=seq(0,40,2))+
scale_color_discrete(name="tau factor")+
labs(x=expression(Delta~pCO[2]~("%"~of~absolute~value)), y="Depth [m]",
title = str_c("Date: ",i_ID," | Station: ",i_station))+
geom_vline(xintercept = 0)+
geom_vline(xintercept = c(-10,10), col="red")+
facet_wrap(~RT, labeller = label_both)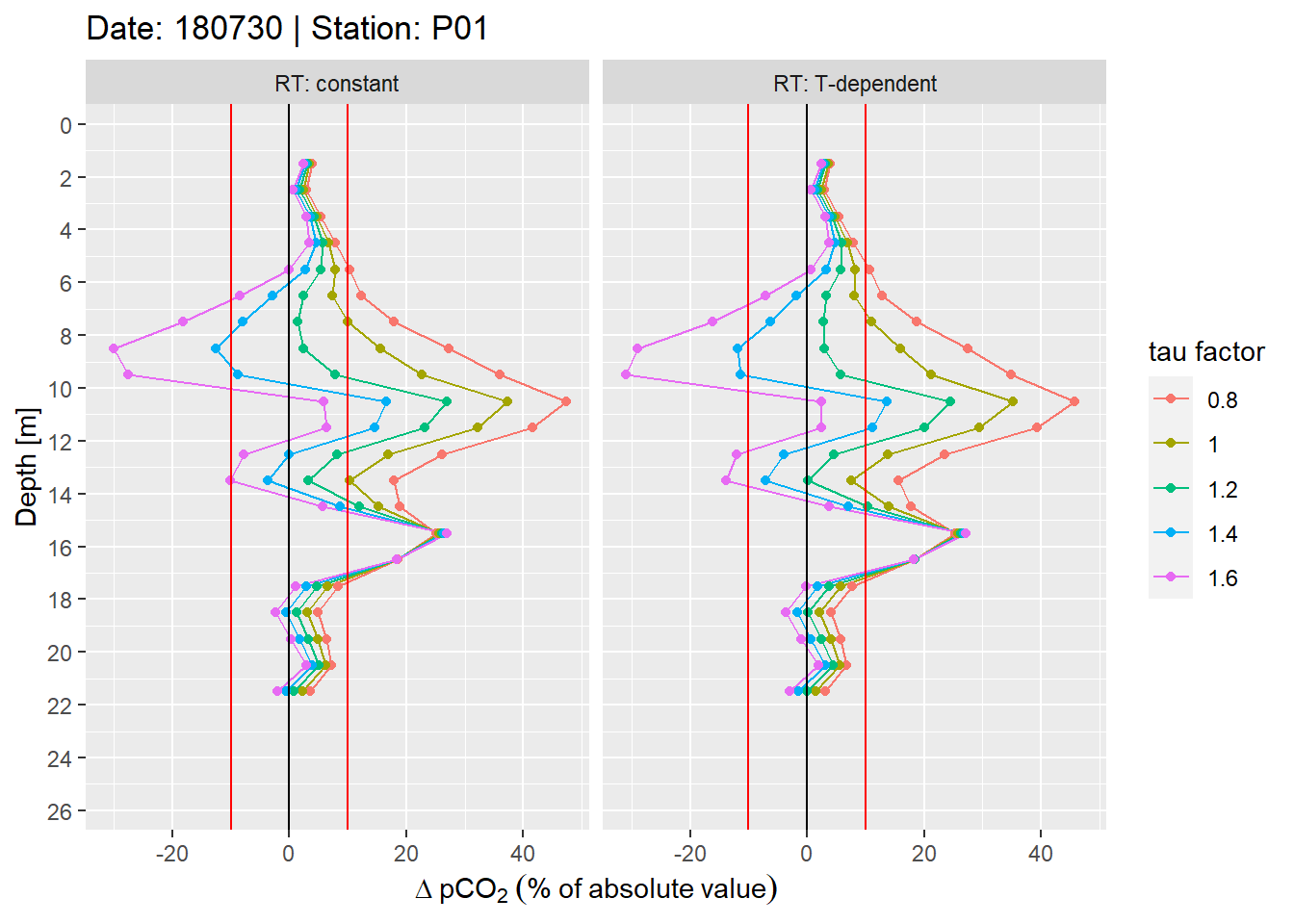
Example plot of relative offset pCO2 profiles. Panels highlight the effect of constant vs T-dependent tau estimates. Colour indicates the optimization by applying a constant factor to tau. Vertical red lines mark an arbitray 10% threshold.
A pdf with all relative pCO2 offset profiles can be assessed here.
pdf(file=here::here("output/Plots/response_time",
"RT_correction_delta_pCO2_relative_profiles_discrete.pdf"), onefile = TRUE, width = 7, height = 7)
for(i_ID in unique(RT_diff$ID)){
for(i_station in unique(RT_diff$station)){
if (nrow(RT_diff %>% filter(ID == i_ID, station == i_station)) > 0){
print(
RT_diff %>%
filter(ID == i_ID,
station == i_station,
correction == "pCO2_RT_mean") %>%
arrange(dep_int) %>%
ggplot(aes(d_pCO2_rel, dep_int, col=as.factor(tau_factor)))+
geom_path()+
geom_point()+
scale_y_reverse(breaks=seq(0,40,2))+
scale_color_discrete(name="tau factor")+
labs(x = "delta pCO2 [% of absolute value]", y="Depth [m]", title = str_c("Date: ",i_ID," | Station: ",i_station))+
geom_vline(xintercept = 0)+
geom_vline(xintercept = c(-10,10), col="red")+
theme_bw()+
facet_wrap(~RT, labeller = label_both)
)
}
}
}
dev.off()4.2 Downcast vs reference value
equi_diff <- full_join(RT_diff, df_equi_int) %>%
filter(!is.na(pCO2_equi)) %>%
mutate(d_pCO2_equi = down - pCO2_equi,
d_pCO2_equi_rel = 100 * d_pCO2_equi / pCO2_equi)equi_diff %>%
filter(RT == "T-dependent", tau_factor == 1.2, correction=="pCO2_RT_mean") %>%
ggplot(aes(pCO2_equi, d_pCO2_equi))+
geom_hline(yintercept = 0)+
geom_point()+
labs(x=expression(Reference~pCO[2]~(µatm)), y=expression(Delta~pCO[2]~from~reference~(µatm)))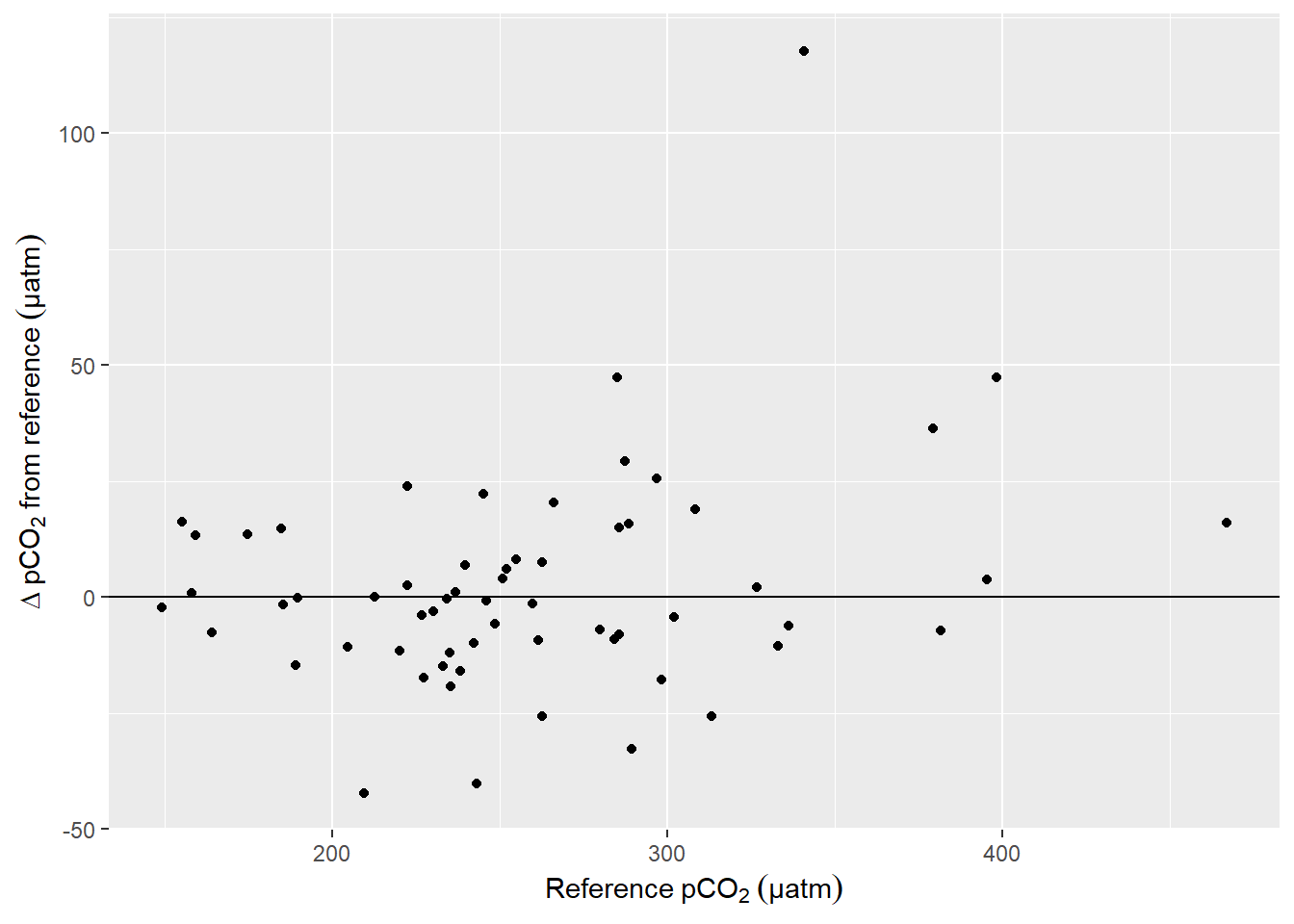
Offset between pCO2 downcast and upcast reference value as a function of absolute pCO2. (Conditions: T-dependent tau, Factor = 1.2.
equi_diff %>%
ggplot(aes(as.factor(tau_factor), d_pCO2_equi, fill=correction))+
geom_hline(yintercept = 0)+
geom_violin()+
labs(y=expression(Delta~pCO[2]~from~reference~(µatm)), x="Tau factor")+
scale_fill_brewer(palette = "Set1")+
facet_wrap(~RT, labeller = label_both)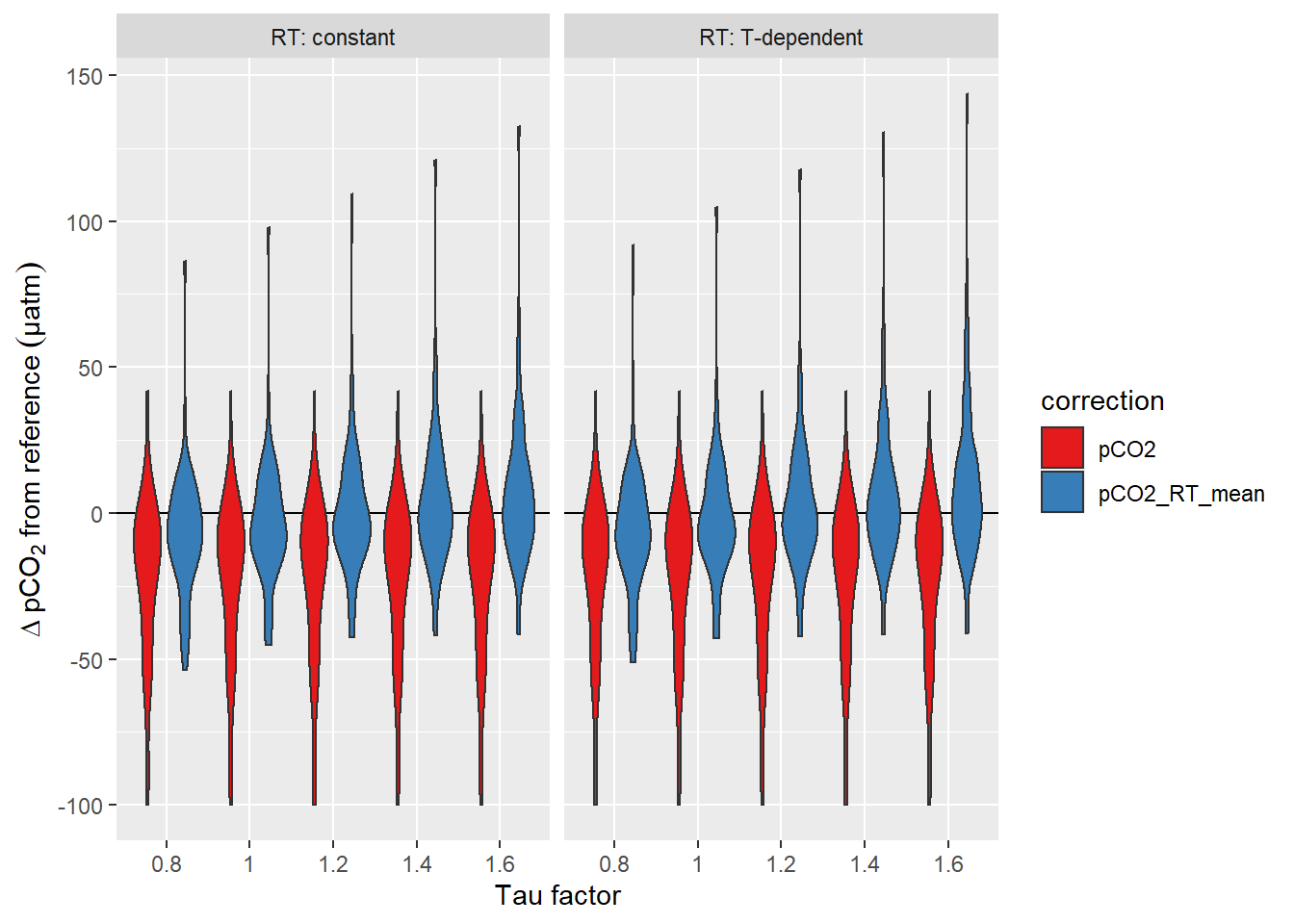
Offset between pCO2 downcast and upcast reference value. Panels highlight the effect of constant vs T-dependent tau estimates. Colour distinguish raw and corrected offsets.
4.3 Summary metrics
In order to decide, which conditions resulted in the best response correction the mean absoulte and relative pCO2 offset across all profiles was calculated for:
- the offset between downcast and reference value
- the offset between downcast and upcast
- constant and T-dependent tau
- applied tau factors
Summary statistics were restricted to complete shallow profiles (not more than 2 observations missing from 1m depth intervals, maximum depth 20m).
RT_diff_20 <- RT_diff %>%
filter(dep_int <= 20) %>%
group_by(ID, station, RT, tau_factor, correction) %>%
mutate(nr_na = sum(is.na(d_pCO2))) %>%
ungroup() %>%
filter(nr_na <= 2)
RT_diff_30 <- RT_diff %>%
filter(dep_int <= 30) %>%
group_by(ID, station, RT, tau_factor, correction) %>%
mutate(nr_na = sum(is.na(d_pCO2))) %>%
ungroup() %>%
filter(nr_na <= 2)
RT_diff_sum_profile_30 <- RT_diff_30 %>%
mutate(d_pCO2_abs = abs(d_pCO2),
d_pCO2_rel_abs = abs(d_pCO2_rel)) %>%
group_by(RT, tau_factor, dep_int, correction) %>%
summarise(mean = mean(d_pCO2, na.rm = TRUE),
sd = sd(d_pCO2, na.rm = TRUE),
mean_abs = mean(d_pCO2_abs, na.rm = TRUE),
mean_rel = mean(d_pCO2_rel, na.rm = TRUE),
sd_rel = sd(d_pCO2_rel, na.rm = TRUE),
mean_rel_abs = mean(d_pCO2_rel_abs, na.rm = TRUE)) %>%
ungroup() %>%
pivot_longer(cols = 5:10, names_to = "estimate", values_to = "dpCO2")
RT_diff_sum_profile_20 <- RT_diff_20 %>%
mutate(d_pCO2_abs = abs(d_pCO2),
d_pCO2_rel_abs = abs(d_pCO2_rel)) %>%
group_by(RT, tau_factor, dep_int, correction) %>%
summarise(mean = mean(d_pCO2, na.rm = TRUE),
sd = sd(d_pCO2, na.rm = TRUE),
mean_abs = mean(d_pCO2_abs, na.rm = TRUE),
mean_rel = mean(d_pCO2_rel, na.rm = TRUE),
sd_rel = sd(d_pCO2_rel, na.rm = TRUE),
mean_rel_abs = mean(d_pCO2_rel_abs, na.rm = TRUE)) %>%
ungroup() %>%
pivot_longer(cols = 5:10, names_to = "estimate", values_to = "dpCO2")
equi_diff_sum <- equi_diff %>%
mutate(d_pCO2_equi_abs = abs(d_pCO2_equi),
d_pCO2_equi_rel_abs = abs(d_pCO2_equi_rel)) %>%
group_by(correction, RT, tau_factor) %>%
summarise(mean = mean(d_pCO2_equi, na.rm = TRUE),
mean_abs = mean(d_pCO2_equi_abs, na.rm = TRUE),
mean_rel = mean(d_pCO2_equi_rel, na.rm = TRUE),
mean_rel_abs = mean(d_pCO2_equi_rel_abs, na.rm = TRUE)) %>%
ungroup() %>%
pivot_longer(cols = 4:7, names_to = "estimate", values_to = "dpCO2")RT_diff_sum_profile_30 %>%
filter(correction == "pCO2_RT_mean",
estimate %in% c("mean_abs", "mean_rel_abs", "sd", "sd_rel")) %>%
ggplot()+
geom_vline(xintercept = 0)+
geom_hline(yintercept = 20)+
geom_vline(xintercept = c(10), col="red")+
geom_path(aes(dpCO2, dep_int, col=as.factor(tau_factor)))+
scale_y_reverse()+
scale_color_discrete(name="Tau factor")+
labs(x=expression(Delta~pCO[2]~(µatm)), y="Depth intervals (1m)")+
facet_grid(estimate~RT)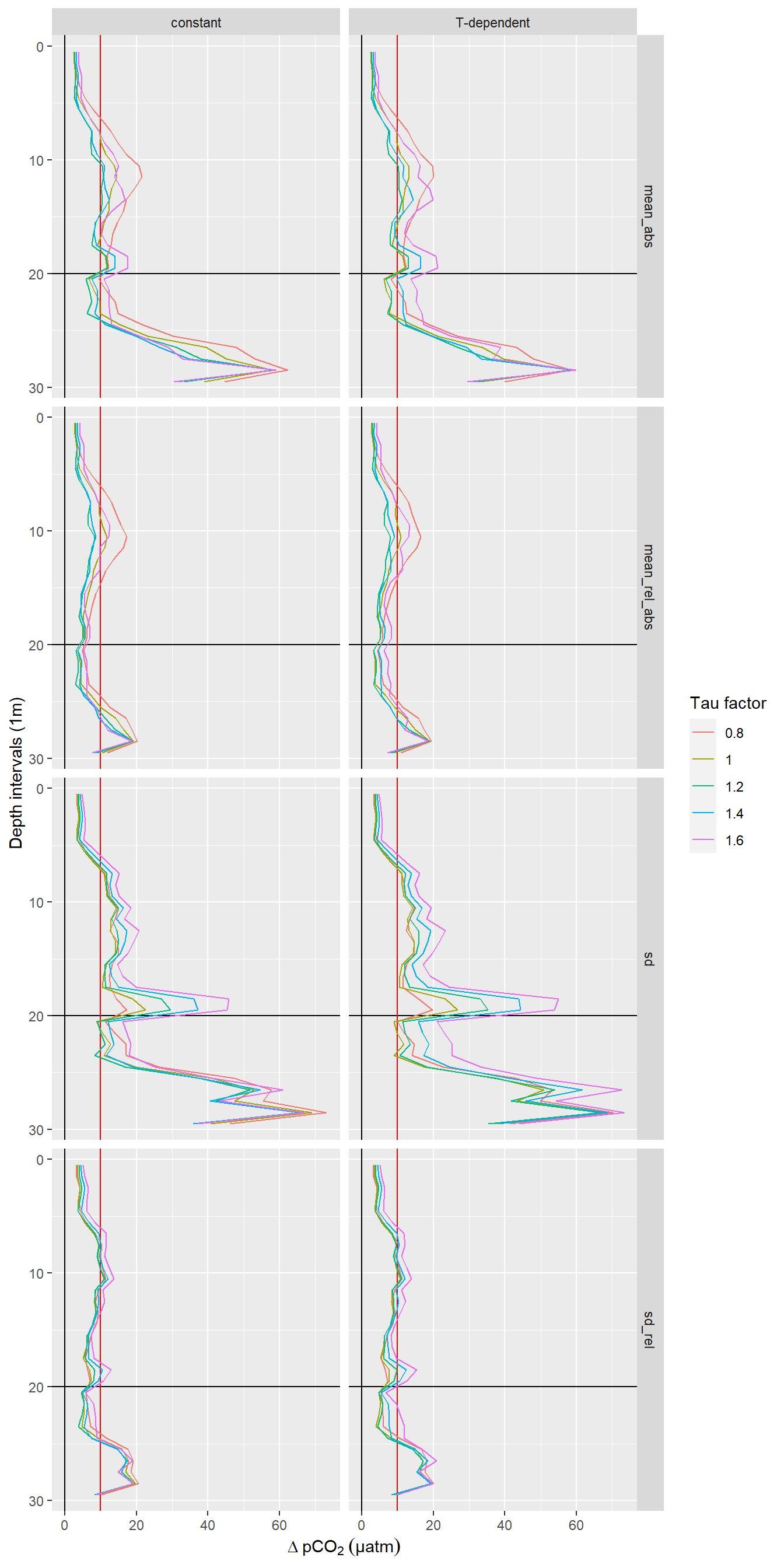
Offset between up- and downcast. Panel columns: Constant and T-dependent tau. Panel rows from top to bottom: Mean of absolute offset, mean of relative absolute offset, standard deviation of offset, standard deviation of relative offset.
RT_diff_sum_mean_highres <-
read_csv(here::here("data/_merged_data_files",
"X_BloomSail_CTD_HydroC_profiles_RT_cast-offset_highres_taufactor_mean.csv")) %>%
filter(estimate %in% c("mean_abs", "mean_rel_abs"))
RT_diff_sum_mean <- RT_diff_sum_profile_20 %>%
group_by(RT, estimate, correction, tau_factor) %>%
summarise(mean_dpCO2 = mean(dpCO2)) %>%
ungroup()
RT_diff_sum_mean %>%
filter(estimate %in% c("mean_abs", "mean_rel_abs")) %>%
ggplot(aes(tau_factor, mean_dpCO2, col=RT, linetype=correction, shape=correction))+
geom_line(data = RT_diff_sum_mean_highres,
aes(tau_factor, mean_dpCO2))+
geom_point()+
geom_hline(yintercept = 0)+
labs(x="Tau factor", y=expression(Mean~Delta~pCO[2]))+
facet_wrap(~estimate)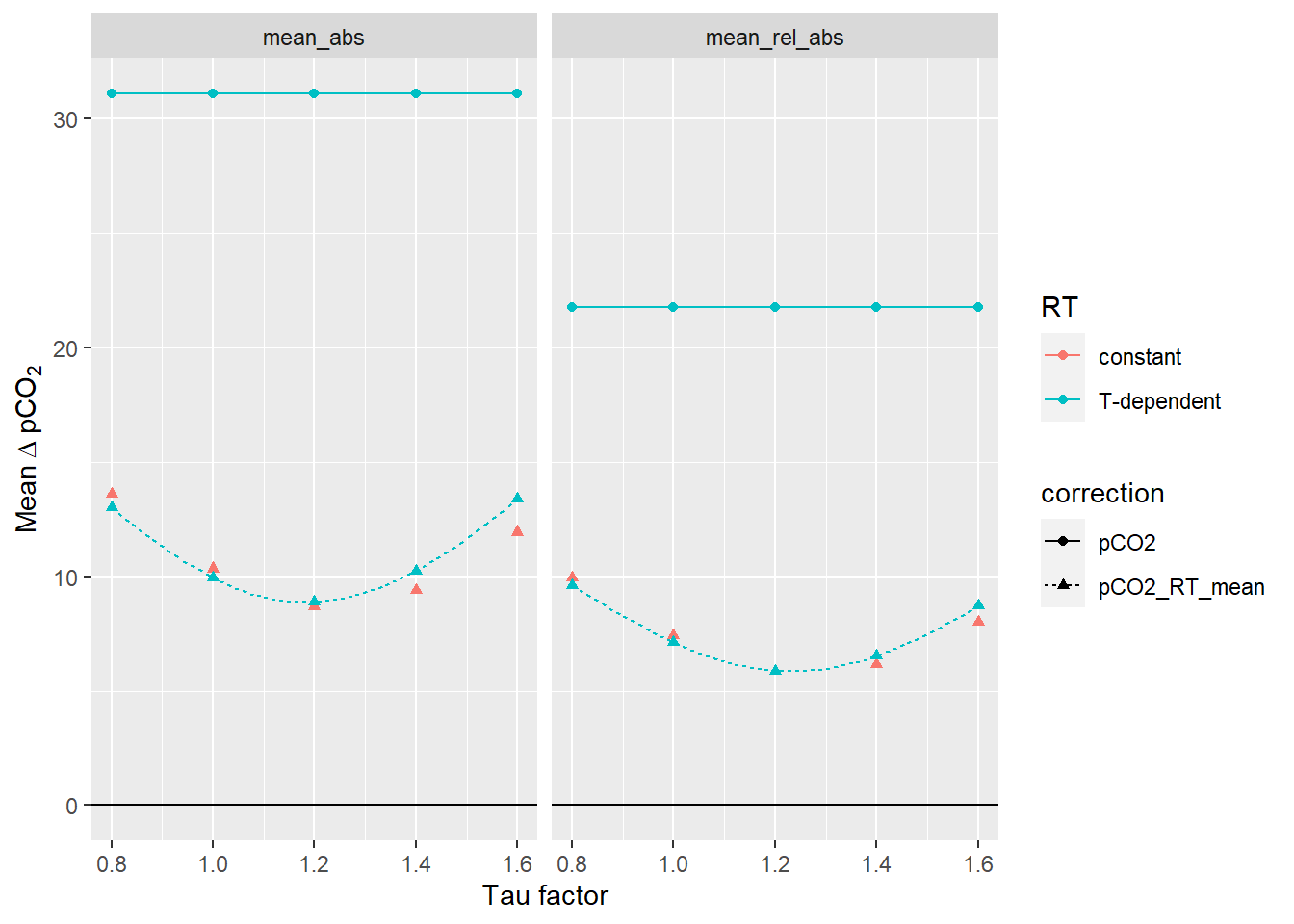
Mean offset between up- and downcast for all profiles up to 20m water depth. The lines between discrete tau factors result from the same analysis performed with high resolution of the tau factor. Left Panel: Mean absolute offset (µatm). Right panel: Mean relative offset (% of absolute value).
Below we determined the tau factor that corresponds to lowest absolute and relative mean offsets, respectively.
RT_diff_sum_mean_highres %>%
filter(correction == "pCO2_RT_mean", estimate %in% c("mean_abs")) %>%
slice(which.min(mean_dpCO2)) %>%
select(tau_factor, mean_dpCO2) %>%
rename(mean_abs=mean_dpCO2)# A tibble: 1 x 2
tau_factor mean_abs
<dbl> <dbl>
1 1.18 8.89RT_diff_sum_mean_highres %>%
filter(correction == "pCO2_RT_mean", estimate == "mean_rel_abs") %>%
slice(which.min(mean_dpCO2)) %>%
select(tau_factor, mean_dpCO2) %>%
rename(mean_rel_abs=mean_dpCO2)# A tibble: 1 x 2
tau_factor mean_rel_abs
<dbl> <dbl>
1 1.24 5.85Likewise, we analyse the offset from the pCO2 reference value:
equi_diff_sum_highres <-
read_csv(here::here("data/_merged_data_files",
"X_BloomSail_CTD_HydroC_profiles_RT_reference-offset_highres_taufactor_mean.csv")) %>%
pivot_longer(cols = 4:7, names_to = "estimate", values_to = "dpCO2") %>%
filter(estimate %in% c("mean_abs", "mean_rel_abs"))
equi_diff_sum %>%
filter(estimate %in% c("mean_abs", "mean_rel_abs")) %>%
ggplot(aes(tau_factor, dpCO2, col=RT, linetype=correction, shape=correction))+
geom_line(data = equi_diff_sum_highres,
aes(tau_factor, dpCO2))+
geom_point()+
geom_hline(yintercept = 0)+
labs(x="Tau factor", y=expression(Mean~Delta~pCO[2]))+
facet_wrap(~estimate)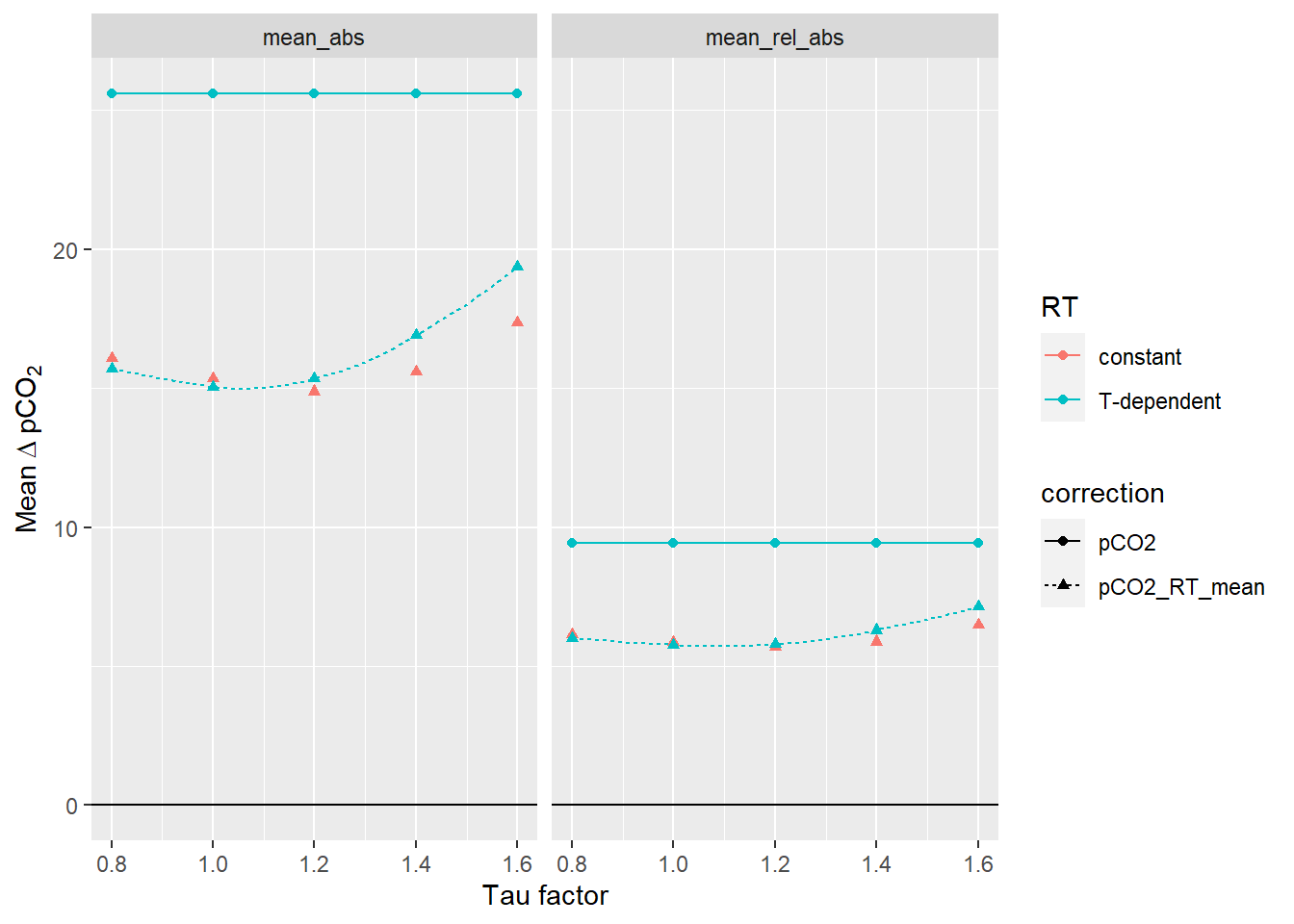
Mean pCO2 offset from reference values as a function of the factor applied to tau. The lines between discrete tau factors result from the same analysis performed with high resolution of the tau factor. Left Panel: Mean absolute offset (µatm). Right panel: Mean relative offset (% of absolute value).
Below we determined the tau factor that corresponds to lowest absolute and relative mean offsets, respectively.
equi_diff_sum_highres %>%
filter(correction == "pCO2_RT_mean", estimate %in% c("mean_abs")) %>%
slice(which.min(dpCO2)) %>%
select(tau_factor, dpCO2) %>%
rename(mean_abs=dpCO2)# A tibble: 1 x 2
tau_factor mean_abs
<dbl> <dbl>
1 1.04 15.0equi_diff_sum_highres %>%
filter(correction == "pCO2_RT_mean", estimate == "mean_rel_abs") %>%
slice(which.min(dpCO2)) %>%
select(tau_factor, dpCO2) %>%
rename(mean_rel_abs=dpCO2)# A tibble: 1 x 2
tau_factor mean_rel_abs
<dbl> <dbl>
1 1.1 5.725 Conclusion
- Taking the temperature dependence of tau into account resulted in a slightly better agreement between up- and downcast, as well as downcast and reference value
- For all quality metrics we find improved agreement for slightly positive tau factor ranging from 1.04 - 1.24
- As the focus is on pCO2 changes in the upper 10 m of the water column, we will apply the tau factor 1.24 leading to the lowest relative offset between up- and downcast
6 Correct entire data set
Finally, the response time correction was applied to the full data set (not only profile data) based on the optimum parameterization determined above.
# Response time correction approach after Bittig --------------------------
RT_corr <- function(c1, c0, dt, tau) {
( 1 / ( 2* (( 1+(2*tau/dt) )^(-1) ))) * (c1 - (1-(2* (( 1+(2*tau/dt) )^(-1) ))) * c0)
}
# load data and response times
df <-
read_csv(here::here("Data/_merged_data_files", "BloomSail_CTD_HydroC_track.csv"),
col_types = cols(ID = col_character(),
pCO2_analog = col_double(),
pCO2 = col_double(),
Zero = col_factor(),
Flush = col_factor(),
mixing = col_factor(),
Zero_ID = col_integer(),
deployment = col_integer(),
duration = col_double(),
lon = col_double(),
lat = col_double()))
df <- df %>%
group_by(ID) %>%
mutate(duration = as.numeric(date_time - min(date_time)),
pump_power = if_else(date_time < ymd_hms("2018-07-17;13:08:34"), "1W", "8W")) %>%
arrange(date_time)
RT_fit <- read_csv(here::here("data/_summarized_data_files", "Tina_V_HydroC_RT_fit.csv"))
# Assign T-dependent response time (tau) values ----------------------------------------------
RT_fit <- RT_fit %>%
rename(tau_intercept = `(Intercept)`, tau_slope=tem)
df <- full_join(df, RT_fit)
#Assign tau
df <- df %>%
mutate(tau = tau_intercept + tau_slope *tem) %>%
select(-tau_intercept, -tau_slope)
# Prepare data set for RT correction --------------------------------------
df <- df %>%
group_by(ID, station) %>%
arrange(date_time) %>%
mutate(dt = as.numeric(as.character(date_time - lag(date_time)))) %>%
ungroup()
# measurement frequency
freq <- df %>%
filter(dt < 13) %>%
group_by(ID) %>%
summarise(dt_mean = round(mean(dt, na.rm = TRUE),0))
df <- full_join(df, freq)
# tau factors
df <- expand_grid(df, tau_factor = seq(1.2))
df <- df %>%
mutate(tau_test = tau*tau_factor)
# Apply RT correction to entire data set
for(i_ID in unique(df$ID)){
#i_ID <- "180716"
freq_sub <- freq %>% filter(ID == i_ID) %>% pull(dt_mean)
window <- 30 / freq_sub
rolling_mean <- rollify(~mean(.x, na.rm = TRUE), window = window)
df_sub <- df %>%
filter(ID == i_ID) %>%
group_by(station) %>%
mutate(pCO2_RT = RT_corr(pCO2, lag(pCO2), dt, tau_test),
pCO2_RT = if_else(pCO2_RT %in% c(Inf, -Inf), NaN, pCO2_RT),
window = window,
pCO2_RT_mean = rolling_mean(pCO2_RT)
#pCO2_RT_median = rolling_median(pCO2_RT)
) %>%
ungroup()
# time shift RT corrected data
shift <- as.integer(as.character(window/2))
df_sub <- df_sub %>%
group_by(station) %>%
mutate(pCO2_RT_mean = lead(pCO2_RT_mean, shift)) %>%
ungroup()
if (exists("df_corr")){df_corr <- bind_rows(df_corr, df_sub)}
else{df_corr <- df_sub}
rm(df_sub, freq_sub, rolling_mean, shift, window)
}
df <- df_corr
rm(RT_corr, i_ID, freq, df_corr)
df <- df %>%
select(-c(tau, tau_factor, tau_test, window))
df %>%
write_csv(here::here("data/_merged_data_files",
"BloomSail_CTD_HydroC_track_RT.csv"))
rm(df)7 List of relevant parameters
Response time determination
- Fit interval length: Use tau from one or all fit interval length? Scale fit interval length to expected tau?
- tau residual threshold (mean absolute residula <1% of final pCO2, entire group removed)
- Mean vs T-dependent tau
Response time correction
- correction procedure (Bittig vs. Fiedler, Miloshevich, Fietzek)
- Smoothing
Quality assesment of response time correction
- Down-Up-difference vs reference value
- Depth interval width for offset calculation
- Max depth for Down-Up-difference (currently upper 20m)
- NA criterion for included Down-Up-difference (currently 2)
8 Open tasks / questions
- Condering the summary metrics: If the standard deviation of the offset between up- and downcast is as large as the offset itself, does it make sense to apply the tau factor? In other words: Does it make the profiles significantly better?
- Compare Contros and own response time estimates
sessionInfo()R version 3.5.0 (2018-04-23)
Platform: x86_64-w64-mingw32/x64 (64-bit)
Running under: Windows 10 x64 (build 18363)
Matrix products: default
locale:
[1] LC_COLLATE=English_United States.1252
[2] LC_CTYPE=English_United States.1252
[3] LC_MONETARY=English_United States.1252
[4] LC_NUMERIC=C
[5] LC_TIME=English_United States.1252
attached base packages:
[1] stats graphics grDevices utils datasets methods base
other attached packages:
[1] patchwork_1.0.0 tibbletime_0.1.3 lubridate_1.7.4 broom_0.5.3
[5] data.table_1.12.6 seacarb_3.2.12 oce_1.2-0 gsw_1.0-5
[9] testthat_2.3.1 forcats_0.4.0 stringr_1.4.0 dplyr_0.8.3
[13] purrr_0.3.3 readr_1.3.1 tidyr_1.0.0 tibble_2.1.3
[17] ggplot2_3.3.0 tidyverse_1.3.0
loaded via a namespace (and not attached):
[1] Rcpp_1.0.2 here_0.1 lattice_0.20-35 utf8_1.1.4
[5] assertthat_0.2.1 zeallot_0.1.0 rprojroot_1.3-2 digest_0.6.22
[9] R6_2.4.0 cellranger_1.1.0 backports_1.1.5 reprex_0.3.0
[13] evaluate_0.14 highr_0.8 httr_1.4.1 pillar_1.4.2
[17] rlang_0.4.5 readxl_1.3.1 rstudioapi_0.10 Matrix_1.2-14
[21] rmarkdown_2.0 labeling_0.3 munsell_0.5.0 compiler_3.5.0
[25] httpuv_1.5.2 modelr_0.1.5 xfun_0.10 pkgconfig_2.0.3
[29] mgcv_1.8-23 htmltools_0.4.0 tidyselect_0.2.5 workflowr_1.6.0
[33] fansi_0.4.0 viridisLite_0.3.0 crayon_1.3.4 dbplyr_1.4.2
[37] withr_2.1.2 later_1.0.0 grid_3.5.0 nlme_3.1-137
[41] jsonlite_1.6 gtable_0.3.0 lifecycle_0.1.0 DBI_1.0.0
[45] git2r_0.26.1 magrittr_1.5 scales_1.0.0 cli_1.1.0
[49] stringi_1.4.3 fs_1.3.1 promises_1.1.0 xml2_1.2.2
[53] generics_0.0.2 vctrs_0.2.0 RColorBrewer_1.1-2 tools_3.5.0
[57] glue_1.3.1 hms_0.5.2 yaml_2.2.0 colorspace_1.4-1
[61] rvest_0.3.5 knitr_1.26 haven_2.2.0