Methods
Tina Lasisi
2023-03-04 20:58:44
Last updated: 2023-03-04
Checks: 7 0
Knit directory: PODFRIDGE/
This reproducible R Markdown analysis was created with workflowr (version 1.7.0). The Checks tab describes the reproducibility checks that were applied when the results were created. The Past versions tab lists the development history.
Great! Since the R Markdown file has been committed to the Git repository, you know the exact version of the code that produced these results.
Great job! The global environment was empty. Objects defined in the global environment can affect the analysis in your R Markdown file in unknown ways. For reproduciblity it’s best to always run the code in an empty environment.
The command set.seed(20230302) was run prior to running
the code in the R Markdown file. Setting a seed ensures that any results
that rely on randomness, e.g. subsampling or permutations, are
reproducible.
Great job! Recording the operating system, R version, and package versions is critical for reproducibility.
Nice! There were no cached chunks for this analysis, so you can be confident that you successfully produced the results during this run.
Great job! Using relative paths to the files within your workflowr project makes it easier to run your code on other machines.
Great! You are using Git for version control. Tracking code development and connecting the code version to the results is critical for reproducibility.
The results in this page were generated with repository version c02c427. See the Past versions tab to see a history of the changes made to the R Markdown and HTML files.
Note that you need to be careful to ensure that all relevant files for
the analysis have been committed to Git prior to generating the results
(you can use wflow_publish or
wflow_git_commit). workflowr only checks the R Markdown
file, but you know if there are other scripts or data files that it
depends on. Below is the status of the Git repository when the results
were generated:
Ignored files:
Ignored: .DS_Store
Ignored: .Rproj.user/
Ignored: data/.DS_Store
Note that any generated files, e.g. HTML, png, CSS, etc., are not included in this status report because it is ok for generated content to have uncommitted changes.
These are the previous versions of the repository in which changes were
made to the R Markdown (analysis/methods.Rmd) and HTML
(docs/methods.html) files. If you’ve configured a remote
Git repository (see ?wflow_git_remote), click on the
hyperlinks in the table below to view the files as they were in that
past version.
| File | Version | Author | Date | Message |
|---|---|---|---|---|
| Rmd | c02c427 | Tina Lasisi | 2023-03-04 | update methods |
| html | 342c5a3 | Tina Lasisi | 2023-03-04 | Build site. |
| Rmd | ea3444e | Tina Lasisi | 2023-03-04 | update methods |
| html | 2b161f2 | Tina Lasisi | 2023-03-04 | Build site. |
| Rmd | d8748aa | Tina Lasisi | 2023-03-04 | wflow_publish("analysis/methods.Rmd") |
| html | c3948af | Tina Lasisi | 2023-03-04 | Build site. |
| Rmd | ce722bc | Tina Lasisi | 2023-03-04 | update website |
| Rmd | a3af2d6 | Tina Lasisi | 2023-03-02 | Updating images and methods page |
| html | a3af2d6 | Tina Lasisi | 2023-03-02 | Updating images and methods page |
| html | f02bc38 | Tina Lasisi | 2023-03-02 | Build site. |
| html | c9130d5 | Tina Lasisi | 2023-03-02 | wflow_git_commit(all = TRUE) |
| html | a4a7d45 | Tina Lasisi | 2023-03-02 | Build site. |
| html | 00073fd | Tina Lasisi | 2023-03-02 | Build site. |
| Rmd | d6a84df | Tina Lasisi | 2023-03-02 | Update website |
| html | 51ed5a6 | Tina Lasisi | 2023-03-02 | Build site. |
| Rmd | 13ed9ae | Tina Lasisi | 2023-03-02 | Publishing POPFORGE |
| html | 13ed9ae | Tina Lasisi | 2023-03-02 | Publishing POPFORGE |
Coop & Edge
Coop & Edge (2019) use a population genetics approach to estimate the likelihood of finding a genetic relative in a database. They assumes that two individuals are related if they share a certain number of genetic blocks, which is determined by the degree of relatedness (e.g. first cousin, second cousin, etc.). Using this assumption, they calculates the expected number of blocks shared between two individuals of a given degree of relatedness based on the size of the genetic database and the population size. They then uses the Poisson distribution to estimate the probability of finding at least one relative of a given degree of relatedness in a database of a certain size.
The original code can be found here.
Below is an adaptation of the code for demonstration purposes with annotations for clarification.
Population and Database Size Estimation
In the code chunk below, we first read in data on US population sizes by year and calculate the number of grandparents by generation based on the cousin degree. We then determine which years match the grandparents’ generation and get the population sizes by year for this generation. The population size is then scaled down by 50% to account for sex and age. For small populations (less than 1 million), the minimum population size is set to 1 million. We also set up a vector of database sizes to test.
# Load necessary packages
library(wesanderson) # for color palettes
# Set path to the data file
path <- "./data/"
savepath <- "./output/"
# Set up vector for cousin degree
p <- c(1:8)
# Set up initial population size
N <- 76e6
# Read in data on US population sizes by year
US_pop <- read.csv(paste(path, "US_popsize.csv", sep = ""))
# Calculate number of grandparents by generation
p_grandpar_gen <- 1950 - 30 * (p + 1)
# Determine which years match the grandparents' generation
these.years <- match(p_grandpar_gen, US_pop$year)
# Get population sizes by year for grandparents' generation
US_Ns <- US_pop$Population[these.years]
# Scale population size down by 50% to account for sex and age
N <- US_Ns
N <- N * 0.5 * 0.9
# Set minimum population size for small populations
N[US_Ns < 1e6] <- 1e6
# Set up vector of database sizes to test
DB.sizes <- c(1e6, 5e6, 10e6)
# Set color palette for graphs
my.cols <- wes_palette("Darjeeling1")Probability of p-th degree cousin and number of p-th degree cousins
The code below calculates the probability of having at least one p-th cousin in the database and the expected number of p-th cousins in the sample for different database sizes. The first plot shows the probability of having at least one p-th cousin in the database based on the degree of relatedness and the size of the database. The second plot shows the expected number of p-th cousins in the sample for different database sizes.
layout(t(1:2))
# Plot probability of having at least one p-th cousin in database
plot(c(1, 8), c(0, 1), type = "n", ylab = "Probability of at least one p-th cousin in database", xlab = "p (degree of cousin)")
sapply(1:length(DB.sizes), function(i) {
DB.size <- DB.sizes[i]
prob.no.rellys <- exp(-2^(2*p - 2) * DB.size / N)
points(p, 1 - prob.no.rellys, type = "b", col = my.cols[i], pch = 19, lwd = 1.5)
})[[1]]
NULL
[[2]]
NULL
[[3]]
NULLlegend(x = "bottomright", legend = c("Database size (Millions) =", format(DB.sizes / 1e6, dig = 1)), col = c(NA, my.cols), pch = 19)
# Plot of expected number of p-th cousins in sample
plot(c(1,8),c(0,1000),type="n",ylab="Expected number of p-th cousins in database",xlab="p.(degree of cousin)")
sapply(1:length(DB.sizes),function(i){
num.cousins<-4^(p)*DB.sizes[i]/(N/2)
points(p,num.cousins,type="b",col=my.cols[i],lwd=1.5,pch=19)
# points(p,4^(p),type="b",col="black")
})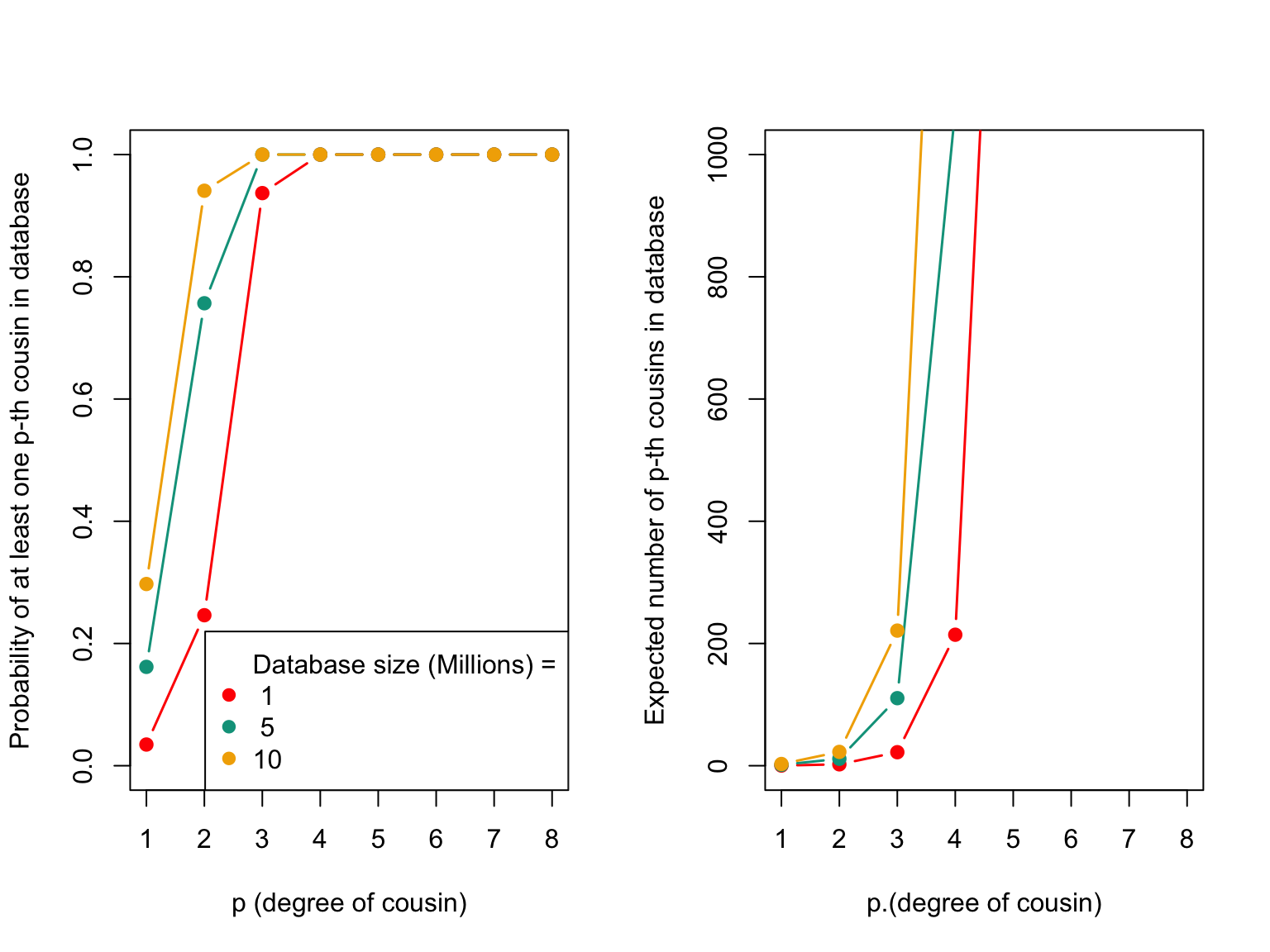
The plot above displays the probability of having at least one p-th cousin in a genetic database and the expected number of p-th cousins in a database. The left plot shows the probability of finding at least one p-th cousin in a database of a given size, and the right plot shows the expected number of p-th cousins in a database of a given size based on the number of genetic blocks shared.
| Version | Author | Date |
|---|---|---|
| 342c5a3 | Tina Lasisi | 2023-03-04 |
[[1]]
NULL
[[2]]
NULL
[[3]]
NULLProbability of a genetically detectable cousin
Below, we calculate the expected number of shared blocks of genetic material between cousins of varying degrees of relatedness. This is important because the probability of detecting genetic material that is shared between two individuals decreases as the degree of relatedness between them decreases. The code uses a Poisson distribution assumption to estimate the probability of two cousins sharing at least one, two, or three blocks of genetic material, based on the expected number of shared blocks of genetic material calculated from previous research.
# The variable 'meiosis' represents the number of meiosis events between cousins, where 'p' is the degree of relatedness (i.e. p = 1 for first cousins, p = 2 for second cousins, etc.)
meiosis <- p + 1
## Expected number of blocks shared between cousins
# 'E.num.blocks' is the expected number of blocks of shared genetic material between cousins based on the degree of relatedness and the number of meiosis events between them. This value is calculated based on previous research and is not calculated in this code.
E.num.blocks <- 2 * (33.8 * (2 * meiosis) + 22) / (2^(2 * meiosis - 1))
## Use Poisson assumption
# 'Prob.genetic' is the probability of two cousins sharing at least one block of genetic material based on the expected number of shared blocks calculated in the previous step. The calculation uses a Poisson distribution assumption.
Prob.genetic <- 1 - exp(-E.num.blocks)
# 'prob.g.e.2.blocks' is the probability of two cousins sharing at least two blocks of genetic material based on the expected number of shared blocks calculated in the previous step. The calculation uses a Poisson distribution assumption.
prob.g.e.2.blocks <- 1 - sapply(E.num.blocks, function(expected.num) {sum(dpois(0:1, expected.num))})
# 'prob.g.e.3.blocks' is the probability of two cousins sharing at least three blocks of genetic material based on the expected number of shared blocks calculated in the previous step. The calculation uses a Poisson distribution assumption.
prob.g.e.3.blocks <- 1 - sapply(E.num.blocks, function(expected.num) {sum(dpois(0:2, expected.num))})## Plot for number of shared blocks with p-th degree cousins
# Set layout of plot
layout(t(1))
# Set color palette for plot
my.cols2<-wes_palette("FantasticFox1")[3:5]
# Create a blank plot with labeled axes
plot(c(1,8),c(0,1),type="n",ylab="Probability p-th cousin \"detectable\"",xlab="p.(degree of cousin)")
# Add points for probability of detecting pth cousin with genomic blocks using colors from my.cols2
points(p,Prob.genetic,col=my.cols2[1],pch=19,type="b",lwd=2)
points(p,prob.g.e.2.blocks,col=my.cols2[2],pch=19,type="b",lwd=2)
points(p,prob.g.e.3.blocks,col=my.cols2[3],pch=19,type="b",lwd=2)
# Add a legend to the plot
legend(x="topright",legend=c("Cousins (w. >0 genomic blocks)","Cousins (w. >1 genomic blocks)","Cousins (w. >2 genomic blocks)"),col=my.cols2[1:3],lty=1)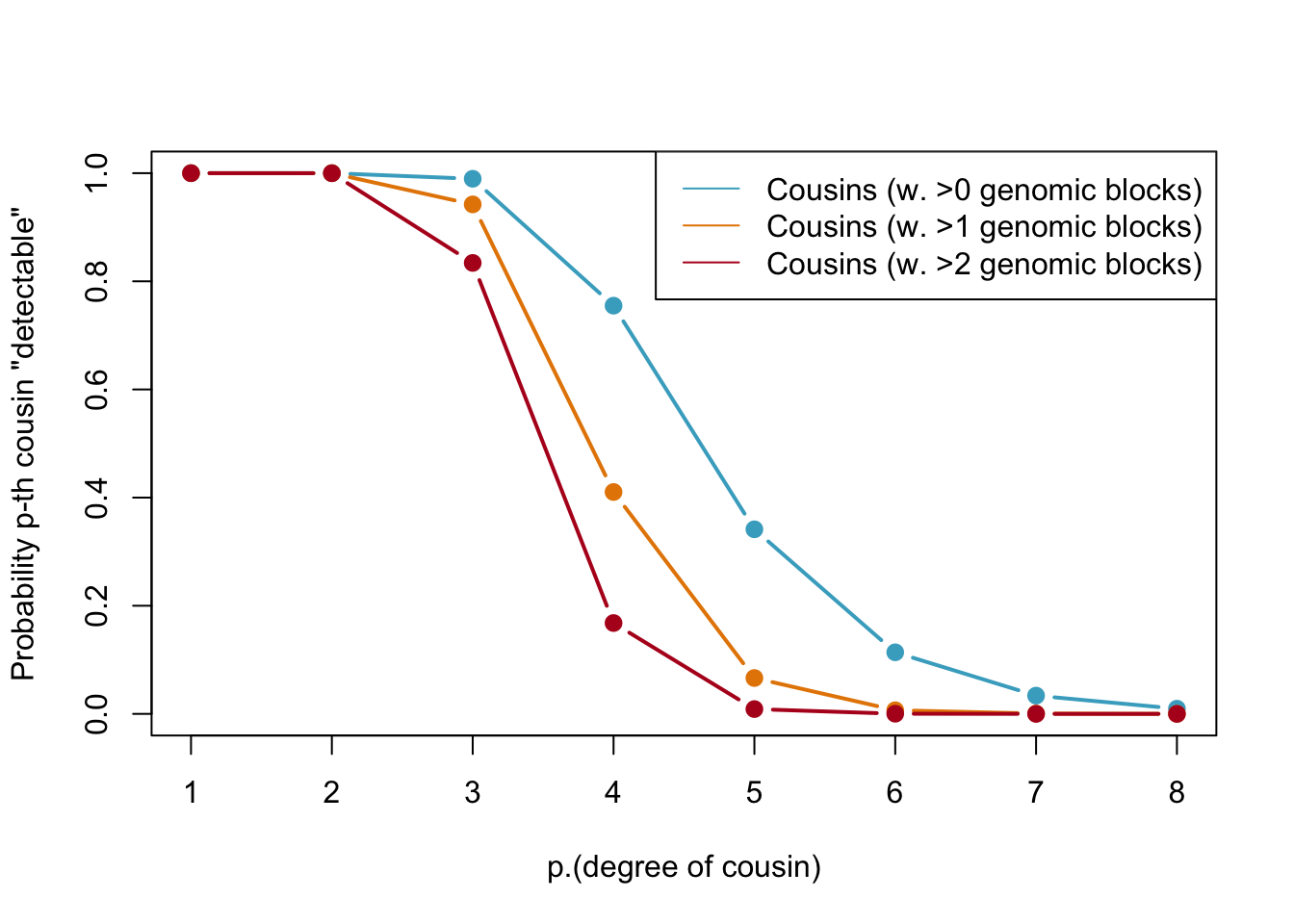
Probabilities of detecting a genetic cousin in a database based on shared genomic blocks. Blue lines represent cousins with at least one genomic block, orange dotted and red lines represent cousins with at least two and three genomic blocks, respectively. The legend specifies the type of cousin being represented by each line.
| Version | Author | Date |
|---|---|---|
| 342c5a3 | Tina Lasisi | 2023-03-04 |
## Plot for expected number of p-th degree cousins in a given database
# Set the layout of the plot
layout(t(1))
# Create a plot with the y-axis ranging from 0 to 350 and the x-axis ranging from 1 to 8, labeled as "Expected number of genetic p-th cousins in database" and "p. (degree of cousin)", respectively
plot(c(1,8),c(0,350),type="n",ylab="Expected number of genetic p-th cousins in database",xlab="p. (degree of cousin)")
# For each database size, calculate the expected number of genetic cousins based on the size of the database, the total number of individuals in the population, and the expected number of blocks of shared genetic material between cousins. Multiply the number of expected genetic cousins by the probability of sharing at least three blocks of genetic material with a cousin, and plot the result as a line on the plot. Repeat this for each database size.
sapply(1:length(DB.sizes),function(i){
num.cousins<-4^(p)*DB.sizes[i]/(N/2)
points(p,num.cousins*prob.g.e.3.blocks,type="b",lty=1,col=my.cols[i])
})[[1]]
NULL
[[2]]
NULL
[[3]]
NULL# Create a legend for the plot that explains what each line represents, including the legend for the database size
my.leg <- c(c("Genetic Cousins", ">2 blocks"), c("Database size (Millions)=", format(DB.sizes/1e6, dig=1)))
legend(x="topright",legend=my.leg,col=c(NA,rep("black",1),NA,my.cols),lty=c(NA,1:2,rep(NA,3)),pch=c(rep(NA,3),rep(19,3)))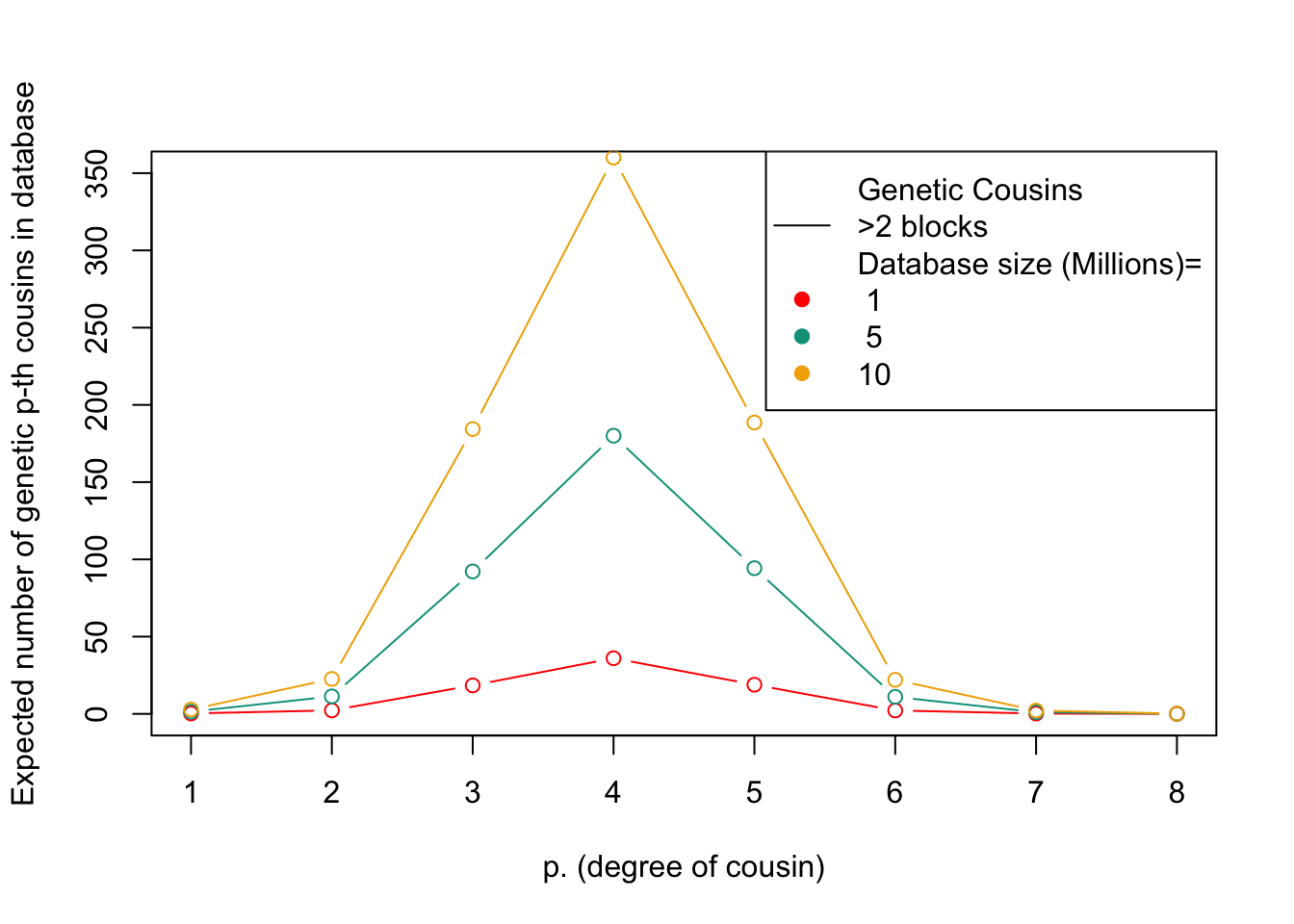
This figure shows the expected number of genetic relatives of degree p in a database of a given size. The x-axis represents the degree of relatedness, while the y-axis represents the expected number of genetic relatives. Each line represents a different database size.
| Version | Author | Date |
|---|---|---|
| 342c5a3 | Tina Lasisi | 2023-03-04 |
sessionInfo()R version 4.2.2 (2022-10-31)
Platform: aarch64-apple-darwin20 (64-bit)
Running under: macOS Ventura 13.0.1
Matrix products: default
BLAS: /Library/Frameworks/R.framework/Versions/4.2-arm64/Resources/lib/libRblas.0.dylib
LAPACK: /Library/Frameworks/R.framework/Versions/4.2-arm64/Resources/lib/libRlapack.dylib
locale:
[1] en_US.UTF-8/en_US.UTF-8/en_US.UTF-8/C/en_US.UTF-8/en_US.UTF-8
attached base packages:
[1] stats graphics grDevices utils datasets methods base
other attached packages:
[1] wesanderson_0.3.6 workflowr_1.7.0
loaded via a namespace (and not attached):
[1] Rcpp_1.0.9 highr_0.9 compiler_4.2.2 pillar_1.8.1
[5] bslib_0.4.1 later_1.3.0 git2r_0.30.1 jquerylib_0.1.4
[9] tools_4.2.2 getPass_0.2-2 digest_0.6.30 jsonlite_1.8.3
[13] evaluate_0.18 lifecycle_1.0.3 tibble_3.1.8 pkgconfig_2.0.3
[17] rlang_1.0.6 cli_3.4.1 rstudioapi_0.14 yaml_2.3.6
[21] xfun_0.35 fastmap_1.1.0 httr_1.4.4 stringr_1.5.0
[25] knitr_1.41 fs_1.5.2 vctrs_0.5.1 sass_0.4.4
[29] rprojroot_2.0.3 glue_1.6.2 R6_2.5.1 processx_3.8.0
[33] fansi_1.0.3 rmarkdown_2.18 callr_3.7.3 magrittr_2.0.3
[37] whisker_0.4 ps_1.7.2 promises_1.2.0.1 htmltools_0.5.3
[41] httpuv_1.6.6 utf8_1.2.2 stringi_1.7.8 cachem_1.0.6