Scalar Encoder/Decoder (Linear Interpolation Spline)
Ross Gayler
2021-08-12
Last updated: 2021-08-18
Checks: 6 1
Knit directory:
VSA_altitude_hold/
This reproducible R Markdown analysis was created with workflowr (version 1.6.2). The Checks tab describes the reproducibility checks that were applied when the results were created. The Past versions tab lists the development history.
The R Markdown file has unstaged changes.
To know which version of the R Markdown file created these
results, you’ll want to first commit it to the Git repo. If
you’re still working on the analysis, you can ignore this
warning. When you’re finished, you can run
wflow_publish to commit the R Markdown file and
build the HTML.
Great job! The global environment was empty. Objects defined in the global environment can affect the analysis in your R Markdown file in unknown ways. For reproduciblity it’s best to always run the code in an empty environment.
The command set.seed(20210617) was run prior to running the code in the R Markdown file.
Setting a seed ensures that any results that rely on randomness, e.g.
subsampling or permutations, are reproducible.
Great job! Recording the operating system, R version, and package versions is critical for reproducibility.
Nice! There were no cached chunks for this analysis, so you can be confident that you successfully produced the results during this run.
Great job! Using relative paths to the files within your workflowr project makes it easier to run your code on other machines.
Great! You are using Git for version control. Tracking code development and connecting the code version to the results is critical for reproducibility.
The results in this page were generated with repository version 9c30ab0. See the Past versions tab to see a history of the changes made to the R Markdown and HTML files.
Note that you need to be careful to ensure that all relevant files for the
analysis have been committed to Git prior to generating the results (you can
use wflow_publish or wflow_git_commit). workflowr only
checks the R Markdown file, but you know if there are other scripts or data
files that it depends on. Below is the status of the Git repository when the
results were generated:
Ignored files:
Ignored: .Rhistory
Ignored: .Rproj.user/
Ignored: renv/library/
Ignored: renv/local/
Ignored: renv/staging/
Unstaged changes:
Modified: R/functions.R
Modified: analysis/encoder_spline.Rmd
Note that any generated files, e.g. HTML, png, CSS, etc., are not included in this status report because it is ok for generated content to have uncommitted changes.
These are the previous versions of the repository in which changes were made
to the R Markdown (analysis/encoder_spline.Rmd) and HTML (docs/encoder_spline.html)
files. If you’ve configured a remote Git repository (see
?wflow_git_remote), click on the hyperlinks in the table below to
view the files as they were in that past version.
| File | Version | Author | Date | Message |
|---|---|---|---|---|
| Rmd | 9c30ab0 | Ross Gayler | 2021-08-17 | WIP |
| html | 9c30ab0 | Ross Gayler | 2021-08-17 | WIP |
| html | dd93727 | Ross Gayler | 2021-08-16 | WIP |
| Rmd | 271e9ef | Ross Gayler | 2021-08-16 | WIP |
| html | 271e9ef | Ross Gayler | 2021-08-16 | WIP |
| html | 73ca387 | Ross Gayler | 2021-08-15 | WIP |
| Rmd | 56137f3 | Ross Gayler | 2021-08-15 | WIP |
| Rmd | 4d2ad68 | Ross Gayler | 2021-08-15 | WIP |
This notebook documents the implementation of the linear interpolation spline scalar encoder/decoder.
The reasoning behind the design choices is explained in XXX.
1 Make encoder specification
The encoder will map each unique scalar input value to a VSA vector such that similar input values are mapped to similar output VSA vectors.
For programming purposes, the mapping is represented by a spline_spec
object, which is created by vsa_mk_scalar_encoder_spline_spec().
The encoder specification represents a piecewise linear function from the input scalar value to another scalar value.
The piecewise linear function has \(k\) knots, which must be unique scalar values and given in increasing order.
Values of the input scalar that are outside the range of the knots are treated identically to the nearest extreme value of the knots.
There is a unique atomic VSA vector associated with each knot.
If the input scalar is exactly equal to a knot value then the encoder will return the corresponding VSA vector.
If the input scalar lies between two knot value then the encoder will return the weighted sum of the two corresponding VSA vectors with the weighting reflecting the position of the scalar value relative to the two knot values..
The piecewise linear function is specified by the knots given as an
argument to vsa_mk_scalar_encoder_spline_spec() and the VSA vectors
corresponding to the knots are randomly generated. The spline_spec
object captures these two components, which remain constant over the
simulation.
# function to make the specification for a piecewise linear spline encoder
vsa_mk_scalar_encoder_spline_spec <- function(
vsa_dim, # integer - dimensionality of VSA vectors
knots, # numeric vector - scalar knot locations (in increasing order)
seed = NULL # integer - seed for random number generator
) # value # data structure representing linear spline encoder specification
{
### Set up the arguments ###
# The OCD error checking is probably more useful as documentation
if(missing(vsa_dim))
stop("vsa_dim must be specified")
if(!(is.vector(vsa_dim, mode = "integer") && length(vsa_dim) == 1))
stop("vsa_dim must be an integer")
if(vsa_dim < 1)
stop("vsa_dim must be (much) greater than zero")
if(!is.vector(knots, mode = "numeric"))
stop("knots must be a numeric vector")
if(length(knots) < 2)
stop("length(knots) must be >= 2")
if(!all(is.finite(knots)))
stop("all knot values must be nonmissing and finite")
if(length(knots) != length(unique(knots)))
stop("all knot values must be unique")
if(!all(order(knots) == 1:length(knots)))
stop("knot values must be in increasing order")
# check that the specified seed is an integer
if(!is.null(seed) && !(is.vector(seed, mode = "integer") && length(seed) == 1))
stop("seed must be an integer")
# set the seed if it has been specified
if (!is.null(seed))
set.seed(seed)
# generate VSA atoms corresponding to each of the knots
tibble::tibble(
knots_scalar = knots,
knots_vsa = purrr::map(knots, ~ vsa_mk_atom_bipolar(vsa_dim = vsa_dim))
)
}Do some very small scale testing.
Generate a tiny spline_spec object and display the contents.
ss <- vsa_mk_scalar_encoder_spline_spec(vsa_dim = 10L, knots = c(-1, 1, 2))
ss# A tibble: 3 × 2
knots_scalar knots_vsa
<dbl> <list>
1 -1 <int [10]>
2 1 <int [10]>
3 2 <int [10]>ss$knots_vsa[[1]] [1] 1 -1 -1 -1 1 1 1 1 -1 -1ss$knots_vsa[[2]] [1] 1 1 1 -1 1 1 -1 1 -1 1ss$knots_vsa[[3]] [1] 1 1 -1 -1 -1 1 -1 -1 -1 -1- The contents are as expected.
2 Apply encoding
# function to encode a scalar numeric value to a VSA vector
# This function uses a linear interpolation spline
# to interpolate between a sequence of VSA vectors corresponding to the spline knots
vsa_encode_scalar_spline <- function(
x, # numeric[1] - scalar value to be encoded
spline_spec # data frame - spline spec created by vsa_mk_scalar_encoder_spline_spec()
) # numeric # one VSA vector, the encoding of the scalar value
{
### Set up the arguments ###
# The OCD error checking is probably more useful as documentation
if (missing(x))
stop("x must be specified")
if (!(is.vector(x, mode = "numeric") && length(x) == 1))
stop("x must be a numeric scalar")
if (is.na(x))
stop("x must be non-missing")
if (!is.finite(x))
stop("x must be finite")
if (missing(spline_spec))
stop("spline_spec must be specified")
if (
!(
is_tibble(spline_spec) &&
all(c("knots_scalar", "knots_vsa") %in% names(spline_spec))
)
)
stop("spline_spec must be a spline specification object")
# Map the scalar into a continuous index across the knots
# Linearly interpolate the input scalar onto a scale in which knots correspond to 1:n
i <- approx(
x = spline_spec$knots_scalar, y = seq_along(spline_spec$knots_scalar),
rule = 2, # clip x to fit the range of the knots
xout = x
)$y # get the interpolated value only
# Get the knot indices immediately above and below the index value
i_lo <- floor(i)
i_hi <- ceiling(i)
# Return the VSA vector corresponding to the index value
if (i_lo == i_hi) # check if index is on a knot
# Exactly on a knot so return the corresponding knot VSA vector
spline_spec$knots_vsa[[i]]
else {
# Between two knots
# Return the weighted sum of the corresponding knot VSA vectors
i_offset <- i - i_lo
vsa_add(
spline_spec$knots_vsa[[i_lo]], spline_spec$knots_vsa[[i_hi]],
sample_wt = c(1 - i_offset, i_offset)
)
}
}Do some very small scale testing.
Test what happens when the input scalar lies exactly on a knot.
vsa_encode_scalar_spline(-1.0, ss) [1] 1 -1 -1 -1 1 1 1 1 -1 -1vsa_encode_scalar_spline( 1.0, ss) [1] 1 1 1 -1 1 1 -1 1 -1 1vsa_encode_scalar_spline( 2.0, ss) [1] 1 1 -1 -1 -1 1 -1 -1 -1 -1- The returned values are equal to the VSA vectors at the corresponding knots.
Test what happens when the input scalar falls outside the range of the knots.
vsa_encode_scalar_spline(-1.1, ss) [1] 1 -1 -1 -1 1 1 1 1 -1 -1vsa_encode_scalar_spline( 2.1, ss) [1] 1 1 -1 -1 -1 1 -1 -1 -1 -1- Input values outside the range of the knots are mapped to the nearest extreme knot.
Check that intermediate values are random (because of the random
sampling in vsa_add()).
# remind us of the knot values
ss$knots_vsa[[1]] [1] 1 -1 -1 -1 1 1 1 1 -1 -1ss$knots_vsa[[2]] [1] 1 1 1 -1 1 1 -1 1 -1 1# identify which elements are identical for the two knots
ss$knots_vsa[[1]] == ss$knots_vsa[[2]] [1] TRUE FALSE FALSE TRUE TRUE TRUE FALSE TRUE TRUE FALSE# interpolate midway between those two knots
vsa_encode_scalar_spline(0, ss) [1] 1 -1 1 -1 1 1 1 1 -1 -1vsa_encode_scalar_spline(0, ss) [1] 1 1 1 -1 1 1 1 1 -1 1vsa_encode_scalar_spline(0, ss) [1] 1 -1 -1 -1 1 1 -1 1 -1 -1vsa_encode_scalar_spline(0, ss) [1] 1 -1 -1 -1 1 1 -1 1 -1 1Elements 3, 4, 6, 7, and 8 of the first and second knot vectors are identical, so the result of adding them is constant.
The other element values vary between the two knot vectors, so the corresponding interpolated values will vary because of the random sampling in
vsa_add()(although some may be identical by chance)
Check that interpolation has the expected effect on the angles of the vectors.
Initially, use relatively low dimensional VSA vectors (vsa_dim = 1e3)
to give greater variability to the results.
# make an encoder specification with realistic vector dimension
ss <- vsa_mk_scalar_encoder_spline_spec(vsa_dim = 1e3L, knots = c(-1, 1, 2, 4))
# get the vectors corresponding to the knots
v1 <- ss$knots_vsa[[1]]
v2 <- ss$knots_vsa[[2]]
v3 <- ss$knots_vsa[[3]]
v4 <- ss$knots_vsa[[4]]
# make a sequence of scalar values that (more than) span the knot range
d <- tibble::tibble(
x = seq(from = -1.5, to = 4.5, by = 0.05)
) %>%
dplyr::rowwise() %>%
dplyr::mutate(
# encode each value of x
v_x = vsa_encode_scalar_spline(x[[1]], ss) %>% list(),
# get the cosine between the encoded x and each of the knot vectors
cos_1 = vsa_cos_sim(v_x, v1),
cos_2 = vsa_cos_sim(v_x, v2),
cos_3 = vsa_cos_sim(v_x, v3),
cos_4 = vsa_cos_sim(v_x, v4)
) %>%
dplyr::ungroup() %>%
dplyr::select(-v_x) %>%
tidyr::pivot_longer(cos_1:cos_4,
names_to = "knot", names_prefix = "cos_",
values_to = "cos")
d %>% ggplot(aes(x = x)) +
geom_hline(yintercept = c(0, 1), alpha = 0.3) +
geom_vline(xintercept = c(-1, 1, 2, 4), alpha = 0.3) +
geom_point(aes(y = cos, colour = knot))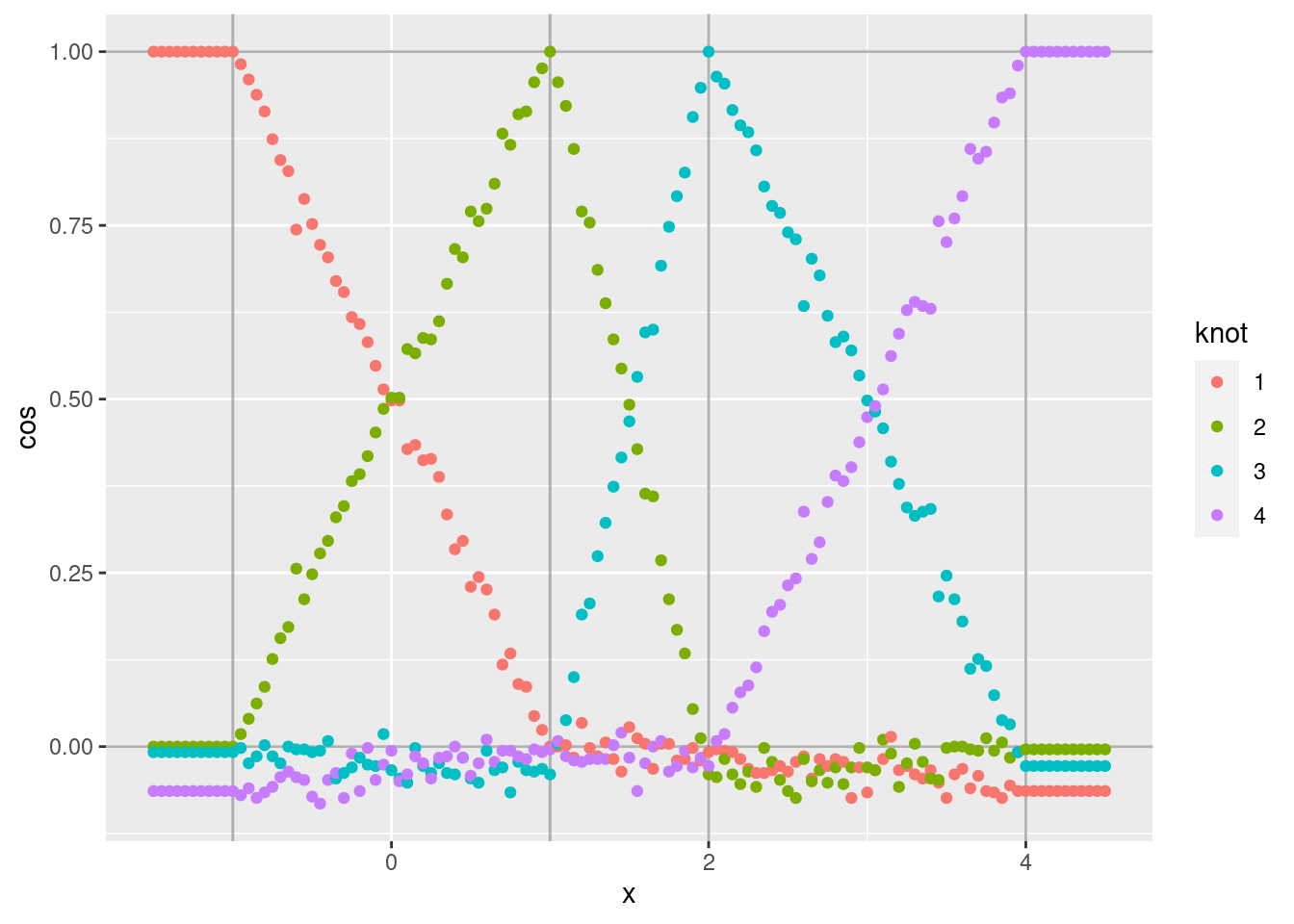
Each curve shows the cosine similarity of the encoded scalar (\(x\)) to the VSA vector corresponding to one of the knots.
- Each curve shows the expected linear ramp as it moves between the two bounding knots.
- The cosine similarity at the peak of each curve is exactly one because the encoded scalar is identical to the corresponding knot vector.
- The curves corresponding to intermediate values of \(x\) are noisy
around a straight line. The noise is due to the encoding being a
random weighted blend of the bounding knot vectors (due to applying
vsa_add()). - The minimum values of each curve are not exactly zero, because
they correspond to the angle between two randomly selected vectors.
That is, the cosine similarity is distributed around zero. Repeat
that analysis using relatively high dimensional VSA vectors
(
vsa_dim = 1e5) to reduce the variability of the results.
# make an encoder specification with realistic vector dimension
ss <- vsa_mk_scalar_encoder_spline_spec(vsa_dim = 1e5L, knots = c(-1, 1, 2, 4))
# get the vectors corresponding to the knots
v1 <- ss$knots_vsa[[1]]
v2 <- ss$knots_vsa[[2]]
v3 <- ss$knots_vsa[[3]]
v4 <- ss$knots_vsa[[4]]
# make a sequence of scalar values that (more than) span the knot range
d <- tibble::tibble(
x = seq(from = -1.5, to = 4.5, by = 0.05)
) %>%
dplyr::rowwise() %>%
dplyr::mutate(
# encode each value of x
v_x = vsa_encode_scalar_spline(x[[1]], ss) %>% list(),
# get the cosine between the encoded x and each of the knot vectors
cos_1 = vsa_cos_sim(v_x, v1),
cos_2 = vsa_cos_sim(v_x, v2),
cos_3 = vsa_cos_sim(v_x, v3),
cos_4 = vsa_cos_sim(v_x, v4)
) %>%
dplyr::ungroup() %>%
dplyr::select(-v_x) %>%
tidyr::pivot_longer(cos_1:cos_4,
names_to = "knot", names_prefix = "cos_",
values_to = "cos")
d %>% ggplot(aes(x = x)) +
geom_hline(yintercept = c(0, 1), alpha = 0.3) +
geom_vline(xintercept = c(-1, 1, 2, 4), alpha = 0.3) +
geom_point(aes(y = cos, colour = knot))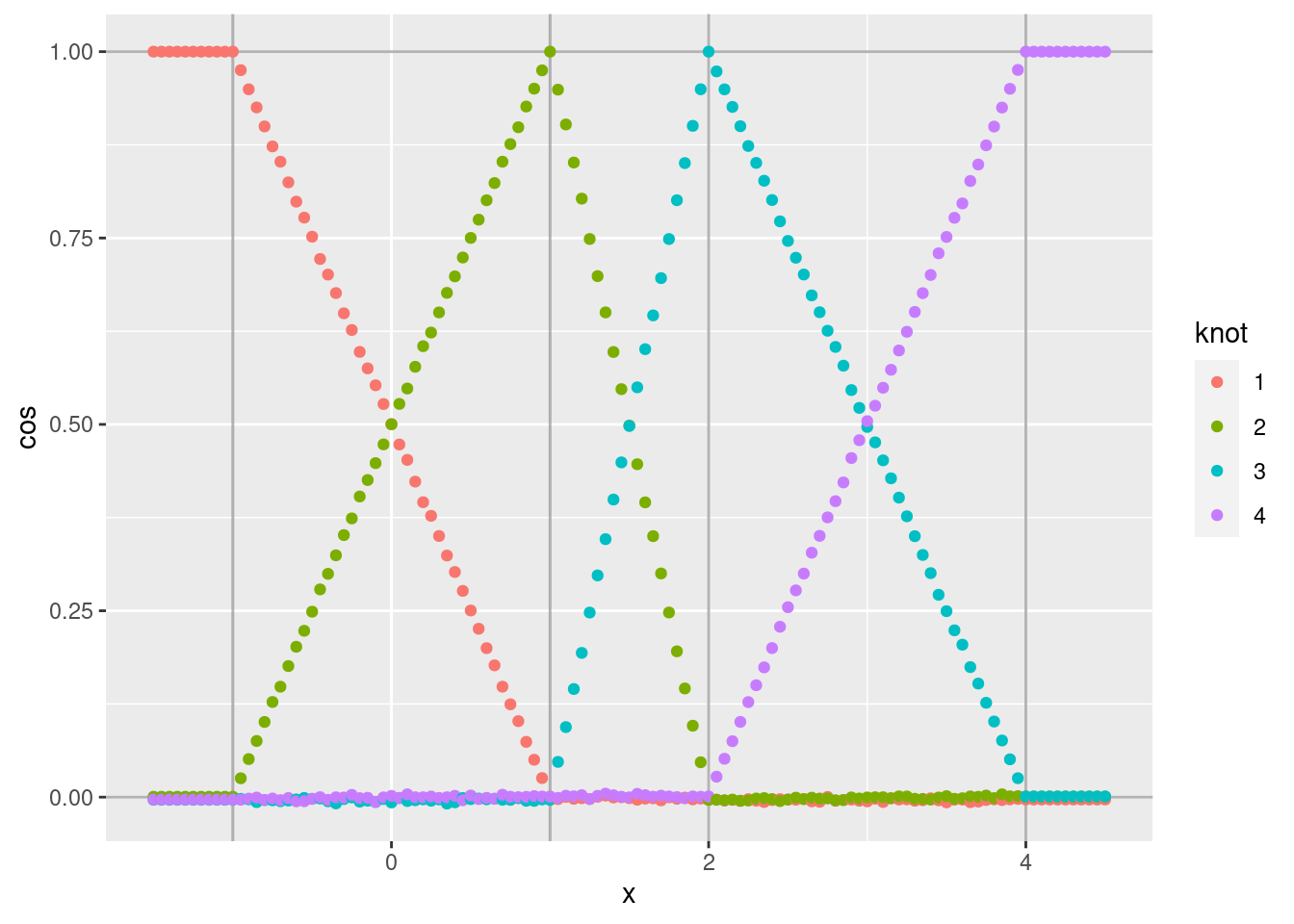
- As expected, the noise is greatly reduced.
With the linear spline encoding, the representations at the knots are
always identical to the knot vectors. For intermediate values of the
numeric scalar the encoding is a weighted blend of the bounding knot
vectors. This blending is implemented by vsa_add(), so the encoding
will be different on each occasion the encoding is generated.
Demonstrate the distribution of cosine similarity between encodings of the same scalar value. Use a scalar value midway between the bounding knots to maximise the variation between encodings.
Use VSA vectors with dimensionality \(10^4\) to match the default dimensionality we intend to use.
# make an encoder specification with realistic vector dimension
ss <- vsa_mk_scalar_encoder_spline_spec(vsa_dim = 1e4L, knots = c(0, 1))
# generate n pairs of encodings of the same scalar (x)
x <- 0.5 # scalar to encode (in the range 0 .. 1)
n <- 1e3 # number of pairs to create
# make a one-column data frame with the cos similarity of each vector pair
d <- tibble::tibble(
cos = purrr::map_dbl(1:n, ~
vsa_cos_sim(
vsa_encode_scalar_spline(x, ss),
vsa_encode_scalar_spline(x, ss)
)
)
)
d %>% ggplot() +
geom_histogram(aes(x = cos))`stat_bin()` using `bins = 30`. Pick better value with `binwidth`.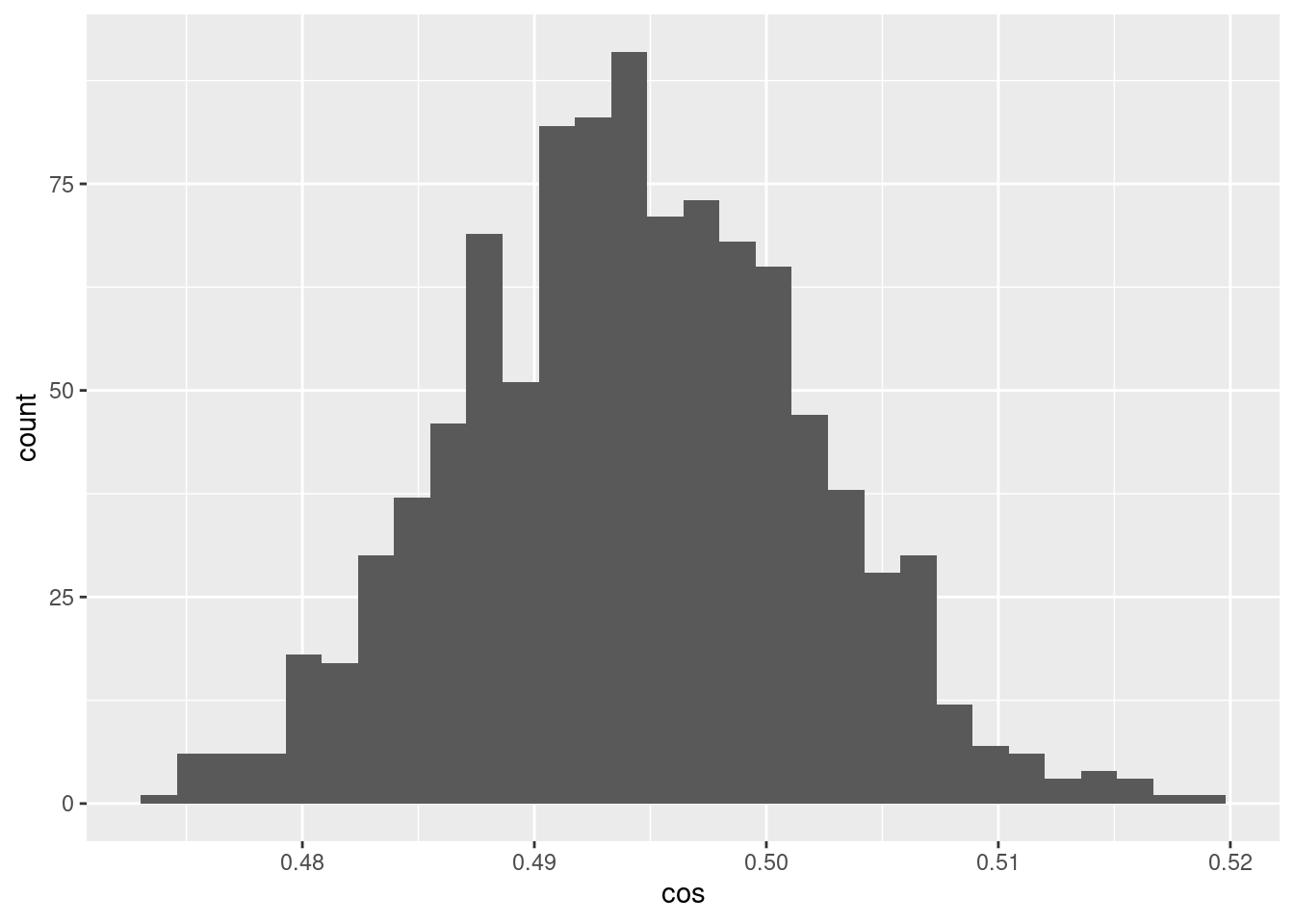
- The encoded values of the scalar midway between the bounding knots differ randomly and have a distribution of cosine similarities to each other that are fairly tightly bounded around 0.5
Repeat the analysis for a scalar much nearer one of the knots.
# make an encoder specification with realistic vector dimension
ss <- vsa_mk_scalar_encoder_spline_spec(vsa_dim = 1e4L, knots = c(0, 1))
# generate n pairs of encodings of the same scalar (x)
x <- 0.05 # scalar to encode (in the range 0 .. 1)
n <- 1e3 # number of pairs to create
# make a one-column data frame with the cos similarity of each vector pair
d <- tibble::tibble(
cos = purrr::map_dbl(1:n, ~
vsa_cos_sim(
vsa_encode_scalar_spline(x, ss),
vsa_encode_scalar_spline(x, ss)
)
)
)
d %>% ggplot() +
geom_histogram(aes(x = cos))`stat_bin()` using `bins = 30`. Pick better value with `binwidth`.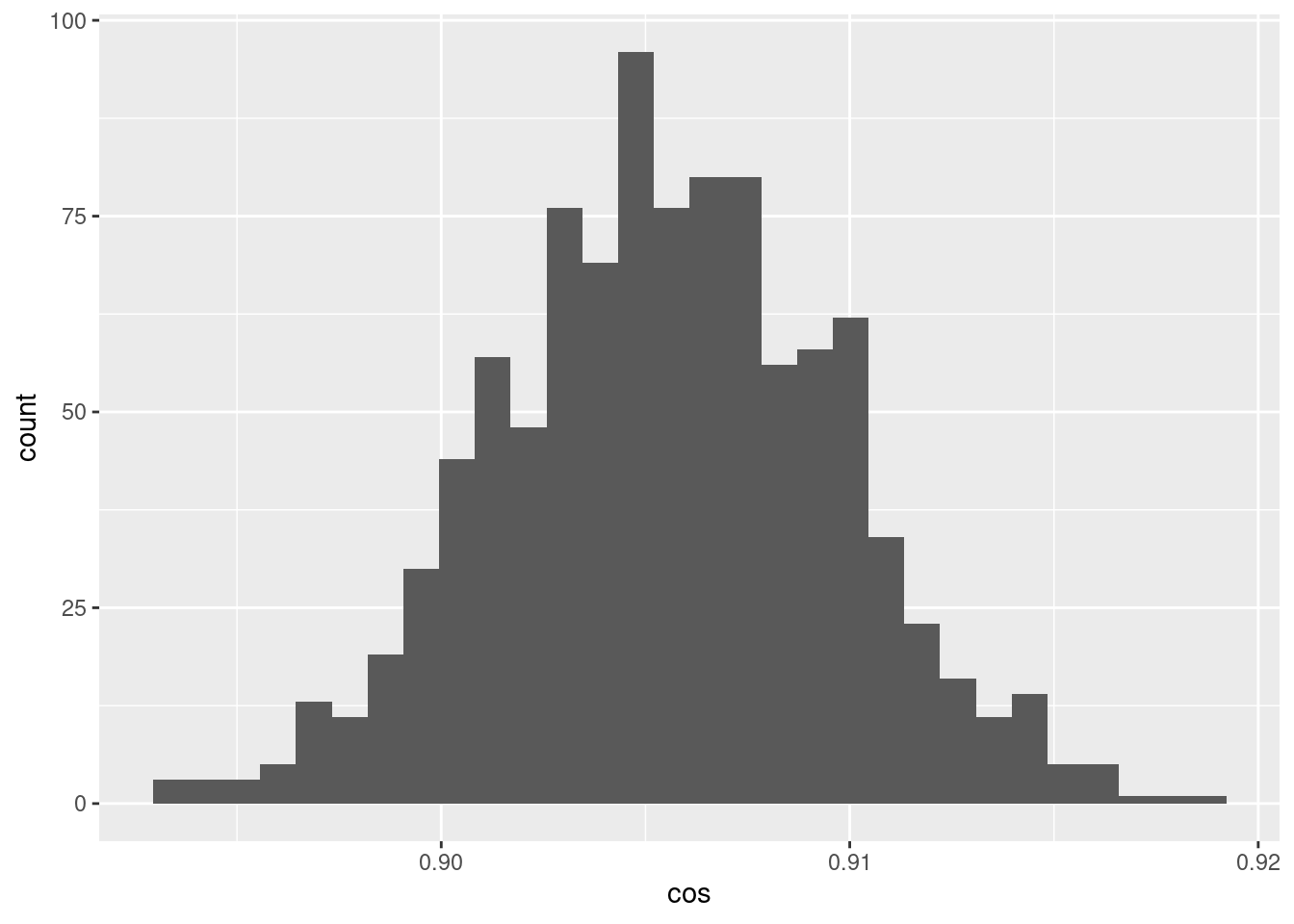
- The cosine similarities between pairs of encodings of the scalar 0.05 is a much tighter distribution around ~0.905
The fact that the encoding is constant at the knots and more variable
between knots seems rather odd. If this is a problem the encoding could
be made constant by using a fixed seed to vsa_add().
3 Apply decoding
The decoder applies the spline specification to a VSA vector and returns a numeric scalar value.
The input VSA vector is compared to each of the knot vectors and the dot product calculated for each comparison. Dot products less than a threshold (close to zero) are set to zero, then all the dot products are normalised to sum to one. The normalised dot products are then used with the scalar knot values to calculate the weighted mean of the scalar knot values. The weighted mean is returned as the output of the decoder.
# function to encode a scalar numeric value to a VSA vector
# This function uses a linear interpolation spline
# to interpolate between a sequence of VSA vectors corresponding to the spline knots
vsa_decode_scalar_spline <- function(
v, # numeric - VSA vector (not necessarily bipolar)
spline_spec, # data frame - spline spec created by vsa_mk_scalar_encoder_spline_spec()
zero_thresh = 4 # numeric[1] - zero threshold (in standard deviations)
) # numeric[1] - scalar value decoded from v
{
### Set up the arguments ###
# The OCD error checking is probably more useful as documentation
if(missing(v))
stop("VSA vector argument (v) must be specified")
if(!is.vector(v, mode = "numeric"))
stop("v must be an numeric vector")
if (missing(spline_spec))
stop("spline_spec must be specified")
if (
!(
is_tibble(spline_spec) &&
all(c("knots_scalar", "knots_vsa") %in% names(spline_spec))
)
)
stop("spline_spec must be a spline specification object")
# get the dot product of the encoded scalar with each of the knot vectors
dotprod <- spline_spec$knots_vsa %>%
purrr::map_dbl(.f = vsa_dotprod, v2 = v)
# set dot products below the zero threshold to 0.5
zero_thresh <- zero_thresh * sqrt(length(v) * 0.5) # sd = sqrt(n p q) = sqrt(vsa_dim 0.5 0.5)
dotprod <- ifelse(dotprod < zero_thresh, 0, dotprod)
# normalise the dot products
dotprod <- dotprod / sum(dotprod)
# return the weighted sum of the knot scalara
sum(dotprod * spline_spec$knots_scalar)
}Do some very small scale testing.
3.1 Values decoded correctly
Chcek that encoded values are decoded correctly across the range of the knots.
# make an encoder specification with realistic vector dimension
ss <- vsa_mk_scalar_encoder_spline_spec(vsa_dim = 1e4L, knots = c(-1, 1, 2, 4))
-1.5 %>% vsa_encode_scalar_spline(ss) %>% vsa_decode_scalar_spline(ss)[1] -1-1 %>% vsa_encode_scalar_spline(ss) %>% vsa_decode_scalar_spline(ss)[1] -10 %>% vsa_encode_scalar_spline(ss) %>% vsa_decode_scalar_spline(ss)[1] -0.0035985611 %>% vsa_encode_scalar_spline(ss) %>% vsa_decode_scalar_spline(ss)[1] 11.5 %>% vsa_encode_scalar_spline(ss) %>% vsa_decode_scalar_spline(ss)[1] 1.5062842 %>% vsa_encode_scalar_spline(ss) %>% vsa_decode_scalar_spline(ss)[1] 23 %>% vsa_encode_scalar_spline(ss) %>% vsa_decode_scalar_spline(ss)[1] 3.0187774 %>% vsa_encode_scalar_spline(ss) %>% vsa_decode_scalar_spline(ss)[1] 44.5 %>% vsa_encode_scalar_spline(ss) %>% vsa_decode_scalar_spline(ss)[1] 4- The decoded values at the knots are exactly correct.
- The decoded values between the knots are approximately correct.
Check the random variation of intermediate values.
0 %>% vsa_encode_scalar_spline(ss) %>% vsa_decode_scalar_spline(ss)[1] 0.032387050 %>% vsa_encode_scalar_spline(ss) %>% vsa_decode_scalar_spline(ss)[1] 0.020391840 %>% vsa_encode_scalar_spline(ss) %>% vsa_decode_scalar_spline(ss)[1] 0.013594560 %>% vsa_encode_scalar_spline(ss) %>% vsa_decode_scalar_spline(ss)[1] -0.0047980810 %>% vsa_encode_scalar_spline(ss) %>% vsa_decode_scalar_spline(ss)[1] -0.02319072- The decoded values are tightly clustered around the encoded value.
3.2 Zero threshold
Look at the effect of the zero threshold.
When there are more than two knots there is more than one interval bounded by knots. When decoding, we are only interested in the knots bounding the interval containing the encoded value. The other knots should be ignored.
These irrelevant knots will have small dot products with the encoded scalar value. Unfortunately, the dot products will not be exactly zero. They will be distributed in a small range around zero.
The aim of the zero threshold is to treat dot products in the range that would be produced by approximately orthogonal vectors as exactly zero.
In the following analyses I will make life gard for the decoder by having 101 knots. This makes it more likely that at least one of the irrelevant knots will have a dot product above the zero threshold.
Make the zero threshold ridiculously large (10).
ss <- vsa_mk_scalar_encoder_spline_spec(vsa_dim = 1e4L, knots = 0:100)
# encode and decode random values over the first knot interval
runif(n = 1e3, min = -0.1, max = 1.1) %>%
tibble::tibble(x_in = .) %>%
dplyr::rowwise() %>%
dplyr::mutate(
x_out = x_in %>%
vsa_encode_scalar_spline(ss) %>%
vsa_decode_scalar_spline(ss, zero_thresh = 8)
) %>%
dplyr::ungroup() %>%
ggplot() +
geom_vline(xintercept = 0:1, alpha = 0.3) +
geom_abline(slope = 1, intercept = 0, colour = "red", alpha = 0.5) +
geom_point(aes(x = x_in, y = x_out), size = 0.1, alpha = 0.5) +
ggtitle("zero_thresh = 8")
- Encoded values close to the knots are treated as though they are exactly equal to the knots (because the dot product with the knot vector at the other end of the interval is close to zero).
- The decoded values not close to the knots lie along the expected line.
runif(n = 1e3, min = -0.1, max = 1.1) %>%
tibble::tibble(x_in = .) %>%
dplyr::rowwise() %>%
dplyr::mutate(
x_out = x_in %>%
vsa_encode_scalar_spline(ss) %>%
vsa_decode_scalar_spline(ss, zero_thresh = 6)
) %>%
dplyr::ungroup() %>%
ggplot() +
geom_vline(xintercept = 0:1, alpha = 0.3) +
geom_abline(slope = 1, intercept = 0, colour = "red", alpha = 0.5) +
geom_point(aes(x = x_in, y = x_out), size = 0.1, alpha = 0.5) +
ggtitle("zero_thresh = 6")
- The region considered identical to the knot value is smaller.
- A small number of points are way off the expected line because some irrelevant knots have had dot products above the zero threshold.
runif(n = 1e3, min = -0.1, max = 1.1) %>%
tibble::tibble(x_in = .) %>%
dplyr::rowwise() %>%
dplyr::mutate(
x_out = x_in %>%
vsa_encode_scalar_spline(ss) %>%
vsa_decode_scalar_spline(ss, zero_thresh = 5)
) %>%
dplyr::ungroup() %>%
ggplot() +
geom_vline(xintercept = 0:1, alpha = 0.3) +
geom_abline(slope = 1, intercept = 0, colour = "red", alpha = 0.5) +
geom_point(aes(x = x_in, y = x_out), size = 0.1, alpha = 0.5) +
ggtitle("zero_thresh = 5")
Try a smaller number of knots, which will make life easier for the decoder.
ss <- vsa_mk_scalar_encoder_spline_spec(vsa_dim = 1e4L, knots = 0:2)
# encode and decode random values over the knot range
runif(n = 1e3, min = -0.1, max = 2.1) %>%
tibble::tibble(x_in = .) %>%
dplyr::rowwise() %>%
dplyr::mutate(
x_out = x_in %>%
vsa_encode_scalar_spline(ss) %>%
vsa_decode_scalar_spline(ss, zero_thresh = 4)
) %>%
dplyr::ungroup() %>%
ggplot() +
geom_vline(xintercept = 0:2, alpha = 0.3) +
geom_abline(slope = 1, intercept = 0, colour = "red", alpha = 0.5) +
geom_point(aes(x = x_in, y = x_out), size = 0.1, alpha = 0.5) +
ggtitle("zero_thresh = 4")
runif(n = 1e3, min = -0.1, max = 2.1) %>%
tibble::tibble(x_in = .) %>%
dplyr::rowwise() %>%
dplyr::mutate(
x_out = x_in %>%
vsa_encode_scalar_spline(ss) %>%
vsa_decode_scalar_spline(ss, zero_thresh = 2)
) %>%
dplyr::ungroup() %>%
ggplot() +
geom_vline(xintercept = 0:2, alpha = 0.3) +
geom_abline(slope = 1, intercept = 0, colour = "red", alpha = 0.5) +
geom_point(aes(x = x_in, y = x_out), size = 0.1, alpha = 0.5) +
ggtitle("zero_thresh = 2")
- The decoded values are not quite aligned with the expected line.
Now try a zero threshold where we expect to see random values above the threshold.
runif(n = 1e3, min = -0.1, max = 2.1) %>%
tibble::tibble(x_in = .) %>%
dplyr::rowwise() %>%
dplyr::mutate(
x_out = x_in %>%
vsa_encode_scalar_spline(ss) %>%
vsa_decode_scalar_spline(ss, zero_thresh = 1)
) %>%
dplyr::ungroup() %>%
ggplot() +
geom_vline(xintercept = 0:2, alpha = 0.3) +
geom_abline(slope = 1, intercept = 0, colour = "red", alpha = 0.5) +
geom_point(aes(x = x_in, y = x_out), size = 0.1, alpha = 0.5) +
ggtitle("zero_thresh = 1")
- The decoded values are not quite aligned with the expected line.
- The decoded values corresponding to the knots are not quite right.
Now set the zero threshold to zero. This avoids negative dot products, which is required to make the weighted sum meaningful.
runif(n = 1e3, min = -0.1, max = 2.1) %>%
tibble::tibble(x_in = .) %>%
dplyr::rowwise() %>%
dplyr::mutate(
x_out = x_in %>%
vsa_encode_scalar_spline(ss) %>%
vsa_decode_scalar_spline(ss, zero_thresh = 0)
) %>%
dplyr::ungroup() %>%
ggplot() +
geom_vline(xintercept = 0:2, alpha = 0.3) +
geom_abline(slope = 1, intercept = 0, colour = "red", alpha = 0.5) +
geom_point(aes(x = x_in, y = x_out), size = 0.1, alpha = 0.5) +
ggtitle("zero_thresh = 0")
Now try disabling the zero threshold.
runif(n = 1e3, min = -0.1, max = 2.1) %>%
tibble::tibble(x_in = .) %>%
dplyr::rowwise() %>%
dplyr::mutate(
x_out = x_in %>%
vsa_encode_scalar_spline(ss) %>%
vsa_decode_scalar_spline(ss, zero_thresh = -Inf)
) %>%
dplyr::ungroup() %>%
ggplot() +
geom_vline(xintercept = 0:2, alpha = 0.3) +
geom_abline(slope = 1, intercept = 0, colour = "red", alpha = 0.5) +
geom_point(aes(x = x_in, y = x_out), size = 0.1, alpha = 0.5) +
ggtitle("zero_thresh = -Inf")
- That’s not obviously different to setting the threshold to zero.
4 Random vectors
Try to decode a random vector (i.e. not a valid encoding of a scalar).
Setting a high zero threshold means that with high probability we will end up dividing by zero in the decoder.
vsa_mk_atom_bipolar(1e4L) %>% vsa_decode_scalar_spline(ss, zero_thresh = 4)[1] NaNvsa_mk_atom_bipolar(1e4L) %>% vsa_decode_scalar_spline(ss, zero_thresh = 4)[1] NaNvsa_mk_atom_bipolar(1e4L) %>% vsa_decode_scalar_spline(ss, zero_thresh = 4)[1] NaNvsa_mk_atom_bipolar(1e4L) %>% vsa_decode_scalar_spline(ss, zero_thresh = 4)[1] NaNvsa_mk_atom_bipolar(1e4L) %>% vsa_decode_scalar_spline(ss, zero_thresh = 4)[1] NaNSetting a zero threshold means that approximately half the dot products will be set to zero.
vsa_mk_atom_bipolar(1e4L) %>% vsa_decode_scalar_spline(ss, zero_thresh = 0)[1] 0vsa_mk_atom_bipolar(1e4L) %>% vsa_decode_scalar_spline(ss, zero_thresh = 0)[1] NaNvsa_mk_atom_bipolar(1e4L) %>% vsa_decode_scalar_spline(ss, zero_thresh = 0)[1] 1.552239vsa_mk_atom_bipolar(1e4L) %>% vsa_decode_scalar_spline(ss, zero_thresh = 0)[1] NaNvsa_mk_atom_bipolar(1e4L) %>% vsa_decode_scalar_spline(ss, zero_thresh = 0)[1] NaN- The probability of dividing by zero is nonzero.
- The “decoded” values lie in the range of the knots.
Disabling the zero threshold results in a very small probability of dividing by zero. The weighted sum no longer makes sense because the weights can be negative. Consequently, the returned value can lie outside the range of the knots.
vsa_mk_atom_bipolar(1e4L) %>% vsa_decode_scalar_spline(ss, zero_thresh = -Inf)[1] -10.25vsa_mk_atom_bipolar(1e4L) %>% vsa_decode_scalar_spline(ss, zero_thresh = -Inf)[1] 0.1315789vsa_mk_atom_bipolar(1e4L) %>% vsa_decode_scalar_spline(ss, zero_thresh = -Inf)[1] -1.625vsa_mk_atom_bipolar(1e4L) %>% vsa_decode_scalar_spline(ss, zero_thresh = -Inf)[1] 0.9927536vsa_mk_atom_bipolar(1e4L) %>% vsa_decode_scalar_spline(ss, zero_thresh = -Inf)[1] 5.804878- Some of the decoded values lie outside the range of the knots.
sessionInfo()R version 4.1.1 (2021-08-10)
Platform: x86_64-pc-linux-gnu (64-bit)
Running under: Ubuntu 21.04
Matrix products: default
BLAS: /usr/lib/x86_64-linux-gnu/blas/libblas.so.3.9.0
LAPACK: /usr/lib/x86_64-linux-gnu/lapack/liblapack.so.3.9.0
locale:
[1] LC_CTYPE=en_AU.UTF-8 LC_NUMERIC=C
[3] LC_TIME=en_AU.UTF-8 LC_COLLATE=en_AU.UTF-8
[5] LC_MONETARY=en_AU.UTF-8 LC_MESSAGES=en_AU.UTF-8
[7] LC_PAPER=en_AU.UTF-8 LC_NAME=C
[9] LC_ADDRESS=C LC_TELEPHONE=C
[11] LC_MEASUREMENT=en_AU.UTF-8 LC_IDENTIFICATION=C
attached base packages:
[1] stats graphics grDevices datasets utils methods base
other attached packages:
[1] tibble_3.1.3 Matrix_1.3-4 dplyr_1.0.7 DiagrammeR_1.0.6.1
[5] ggplot2_3.3.5 purrr_0.3.4 magrittr_2.0.1 here_1.0.1
loaded via a namespace (and not attached):
[1] Rcpp_1.0.7 highr_0.9 RColorBrewer_1.1-2 pillar_1.6.2
[5] compiler_4.1.1 later_1.2.0 git2r_0.28.0 workflowr_1.6.2
[9] tools_4.1.1 digest_0.6.27 lattice_0.20-44 jsonlite_1.7.2
[13] evaluate_0.14 lifecycle_1.0.0 gtable_0.3.0 pkgconfig_2.0.3
[17] rlang_0.4.11 rstudioapi_0.13 cli_3.0.1 yaml_2.2.1
[21] xfun_0.25 withr_2.4.2 stringr_1.4.0 knitr_1.33
[25] htmlwidgets_1.5.3 generics_0.1.0 fs_1.5.0 vctrs_0.3.8
[29] tidyselect_1.1.1 rprojroot_2.0.2 grid_4.1.1 glue_1.4.2
[33] R6_2.5.0 fansi_0.5.0 rmarkdown_2.10 bookdown_0.22
[37] farver_2.1.0 tidyr_1.1.3 whisker_0.4 scales_1.1.1
[41] promises_1.2.0.1 ellipsis_0.3.2 htmltools_0.5.1.1 colorspace_2.0-2
[45] renv_0.14.0 httpuv_1.6.1 labeling_0.4.2 utf8_1.2.2
[49] stringi_1.7.3 visNetwork_2.0.9 munsell_0.5.0 crayon_1.4.1