Biological Significance
Tina Lasisi
2020-11-24 20:03:18
Last updated: 2020-11-24
Checks: 7 0
Knit directory: 2020_HairPheno_manuscript/analysis/
This reproducible R Markdown analysis was created with workflowr (version 1.6.2). The Checks tab describes the reproducibility checks that were applied when the results were created. The Past versions tab lists the development history.
Great! Since the R Markdown file has been committed to the Git repository, you know the exact version of the code that produced these results.
Great job! The global environment was empty. Objects defined in the global environment can affect the analysis in your R Markdown file in unknown ways. For reproduciblity it’s best to always run the code in an empty environment.
The command set.seed(12345) was run prior to running the code in the R Markdown file. Setting a seed ensures that any results that rely on randomness, e.g. subsampling or permutations, are reproducible.
Great job! Recording the operating system, R version, and package versions is critical for reproducibility.
Nice! There were no cached chunks for this analysis, so you can be confident that you successfully produced the results during this run.
Great job! Using relative paths to the files within your workflowr project makes it easier to run your code on other machines.
Great! You are using Git for version control. Tracking code development and connecting the code version to the results is critical for reproducibility.
The results in this page were generated with repository version 4b704ad. See the Past versions tab to see a history of the changes made to the R Markdown and HTML files.
Note that you need to be careful to ensure that all relevant files for the analysis have been committed to Git prior to generating the results (you can use wflow_publish or wflow_git_commit). workflowr only checks the R Markdown file, but you know if there are other scripts or data files that it depends on. Below is the status of the Git repository when the results were generated:
Ignored files:
Ignored: .Rproj.user/
Ignored: output/
Untracked files:
Untracked: .DS_Store
Untracked: .gitignore
Untracked: 2020_HairPheno_manuscript.Rproj
Untracked: analysis/
Untracked: code/
Untracked: data/
Note that any generated files, e.g. HTML, png, CSS, etc., are not included in this status report because it is ok for generated content to have uncommitted changes.
There are no past versions. Publish this analysis with wflow_publish() to start tracking its development.
To explore the significance of quantifying hair fiber morphology, we explore the relationship between various quantitative hair traits, categorical data and genotype data on the same sample.
Our data consists of 193 individuals for whom we have quantitative hair phenotype data. In our first data quality control step, we filter to keep individuals who have more than 4 hair fragments in their curvature image and over 10% African ancestry. We calculate mean and median values for the cross-sectional data we have collected for individuals (~ 6 sectioned hair fibers). In our analyses, we use median values as they are less affected by intra-individual outliers.
1 Self-reported hair texture vs. quantitative
We compare the self-reported hair texture with mean and median curvature for our sample.
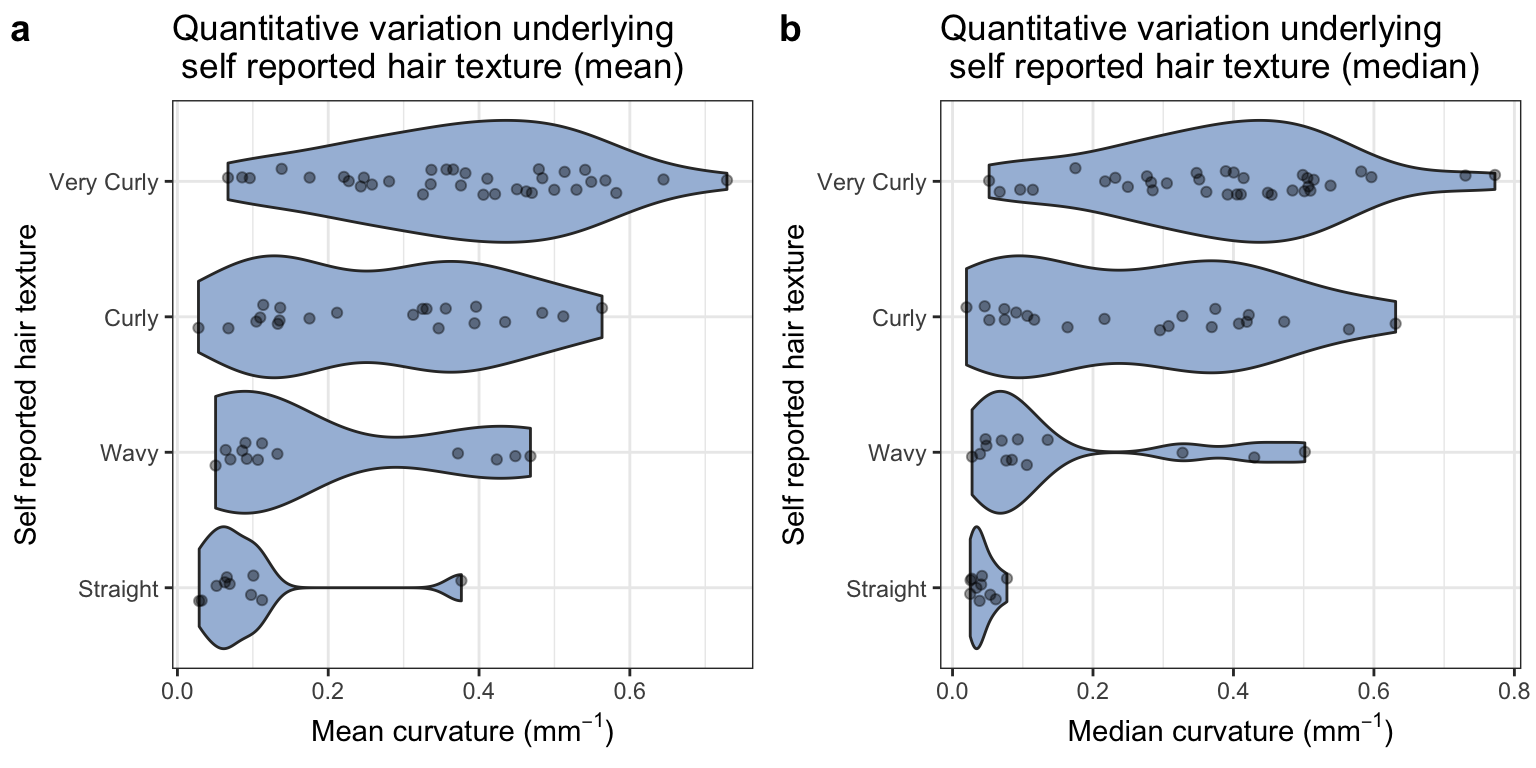
The single individual with a high mean curvature in the straight group is the result of an artefact in the image.

The red arrow points to a stray fiber that likely contaminated the sample and was missed during imaging. Such potential outliers are the reason we chose to use the median curvature for a sample in our analyses.
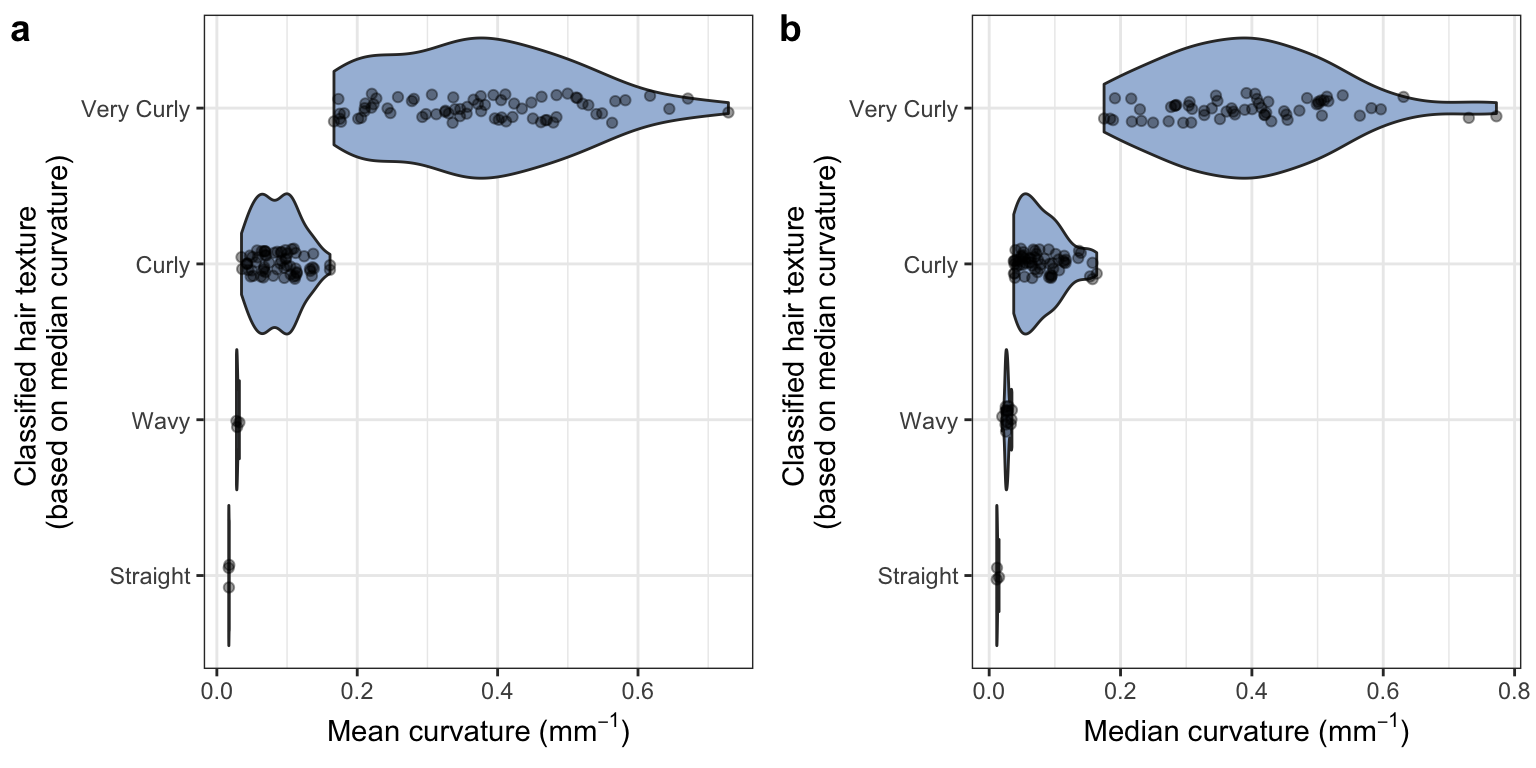
2 Objective hair texture vs. quantitative
To explore how much data is lost when binning continuous variation, we compared mean and median curvature to classified hair texture. This classification is based on Loussouarn et al.’s 2007 paper "Worldwide diversity of hair curliness: a new method of assessment.
While the authors propose a number of parameters to distinguish curlier hair types (based on number of twists and waves among other factors), their primary classification is based on curvature. We demonstrate that, regardless of additional parameters, a considerable range of curvature is obscured when collapsing hair variation according to their curvature thresholds.
3 Ancestry vs. hair morphology
We carried out a number of analyses using the genotype data collected for this diverse sample. In an admixed sample where a continuous trait has divergent distributions in the parental ancestry groups, the resulting admixed population can show a correlation between ancestry and that trait. Finding such a correlation suggests may imply a polygenic trait with high heritability.
3.1 Admixture components
Our sample consists of admixed individuals with primarily African and European ancestry.
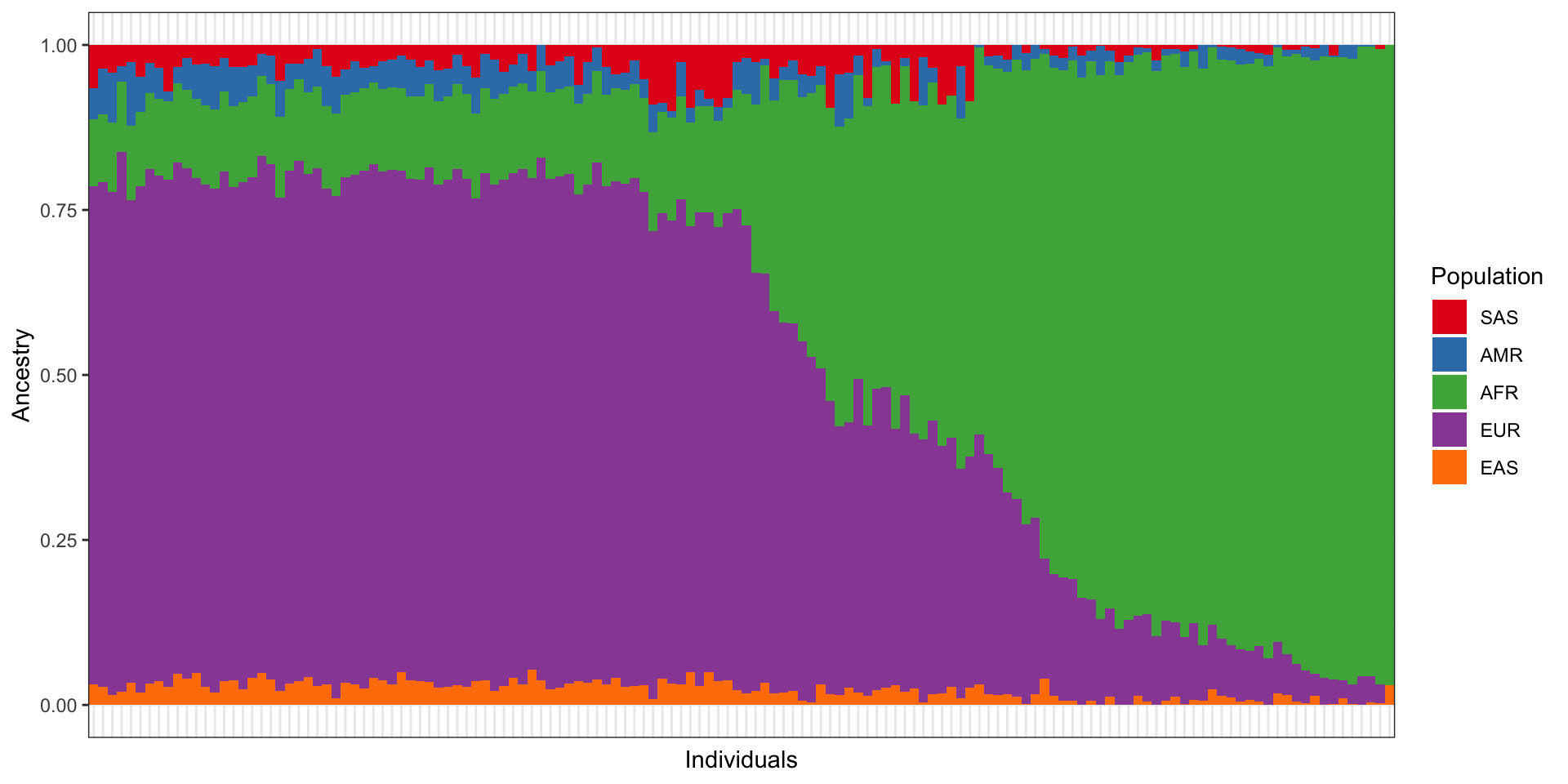
The colors represent ancestries that correspond to the following 1000 Genomes populations: - SAS = South Asian - AMR = American - AFR = African - EUR = European - EAS = East Asian
Each of these are metapopulations based on the grouping of multiple (sub)continental population groups in the 1000 Genomes repository.
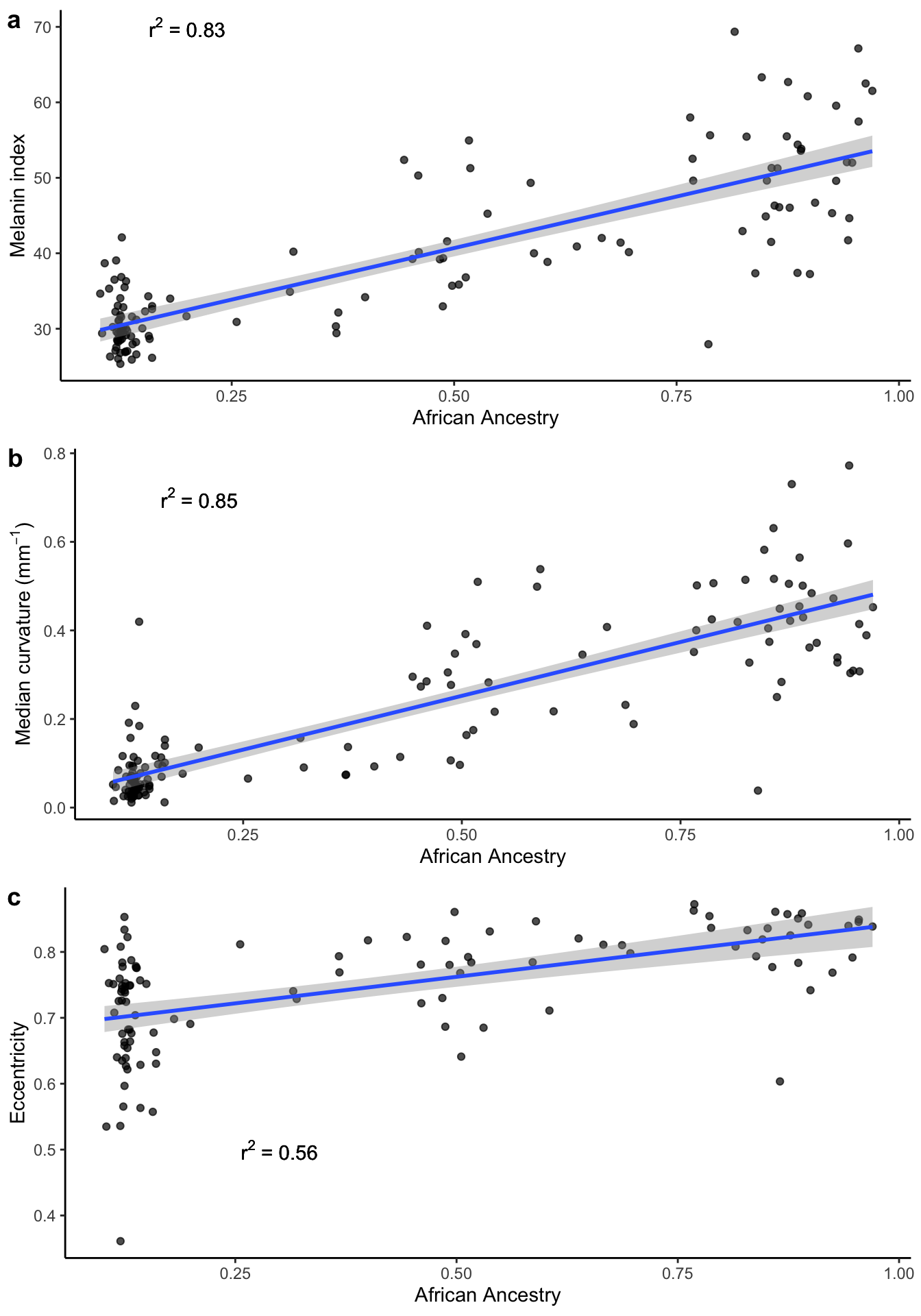
3.2 Ancestry vs. curvature
Here we plot the correlation between proportion of African ancestry and m-index, median curvature, and eccentricity.
3.3 Curvature vs. eccentricity
The relationship between cross-sectional shape (eccentricity) and curvature has long been debated. Due to the coincidence of cross-sectional shape and curvature in various populations that are often contrasted (i.e. East Asian vs. North European vs. West African), it has been unclear whether these traits have a causal relationship (specifically that higher eccentricity predicts higher curvature). In our admixed sample, we have the opportunity to test this question and fit a model between these traits with and without ancestry.
3.3.1 Uncorrected
First we examine the data without correcting for ancestry.
Call:
lm(formula = curv_median ~ eccentricity_median, data = df_curv_ecc)
Residuals:
Min 1Q Median 3Q Max
-0.2843 -0.1245 -0.0264 0.1125 0.4770
Coefficients:
Estimate Std. Error t value Pr(>|t|)
(Intercept) -0.5682 0.1270 -4.474 1.94e-05 ***
eccentricity_median 1.0284 0.1692 6.076 1.96e-08 ***
---
Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
Residual standard error: 0.1576 on 106 degrees of freedom
Multiple R-squared: 0.2583, Adjusted R-squared: 0.2513
F-statistic: 36.92 on 1 and 106 DF, p-value: 1.959e-08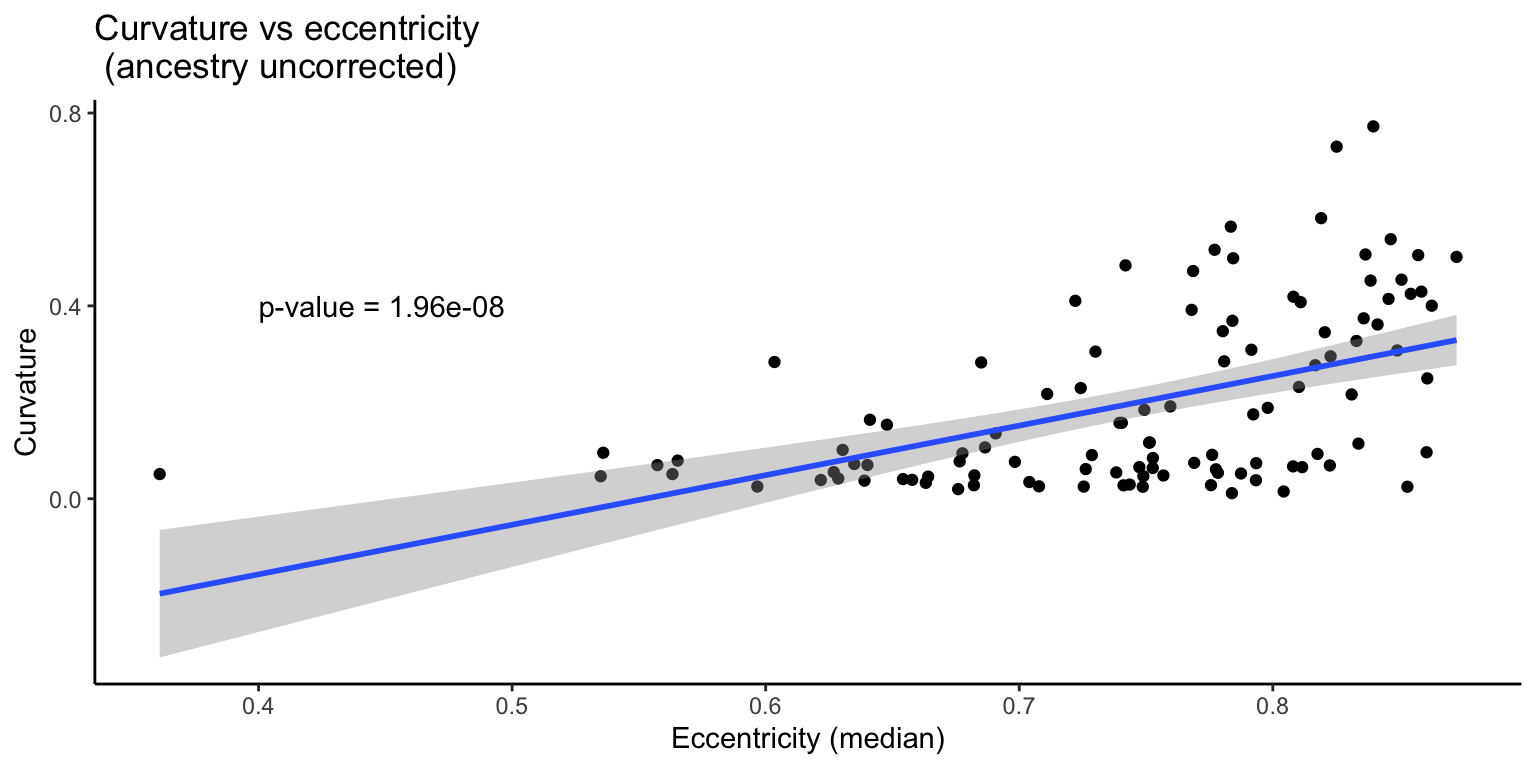
If we consider the relationship between curvature and eccentricity without taking into account ancestry, we find that eccentricity is a significant predictor of curvature.
3.3.2 Corrected
We then re-analyze the data with ancestry as a covariate.
Call:
lm(formula = curv_median ~ eccentricity_median + AFR, data = df_curv_ecc)
Residuals:
Min 1Q Median 3Q Max
-0.37902 -0.04122 -0.00657 0.03606 0.29971
Coefficients:
Estimate Std. Error t value Pr(>|t|)
(Intercept) -0.07237 0.08661 -0.836 0.405
eccentricity_median 0.10891 0.12511 0.871 0.386
AFR 0.48101 0.03632 13.243 <2e-16 ***
---
Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
Residual standard error: 0.09693 on 105 degrees of freedom
Multiple R-squared: 0.7222, Adjusted R-squared: 0.7169
F-statistic: 136.5 on 2 and 105 DF, p-value: < 2.2e-16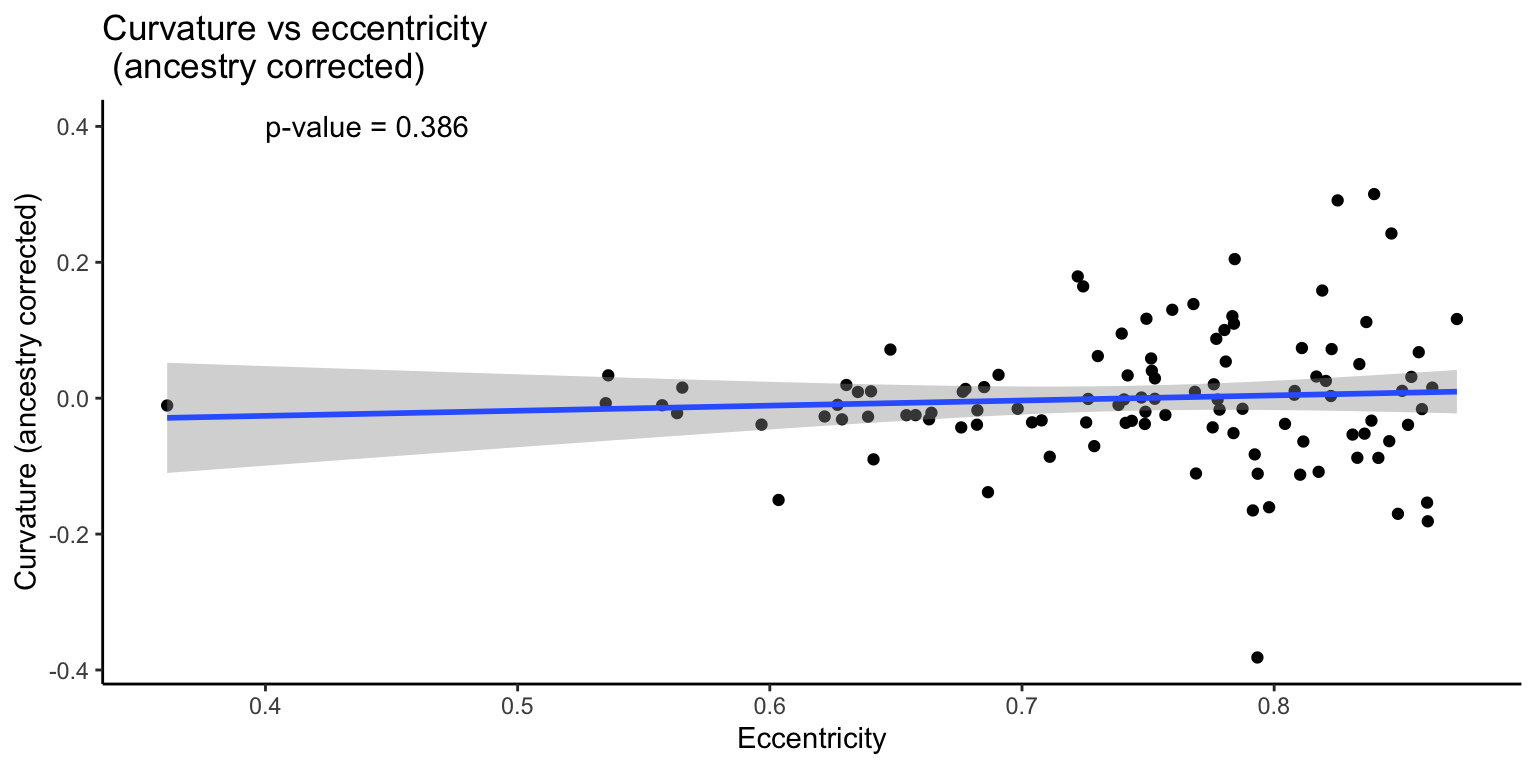
However, when we correct for ancestry, this correlation is no longer significant. This supports the idea that these traits may be independent.
3.4 Curvature vs. skin pigmentation
To demonstrate the potential effect of population stratification on traits, we compare hair curvature with skin pigmentation (m-index). These two traits are not biologically related, yet, in an admixed population, we may see a correlation that is due to population stratification of these polygenic traits.
3.4.1 Uncorrected
First we examine the relationship between curvature and skin pigmentation without correcting for ancestry.
Call:
lm(formula = curv_median ~ m_index, data = df_curv_mindex)
Residuals:
Min 1Q Median 3Q Max
-0.20715 -0.06804 -0.03471 0.04818 0.51483
Coefficients:
Estimate Std. Error t value Pr(>|t|)
(Intercept) -0.280232 0.041533 -6.747 4.91e-10 ***
m_index 0.012887 0.001031 12.501 < 2e-16 ***
---
Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
Residual standard error: 0.1261 on 126 degrees of freedom
Multiple R-squared: 0.5536, Adjusted R-squared: 0.5501
F-statistic: 156.3 on 1 and 126 DF, p-value: < 2.2e-16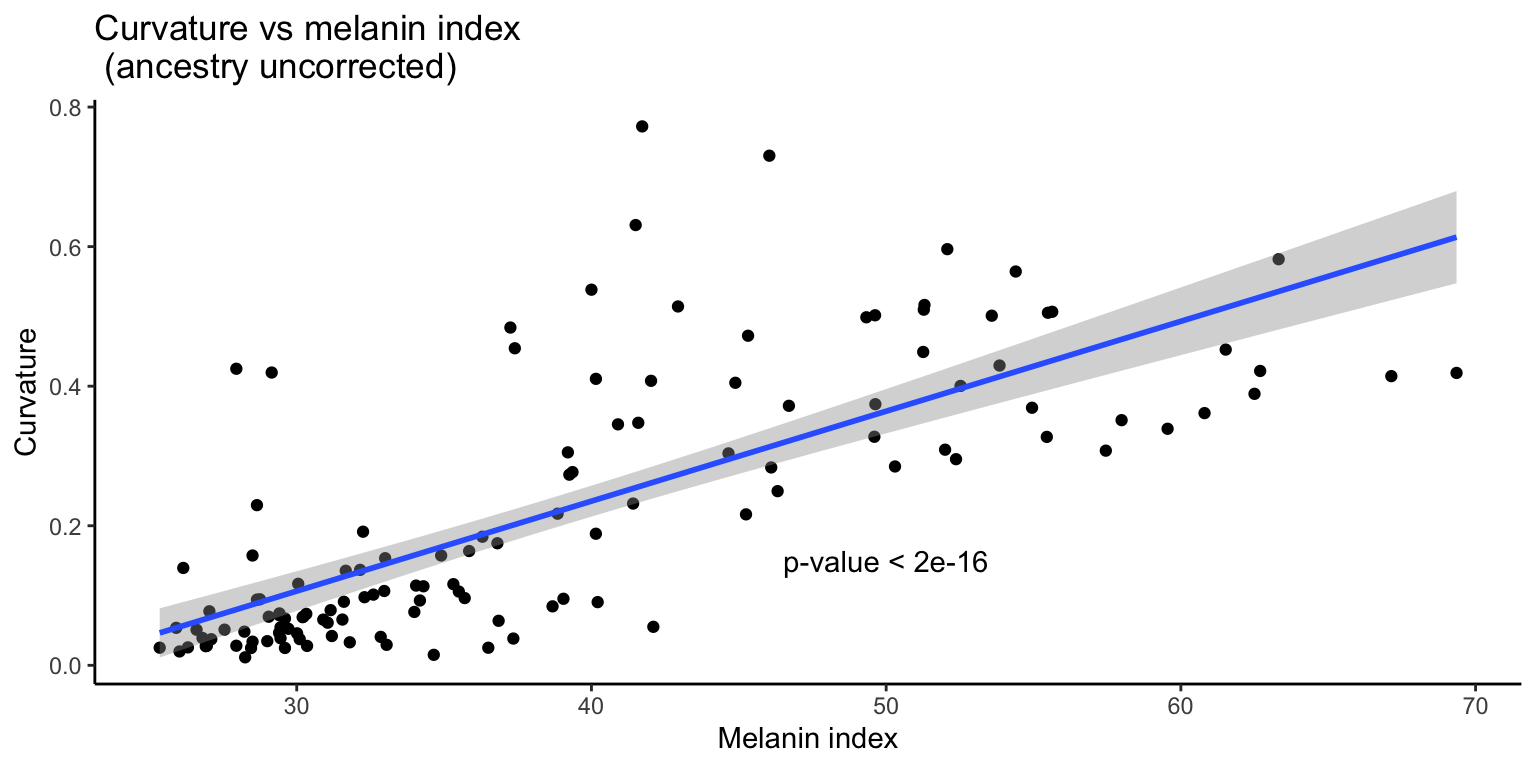
As expected, we see a significant correlation between the two traits.
3.4.2 Corrected
We then apply a correction for ancestry and re-analyze the data.
Call:
lm(formula = curv_median ~ m_index + AFR, data = df_curv_mindex)
Residuals:
Min 1Q Median 3Q Max
-0.34321 -0.04877 -0.01348 0.03562 0.34806
Coefficients:
Estimate Std. Error t value Pr(>|t|)
(Intercept) -0.061501 0.042384 -1.451 0.149
m_index 0.002734 0.001469 1.862 0.065 .
AFR 0.406609 0.048561 8.373 9.63e-14 ***
---
Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
Residual standard error: 0.1014 on 125 degrees of freedom
Multiple R-squared: 0.714, Adjusted R-squared: 0.7094
F-statistic: 156 on 2 and 125 DF, p-value: < 2.2e-16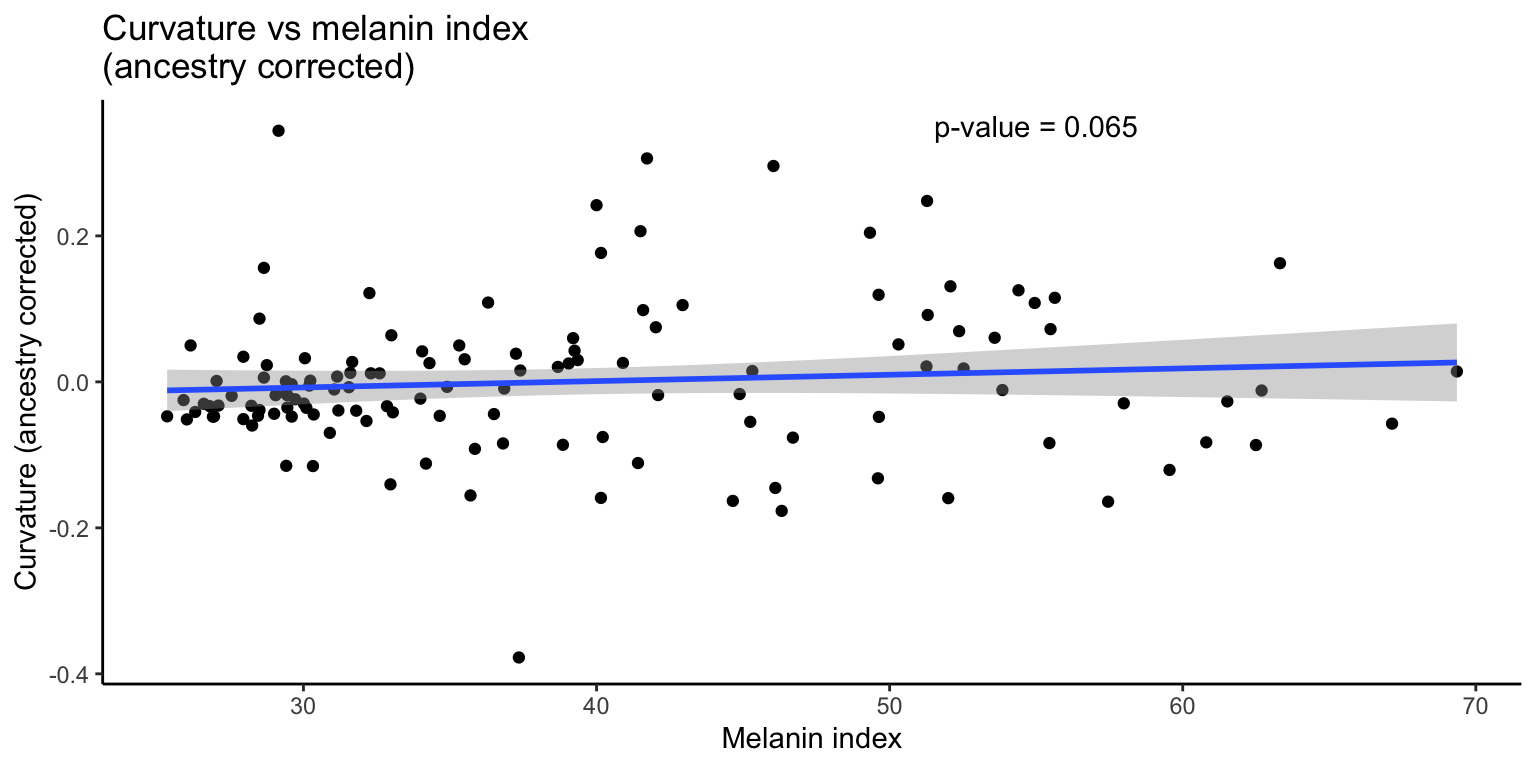
Like with curvature and eccentricity, the relationship between curvature and skin pigmentation is no longer significant when ancestry is taken into account.
R version 3.6.3 (2020-02-29)
Platform: x86_64-apple-darwin15.6.0 (64-bit)
Running under: macOS Mojave 10.14.6
Matrix products: default
BLAS: /Library/Frameworks/R.framework/Versions/3.6/Resources/lib/libRblas.0.dylib
LAPACK: /Library/Frameworks/R.framework/Versions/3.6/Resources/lib/libRlapack.dylib
locale:
[1] en_US.UTF-8/en_US.UTF-8/en_US.UTF-8/C/en_US.UTF-8/en_US.UTF-8
attached base packages:
[1] stats graphics grDevices utils datasets methods base
other attached packages:
[1] cowplot_1.1.0 knitr_1.30 forcats_0.5.0 stringr_1.4.0
[5] dplyr_1.0.2 purrr_0.3.4 readr_1.4.0 tidyr_1.1.2
[9] tibble_3.0.4 ggplot2_3.3.2 tidyverse_1.3.0
loaded via a namespace (and not attached):
[1] Rcpp_1.0.5 lattice_0.20-38 lubridate_1.7.9.2 assertthat_0.2.1
[5] rprojroot_2.0.2 digest_0.6.27 R6_2.5.0 cellranger_1.1.0
[9] plyr_1.8.6 backports_1.2.0 reprex_0.3.0 evaluate_0.14
[13] httr_1.4.2 pillar_1.4.6 rlang_0.4.8 readxl_1.3.1
[17] rstudioapi_0.13 Matrix_1.2-18 rmarkdown_2.5 labeling_0.4.2
[21] splines_3.6.3 munsell_0.5.0 broom_0.7.2 compiler_3.6.3
[25] httpuv_1.5.4 modelr_0.1.8 xfun_0.19 pkgconfig_2.0.3
[29] mgcv_1.8-31 htmltools_0.5.0 tidyselect_1.1.0 workflowr_1.6.2
[33] fansi_0.4.1 crayon_1.3.4 dbplyr_2.0.0 withr_2.3.0
[37] later_1.1.0.1 grid_3.6.3 nlme_3.1-144 jsonlite_1.7.1
[41] gtable_0.3.0 lifecycle_0.2.0 DBI_1.1.0 git2r_0.27.1
[45] magrittr_1.5 scales_1.1.1 cli_2.1.0 stringi_1.5.3
[49] farver_2.0.3 reshape2_1.4.4 fs_1.5.0 promises_1.1.1
[53] xml2_1.3.2 ellipsis_0.3.1 generics_0.1.0 vctrs_0.3.4
[57] tools_3.6.3 glue_1.4.2 hms_0.5.3 yaml_2.2.1
[61] colorspace_2.0-0 rvest_0.3.6 haven_2.3.1