Last updated: 2021-08-01

Checks: 7 0

Knit directory: 2021/

This reproducible R Markdown analysis was created with workflowr (version 1.6.2). The Checks tab describes the reproducibility checks that were applied when the results were created. The Past versions tab lists the development history.

R Markdown file: up-to-date

Great! Since the R Markdown file has been committed to the Git repository, you know the exact version of the code that produced these results.

Environment: empty

Great job! The global environment was empty. Objects defined in the global environment can affect the analysis in your R Markdown file in unknown ways. For reproduciblity it’s best to always run the code in an empty environment.

Seed: set.seed(20210412)

The command set.seed(20210412) was run prior to running the code in the R Markdown file. Setting a seed ensures that any results that rely on randomness, e.g. subsampling or permutations, are reproducible.

Session information: recorded

Great job! Recording the operating system, R version, and package versions is critical for reproducibility.

Cache: none

Nice! There were no cached chunks for this analysis, so you can be confident that you successfully produced the results during this run.

File paths: relative

Great job! Using relative paths to the files within your workflowr project makes it easier to run your code on other machines.

Repository version: 7628720

Great! You are using Git for version control. Tracking code development and connecting the code version to the results is critical for reproducibility.

The results in this page were generated with repository version 7628720. See the Past versions tab to see a history of the changes made to the R Markdown and HTML files.

Note that you need to be careful to ensure that all relevant files for the analysis have been committed to Git prior to generating the results (you can use wflow_publish or wflow_git_commit). workflowr only checks the R Markdown file, but you know if there are other scripts or data files that it depends on. Below is the status of the Git repository when the results were generated:


Ignored files:
    Ignored:    .Rhistory
    Ignored:    .Rproj.user/
    Ignored:    analysis/hero-image.html
    Ignored:    analysis/poke_logo.png

Untracked files:
    Untracked:  Curso_Bioestadistica_MTripp_cuatriII.docx
    Untracked:  Curso_Bioestadistica_MTripp_cuatriII.pdf
    Untracked:  Diapositivas/
    Untracked:  Prueba_markdown.Rmd
    Untracked:  Prueba_markdown.pdf
    Untracked:  README.html
    Untracked:  Resources/
    Untracked:  Tarea_Tstudent.Rmd
    Untracked:  Tarea_Tstudent.docx
    Untracked:  Tarea_Tstudent.html
    Untracked:  Tarea_Tstudent.pdf
    Untracked:  analysis/Clase13_noParam.Rmd
    Untracked:  analysis/hero_backgroud.jpg
    Untracked:  analysis/images/
    Untracked:  analysis/style.css
    Untracked:  analysis/test.Rmd
    Untracked:  code/tarea_macrograd.R
    Untracked:  data/CS_subset.csv
    Untracked:  data/Consumo_oxigeno_wide.csv
    Untracked:  data/Darwin_esp.csv
    Untracked:  data/Data_enzimas_Experimento1.txt
    Untracked:  data/Data_enzimas_Experimento2.txt
    Untracked:  data/Data_enzimas_Experimento3.txt
    Untracked:  data/Data_enzimas_Experimento4.txt
    Untracked:  data/DownloadFestival(No Outlier).dat
    Untracked:  data/Festival.csv
    Untracked:  data/Hful_metabolitos_ver2.csv
    Untracked:  data/Longitud_noParam.csv
    Untracked:  data/LungCapData.txt
    Untracked:  data/LungCapDataEsp.csv
    Untracked:  data/PalmerPenguins.csv
    Untracked:  data/Pokemon_tabla.csv
    Untracked:  data/Pokemon_tabla.xls
    Untracked:  data/RExam.dat
    Untracked:  data/Rexamendat.csv
    Untracked:  data/Tabla1_Muestreo.txt
    Untracked:  data/Transcriptome_Anotacion.csv
    Untracked:  data/Transcriptome_DGE.csv
    Untracked:  data/Vinogradov_2004_Titanic.tab
    Untracked:  data/Vinogradov_2004_Titanic.tab.csv
    Untracked:  data/data_tukey.txt
    Untracked:  data/exp_macrogard_growth.tab
    Untracked:  data/exp_macrogard_rna-dna.tab
    Untracked:  data/fertilizantes_luz.csv
    Untracked:  data/gatos_sueno.csv
    Untracked:  data/macrogard_crecimiento.csv
    Untracked:  data/pokemon_extended.csv
    Untracked:  output/Plot_all_penguins.pdf
    Untracked:  output/Plot_all_penguins.tiff
    Untracked:  output/graficos/

Unstaged changes:
    Modified:   analysis/_site.yml

Note that any generated files, e.g. HTML, png, CSS, etc., are not included in this status report because it is ok for generated content to have uncommitted changes.

These are the previous versions of the repository in which changes were made to the R Markdown (analysis/Clase14_PCA.Rmd) and HTML (docs/Clase14_PCA.html) files. If you’ve configured a remote Git repository (see ?wflow_git_remote), click on the hyperlinks in the table below to view the files as they were in that past version.

File	Version	Author	Date	Message
Rmd	7628720	Miguel Tripp	2021-08-01	workflowr::wflow_publish(c(“analysis/index.Rmd”, “analysis/about.Rmd”,
html	5aafed2	Miguel Tripp	2021-08-01	Build site.
html	2bc601a	Miguel Tripp	2021-07-31	Build site.
Rmd	b4e67dc	Miguel Tripp	2021-07-31	workflowr::wflow_publish(c(“analysis/index.Rmd”, “analysis/about.Rmd”,
html	03db7ff	Miguel Tripp	2021-07-25	Build site.
html	fcb9047	Miguel Tripp	2021-07-25	Build site.
html	2adc7a9	Miguel Tripp	2021-07-24	Build site.
html	9d09420	Miguel Tripp	2021-07-22	Build site.
Rmd	9a3bbe1	Miguel Tripp	2021-07-22	workflowr::wflow_publish(c(“analysis/index.Rmd”, “analysis/about.Rmd”,

1 Generalidades

¿Que es un PCA?

El análisis de componentes principales (Principal Component Analysis) o PCA es una herramienta para el análisis exploratorio de los datos que permite visualizar la variación presente de un set de datos con muchas variables.

El PCA pertenece a la familia de técnicas conocidas como no supervisadas (unsupervised) ya que a diferencia de métodos anteriores de regresión, donde se utilizan una serie de predictores para predecir una variables de respuesta $Y$, en estos métodos no supervisados la variable de respuesta $Y$ no se toma en cuenta ya que el objetivo no es predecir $Y$ sino extraer información empleando los predictores para identificar subgrupos 1.

De manera general, el PCA es un tipo de transformación lineal de un set de datos con un cierto número de variables. Dicha transformación ajusta el set de datos a un nuevo sistema de coordenadas de manera que la mayor proporción de la varianza se explica en la primera coordenada y cada coordenada subsiguiente es ortogonal a la anterior y explica una menor variabilidad.

¿Cuando se usa un PCA?

Una de las principales aplicaciones de PCA es la reducción de dimensionalidad (es decir, variables): cuando contamos con un gran número de variables cuantitativs posiblemente correlacionadas (indicativo de exstencia de información redundante), un PCA permite “reducirlas” a un número menor de variables transformadas (componentes principales) que expliquen gran parte de la variabilidad de los datos.

Cada dimensión o componente principal generado por PCA será una combinación lineal de las variables originales. El PCA puede considerarse como una rotación de los ejes del sistema de coordenadas de las variables originales a nuevos ejes ortogonales, de manera que estos ejes coincidan con la dirección de máxima varianza de los datos.

Es importante recordar que el PCA reduce la dimensionalidad pero no reduce el número de variables en los datos. Esto significa que puedes explicar el 99% de la variabilidad de un set de datos con 1,000 variables usando solamente los tres componentes principales, pero aún necesitas esos 1,000 variables para construir los componentes principales.

2 Metabolitos de abulon

Para este ejercicio utilizaremos la base de datos Hful_meabolitos_ver2.csv la cual se puede descargar aquí contiene información de la concentración (Unidades arbitrarias) de diversos metabolitos endógenos de muestras de tejido de abulón (Haliotis fulgens) expuestos a un incremento en la temperatura. Para esto, se tomaron muestras de branquia de abulón a 18°C, 24°C, 30°C y 32°C. El PCA nos permitirá evaluar si hay diferencias en el perfíl de metabolítos entre cada temperatura.

library(tidyverse)

metabolitos <- read_csv("data/Hful_metabolitos_ver2.csv")


-- Column specification --------------------------------------------------------
cols(
  ind.names = col_character(),
  Group = col_character(),
  ATP = col_double(),
  Acetate = col_double(),
  Alanine = col_double(),
  Homarine = col_double(),
  Isoleucine = col_double(),
  Lactate = col_double(),
  Leucine = col_double(),
  Succinate = col_double(),
  Taurine = col_double(),
  Threonine = col_double(),
  Tyrosine = col_double(),
  Valine = col_double()
)

2.1 Normalización de los datos

Un aspecto fundamenta al aplicar un PCA es que las observaciones tienen que moverse al centro del eje de coordenadas, esto es, centrarlas para que tengan media de 0, para así eliminar posibles sesgos en las mediciones.

Los datos también se escalan a una varianza unitaria para eliminar el efecto de las distintas unidades en las que puedan estar medidas los datos.

Para entender este concepto, vamos a visualizar nuestros datos. Primero será necesario transformar la tabla a formato largo (long).

metabolitos_long <- metabolitos %>% 
  pivot_longer(-c(1,2), names_to = "metabolito", values_to = "concentracion")

Y posteriomente visualizamos la concentración de cada metabolito

ggplot(metabolitos_long, aes(y = metabolito, x = concentracion))+
  geom_boxplot()+
  labs(title = "concentración relativa de cada metabolito", y = "Concentración de metabolitos (U.A.)")

ggplot(metabolitos_long, aes(x = concentracion))+
  geom_density()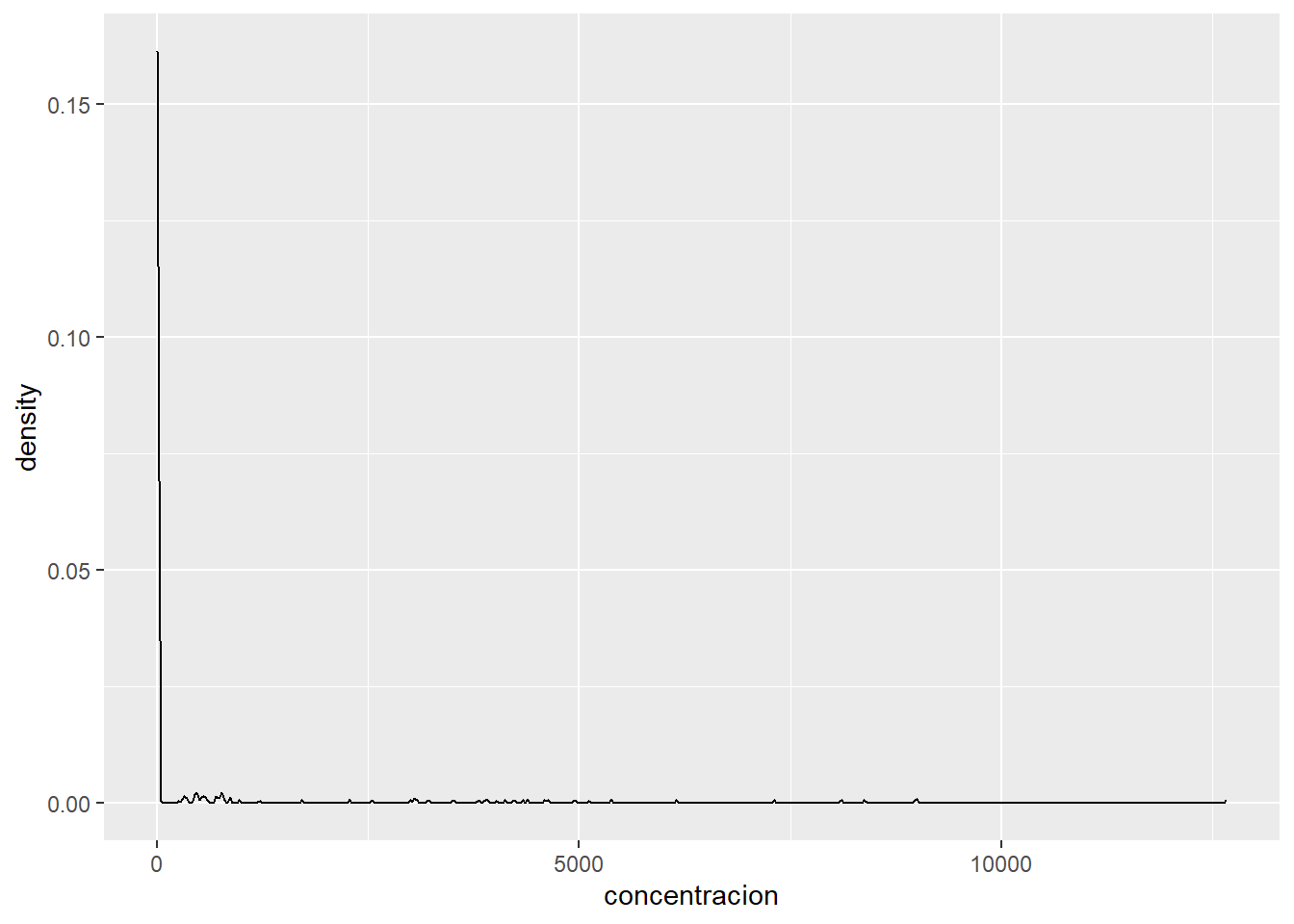

Como puedes observar, la concentración de la homarina es mucho mayor que la del resto de los metabolítos. Esto es una situación de la que tenemos que tener cuidado ya que la homarina cargaría todo el peso del PCA

Este proceso de normalización y escalar se aplican directamente dentro de la función para hacer el PCA, pero para visualizar este efecto, vamos a hacer el siguiente ejercicio:

metabolitos_scale <- data.frame(metabolitos$Group, scale(metabolitos[,-c(1:2)], center = TRUE, scale = TRUE))


metabolitos_long_scale <- metabolitos_scale %>% 
  pivot_longer(- metabolitos.Group, names_to = "metabolito", values_to = "concentracion")

ggplot(metabolitos_long_scale, aes(y = metabolito, x = concentracion))+
  geom_boxplot()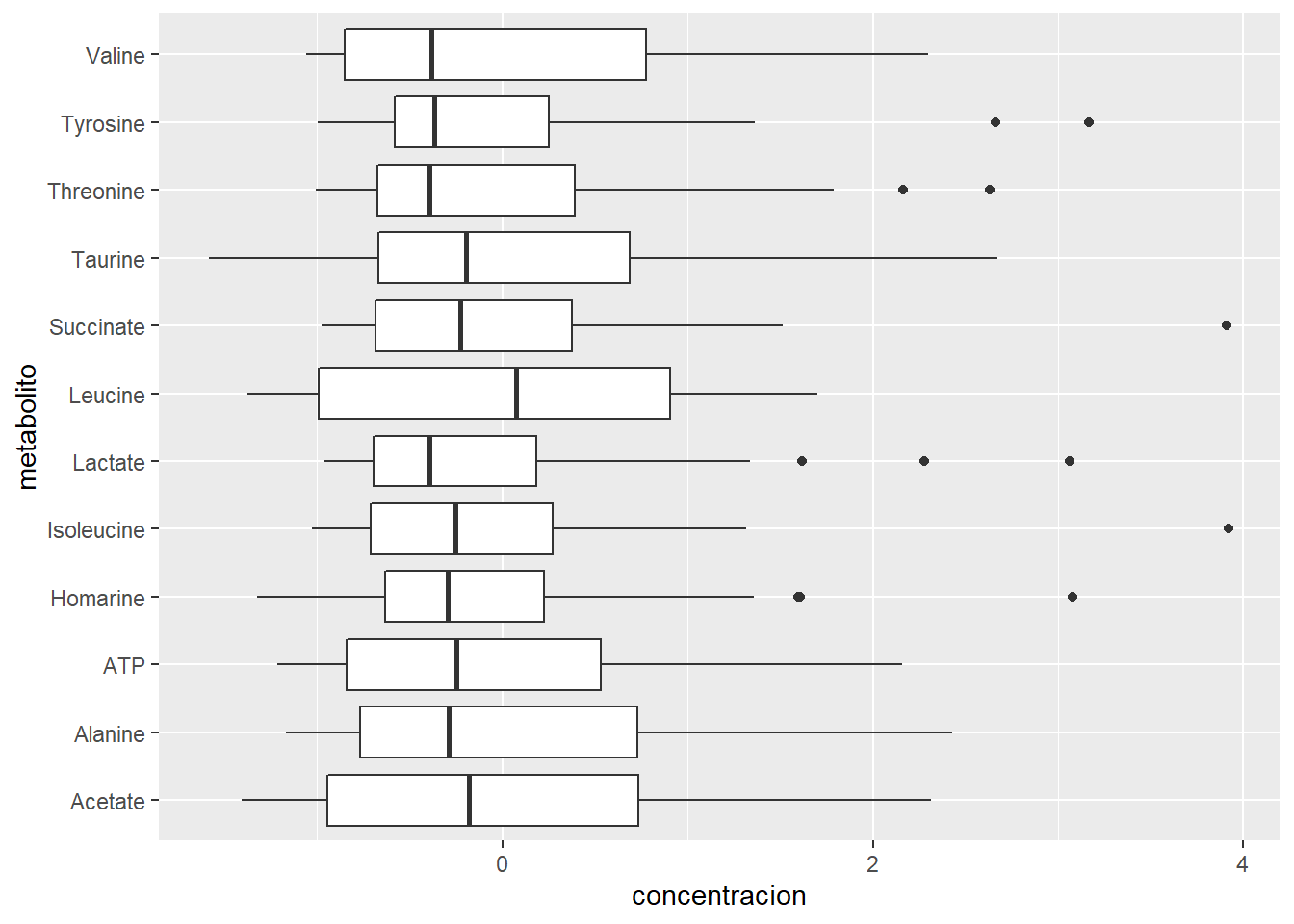

ggplot(metabolitos_long_scale, aes(x = concentracion))+
  geom_density()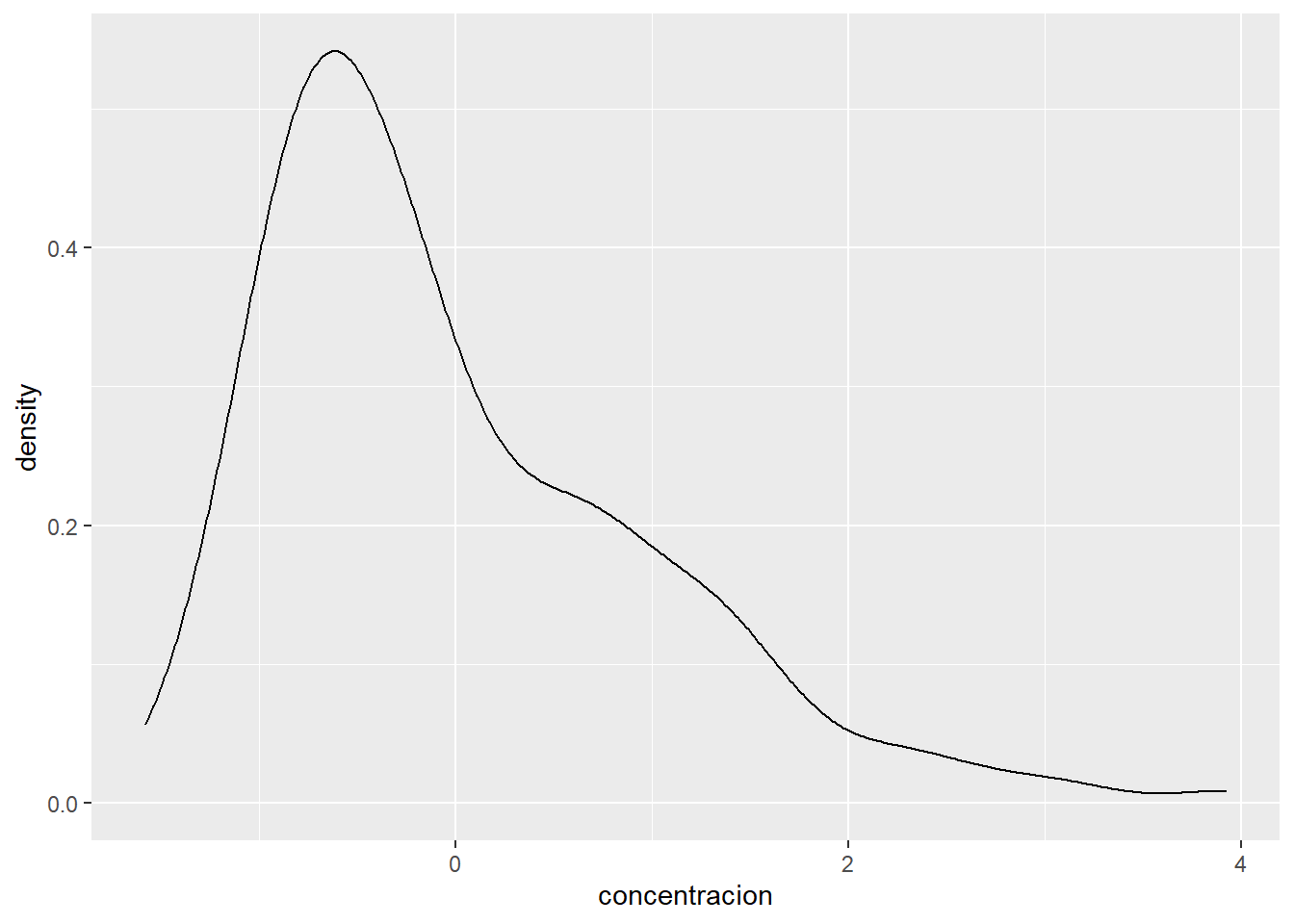

Como puedes ver, al escalar los datos a pesar de las diferencias iniciales en la concentración, ahora todos tienen una media de $0$ lo que nos permite que todas las variables tengan contribución similar al PCA

2.2 PCA con `prcomp()`

Existe una gran número de alternativas para realizar un análisis de componentes principales en R, pero para fines practicos, iniciaremos usando la función de R base prcomp().

Dado que esta función trabaja sobre una matriz, le indicaremos que no tome en cuenta las primeras dos columnas de la tabla original:

metabolitos_pca <- prcomp(metabolitos[,-c(1:2)], center = TRUE, scale. = TRUE)


summary(metabolitos_pca)

Importance of components:
                          PC1    PC2    PC3     PC4     PC5     PC6     PC7
Standard deviation     2.1470 1.5718 1.2163 0.92162 0.88165 0.77621 0.65618
Proportion of Variance 0.3841 0.2059 0.1233 0.07078 0.06478 0.05021 0.03588
Cumulative Proportion  0.3841 0.5900 0.7133 0.78406 0.84883 0.89904 0.93492
                          PC8    PC9    PC10    PC11   PC12
Standard deviation     0.4850 0.4608 0.39208 0.31696 0.2813
Proportion of Variance 0.0196 0.0177 0.01281 0.00837 0.0066
Cumulative Proportion  0.9545 0.9722 0.98503 0.99340 1.0000

En este caso obtuvimos 12 componentes principales. Cada uno de ellos explica cierto porcentaje de la variación total del set de datos. Es decir, el PC1 explica 38% de la varianza total, mientras que el PC2 explica un 20% de la varianza, por lo que ambos componentes explicar mas de un 50% de la varianza total.

Esto se puede visualizar en forma de un scree plot

screeplot(metabolitos_pca, type = "l", main = "scree plot con los componentes principales")
abline(h = 1, col="red", lty=5)
legend("topright", legend=c("Eigenvalor = 1"),
       col=c("red"), lty=5, cex=0.6)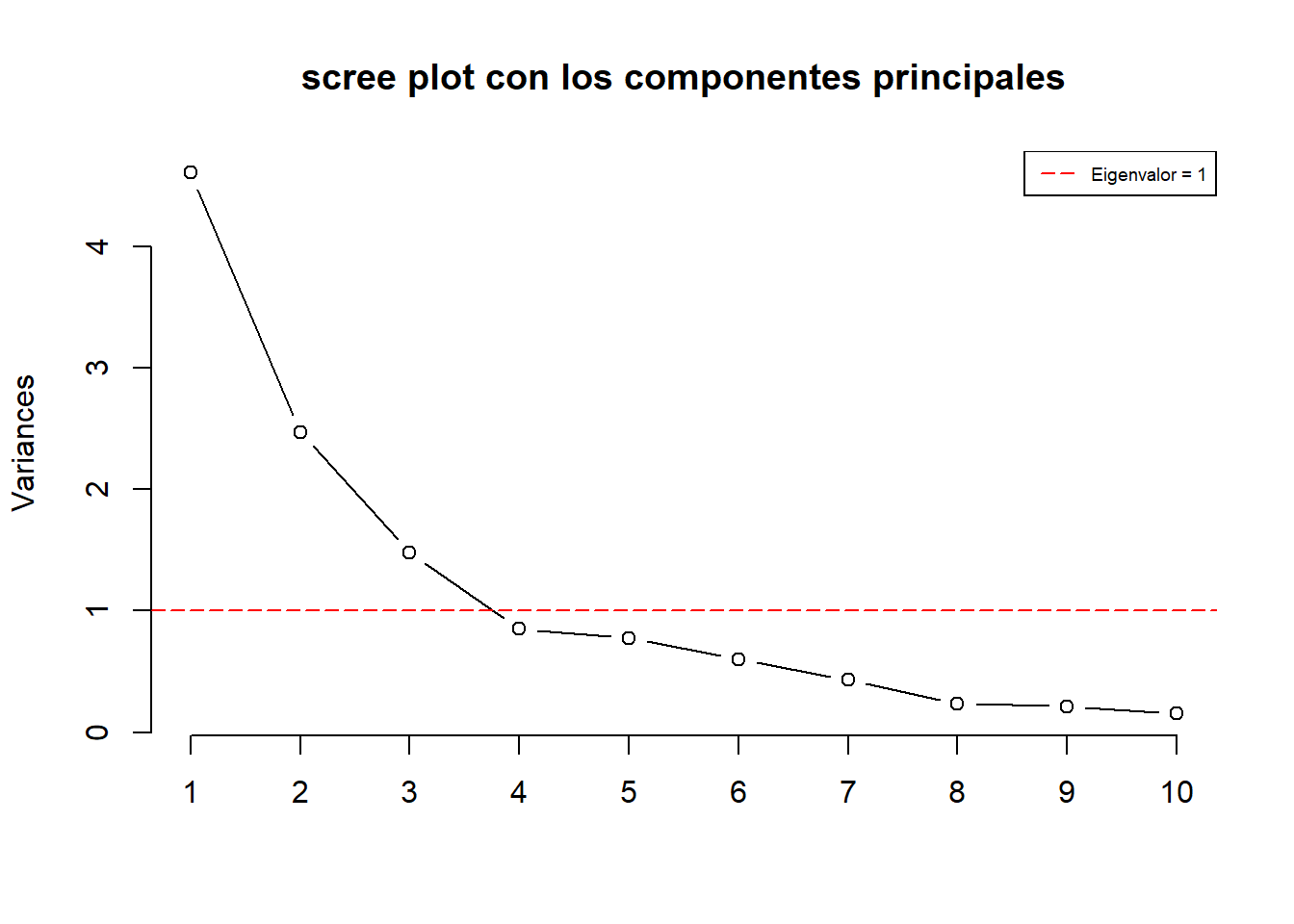

O podemos calcular manualmente la proporción de la varianza explicada por cada componente

La varianza explicada por cada componente principal (correspondiente a los eigenvalores) la obtenemos elevando al cuadrado la desviación estándar.

prop_varianza <- metabolitos_pca$sdev^2 / sum(metabolitos_pca$sdev^2)

prop_varianza <- data.frame(prop_varianza, pc = 1:12)

ggplot(prop_varianza, aes(x = pc, y = prop_varianza))+
  geom_bar(stat = "identity")+
  theme_bw()+
  labs(x = "Componente principal", y = "Prop. de varianza explicada")

y la proporción acumulada de la varianza

prop_varianza$accum <- cumsum(prop_varianza$prop_varianza)

ggplot(prop_varianza, aes(x = pc, y = accum))+
  geom_point()+
  geom_line()+
  geom_label(aes(label = round(accum,2))) +
  theme_bw()+
  labs(x = "Componente principal",
       y = "Prop. varianza explicada acumulada")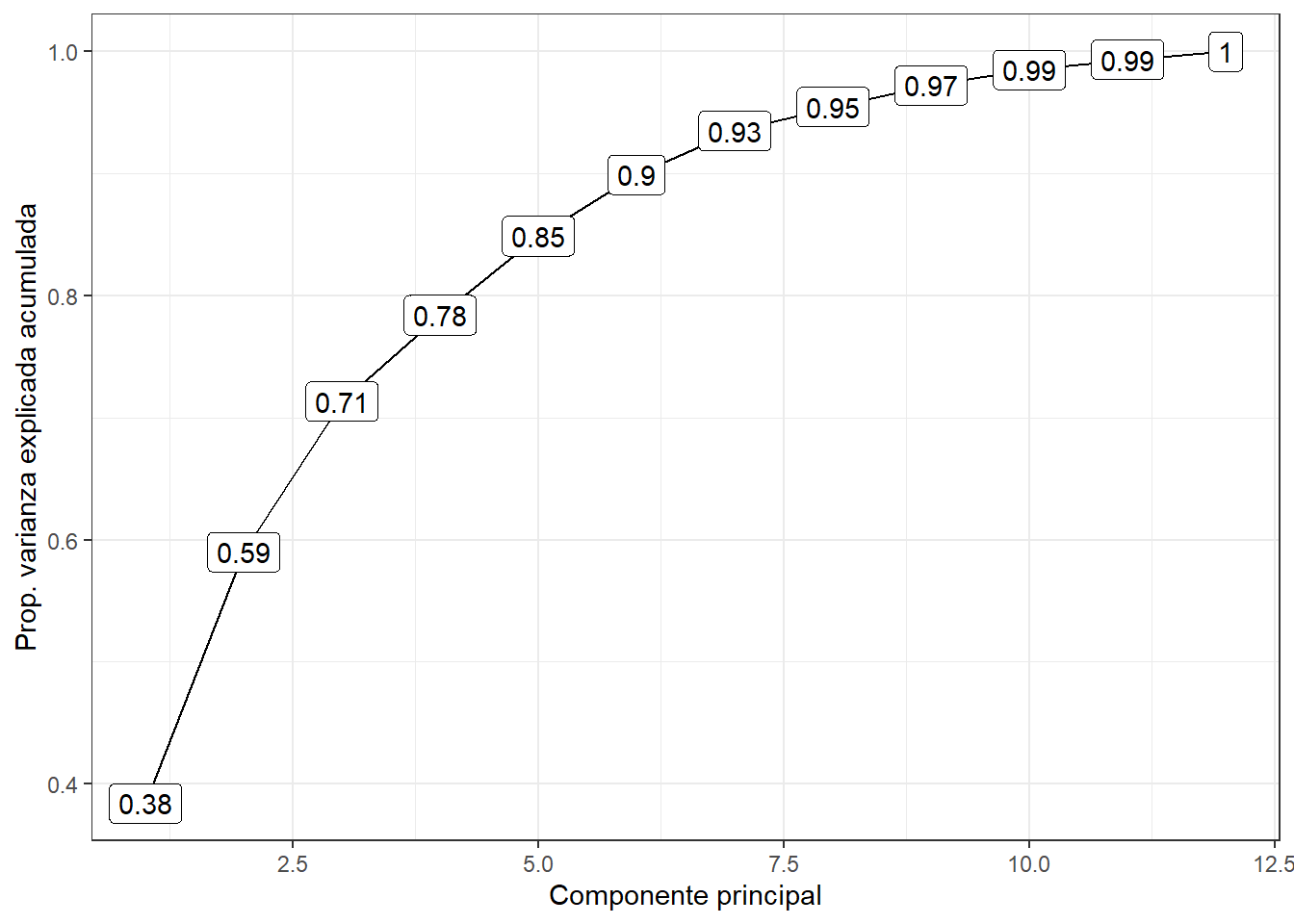

Como es de esperar, la varianza explicada es mayor en el primer componente que en las subsiguientes.

No existe un método objetivo para escoger el número de componentes principales que son suficientes para un análisis, por lo que depende del juicio del analista y del problema en cuestión. Si explican suficiente variabilidad y el objetivo es la visualización de los datos, no se suelen escoger más de tres componentes principales, para así facilitar la representación gráfica y la interpretación.

Ahora, analicemos a mayor detalle el objeto pca que acabamos de generas

names(metabolitos_pca)

[1] "sdev"     "rotation" "center"   "scale"    "x"

El objeto prcomp contiene la información necesario:

Centro ($center), la escala (scale), desviación estandar ($dev) de cada componente principal.
La relación (correlación o anticorrelación) entre las variables iniciales y el componente principal ($rotation)
El valor de cada muestra en función del componente principal ($x)

Los elementos center y scale se corresponden con las medias y las desviaciones estándar originales de las variables previo escalado e implementación del PCA.

La matriz rotation proporciona los loadings de los componentes principales (cada columna contiene el vector de loadings de cada componente principal). La función los denomina matriz de rotación ya que si multiplicáramos la matriz de datos por $rotation, obtendríamos las coordenadas de los datos en el nuevo sistema rotado de coordenadas. Estas coordenadas se corresponden con los scores de los componentes principales.

De manera que:

metabolitos_pca$rotation

                    PC1          PC2         PC3          PC4         PC5
ATP        -0.070685562  0.479974506 -0.04687200  0.327201217 -0.29836992
Acetate    -0.324755039  0.165290878  0.28385534  0.041713707 -0.07123331
Alanine     0.328378334  0.266153017  0.07642588  0.421653115  0.33359945
Homarine   -0.286651681  0.361836185 -0.28681415  0.035405924 -0.03021160
Isoleucine -0.347649618 -0.066523746  0.21734203  0.378239502  0.37908584
Lactate    -0.319708823  0.278323765  0.26098969  0.001400924 -0.26282914
Leucine    -0.315770470 -0.376408246 -0.01456305 -0.111985294 -0.32958349
Succinate  -0.216637920 -0.014155443 -0.55389486 -0.162844001  0.50435964
Taurine    -0.008570964 -0.228759485 -0.50677579  0.633289470 -0.30223829
Threonine  -0.410405185  0.006835562  0.15271445  0.105312352  0.34526274
Tyrosine   -0.284978138  0.266071154 -0.34545093 -0.272150544 -0.08317614
Valine     -0.283020877 -0.439995442  0.08533091  0.209323386 -0.02093078
                   PC6         PC7           PC8         PC9        PC10
ATP         0.50870283 -0.33441840  0.3354882279 -0.22186801  0.04857953
Acetate     0.42177543  0.65871377 -0.0003270073  0.30887554 -0.07656480
Alanine    -0.11680975  0.09305641 -0.0765090655 -0.26812909 -0.49867075
Homarine   -0.04007653 -0.31091568 -0.6104955686  0.43289941 -0.09962305
Isoleucine -0.18682142 -0.33839267  0.2727932823  0.23071977  0.25588950
Lactate    -0.39669272  0.10024969 -0.2845229360 -0.47305870 -0.04784806
Leucine     0.13181149 -0.20900202 -0.0612149434 -0.35304246 -0.03306915
Succinate   0.33699277  0.09821686 -0.0848058779 -0.33871951 -0.02314957
Taurine    -0.18790566  0.34211252 -0.0349247181  0.01535670  0.20907203
Threonine  -0.08452254  0.15302004 -0.0290742509 -0.24173140  0.25420418
Tyrosine   -0.41260553  0.11215091  0.5831321850  0.10596301 -0.29694198
Valine      0.11033857 -0.13420324  0.0217276395  0.09895093 -0.68357650
                   PC11        PC12
ATP        -0.164854790 -0.06645838
Acetate     0.246085745  0.07875348
Alanine     0.206282921  0.36760490
Homarine   -0.037398968  0.18102997
Isoleucine  0.431816658 -0.10817063
Lactate     0.142711183 -0.43395454
Leucine     0.363228032  0.56103230
Succinate   0.203006497 -0.27980375
Taurine    -0.006810428 -0.02842208
Threonine  -0.634046747  0.34846591
Tyrosine   -0.002904511  0.15936636
Valine     -0.293708927 -0.28421331

el primer componente es el resultado de la siguiente combinación lineal de las variables originales:

$PC1 = -0.070 ATP - 0.324 Acetate + 0.328 Alanine... etc$

2.3 Visualización del PCA

Una de las formas de visualizar los resultados de un PCA es mediante el llamado biplot. Este permite visualizar la posición de cada muestra en relación al PC1 y PC2 y como contribuye cada variable a cada componente principal.

biplot(metabolitos_pca, scale = 0)

La comparación de la distancia entre puntuaciones y vectores no es relevante en la interpretación de los biplots, teniendo en cuenta que hay varias versiones de biplots que se pueden obtener según como se escalen sus elementos (ya que esto afecta a la compactación o dispersión de la representación). Las interpretaciones se centran en las direcciones y agrupamientos tanto de unos como de otros.

Para los vectores (variables), nos fijamos en su longitud y en el ángulo con respecto a los ejes de las componentes principales y entre ellos mismos:

Ángulo: cuanto más paralelo es un vector al eje de una componente, más ha contribuido a la creación de la misma. Con ello obtienes información sobre qué variable(s) ha sido más determinante para crear cada componente, y si entre las variables (y cuales) hay correlaciones. Ángulos pequeños entre vectores representa alta correlación entre las variables implicadas (observaciones con valores altos en una de esas variables tendrá valores altos en la variable o variables correlacionadas); ángulos rectos representan falta de correlación, y ángulos opuestos representan correlación negativa (una observación con valores altos en una de las variables irá acompañado de valores bajos en la otra).
Longitud: cuanto mayor la longitud de un vector relacionado con x variable (en un rango normalizado de 0 a 1), mayor variabilidad de dicha variable está contenida en la representación de las dos componentes del biplot, es decir, mejor está representada su información en el gráfico.

Para los scores (observaciones), nos fijamos en los posibles agrupamientos. Puntuaciones próximas representan observaciones de similares características. Puntuaciones con valores de las variables próximas a la media se sitúan más cerca del centro del biplot (0, 0). El resto representan variabilidades normales o extremas (outliers). Por otro lado, la relación de las observaciones con las variables se puede estudiar proyectando las observaciones sobre la dirección de los vectores[1].

El paso siguiente es extraer los PCs 1 y 2, los cuales son los que explican la mayor variabilidad de los datos y graficarlo usarlo ggplot. Para esto, necesitamos extraer los PC 1 y 2 de nuestro objecto pca y unirlos a nuestra tabla original de metabolitos

metabolitos_PCs <- cbind(metabolitos, metabolitos_pca$x[, 1:2])

head(metabolitos_PCs)

  ind.names Group      ATP   Acetate Alanine Homarine Isoleucine   Lactate
1    Hf10BG   18C 3.991304 0.9086957 11.6589 3044.326  0.9391304 1.2695652
2     Hf2BG   18C 2.931579 0.8000000 15.2360 4593.174  0.3947368 1.6315789
3     Hf4BG   18C 1.450000 1.3205882 16.3250 2537.371  0.1470588 1.0117647
4     Hf5BG   18C 2.466667 0.8076923 11.3650 3063.985  0.3076923 0.5948718
5     Hf6BG   18C 4.776190 0.9142857 14.6588 4023.495  0.7666667 2.5428571
6     Hf7BG   18C 3.823810 0.7857143 14.3658 7304.200  0.5476190 2.4523810
    Leucine Succinate  Taurine Threonine Tyrosine    Valine      PC1
1 1.0826087 0.2173913 758.2365 0.6869565 2.086957 0.7565217 2.245430
2 0.5894737 0.4000000 689.1245 0.5736842 9.657895 0.3526316 2.284984
3 0.3617647 0.1176471 865.3210 0.4529412 4.502941 0.2441176 3.200969
4 0.7333333 0.1102564 751.2350 0.3333333 4.564103 0.6897436 2.827378
5 0.8952381 0.5952381 569.1234 0.7857143 4.485714 1.4047619 1.764634
6 1.1190476 0.6523810 713.2286 1.1000000 3.642857 1.1666667 1.441144
          PC2
1  0.25398388
2  0.94070763
3 -0.08366326
4 -0.12111761
5  1.18767384
6  1.11936471

Ahora graficamos con ggplot

ggplot(metabolitos_PCs, aes(x = PC1, y = PC2, col = Group, fill = Group))+
stat_ellipse(geom = "polygon", col = "black", alpha = 0.3)+
  geom_point(shape = 21, col = "black")

Alternativamente, podemos usar el paquete ggbiplot para graficar el biplot

#library(devtools)
#install_github("vqv/ggbiplot")

library(ggbiplot)

ggbiplot(metabolitos_pca, labels = metabolitos$ind.names, ellipse = TRUE, groups = metabolitos$Group, scale = 0)+
  theme_bw()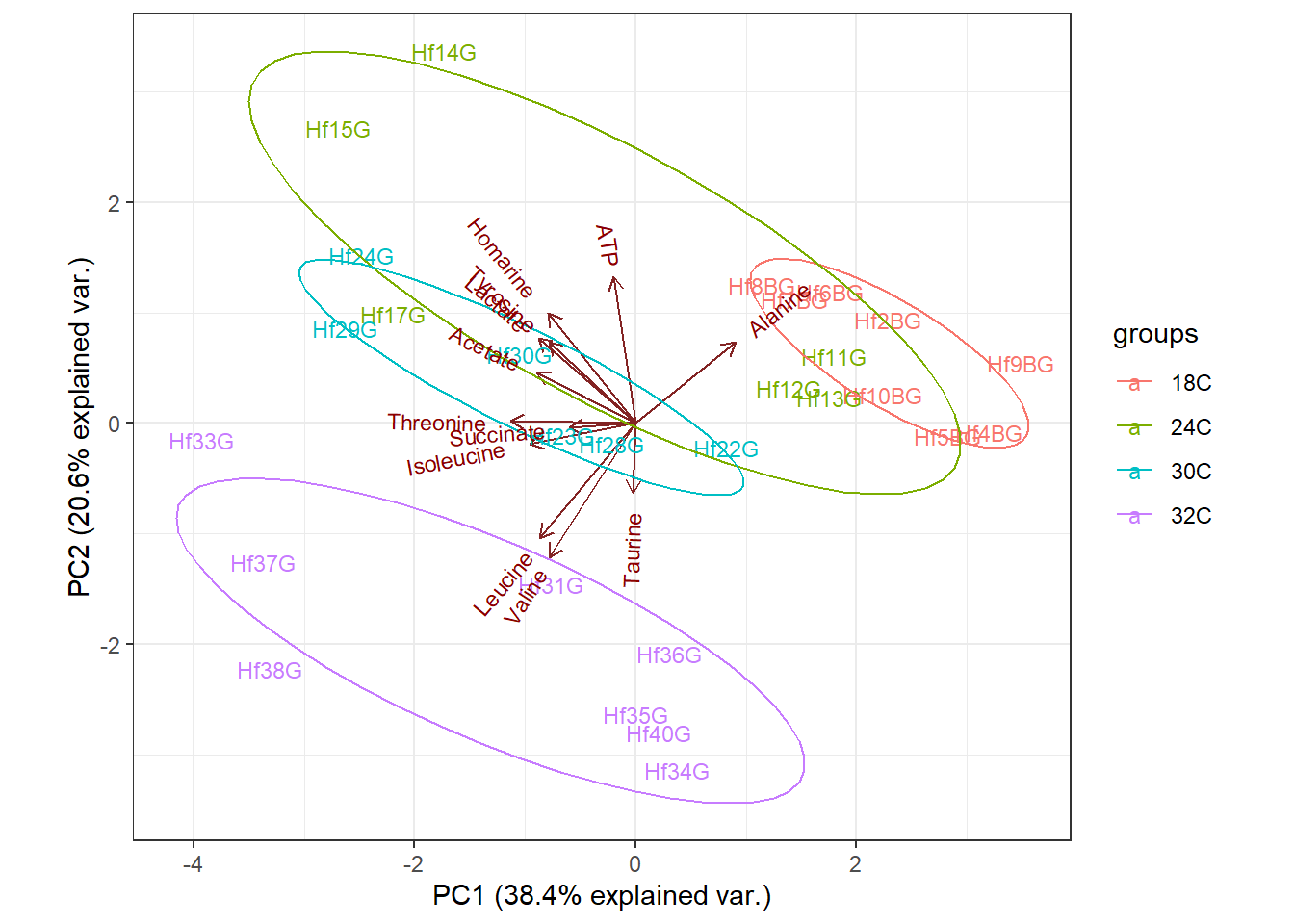

Con esta función también es posible graficar el segundo y tercer componente principal (PC2 y PC3), los cuales explican un menor porcentaje la variabildiad de los datos.

ggbiplot(metabolitos_pca, choices = c(2,3), labels = metabolitos$ind.names, ellipse = TRUE, groups = metabolitos$Group, scale = 0)+
  theme_bw()

ggbiplot(metabolitos_pca, choices = c(1,2), labels = metabolitos$ind.names, ellipse = TRUE, groups = metabolitos$Group, scale = 0, var.axes = FALSE)+
  theme_bw()

sessionInfo()

R version 4.0.5 (2021-03-31)
Platform: x86_64-w64-mingw32/x64 (64-bit)
Running under: Windows 10 x64 (build 19043)

Matrix products: default

locale:
[1] LC_COLLATE=English_United States.1252 
[2] LC_CTYPE=English_United States.1252   
[3] LC_MONETARY=English_United States.1252
[4] LC_NUMERIC=C                          
[5] LC_TIME=English_United States.1252    

attached base packages:
[1] grid      stats     graphics  grDevices utils     datasets  methods  
[8] base     

other attached packages:
 [1] ggbiplot_0.55   scales_1.1.1    plyr_1.8.6      forcats_0.5.1  
 [5] stringr_1.4.0   dplyr_1.0.5     purrr_0.3.4     readr_1.4.0    
 [9] tidyr_1.1.3     tibble_3.0.4    ggplot2_3.3.5   tidyverse_1.3.1
[13] workflowr_1.6.2

loaded via a namespace (and not attached):
 [1] Rcpp_1.0.5        lubridate_1.7.10  ps_1.5.0          assertthat_0.2.1 
 [5] rprojroot_2.0.2   digest_0.6.27     utf8_1.2.1        R6_2.5.0         
 [9] cellranger_1.1.0  backports_1.2.1   reprex_2.0.0      evaluate_0.14    
[13] httr_1.4.2        pillar_1.6.0      rlang_0.4.11      readxl_1.3.1     
[17] rstudioapi_0.13   whisker_0.4       jquerylib_0.1.4   rmarkdown_2.9    
[21] labeling_0.4.2    munsell_0.5.0     broom_0.7.6       compiler_4.0.5   
[25] httpuv_1.5.4      modelr_0.1.8      xfun_0.23         pkgconfig_2.0.3  
[29] htmltools_0.5.1.1 tidyselect_1.1.1  fansi_0.4.2       crayon_1.4.1     
[33] dbplyr_2.1.1      withr_2.4.2       later_1.1.0.1     MASS_7.3-53      
[37] jsonlite_1.7.2    gtable_0.3.0      lifecycle_1.0.0   DBI_1.1.0        
[41] git2r_0.27.1      magrittr_2.0.1    cli_2.5.0         stringi_1.5.3    
[45] farver_2.0.3      fs_1.5.0          promises_1.1.1    xml2_1.3.2       
[49] bslib_0.2.5.1     ellipsis_0.3.1    generics_0.1.0    vctrs_0.3.8      
[53] tools_4.0.5       glue_1.4.2        hms_1.0.0         yaml_2.2.1       
[57] colorspace_2.0-0  rvest_1.0.0       knitr_1.30        haven_2.3.1      
[61] sass_0.4.0

Análisis de Componentes Principales (PCA)

Miguel Tripp

1 Generalidades

2 Metabolitos de abulon

2.1 Normalización de los datos

2.2 PCA con prcomp()

2.3 Visualización del PCA

2.2 PCA con `prcomp()`