Pseudocounts
Jason Willwerscheid
8/26/2019
Last updated: 2019-09-21
Checks: 6 0
Knit directory: scFLASH/
This reproducible R Markdown analysis was created with workflowr (version 1.2.0). The Report tab describes the reproducibility checks that were applied when the results were created. The Past versions tab lists the development history.
Great! Since the R Markdown file has been committed to the Git repository, you know the exact version of the code that produced these results.
Great job! The global environment was empty. Objects defined in the global environment can affect the analysis in your R Markdown file in unknown ways. For reproduciblity it’s best to always run the code in an empty environment.
The command set.seed(20181103) was run prior to running the code in the R Markdown file. Setting a seed ensures that any results that rely on randomness, e.g. subsampling or permutations, are reproducible.
Great job! Recording the operating system, R version, and package versions is critical for reproducibility.
Nice! There were no cached chunks for this analysis, so you can be confident that you successfully produced the results during this run.
Great! You are using Git for version control. Tracking code development and connecting the code version to the results is critical for reproducibility. The version displayed above was the version of the Git repository at the time these results were generated.
Note that you need to be careful to ensure that all relevant files for the analysis have been committed to Git prior to generating the results (you can use wflow_publish or wflow_git_commit). workflowr only checks the R Markdown file, but you know if there are other scripts or data files that it depends on. Below is the status of the Git repository when the results were generated:
Ignored files:
Ignored: .DS_Store
Ignored: .Rhistory
Ignored: .Rproj.user/
Ignored: code/initialization/
Ignored: data/Ensembl2Reactome.txt
Ignored: data/droplet.rds
Ignored: data/mus_pathways.rds
Ignored: output/backfit/
Ignored: output/lowrank/
Ignored: output/prior_type/
Ignored: output/pseudocount/
Ignored: output/pseudocount_redux/
Ignored: output/size_factors/
Ignored: output/var_type/
Untracked files:
Untracked: analysis/NBapprox.Rmd
Untracked: analysis/deleted.Rmd
Untracked: analysis/trachea4.Rmd
Untracked: code/missing_data.R
Untracked: code/trachea4.R
Unstaged changes:
Modified: analysis/index.Rmd
Note that any generated files, e.g. HTML, png, CSS, etc., are not included in this status report because it is ok for generated content to have uncommitted changes.
These are the previous versions of the R Markdown and HTML files. If you’ve configured a remote Git repository (see ?wflow_git_remote), click on the hyperlinks in the table below to view them.
| File | Version | Author | Date | Message |
|---|---|---|---|---|
| Rmd | 5f88c0d | Jason Willwerscheid | 2019-09-21 | wflow_publish(“analysis/pseudocount_redux.Rmd”) |
| html | de985b0 | Jason Willwerscheid | 2019-09-05 | Build site. |
| html | 9f3dff5 | Jason Willwerscheid | 2019-09-03 | Build site. |
| Rmd | f120ec4 | Jason Willwerscheid | 2019-09-03 | wflow_publish(“analysis/pseudocount_redux.Rmd”) |
Introduction
In the previous analysis, I argued that it’s best to use a more sophisticated approach to calculating size factors (such as scran). It remains to choose a pseudocount. That is, letting \(X\) be the matrix of scaled counts, I consider the family of transformations \[ Y_{ij} = \log \left( X_{ij} + \alpha \right), \] which is, up to a constant, equivalent to the family of sparsity-preserving transformations \[ Y_{ij} = \log \left( \frac{X_{ij}}{\alpha} + 1 \right). \]
Typical choices of \(\alpha\) include 0.5 and 1. Aaron Lun has argued that a somewhat larger pseudocount should be used. Specifically, he proposes setting \[ \alpha = \min \left\{1, 1/s_\min - 1 / s_\max \right\}, \] where \(s_\min\) and \(s_\max\) are the smallest and largest size factors. Using the scran size factors from the previous analysis, this would yield \(\alpha = 3.14\) .
Here I consider a broader range of \(\alpha\), including pseudocounts that are much smaller (\(\alpha = 1/100\)) and larger (\(\alpha = 100\)) than are probably reasonable. Each fit was produced by adding 20 “greedy” factors to the Montoro et al. droplet dataset and backfitting. The code can be viewed here.
source("./code/utils.R")
droplet <- readRDS("./data/droplet.rds")
droplet <- preprocess.droplet(droplet)
res <- readRDS("./output/pseudocount/pseudocount_fits.rds")Previous results
In a previous exploration of pseudocounts, I made the following observations:
- The ELBO is monotonically decreasing as a function of the pseudocount.
- Comparing fits by randomly deleting data, imputing the missing values, and then calculating the Spearman rank correlation between the imputed and true values suggests that an \(\alpha\) between 0.35 and 1 is best.
- Smaller pseudocounts will more strongly shrink small counts, while larger pseudocounts more strongly shrink large counts. The transition between “small” and “large” counts is around 10.
- Smaller pseudocounts favor larger loadings for sparser genes, while larger pseudocounts favor more highly expressed genes.
- One can make a theoretical argument for \(\alpha = 0.5\), but the argument is admittedly pretty flimsy on its own.
Intuition
It’s useful to think about how the EBMF fit will change as \(\alpha\) becomes very small or very large.
As \(\alpha \to 0\), the differences between zero and nonzero counts are accentuated, while the respective differences among nonzero counts diminish in importance. In the limit, the transformed matrix becomes binary. Thus, a smaller \(\alpha\) prioritizes fitting zero counts over carefully distinguishing among nonzero counts.
At the other end of the scale, as \(\alpha\) increases, a larger range of counts is pushed towards zero, which amplifies the difference between large counts and small to moderate counts. As a result, a larger \(\alpha\) prioritizes fitting large counts over getting zero counts exactly right.
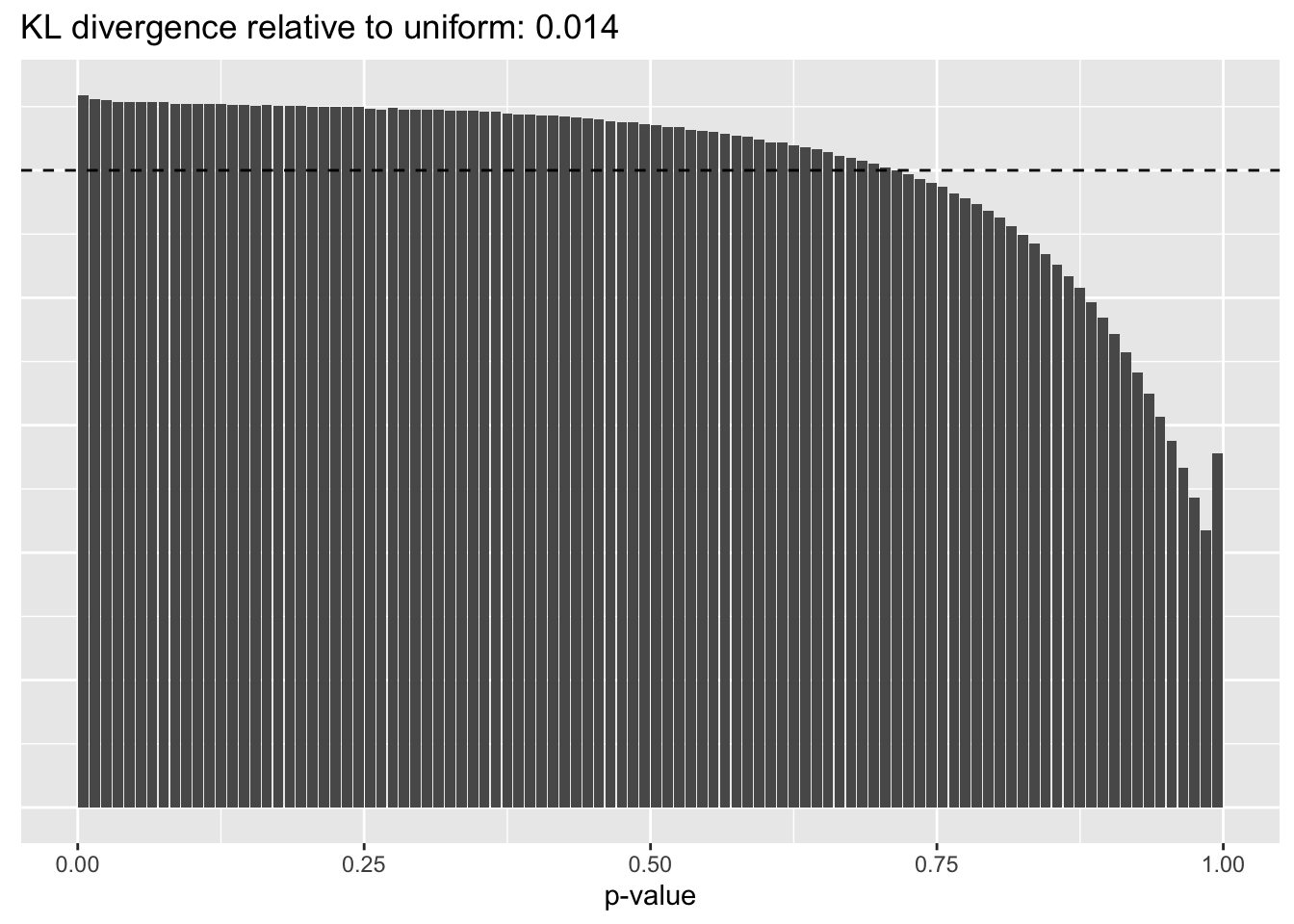
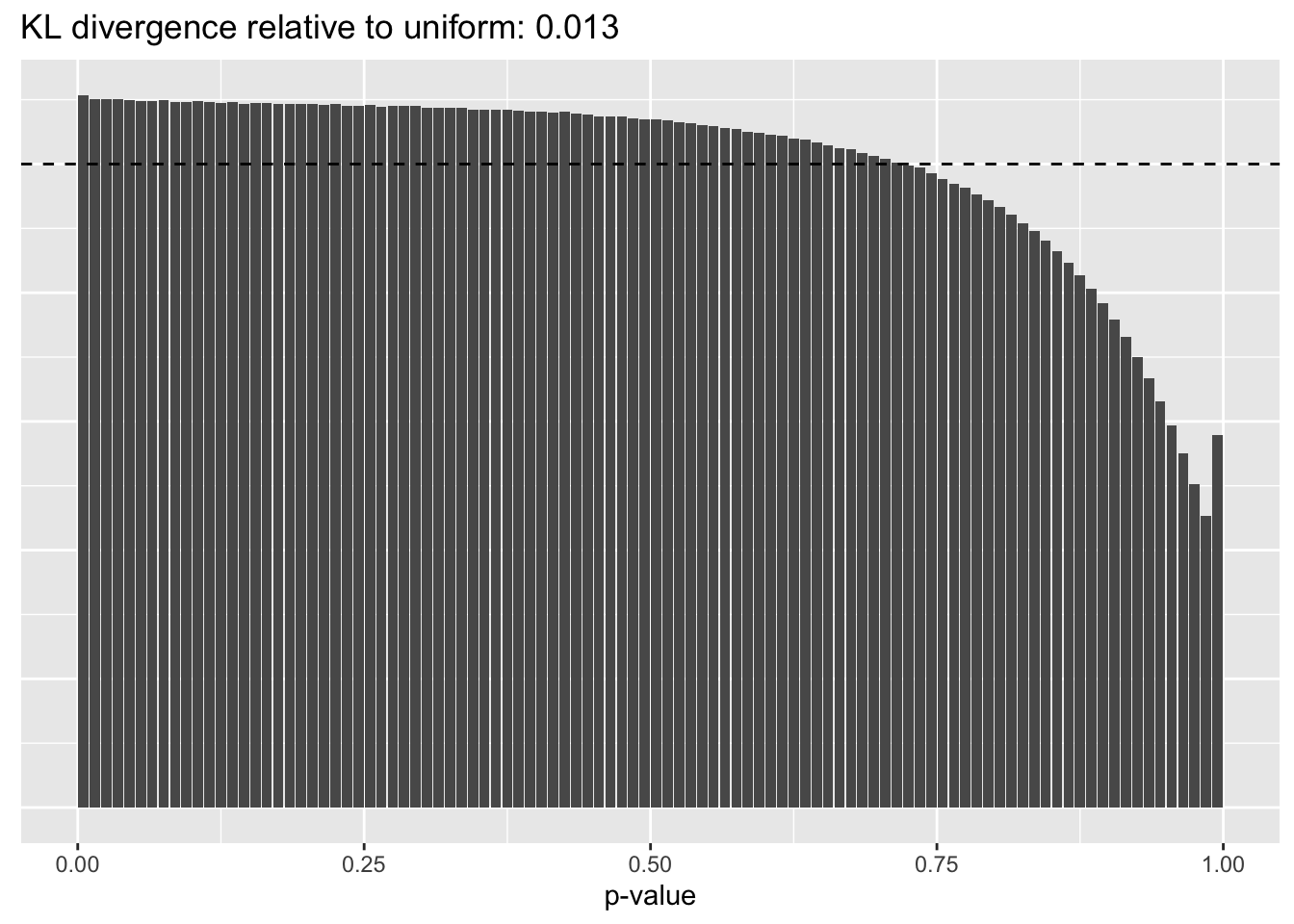
Results: p-values
This intuition is confirmed by the \(p\)-value plots. \(p\)-values near one correspond to fitted values that are much smaller than the true counts, so an overabundance of \(p\)-values near one means that the fitted model is not doing a very good job of fitting large counts. Vice versa, an overabundance of \(p\)-values near zero means that the fitted model is failing to fit zero counts very well. Although I’ve provided the KL divergence between the observed and expected \(p\)-value distributions, it’s not a great metric. In particular, it doesn’t penalize severe under-predictions (\(p \approx 1\)) as much as I’d like.
for (pc in names(res)) {
cat("\n### Pseudocount = ", pc, "\n")
plot(plot.p.vals(res[[pc]][["p.vals"]]))
cat("\n")
}Pseudocount = 0.01
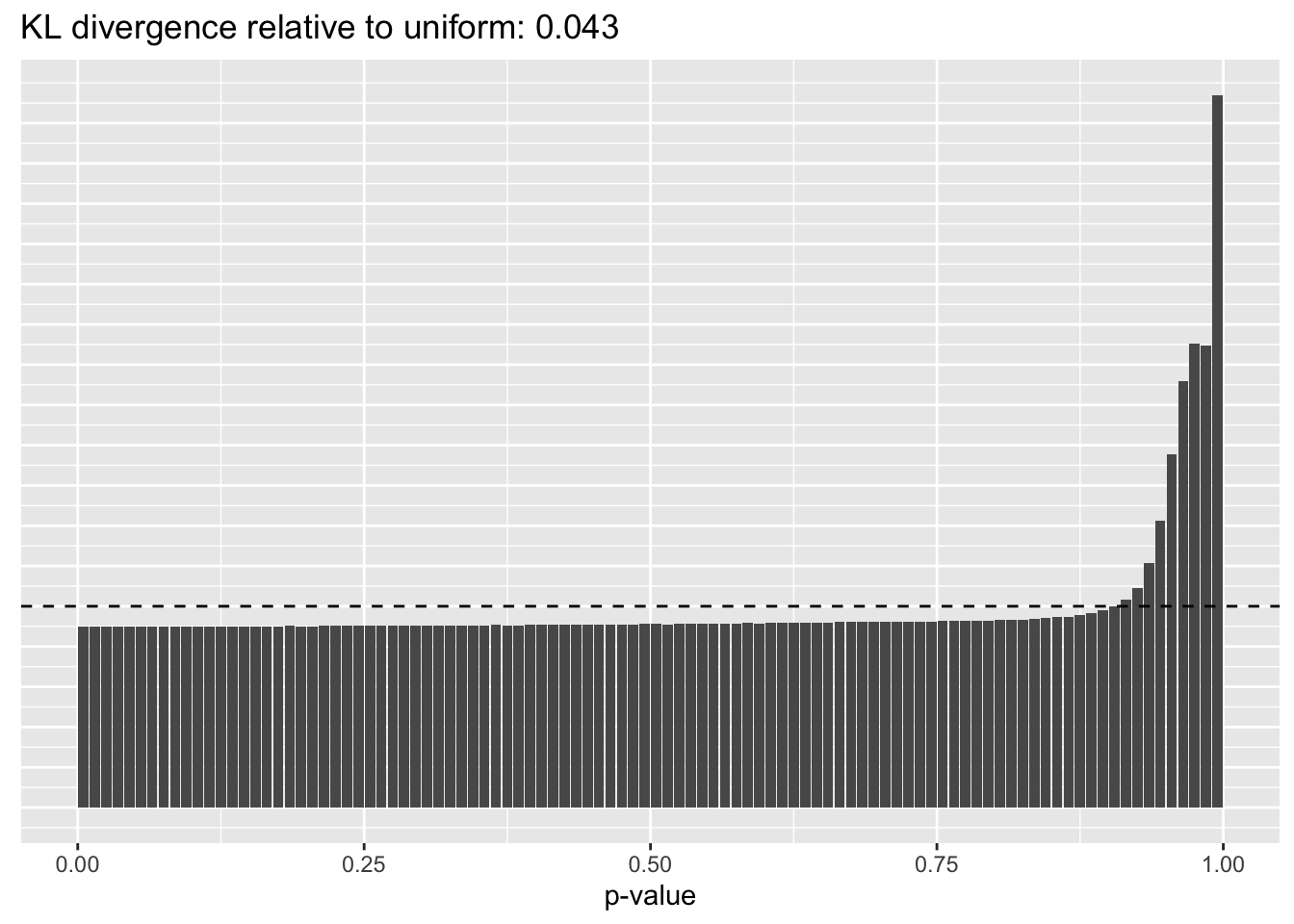
Pseudocount = 0.0625
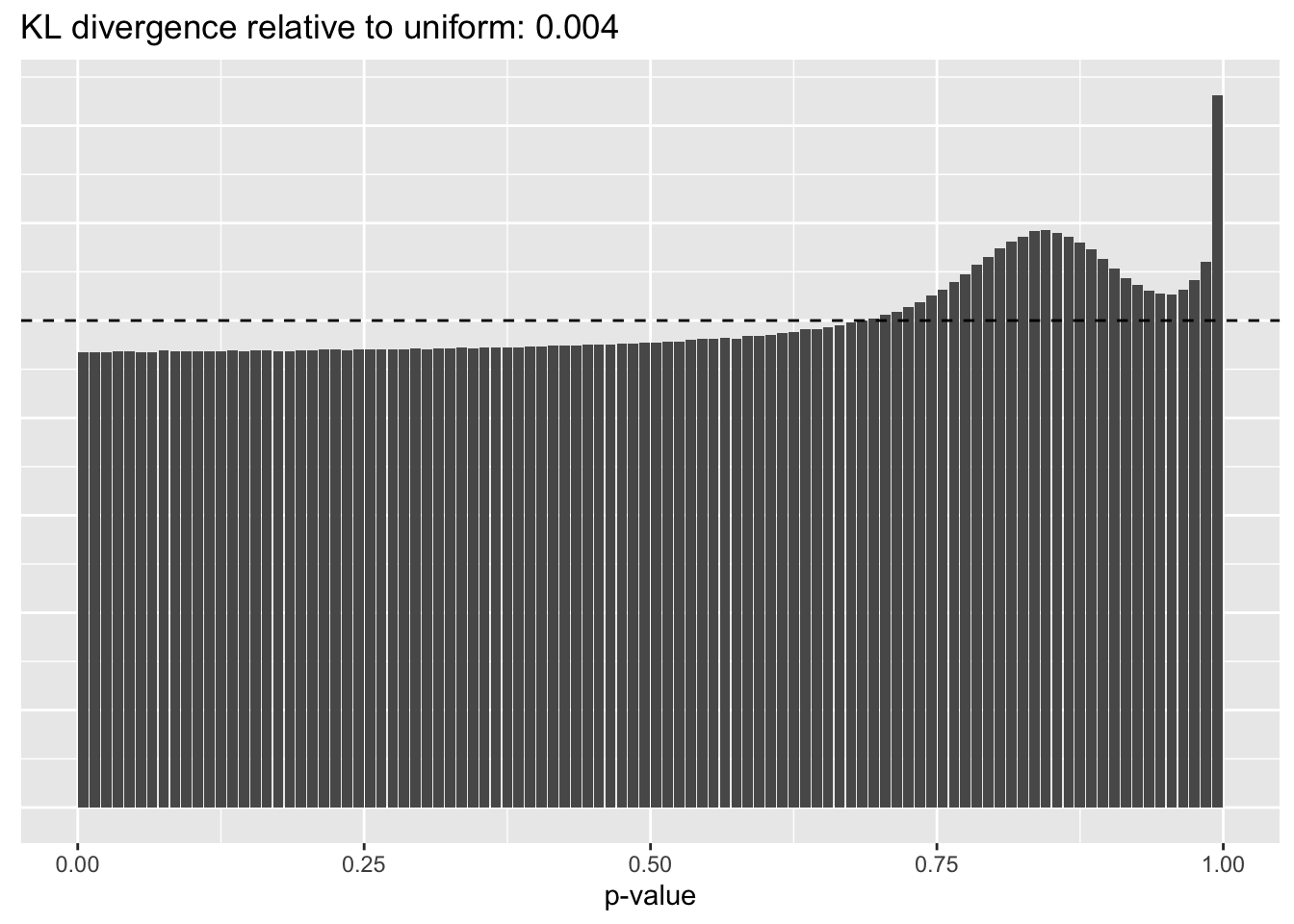
Pseudocount = 0.25
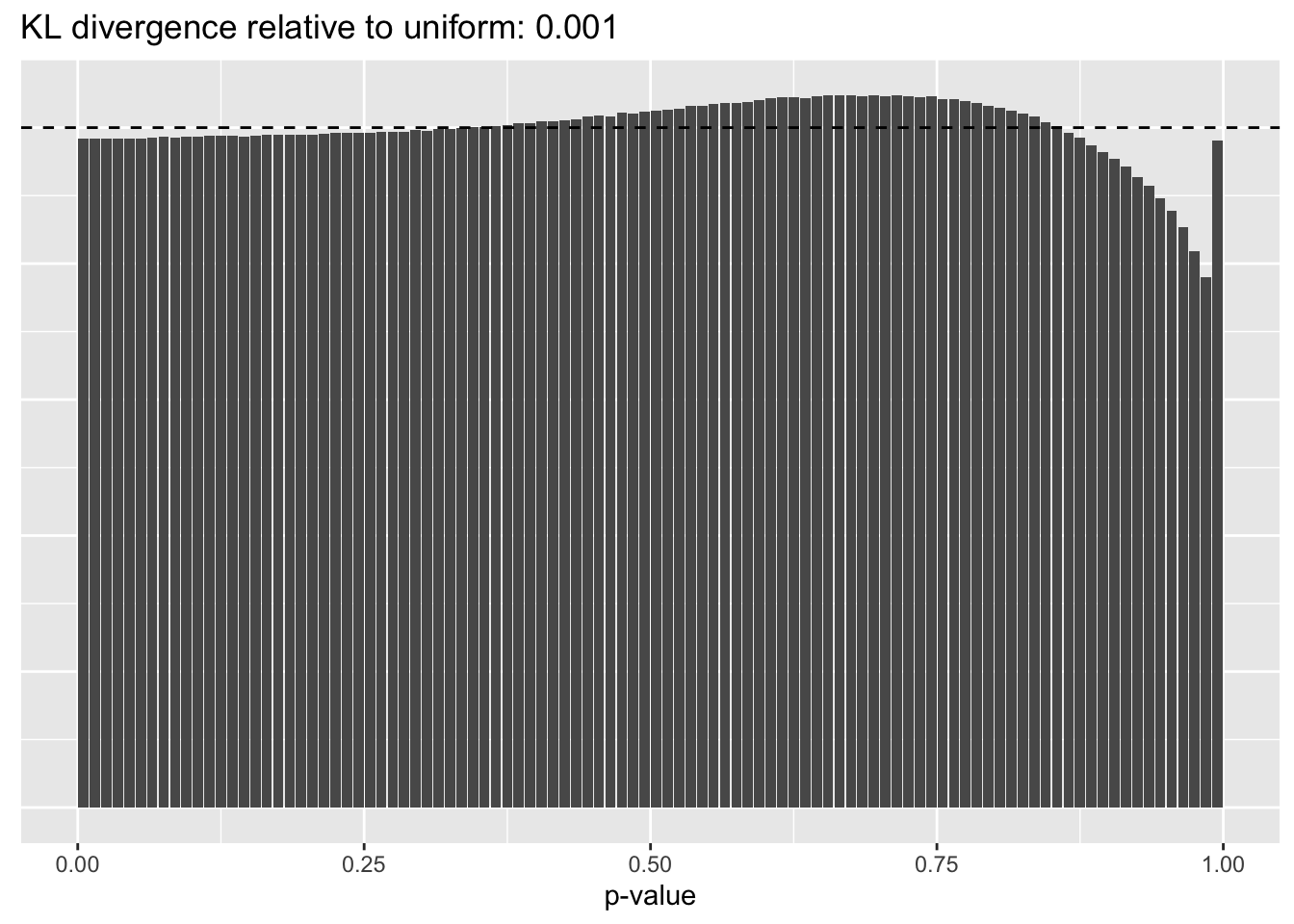
Pseudocount = 0.5
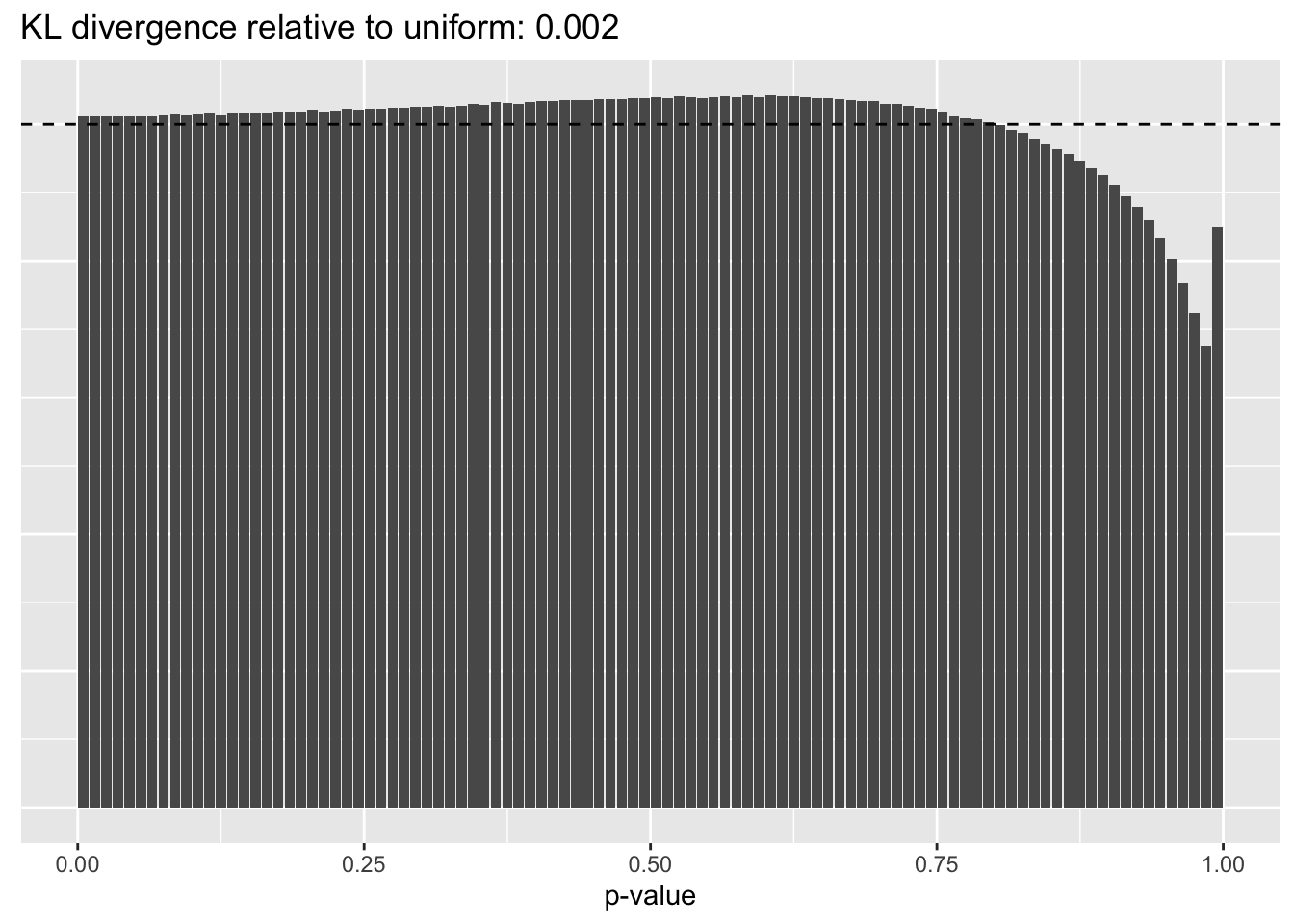
Pseudocount = 1
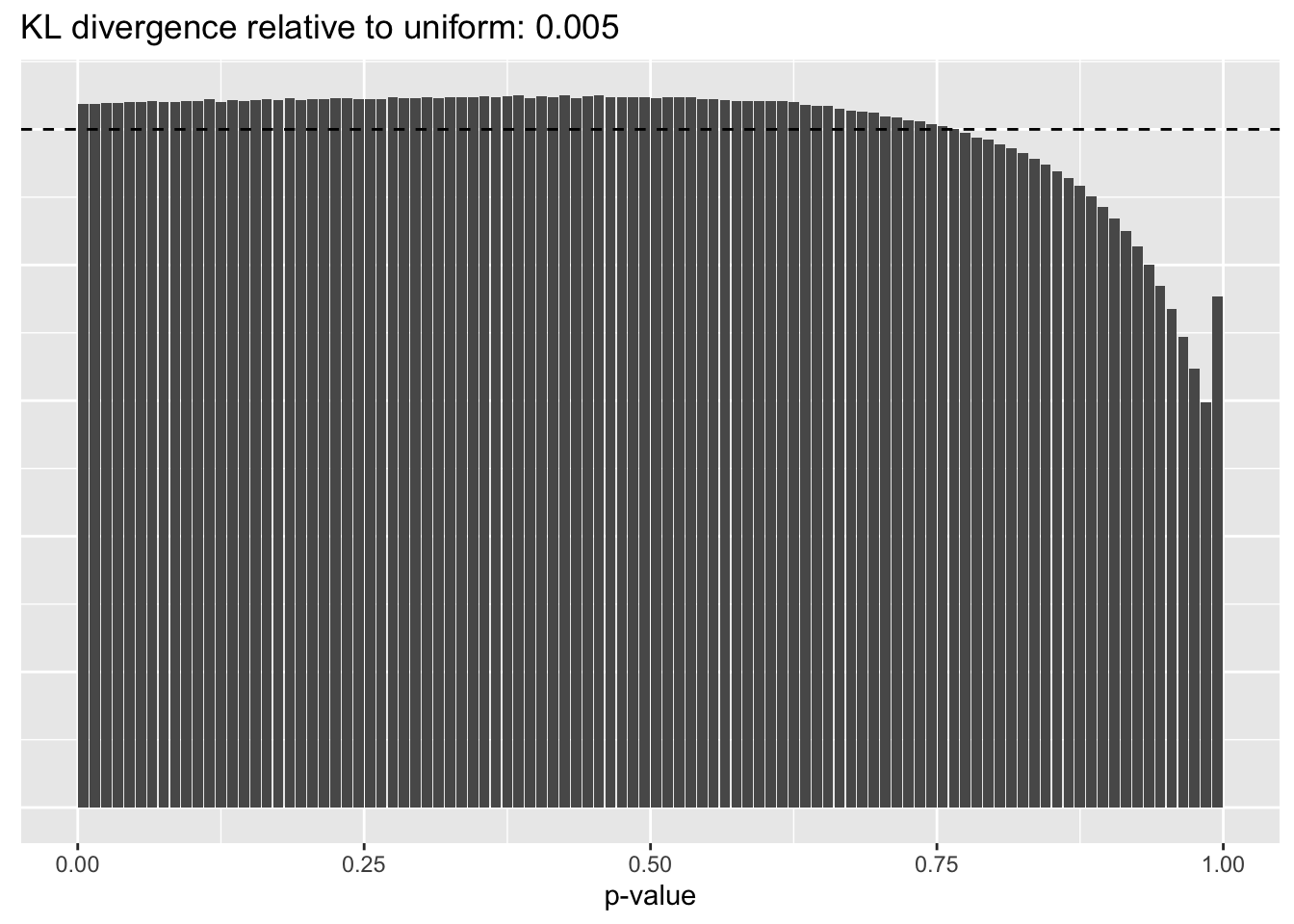
Pseudocount = 2
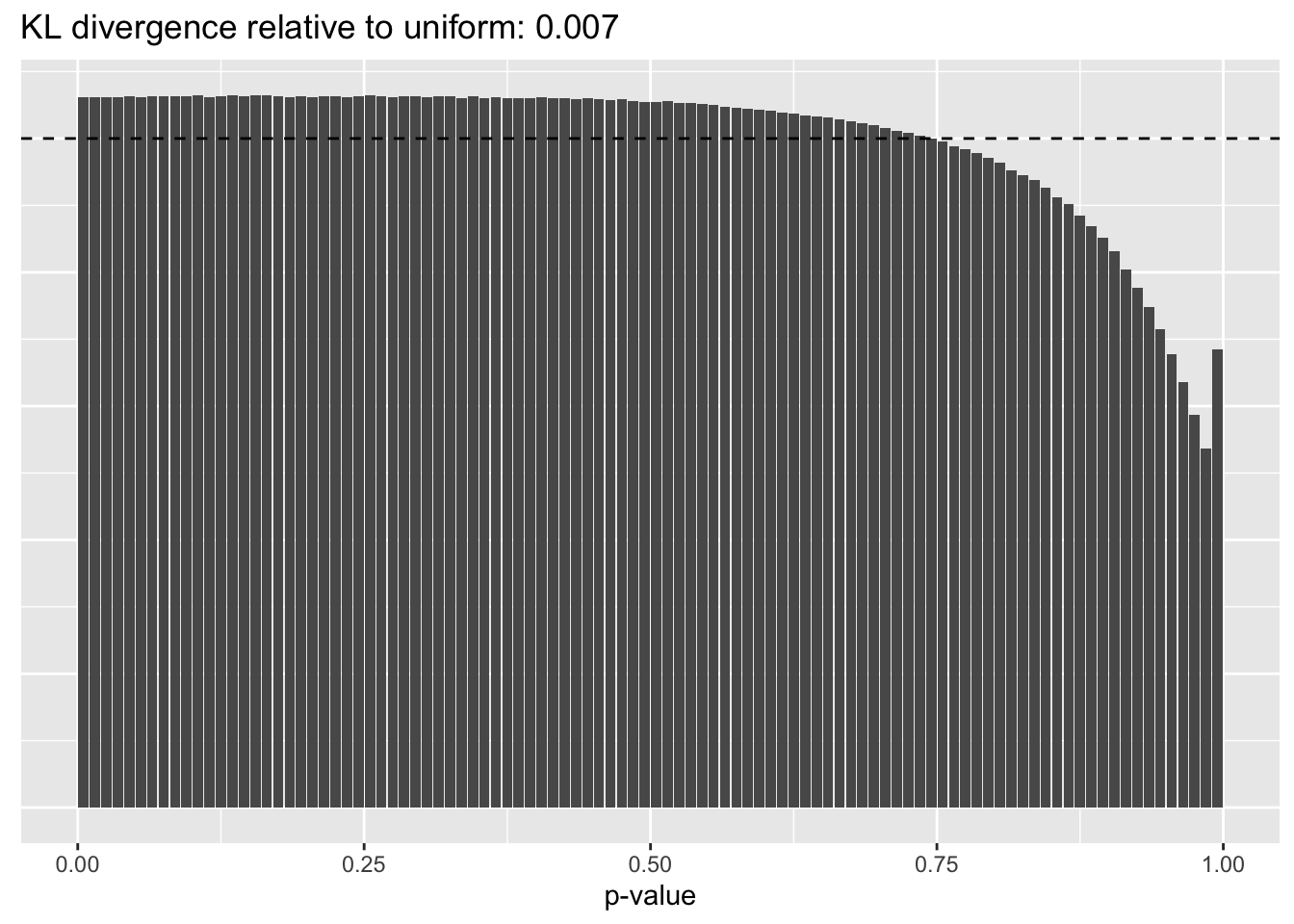
Pseudocount = 4
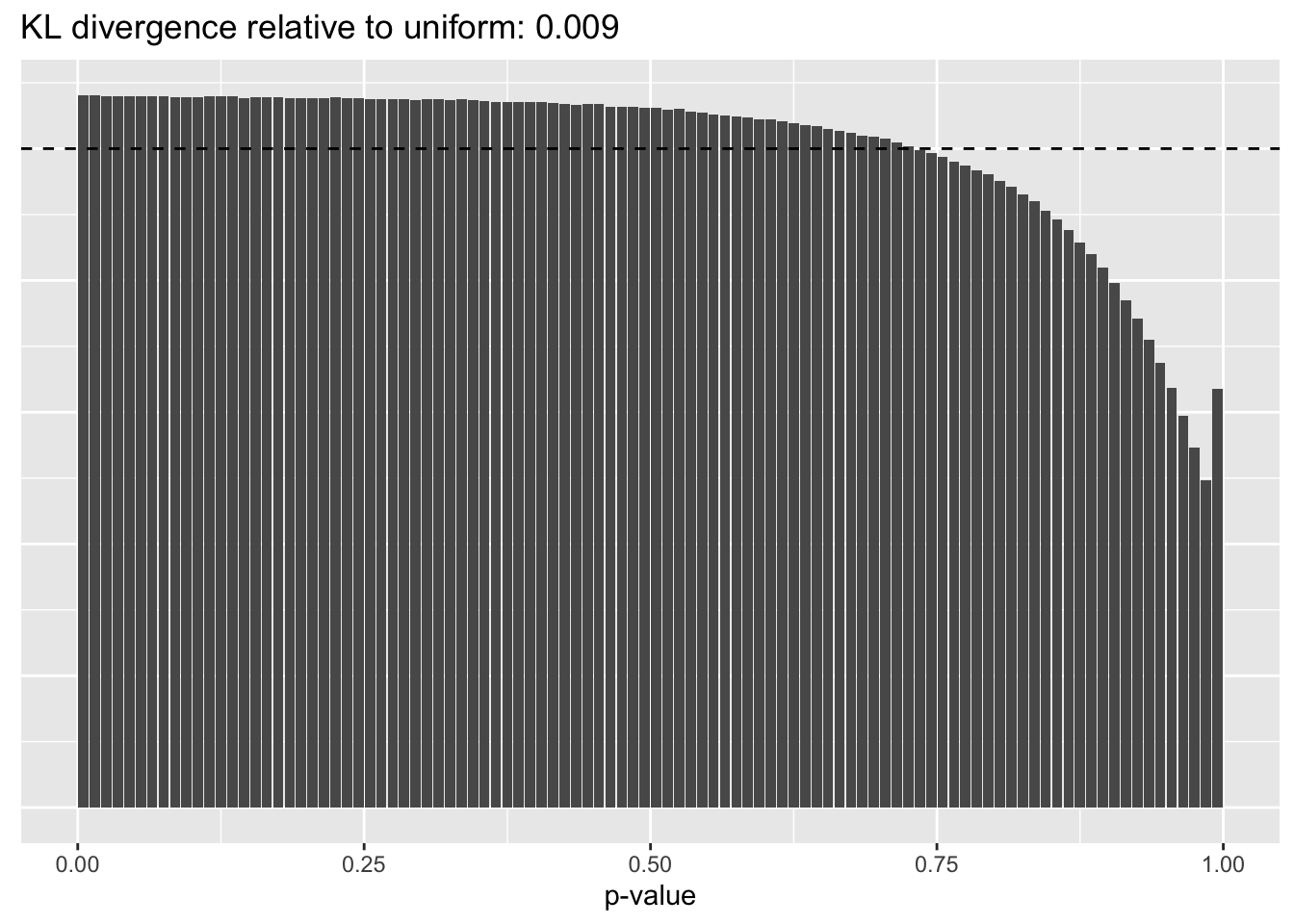
Pseudocount = 16
Results: ELBO
The ELBO is a terrible metric here. Indeed, as I’ve already observed, the ELBO is monotonically decreasing as a function of the pseudocount.
To see why this is the case, imagine fitting a simple rank-one model with a constant variance structure. The data log likelihood (that is, the part of the ELBO that ignores priors) is \[ -\frac{np}{2} \log(2 \pi \sigma^2) - \frac{1}{2 \sigma^2} \sum_{i, j} \mathbb{E} (Y_{ij} - \hat{Y}_{ij})^2. \] Recall that \(\sigma^2\) is estimated (via ML) as the mean expected squared residual, so that the data log likelihood can be written \[ -\frac{np}{2} \log(2 \pi \sigma^2) - \frac{np}{2} = -np \log \sigma + C.\] Meanwhile, the change-of-variables adjustment to the ELBO is \[ np \log (1 / \alpha) - \sum_{i, j} Y_{ij}. \]
Now take \(\alpha \to 0\). Zero entries in \(X\) are always zero in the transformed matrix \(Y\), and nonzero entries are approximately \(\log X_{ij} - \log \alpha \approx -\log \alpha\), so \[ \sum_{i, j} Y_{ij} \approx snp \log (1 / \alpha), \] where \(s\) is the sparsity of \(X\) (that is, the proportion of entries that are nonzero). Next, since the rank-one fit will yield a \(\sigma^2\) that is approximately equal to \(\text{Var}(Y)\), which (in the limit) is \((\log (1 / \alpha))^2 s(1 - s)\), the data log likelihood is approximately \[ -np \log (\sqrt{s} \log (1 / \alpha)) + C = -np \log \log (1 / \alpha) + C. \]
Thus, for \(\alpha\) near zero, the adjusted log likelihood is approximately \[ (1 + s)np \log (1 / \alpha) - np \log \log (1 / \alpha) + C, \] which blows up as \(\alpha \to 0\).
elbo.df <- data.frame(pseudocount = as.numeric(names(res)),
elbo = sapply(res, function(x) x$fl$elbo + x$elbo.adj))
ggplot(elbo.df, aes(x = pseudocount, y = elbo)) +
geom_point() +
scale_x_continuous(trans = "log2") +
labs(y = "ELBO")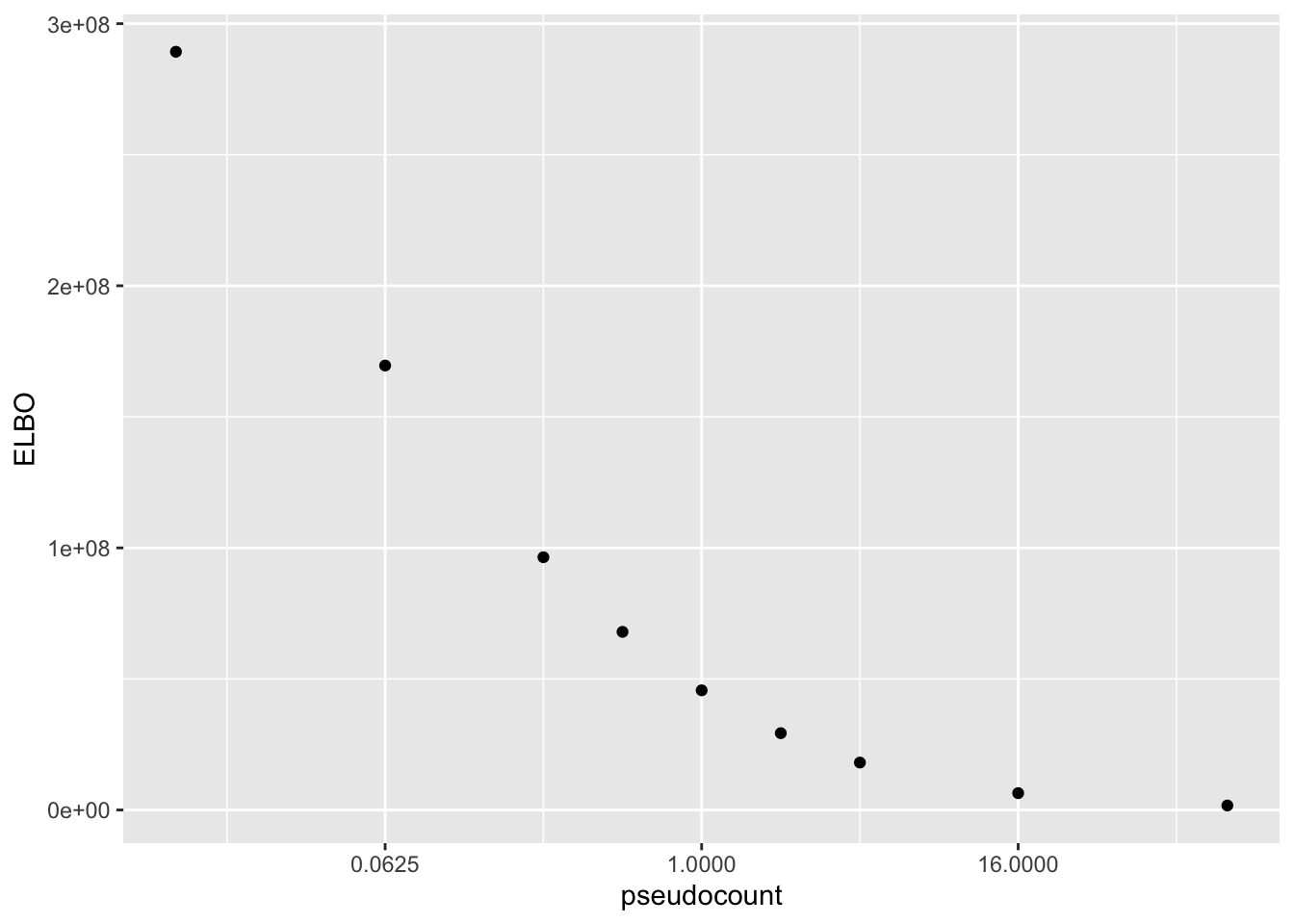
Results: Log likelihood of implied distribution
The log likehood of the implied discrete distribution is a much better metric than the ELBO or the KL-divergence of \(p\)-value distributions. Using this metric, \(\alpha = 0.5\) does best.
llik.df <- data.frame(pseudocount = as.numeric(names(res)),
llik = sapply(res, function(x) x$p.vals$llik))
ggplot(llik.df, aes(x = pseudocount, y = llik)) +
geom_point() +
scale_x_continuous(trans = "log2") +
labs(y = "log likelihood (implied model)")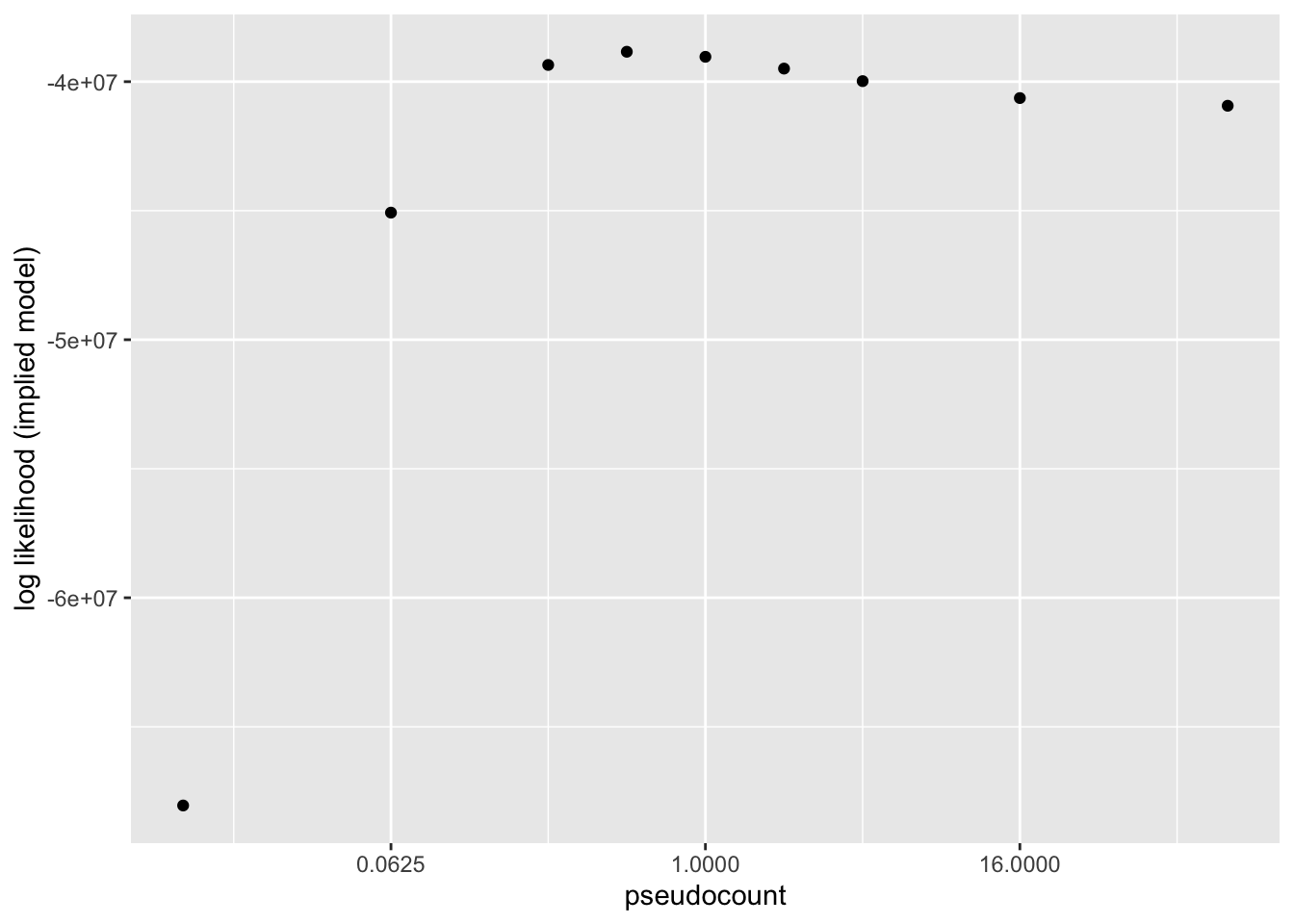
sessionInfo()R version 3.5.3 (2019-03-11)
Platform: x86_64-apple-darwin15.6.0 (64-bit)
Running under: macOS Mojave 10.14.6
Matrix products: default
BLAS: /Library/Frameworks/R.framework/Versions/3.5/Resources/lib/libRblas.0.dylib
LAPACK: /Library/Frameworks/R.framework/Versions/3.5/Resources/lib/libRlapack.dylib
locale:
[1] en_US.UTF-8/en_US.UTF-8/en_US.UTF-8/C/en_US.UTF-8/en_US.UTF-8
attached base packages:
[1] stats graphics grDevices utils datasets methods base
other attached packages:
[1] flashier_0.1.17 ggplot2_3.2.0 Matrix_1.2-15
loaded via a namespace (and not attached):
[1] Rcpp_1.0.1 compiler_3.5.3 pillar_1.3.1
[4] git2r_0.25.2 workflowr_1.2.0 iterators_1.0.10
[7] tools_3.5.3 digest_0.6.18 evaluate_0.13
[10] tibble_2.1.1 gtable_0.3.0 lattice_0.20-38
[13] pkgconfig_2.0.2 rlang_0.3.1 foreach_1.4.4
[16] parallel_3.5.3 yaml_2.2.0 ebnm_0.1-24
[19] xfun_0.6 withr_2.1.2 stringr_1.4.0
[22] dplyr_0.8.0.1 knitr_1.22 fs_1.2.7
[25] rprojroot_1.3-2 grid_3.5.3 tidyselect_0.2.5
[28] glue_1.3.1 R6_2.4.0 rmarkdown_1.12
[31] mixsqp_0.1-119 ashr_2.2-38 purrr_0.3.2
[34] magrittr_1.5 whisker_0.3-2 MASS_7.3-51.1
[37] codetools_0.2-16 backports_1.1.3 scales_1.0.0
[40] htmltools_0.3.6 assertthat_0.2.1 colorspace_1.4-1
[43] labeling_0.3 stringi_1.4.3 pscl_1.5.2
[46] doParallel_1.0.14 lazyeval_0.2.2 munsell_0.5.0
[49] truncnorm_1.0-8 SQUAREM_2017.10-1 crayon_1.3.4