Introduction to R
Anthony Hung
2019-04-25
Last updated: 2019-05-30
Checks: 5 1
Knit directory: MSTPsummerstatistics/
This reproducible R Markdown analysis was created with workflowr (version 1.3.0). The Checks tab describes the reproducibility checks that were applied when the results were created. The Past versions tab lists the development history.
The R Markdown file has unstaged changes. To know which version of the R Markdown file created these results, you’ll want to first commit it to the Git repo. If you’re still working on the analysis, you can ignore this warning. When you’re finished, you can run wflow_publish to commit the R Markdown file and build the HTML.
Great job! The global environment was empty. Objects defined in the global environment can affect the analysis in your R Markdown file in unknown ways. For reproduciblity it’s best to always run the code in an empty environment.
The command set.seed(20180927) was run prior to running the code in the R Markdown file. Setting a seed ensures that any results that rely on randomness, e.g. subsampling or permutations, are reproducible.
Great job! Recording the operating system, R version, and package versions is critical for reproducibility.
Nice! There were no cached chunks for this analysis, so you can be confident that you successfully produced the results during this run.
Great! You are using Git for version control. Tracking code development and connecting the code version to the results is critical for reproducibility. The version displayed above was the version of the Git repository at the time these results were generated.
Note that you need to be careful to ensure that all relevant files for the analysis have been committed to Git prior to generating the results (you can use wflow_publish or wflow_git_commit). workflowr only checks the R Markdown file, but you know if there are other scripts or data files that it depends on. Below is the status of the Git repository when the results were generated:
Ignored files:
Ignored: .DS_Store
Ignored: .Rhistory
Ignored: .Rproj.user/
Ignored: analysis/.RData
Ignored: analysis/.Rhistory
Unstaged changes:
Modified: analysis/Bayes.Rmd
Modified: analysis/introR.Rmd
Modified: analysis/markov.Rmd
Note that any generated files, e.g. HTML, png, CSS, etc., are not included in this status report because it is ok for generated content to have uncommitted changes.
These are the previous versions of the R Markdown and HTML files. If you’ve configured a remote Git repository (see ?wflow_git_remote), click on the hyperlinks in the table below to view them.
| File | Version | Author | Date | Message |
|---|---|---|---|---|
| html | 6d3e1c8 | Anthony Hung | 2019-05-28 | Build site. |
| html | c117ef1 | Anthony Hung | 2019-05-27 | Build site. |
| html | b291d24 | Anthony Hung | 2019-05-24 | Build site. |
| html | 4e210d6 | Anthony Hung | 2019-05-24 | Build site. |
| html | c4bdfdc | Anthony Hung | 2019-05-22 | Build site. |
| Rmd | dd1e411 | Anthony Hung | 2019-05-22 | before republishing syllabus |
| html | dd1e411 | Anthony Hung | 2019-05-22 | before republishing syllabus |
| Rmd | 4ce8e85 | Anthony Hung | 2019-05-21 | bandersnatch add |
| html | 4ce8e85 | Anthony Hung | 2019-05-21 | bandersnatch add |
| html | 096760a | Anthony Hung | 2019-05-18 | Build site. |
| html | da98ae8 | Anthony Hung | 2019-05-17 | Build site. |
| html | bb90220 | Anthony Hung | 2019-05-17 | commit before publishing |
| Rmd | 239723e | Anthony Hung | 2019-05-08 | Update learning objectives |
| html | 239723e | Anthony Hung | 2019-05-08 | Update learning objectives |
| html | 2ec7944 | Anthony Hung | 2019-05-06 | Build site. |
| html | 536085f | Anthony Hung | 2019-05-06 | Build site. |
| html | ee75486 | Anthony Hung | 2019-05-04 | Build site. |
| html | 5ea5f30 | Anthony Hung | 2019-04-29 | Build site. |
| html | e0e8156 | Anthony Hung | 2019-04-29 | Build site. |
| html | e746cf5 | Anthony Hung | 2019-04-28 | Build site. |
| Rmd | 133df4a | Anthony Hung | 2019-04-28 | introR |
| html | 133df4a | Anthony Hung | 2019-04-28 | introR |
| html | 22b3720 | Anthony Hung | 2019-04-26 | Build site. |
| html | ddb3114 | Anthony Hung | 2019-04-26 | Build site. |
| html | 413d065 | Anthony Hung | 2019-04-26 | Build site. |
| html | 6b98d6c | Anthony Hung | 2019-04-26 | Build site. |
| Rmd | 9f13e70 | Anthony Hung | 2019-04-25 | finish CLT |
| html | 9f13e70 | Anthony Hung | 2019-04-25 | finish CLT |
Introduction
Here, we introduce R, a statistical programming language. Doing statistics within a programming language brings many advantages, including allowing one to organize all analyses into program files that can be rerun to replicate analyses. In addition to using R, we will be using RStudio, an integrated development environment (IDE), which assists us in working with R and outputs of our code as we develop it. Our objective today is to get everyone up to speed with working knowledge of R and programming to be able to do exercises as a part of the rest of the course.
Both R and RStudio are freely available online.
Downloading/Installing R and RStudio
Download the appropriate “base” version of R for your operating system from CRAN: https://cran.r-project.org/
Install the software with default settings.
Download the appropriate RStudio version for your operating system: https://www.rstudio.com/products/rstudio/download/#download
R Basics
Follow along in your R console with the code in each of the code chunks as we explore the different aspects of R! Clicking on the github logo on the top right corner of the webpage will take you to the repository for this website, where you can download the R markdown file for this page to load into RStudio to follow along.
Mathematical operations in R
Many familiar operators work in R, allowing you to work with numbers like you would in a calculator. Operators such as inequalities also work, returning “TRUE” if the proposed logical expression is true and “FALSE” otherwise.
2+4 #addition[1] 62-4 #subtraction[1] -22*4 #multiplication[1] 82/4 #division[1] 0.52^4 #exponentiation[1] 16log(2) #the default log base is the natural log[1] 0.69314722 < 4[1] TRUE2 > 4[1] FALSE2 >= 4 #greater than or equal to [1] FALSE2 == 2 #is equal to (notice that there are two equal signs, as a single equal sign denotes assignment)[1] TRUE2 != 4 #is not equal to [1] TRUE2 != 4 | 2 + 2 == 4 #OR[1] TRUE2 != 4 & 2 + 2 == 4 #AND[1] TRUE"Red" == "Red"[1] TRUEObjects
In addition to being able to work with actual numbers, R works in objects, which can represent anything from numbers to strings to vectors to matrices. Everything in R is an object. The best practice for assigning variable names to objects is the “<-” operator. After objects are created, they are stored in in the “Environment” tab in your RStudio console and can be called upon to perform different operations.
R has many data structures, including:
- atomic vector
- list
- matrix
- data frame
- factors
R has 6 atomic vector types, or classes. Atomic means that a vector only contains elements of one class (i.e. the elements inside the vector do not come from mutliple classes).
- character
- numeric (real or decimal)
- integer
- logical (TRUE or FALSE)
- complex (containing i)
a <- 2
b <- 3
a + b[1] 5class(a) #the "class" function tells you what class of object a is[1] "numeric"d <- c(1,2,3,4,5) #the "c" function concatenates the arguments contained within it into a vector
d[1] 1 2 3 4 5d <- c(d, 1) #The "c" function also allows you to append items to an existing vector
d[1] 1 2 3 4 5 1class(d)[1] "numeric"d[3] #brackets allow you index vectors or matrices. Here, we call the third value from our d vector.[1] 3#Matrices are just like vectors, but with two dimensions
my_matrix <- matrix(seq(1:9), ncol = 3)
my_matrix [,1] [,2] [,3]
[1,] 1 4 7
[2,] 2 5 8
[3,] 3 6 9#vectors and matrices can only contain objects of one class. If you include objects of multiple types into the same vector, R will perform coersion to force all the objects contained in the vector into a shared class
x <- c(1.7, "a")
x[1] "1.7" "a" class("a")[1] "character"class(1.7)[1] "numeric"class(x)[1] "character"y <- c(TRUE, 2)
y[1] 1 2z <- c("a", TRUE)
z[1] "a" "TRUE"#If you would like to store objects of multiple classes into one object, a list can accomodate such a task.
x_y_z_list <- list(x,y,z)
x_y_z_list[[1]]
[1] "1.7" "a"
[[2]]
[1] 1 2
[[3]]
[1] "a" "TRUE"#to index an element in a list, use double brackets [[]]. You can further index elements within an element of a list.
x_y_z_list[[1]][1] "1.7" "a" x_y_z_list[[1]][2][1] "a"#elements in a list can be assigned names
x_y_z_list <- list(a=x, b=y, c=z)
x_y_z_list$a
[1] "1.7" "a"
$b
[1] 1 2
$c
[1] "a" "TRUE"#Dataframes are a very commonly used type of object in R. You can think of a dataframe as a rectangular combination of lists.
#The below code stores the stated values in a dataframe which contains employee ids, names, salaries, and start dates for 5 employees
emp.data <- data.frame(
emp_id = c (1:5),
emp_name = c("Rick","Dan","Michelle","Ryan","Gary"),
salary = c(623.3,515.2,611.0,729.0,843.25),
start_date = as.Date(c("2012-01-01", "2013-09-23", "2014-11-15", "2014-05-11",
"2015-03-27")),
stringsAsFactors = FALSE
)
emp.data emp_id emp_name salary start_date
1 1 Rick 623.30 2012-01-01
2 2 Dan 515.20 2013-09-23
3 3 Michelle 611.00 2014-11-15
4 4 Ryan 729.00 2014-05-11
5 5 Gary 843.25 2015-03-27emp.data$emp_id #the $ operator calls on a certain column of a dataframe[1] 1 2 3 4 5class(emp.data$emp_id) #As noted earlier, a dataframe can be thought of as a rectangular list, combining different data classes together, each in a different column.[1] "integer"class(emp.data$salary)[1] "numeric"emp.data$emp_name[emp.data$salary > 620] #You can combine logical operators, brackets, and the $ sign to subset your dataframe in any way you choose! Here, we print out all the employee names for employees who have a salary greater than 620.[1] "Rick" "Ryan" "Gary"ls() #ls lists all the variable names that have been assigned to objects in your workspace[1] "a" "b" "d" "emp.data" "my_matrix"
[6] "x" "x_y_z_list" "y" "z" Using Packages in R
In addition to the basic functions provided in R, oftentimes we will be working with packages that contain functions written by other people to perform common tasks or specific analyses. Packages can also contain datasets. We can load these packages into our R environment after installing them in R.
usePackage <- function(p)
{
if (!is.element(p, installed.packages()[,1]))
install.packages(p, dep = TRUE)
require(p, character.only = TRUE)
}
usePackage("gapminder")#This code installs the gapminder packages, which contains vital statistics data from multiple countries. install.packages() is the function that will install a package for you if you know it's name.Loading required package: gapminderlibrary("gapminder") #After installing the package, we need to tell R to load it into our current environment with this function.
head(gapminder) #The package gapminder contains a dataset called gapminder. We can use the "head" function to print out the first 6 rows of this dataset.# A tibble: 6 x 6
country continent year lifeExp pop gdpPercap
<fct> <fct> <int> <dbl> <int> <dbl>
1 Afghanistan Asia 1952 28.8 8425333 779.
2 Afghanistan Asia 1957 30.3 9240934 821.
3 Afghanistan Asia 1962 32.0 10267083 853.
4 Afghanistan Asia 1967 34.0 11537966 836.
5 Afghanistan Asia 1972 36.1 13079460 740.
6 Afghanistan Asia 1977 38.4 14880372 786.?gapminder #the ? operator lauches a help page to describe a particular function, including the arguments it takes. Whenever using a new function, it is good practice to first explore it through ?.Loops
Oftentimes, we may want to perform the same operation or function many many times. Rather than having to explicitly write out each individual operation, we can make use of loops. For example, let’s say that we want to raise the number 2 to the power of each integer from 0 to 20. We could either write out 2^0, 2^1, 2^2 …, or make use of a for loop to condense our code while getting the same result.
2^0[1] 12^1[1] 22^2[1] 42^3[1] 8# ...
#This is a for loop. in the parentheses after the for function, we specify over what range of values we want to loop over, and assign a dummy variable name to take on each of those values in sequence. Within the curly braces, we state what operation we want to perform over all the values taken on by the dummy variable.
for(i in 0:20){
print(2^i)
}[1] 1
[1] 2
[1] 4
[1] 8
[1] 16
[1] 32
[1] 64
[1] 128
[1] 256
[1] 512
[1] 1024
[1] 2048
[1] 4096
[1] 8192
[1] 16384
[1] 32768
[1] 65536
[1] 131072
[1] 262144
[1] 524288
[1] 1048576User-defined Functions (UDF)
Another way to avoid writing out or copy-pasting the same exact thing over and over again when working with data is to write a function to contain a certain combination of operations you find yourself running mutliple times. For example, you may find yourself needing to calculate the Hardy-Weinberg Equillibrium genotype frequencies of a population given the allele frequencies. We can wrap up all the code that you would need to calculate this in a function that we can call upon again and again.
calc_HWE_geno <- function(p = 0.5){
q <- 1-p
pp <- p^2
pq <- 2*p*q
qq <- q^2
return(c(pp, pq, qq))
}
calc_HWE_geno(p = 0.1)[1] 0.01 0.18 0.81#note that in our UDF we assigned a default value to p (p = 0.5). This means that if we do not specify a value for our argument of p, it will default to using that value.
calc_HWE_geno()[1] 0.25 0.50 0.25Plots
In addition to mathematical operations, R can help with data visualization. Base R has a few useful plotting functions, but popular packages such as ggplot2 give more customization and control to the user.
hist(gapminder$lifeExp)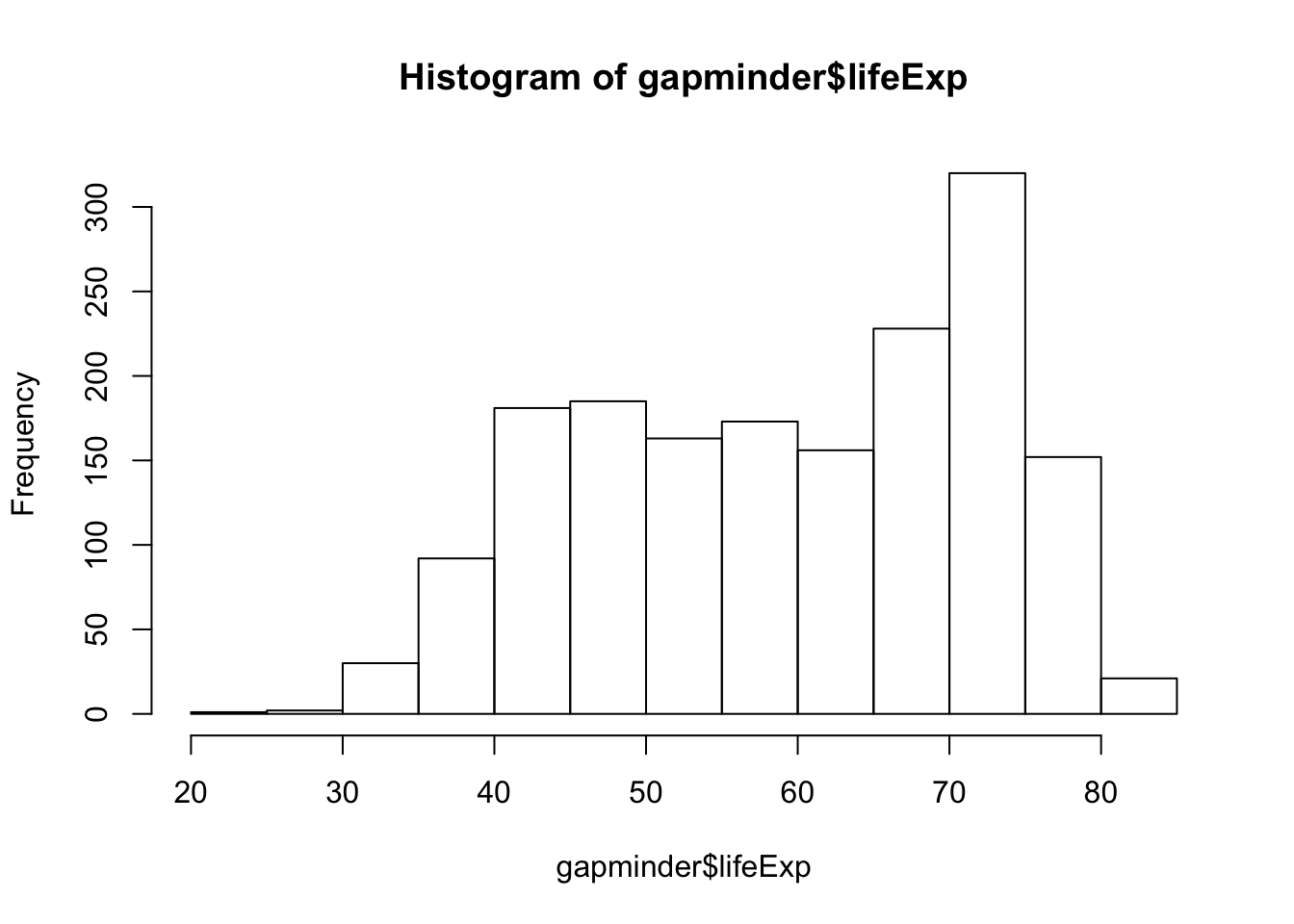
| Version | Author | Date |
|---|---|---|
| 133df4a | Anthony Hung | 2019-04-28 |
boxplot(lifeExp ~ continent, data = gapminder) #box plot for the life expectancies of all years per continent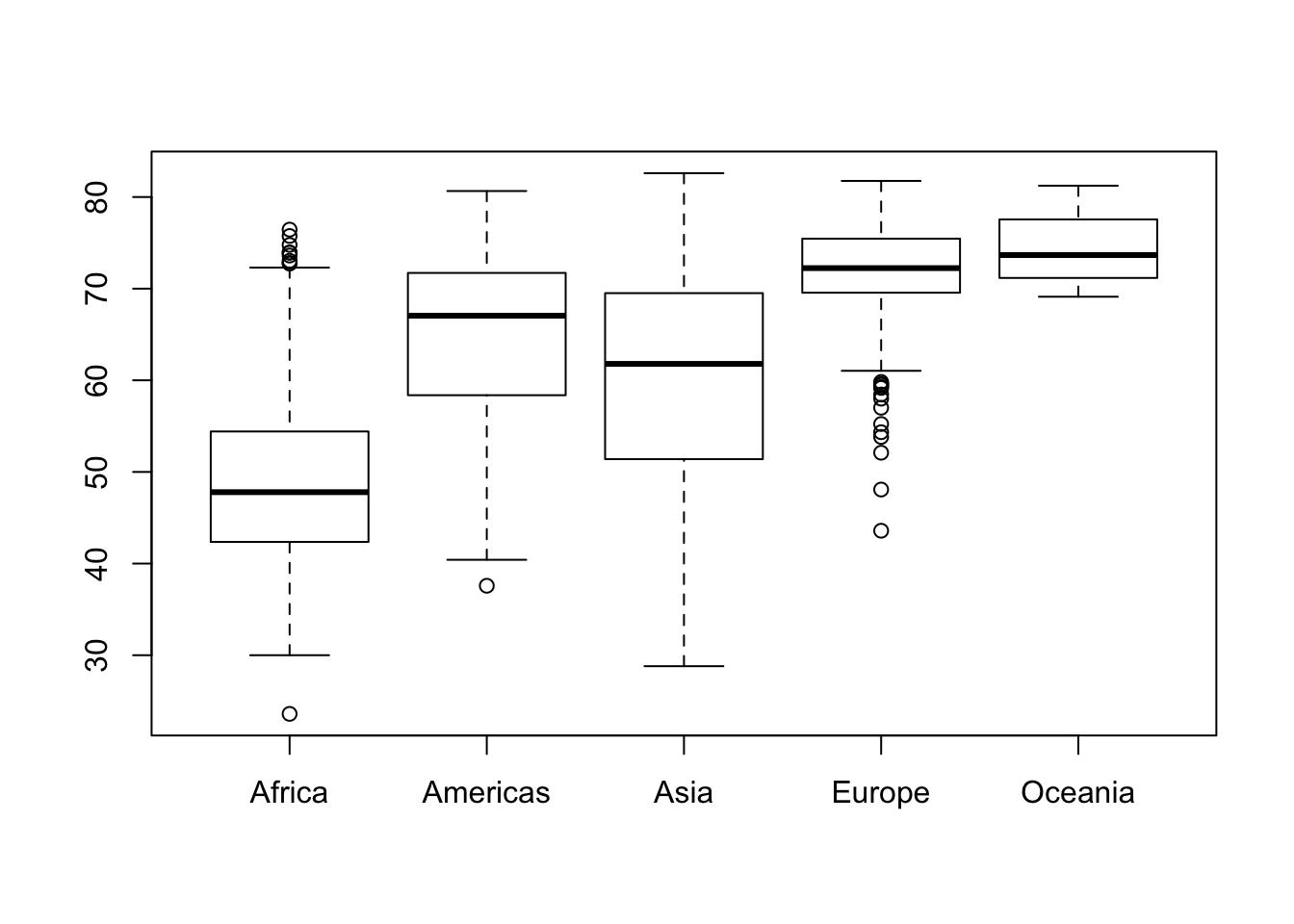
| Version | Author | Date |
|---|---|---|
| 133df4a | Anthony Hung | 2019-04-28 |
Setting a random seed
R has many functions that use a random number generator to generate an output. For example, the r____ functions (e.g. rbinom, runif) pull numbers from a probability distribution of your choice. In order to create reproducible analyses, it is often advantageous to be able to reliably obtain the same “random” number after running the same function over again. In order to do so, we can set a seed for the random number generator.
runif(1,0,1) #runif pulls a number from the uniform distribution with a set of given parameters[1] 0.1944457runif(1,0,1) #we can see that running runif twice gives you differnt results[1] 0.205278set.seed(1234) #setting a seed allows us to obtain reproducible results from functions that use the random number generator
runif(1,0,1)[1] 0.1137034set.seed(1234)
runif(1,0,1)[1] 0.1137034Reading and writing data in R
Finally, let us address probably one of the most important points when working with statistics in science: how to get the data you have collected into your R environment. For this part of the lesson, we will be working with the bandersnatch.csv file (created by Katie Long) located here: https://raw.githubusercontent.com/anthonyhung/MSTPsummerstatistics/master/data/bandersnatch.csv. If you would like to have your own copy of this dataset, you can open up a terminal window and run the commands.
cd ~/Desktop
mkdir data
cd data
wget https://raw.githubusercontent.com/anthonyhung/MSTPsummerstatistics/master/data/bandersnatch.csv--2019-05-30 13:39:30-- https://raw.githubusercontent.com/anthonyhung/MSTPsummerstatistics/master/data/bandersnatch.csv
Resolving raw.githubusercontent.com... 151.101.184.133
Connecting to raw.githubusercontent.com|151.101.184.133|:443... connected.
HTTP request sent, awaiting response... 200 OK
Length: 13511471 (13M) [text/plain]
Saving to: ‘bandersnatch.csv’
0K .......... .......... .......... .......... .......... 0% 2.83M 5s
50K .......... .......... .......... .......... .......... 0% 3.60M 4s
100K .......... .......... .......... .......... .......... 1% 1.33M 6s
150K .......... .......... .......... .......... .......... 1% 59.2M 4s
200K .......... .......... .......... .......... .......... 1% 4.53M 4s
250K .......... .......... .......... .......... .......... 2% 4.09M 4s
300K .......... .......... .......... .......... .......... 2% 4.05M 4s
350K .......... .......... .......... .......... .......... 3% 3.72M 4s
400K .......... .......... .......... .......... .......... 3% 3.99M 4s
450K .......... .......... .......... .......... .......... 3% 1.27M 4s
500K .......... .......... .......... .......... .......... 4% 5.33M 4s
550K .......... .......... .......... .......... .......... 4% 1.96M 4s
600K .......... .......... .......... .......... .......... 4% 3.63M 4s
650K .......... .......... .......... .......... .......... 5% 4.68M 4s
700K .......... .......... .......... .......... .......... 5% 3.84M 4s
750K .......... .......... .......... .......... .......... 6% 572K 5s
800K .......... .......... .......... .......... .......... 6% 23.1M 5s
850K .......... .......... .......... .......... .......... 6% 12.5M 5s
900K .......... .......... .......... .......... .......... 7% 5.18M 4s
950K .......... .......... .......... .......... .......... 7% 4.06M 4s
1000K .......... .......... .......... .......... .......... 7% 5.41M 4s
1050K .......... .......... .......... .......... .......... 8% 1015K 5s
1100K .......... .......... .......... .......... .......... 8% 2.00M 5s
1150K .......... .......... .......... .......... .......... 9% 4.86M 4s
1200K .......... .......... .......... .......... .......... 9% 1.97M 4s
1250K .......... .......... .......... .......... .......... 9% 51.4M 4s
1300K .......... .......... .......... .......... .......... 10% 4.88M 4s
1350K .......... .......... .......... .......... .......... 10% 3.05M 4s
1400K .......... .......... .......... .......... .......... 10% 1.12M 4s
1450K .......... .......... .......... .......... .......... 11% 4.91M 4s
1500K .......... .......... .......... .......... .......... 11% 3.01M 4s
1550K .......... .......... .......... .......... .......... 12% 4.74M 4s
1600K .......... .......... .......... .......... .......... 12% 1.39M 4s
1650K .......... .......... .......... .......... .......... 12% 3.01M 4s
1700K .......... .......... .......... .......... .......... 13% 3.02M 4s
1750K .......... .......... .......... .......... .......... 13% 1.65M 4s
1800K .......... .......... .......... .......... .......... 14% 3.46M 4s
1850K .......... .......... .......... .......... .......... 14% 3.29M 4s
1900K .......... .......... .......... .......... .......... 14% 2.20M 4s
1950K .......... .......... .......... .......... .......... 15% 1.53M 4s
2000K .......... .......... .......... .......... .......... 15% 6.96M 4s
2050K .......... .......... .......... .......... .......... 15% 1.92M 4s
2100K .......... .......... .......... .......... .......... 16% 1.78M 4s
2150K .......... .......... .......... .......... .......... 16% 1.41M 4s
2200K .......... .......... .......... .......... .......... 17% 3.45M 4s
2250K .......... .......... .......... .......... .......... 17% 1.66M 4s
2300K .......... .......... .......... .......... .......... 17% 3.23M 4s
2350K .......... .......... .......... .......... .......... 18% 1.26M 4s
2400K .......... .......... .......... .......... .......... 18% 2.68M 4s
2450K .......... .......... .......... .......... .......... 18% 3.61M 4s
2500K .......... .......... .......... .......... .......... 19% 4.53M 4s
2550K .......... .......... .......... .......... .......... 19% 1.90M 4s
2600K .......... .......... .......... .......... .......... 20% 4.24M 4s
2650K .......... .......... .......... .......... .......... 20% 1.50M 4s
2700K .......... .......... .......... .......... .......... 20% 2.80M 4s
2750K .......... .......... .......... .......... .......... 21% 5.68M 4s
2800K .......... .......... .......... .......... .......... 21% 4.30M 4s
2850K .......... .......... .......... .......... .......... 21% 2.92M 4s
2900K .......... .......... .......... .......... .......... 22% 4.30M 4s
2950K .......... .......... .......... .......... .......... 22% 3.66M 4s
3000K .......... .......... .......... .......... .......... 23% 2.36M 4s
3050K .......... .......... .......... .......... .......... 23% 3.69M 4s
3100K .......... .......... .......... .......... .......... 23% 4.46M 4s
3150K .......... .......... .......... .......... .......... 24% 6.09M 4s
3200K .......... .......... .......... .......... .......... 24% 3.20M 4s
3250K .......... .......... .......... .......... .......... 25% 5.05M 4s
3300K .......... .......... .......... .......... .......... 25% 4.00M 4s
3350K .......... .......... .......... .......... .......... 25% 3.31M 4s
3400K .......... .......... .......... .......... .......... 26% 5.18M 4s
3450K .......... .......... .......... .......... .......... 26% 5.51M 3s
3500K .......... .......... .......... .......... .......... 26% 5.02M 3s
3550K .......... .......... .......... .......... .......... 27% 4.67M 3s
3600K .......... .......... .......... .......... .......... 27% 4.13M 3s
3650K .......... .......... .......... .......... .......... 28% 8.93M 3s
3700K .......... .......... .......... .......... .......... 28% 5.74M 3s
3750K .......... .......... .......... .......... .......... 28% 3.94M 3s
3800K .......... .......... .......... .......... .......... 29% 5.62M 3s
3850K .......... .......... .......... .......... .......... 29% 2.44M 3s
3900K .......... .......... .......... .......... .......... 29% 5.50M 3s
3950K .......... .......... .......... .......... .......... 30% 6.96M 3s
4000K .......... .......... .......... .......... .......... 30% 7.56M 3s
4050K .......... .......... .......... .......... .......... 31% 4.38M 3s
4100K .......... .......... .......... .......... .......... 31% 5.29M 3s
4150K .......... .......... .......... .......... .......... 31% 2.65M 3s
4200K .......... .......... .......... .......... .......... 32% 2.52M 3s
4250K .......... .......... .......... .......... .......... 32% 2.59M 3s
4300K .......... .......... .......... .......... .......... 32% 5.96M 3s
4350K .......... .......... .......... .......... .......... 33% 4.31M 3s
4400K .......... .......... .......... .......... .......... 33% 4.29M 3s
4450K .......... .......... .......... .......... .......... 34% 5.09M 3s
4500K .......... .......... .......... .......... .......... 34% 13.8M 3s
4550K .......... .......... .......... .......... .......... 34% 1.60M 3s
4600K .......... .......... .......... .......... .......... 35% 6.31M 3s
4650K .......... .......... .......... .......... .......... 35% 3.72M 3s
4700K .......... .......... .......... .......... .......... 35% 5.99M 3s
4750K .......... .......... .......... .......... .......... 36% 6.33M 3s
4800K .......... .......... .......... .......... .......... 36% 2.69M 3s
4850K .......... .......... .......... .......... .......... 37% 91.4M 3s
4900K .......... .......... .......... .......... .......... 37% 4.16M 3s
4950K .......... .......... .......... .......... .......... 37% 5.58M 3s
5000K .......... .......... .......... .......... .......... 38% 6.19M 3s
5050K .......... .......... .......... .......... .......... 38% 6.85M 3s
5100K .......... .......... .......... .......... .......... 39% 4.39M 3s
5150K .......... .......... .......... .......... .......... 39% 7.07M 3s
5200K .......... .......... .......... .......... .......... 39% 7.16M 2s
5250K .......... .......... .......... .......... .......... 40% 2.71M 2s
5300K .......... .......... .......... .......... .......... 40% 15.1M 2s
5350K .......... .......... .......... .......... .......... 40% 3.05M 2s
5400K .......... .......... .......... .......... .......... 41% 1.22M 2s
5450K .......... .......... .......... .......... .......... 41% 83.0M 2s
5500K .......... .......... .......... .......... .......... 42% 6.27M 2s
5550K .......... .......... .......... .......... .......... 42% 4.24M 2s
5600K .......... .......... .......... .......... .......... 42% 3.02M 2s
5650K .......... .......... .......... .......... .......... 43% 5.78M 2s
5700K .......... .......... .......... .......... .......... 43% 2.43M 2s
5750K .......... .......... .......... .......... .......... 43% 1.85M 2s
5800K .......... .......... .......... .......... .......... 44% 3.82M 2s
5850K .......... .......... .......... .......... .......... 44% 3.91M 2s
5900K .......... .......... .......... .......... .......... 45% 5.59M 2s
5950K .......... .......... .......... .......... .......... 45% 3.41M 2s
6000K .......... .......... .......... .......... .......... 45% 4.87M 2s
6050K .......... .......... .......... .......... .......... 46% 3.15M 2s
6100K .......... .......... .......... .......... .......... 46% 2.77M 2s
6150K .......... .......... .......... .......... .......... 46% 5.24M 2s
6200K .......... .......... .......... .......... .......... 47% 5.92M 2s
6250K .......... .......... .......... .......... .......... 47% 3.01M 2s
6300K .......... .......... .......... .......... .......... 48% 4.09M 2s
6350K .......... .......... .......... .......... .......... 48% 5.94M 2s
6400K .......... .......... .......... .......... .......... 48% 4.64M 2s
6450K .......... .......... .......... .......... .......... 49% 4.66M 2s
6500K .......... .......... .......... .......... .......... 49% 8.03M 2s
6550K .......... .......... .......... .......... .......... 50% 4.57M 2s
6600K .......... .......... .......... .......... .......... 50% 4.17M 2s
6650K .......... .......... .......... .......... .......... 50% 6.82M 2s
6700K .......... .......... .......... .......... .......... 51% 5.55M 2s
6750K .......... .......... .......... .......... .......... 51% 6.18M 2s
6800K .......... .......... .......... .......... .......... 51% 794K 2s
6850K .......... .......... .......... .......... .......... 52% 63.8M 2s
6900K .......... .......... .......... .......... .......... 52% 3.51M 2s
6950K .......... .......... .......... .......... .......... 53% 3.20M 2s
7000K .......... .......... .......... .......... .......... 53% 2.69M 2s
7050K .......... .......... .......... .......... .......... 53% 2.25M 2s
7100K .......... .......... .......... .......... .......... 54% 4.17M 2s
7150K .......... .......... .......... .......... .......... 54% 2.05M 2s
7200K .......... .......... .......... .......... .......... 54% 4.72M 2s
7250K .......... .......... .......... .......... .......... 55% 2.49M 2s
7300K .......... .......... .......... .......... .......... 55% 3.77M 2s
7350K .......... .......... .......... .......... .......... 56% 3.35M 2s
7400K .......... .......... .......... .......... .......... 56% 4.38M 2s
7450K .......... .......... .......... .......... .......... 56% 3.67M 2s
7500K .......... .......... .......... .......... .......... 57% 3.64M 2s
7550K .......... .......... .......... .......... .......... 57% 3.22M 2s
7600K .......... .......... .......... .......... .......... 57% 5.43M 2s
7650K .......... .......... .......... .......... .......... 58% 3.06M 2s
7700K .......... .......... .......... .......... .......... 58% 4.58M 2s
7750K .......... .......... .......... .......... .......... 59% 1.91M 2s
7800K .......... .......... .......... .......... .......... 59% 5.19M 2s
7850K .......... .......... .......... .......... .......... 59% 1.05M 2s
7900K .......... .......... .......... .......... .......... 60% 5.11M 2s
7950K .......... .......... .......... .......... .......... 60% 1.96M 2s
8000K .......... .......... .......... .......... .......... 61% 1.57M 2s
8050K .......... .......... .......... .......... .......... 61% 1.22M 2s
8100K .......... .......... .......... .......... .......... 61% 99.9M 2s
8150K .......... .......... .......... .......... .......... 62% 16.9M 2s
8200K .......... .......... .......... .......... .......... 62% 2.69M 2s
8250K .......... .......... .......... .......... .......... 62% 3.34M 2s
8300K .......... .......... .......... .......... .......... 63% 5.00M 1s
8350K .......... .......... .......... .......... .......... 63% 3.23M 1s
8400K .......... .......... .......... .......... .......... 64% 2.59M 1s
8450K .......... .......... .......... .......... .......... 64% 4.13M 1s
8500K .......... .......... .......... .......... .......... 64% 2.78M 1s
8550K .......... .......... .......... .......... .......... 65% 1.60M 1s
8600K .......... .......... .......... .......... .......... 65% 2.65M 1s
8650K .......... .......... .......... .......... .......... 65% 954K 1s
8700K .......... .......... .......... .......... .......... 66% 2.69M 1s
8750K .......... .......... .......... .......... .......... 66% 2.85M 1s
8800K .......... .......... .......... .......... .......... 67% 3.46M 1s
8850K .......... .......... .......... .......... .......... 67% 2.88M 1s
8900K .......... .......... .......... .......... .......... 67% 3.44M 1s
8950K .......... .......... .......... .......... .......... 68% 2.48M 1s
9000K .......... .......... .......... .......... .......... 68% 1.63M 1s
9050K .......... .......... .......... .......... .......... 68% 1.92M 1s
9100K .......... .......... .......... .......... .......... 69% 8.77M 1s
9150K .......... .......... .......... .......... .......... 69% 2.41M 1s
9200K .......... .......... .......... .......... .......... 70% 2.34M 1s
9250K .......... .......... .......... .......... .......... 70% 1.88M 1s
9300K .......... .......... .......... .......... .......... 70% 741K 1s
9350K .......... .......... .......... .......... .......... 71% 2.00M 1s
9400K .......... .......... .......... .......... .......... 71% 2.04M 1s
9450K .......... .......... .......... .......... .......... 71% 2.15M 1s
9500K .......... .......... .......... .......... .......... 72% 2.41M 1s
9550K .......... .......... .......... .......... .......... 72% 2.45M 1s
9600K .......... .......... .......... .......... .......... 73% 2.92M 1s
9650K .......... .......... .......... .......... .......... 73% 3.33M 1s
9700K .......... .......... .......... .......... .......... 73% 2.79M 1s
9750K .......... .......... .......... .......... .......... 74% 3.41M 1s
9800K .......... .......... .......... .......... .......... 74% 3.31M 1s
9850K .......... .......... .......... .......... .......... 75% 3.47M 1s
9900K .......... .......... .......... .......... .......... 75% 3.41M 1s
9950K .......... .......... .......... .......... .......... 75% 4.64M 1s
10000K .......... .......... .......... .......... .......... 76% 3.45M 1s
10050K .......... .......... .......... .......... .......... 76% 4.82M 1s
10100K .......... .......... .......... .......... .......... 76% 4.02M 1s
10150K .......... .......... .......... .......... .......... 77% 2.88M 1s
10200K .......... .......... .......... .......... .......... 77% 3.84M 1s
10250K .......... .......... .......... .......... .......... 78% 6.14M 1s
10300K .......... .......... .......... .......... .......... 78% 1.58M 1s
10350K .......... .......... .......... .......... .......... 78% 4.17M 1s
10400K .......... .......... .......... .......... .......... 79% 2.60M 1s
10450K .......... .......... .......... .......... .......... 79% 6.02M 1s
10500K .......... .......... .......... .......... .......... 79% 4.51M 1s
10550K .......... .......... .......... .......... .......... 80% 2.80M 1s
10600K .......... .......... .......... .......... .......... 80% 3.02M 1s
10650K .......... .......... .......... .......... .......... 81% 6.24M 1s
10700K .......... .......... .......... .......... .......... 81% 5.10M 1s
10750K .......... .......... .......... .......... .......... 81% 5.27M 1s
10800K .......... .......... .......... .......... .......... 82% 5.16M 1s
10850K .......... .......... .......... .......... .......... 82% 3.83M 1s
10900K .......... .......... .......... .......... .......... 82% 5.70M 1s
10950K .......... .......... .......... .......... .......... 83% 3.01M 1s
11000K .......... .......... .......... .......... .......... 83% 5.29M 1s
11050K .......... .......... .......... .......... .......... 84% 5.19M 1s
11100K .......... .......... .......... .......... .......... 84% 5.95M 1s
11150K .......... .......... .......... .......... .......... 84% 4.54M 1s
11200K .......... .......... .......... .......... .......... 85% 2.60M 1s
11250K .......... .......... .......... .......... .......... 85% 8.61M 1s
11300K .......... .......... .......... .......... .......... 86% 3.40M 1s
11350K .......... .......... .......... .......... .......... 86% 2.74M 1s
11400K .......... .......... .......... .......... .......... 86% 4.28M 1s
11450K .......... .......... .......... .......... .......... 87% 7.37M 1s
11500K .......... .......... .......... .......... .......... 87% 6.29M 1s
11550K .......... .......... .......... .......... .......... 87% 3.82M 1s
11600K .......... .......... .......... .......... .......... 88% 3.65M 0s
11650K .......... .......... .......... .......... .......... 88% 5.60M 0s
11700K .......... .......... .......... .......... .......... 89% 6.98M 0s
11750K .......... .......... .......... .......... .......... 89% 3.95M 0s
11800K .......... .......... .......... .......... .......... 89% 3.92M 0s
11850K .......... .......... .......... .......... .......... 90% 5.91M 0s
11900K .......... .......... .......... .......... .......... 90% 2.75M 0s
11950K .......... .......... .......... .......... .......... 90% 4.46M 0s
12000K .......... .......... .......... .......... .......... 91% 32.4M 0s
12050K .......... .......... .......... .......... .......... 91% 4.54M 0s
12100K .......... .......... .......... .......... .......... 92% 2.94M 0s
12150K .......... .......... .......... .......... .......... 92% 2.20M 0s
12200K .......... .......... .......... .......... .......... 92% 4.29M 0s
12250K .......... .......... .......... .......... .......... 93% 4.22M 0s
12300K .......... .......... .......... .......... .......... 93% 8.19M 0s
12350K .......... .......... .......... .......... .......... 93% 2.16M 0s
12400K .......... .......... .......... .......... .......... 94% 4.26M 0s
12450K .......... .......... .......... .......... .......... 94% 1.30M 0s
12500K .......... .......... .......... .......... .......... 95% 2.02M 0s
12550K .......... .......... .......... .......... .......... 95% 1.82M 0s
12600K .......... .......... .......... .......... .......... 95% 2.34M 0s
12650K .......... .......... .......... .......... .......... 96% 910K 0s
12700K .......... .......... .......... .......... .......... 96% 1.21M 0s
12750K .......... .......... .......... .......... .......... 97% 2.54M 0s
12800K .......... .......... .......... .......... .......... 97% 2.50M 0s
12850K .......... .......... .......... .......... .......... 97% 2.47M 0s
12900K .......... .......... .......... .......... .......... 98% 2.62M 0s
12950K .......... .......... .......... .......... .......... 98% 3.53M 0s
13000K .......... .......... .......... .......... .......... 98% 1.18M 0s
13050K .......... .......... .......... .......... .......... 99% 3.33M 0s
13100K .......... .......... .......... .......... .......... 99% 2.45M 0s
13150K .......... .......... .......... .......... .... 100% 4.60M=4.2s
2019-05-30 13:39:35 (3.04 MB/s) - ‘bandersnatch.csv’ saved [13511471/13511471]Now that we have a copy of the data in a data directory on our desktop, we can load it into R using a relative or absolute directory path and the read.csv function.
data <- read.csv("~/Desktop/data/bandersnatch.csv")
#let's take a look at the dataset we've just loaded
head(data) Color Fur Baseline.Frumiosity Post.Frumiosity
1 Red Nude 4.477127 11.46590
2 Red Nude 4.113727 11.09354
3 Red Nude 4.806221 11.81268
4 Red Nude 5.357348 12.36704
5 Red Nude 5.951754 12.96135
6 Red Nude 3.593995 10.62375summary(data) Color Fur Baseline.Frumiosity Post.Frumiosity
Blue:200000 Furry:200000 Min. :-1.108 Min. : 1.887
Red :200000 Nude :200000 1st Qu.: 4.001 1st Qu.: 4.044
Median : 6.980 Median : 8.976
Mean : 6.001 Mean : 9.001
3rd Qu.: 8.961 3rd Qu.:13.956
Max. : 9.174 Max. :16.192 #what is the difference between these two function calls?
head(read.csv("~/Desktop/data/bandersnatch.csv", header = T)) Color Fur Baseline.Frumiosity Post.Frumiosity
1 Red Nude 4.477127 11.46590
2 Red Nude 4.113727 11.09354
3 Red Nude 4.806221 11.81268
4 Red Nude 5.357348 12.36704
5 Red Nude 5.951754 12.96135
6 Red Nude 3.593995 10.62375head(read.csv("~/Desktop/data/bandersnatch.csv", header = F)) V1 V2 V3 V4
1 Color Fur Baseline Frumiosity Post-Frumiosity
2 Red Nude 4.477127244 11.46590322
3 Red Nude 4.113726932 11.09353649
4 Red Nude 4.806220524 11.81268077
5 Red Nude 5.357347878 12.36703951
6 Red Nude 5.951754455 12.96134984#let's look at the structure of the data
class(data)[1] "data.frame"class(data$Color)[1] "factor"class(data$Baseline.Frumiosity)[1] "numeric"#let's make some plots with the data
hist(data$Baseline.Frumiosity)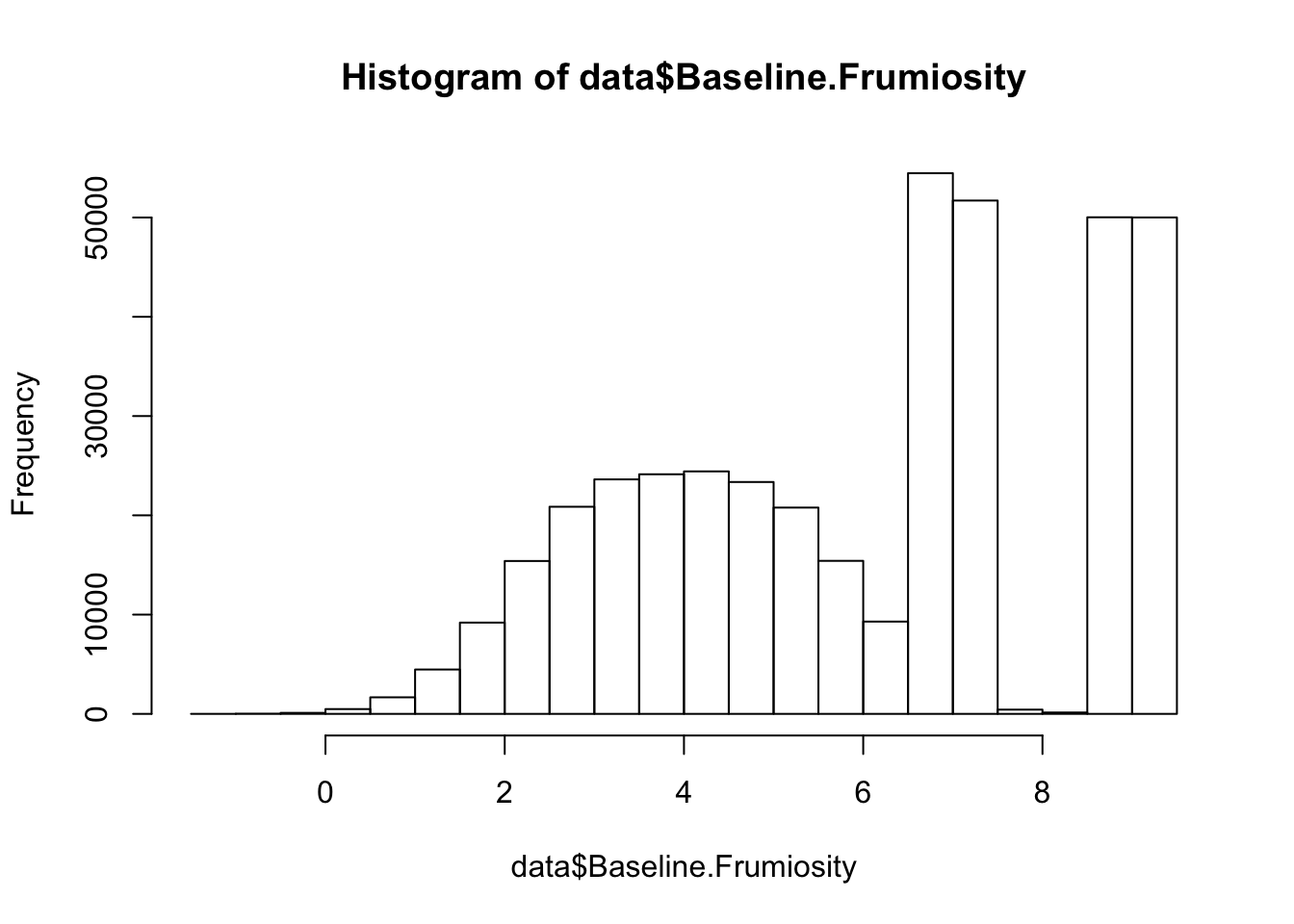
| Version | Author | Date |
|---|---|---|
| dd1e411 | Anthony Hung | 2019-05-22 |
hist(data$Post.Frumiosity)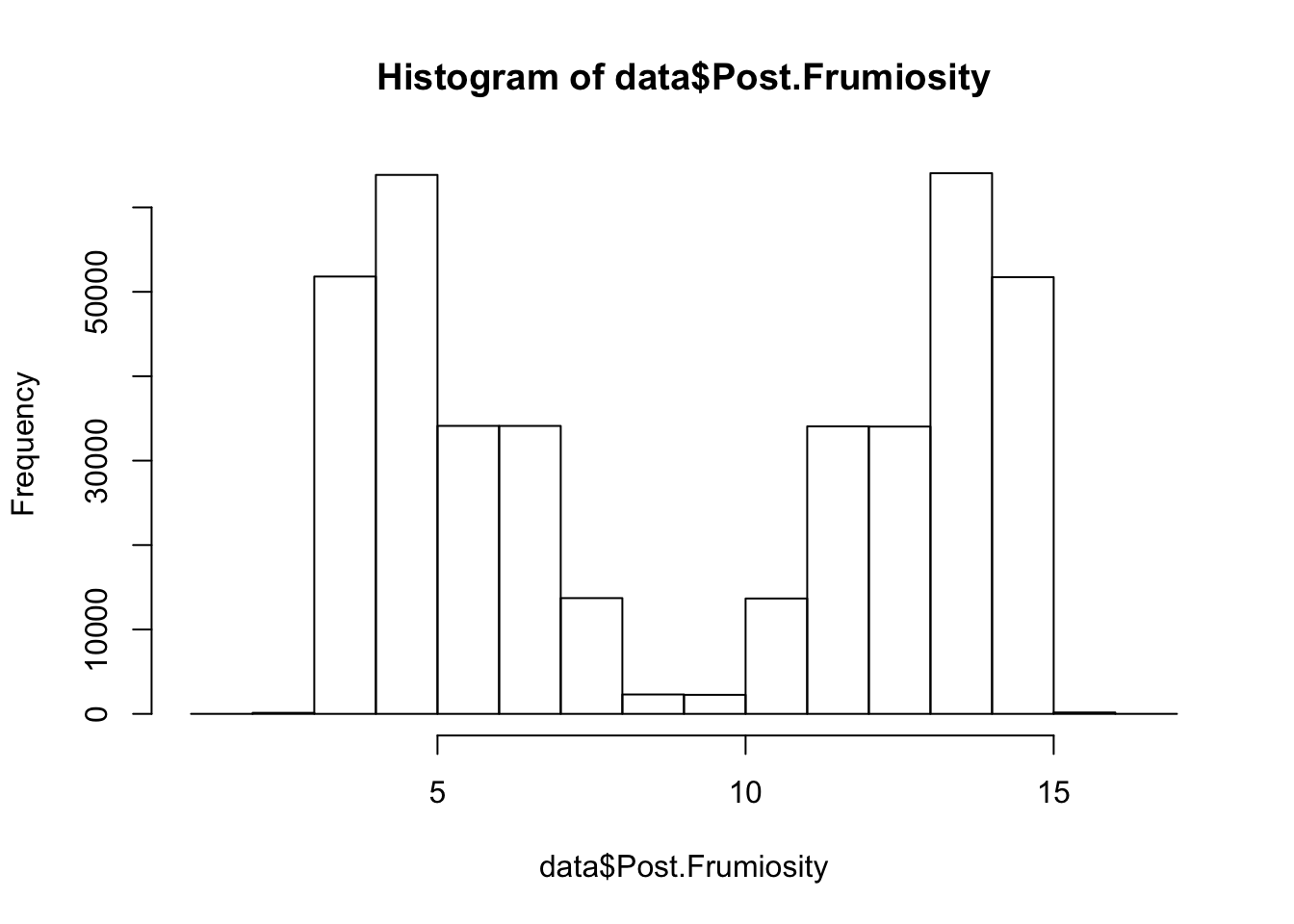
| Version | Author | Date |
|---|---|---|
| dd1e411 | Anthony Hung | 2019-05-22 |
plot(data$Baseline.Frumiosity, data$Post.Frumiosity)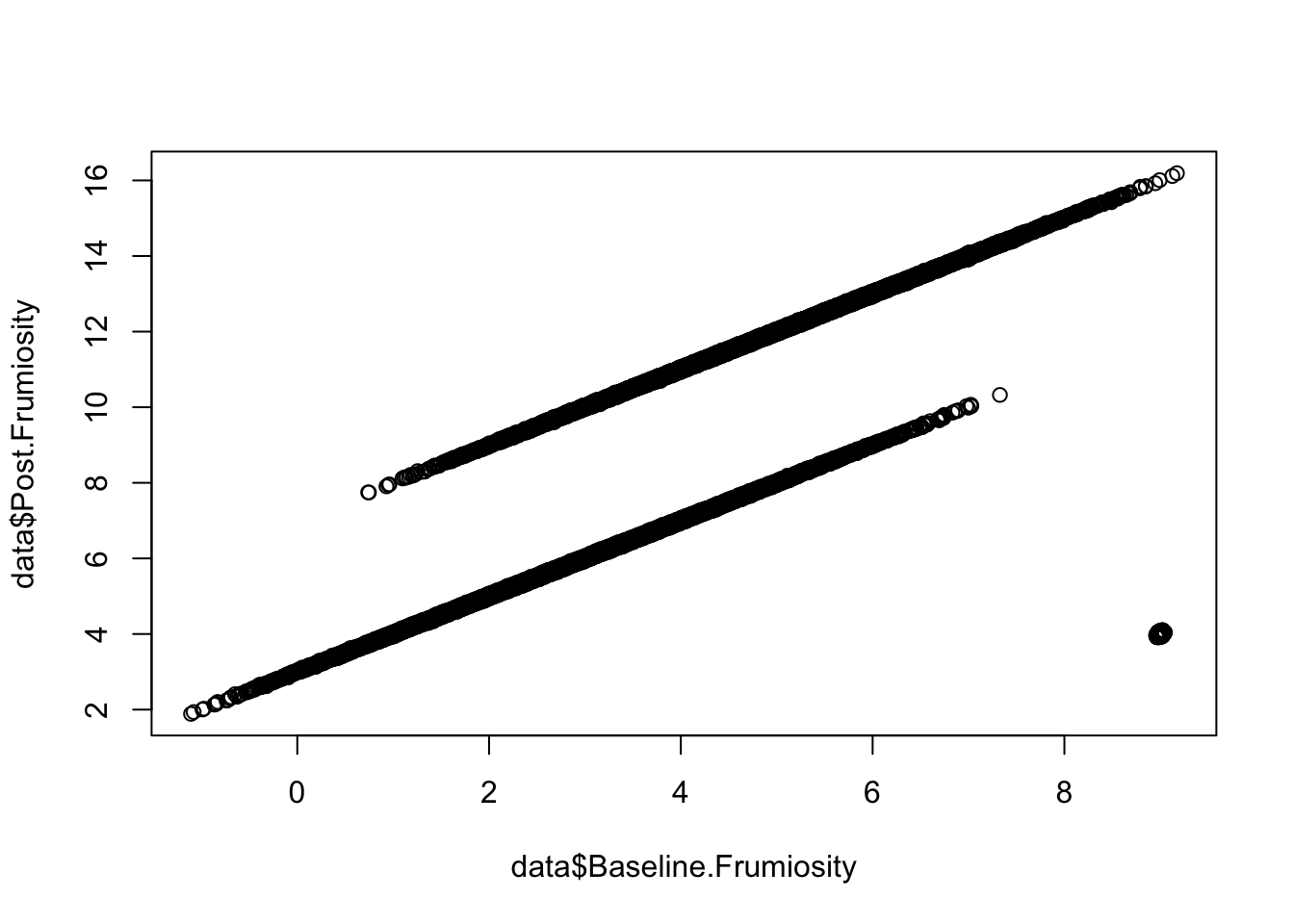
| Version | Author | Date |
|---|---|---|
| dd1e411 | Anthony Hung | 2019-05-22 |
#we can also write data files and export them using R
data$Size <- rnorm(nrow(data))
write.csv(data, "~/Desktop/data/new_bandersnatch.csv")Exercises:
Write a function called calc_KE that takes as arguments the mass (in kg) and velocity (in m/s) of an object and returns the kinetic energy (in Joules) of an object. Use it to find the KE of a 0.5 kg rock moving at 1.2 m/s.
0.36 Joules Working with the gapminder dataset, find the country with the highest life expectancy in 1962.
Iceland
If time permits: Introduction to Unix terminal and git/github
sessionInfo()R version 3.5.1 (2018-07-02)
Platform: x86_64-apple-darwin15.6.0 (64-bit)
Running under: macOS 10.14.5
Matrix products: default
BLAS: /Library/Frameworks/R.framework/Versions/3.5/Resources/lib/libRblas.0.dylib
LAPACK: /Library/Frameworks/R.framework/Versions/3.5/Resources/lib/libRlapack.dylib
locale:
[1] en_US.UTF-8/en_US.UTF-8/en_US.UTF-8/C/en_US.UTF-8/en_US.UTF-8
attached base packages:
[1] stats graphics grDevices utils datasets methods base
other attached packages:
[1] gapminder_0.3.0
loaded via a namespace (and not attached):
[1] Rcpp_0.12.18 knitr_1.20 whisker_0.3-2 magrittr_1.5
[5] workflowr_1.3.0 rlang_0.2.2 fansi_0.3.0 stringr_1.3.1
[9] tools_3.5.1 utf8_1.1.4 cli_1.0.0 git2r_0.23.0
[13] htmltools_0.3.6 yaml_2.2.0 rprojroot_1.3-2 digest_0.6.16
[17] assertthat_0.2.1 tibble_1.4.2 crayon_1.3.4 fs_1.2.7
[21] glue_1.3.0 evaluate_0.11 rmarkdown_1.10 stringi_1.2.4
[25] compiler_3.5.1 pillar_1.3.0 backports_1.1.2