Estimating Differences in the Distribution of First-degree Relatives

workflowr

• Summary
• Checks
• Past versions

Last updated: 2025-01-09

Checks: 6 1

Knit directory: PODFRIDGE/

This reproducible R Markdown analysis was created with workflowr (version 1.7.1). The Checks tab describes the reproducibility checks that were applied when the results were created. The Past versions tab lists the development history.

---

R Markdown file: uncommitted changes

The R Markdown file has unstaged changes. To know which version of the R Markdown file created these results, you’ll want to first commit it to the Git repo. If you’re still working on the analysis, you can ignore this warning. When you’re finished, you can run wflow_publish to commit the R Markdown file and build the HTML.

Environment: empty

Great job! The global environment was empty. Objects defined in the global environment can affect the analysis in your R Markdown file in unknown ways. For reproduciblity it’s best to always run the code in an empty environment.

Seed: set.seed(20230302)

The command set.seed(20230302) was run prior to running the code in the R Markdown file. Setting a seed ensures that any results that rely on randomness, e.g. subsampling or permutations, are reproducible.

Session information: recorded

Great job! Recording the operating system, R version, and package versions is critical for reproducibility.

Cache: none

Nice! There were no cached chunks for this analysis, so you can be confident that you successfully produced the results during this run.

File paths: relative

Great job! Using relative paths to the files within your workflowr project makes it easier to run your code on other machines.

Repository version: 0c90de8

Great! You are using Git for version control. Tracking code development and connecting the code version to the results is critical for reproducibility.

The results in this page were generated with repository version 0c90de8. See the Past versions tab to see a history of the changes made to the R Markdown and HTML files.

Note that you need to be careful to ensure that all relevant files for the analysis have been committed to Git prior to generating the results (you can use wflow_publish or wflow_git_commit). workflowr only checks the R Markdown file, but you know if there are other scripts or data files that it depends on. Below is the status of the Git repository when the results were generated:

Ignored files:
    Ignored:    .DS_Store
    Ignored:    .Rhistory
    Ignored:    .Rproj.user/
    Ignored:    analysis/.Rhistory
    Ignored:    data/.DS_Store

Unstaged changes:
    Modified:   analysis/relative-distribution.Rmd

Note that any generated files, e.g. HTML, png, CSS, etc., are not included in this status report because it is ok for generated content to have uncommitted changes.

---

These are the previous versions of the repository in which changes were made to the R Markdown (analysis/relative-distribution.Rmd) and HTML (docs/relative-distribution.html) files. If you’ve configured a remote Git repository (see ?wflow_git_remote), click on the hyperlinks in the table below to view the files as they were in that past version.

File	Version	Author	Date	Message
Rmd	0c90de8	linmatch	2024-12-18	clean and organize the document
Rmd	f567c4a	linmatch	2024-12-16	update
html	f567c4a	linmatch	2024-12-16	update
Rmd	231390a	linmatch	2024-12-11	update analysis
html	231390a	linmatch	2024-12-11	update analysis
Rmd	8007864	linmatch	2024-12-03	update workflow page
html	8007864	linmatch	2024-12-03	update workflow page
Rmd	e553adc	linmatch	2024-11-21	Update relative-distribution.Rmd
Rmd	e76576b	linmatch	2024-11-21	Update relative-distribution.Rmd
Rmd	21f0f4f	linmatch	2024-11-19	Update relative-distribution.Rmd
Rmd	f583798	linmatch	2024-11-14	Update relative-distribution.Rmd
Rmd	900b2e4	linmatch	2024-11-14	Update relative-distribution.Rmd
Rmd	776920f	linmatch	2024-11-12	update the model fit analysis in children’s part
html	776920f	linmatch	2024-11-12	update the model fit analysis in children’s part
Rmd	06a8f96	linmatch	2024-11-05	update sibling’s part
html	06a8f96	linmatch	2024-11-05	update sibling’s part
Rmd	1741cb1	linmatch	2024-11-05	fix test
Rmd	4e68621	linmatch	2024-11-05	fix chisq-test in cohort stability
html	4e68621	linmatch	2024-11-05	fix chisq-test in cohort stability
Rmd	6fb5b40	linmatch	2024-10-29	update sibling’s distribution plot
Rmd	570abb0	linmatch	2024-10-22	update sibling part
Rmd	2e09e08	linmatch	2024-10-22	workflow build
html	2e09e08	linmatch	2024-10-22	workflow build
Rmd	bb2c61b	linmatch	2024-10-21	complete fertility shift analysis
Rmd	842d935	linmatch	2024-10-17	update fertility shift
Rmd	2ae8460	linmatch	2024-10-16	fix the chisq-test
Rmd	9632ae1	linmatch	2024-10-12	update cohort stability
Rmd	9852339	linmatch	2024-10-08	update cohort stability
html	9852339	linmatch	2024-10-08	update cohort stability
Rmd	7ec169f	linmatch	2024-10-03	update sibling distribution
Rmd	27b986f	linmatch	2024-10-01	update stability cohort analysis
Rmd	57a97db	linmatch	2024-09-30	Update relative-distribution.Rmd
Rmd	52aa7f8	linmatch	2024-09-27	improving code on Part1
Rmd	c54a746	linmatch	2024-09-26	update and fix step 2
Rmd	94d00b3	linmatch	2024-09-24	fix step1
Rmd	1225480	linmatch	2024-09-23	update on step1
Rmd	83174c0	Tina Lasisi	2024-09-22	Instructions and layout for relative distribution
html	83174c0	Tina Lasisi	2024-09-22	Instructions and layout for relative distribution
Rmd	78c1621	Tina Lasisi	2024-09-21	Update relative-distribution.Rmd
Rmd	f4c2830	Tina Lasisi	2024-09-21	Update relative-distribution.Rmd
Rmd	2851385	Tina Lasisi	2024-09-21	rename old analysis
html	2851385	Tina Lasisi	2024-09-21	rename old analysis

---

Introduction

The relative genetic surveillance of a population is influenced by the number of genetically detectable relatives individuals have. First-degree relatives (parents, siblings, and children) are especially relevant in forensic analyses using short tandem repeat (STR) loci, where close familial searches are commonly employed. To explore potential disparities in genetic detectability between African American and European American populations, we examined U.S. Census data from four census years (1960, 1970, 1980, and 1990) focusing on the number of children born to women over the age of 40.

Data Sources

We used publicly available data from the Integrated Public Use Microdata Series (IPUMS) for the U.S. Census years 1960, 1970, 1980, and 1990. The datasets include information on:

• AGE: Age of the respondent.
• RACE: Self-identified race of the respondent.
• chborn_num: Number of children ever born to the respondent.

Data citation: Steven Ruggles, Sarah Flood, Matthew Sobek, Daniel Backman, Annie Chen, Grace Cooper, Stephanie Richards, Renae Rogers, and Megan Schouweiler. IPUMS USA: Version 14.0 [dataset]. Minneapolis, MN: IPUMS, 2023. https://doi.org/10.18128/D010.V14.0

Data Preparation

Filtering Criteria: We selected women aged 40 and above to ensure that most had completed childbearing.

Due to the terms of agreement for using this data, we cannot share the full dataset but our repo contains the subset that was used to calculate the mean number of offspring and variance.

Race Classification: We categorized individuals into two groups:

• African American: Those who identified as “Black” or “African American”.
• European American: Those who identified as “White”.

Calculating Number of Siblings: For each child of these women, the number of siblings (n_sib) is one less than the number of children born to the mother:

\[ n_{sib} = chborn_{num} - 1 \]

path <- file.path(".", "data")
savepath <- file.path(".", "output")

prop_race_year <- file.path(path, "proportions_table_by_race_year.csv")
data_filter <- file.path(path, "data_filtered_recoded.csv")

children_data = read.csv(prop_race_year)
mother_data = read.csv(data_filter)

df <- mother_data %>%
  # Filter for women aged 40 and above
  filter(AGE >= 40) %>%
  mutate(
    # Create new age ranges
    AGE_RANGE = case_when(
      AGE >= 70 ~ "70+",
      AGE >= 60 ~ "60-69",
      AGE >= 50 ~ "50-59",
      AGE >= 40 ~ "40-49",
      TRUE ~ as.character(AGE_RANGE)  # This shouldn't occur due to the filter, but included for completeness
    ),
    # Convert CHBORN to ordered factor
    CHBORN = factor(case_when(
      chborn_num == 0 ~ "No children",
      chborn_num == 1 ~ "1 child",
      chborn_num == 2 ~ "2 children",
      chborn_num == 3 ~ "3 children",
      chborn_num == 4 ~ "4 children",
      chborn_num == 5 ~ "5 children",
      chborn_num == 6 ~ "6 children",
      chborn_num == 7 ~ "7 children",
      chborn_num == 8 ~ "8 children",
      chborn_num == 9 ~ "9 children",
      chborn_num == 10 ~ "10 children",
      chborn_num == 11 ~ "11 children",
      chborn_num >= 12 ~ "12+ children"
    ), levels = c("No children", "1 child", "2 children", "3 children", 
                  "4 children", "5 children", "6 children", "7 children", 
                  "8 children", "9 children", "10 children", "11 children", 
                  "12+ children"), ordered = TRUE),
    
    # Ensure RACE variable is correctly formatted and filtered
    RACE = factor(RACE, levels = c("White", "Black/African American"))
  ) %>%
  # Filter for African American and European American women
  filter(RACE %in% c("Black/African American", "White")) %>%
  # Select and reorder columns
  dplyr::select(YEAR, SEX, AGE, BIRTHYR, RACE, CHBORN, AGE_RANGE, chborn_num)

# Display the first few rows of the processed data
head(df)

  YEAR    SEX AGE BIRTHYR  RACE      CHBORN AGE_RANGE chborn_num
1 1960 Female  65    1894 White No children     60-69          0
2 1960 Female  49    1911 White  2 children     40-49          2
3 1960 Female  54    1905 White No children     50-59          0
4 1960 Female  56    1903 White     1 child     50-59          1
5 1960 Female  54    1905 White     1 child     50-59          1
6 1960 Female  50    1910 White No children     50-59          0

# Summary of the processed data
summary(df)

      YEAR          SEX                 AGE            BIRTHYR    
 Min.   :1960   Length:1917477     Min.   : 41.00   Min.   :1859  
 1st Qu.:1970   Class :character   1st Qu.: 49.00   1st Qu.:1905  
 Median :1970   Mode  :character   Median : 58.00   Median :1916  
 Mean   :1976                      Mean   : 59.24   Mean   :1916  
 3rd Qu.:1980                      3rd Qu.: 68.00   3rd Qu.:1926  
 Max.   :1990                      Max.   :100.00   Max.   :1949  
                                                                  
                     RACE                 CHBORN        AGE_RANGE        
 White                 :1740755   2 children :452594   Length:1917477    
 Black/African American: 176722   No children:343319   Class :character  
                                  3 children :335119   Mode  :character  
                                  1 child    :292001                     
                                  4 children :204983                     
                                  5 children :113593                     
                                  (Other)    :175868                     
   chborn_num   
 Min.   : 0.00  
 1st Qu.: 1.00  
 Median : 2.00  
 Mean   : 2.57  
 3rd Qu.: 4.00  
 Max.   :12.00  
                

# Check the levels of the RACE factor
levels(df$RACE)

[1] "White"                  "Black/African American"

# Count of observations by RACE
table(df$RACE)

                 White Black/African American 
               1740755                 176722 

# Count of observations by AGE_RANGE
table(df$AGE_RANGE)

 40-49  50-59  60-69    70+ 
529160 517620 436829 433868 

Distribution of Number of Children Across Census Years

First we visualize the general trends in the frequency of the number of children for African American and European American mothers across the Census years by age group.

# Calculate proportions within each group, ensuring proper normalization
df_proportions <- df %>%
  group_by(YEAR, RACE, AGE_RANGE, chborn_num) %>%
  summarise(count = n(), .groups = "drop") %>%
  group_by(YEAR, RACE, AGE_RANGE) %>%
  mutate(proportion = count / sum(count)) %>%
  ungroup()

# Reshape data for the mirror plot
df_mirror <- df_proportions %>%
  mutate(proportion = if_else(RACE == "White", -proportion, proportion))

# Create color palette
my_colors <- colorRampPalette(c("#FFB000", "#F77A2E", "#DE3A8A", "#7253FF", "#5E8BFF"))(13)

# Create the plot
child_plot <- ggplot(df_mirror, aes(x = chborn_num, y = proportion, fill = as.factor(chborn_num))) +
  geom_col(aes(alpha = RACE)) +
  geom_hline(yintercept = 0, color = "black", size = 0.5) +
  facet_grid(AGE_RANGE ~ YEAR, scales = "free_y") +
  coord_flip() +
  scale_y_continuous(
    labels = function(x) abs(x),
    limits = function(x) c(-max(abs(x)), max(abs(x)))
  ) +
  scale_x_continuous(breaks = 0:12, labels = c(0:11, "12+")) +
  scale_fill_manual(values = my_colors) +
  scale_alpha_manual(values = c("White" = 0.7, "Black/African American" = 1), guide = "none") +
  labs(
    title = "Distribution of Number of Children by Census Year, Race, and Age Range",
    x = "Number of Children",
    y = "Proportion",
    fill = "Number of Children",
    caption = "White population shown on left (negative values), Black/African American on right (positive values)\nProportions normalized within each age range, race, and census year\nFootnote: The category '12+' includes families with 12 or more children."
  ) +
  theme_minimal() +
  theme(
    plot.title = element_text(size = 14, hjust = 0.5),
    axis.text.y = element_text(size = 8),
    strip.text = element_text(size = 10),
    legend.position = "none",
    panel.grid.major.y = element_blank(),
    panel.grid.minor.y = element_blank()
  )

print(child_plot)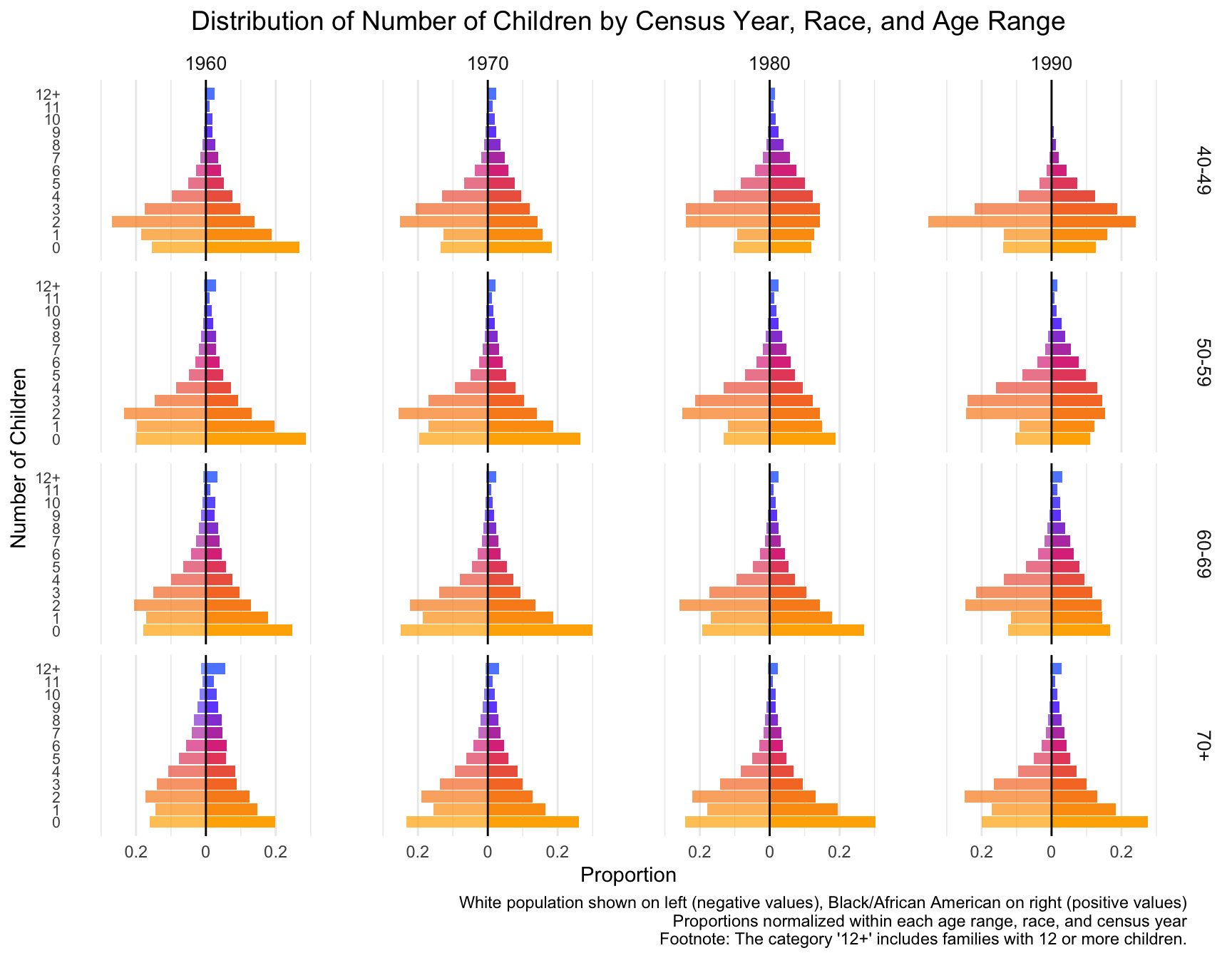

Past versions of unnamed-chunk-3-1.png

Version	Author	Date
f567c4a	linmatch	2024-12-16

# Print summary to check age ranges and normalization
print(df_proportions %>%
  group_by(YEAR, RACE, AGE_RANGE) %>%
  summarise(total_proportion = sum(proportion), .groups = "drop") %>%
  arrange(YEAR, RACE, AGE_RANGE))

# A tibble: 32 × 4
    YEAR RACE                   AGE_RANGE total_proportion
   <int> <fct>                  <chr>                <dbl>
 1  1960 White                  40-49                    1
 2  1960 White                  50-59                    1
 3  1960 White                  60-69                    1
 4  1960 White                  70+                      1
 5  1960 Black/African American 40-49                    1
 6  1960 Black/African American 50-59                    1
 7  1960 Black/African American 60-69                    1
 8  1960 Black/African American 70+                      1
 9  1970 White                  40-49                    1
10  1970 White                  50-59                    1
# ℹ 22 more rows

With this visualization of the distribution of the data, we can see that there are differences between White and Black Americans.

# Mean Number of Children By race and Year
df %>% group_by(RACE, YEAR) %>% summarise(Mean = mean(chborn_num))

`summarise()` has grouped output by 'RACE'. You can override using the
`.groups` argument.

# A tibble: 8 × 3
# Groups:   RACE [2]
  RACE                    YEAR  Mean
  <fct>                  <int> <dbl>
1 White                   1960  2.62
2 White                   1970  2.45
3 White                   1980  2.55
4 White                   1990  2.53
5 Black/African American  1960  3.02
6 Black/African American  1970  3.00
7 Black/African American  1980  3.21
8 Black/African American  1990  3.20

We will now test for differences in 1) the mean and variance, and 2) zero-inflation.

Model Fit Across Census Years

For each combination of race, census year, and age range, we fit the following candidate models:

• Poisson Model
• Negative Binomial (NB) Model
• Zero-Inflated Poisson (ZIP) Model
• Zero-Inflated Negative Binomial (ZINB) Model

Fit and Compare Models

combinations <- df %>%
  group_by(YEAR, RACE, AGE_RANGE) %>%
  group_split()

# Initialize the data frame to store results
best_models <- data.frame(
  Race = character(),
  Census_Year = numeric(),
  Age_Range = character(),
  AIC_poisson = numeric(),
  AIC_nb = numeric(),
  AIC_zip = numeric(),
  AIC_zinb = numeric(),
  stringsAsFactors = FALSE
)

# Loop through each subset of data
for (i in seq_along(combinations)) {
  subset_data <- combinations[[i]]
  
  # Fit Poisson model
  poisson_model <- glm(chborn_num ~ 1, family = poisson, data = subset_data)
  # Fit Negative Binomial model
  nb_model <- glm.nb(chborn_num ~ 1, data = subset_data)

  # Fit Zero-Inflated Poisson model
  zip_model <- zeroinfl(chborn_num ~ 1 | 1, data = subset_data, dist = "poisson")

  # Fit Zero-Inflated Negative Binomial model
  zinb_model <- zeroinfl(chborn_num ~ 1 | 1, data = subset_data, dist = "negbin")
  
  # Append the result to the best_models data frame
  best_models <- rbind(
    best_models,
    data.frame(
      Race = unique(subset_data$RACE),
      Census_Year = unique(subset_data$YEAR),
      Age_Range = unique(subset_data$AGE_RANGE),
      AIC_poisson = AIC(poisson_model),
      AIC_nb = AIC(nb_model),
      AIC_zip = AIC(zip_model),
      AIC_zinb = AIC(zinb_model),
      stringsAsFactors = FALSE
    )
  )
}

Record the Best Model for Each Subset

# Add a Best_Model column to store the best model based on minimum AIC
best_models$Best_Model <- apply(best_models, 1, function(row) {
  # Get AIC values for Poisson, NB, ZIP, and ZINB models
  aic_values <- c(Poisson = as.numeric(row['AIC_poisson']),
                  Negative_Binomial = as.numeric(row['AIC_nb']),
                  Zero_Inflated_Poisson = as.numeric(row['AIC_zip']),
                  Zero_Inflated_NB= as.numeric(row['AIC_zinb']))
  
  # Find the name of the model with the minimum AIC value
  best_model <- names(which.min(aic_values))
  
  return(best_model)
})

best_models <- best_models %>% dplyr::select(Race, Census_Year, Age_Range, Best_Model)
# View the updated table with the Best_Model column
print(best_models)

                     Race Census_Year Age_Range            Best_Model
1                   White        1960     40-49      Zero_Inflated_NB
2                   White        1960     50-59      Zero_Inflated_NB
3                   White        1960     60-69      Zero_Inflated_NB
4                   White        1960       70+      Zero_Inflated_NB
5  Black/African American        1960     40-49      Zero_Inflated_NB
6  Black/African American        1960     50-59      Zero_Inflated_NB
7  Black/African American        1960     60-69      Zero_Inflated_NB
8  Black/African American        1960       70+      Zero_Inflated_NB
9                   White        1970     40-49      Zero_Inflated_NB
10                  White        1970     50-59      Zero_Inflated_NB
11                  White        1970     60-69      Zero_Inflated_NB
12                  White        1970       70+      Zero_Inflated_NB
13 Black/African American        1970     40-49      Zero_Inflated_NB
14 Black/African American        1970     50-59      Zero_Inflated_NB
15 Black/African American        1970     60-69      Zero_Inflated_NB
16 Black/African American        1970       70+      Zero_Inflated_NB
17                  White        1980     40-49 Zero_Inflated_Poisson
18                  White        1980     50-59      Zero_Inflated_NB
19                  White        1980     60-69      Zero_Inflated_NB
20                  White        1980       70+      Zero_Inflated_NB
21 Black/African American        1980     40-49      Zero_Inflated_NB
22 Black/African American        1980     50-59      Zero_Inflated_NB
23 Black/African American        1980     60-69      Zero_Inflated_NB
24 Black/African American        1980       70+      Zero_Inflated_NB
25                  White        1990     40-49 Zero_Inflated_Poisson
26                  White        1990     50-59 Zero_Inflated_Poisson
27                  White        1990     60-69      Zero_Inflated_NB
28                  White        1990       70+      Zero_Inflated_NB
29 Black/African American        1990     40-49      Zero_Inflated_NB
30 Black/African American        1990     50-59      Zero_Inflated_NB
31 Black/African American        1990     60-69      Zero_Inflated_NB
32 Black/African American        1990       70+      Zero_Inflated_NB

Analyze the Effect of Race, Census Year, and Age Range

# Recode Best_Model to a binary variable (e.g., "Zero_Inflated_NB" vs. "Other")
best_models$Best_Model_Binary <- ifelse(best_models$Best_Model == "Zero_Inflated_NB", 1, 0)

# Fit binary logistic regression
model_logistic <- glm(Best_Model_Binary ~ Race + Census_Year + Age_Range, family = binomial(), data = best_models)

# Summary of the logistic regression model
summary(model_logistic)

Call:
glm(formula = Best_Model_Binary ~ Race + Census_Year + Age_Range, 
    family = binomial(), data = best_models)

Coefficients:
                             Estimate Std. Error z value Pr(>|z|)
(Intercept)                 8.741e+03  7.710e+06   0.001    0.999
RaceBlack/African American  8.903e+01  8.227e+04   0.001    0.999
Census_Year                -4.426e+00  3.902e+03  -0.001    0.999
Age_Range50-59              4.390e+01  5.002e+04   0.001    0.999
Age_Range60-69              8.990e+01  1.045e+05   0.001    0.999
Age_Range70+                8.990e+01  1.045e+05   0.001    0.999

(Dispersion parameter for binomial family taken to be 1)

    Null deviance: 1.9912e+01  on 31  degrees of freedom
Residual deviance: 2.4509e-09  on 26  degrees of freedom
AIC: 12

Number of Fisher Scoring iterations: 25

RESULT:The p-value for each variable is larger than 0.05, indicating non-significant effects on best model fitting.

Visualize the Results

ggplot(best_models, aes(x = Census_Year, y = Age_Range, fill = Best_Model)) +
  geom_tile(color = "white", lwd = 0.5, linetype = 1) + 
  facet_wrap(~Race, nrow = 2) +  
  scale_fill_manual(values = c("Zero_Inflated_Poisson" = "#0072B2", "Zero_Inflated_NB" = "#F0E442")) + 
  labs(
    title = "Best Model by Race, Census Year, and Age Range",
    x = "Census Year",
    y = "Age Range",
    fill = "Best Model"
  ) +
  theme_minimal() +
  theme(
    plot.title = element_text(size = 14, face = "bold"),
    legend.position = "bottom"
  )

Past versions of unnamed-chunk-8-1.png

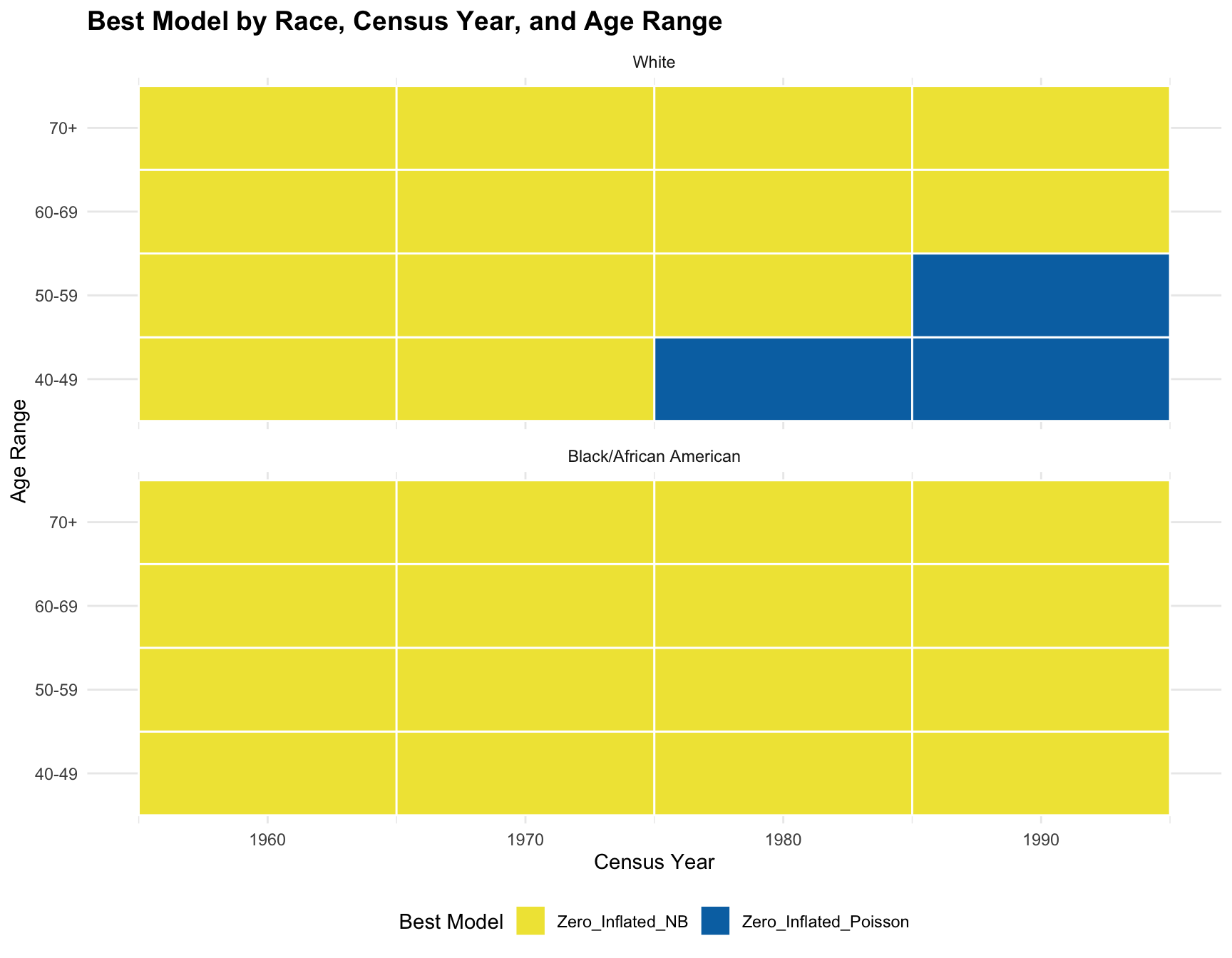
Version	Author	Date
2851385	Tina Lasisi	2024-09-21

Conclusion

The logistics regression shows that there isn’t a significant association between the predictors(races, age ranges, and census year) and the best-fitting model. According to the resulting visualization, the ZINB model is the best fit for the black population across census year and age group. However, the ZINB model perform the best among the white population only across year 1960 and 1970, and age group 60-69 and 70+.

Cohort Stability Analysis

The goal is to determine if there is a significant change in zero inflation, family size, or model fit for the same cohort across different census years, given race.

Table with Birth-Year (Cohort)

calculate_cohort <- function(census_year, age_range) {
  age_limits <- as.numeric(unlist(strsplit(age_range, "-|\\+")))
  
  if (length(age_limits) == 1) {
    lower_age <- age_limits
    upper_age <- Inf  
  } else {
    lower_age <- age_limits[1]
    upper_age <- age_limits[2]
  }
  
  lower_cohort <- census_year - upper_age
  upper_cohort <- census_year - lower_age
  
  
  if (upper_age == Inf) {
    upper_cohort <- census_year - 70
  }
  
  return(paste(lower_cohort, upper_cohort, sep = "-"))
}

best_models <- best_models %>%
  mutate(Cohort = mapply(calculate_cohort, Census_Year, Age_Range)) %>% 
  dplyr::select(Race, Census_Year, Age_Range, Best_Model, Cohort)

print(best_models)

                     Race Census_Year Age_Range            Best_Model    Cohort
1                   White        1960     40-49      Zero_Inflated_NB 1911-1920
2                   White        1960     50-59      Zero_Inflated_NB 1901-1910
3                   White        1960     60-69      Zero_Inflated_NB 1891-1900
4                   White        1960       70+      Zero_Inflated_NB -Inf-1890
5  Black/African American        1960     40-49      Zero_Inflated_NB 1911-1920
6  Black/African American        1960     50-59      Zero_Inflated_NB 1901-1910
7  Black/African American        1960     60-69      Zero_Inflated_NB 1891-1900
8  Black/African American        1960       70+      Zero_Inflated_NB -Inf-1890
9                   White        1970     40-49      Zero_Inflated_NB 1921-1930
10                  White        1970     50-59      Zero_Inflated_NB 1911-1920
11                  White        1970     60-69      Zero_Inflated_NB 1901-1910
12                  White        1970       70+      Zero_Inflated_NB -Inf-1900
13 Black/African American        1970     40-49      Zero_Inflated_NB 1921-1930
14 Black/African American        1970     50-59      Zero_Inflated_NB 1911-1920
15 Black/African American        1970     60-69      Zero_Inflated_NB 1901-1910
16 Black/African American        1970       70+      Zero_Inflated_NB -Inf-1900
17                  White        1980     40-49 Zero_Inflated_Poisson 1931-1940
18                  White        1980     50-59      Zero_Inflated_NB 1921-1930
19                  White        1980     60-69      Zero_Inflated_NB 1911-1920
20                  White        1980       70+      Zero_Inflated_NB -Inf-1910
21 Black/African American        1980     40-49      Zero_Inflated_NB 1931-1940
22 Black/African American        1980     50-59      Zero_Inflated_NB 1921-1930
23 Black/African American        1980     60-69      Zero_Inflated_NB 1911-1920
24 Black/African American        1980       70+      Zero_Inflated_NB -Inf-1910
25                  White        1990     40-49 Zero_Inflated_Poisson 1941-1950
26                  White        1990     50-59 Zero_Inflated_Poisson 1931-1940
27                  White        1990     60-69      Zero_Inflated_NB 1921-1930
28                  White        1990       70+      Zero_Inflated_NB -Inf-1920
29 Black/African American        1990     40-49      Zero_Inflated_NB 1941-1950
30 Black/African American        1990     50-59      Zero_Inflated_NB 1931-1940
31 Black/African American        1990     60-69      Zero_Inflated_NB 1921-1930
32 Black/African American        1990       70+      Zero_Inflated_NB -Inf-1920

Summary Statistics for Each Subset

df_merg <- df %>%
  rename(Census_Year = YEAR, Race = RACE, Age_Range = AGE_RANGE)

# Perform a left join to merge the data frames
merged_data <- left_join(df_merg, best_models, by = c("Race", "Census_Year", "Age_Range"))

calculate_mode <- function(x) {
  ux <- unique(x)
  ux[which.max(tabulate(match(x, ux)))]
}

summary_table <- merged_data %>% group_by(Race, Cohort, Census_Year) %>%
  summarise(
    Mean = mean(chborn_num),
    Variance = var(chborn_num),
    Mode = calculate_mode(chborn_num),
    Prob_0 = mean(chborn_num == 0),
    Prob_1 = mean(chborn_num == 1),
    Prob_2 = mean(chborn_num == 2),
    Prob_3 = mean(chborn_num == 3),
    Prob_4 = mean(chborn_num == 4),
    Prob_5 = mean(chborn_num == 5),
    Prob_6 = mean(chborn_num == 6),
    Prob_7 = mean(chborn_num == 7),
    Prob_8 = mean(chborn_num == 8),
    Prob_9 = mean(chborn_num == 9),
    Prob_10 = mean(chborn_num == 10),
    Prob_11 = mean(chborn_num == 11),
    Prob_12plus = mean(chborn_num >= 12)
    #Total_Prob = Prob_0 + Prob_1 + Prob_2 + Prob_3 + Prob_4 + Prob_5 + Prob_6 + 
                # Prob_7 + Prob_8 + Prob_9 + Prob_10 + Prob_11 + Prob_12plus
  ) %>%
  ungroup() %>% as.data.frame()

`summarise()` has grouped output by 'Race', 'Cohort'. You can override using
the `.groups` argument.

# View the summary table
print(summary_table)

                     Race    Cohort Census_Year     Mean  Variance Mode
1                   White -Inf-1890        1960 3.295149  8.035775    2
2                   White -Inf-1900        1970 2.619220  6.411794    0
3                   White -Inf-1910        1980 2.259255  4.905316    0
4                   White -Inf-1920        1990 2.310209  4.125397    2
5                   White 1891-1900        1960 2.749532  6.109824    2
6                   White 1901-1910        1960 2.357718  4.870047    2
7                   White 1901-1910        1970 2.198574  4.786569    0
8                   White 1911-1920        1960 2.383745  3.784971    2
9                   White 1911-1920        1970 2.290355  3.947823    2
10                  White 1911-1920        1980 2.299697  3.885418    2
11                  White 1921-1930        1970 2.697188  3.906783    2
12                  White 1921-1930        1980 2.728259  3.886124    2
13                  White 1921-1930        1990 2.796851  3.950610    2
14                  White 1931-1940        1980 2.901081  3.393930    2
15                  White 1931-1940        1990 2.894691  3.351678    2
16                  White 1941-1950        1990 2.204755  2.090623    2
17 Black/African American -Inf-1890        1960 3.902162 13.245048    0
18 Black/African American -Inf-1900        1970 3.087770 10.564482    0
19 Black/African American -Inf-1910        1980 2.613889  9.158011    0
20 Black/African American -Inf-1920        1990 2.856028  9.809749    0
21 Black/African American 1891-1900        1960 3.166572 10.973569    0
22 Black/African American 1901-1910        1960 2.741205  9.730068    0
23 Black/African American 1901-1910        1970 2.618036  9.023970    0
24 Black/African American 1911-1920        1960 2.820761  9.475099    0
25 Black/African American 1911-1920        1970 2.795064  9.124200    0
26 Black/African American 1911-1920        1980 2.817014  9.453284    0
27 Black/African American 1921-1930        1970 3.411675  9.564633    0
28 Black/African American 1921-1930        1980 3.400445  9.646242    0
29 Black/African American 1921-1930        1990 3.643816 10.234543    0
30 Black/African American 1931-1940        1980 3.721409  7.972764    3
31 Black/African American 1931-1940        1990 3.723892  7.741557    2
32 Black/African American 1941-1950        1990 2.690402  3.955388    2
      Prob_0     Prob_1    Prob_2     Prob_3     Prob_4     Prob_5     Prob_6
1  0.1601171 0.14383842 0.1735320 0.14095304 0.10820180 0.07719472 0.05585582
2  0.2337344 0.15563563 0.1907270 0.13766146 0.09400089 0.06100962 0.04147614
3  0.2425410 0.17905944 0.2217025 0.14213617 0.08185637 0.04957835 0.03016161
4  0.2003224 0.17086054 0.2495743 0.16517318 0.09503183 0.05020253 0.02764322
5  0.1790942 0.17183505 0.2064320 0.14997168 0.10013557 0.06473203 0.04249112
6  0.2000759 0.19774610 0.2351671 0.14591432 0.08571877 0.04872973 0.03009123
7  0.2484123 0.18579166 0.2226615 0.13859746 0.08031093 0.04560480 0.02848213
8  0.1548323 0.18555184 0.2691760 0.17613893 0.09801059 0.05041189 0.02763336
9  0.1967171 0.16973904 0.2562944 0.16982255 0.09505741 0.04905532 0.02524530
10 0.1926550 0.16842906 0.2583952 0.17291618 0.09513579 0.04901138 0.02691150
11 0.1351880 0.12673286 0.2507330 0.20721415 0.13102862 0.06863779 0.03679984
12 0.1318459 0.12042477 0.2503092 0.21324354 0.13229042 0.07044023 0.03706567
13 0.1234195 0.11569770 0.2477657 0.21626065 0.13752802 0.07369103 0.03953569
14 0.1037357 0.09351712 0.2399871 0.23964134 0.16043259 0.08265468 0.04216199
15 0.1031027 0.09122701 0.2441949 0.24135347 0.15966028 0.08278604 0.04035221
16 0.1389518 0.13595406 0.3532313 0.22043189 0.09474345 0.03452663 0.01315010
17 0.1979522 0.14761092 0.1242890 0.08902162 0.08447099 0.05830489 0.06058020
18 0.2601452 0.16502234 0.1285369 0.09959047 0.08460536 0.05835815 0.04579300
19 0.3019568 0.19414247 0.1310909 0.09464126 0.06778360 0.04744852 0.03824018
20 0.2758865 0.18308004 0.1298886 0.09979737 0.07163121 0.05420466 0.04346505
21 0.2480664 0.17732503 0.1284663 0.09677419 0.07508017 0.05715903 0.04584041
22 0.2864718 0.19580962 0.1319193 0.09169684 0.07281428 0.04837041 0.03879979
23 0.2998207 0.18659938 0.1367953 0.09436218 0.07231556 0.05491733 0.03625739
24 0.2685870 0.18750000 0.1383696 0.09891304 0.07510870 0.05206522 0.04413043
25 0.2644968 0.18741749 0.1396872 0.10373718 0.07936427 0.05255408 0.04305880
26 0.2708013 0.17914380 0.1436883 0.10406147 0.07178924 0.05433589 0.04368825
27 0.1825328 0.15683751 0.1417145 0.12075385 0.09643760 0.07621236 0.05796369
28 0.1890040 0.15089492 0.1437869 0.12280552 0.09454483 0.07185065 0.05917616
29 0.1674815 0.14605222 0.1425153 0.11640487 0.09497555 0.07968376 0.06407989
30 0.1190148 0.12667930 0.1436445 0.14424733 0.12435412 0.10032725 0.07543920
31 0.1110096 0.12261307 0.1537688 0.14536318 0.13001370 0.09821836 0.07747830
32 0.1258126 0.15923518 0.2409178 0.18860421 0.12466539 0.07319312 0.04221797
        Prob_7      Prob_8       Prob_9      Prob_10      Prob_11  Prob_12plus
1  0.041084387 0.034021662 0.0232983786 0.0170538963 0.0107017506 0.0141469822
2  0.027730366 0.021085755 0.0136685140 0.0098475111 0.0061248428 0.0072978345
3  0.018016649 0.012731042 0.0087478429 0.0054809686 0.0032668743 0.0047212303
4  0.015665041 0.009936348 0.0059849549 0.0041084566 0.0023807556 0.0031164752
5  0.028642035 0.019752536 0.0133514098 0.0101079439 0.0054400988 0.0080142781
6  0.019685606 0.013481499 0.0084292090 0.0063219068 0.0035732517 0.0050653787
7  0.016949039 0.011846964 0.0078935242 0.0056162892 0.0031186767 0.0047147446
8  0.015027420 0.008985590 0.0057688199 0.0033710799 0.0022909100 0.0028013199
9  0.014739040 0.009003132 0.0055114823 0.0034551148 0.0020929019 0.0032672234
10 0.013830609 0.009086128 0.0053711101 0.0032338559 0.0018127497 0.0032114763
11 0.018971640 0.010663352 0.0060738619 0.0036086503 0.0017938349 0.0025543789
12 0.019924245 0.010812430 0.0055849728 0.0036524562 0.0019035288 0.0025026089
13 0.019747920 0.011179196 0.0063567977 0.0038260350 0.0019827629 0.0030090171
14 0.019447458 0.009181204 0.0046502200 0.0023370336 0.0011565932 0.0010969750
15 0.019026010 0.009492189 0.0043714027 0.0021336608 0.0010720345 0.0012281560
16 0.005115379 0.002117610 0.0008191578 0.0004008645 0.0002875767 0.0002701478
17 0.047781570 0.044368601 0.0346985210 0.0315699659 0.0236063709 0.0557451650
18 0.037043931 0.029318690 0.0252233805 0.0209419211 0.0134028295 0.0320178704
19 0.034531270 0.023404527 0.0170098478 0.0170098478 0.0092083387 0.0235324210
20 0.037082067 0.029078014 0.0217831814 0.0163120567 0.0094224924 0.0283687943
21 0.039615167 0.034899076 0.0239577438 0.0260328240 0.0130164120 0.0337672137
22 0.029487843 0.028711847 0.0210812209 0.0165545784 0.0102172788 0.0280651837
23 0.029749651 0.023109104 0.0184607212 0.0138787436 0.0094959825 0.0242379972
24 0.035434783 0.026847826 0.0191304348 0.0186956522 0.0103260870 0.0248913043
25 0.031938662 0.028688941 0.0201076470 0.0160454961 0.0108662537 0.0220371687
26 0.031503842 0.025795829 0.0222832053 0.0171240395 0.0107574094 0.0250274424
27 0.049046196 0.036037692 0.0242702827 0.0204091014 0.0130085038 0.0247759136
28 0.047529331 0.036139419 0.0262053610 0.0196968399 0.0139590648 0.0244069538
29 0.052637054 0.039633829 0.0263185270 0.0241339852 0.0160199730 0.0300634557
30 0.057698932 0.040475370 0.0259214606 0.0170513262 0.0102480193 0.0148983810
31 0.055824577 0.039013248 0.0278666058 0.0152581087 0.0074920055 0.0160804020
32 0.020573614 0.012848948 0.0061185468 0.0022944551 0.0014531549 0.0020650096

Test for Significant Changes Over Time Within Each Cohort

The goal is to determine if there is a significant change in any of the following across census years for the same cohort:

1. Zero Inflation: Check if the proportion of women with zero children changes significantly over time for the same cohort.
2. Family Size: Test if the mean or variance in the number of children changes for the same cohort over time.
3. Model Fit: Analyze if the best-fitting model for the cohort changes over time.

a. Zero-Inflation Analysis

## divided the corhort by race
merged_df_black <- merged_data %>% filter(Race == "Black/African American")
merged_df_white <- merged_data %>% filter(Race == "White")

# Data frame to store proportions
proportions_df_b <- data.frame(Cohort = character(), Census_Year = character(), 
                             Proportion_Zero_Children = numeric(), Race = character(), stringsAsFactors = FALSE)

# Filter cohorts with more than one census year
cohort_counts <- merged_df_black %>%
  group_by(Cohort) %>%
  summarise(Unique_Census_Years = n_distinct(Census_Year)) %>%
  filter(Unique_Census_Years > 1)

# Get the list of cohorts for testing
cohorts_for_test <- cohort_counts$Cohort

# Initialize results data frame
results_black <- data.frame(RACE = character(), Cohort = character(), Chi_Square = numeric(), p_value = numeric(), stringsAsFactors = FALSE)

# Loop through each cohort and run the chi-square test
for (cohort in cohorts_for_test) {
  cohort_data <- merged_df_black %>% filter(Cohort == cohort)
  
  # Create contingency table
  contingency_table <- table(cohort_data$Census_Year, cohort_data$chborn_num == "0")
  
  # Perform the chi-square test only if more than one row is in the table
  if (nrow(contingency_table) > 1) {
    test_result <- chisq.test(contingency_table)
    
    # Append results to the results data frame
    results_black <- rbind(results_black, data.frame(
      RACE = "Black/African American",
      Cohort = cohort,
      Chi_Square = test_result$statistic,
      p_value = test_result$p.value
    ))
    
    # proportion across year
    proportions <- cohort_data %>%
      group_by(Census_Year) %>%
      summarise(Proportion_Zero_Children = mean(chborn_num == "0"))
    
    proportions$Cohort <- cohort
    proportions$Race <- "Black"
    
    # Combine into one data frame
    proportions_df_b <- rbind(proportions_df_b, proportions)
  
    # Print proportions for review
    print(paste("Proportions for cohort:", cohort))
    print(proportions)
  }
}

[1] "Proportions for cohort: 1901-1910"
# A tibble: 2 × 4
  Census_Year Proportion_Zero_Children Cohort    Race 
        <int>                    <dbl> <chr>     <chr>
1        1960                    0.286 1901-1910 Black
2        1970                    0.300 1901-1910 Black
[1] "Proportions for cohort: 1911-1920"
# A tibble: 3 × 4
  Census_Year Proportion_Zero_Children Cohort    Race 
        <int>                    <dbl> <chr>     <chr>
1        1960                    0.269 1911-1920 Black
2        1970                    0.264 1911-1920 Black
3        1980                    0.271 1911-1920 Black
[1] "Proportions for cohort: 1921-1930"
# A tibble: 3 × 4
  Census_Year Proportion_Zero_Children Cohort    Race 
        <int>                    <dbl> <chr>     <chr>
1        1970                    0.183 1921-1930 Black
2        1980                    0.189 1921-1930 Black
3        1990                    0.167 1921-1930 Black
[1] "Proportions for cohort: 1931-1940"
# A tibble: 2 × 4
  Census_Year Proportion_Zero_Children Cohort    Race 
        <int>                    <dbl> <chr>     <chr>
1        1980                    0.119 1931-1940 Black
2        1990                    0.111 1931-1940 Black

results_black <- results_black %>%
  mutate(Significance = ifelse(p_value > 0.05, "No", "Yes"))

print(results_black)

                             RACE    Cohort Chi_Square      p_value
X-squared  Black/African American 1901-1910   4.310851 0.0378700083
X-squared1 Black/African American 1911-1920   1.421550 0.4912633533
X-squared2 Black/African American 1921-1930  17.245995 0.0001799202
X-squared3 Black/African American 1931-1940   3.466056 0.0626405054
           Significance
X-squared           Yes
X-squared1           No
X-squared2          Yes
X-squared3           No

# Function to determine the nature of change
determine_nature_of_change <- function(proportions) {
  if (nrow(proportions) > 1) {
    if (all(diff(proportions$Proportion_Zero_Children) > 0)) {
      return("Increase")
    } else if (all(diff(proportions$Proportion_Zero_Children) < 0)) {
      return("Decrease")
    } else {
      return("Mixed/No Change")
    }
  } else {
    return("Not Applicable")
  }
}

# Add the Nature_of_Change column
results_black$Nature_of_Change <- NA  # Initialize the column

# Loop through each cohort in results_black
for (i in 1:nrow(results_black)) {
  cohort <- results_black$Cohort[i]
  cohort_data <- merged_df_black %>% filter(Cohort == cohort)
  
  # Calculate proportions for the cohort
  proportions <- cohort_data %>%
    group_by(Census_Year) %>%
    summarise(Proportion_Zero_Children = mean(chborn_num == "0"))
    
  # Determine nature of change
  results_black$Nature_of_Change[i] <- determine_nature_of_change(proportions)
}

# View the updated results_black
print(results_black)

                             RACE    Cohort Chi_Square      p_value
X-squared  Black/African American 1901-1910   4.310851 0.0378700083
X-squared1 Black/African American 1911-1920   1.421550 0.4912633533
X-squared2 Black/African American 1921-1930  17.245995 0.0001799202
X-squared3 Black/African American 1931-1940   3.466056 0.0626405054
           Significance Nature_of_Change
X-squared           Yes         Increase
X-squared1           No  Mixed/No Change
X-squared2          Yes  Mixed/No Change
X-squared3           No         Decrease

# Data frame to store proportions
proportions_df_w <- data.frame(Cohort = character(), Census_Year = character(), 
                             Proportion_Zero_Children = numeric(), Race = character(), stringsAsFactors = FALSE)

# Filter cohorts with more than one census year
cohort_counts2 <- merged_df_white %>%
  group_by(Cohort) %>%
  summarise(Unique_Census_Years = n_distinct(Census_Year)) %>%
  filter(Unique_Census_Years > 1)

# Get the list of cohorts for testing
cohorts_for_test2 <- cohort_counts2$Cohort

# Initialize results data frame
results_white <- data.frame(RACE = character(), Cohort = character(), Chi_Square = numeric(), p_value = numeric(), stringsAsFactors = FALSE)

# Loop through each cohort and run the chi-square test
for (cohort in cohorts_for_test2) {
  cohort_data <- merged_df_white %>% filter(Cohort == cohort)
  
  # Create contingency table
  contingency_table <- table(cohort_data$Census_Year, cohort_data$chborn_num == "0")
  
  # Perform the chi-square test only if more than one row is in the table
  if (nrow(contingency_table) > 1) {
    test_result <- chisq.test(contingency_table)
    
    # Append results to the results data frame
    results_white <- rbind(results_white, data.frame(
      RACE = "White",
      Cohort = cohort,
      Chi_Square = test_result$statistic,
      p_value = test_result$p.value
    ))
    
    # proportion across year
    proportions <- cohort_data %>%
      group_by(Census_Year) %>%
      summarise(Proportion_Zero_Children = mean(chborn_num == "0"))
    
    proportions$Cohort <- cohort
    proportions$Race <- "White"
    
    # Combine into one data frame
    proportions_df_w <- rbind(proportions_df_w, proportions)
  
    # Print proportions for review
    print(paste("Proportions for cohort:", cohort))
    print(proportions)
  }
}

[1] "Proportions for cohort: 1901-1910"
# A tibble: 2 × 4
  Census_Year Proportion_Zero_Children Cohort    Race 
        <int>                    <dbl> <chr>     <chr>
1        1960                    0.200 1901-1910 White
2        1970                    0.248 1901-1910 White
[1] "Proportions for cohort: 1911-1920"
# A tibble: 3 × 4
  Census_Year Proportion_Zero_Children Cohort    Race 
        <int>                    <dbl> <chr>     <chr>
1        1960                    0.155 1911-1920 White
2        1970                    0.197 1911-1920 White
3        1980                    0.193 1911-1920 White
[1] "Proportions for cohort: 1921-1930"
# A tibble: 3 × 4
  Census_Year Proportion_Zero_Children Cohort    Race 
        <int>                    <dbl> <chr>     <chr>
1        1970                    0.135 1921-1930 White
2        1980                    0.132 1921-1930 White
3        1990                    0.123 1921-1930 White
[1] "Proportions for cohort: 1931-1940"
# A tibble: 2 × 4
  Census_Year Proportion_Zero_Children Cohort    Race 
        <int>                    <dbl> <chr>     <chr>
1        1980                    0.104 1931-1940 White
2        1990                    0.103 1931-1940 White

results_white <- results_white %>%
  mutate(Significance = ifelse(p_value > 0.05, "No", "Yes"))

print(results_white)

            RACE    Cohort  Chi_Square       p_value Significance
X-squared  White 1901-1910 662.9400598 3.427247e-146          Yes
X-squared1 White 1911-1920 711.8344845 2.673657e-155          Yes
X-squared2 White 1921-1930  80.1733778  3.895581e-18          Yes
X-squared3 White 1931-1940   0.1867867  6.656046e-01           No

# Add the Nature_of_Change column
results_white$Nature_of_Change <- NA  # Initialize the column

# Loop through each cohort in results_white
for (i in 1:nrow(results_white)) {
  cohort <- results_white$Cohort[i]
  cohort_data <- merged_df_white %>% filter(Cohort == cohort)
  
  # Calculate proportions for the cohort
  proportions <- cohort_data %>%
    group_by(Census_Year) %>%
    summarise(Proportion_Zero_Children = mean(chborn_num == "0"))
  
  # Determine nature of change
  results_white$Nature_of_Change[i] <- determine_nature_of_change(proportions)
}

# View the updated results_white
print(results_white)

            RACE    Cohort  Chi_Square       p_value Significance
X-squared  White 1901-1910 662.9400598 3.427247e-146          Yes
X-squared1 White 1911-1920 711.8344845 2.673657e-155          Yes
X-squared2 White 1921-1930  80.1733778  3.895581e-18          Yes
X-squared3 White 1931-1940   0.1867867  6.656046e-01           No
           Nature_of_Change
X-squared          Increase
X-squared1  Mixed/No Change
X-squared2         Decrease
X-squared3         Decrease

# Combine the two data frames
combined_result <- rbind(results_black, results_white)

# Create the plot
ggplot(combined_result, aes(x = Cohort, y = p_value, color = RACE, shape = Significance)) +
  geom_point(size = 2) +
  geom_line(aes(group = RACE)) +
    annotate("text", x = Inf, y = 0.05, label = "p = 0.05", hjust = 1.1, vjust = -0.5, color = "red", size = 3) +
  geom_hline(yintercept = 0.05, linetype = "dashed", color = "red", size = 0.5) + 
  scale_y_log10() +  # Use log scale for better visualization if p-values vary widely
  labs(
    title = "Change of p-values by Cohort",
    x = "Cohort",
    y = "p-value (log scale)",
    color = "Race",
    shape = "Significance"
  ) +
  theme_minimal() +
  theme(axis.text.x = element_text(angle = 45, hjust = 1))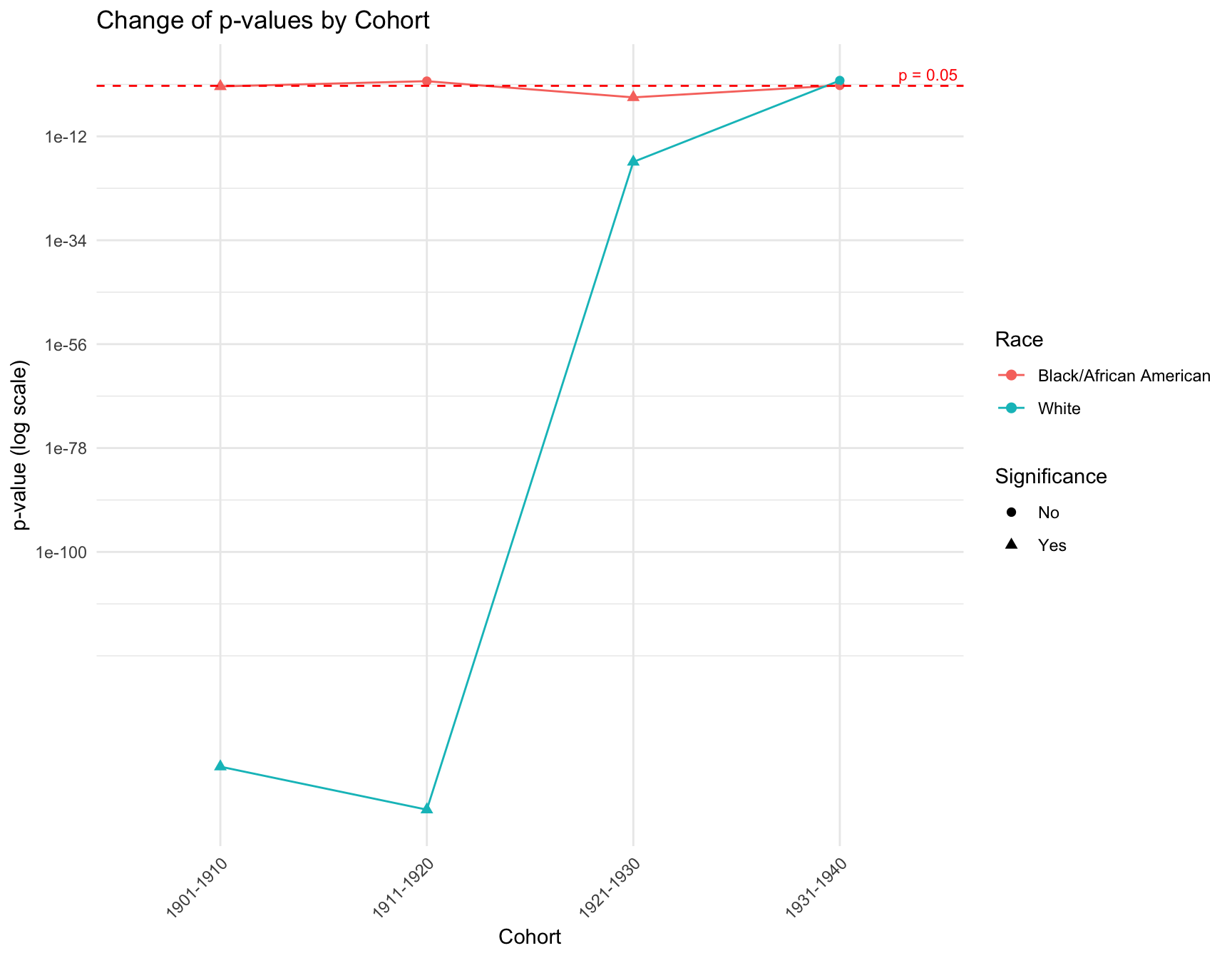

Past versions of unnamed-chunk-17-1.png

Version	Author	Date
2851385	Tina Lasisi	2024-09-21

RESULT: The graph shows that there is a discrepancy in the p-value within the cohorts like 1901-1910, 1911-1920 and 1921-1930 by race. However, in cohort 1931-1941, the p-value of each race is pretty close to each other. The overall trend of the p-value for black population is stable across cohort, while the trend for white population fluctuate a lot.

b. Family Size Analysis

merged_data2 <- left_join(merged_data, summary_table, by = c("Race","Cohort","Census_Year")) %>% dplyr::select(Race, Cohort, Census_Year, Mean, Variance)
merged_black = merged_data2 %>% filter(Race == "Black/African American")
merged_white = merged_data2 %>% filter(Race == "White")

cohorts1 <- unique(merged_black$Cohort)

# Loop through each cohort and apply ANOVA for Mean and Variance
for (cohort in cohorts1) {
  
  # Filter data for the specific cohort
  cohort_data_b <- merged_black[merged_black$Cohort == cohort, ]
  
  # Check if there are at least two unique Census_Year values
  if (length(unique(cohort_data_b$Census_Year)) < 2) {
    cat("\nCohort:", cohort, "has only one Census Year. Skipping ANOVA.\n")
    next
  }
  
  # Perform ANOVA for Mean
  anova_mean_result <- aov(Mean ~ factor(Census_Year), data = cohort_data_b)
  
  # Perform ANOVA for Variance
  anova_variance_result <- aov(Variance ~ factor(Census_Year), data = cohort_data_b)
  
  # Output the results
  cat("\nCohort:", cohort)
  cat("\nANOVA for Mean Family Size:\n")
  print(summary(anova_mean_result))
}

Cohort: 1891-1900 has only one Census Year. Skipping ANOVA.

Cohort: 1911-1920
ANOVA for Mean Family Size:
                       Df Sum Sq Mean Sq   F value Pr(>F)    
factor(Census_Year)     2  5.453   2.727 8.507e+23 <2e-16 ***
Residuals           38001  0.000   0.000                     
---
Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

Cohort: 1901-1910
ANOVA for Mean Family Size:
                       Df Sum Sq Mean Sq   F value Pr(>F)    
factor(Census_Year)     1  77.51   77.51 7.094e+25 <2e-16 ***
Residuals           22789   0.00    0.00                     
---
Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

Cohort: -Inf-1890 has only one Census Year. Skipping ANOVA.

Cohort: 1921-1930
ANOVA for Mean Family Size:
                       Df Sum Sq Mean Sq   F value Pr(>F)    
factor(Census_Year)     2    417   208.5 4.477e+26 <2e-16 ***
Residuals           43042      0     0.0                     
---
Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

Cohort: -Inf-1900 has only one Census Year. Skipping ANOVA.

Cohort: 1931-1940
ANOVA for Mean Family Size:
                       Df  Sum Sq Mean Sq   F value Pr(>F)    
factor(Census_Year)     1 0.03475 0.03475 1.223e+22 <2e-16 ***
Residuals           22555 0.00000 0.00000                     
---
Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

Cohort: -Inf-1910 has only one Census Year. Skipping ANOVA.

Cohort: 1941-1950 has only one Census Year. Skipping ANOVA.

Cohort: -Inf-1920 has only one Census Year. Skipping ANOVA.

cohorts2 <- unique(merged_white$Cohort)

# Loop through each cohort and apply ANOVA for Mean and Variance
for (cohort in cohorts2) {
  
  # Filter data for the specific cohort
  cohort_data_w <- merged_white[merged_white$Cohort == cohort, ]
  
  # Check if there are at least two unique Census_Year values
  if (length(unique(cohort_data_w$Census_Year)) < 2) {
    cat("\nCohort:", cohort, "has only one Census Year. Skipping ANOVA.\n")
    next
  }
  
  # Perform ANOVA for Mean
  anova_mean_result <- aov(Mean ~ factor(Census_Year), data = cohort_data_w)
  
  # Output the results
  cat("\nCohort:", cohort)
  cat("\nANOVA for Mean Family Size:\n")
  print(summary(anova_mean_result))
}

Cohort: 1891-1900 has only one Census Year. Skipping ANOVA.

Cohort: 1911-1920
ANOVA for Mean Family Size:
                        Df Sum Sq Mean Sq   F value Pr(>F)    
factor(Census_Year)      2  535.2   267.6 4.546e+24 <2e-16 ***
Residuals           365210    0.0     0.0                     
---
Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

Cohort: 1901-1910
ANOVA for Mean Family Size:
                        Df Sum Sq Mean Sq   F value Pr(>F)    
factor(Census_Year)      1   1281    1281 9.604e+25 <2e-16 ***
Residuals           226142      0       0                     
---
Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

Cohort: -Inf-1890 has only one Census Year. Skipping ANOVA.

Cohort: -Inf-1900 has only one Census Year. Skipping ANOVA.

Cohort: 1921-1930
ANOVA for Mean Family Size:
                        Df Sum Sq Mean Sq   F value Pr(>F)    
factor(Census_Year)      2  653.9     327 8.029e+23 <2e-16 ***
Residuals           394507    0.0       0                     
---
Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

Cohort: 1931-1940
ANOVA for Mean Family Size:
                        Df Sum Sq Mean Sq   F value Pr(>F)    
factor(Census_Year)      1  1.829   1.829 8.533e+22 <2e-16 ***
Residuals           179944  0.000   0.000                     
---
Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

Cohort: -Inf-1910 has only one Census Year. Skipping ANOVA.

Cohort: -Inf-1920 has only one Census Year. Skipping ANOVA.

Cohort: 1941-1950 has only one Census Year. Skipping ANOVA.

RESULT: 1.In both racial group, the ANOVA is not applicable for the following cohort since there is only one census year available in the data for those cohorts:-Inf-1910, 1941-1950, -Inf-1920, -Inf-1890, -Inf-1900, and 1891-1900 2.By looking at the ANOVA for mean family size in both racial group, the p-value of the rest cohorts (1901-1910, 1911-1920, 1921-1930, 1931-1940) are smaller than 0.05, indicating mean family size for these cohort has significantly changed over different census years in both population.

c. Model Fit Analysis

# Due to the due lack of data variability, I use visualization instead of test

ggplot(best_models, aes(x = Census_Year, y = Cohort, fill = Best_Model)) +
  geom_tile(color = "white", lwd = 0.5, linetype = 1) + # Create the tiles
  facet_wrap(~Race, nrow = 2) + # Facet by Race
  scale_fill_manual(values = c("Zero_Inflated_Poisson" = "#0072B2", "Zero_Inflated_NB" = "#F0E442")) + 
  labs(
    title = "Best Model by Race, Census Year, and Cohort(Birth Range)",
    x = "Census Year",
    y = "Birth Range",
    fill = "Best Model"
  ) +
  theme_minimal() +
  theme(
    plot.title = element_text(size = 14, face = "bold"),
    legend.position = "bottom"
  )

Past versions of unnamed-chunk-21-1.png

Version	Author	Date
f567c4a	linmatch	2024-12-16
231390a	linmatch	2024-12-11
776920f	linmatch	2024-11-12
2851385	Tina Lasisi	2024-09-21

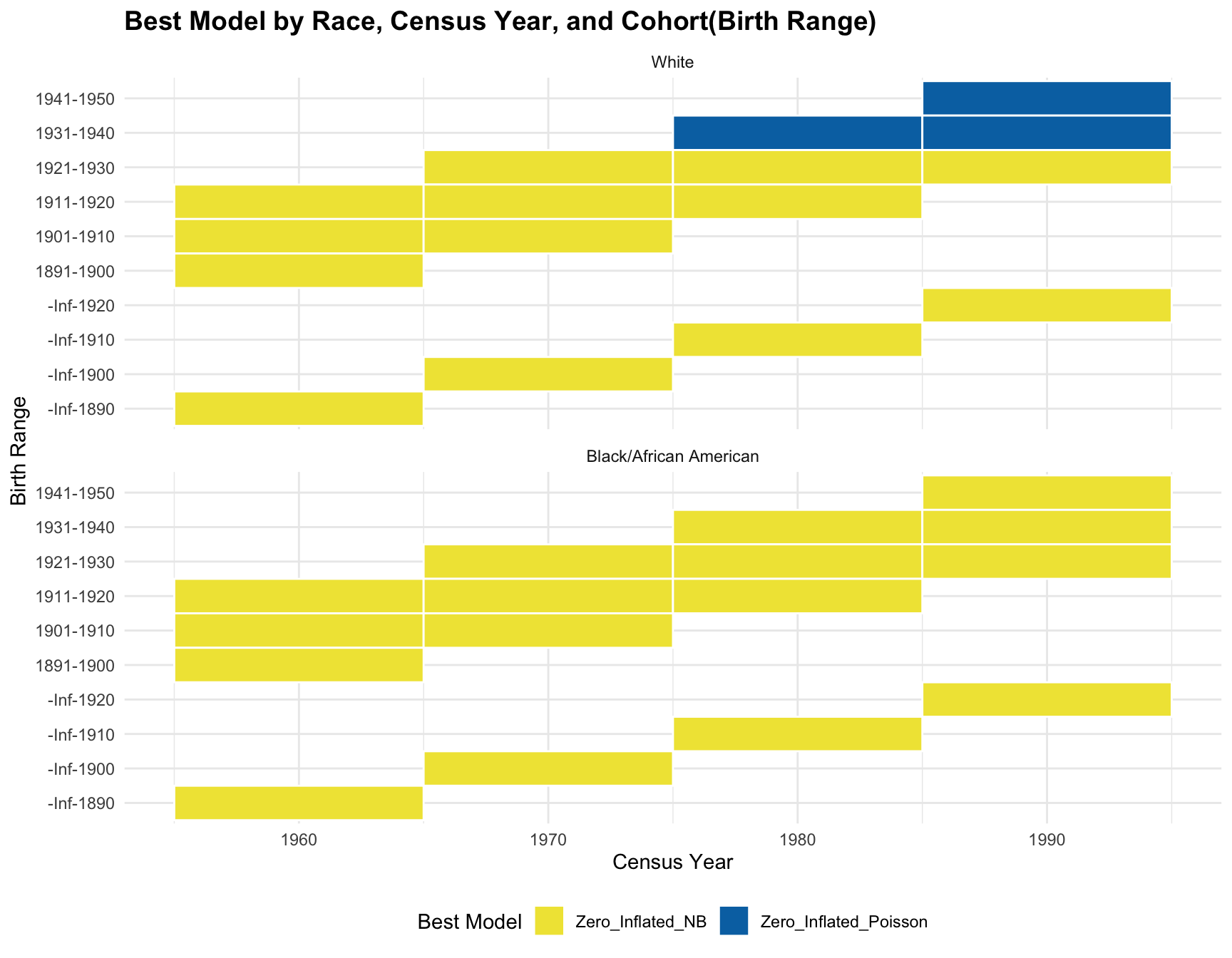
RESULT: Based on the heatmap created, we can see that the model fit for each cohort(cohort with 2+ corresponding census year) across year does not change.

Conclusion

• Zero-inflation: We observe that the proportion of women with zero children change significantly across census year in the following cohort by race: -black population:1901-1910, 1921-1930 -white population:1901-1910, 1911-1920, 1921-1930
• Family size: Cohorts 1901-1910, 1911-1920, 1921-1930, and 1931-1940 present significant change in mean family size across year for both races.
• Best-fitting Model: Model fit for each cohort(cohort with 2+ corresponding census year) across year does not change in both racial group.

Analyzing and Visualizing Significant Fertility Shifts

The goal is to summarize the previous information and create visualization that illustrates significant fertility shifts in cohorts, compares fertility patterns of 40-49 year-olds to 50-59 year-olds in the 1990 census so we can pick the set of fertility distributions we want to use to visualize the sibling distribution and do the math on the genetic surveillance.

Panel A: Fertility Distribution Shifts Across Cohorts

part1<- child_plot +
  geom_rect(data = df_mirror %>% filter((YEAR == 1960 & AGE_RANGE == "50-59")|
                                        (YEAR == 1970 & AGE_RANGE == "40-49")|
                                        (YEAR == 1970 & AGE_RANGE == "60-69")|
                                        (YEAR == 1980 & AGE_RANGE == "50-59")|
                                        (YEAR == 1990 & AGE_RANGE == "60-69")),
            aes(xmin = -0.45, xmax = 0.45, ymin = -0.3, ymax = 0.3), 
            fill = "blue", alpha = 0.03)

part2<- part1 +
  geom_rect(data = df_mirror %>% filter((YEAR == 1960 & AGE_RANGE == "40-49")|
                                        (YEAR == 1970 & AGE_RANGE == "50-59")|
                                        (YEAR == 1980 & AGE_RANGE == "60-69")),
            aes(xmin = -0.45, xmax = 0.45, ymin = -0.3, ymax = 0), 
            fill = "blue", alpha = 0.03) + 
  labs(title = "Fertility Distribution Shifts",
       subtitle = "Highlighted significant shifts in Number of zero Children",
       caption = "Annotations indicate key shifts in number of zero children across census years. White population shown on left (negative values), Black/African American on right (positive values)\nProportions normalized within each age range, race, and census year\nFootnote: The category '12+' includes families with 12 or more children.") +
  theme_minimal()+
  theme(
    plot.title = element_text(size = 14, hjust = 0.5),
    plot.subtitle = element_text(size = 12, hjust = 0.5), 
    plot.caption = element_text(size = 9, hjust = 0.5),  
    axis.text.y = element_text(size = 8),
    strip.text = element_text(size = 10)
  )
part2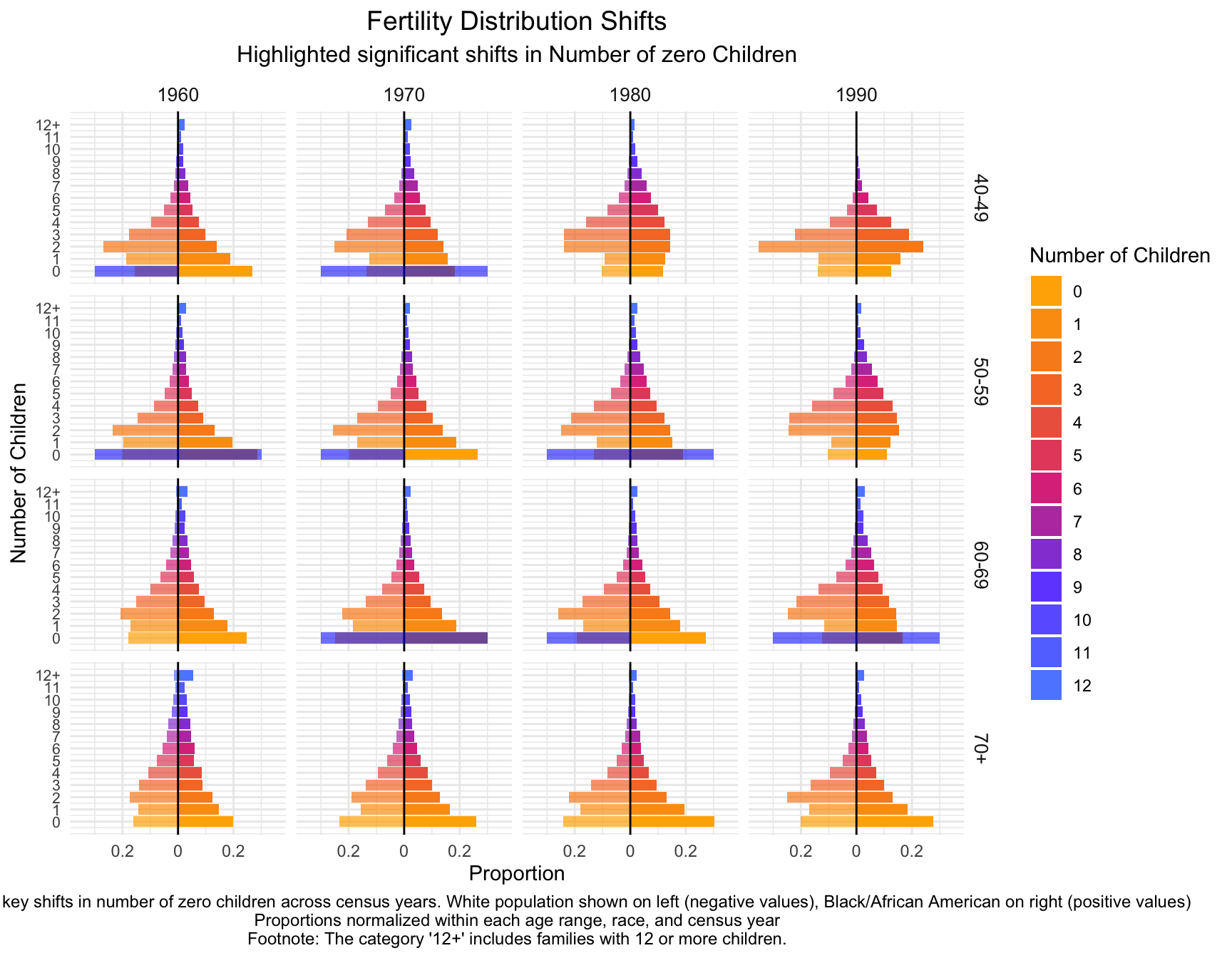

Past versions of unnamed-chunk-23-1.png

Version	Author	Date
2851385	Tina Lasisi	2024-09-21

child_plot +
  geom_rect(data = df_mirror %>% filter((YEAR == 1960 & AGE_RANGE == "40-49")|
                                        (YEAR == 1960 & AGE_RANGE == "50-59")|
                                        (YEAR == 1970 & AGE_RANGE == "40-49")|
                                        (YEAR == 1970 & AGE_RANGE == "50-59")|
                                        (YEAR == 1970 & AGE_RANGE == "60-69")|
                                        (YEAR == 1980 & AGE_RANGE == "40-49")|
                                        (YEAR == 1980 & AGE_RANGE == "50-59")|
                                        (YEAR == 1980 & AGE_RANGE == "60-69")|
                                        (YEAR == 1990 & AGE_RANGE == "50-59")|
                                        (YEAR == 1990 & AGE_RANGE == "60-69")),
            aes(xmin = -0.45, xmax = 13, ymin = -0.3, ymax = 0.3), 
            fill = "blue", alpha = 0.01) + 
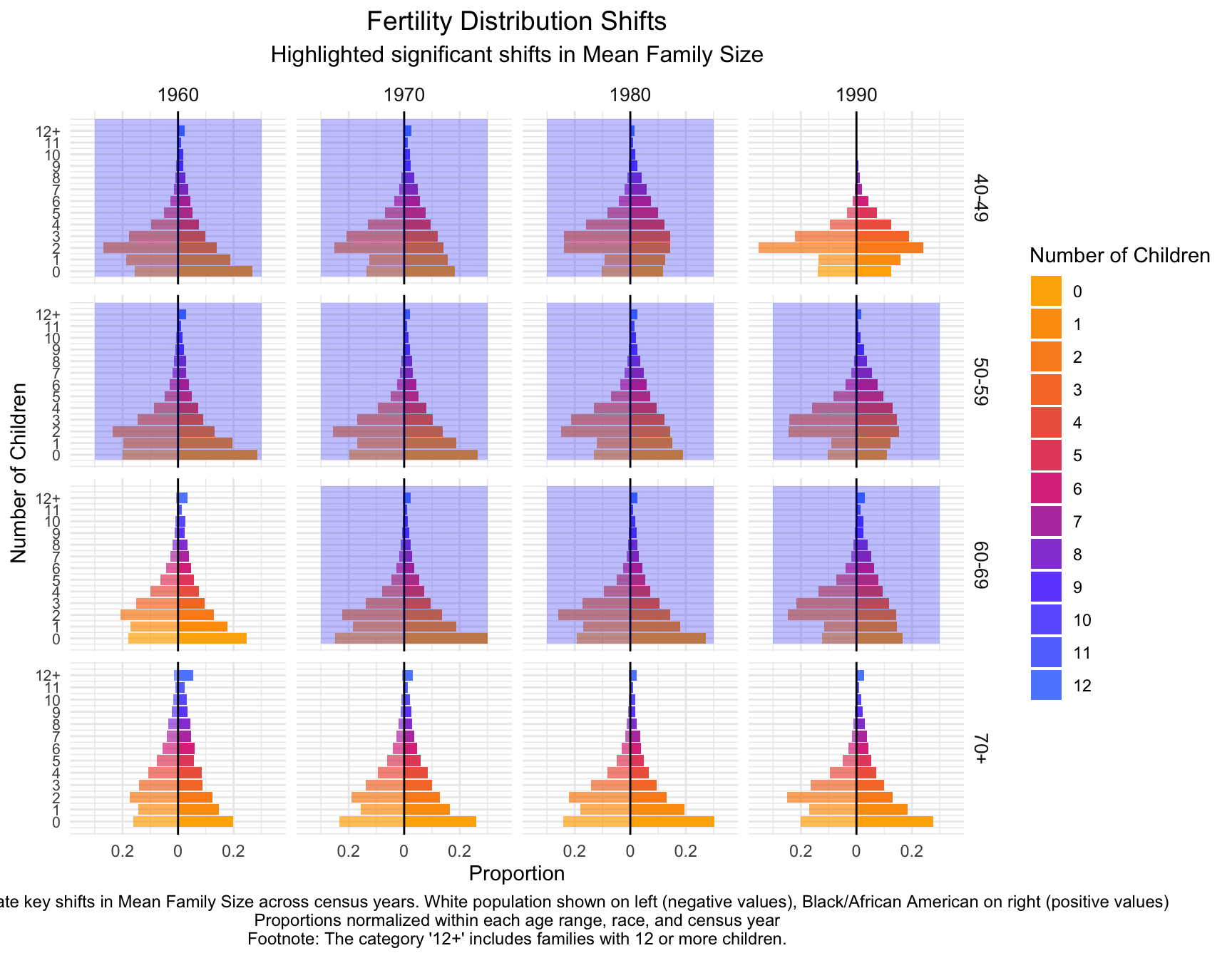
  labs(title = "Fertility Distribution Shifts",
       subtitle = "Highlighted significant shifts in Mean Family Size",
       caption = "Annotations indicate key shifts in Mean Family Size across census years. White population shown on left (negative values), Black/African American on right (positive values)\nProportions normalized within each age range, race, and census year\nFootnote: The category '12+' includes families with 12 or more children.") +
  theme_minimal()+
  theme(
    plot.title = element_text(size = 14, hjust = 0.5),
    plot.subtitle = element_text(size = 12, hjust = 0.5), 
    plot.caption = element_text(size = 9, hjust = 0.5),  
    axis.text.y = element_text(size = 8),
    strip.text = element_text(size = 10)
  )

Past versions of unnamed-chunk-24-1.png

Version	Author	Date
2851385	Tina Lasisi	2024-09-21

Additional Visualization: Nature of Significant Change across Year for Cohorts by Race

# Significant Change in Zero Inflation
## Balck population
filter_prop_b <- proportions_df_b %>% 
  filter(Cohort %in% c("1901-1910", "1921-1930"))

## White population
filter_prop_w <- proportions_df_w %>% 
  filter(Cohort %in% c("1901-1910", "1911-1920", "1921-1930"))

combined_data <- bind_rows(filter_prop_b, filter_prop_w)

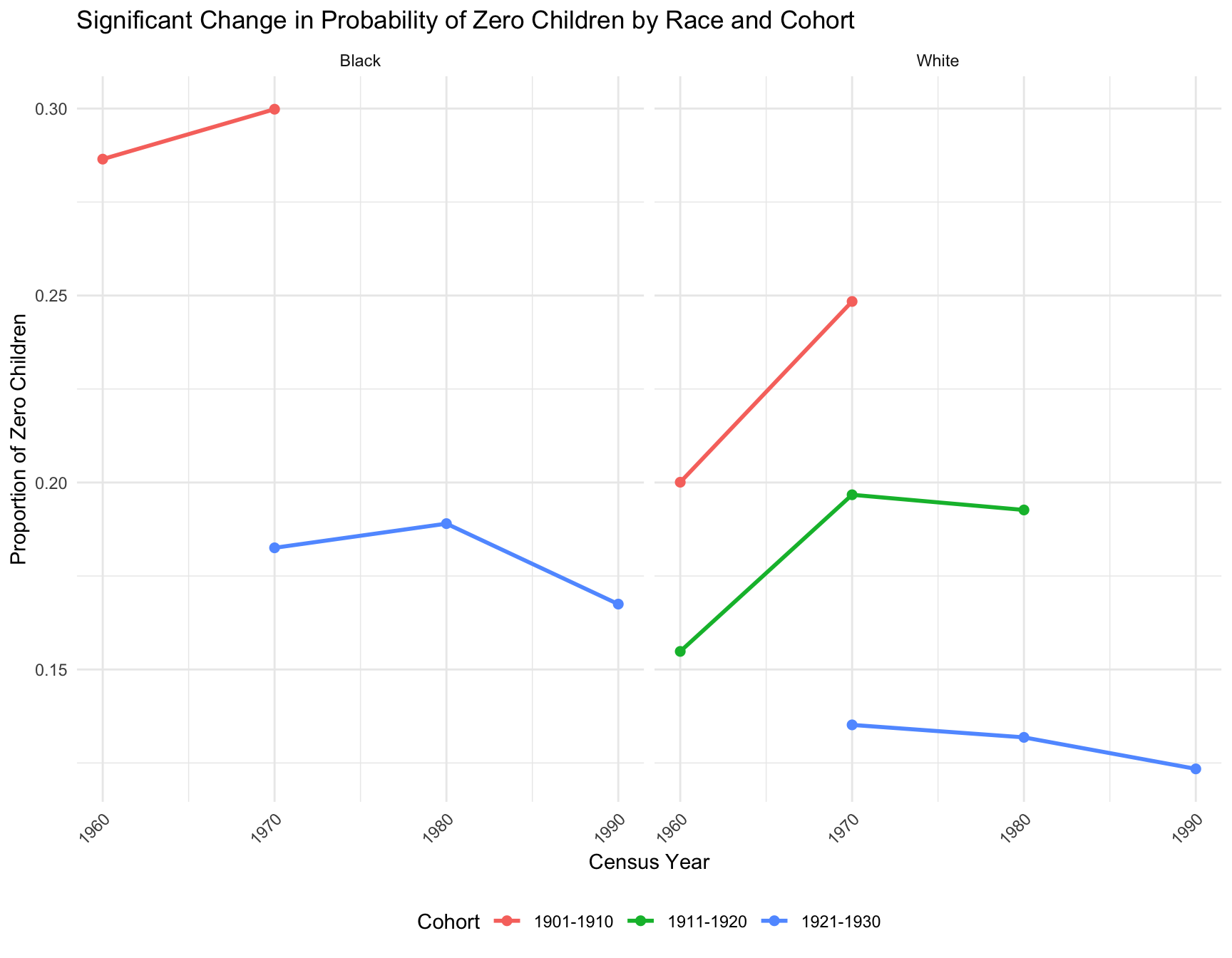
ggplot(combined_data, aes(x = Census_Year, y = Proportion_Zero_Children, color = Cohort)) +
  geom_line(size = 1) +
  geom_point(size = 2) +
  facet_wrap(~ Race, scales = "free_x") +
  labs(
    title = "Significant Change in Probability of Zero Children by Race and Cohort",
    x = "Census Year",
    y = "Proportion of Zero Children",
    color = "Cohort"
  ) +
  theme_minimal() +
  theme(
    axis.text.x = element_text(angle = 45, hjust = 1),
    legend.position = "bottom"
  )

Past versions of unnamed-chunk-25-1.png

Version	Author	Date
2851385	Tina Lasisi	2024-09-21

# Significant Change in mean family size

significant_cohorts <- c("1901-1910", "1911-1920", "1921-1930", "1931-1940")  # Replace with actual significant cohorts
filtered_data <- merged_data2 %>% filter(Cohort %in% significant_cohorts)

# Plot for significant cohorts
ggplot(filtered_data, aes(x = as.factor(Census_Year), y = Mean, color = Race, group = interaction(Cohort, Race))) +
  geom_line(size = 1) +
  geom_point(size = 2) +
  facet_wrap(~ Cohort, scales = "free_x") + 
  labs(
    title = "Significant Changes in Mean Family Size Over Census Years",
    x = "Census Year",
    y = "Mean Family Size",
    color = "Race"
  ) +
  theme_minimal() +
  theme(axis.text.x = element_text(angle = 45, hjust = 1))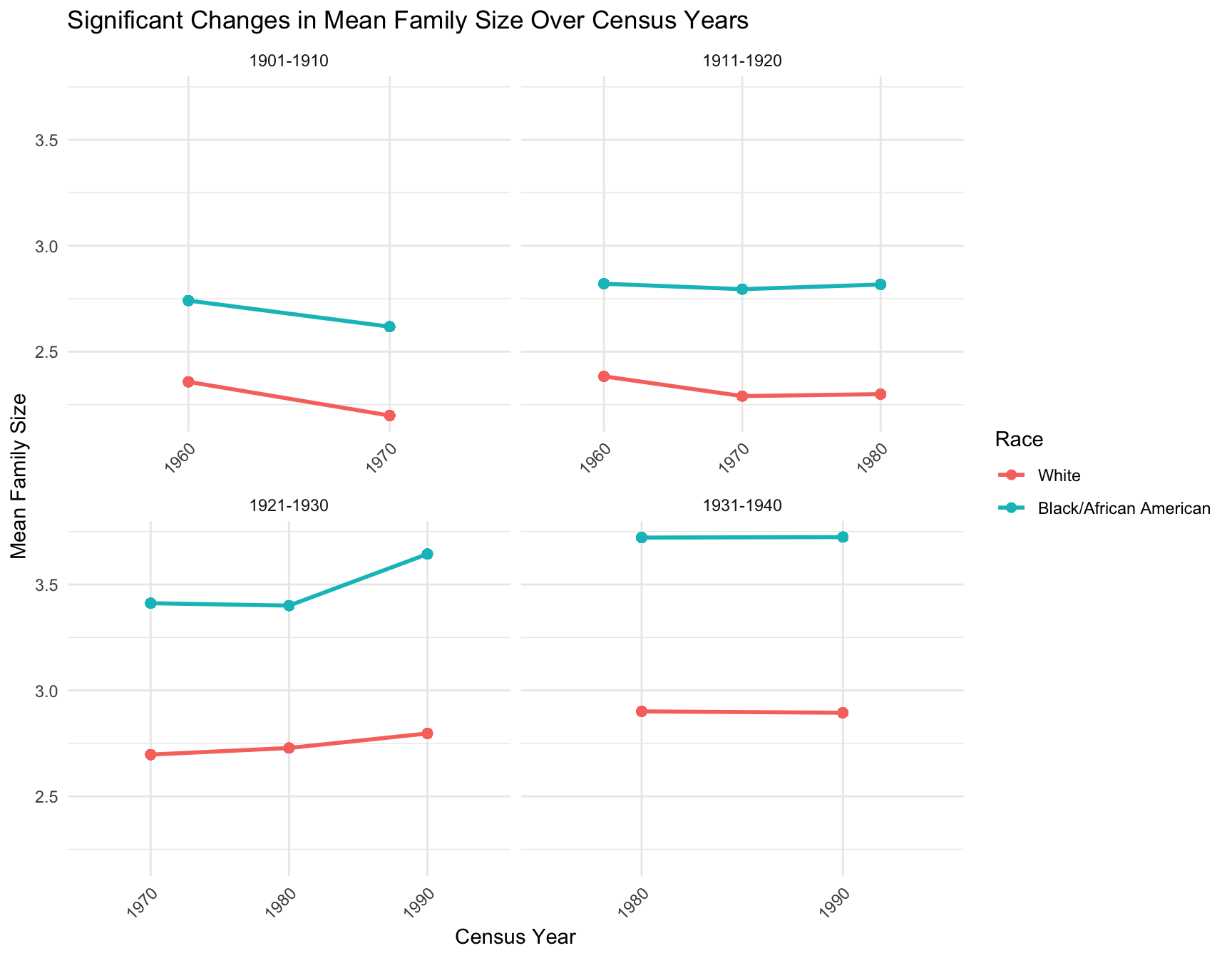

Past versions of unnamed-chunk-26-1.png

Version	Author	Date
8007864	linmatch	2024-12-03
2851385	Tina Lasisi	2024-09-21

Panel B: Comparison of 40-49 and 50-59 Age Groups in 1990

Visulization of Distribution

filter_df <- df_proportions %>% 
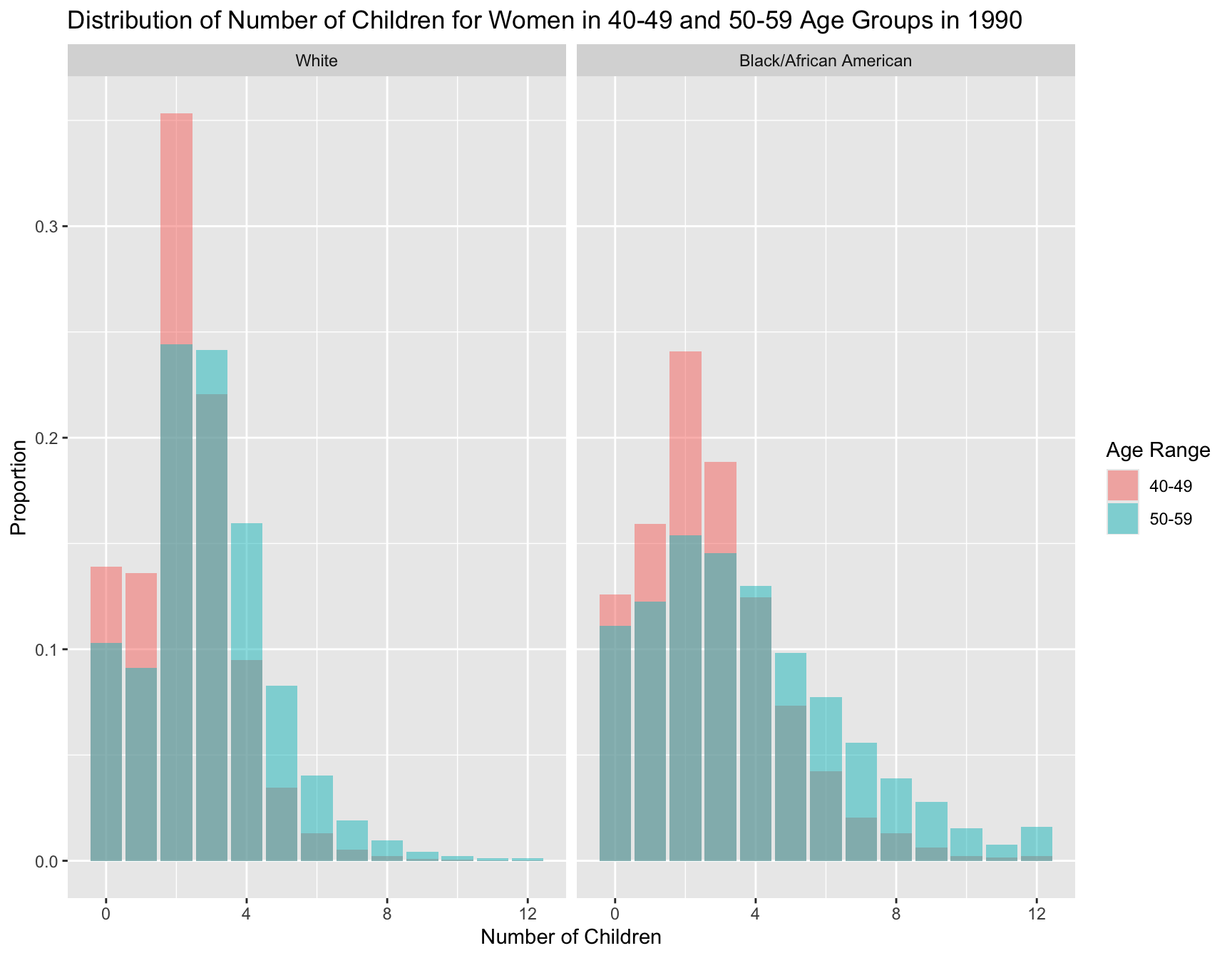
  filter(YEAR == "1990", AGE_RANGE %in% c("40-49", "50-59")) 

ggplot(filter_df, aes(x = chborn_num, y = proportion, fill = AGE_RANGE)) +
  geom_col(position = "identity", alpha = 0.5) +  
  facet_wrap(~ RACE) +  
  labs(
    title = "Distribution of Number of Children for Women in 40-49 and 50-59 Age Groups in 1990",
    x = "Number of Children",
    y = "Proportion",
    fill = "Age Range"
  ) 

Past versions of unnamed-chunk-28-1.png

Version	Author	Date
231390a	linmatch	2024-12-11
8007864	linmatch	2024-12-03

Summary Statistics Table

summary_stats <- filter_df %>%
  group_by(AGE_RANGE, RACE) %>%
  summarise(
    mean_children = weighted.mean(chborn_num, count),  # Mean number of children
    variance_children = sum(count * (chborn_num - weighted.mean(chborn_num, count))^2) / sum(count),  # Variance
    zero_inflation = sum(count[chborn_num == 0]) / sum(count)  # Proportion of women with 0 children
  )

`summarise()` has grouped output by 'AGE_RANGE'. You can override using the
`.groups` argument.

# Print summary statistics table
summary_stats

# A tibble: 4 × 5
# Groups:   AGE_RANGE [2]
  AGE_RANGE RACE                  mean_children variance_children zero_inflation
  <chr>     <fct>                         <dbl>             <dbl>          <dbl>
1 40-49     White                          2.20              2.09          0.139
2 40-49     Black/African Americ…          2.69              3.96          0.126
3 50-59     White                          2.89              3.35          0.103
4 50-59     Black/African Americ…          3.72              7.74          0.111

Test for Difference in Means

## Check the normality assumption for black population
# Subset data for the 40-49 and 50-59 age groups
data_40_49_b <- df %>% filter(AGE_RANGE == "40-49", RACE == "Black/African American")
data_50_59_b <- df %>% filter(AGE_RANGE == "50-59", RACE == "Black/African American")

qqnorm(data_40_49_b$chborn_num, main = "QQ Plot: 40-49 Age Group (Black/African American)")
qqline(data_40_49_b$chborn_num)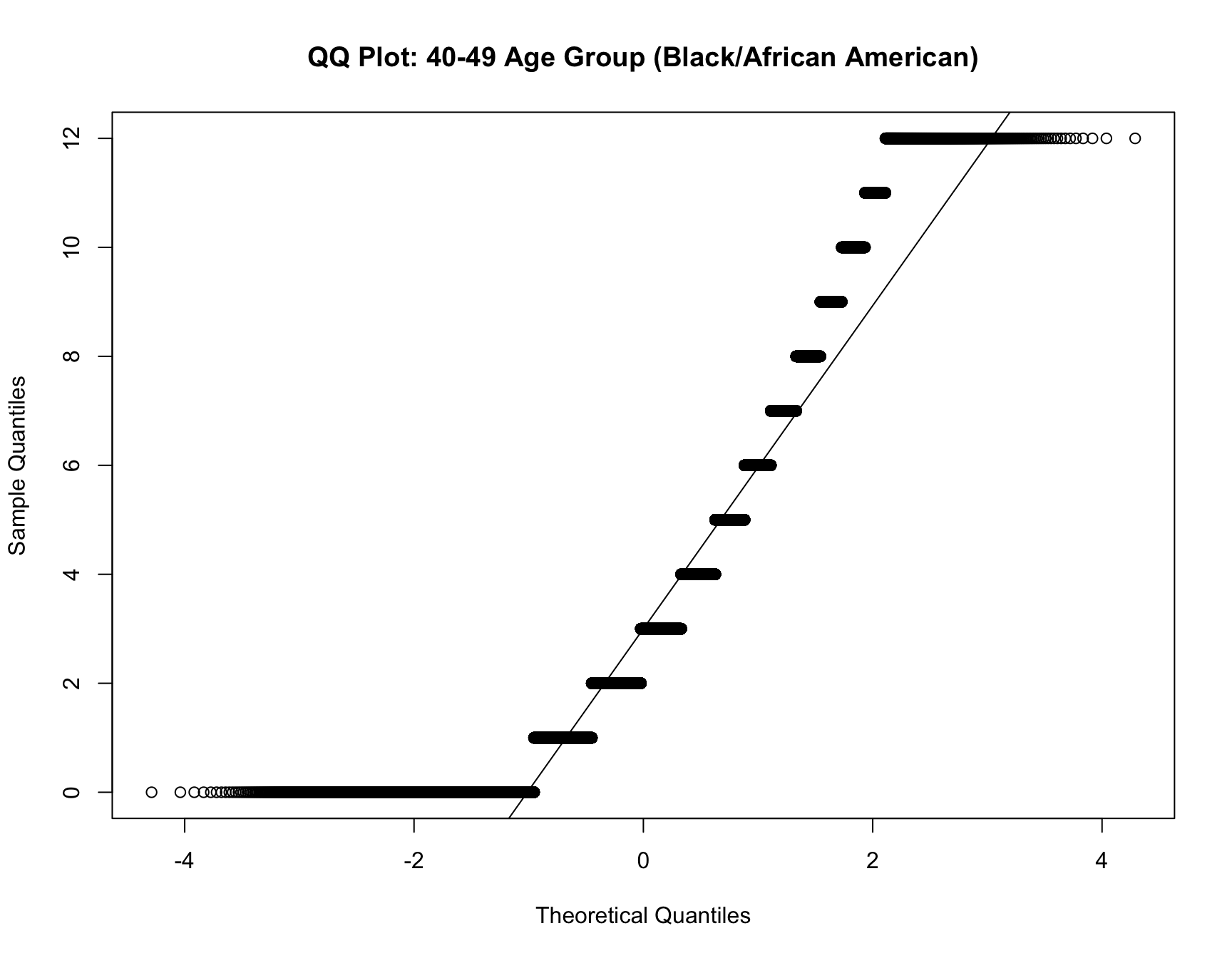

Past versions of unnamed-chunk-30-1.png

Version	Author	Date
231390a	linmatch	2024-12-11
776920f	linmatch	2024-11-12

# QQ plot for the 50-59 age group
qqnorm(data_50_59_b$chborn_num, main = "QQ Plot: 50-59 Age Group (Black/African American)")
qqline(data_50_59_b$chborn_num)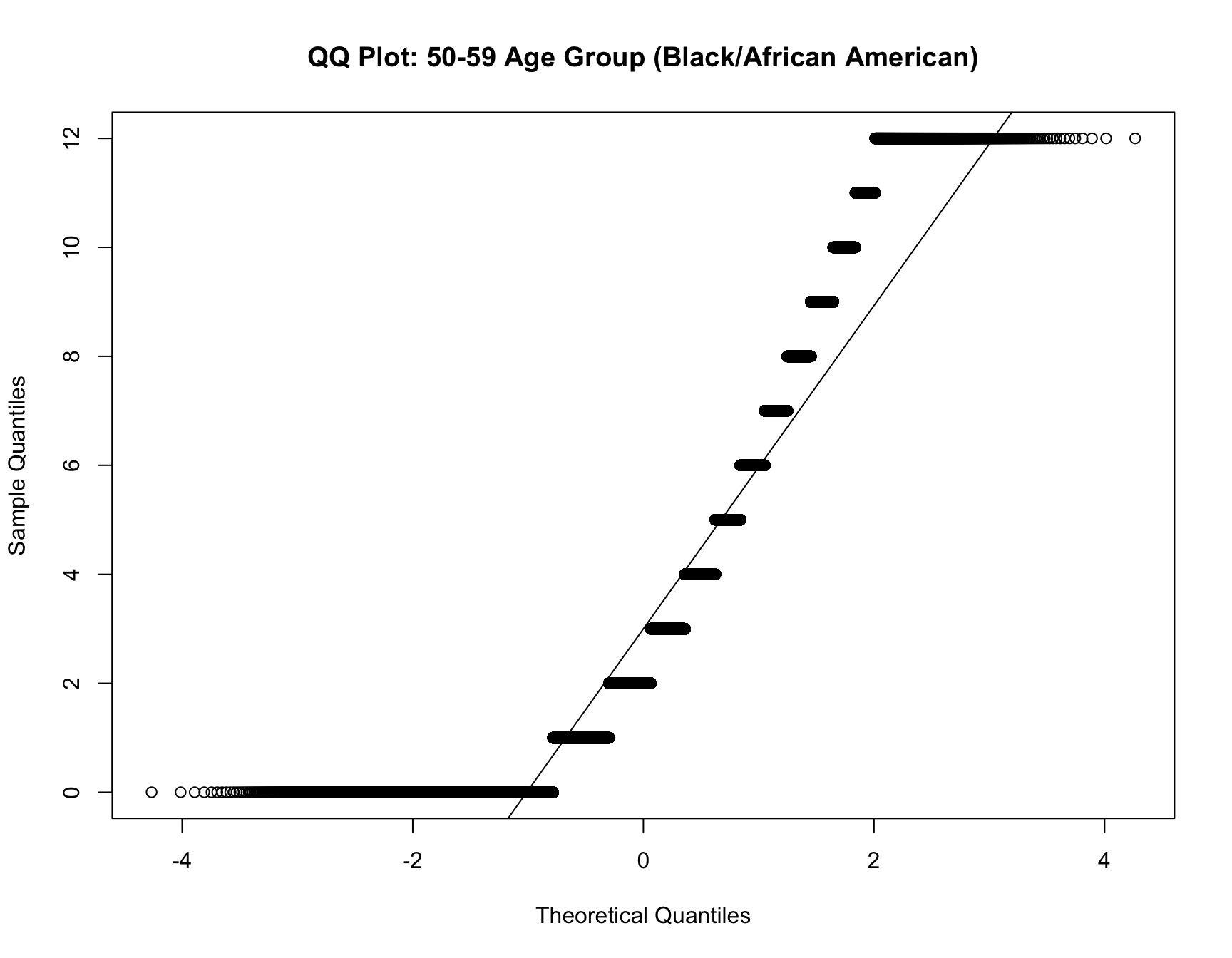

## Check the normality assumption for white population
data_40_49_w <- df %>% filter(AGE_RANGE == "40-49", RACE == "White")
data_50_59_w <- df %>% filter(AGE_RANGE == "50-59", RACE == "White")

qqnorm(data_40_49_w$chborn_num, main = "QQ Plot: 40-49 Age Group (White)")
qqline(data_40_49_w$chborn_num)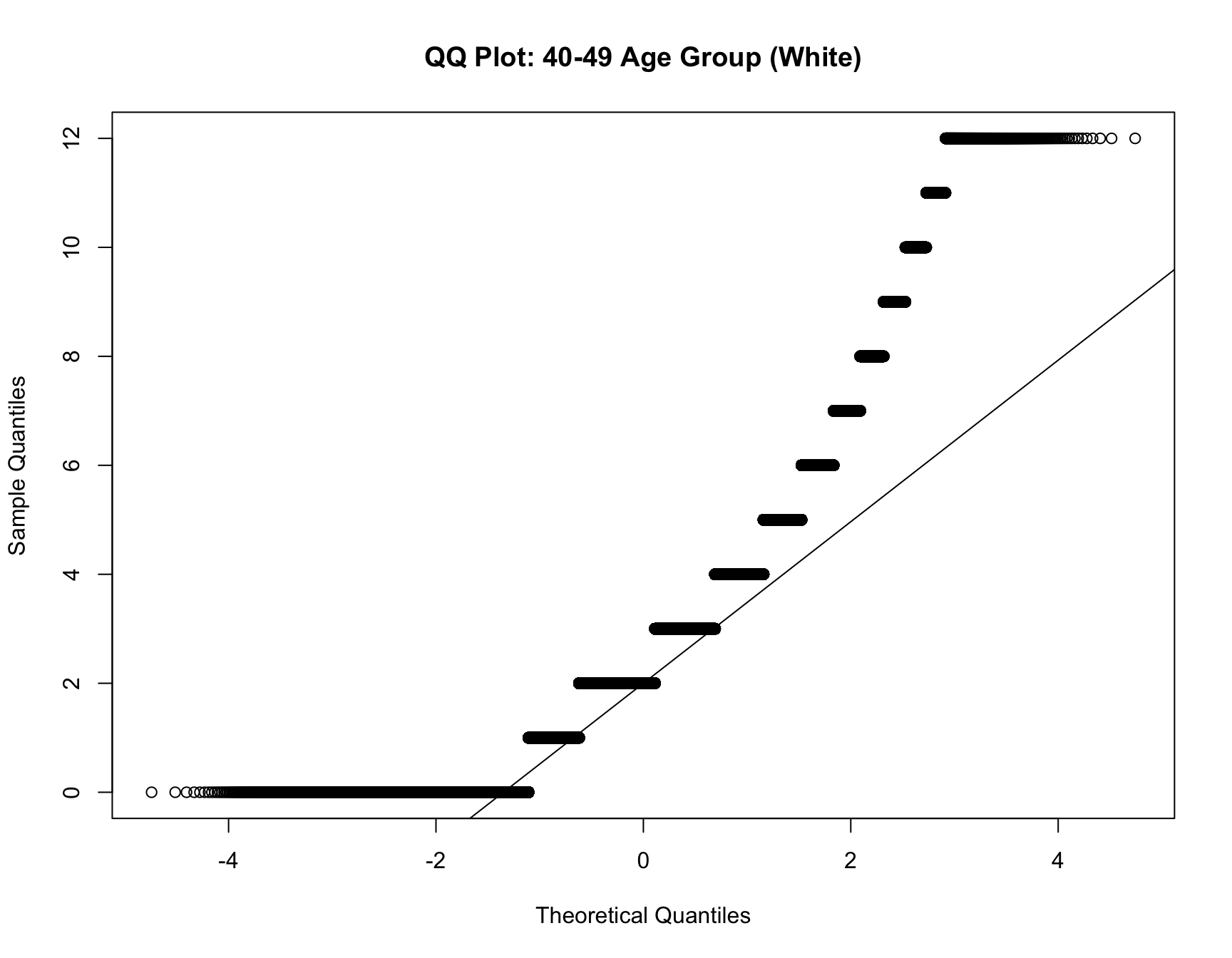

Past versions of unnamed-chunk-31-1.png

Version	Author	Date
f567c4a	linmatch	2024-12-16
231390a	linmatch	2024-12-11
8007864	linmatch	2024-12-03
776920f	linmatch	2024-11-12

# QQ plot for the 50-59 age group
qqnorm(data_50_59_w$chborn_num, main = "QQ Plot: 50-59 Age Group (White)")
qqline(data_50_59_w$chborn_num)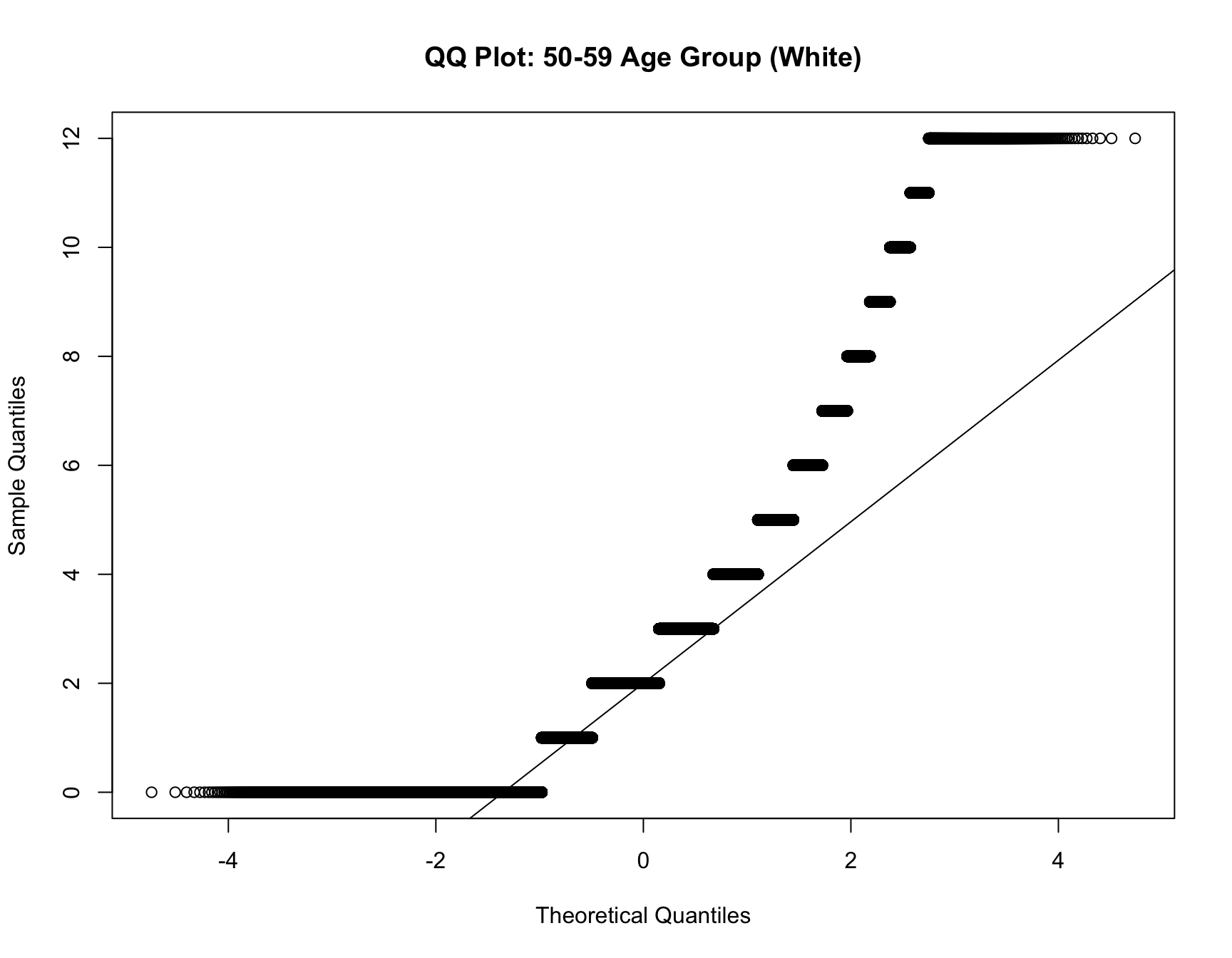

Since the data for black population and white population violate normality assumption, we perform a Mann-Whitney U test for both racial groups in the follwoing:

wilcox_test_result <- wilcox.test(data_40_49_b$chborn_num, data_50_59_b$chborn_num)$p.value
wilcox_test_result2 <- wilcox.test(data_40_49_w$chborn_num, data_50_59_w$chborn_num)$p.value
print(c(wilcox_test_result, wilcox_test_result2))

[1]  1.012022e-31 3.463246e-126

RESULT: These p-values are both extremely small (close to zero), meaning there is a very strong statistical difference between the two age groups (40-49 and 50-59) in terms of the mean number of children within each racial group.

Test for Difference in Variances

## Apply Levene's test since non-normality
df_w <- df %>% filter(RACE == "White")
df_b <- df %>% filter(RACE == "Black/African American")

# Levene's test for Black group
levene_test_b <- leveneTest(chborn_num ~ as.factor(AGE_RANGE), data = df_b)

# Levene's test for White group
levene_test_w <- leveneTest(chborn_num ~ as.factor(AGE_RANGE), data = df_w)

# Print results
print(levene_test_b)

Levene's Test for Homogeneity of Variance (center = median)
          Df F value    Pr(>F)    
group      3  93.887 < 2.2e-16 ***
      176718                      
---
Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

print(levene_test_w)

Levene's Test for Homogeneity of Variance (center = median)
           Df F value    Pr(>F)    
group       3  4205.8 < 2.2e-16 ***
      1740751                      
---
Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

RESULT: Since the p values are smaller than 0.05 for both racial group, we have enough evidence to reject the null hypothesis, indicating that the variances of the number of children between the two age groups within each racial group are significantly different.

Chi-Square Test for Difference in Zero Inflation

# contingency tables showing the counts of women with zero children and those with one or more children for each age group 
ZI_table <- df %>% filter(YEAR == "1990", AGE_RANGE %in% c("40-49", "50-59")) %>% 
  mutate(childlessness = ifelse(chborn_num == 0, "0 Children", "1+ Children")) %>%       group_by(RACE, AGE_RANGE, childlessness) %>%
  summarise(count = n())

`summarise()` has grouped output by 'RACE', 'AGE_RANGE'. You can override using
the `.groups` argument.

ZI_table

# A tibble: 8 × 4
# Groups:   RACE, AGE_RANGE [4]
  RACE                   AGE_RANGE childlessness count
  <fct>                  <chr>     <chr>         <int>
1 White                  40-49     0 Children    15945
2 White                  40-49     1+ Children   98807
3 White                  50-59     0 Children     9906
4 White                  50-59     1+ Children   86173
5 Black/African American 40-49     0 Children     1645
6 Black/African American 40-49     1+ Children   11430
7 Black/African American 50-59     0 Children     1215
8 Black/African American 50-59     1+ Children    9730

ZI_table_b <- ZI_table %>%
  filter(RACE == "Black/African American")

cont_table_b <- xtabs(count ~ AGE_RANGE + childlessness, data = ZI_table_b)
chi_test_b <- chisq.test(cont_table_b)
chi_test_b

    Pearson's Chi-squared test with Yates' continuity correction

data:  cont_table_b
X-squared = 12.306, df = 1, p-value = 0.0004515

ZI_table_w <- ZI_table %>%
  filter(RACE == "White")

cont_table_w <- xtabs(count ~ AGE_RANGE + childlessness, data = ZI_table_w)
chi_test_w <- chisq.test(cont_table_w)
chi_test_w

    Pearson's Chi-squared test with Yates' continuity correction

data:  cont_table_w
X-squared = 624.38, df = 1, p-value < 2.2e-16

RESULT: The p-values for both tests are extremely low, suggests that there is a significant difference in the proportion of women with 0 children across age ranges (40-49 vs. 50-59) for both the Black/African American and White racial groups. The results imply that childlessness is not uniformly distributed across age groups.

Step 4: Summarize Findings

Write a clear and concise summary addressing the following points.

4.1 Significant Fertility Shifts Across Cohorts

• Identify Timing of Shifts:
  • Specify when significant fertility shifts occurred for each racial group based on your analysis in Question 2.
• Describe Nature of Shifts:
  • Detail the characteristics of the shifts, such as:
    • Decrease in mean number of children
    • Increase in childlessness (zero inflation)
    • Changes in variance or distribution shape
• Highlight Differences Between Racial Groups:
  • Compare the timing and nature of shifts between African American and European American women.
  • Discuss any patterns or discrepancies observed.

4.2 Comparison of 40-49 and 50-59 Age Groups in 1990

• Summarize Key Differences:
  • Present the differences in fertility patterns between the two age groups for each racial group.
  • Include comparisons of:
    • Distribution shapes
    • Mean number of children
    • Variance
    • Zero inflation
• Report Statistical Test Results:
  • Provide the results of the t-tests, F-tests, and chi-square tests.
  • Interpret the significance of these results in the context of your analysis.
• Discuss Implications:
  • Consider what these differences suggest about fertility trends and behaviors.
  • Reflect on whether the older age group represents completed fertility patterns.

4.3 Synthesis and Implications

• Integrate Findings:
  • Connect the insights from the cohort analysis with the age group comparison.
  • Discuss how the patterns observed in the 1990 census relate to the shifts identified across cohorts.
• Consider Contributing Factors:
  • Explore potential social, economic, or policy factors that may have contributed to the observed fertility shifts.
    • For example, changes in access to education, employment opportunities, or family planning resources.
• Reflect on Broader Implications:
  • Discuss how these fertility trends might impact your broader research topic, such as genetic surveillance disparities.
  • Consider the implications for future demographic research or policy development.

Additional Considerations

• Visual Clarity:
  • Ensure all visualizations are easy to interpret.
  • Use clear labels, legends, and annotations.
• Contextualize Statistical Significance:
  • Explain not just whether results are statistically significant, but also what they mean in practical terms.
• Acknowledge Data Limitations:
  • Discuss any limitations or biases in the data that could affect your findings.
    • For instance, sample size constraints or missing data.
• Ethical Considerations:
  • Approach discussions of race and fertility sensitively and responsibly.
  • Avoid drawing causal conclusions without robust evidence.

Integration with Previous Work

• Leverage Previous Analyses:
  • Use the visualizations and statistical summaries from Questions 1 and 2 as foundations for this analysis.
• Create a Cohesive Narrative:
  • Ensure that your findings from all questions are connected and build upon each other.
  • Tell a comprehensive story about fertility trends across cohorts and racial groups.

Final Deliverables

• Multi-Panel Visualization:
  • Panel A: Fertility distribution shifts across cohorts with highlighted significant shifts.
  • Panel B: Comparative distribution plots for 40-49 and 50-59 age groups in 1990, including summary statistics.
• Written Summary:
  • A concise report that addresses the points outlined in Step 4.
  • Include interpretations of statistical analyses and discuss broader implications.
• Statistical Analysis Documentation:
  • Provide details of the statistical tests conducted, including test assumptions, results, and interpretations.
• Annotated Code (if applicable):
  • While not the focus, include any new code used for this analysis with appropriate comments.

Distribution of Number of Siblings Across Census Years

Having analyzed the distribution of the number of children, we now turn our attention to the distribution of the number of siblings. We will explore the trends in the frequency of the number of siblings for African American and European American mothers across the Census years by age group.

Frequency of siblings is calculated as follows.

\[ \text{freq}_{n_{\text{sib}}} = \text{freq}_{\text{mother}} \cdot \text{chborn}_{\text{num}} \]

For example, suppose 10 mothers (generation 0) have 7 children, then there will be 70 children (generation 1) in total who each have 6 siblings.

We take our original data and calculate the frequency of siblings for each mother based on the number of children they have. We then aggregate this data to get the frequency of siblings for each generation along with details on the birth years of the relevant children to visualize the distribution of the number of siblings across generations.

Data Preparation

Calculate Sibling Frequencies

df2 <- df %>% 
  dplyr::select(RACE, YEAR, AGE_RANGE, chborn_num)

df2 <- df2 %>%
 mutate(n_siblings = chborn_num - 1)

df2 <- df2 %>%
mutate(sibling_freq = ifelse(chborn_num != 1, n_siblings * 1, 1))  # Assuming each mother represents 1 in frequency

Aggregate Sibling Data

# Group the data and calculate sibling frequencies
df_siblings <- df2 %>%
 group_by(YEAR, RACE, AGE_RANGE, n_siblings) %>%
 summarise(
   sibling_count = sum(sibling_freq),
   .groups = "drop"
 )

# Calculate proportions within each group
df_sibling_proportions <- df_siblings %>%
 group_by(YEAR, RACE, AGE_RANGE) %>%
 mutate(proportion = sibling_count / sum(sibling_count)) %>%
 ungroup()

Check Normalization

normalization_check <- df_sibling_proportions %>%
  group_by(YEAR, RACE, AGE_RANGE) %>%
  summarise(total_proportion = sum(proportion), .groups = "drop") %>%
  arrange(YEAR, RACE, AGE_RANGE)

print(normalization_check)

# A tibble: 32 × 4
    YEAR RACE                   AGE_RANGE total_proportion
   <int> <fct>                  <chr>                <dbl>
 1  1960 White                  40-49                    1
 2  1960 White                  50-59                    1
 3  1960 White                  60-69                    1
 4  1960 White                  70+                      1
 5  1960 Black/African American 40-49                    1
 6  1960 Black/African American 50-59                    1
 7  1960 Black/African American 60-69                    1
 8  1960 Black/African American 70+                      1
 9  1970 White                  40-49                    1
10  1970 White                  50-59                    1
# ℹ 22 more rows

Visualization of Distribution of Number of Siblings

df_sibling_mirror <- df_sibling_proportions %>%
  mutate(proportion = if_else(RACE == "White", -proportion, proportion))

my_colors <- colorRampPalette(c("#FFB000", "#F77A2E", "#DE3A8A", "#7253FF", "#5E8BFF"))(13)

ggplot(data = df_sibling_mirror %>% filter(n_siblings != "-1"), aes(x = n_siblings, y = proportion, fill = as.factor(n_siblings))) +
 geom_col(aes(alpha = RACE)) +
 geom_hline(yintercept = 0, color = "black", size = 0.5) +
 facet_grid(AGE_RANGE ~ YEAR, scales = "free_y") +
 coord_flip() +
 scale_y_continuous(
   labels = function(x) abs(x),
   limits = function(x) c(-max(abs(x)), max(abs(x)))
 ) +
 scale_x_continuous(breaks = 0:11, labels = c(0:10, "11+")) +
 scale_fill_manual(values = my_colors) +
 scale_alpha_manual(values = c("White" = 0.7, "Black/African American" = 1)) +
 labs(
   title = "Distribution of Number of Siblings by Census Year, Race, and Age Range",
   x = "Number of Siblings",
   y = "Proportion",
   fill = "Number of Siblings",
   caption = "White population shown on left (negative values), Black/African American on right (positive values)\nProportions normalized within each age range, race, and census year\nFootnote: The category '11+' includes individuals with 11 or more siblings."
 ) +
 theme_minimal() +
 theme(
   plot.title = element_text(size = 14, hjust = 0.5),
   axis.text.y = element_text(size = 8),
   strip.text = element_text(size = 10),
   legend.position = "none",
   panel.grid.major.y = element_blank(),
   panel.grid.minor.y = element_blank()
 )

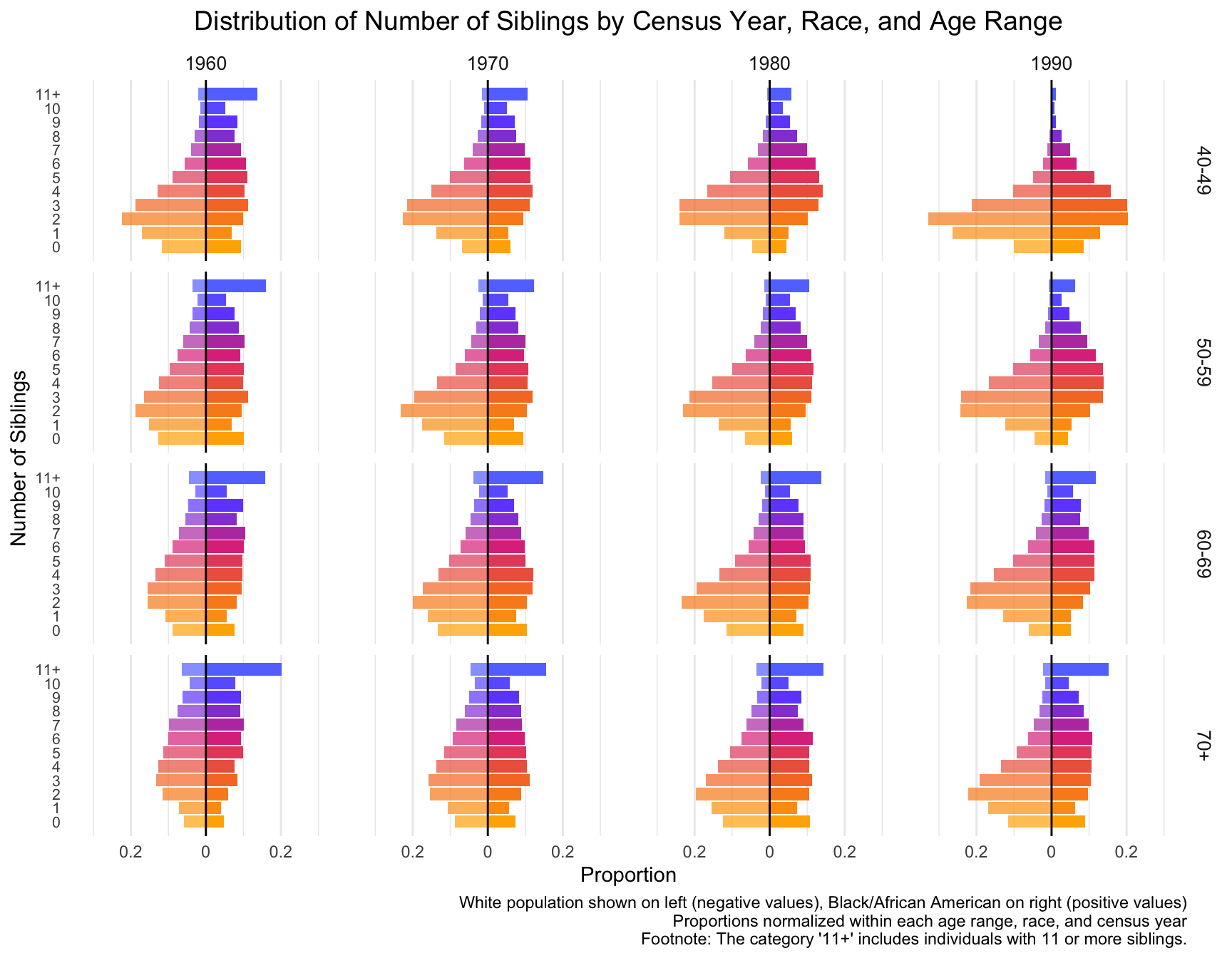
# Mean Number of Sibling By race only
df2 %>% filter(RACE == "Black/African American" & n_siblings >= 0) %>% summarise(Mean = mean(n_siblings))

      Mean
1 2.970941

df2 %>% filter(RACE == "White" & n_siblings >= 0) %>% summarise(Mean = mean(n_siblings))

      Mean
1 2.049651

RESULT:

-By Census Year: In 1960 and 1970, individuals are more likely to have higher number of siblings, especially in the 5-10 range. This trend diminishes over time.

By 1980 and 1990, the distribution shifts toward smaller family sizes, with a growing proportion of individuals having fewer siblings.

-By age range:

40-49 Age Group: For this group, the number of individuals with 0-2 siblings increases across census years, especially in 1980 and 1990, while the proportion of individuals with larger sibling counts decreases.

50-59 and 60-69 Age Groups: These groups show a similar shift toward smaller family sizes, but the trend is slightly more gradual compared to the younger age group.

70+ Age Group: The shift to fewer siblings is noticeable, although the trend is less pronounced. The distribution remains relatively stable across the census years, with a significant portion of individuals still coming from large families in 1960 and 1970.

2. Compare the distributions between White and Black/African American populations.

RESULT: -Black/African American Populations (right side of each pair) consistently show a higher proportion of individuals with larger sibling counts (5-10 siblings) compared to White populations. However, similar to the White population, the number of individuals with fewer siblings increases over time.

3. Note any significant changes or trends in the number of siblings over time.

RESULT: -White Populations: (left side of each pair) have a more marked shift toward smaller families by 1990, with a larger proportion of individuals having 0-2 siblings compared to the Black/African American population. The decline in larger family sizes (5+ siblings) is more pronounced among Whites, particularly by 1980 and 1990.

4. Consider how these sibling distributions might differ from the children distributions you analyzed earlier, and think about potential reasons for these differences.

RESULT: While both distributions show a trend toward smaller families, the sibling distribution is more spread out across different sibling counts, suggesting potential difference in the distribution.

Model Fit Across Census Years

We repeat the model fitting process we performed for the children distribution, this time using the sibling distribution data.

combinations2 <- df2 %>%
  # treat number of sib = -1 as NA
  filter(n_siblings != -1) %>%
  group_by(YEAR, RACE, AGE_RANGE) %>%
  group_split()

# Initialize the data frame to store results
best_models_sib <- data.frame(
  Race = character(),
  Census_Year = numeric(),
  AGE_RANGE = character(),
  AIC_poisson = numeric(),
  AIC_nb = numeric(),
  AIC_zip = numeric(),
  AIC_zinb = numeric(),
  stringsAsFactors = FALSE
)

# Loop through each subset of data
for (i in seq_along(combinations2)) {
  subset_data <- combinations2[[i]]
  
  # Fit Poisson model
  poisson_model <- glm(n_siblings ~ 1, family = poisson, data = subset_data)
  # Fit Negative Binomial model
  nb_model <- glm.nb(n_siblings ~ 1, data = subset_data)

  # Fit Zero-Inflated Poisson model
  zip_model <- zeroinfl(n_siblings ~ 1 | 1, data = subset_data, dist = "poisson",control = zeroinfl.control(maxit = 100))
  
  # Fit Zero-Inflated Negative Binomial model with increased max iterations
  zinb_model <- zeroinfl(n_siblings ~ 1 | 1, data = subset_data, dist = "negbin",control = zeroinfl.control(maxit = 100))
  
  # Append the result to the best_models data frame
  best_models_sib <- rbind(
    best_models_sib,
    data.frame(
      Race = unique(subset_data$RACE),
      Census_Year = unique(subset_data$YEAR),
      AGE_RANGE = unique(subset_data$AGE_RANGE),
      AIC_poisson = AIC(poisson_model),
      AIC_nb = AIC(nb_model),
      AIC_zip = AIC(zip_model),
      AIC_zinb = AIC(zinb_model),
      stringsAsFactors = FALSE
    )
  )
}

Identify Best-Fitting Models by comparing AIC

# Add a Best_Model column to store the best model based on minimum AIC
best_models_sib$Best_Model <- apply(best_models_sib, 1, function(row) {
  # Get AIC values for Poisson, NB, ZIP, and ZINB models
  aic_values <- c(Poisson = as.numeric(row['AIC_poisson']),
                  Negative_Binomial = as.numeric(row['AIC_nb']),
                  Zero_Inflated_Poisson = as.numeric(row['AIC_zip']),
                  Zero_Inflated_NB= as.numeric(row['AIC_zinb']))
  
  # Find the name of the model with the minimum AIC value
  best_models_sib <- names(which.min(aic_values))
  
  return(best_models_sib)
})

best_models_sib <- best_models_sib %>% dplyr::select(Race, Census_Year, AGE_RANGE, Best_Model)
# View the updated table with the Best_Model column
print(best_models_sib)

                     Race Census_Year AGE_RANGE        Best_Model
1                   White        1960     40-49 Negative_Binomial
2                   White        1960     50-59 Negative_Binomial
3                   White        1960     60-69 Negative_Binomial
4                   White        1960       70+ Negative_Binomial
5  Black/African American        1960     40-49  Zero_Inflated_NB
6  Black/African American        1960     50-59  Zero_Inflated_NB
7  Black/African American        1960     60-69  Zero_Inflated_NB
8  Black/African American        1960       70+  Zero_Inflated_NB
9                   White        1970     40-49 Negative_Binomial
10                  White        1970     50-59 Negative_Binomial
11                  White        1970     60-69 Negative_Binomial
12                  White        1970       70+ Negative_Binomial
13 Black/African American        1970     40-49  Zero_Inflated_NB
14 Black/African American        1970     50-59  Zero_Inflated_NB
15 Black/African American        1970     60-69  Zero_Inflated_NB
16 Black/African American        1970       70+  Zero_Inflated_NB
17                  White        1980     40-49 Negative_Binomial
18                  White        1980     50-59 Negative_Binomial
19                  White        1980     60-69 Negative_Binomial
20                  White        1980       70+ Negative_Binomial
21 Black/African American        1980     40-49  Zero_Inflated_NB
22 Black/African American        1980     50-59  Zero_Inflated_NB
23 Black/African American        1980     60-69  Zero_Inflated_NB
24 Black/African American        1980       70+  Zero_Inflated_NB
25                  White        1990     40-49           Poisson
26                  White        1990     50-59 Negative_Binomial
27                  White        1990     60-69 Negative_Binomial
28                  White        1990       70+ Negative_Binomial
29 Black/African American        1990     40-49 Negative_Binomial
30 Black/African American        1990     50-59  Zero_Inflated_NB
31 Black/African American        1990     60-69  Zero_Inflated_NB
32 Black/African American        1990       70+  Zero_Inflated_NB

Visualize Results

ggplot(best_models_sib, aes(x = Census_Year, y = AGE_RANGE, fill = Best_Model)) +
  geom_tile(color = "white", lwd = 0.5, linetype = 1) + # Create the tiles
  facet_wrap(~Race, nrow = 2) + # Facet by Race
  scale_fill_manual(values = c("Poisson" = "#0072B2", "Zero_Inflated_NB" = "#F0E442", "Negative_Binomial" = "grey")) + 
  labs(
    title = "Best Model(siblings) by Race, Census Year, and Birth Range",
    x = "Census Year",
    y = "Age Range",
    fill = "Best Model"
  ) +
  theme_minimal() +
  theme(
    axis.text.x = element_text(angle = 45, hjust = 1), # Rotate x-axis labels for readability
    plot.title = element_text(size = 14, face = "bold"),
    legend.position = "bottom"
  )

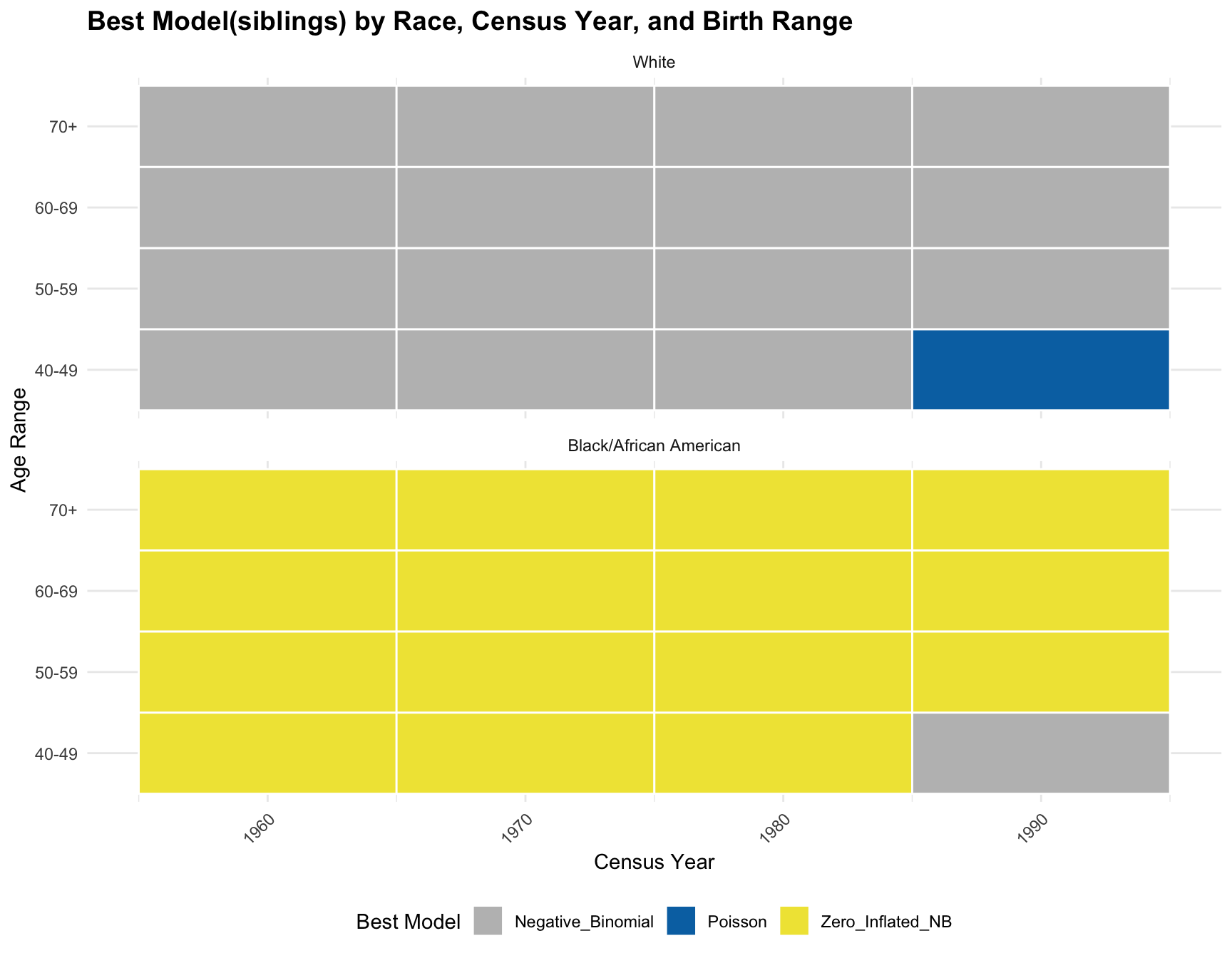
RESULT: By comparing the pattern of best-fitting models between the sibling and children distributions, we observe that the best model for black population has the same best model(zero-inlfated NB) across year and age range except on one subset(age 40-49 in 1990) in siblings distribution. However, there is a large difference in best model for white population. A large portion of best model in children distribution for white population is zero-inlfated NB, while negative-binomial is the best model fitted for siblings distribution except for one subset(age 40-49 in 1990).

Cohort Stability Analysis Siblings

Analyze the stability of sibling distributions across cohorts, similar to the analysis performed for children.

1. Zero Inflation: Check if the proportion of individuals with zero siblings changes significantly over time for the same cohort
2. Family Size: Test if the mean or variance in the number of siblings changes for the same cohort over time.
3. Model Fit: Analyze if the best-fitting model for the cohort changes over time.

a. Zero-Inflation Analysis

best_models_sib <- best_models_sib %>%
  mutate(Cohort = mapply(calculate_cohort, Census_Year, AGE_RANGE)) %>% 
  dplyr::select(Race, Census_Year, AGE_RANGE, Best_Model, Cohort)

df_merg2 <- df2 %>%
  rename(Census_Year = YEAR, Race = RACE)

# Perform a left join to merge the data frames
merged_data_sib <- left_join(df_merg2, best_models_sib, by = c("Race", "Census_Year", "AGE_RANGE"))

## divided the corhort by race
merged_df_black2 <- merged_data_sib %>% filter(Race == "Black/African American")
merged_df_white2 <- merged_data_sib %>% filter(Race == "White")

# Filter cohorts with more than one census year
cohort_counts <- merged_df_black2 %>%
  group_by(Cohort) %>%
  summarise(Unique_Census_Years = n_distinct(Census_Year)) %>%
  filter(Unique_Census_Years > 1)

# Get the list of cohorts for testing
cohorts_for_test <- cohort_counts$Cohort

# Initialize results data frame
results_black2 <- data.frame(RACE = character(), Cohort = character(), Chi_Square = numeric(), p_value = numeric(), stringsAsFactors = FALSE)

# Loop through each cohort and run the chi-square test
for (cohort in cohorts_for_test) {
  cohort_data <- merged_df_black2 %>% filter(Cohort == cohort)
  
  # Create contingency table
  contingency_table <- table(cohort_data$Census_Year, cohort_data$n_siblings == "0")
  
  # Perform the chi-square test only if more than one row is in the table
  if (nrow(contingency_table) > 1) {
    test_result <- chisq.test(contingency_table)
    
    # Append results to the results data frame
    results_black2 <- rbind(results_black2, data.frame(
      RACE = "Black/African American",
      Cohort = cohort,
      Chi_Square = test_result$statistic,
      p_value = test_result$p.value
    ))
  }
}

results_black2 <- results_black2 %>%
  mutate(Significance = ifelse(p_value > 0.05, "No", "Yes"))

print(results_black2)

                             RACE    Cohort Chi_Square    p_value Significance
X-squared  Black/African American 1901-1910  2.7595148 0.09667755           No
X-squared1 Black/African American 1911-1920  3.1588986 0.20608856           No
X-squared2 Black/African American 1921-1930  6.4474388 0.03980673          Yes
X-squared3 Black/African American 1931-1940  0.8166152 0.36617166           No

RESULT: The table shows that only the cohort 1921-1930 has significant change in probability of individuals with zero siblings in black population.

# Filter cohorts with more than one census year
cohort_counts <- merged_df_white2 %>%
  group_by(Cohort) %>%
  summarise(Unique_Census_Years = n_distinct(Census_Year)) %>%
  filter(Unique_Census_Years > 1)

# Get the list of cohorts for testing
cohorts_for_test <- cohort_counts$Cohort

# Initialize results data frame
results_white2 <- data.frame(RACE = character(), Cohort = character(), Chi_Square = numeric(), p_value = numeric(), stringsAsFactors = FALSE)

# Loop through each cohort and run the chi-square test
for (cohort in cohorts_for_test) {
  cohort_data <- merged_df_white2 %>% filter(Cohort == cohort)
  
  # Create contingency table
  contingency_table <- table(cohort_data$Census_Year, cohort_data$n_siblings == "0")
  
  # Perform the chi-square test only if more than one row is in the table
  if (nrow(contingency_table) > 1) {
    test_result <- chisq.test(contingency_table)
    
    # Append results to the results data frame
    results_white2 <- rbind(results_white2, data.frame(
      RACE = "White",
      Cohort = cohort,
      Chi_Square = test_result$statistic,
      p_value = test_result$p.value
    ))
  }
}

results_white2 <- results_white2 %>%
  mutate(Significance = ifelse(p_value > 0.05, "No", "Yes"))

print(results_white2)

            RACE    Cohort Chi_Square      p_value Significance
X-squared  White 1901-1910  46.930953 7.353216e-12          Yes
X-squared1 White 1911-1920 120.015145 8.690450e-27          Yes
X-squared2 White 1921-1930  79.061388 6.792628e-18          Yes
X-squared3 White 1931-1940   2.776021 9.568561e-02           No

RESULT: The table shows that cohorts 1901-1910, 1911-1920, 1921-1930 have significant change in probability of individuals with zero siblings in white population.

b. Family Size Analysis

sum_table_sib <- merged_data_sib %>% group_by(Race, Cohort, Census_Year) %>%
  summarise(
    Mean = mean(chborn_num),
    Variance = var(chborn_num))

`summarise()` has grouped output by 'Race', 'Cohort'. You can override using
the `.groups` argument.

merged_sib <- left_join(merged_data_sib, sum_table_sib, by = c("Race","Cohort","Census_Year")) %>% dplyr::select(Race, Cohort, Census_Year, Mean, Variance)

sum_table_black = merged_sib %>% filter(Race == "Black/African American")
sum_table_white = merged_sib %>% filter(Race == "White")

##Test for Black population
cohorts1 <- unique(sum_table_black$Cohort)

# Loop through each cohort and apply ANOVA for Mean and Variance
for (cohort in cohorts1) {
  
  # Filter data for the specific cohort
  cohort_data_b <- sum_table_black[sum_table_black$Cohort == cohort, ]
  
  # Check if there are at least two unique Census_Year values
  if (length(unique(cohort_data_b$Census_Year)) < 2) {
    cat("\nCohort:", cohort, "has only one Census Year. Skipping ANOVA.\n")
    next
  }
  
  # Perform ANOVA for Mean
  anova_mean_result <- aov(Mean ~ factor(Census_Year), data = cohort_data_b)
  
  # Output the results
  cat("\nCohort:", cohort)
  cat("\nANOVA for Mean number of Siblings:\n")
  print(summary(anova_mean_result))
}

Cohort: 1891-1900 has only one Census Year. Skipping ANOVA.

Cohort: 1911-1920
ANOVA for Mean number of Siblings:
                       Df Sum Sq Mean Sq   F value Pr(>F)    
factor(Census_Year)     2  5.453   2.727 8.507e+23 <2e-16 ***
Residuals           38001  0.000   0.000                     
---
Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

Cohort: 1901-1910
ANOVA for Mean number of Siblings:
                       Df Sum Sq Mean Sq   F value Pr(>F)    
factor(Census_Year)     1  77.51   77.51 7.094e+25 <2e-16 ***
Residuals           22789   0.00    0.00                     
---
Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

Cohort: -Inf-1890 has only one Census Year. Skipping ANOVA.

Cohort: 1921-1930
ANOVA for Mean number of Siblings:
                       Df Sum Sq Mean Sq   F value Pr(>F)    
factor(Census_Year)     2    417   208.5 4.477e+26 <2e-16 ***
Residuals           43042      0     0.0                     
---
Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

Cohort: -Inf-1900 has only one Census Year. Skipping ANOVA.

Cohort: 1931-1940
ANOVA for Mean number of Siblings:
                       Df  Sum Sq Mean Sq   F value Pr(>F)    
factor(Census_Year)     1 0.03475 0.03475 1.223e+22 <2e-16 ***
Residuals           22555 0.00000 0.00000                     
---
Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

Cohort: -Inf-1910 has only one Census Year. Skipping ANOVA.

Cohort: 1941-1950 has only one Census Year. Skipping ANOVA.

Cohort: -Inf-1920 has only one Census Year. Skipping ANOVA.

RESULT: The mean number of siblings change significantly in cohorts 1901-1910, 1911-1920, 1921-1930, 1931-1940 in black population.

##Test for White population
cohorts2 <- unique(sum_table_white$Cohort)

# Loop through each cohort and apply ANOVA for Mean and Variance
for (cohort in cohorts2) {
  
  # Filter data for the specific cohort
  cohort_data_w <- sum_table_white[sum_table_white$Cohort == cohort, ]
  
  # Check if there are at least two unique Census_Year values
  if (length(unique(cohort_data_w$Census_Year)) < 2) {
    cat("\nCohort:", cohort, "has only one Census Year. Skipping ANOVA.\n")
    next
  }
  
  # Perform ANOVA for Mean
  anova_mean_result <- aov(Mean ~ factor(Census_Year), data = cohort_data_w)
  
  # Output the results
  cat("\nCohort:", cohort)
  cat("\nANOVA for Mean number of Siblings:\n")
  print(summary(anova_mean_result))
  
}

Cohort: 1891-1900 has only one Census Year. Skipping ANOVA.

Cohort: 1911-1920
ANOVA for Mean number of Siblings:
                        Df Sum Sq Mean Sq   F value Pr(>F)    
factor(Census_Year)      2  535.2   267.6 4.546e+24 <2e-16 ***
Residuals           365210    0.0     0.0                     
---
Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

Cohort: 1901-1910
ANOVA for Mean number of Siblings:
                        Df Sum Sq Mean Sq   F value Pr(>F)    
factor(Census_Year)      1   1281    1281 9.604e+25 <2e-16 ***
Residuals           226142      0       0                     
---
Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

Cohort: -Inf-1890 has only one Census Year. Skipping ANOVA.

Cohort: -Inf-1900 has only one Census Year. Skipping ANOVA.

Cohort: 1921-1930
ANOVA for Mean number of Siblings:
                        Df Sum Sq Mean Sq   F value Pr(>F)    
factor(Census_Year)      2  653.9     327 8.029e+23 <2e-16 ***
Residuals           394507    0.0       0                     
---
Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

Cohort: 1931-1940
ANOVA for Mean number of Siblings:
                        Df Sum Sq Mean Sq   F value Pr(>F)    
factor(Census_Year)      1  1.829   1.829 8.533e+22 <2e-16 ***
Residuals           179944  0.000   0.000                     
---
Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

Cohort: -Inf-1910 has only one Census Year. Skipping ANOVA.

Cohort: -Inf-1920 has only one Census Year. Skipping ANOVA.

Cohort: 1941-1950 has only one Census Year. Skipping ANOVA.

RESULT: The mean number of siblings change significantly in cohorts 1901-1910, 1911-1920, 1921-1930, 1931-1940 in white population.

c. Model Fit Analysis

ggplot(best_models_sib, aes(x = Census_Year, y = Cohort, fill = Best_Model)) +
  geom_tile(color = "white", lwd = 0.5, linetype = 1) + # Create the tiles
  facet_wrap(~Race, nrow = 2) + # Facet by Race
  scale_fill_manual(values = c("Poisson" = "#0072B2", "Zero_Inflated_NB" = "#F0E442", "Negative_Binomial" = "grey")) + 
  labs(
    title = "Best Model(siblings) by Race, Census Year, and Cohort(Birth Range)",
    x = "Census Year",
    y = "Birth Range",
    fill = "Best Model"
  ) +
  theme_minimal() +
  theme(
    plot.title = element_text(size = 14, face = "bold"),
    legend.position = "bottom"
  )

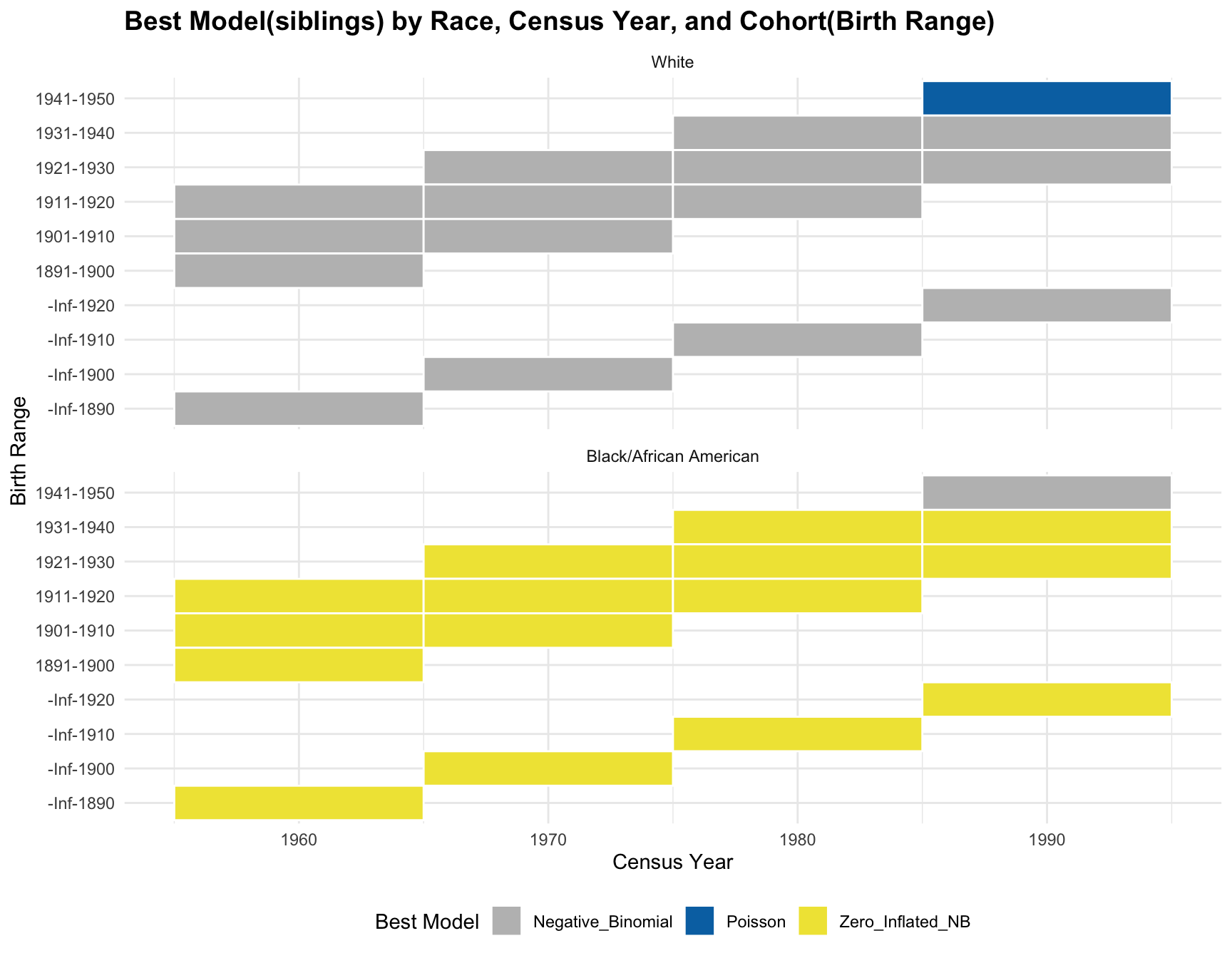RESULT: The best model for each cohort(those with 1+ corresponding census year) is stable over time.

Addtional Analysis on Overall Distribution

We also perform additional analysis to see if the overall distribution is stable across census year for the same cohort

 df_sibling_proportions <- df_sibling_proportions %>%
  mutate(Cohort = mapply(calculate_cohort, YEAR, AGE_RANGE))

df_sibling_proportions %>%
  filter(n_siblings >= 0, sibling_count >= 0, proportion >= 0) %>% group_by(RACE, Cohort) %>%
  ggplot(aes(x = n_siblings, y = proportion, color = as.factor(YEAR))) +
  geom_line() +
  labs(
    title = "Sibling Distribution by Census Year",
    x = "Number of Siblings",
    y = "Proportion",
    color = "Census Year"
  ) +
  facet_grid(RACE ~ Cohort) +
  theme_minimal()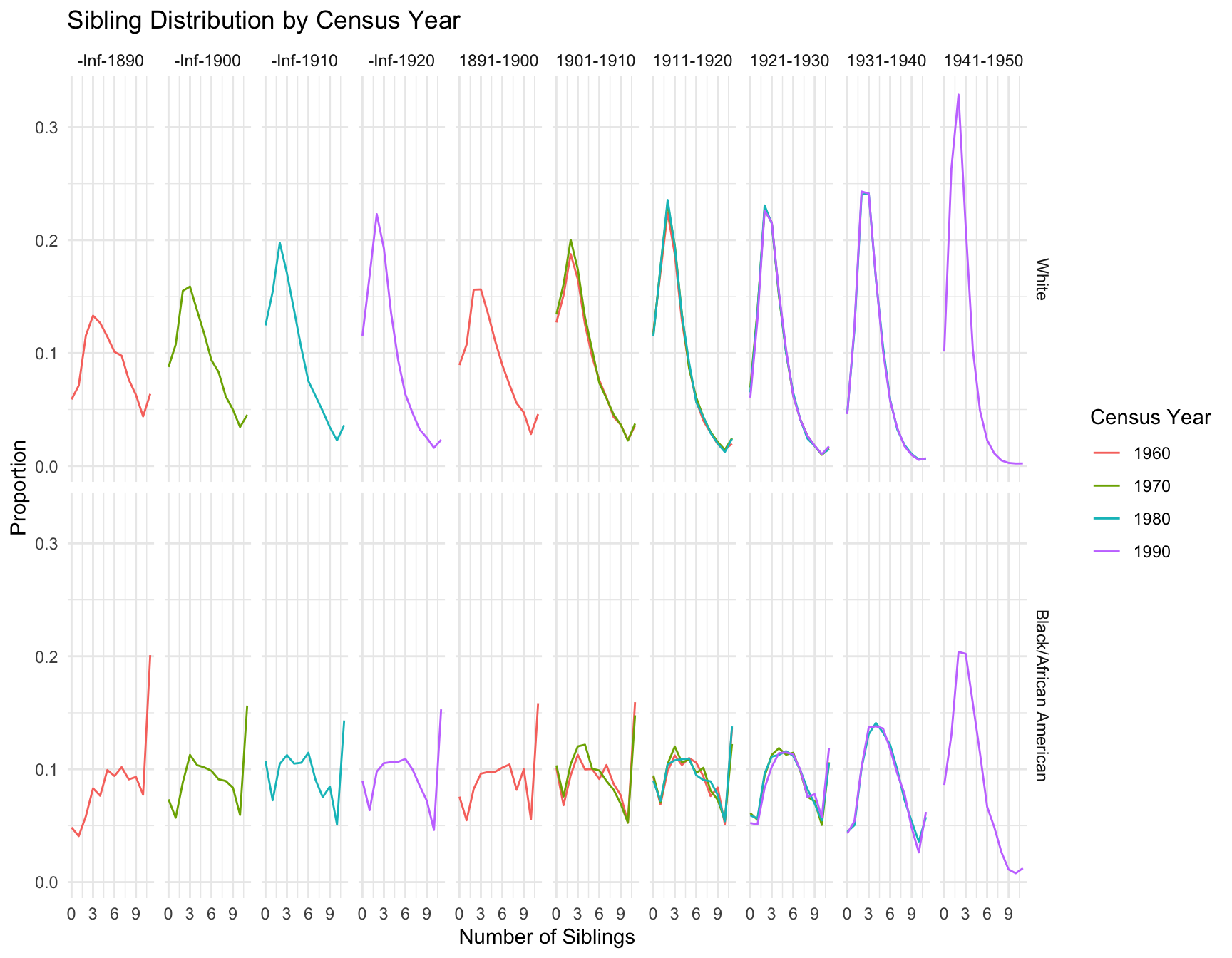

Past versions of unnamed-chunk-59-1.png

Version	Author	Date
f567c4a	linmatch	2024-12-16

df_sibling_b <- df_sibling_proportions %>% filter(RACE == "Black/African American", n_siblings >= 0, sibling_count >= 0, proportion >= 0)

results_sib_b <- list()

cohort_counts2 <- df_sibling_b %>%
  group_by(Cohort) %>%
  summarise(Unique_Census_Years = n_distinct(YEAR)) %>%
  filter(Unique_Census_Years > 1)

for (cohort in cohort_counts2$Cohort) {
  cohort_data <- df_sibling_b %>% filter(Cohort == cohort)
  
  test_result <- kruskal.test(sibling_count ~ YEAR, data = cohort_data)
  
  results_sib_b[[cohort]] <- test_result
}
results_sib_b

$`1901-1910`

    Kruskal-Wallis rank sum test

data:  sibling_count by YEAR
Kruskal-Wallis chi-squared = 13.23, df = 1, p-value = 0.0002755


$`1911-1920`

    Kruskal-Wallis rank sum test

data:  sibling_count by YEAR
Kruskal-Wallis chi-squared = 22.761, df = 2, p-value = 1.141e-05


$`1921-1930`

    Kruskal-Wallis rank sum test

data:  sibling_count by YEAR
Kruskal-Wallis chi-squared = 18.893, df = 2, p-value = 7.895e-05


$`1931-1940`

    Kruskal-Wallis rank sum test

data:  sibling_count by YEAR
Kruskal-Wallis chi-squared = 0.21333, df = 1, p-value = 0.6442

df_sibling_w <- df_sibling_proportions %>% filter(RACE == "White", n_siblings >= 0, sibling_count >= 0, proportion >= 0)

results_sib_w <- list()

cohort_counts2 <- df_sibling_w %>%
  group_by(Cohort) %>%
  summarise(Unique_Census_Years = n_distinct(YEAR)) %>%
  filter(Unique_Census_Years > 1)

for (cohort in cohort_counts2$Cohort) {
  cohort_data <- df_sibling_w %>% filter(Cohort == cohort)
  
  test_result <- kruskal.test(sibling_count ~ YEAR, data = cohort_data)
  
  results_sib_w[[cohort]] <- test_result
}
results_sib_w

$`1901-1910`

    Kruskal-Wallis rank sum test

data:  sibling_count by YEAR
Kruskal-Wallis chi-squared = 3.8533, df = 1, p-value = 0.04965


$`1911-1920`

    Kruskal-Wallis rank sum test

data:  sibling_count by YEAR
Kruskal-Wallis chi-squared = 4.9189, df = 2, p-value = 0.08548


$`1921-1930`

    Kruskal-Wallis rank sum test

data:  sibling_count by YEAR
Kruskal-Wallis chi-squared = 2.7072, df = 2, p-value = 0.2583


$`1931-1940`

    Kruskal-Wallis rank sum test

data:  sibling_count by YEAR
Kruskal-Wallis chi-squared = 0.21333, df = 1, p-value = 0.6442

Summary table showing:

• RACE
• birth_range
• Whether the distribution is stable across census years
• Any significant changes observed

results_summary <- data.frame(
  RACE = character(),
  Cohort = character(),
  Stable_Distribution = character(),
  Significant_Changes = character(),
  stringsAsFactors = FALSE
)

summarize_results <- function(test_results, race) {
  summary_list <- list()
  
  for (birth_range in names(test_results)) {
    test_result <- test_results[[birth_range]]
    
    stable <- ifelse(test_result$p.value >= 0.05, "Yes", "No")
    significant_changes <- ifelse(test_result$p.value < 0.05, "Yes", "No")
    
    summary_list[[birth_range]] <- data.frame(
      RACE = race,
      Cohort = birth_range,
      Stable_Distribution = stable,
      Significant_Changes = significant_changes
    )
  }
  
  do.call(rbind, summary_list)
}

results_summary_black <- summarize_results(results_sib_b, "Black/African American")

results_summary_white <- summarize_results(results_sib_w, "White")

results_summary <- rbind(results_summary, results_summary_black, results_summary_white)

rownames(results_summary) <- NULL 

results_summary

                    RACE    Cohort Stable_Distribution Significant_Changes
1 Black/African American 1901-1910                  No                 Yes
2 Black/African American 1911-1920                  No                 Yes
3 Black/African American 1921-1930                  No                 Yes
4 Black/African American 1931-1940                 Yes                  No
5                  White 1901-1910                  No                 Yes
6                  White 1911-1920                 Yes                  No
7                  White 1921-1930                 Yes                  No
8                  White 1931-1940                 Yes                  No

Visualize stability

ggplot(results_summary, aes(x = Cohort, y = RACE, fill = Significant_Changes)) +
  geom_tile(color = "white") +
  scale_fill_manual(values = c("Yes" = "#e93e3a", "No" = "#fdc70c")) +
  labs(title = "Significant Changes in Sibling Count Distribution Across Years by Race and Birth Range",
       x = "Birth Range",
       y = "Race",
       fill = "Significant Changes") +
  theme_minimal() +
  theme(axis.text.x = element_text(angle = 45, hjust = 1))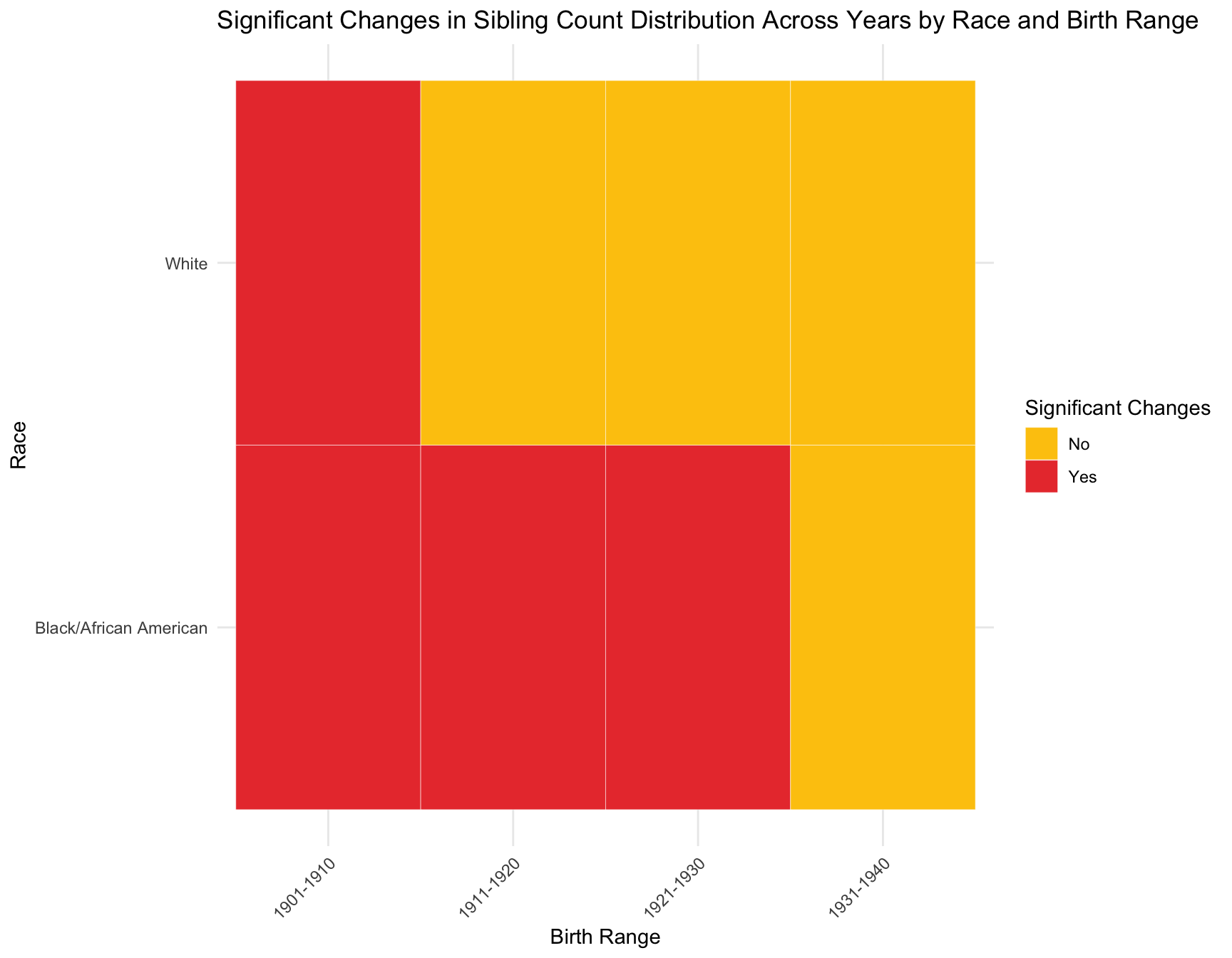

Past versions of unnamed-chunk-63-1.png

Version	Author	Date
f567c4a	linmatch	2024-12-16

Result

From the plot above, we can see the distribution of sibling is stable in the following cohorts by race: -black population:1901-1919, 1911-1920, 1921-1930 -white population:1901-1910

Session information

sessionInfo()

R version 4.3.2 (2023-10-31)
Platform: x86_64-apple-darwin20 (64-bit)
Running under: macOS Sonoma 14.5

Matrix products: default
BLAS:   /Library/Frameworks/R.framework/Versions/4.3-x86_64/Resources/lib/libRblas.0.dylib 
LAPACK: /Library/Frameworks/R.framework/Versions/4.3-x86_64/Resources/lib/libRlapack.dylib;  LAPACK version 3.11.0

locale:
[1] en_US.UTF-8/en_US.UTF-8/en_US.UTF-8/C/en_US.UTF-8/en_US.UTF-8

time zone: America/Detroit
tzcode source: internal

attached base packages:
[1] stats     graphics  grDevices utils     datasets  methods   base     

other attached packages:
 [1] rstatix_0.7.2     car_3.1-3         carData_3.0-5     nnet_7.3-19      
 [5] pscl_1.5.9        MASS_7.3-60       gridExtra_2.3     ggnewscale_0.5.0 
 [9] patchwork_1.2.0   rempsyc_0.1.8     scales_1.3.0      knitr_1.45       
[13] viridis_0.6.5     viridisLite_0.4.2 lubridate_1.9.3   forcats_1.0.0    
[17] stringr_1.5.1     purrr_1.0.2       readr_2.1.5       tidyr_1.3.1      
[21] tibble_3.2.1      ggplot2_3.5.1     tidyverse_2.0.0   dplyr_1.1.4      
[25] workflowr_1.7.1  

loaded via a namespace (and not attached):
 [1] gtable_0.3.4      xfun_0.41         bslib_0.6.1       processx_3.8.3   
 [5] callr_3.7.3       tzdb_0.4.0        vctrs_0.6.5       tools_4.3.2      
 [9] ps_1.7.6          generics_0.1.3    fansi_1.0.6       highr_0.10       
[13] pkgconfig_2.0.3   lifecycle_1.0.4   farver_2.1.1      compiler_4.3.2   
[17] git2r_0.33.0      munsell_0.5.0     getPass_0.2-4     httpuv_1.6.14    
[21] htmltools_0.5.7   sass_0.4.8        yaml_2.3.8        Formula_1.2-5    
[25] later_1.3.2       pillar_1.9.0      jquerylib_0.1.4   whisker_0.4.1    
[29] cachem_1.0.8      abind_1.4-8       tidyselect_1.2.1  digest_0.6.34    
[33] stringi_1.8.3     labeling_0.4.3    rprojroot_2.0.4   fastmap_1.1.1    
[37] grid_4.3.2        colorspace_2.1-0  cli_3.6.2         magrittr_2.0.3   
[41] utf8_1.2.4        broom_1.0.6       withr_3.0.0       backports_1.5.0  
[45] promises_1.2.1    timechange_0.3.0  rmarkdown_2.25    httr_1.4.7       
[49] hms_1.1.3         evaluate_0.23     rlang_1.1.3       Rcpp_1.0.12      
[53] glue_1.7.0        rstudioapi_0.15.0 jsonlite_1.8.9    R6_2.5.1         
[57] fs_1.6.3