Metabolite composition

Last updated: 2020-12-18

Checks: 7 0

Knit directory: exp_evol_respiration/

This reproducible R Markdown analysis was created with workflowr (version 1.6.2). The Checks tab describes the reproducibility checks that were applied when the results were created. The Past versions tab lists the development history.

R Markdown file: up-to-date

Great! Since the R Markdown file has been committed to the Git repository, you know the exact version of the code that produced these results.

Environment: empty

Great job! The global environment was empty. Objects defined in the global environment can affect the analysis in your R Markdown file in unknown ways. For reproduciblity it’s best to always run the code in an empty environment.

Seed: set.seed(20190703)

The command set.seed(20190703) was run prior to running the code in the R Markdown file. Setting a seed ensures that any results that rely on randomness, e.g. subsampling or permutations, are reproducible.

Session information: recorded

Great job! Recording the operating system, R version, and package versions is critical for reproducibility.

Cache: none

Nice! There were no cached chunks for this analysis, so you can be confident that you successfully produced the results during this run.

File paths: relative

Great job! Using relative paths to the files within your workflowr project makes it easier to run your code on other machines.

Repository version: a3b516e

Great! You are using Git for version control. Tracking code development and connecting the code version to the results is critical for reproducibility.

The results in this page were generated with repository version a3b516e. See the Past versions tab to see a history of the changes made to the R Markdown and HTML files.

Note that you need to be careful to ensure that all relevant files for the analysis have been committed to Git prior to generating the results (you can use wflow_publish or wflow_git_commit). workflowr only checks the R Markdown file, but you know if there are other scripts or data files that it depends on. Below is the status of the Git repository when the results were generated:


Ignored files:
    Ignored:    .DS_Store
    Ignored:    .Rapp.history
    Ignored:    .Rproj.user/
    Ignored:    analysis/.DS_Store
    Ignored:    output/.DS_Store

Untracked files:
    Untracked:  output/brms_SEM_respiration.rds
    Untracked:  output/metabolite_interaction_plot.pdf
    Untracked:  output/metabolite_plot.pdf
    Untracked:  output/respiration_figure.pdf
    Untracked:  post_preds_respiration.rds

Unstaged changes:
    Deleted:    output/Figure 2.pdf
    Deleted:    output/bayesian_R2_values.rds
    Deleted:    output/brms_SEM.rds
    Deleted:    output/pairs_plot.pdf

Note that any generated files, e.g. HTML, png, CSS, etc., are not included in this status report because it is ok for generated content to have uncommitted changes.

These are the previous versions of the repository in which changes were made to the R Markdown (analysis/metabolites.Rmd) and HTML (docs/metabolites.html) files. If you’ve configured a remote Git repository (see ?wflow_git_remote), click on the hyperlinks in the table below to view the files as they were in that past version.

File	Version	Author	Date	Message
Rmd	a3b516e	lukeholman	2020-12-18	Neater figures
html	b6cf554	lukeholman	2020-12-11	Build site.
Rmd	dcb0a67	lukeholman	2020-12-11	Tweaks
html	a88f037	lukeholman	2020-12-11	Build site.
Rmd	9588f44	lukeholman	2020-12-11	Tweaks
html	bb96acf	lukeholman	2020-12-11	Build site.
html	e5c580f	lukeholman	2020-12-11	Build site.
Rmd	328e117	lukeholman	2020-12-11	Tweaks
html	49e7792	lukeholman	2020-12-11	Build site.
Rmd	9d65fc7	lukeholman	2020-12-11	Tweaks
html	2911fb9	lukeholman	2020-12-10	Build site.
Rmd	184b0a4	lukeholman	2020-12-10	Tweaks
html	a361e42	lukeholman	2020-12-10	Build site.
Rmd	98c43b5	lukeholman	2020-12-10	Tweaks
html	7fca240	lukeholman	2020-12-10	Build site.
Rmd	125d4a2	lukeholman	2020-12-10	Tweaks
html	31ed22a	lukeholman	2020-12-10	Build site.
Rmd	8464a7f	lukeholman	2020-12-10	Tweaks
html	901053c	lukeholman	2020-12-10	Build site.
Rmd	904af31	lukeholman	2020-12-10	Tweaks
html	f7c88a2	lukeholman	2020-12-10	Build site.
Rmd	68780f6	lukeholman	2020-12-10	Tweaks
html	deb7183	lukeholman	2020-12-09	Build site.
Rmd	720eb6d	lukeholman	2020-12-09	Tweaks
html	b731971	lukeholman	2020-12-09	Build site.
Rmd	398d963	lukeholman	2020-12-09	Tweaks
html	b449eb3	lukeholman	2020-12-09	Build site.
Rmd	15f3c92	lukeholman	2020-12-09	Tweaks
html	43cc270	lukeholman	2020-12-09	Build site.
Rmd	2642c27	lukeholman	2020-12-09	More work
html	4f5ee28	lukeholman	2020-12-04	Build site.
Rmd	d441b69	lukeholman	2020-12-04	Luke metabolites analysis
Rmd	c8feb2d	lukeholman	2020-11-30	Same page with Martin
html	3fdbcb2	lukeholman	2020-11-30	Tweaks Nov 2020

Load packages

# it was slightly harder to install the showtext package. On Mac, I did this:
# installed 'homebrew' using Terminal: ruby -e "$(curl -fsSL https://raw.githubusercontent.com/Homebrew/install/master/install)" 
# installed 'libpng' using Terminal: brew install libpng
# installed 'showtext' in R using: devtools::install_github("yixuan/showtext")  

library(tidyverse)
library(GGally)
library(gridExtra)
library(ggridges)
library(brms)
library(tidybayes)
library(DT)
library(kableExtra)
library(knitrhooks) # install with devtools::install_github("nathaneastwood/knitrhooks")
library(showtext)
output_max_height() # a knitrhook option

# set up nice font for figure
nice_font <- "Lora"
font_add_google(name = nice_font, family = nice_font, regular.wt = 400, bold.wt = 700)
showtext_auto()

options(stringsAsFactors = FALSE)

Load metabolite composition data

This analysis set out to test whether sexual selection treatment had an effect on metabolite composition of flies. We measured fresh and dry fly weight in milligrams, plus the weights of five metabolites which together equal the dry weight. These are:

Lipid_conc (i.e. the weight of the hexane fraction, divided by the full dry weight),
Carbohydrate_conc (i.e. the weight of the aqueous fraction, divided by the full dry weight),
Protein_conc (i.e. \(\mu\)g of protein per milligram as measured by the bicinchoninic acid protein assay),
Glycogen_conc (i.e. \(\mu\)g of glycogen per milligram as measured by the hexokinase assay), and
Chitin_conc (estimated as the difference between the initial and final dry weights)

We expect body weight to vary between the sexes and potentially between treatments. In turn, we expect body weight to affect our five response variables of interest. Heavier flies might contain different proportions of lipids, chitin, etc., and these proportions might vary by sex and treatment (both because of the differences in dry weight, or because of weight-independent effects of sex and treatment on metabolite composition).

metabolites <- read_csv('data/3.metabolite_data.csv') %>%
  mutate(sex = ifelse(sex == "m", "Male", "Female"),
         line = paste(treatment, line, sep = ""),
         treatment = ifelse(treatment == "M", "Monogamy", "Polyandry")) %>%
  # log transform glycogen since it shows a long tail (others are reasonably normal-looking)
  mutate(Glycogen_ug_mg = log(Glycogen_ug_mg)) %>%
  # There was a technical error with flies collected on day 1, 
  # so they are excluded from the whole paper. All the measurements analysed are of 3d-old flies
  filter(time == '2') %>%
  select(-time)

scaled_metabolites <- metabolites %>% 
  # Find proportional metabolites as a proportion of total dry weight
  mutate(
    Dry_weight = dwt_mg,
    Lipid_conc = Hex_frac / Dry_weight,
    Carbohydrate_conc = Aq_frac / Dry_weight,
    Protein_conc = Protein_ug_mg,
    Glycogen_conc = Glycogen_ug_mg,
    Chitin_conc = Chitin_mg_mg) %>% 
  select(sex, treatment, line, Dry_weight, ends_with("conc")) %>%
  mutate_at(vars(ends_with("conc")), ~ as.numeric(scale(.x))) %>%
  mutate(Dry_weight = as.numeric(scale(Dry_weight))) %>%
  mutate(sextreat = paste(sex, treatment),
         sextreat = replace(sextreat, sextreat == "Male Monogamy", "M males"),
         sextreat = replace(sextreat, sextreat == "Male Polyandry", "P males"),
         sextreat = replace(sextreat, sextreat == "Female Monogamy", "M females"),
         sextreat = replace(sextreat, sextreat == "Female Polyandry", "P females"),
         sextreat = factor(sextreat, c("M males", "P males", "M females", "P females")))

Inspect the raw data

Raw numbers

All variables are shown in standard units (i.e. mean = 0, SD = 1).

my_data_table <- function(df){
  datatable(
    df, rownames=FALSE,
    autoHideNavigation = TRUE,
    extensions = c("Scroller",  "Buttons"),
    options = list(
      dom = 'Bfrtip',
      deferRender=TRUE,
      scrollX=TRUE, scrollY=400,
      scrollCollapse=TRUE,
      buttons = 
        list('csv', list(
          extend = 'pdf',
          pageSize = 'A4',
          orientation = 'landscape',
          filename = 'Dpseudo_metabolites')),
      pageLength = 50
    )
  )
}

scaled_metabolites %>%
  select(-sextreat) %>%
  mutate_if(is.numeric, ~ format(round(.x, 3), nsmall = 3)) %>%
  my_data_table()

Simple plots

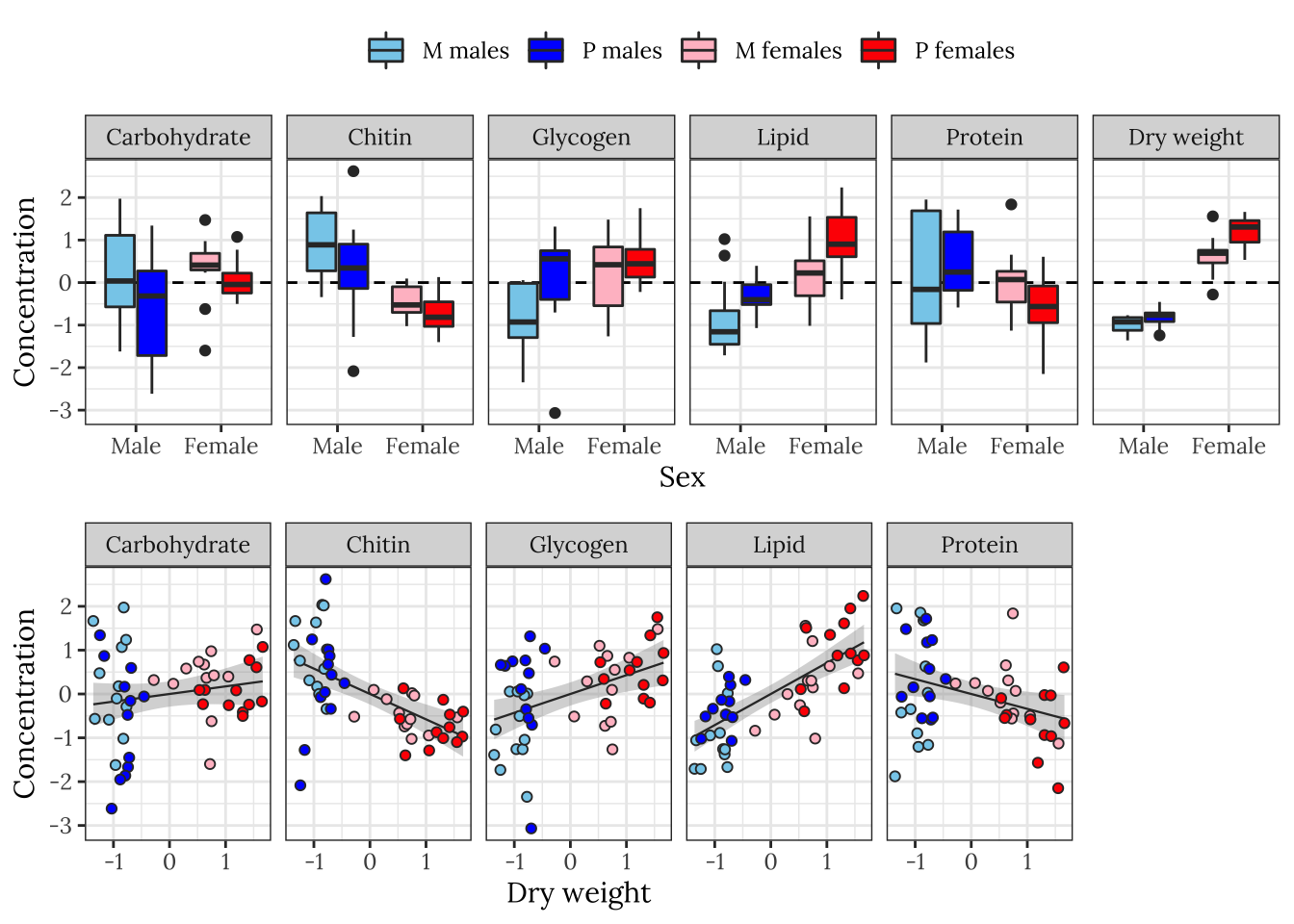
The following plot shows how each metabolite varies between sexes and treatments, and how the consecration of each metabolite co-varies with dry weight across individuals.

levels <- c("Carbohydrate", "Chitin", "Glycogen", "Lipid", "Protein", "Dry weight")

cols <- c("M females" = "pink", 
          "P females" = "red", 
          "M males" = "skyblue", 
          "P males" = "blue")

grid.arrange(
  scaled_metabolites %>% 
    rename_all(~ str_remove_all(.x, "_conc")) %>%
    rename(`Dry weight` = Dry_weight) %>%
    mutate(sex = factor(sex, c("Male", "Female"))) %>%
    reshape2::melt(id.vars = c('sex', 'treatment', 'sextreat', 'line')) %>% 
    mutate(variable = factor(variable, levels)) %>%
    ggplot(aes(x = sex, y = value,  fill  = sextreat)) +
    geom_hline(yintercept = 0, linetype = 2) + 
    geom_boxplot() + 
    facet_grid( ~ variable) +
    theme_bw() +
    xlab("Sex") + ylab("Concentration") +
    theme(legend.position = 'top',
          text = element_text(family = nice_font)) + 
    scale_fill_manual(values = cols, name = ""),
  
  arrangeGrob(
    scaled_metabolites %>% 
      rename_all(~ str_remove_all(.x, "_conc")) %>%
      reshape2::melt(id.vars = c('sex', 'treatment', 'sextreat', 'line', 'Dry_weight')) %>% 
      mutate(variable = factor(variable, levels)) %>%
      ggplot(aes(x = Dry_weight, y = value, colour = sextreat, fill = sextreat)) +
      geom_smooth(method = 'lm', se = TRUE, aes(colour = NULL, fill = NULL), colour = "grey20", size = .4) +
      geom_point(pch = 21, colour = "grey20") +
      facet_grid( ~ variable) +
      theme_bw() +
      xlab("Dry weight") + ylab("Concentration") +
      theme(legend.position = 'none',
            text = element_text(family = nice_font),) + 
      scale_colour_manual(values = cols, name = "") + 
      scale_fill_manual(values = cols, name = ""),
    scaled_metabolites %>% 
      rename_all(~ str_remove_all(.x, "_conc")) %>%
      reshape2::melt(id.vars = c('sex', 'treatment', 'sextreat', 'line', 'Dry_weight')) %>% 
      mutate(variable = factor(variable, levels)) %>%
      ggplot(aes(x = Dry_weight, y = value, colour = sextreat, fill = sextreat)) +
      theme_void() + ylab(NULL), nrow = 1, widths = c(0.84, 0.16)),
  heights = c(0.55, 0.45)
)

Version	Author	Date
49e7792	lukeholman	2020-12-11
deb7183	lukeholman	2020-12-09
43cc270	lukeholman	2020-12-09
4f5ee28	lukeholman	2020-12-04

Plot of correlations between variables

Some of the metabolites, especially lipid concentration, are correlated with dry weight. There is also a large difference in dry weight between sexes (and treatments, to a less extent), and sex and treatment effects are evident for some of the metabolites in the raw data. Some of the metabolites are weakly correlated with other metabolites, e.g. lipid and glycogen concentration.

modified_densityDiag <- function(data, mapping, ...) {
  ggally_densityDiag(data, mapping, colour = "grey10", ...) + 
    scale_fill_manual(values = cols) + 
  scale_x_continuous(guide = guide_axis(check.overlap = TRUE))
}

modified_points <- function(data, mapping, ...) {
  ggally_points(data, mapping, pch = 21, colour = "grey10", ...) +
    scale_fill_manual(values = cols) + 
    scale_x_continuous(guide = guide_axis(check.overlap = TRUE))
}

modified_facetdensity <- function(data, mapping, ...) {
  ggally_facetdensity(data, mapping, ...) + 
    scale_colour_manual(values = cols)
}

modified_box_no_facet <- function(data, mapping, ...) {
  ggally_box_no_facet(data, mapping, colour = "grey10", ...) +
    scale_fill_manual(values = cols)
}

pairs_plot <- scaled_metabolites %>% 
  arrange(sex, treatment) %>%
  select(-line, -sex, -treatment) %>%
  rename(`Sex and treatment` = sextreat) %>%
  rename_all(~ str_replace_all(.x, "_", " ")) %>%
  ggpairs(aes(colour = `Sex and treatment`, fill = `Sex and treatment`),
          diag = list(continuous = wrap(modified_densityDiag, alpha = 0.7),
                      discrete = wrap("blank")),
          lower = list(continuous = wrap(modified_points, alpha = 0.7, size = 1.1), 
                       discrete = wrap("blank"),
                       combo = wrap(modified_box_no_facet, alpha = 0.7)),
          upper = list(continuous = wrap(modified_points, alpha = 0.7, size = 1.1),
                       discrete = wrap("blank"),
                       combo = wrap(modified_box_no_facet, alpha = 0.7, size = 0.5))) 
pairs_plot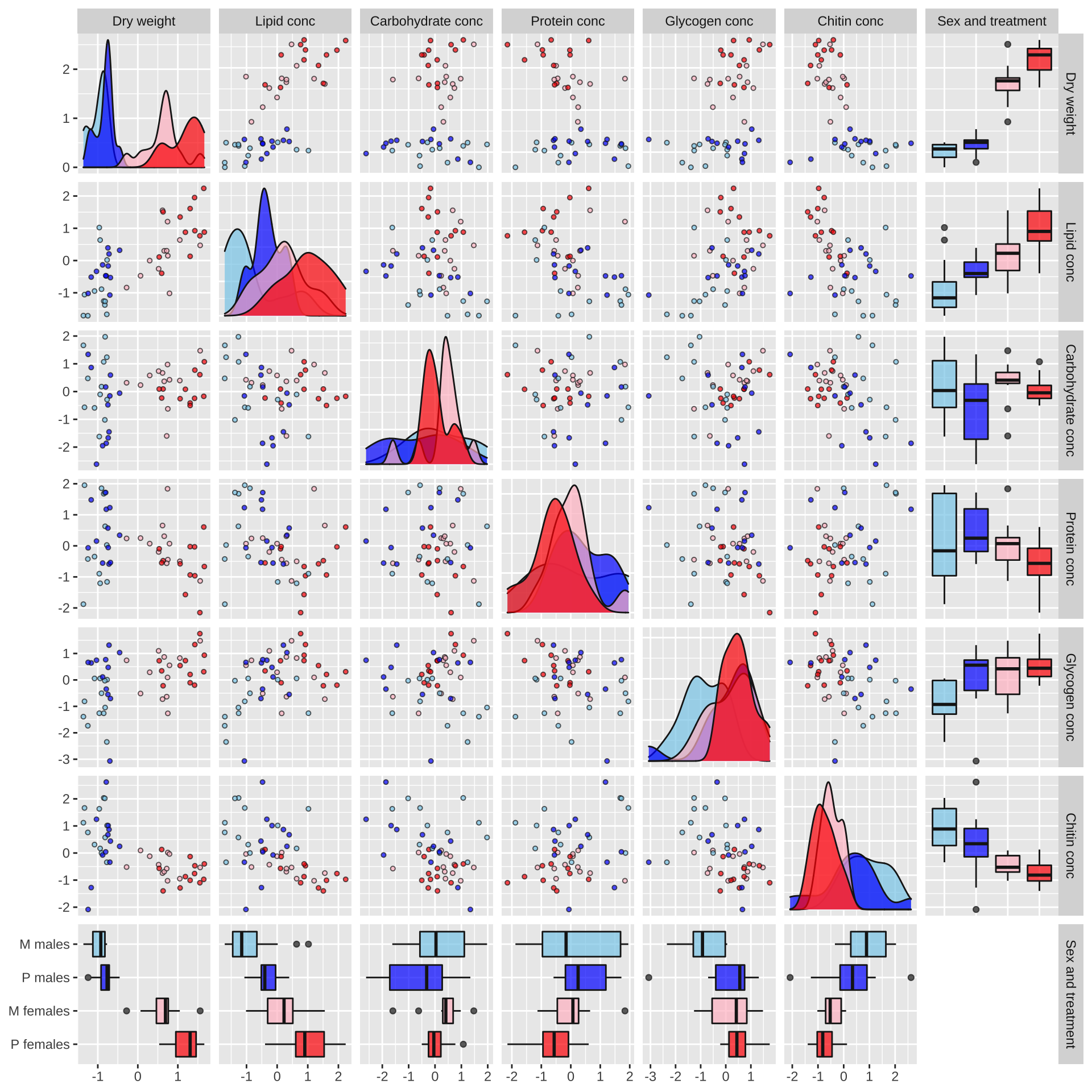

Version	Author	Date
43cc270	lukeholman	2020-12-09

Mean dry weight

se <- function(x) sd(x) / sqrt(length(x))
metabolites %>% 
  group_by(sex, treatment) %>% 
  summarise(mean_dwt = mean(dwt_mg), 
            SE = se(dwt_mg), 
            n = n()) %>% 
  kable(digits = 3) %>% kable_styling(full_width = FALSE)

sex	treatment	mean_dwt	SE	n
Female	Monogamy	0.562	0.019	12
Female	Polyandry	0.644	0.017	12
Male	Monogamy	0.330	0.009	12
Male	Polyandry	0.353	0.009	12

Directed acyclic graph (DAG)

This directed acyclic graph (DAG) illustrates the causal pathways that we observed between the experimental or measured variables (square boxes) and latent variables (ovals). We hypothesise that sex and mating system potentially influence dry weight as well as the metabolite composition (which we assessed by estimating the concentrations of carbohydrates, chitin, glycogen, lipids and protein). Additionally, dry weight is likely correlated with metabolite composition, and so dry weight acts as a ‘mediator variable’ between metabolite composition, and sex and treatment. The structural equation model below is built with this DAG in mind.

DiagrammeR::grViz('digraph {

graph [layout = dot, rankdir = LR]

# define the global styles of the nodes. We can override these in box if we wish
node [shape = rectangle, style = filled, fillcolor = Linen]

"Metabolite\ncomposition" [shape = oval, fillcolor = Beige]

# edge definitions with the node IDs
"Mating system\ntreatment (M vs P)" -> {"Dry weight"}
"Mating system\ntreatment (M vs P)" -> {"Metabolite\ncomposition"} 

"Sex\n(Female vs Male)" -> {"Dry weight"} -> {"Metabolite\ncomposition"}
"Sex\n(Female vs Male)" -> {"Metabolite\ncomposition"}

{"Metabolite\ncomposition"} -> "Carbohydrates"
{"Metabolite\ncomposition"} -> "Chitin"
{"Metabolite\ncomposition"} -> "Glycogen"
{"Metabolite\ncomposition"} -> "Lipids"
{"Metabolite\ncomposition"} -> "Protein"
}')

Fit `brms` structural equation model

Here we fit a model of the five metabolites, which includes dry body weight as a mediator variable. That is, our model estimates the effect of treatment, sex and line (and all the 2- and 3-way interactions) on dry weight, and then estimates the effect of those some predictors (plus dry weight) on the five metabolites. The model assumes that although the different sexes, treatment groups, and lines may differ in their dry weight, the relationship between dry weight and the metabolites does not vary by sex/treatment/line. This assumption was made to constrain the number of parameters in the model, and to reflect out prior beliefs about allometric scaling of metabolites.

Define Priors

We use set fairly tight Normal priors on all fixed effect parameters, which ‘regularises’ the estimates towards zero – this is conservative (because it ensures that a stronger signal in the data is needed to produce a given posterior effect size estimate), and it also helps the model to converge. Similarly, we set a somewhat conservative half-cauchy prior (mean 0, scale 0.01) on the random effects for line (i.e. we consider large differences between lines – in terms of means and treatment effects – to be possible but improbable). We leave all other priors at the defaults used by brms. Note that the Normal priors are slightly wider in the model of dry weight, because we expect larger effect sizes of sex and treatment on dry weight than on the metabolite composition.

prior1 <- c(set_prior("normal(0, 0.5)", class = "b", resp = 'Lipid'),
            set_prior("normal(0, 0.5)", class = "b", resp = 'Carbohydrate'),
            set_prior("normal(0, 0.5)", class = "b", resp = 'Protein'),
            set_prior("normal(0, 0.5)", class = "b", resp = 'Glycogen'),
            set_prior("normal(0, 0.5)", class = "b", resp = 'Chitin'),
            set_prior("normal(0, 1)", class = "b", resp = 'Dryweight'),
            set_prior("cauchy(0, 0.01)", class = "sd", resp = 'Lipid', group = "line"),
            set_prior("cauchy(0, 0.01)", class = "sd", resp = 'Carbohydrate', group = "line"),
            set_prior("cauchy(0, 0.01)", class = "sd", resp = 'Protein', group = "line"),
            set_prior("cauchy(0, 0.01)", class = "sd", resp = 'Glycogen', group = "line"),
            set_prior("cauchy(0, 0.01)", class = "sd", resp = 'Chitin', group = "line"),
            set_prior("cauchy(0, 0.01)", class = "sd", resp = 'Dryweight', group = "line"))

prior1

           prior class coef group         resp dpar nlpar bound source
  normal(0, 0.5)     b                   Lipid                    user
  normal(0, 0.5)     b            Carbohydrate                    user
  normal(0, 0.5)     b                 Protein                    user
  normal(0, 0.5)     b                Glycogen                    user
  normal(0, 0.5)     b                  Chitin                    user
    normal(0, 1)     b               Dryweight                    user
 cauchy(0, 0.01)    sd       line        Lipid                    user
 cauchy(0, 0.01)    sd       line Carbohydrate                    user
 cauchy(0, 0.01)    sd       line      Protein                    user
 cauchy(0, 0.01)    sd       line     Glycogen                    user
 cauchy(0, 0.01)    sd       line       Chitin                    user
 cauchy(0, 0.01)    sd       line    Dryweight                    user

Define the SEM’s sub-models

The fixed effects formula is sex * treatment + Dryweight (or sex * treatment in the case of the model of dry weight). The random effects part of the formula indicates that the 8 independent selection lines may differ in their means, and that the treatment effect may vary in sign/magnitude between lines. The notation | p | means that the model estimates the correlations in line effects (both slopes and intercepts) between the 6 response variables. Finally, the notation set_rescor(TRUE) means that the model should estimate the residual correlations between the response variables.

brms_formula <- 
  
  # Sub-models of the 5 metabolites
  bf(mvbind(Lipid, Carbohydrate, Protein, Glycogen, Chitin) ~ 
       sex*treatment + Dryweight + (treatment | p | line)) +
  
  # dry weight sub-model
   bf(Dryweight ~ sex*treatment + (treatment | p | line)) +
  
  # Allow for (and estimate) covariance between the residuals of the difference response variables
  set_rescor(TRUE)

brms_formula

Lipid ~ sex * treatment + Dryweight + (treatment | p | line) 
Carbohydrate ~ sex * treatment + Dryweight + (treatment | p | line) 
Protein ~ sex * treatment + Dryweight + (treatment | p | line) 
Glycogen ~ sex * treatment + Dryweight + (treatment | p | line) 
Chitin ~ sex * treatment + Dryweight + (treatment | p | line) 
Dryweight ~ sex * treatment + (treatment | p | line)

Running the model

The model is run over 4 chains with 5000 iterations each (with the first 2500 discarded as burn-in), for a total of 2500*4 = 10,000 posterior samples.

if(!file.exists("output/brms_metabolite_SEM.rds")){
  brms_metabolite_SEM <- brm(
    brms_formula,
    data = scaled_metabolites %>% # brms does not like underscores in variable names
      rename(Dryweight = Dry_weight) %>%
      rename_all(~ gsub("_conc", "", .x)),
    iter = 5000, chains = 4, cores = 1,
    prior = prior1,
    control = list(max_treedepth = 20,
                   adapt_delta = 0.99)
  )
  
  saveRDS(brms_metabolite_SEM, "output/brms_metabolite_SEM.rds")
} else {
  brms_metabolite_SEM <- readRDS('output/brms_metabolite_SEM.rds')
}

Posterior predictive check of model fit

The plot below shows that the fitted model is able to produce posterior predictions that have a similar distribution to the original data, for each of the response variables, which is a necessary condition for the model to be used for statistical inference.

grid.arrange(
  pp_check(brms_metabolite_SEM, resp = "Dryweight") + 
    ggtitle("Dry weight") + theme(legend.position = "none"),
  pp_check(brms_metabolite_SEM, resp = "Lipid") + 
    ggtitle("Lipid") + theme(legend.position = "none"),
  pp_check(brms_metabolite_SEM, resp = "Carbohydrate") + 
    ggtitle("Carbohydrate") + theme(legend.position = "none"),
  pp_check(brms_metabolite_SEM, resp = "Protein") + 
    ggtitle("Protein") + theme(legend.position = "none"),
  pp_check(brms_metabolite_SEM, resp = "Glycogen") + 
    ggtitle("Glycogen") + theme(legend.position = "none"),
  pp_check(brms_metabolite_SEM, resp = "Chitin") + 
    ggtitle("Chitin") + theme(legend.position = "none"),
  nrow = 2
)

Version	Author	Date
bb96acf	lukeholman	2020-12-11
e5c580f	lukeholman	2020-12-11
31ed22a	lukeholman	2020-12-10
f7c88a2	lukeholman	2020-12-10

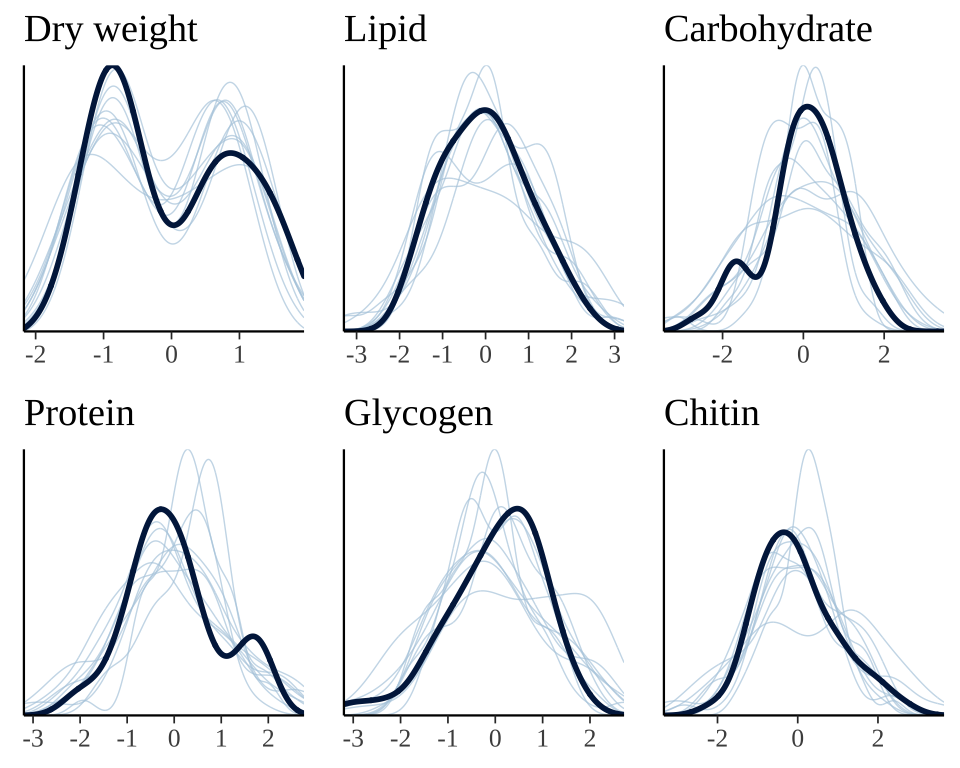
Table of model parameter estimates

Formatted table

This tables shows the fixed effects estimates for the treatment, sex, their interaction, as well as the slope associated with dry weight (where relevant), for each of the six response variables. The p column shows 1 - minus the “probability of direction”, i.e. the posterior probability that the reported sign of the estimate is correct given the data and the prior; subtracting this value from one gives a Bayesian equivalent of a one-sided p-value. For brevity, we have omitted all the parameter estimates involving the predictor variable line, as well as the estimates of residual (co)variance. Click the next tab to see a complete summary of the model and its output.

vars <- c("Lipid", "Carbohydrate", "Glycogen", "Protein", "Chitin")
tests <- c('_Dryweight', '_sexMale',
           '_sexMale:treatmentPolyandry',
           '_treatmentPolyandry')

hypSEM <- data.frame(expand_grid(vars, tests) %>% 
                       mutate(est = NA,
                              err = NA,
                              lwr = NA,
                              upr = NA) %>% 
                       # bind body weight on the end
                       rbind(data.frame(
                         vars = rep('Dryweight', 3),
                         tests = c('_sexMale', 
                                   '_treatmentPolyandry', 
                                   '_sexMale:treatmentPolyandry'),
                         est = NA,
                         err = NA,
                         lwr = NA,
                         upr = NA)))

for(i in 1:nrow(hypSEM)) {
  
  result = hypothesis(brms_metabolite_SEM, 
                      paste0(hypSEM[i, 1], hypSEM[i, 2], ' = 0'))$hypothesis

  hypSEM[i, 3] = round(result$Estimate, 3)
  hypSEM[i, 4] = round(result$Est.Error, 3)
  hypSEM[i, 5] = round(result$CI.Lower, 3)
  hypSEM[i, 6] = round(result$CI.Upper, 3)

}

pvals <- bayestestR::p_direction(brms_metabolite_SEM) %>% 
  as.data.frame() %>%
  mutate(vars = map_chr(str_split(Parameter, "_"), ~ .x[2]),
         tests = map_chr(str_split(Parameter, "_"), ~ .x[3]),
         tests = str_c("_", str_remove_all(tests, "[.]")),
         tests = replace(tests, tests == "_sexMaletreatmentPolyandry", "_sexMale:treatmentPolyandry")) %>%
  filter(!str_detect(tests, "line")) %>%
  mutate(p_val = 1 - pd, star = ifelse(p_val < 0.05, "\\*", "")) %>%
  select(vars, tests, p_val, star)


hypSEM <- hypSEM %>% left_join(pvals, by = c("vars", "tests"))

hypSEM  %>% 
  mutate(Parameter = c(rep(c('Dry weight', 'Sex (M)', 
                             'Sex (M) x Treatment (P)', 
                             'Treatment (P)'), 5), 
                       'Sex (M)', 'Treatment (P)', 'Sex (M) x Treatment (P)'))  %>% 
  mutate(Parameter = factor(Parameter, c("Dry weight", "Sex (M)", "Treatment (P)", "Sex (M) x Treatment (P)")),
         vars = factor(vars, c("Carbohydrate", "Chitin", "Glycogen", "Lipid", "Protein", "Dryweight"))) %>%
  arrange(vars, Parameter) %>%
  select(Parameter, Estimate = est, `Est. error` = err, 
         `CI lower` = lwr, `CI upper` = upr, `p` = p_val, star) %>% 
  rename(` ` = star) %>%
  kable() %>% 
  kable_styling(full_width = FALSE) %>%
  group_rows("Carbohydrates", 1, 4) %>%
  group_rows("Chitin", 5, 8) %>%
  group_rows("Glycogen", 9, 12) %>%
  group_rows("Lipids", 13, 16) %>% 
  group_rows("Protein", 17, 20) %>% 
  group_rows("Dry weight", 21, 23)

Parameter	Estimate	Est. error	CI lower	CI upper	p
Carbohydrates
Dry weight	0.105	0.269	-0.419	0.622	0.3516
Sex (M)	0.024	0.427	-0.812	0.864	0.4771
Treatment (P)	-0.246	0.302	-0.832	0.348	0.2074
Sex (M) x Treatment (P)	-0.414	0.347	-1.090	0.263	0.1172
Chitin
Dry weight	-0.486	0.260	-0.995	0.023	0.0314	*
Sex (M)	0.399	0.420	-0.435	1.206	0.1699
Treatment (P)	-0.113	0.285	-0.673	0.453	0.3405
Sex (M) x Treatment (P)	-0.317	0.328	-0.957	0.320	0.1663
Glycogen
Dry weight	0.332	0.267	-0.180	0.850	0.1096
Sex (M)	-0.267	0.427	-1.096	0.567	0.2652
Treatment (P)	0.220	0.296	-0.367	0.787	0.2244
Sex (M) x Treatment (P)	0.387	0.351	-0.297	1.066	0.1395
Lipids
Dry weight	0.539	0.254	0.041	1.029	0.0171	*
Sex (M)	-0.119	0.411	-0.926	0.680	0.3825
Treatment (P)	0.389	0.276	-0.156	0.919	0.0774
Sex (M) x Treatment (P)	-0.050	0.313	-0.672	0.555	0.4372
Protein
Dry weight	-0.206	0.275	-0.742	0.340	0.2252
Sex (M)	-0.011	0.435	-0.858	0.850	0.4844
Treatment (P)	-0.216	0.306	-0.818	0.378	0.2414
Sex (M) x Treatment (P)	0.352	0.361	-0.347	1.057	0.1667
Dry weight
Sex (M)	-1.614	0.143	-1.895	-1.334	0.0000	*
Treatment (P)	0.525	0.155	0.218	0.827	0.0006	*
Sex (M) x Treatment (P)	-0.354	0.196	-0.733	0.035	0.0378	*

Complete output from `summary.brmsfit()`

‘Group-Level Effects’ (also called random effects): This shows the (co)variances associated with the line-specific intercepts (which have names like sd(Lipid_Intercept)) and slopes (e.g. sd(Dryweight_treatmentPolyandry)), as well as the correlations between these effects (e.g. cor(Lipid_Intercept,Protein_Intercept) is the correlation in line effects on lipids and proteins)
‘Population-Level Effects:’ (also called fixed effects): These give the estimates of the intercept (i.e. for female M flies) and the effects of treatment, sex, dry weight, and the treatment \(\times\) sex interaction, for each response variable.
‘Family Specific Parameters’: This is the parameter sigma for the residual variance for each response variable
‘Residual Correlations:’ This give the correlations between the residuals for each pairs of response variables.

Note that the model has converged (Rhat = 1) and the posterior is adequately samples (high ESS values).

brms_metabolite_SEM

 Family: MV(gaussian, gaussian, gaussian, gaussian, gaussian, gaussian) 
  Links: mu = identity; sigma = identity
         mu = identity; sigma = identity
         mu = identity; sigma = identity
         mu = identity; sigma = identity
         mu = identity; sigma = identity
         mu = identity; sigma = identity 
Formula: Lipid ~ sex * treatment + Dryweight + (treatment | p | line) 
         Carbohydrate ~ sex * treatment + Dryweight + (treatment | p | line) 
         Protein ~ sex * treatment + Dryweight + (treatment | p | line) 
         Glycogen ~ sex * treatment + Dryweight + (treatment | p | line) 
         Chitin ~ sex * treatment + Dryweight + (treatment | p | line) 
         Dryweight ~ sex * treatment + (treatment | p | line) 
   Data: scaled_metabolites %>% rename(Dryweight = Dry_weig (Number of observations: 48) 
Samples: 4 chains, each with iter = 5000; warmup = 2500; thin = 1;
         total post-warmup samples = 10000

Group-Level Effects: 
~line (Number of levels: 8) 
                                                                  Estimate Est.Error l-95% CI u-95% CI Rhat Bulk_ESS Tail_ESS
sd(Lipid_Intercept)                                                   0.09      0.15     0.00     0.52 1.00     1855     2733
sd(Lipid_treatmentPolyandry)                                          0.03      0.07     0.00     0.24 1.00     8128     4958
sd(Carbohydrate_Intercept)                                            0.07      0.14     0.00     0.49 1.00     3043     2670
sd(Carbohydrate_treatmentPolyandry)                                   0.05      0.13     0.00     0.43 1.00     5937     3170
sd(Protein_Intercept)                                                 0.05      0.11     0.00     0.43 1.00     4709     2722
sd(Protein_treatmentPolyandry)                                        0.03      0.07     0.00     0.20 1.00    11030     5733
sd(Glycogen_Intercept)                                                0.03      0.07     0.00     0.22 1.00     8668     4932
sd(Glycogen_treatmentPolyandry)                                       0.03      0.06     0.00     0.18 1.00    10665     4948
sd(Chitin_Intercept)                                                  0.07      0.12     0.00     0.44 1.00     3539     3474
sd(Chitin_treatmentPolyandry)                                         0.04      0.11     0.00     0.35 1.00     6341     3872
sd(Dryweight_Intercept)                                               0.05      0.07     0.00     0.25 1.00     2761     4938
sd(Dryweight_treatmentPolyandry)                                      0.03      0.05     0.00     0.17 1.00     8009     5976
cor(Lipid_Intercept,Lipid_treatmentPolyandry)                         0.00      0.28    -0.53     0.52 1.00    13085     6894
cor(Lipid_Intercept,Carbohydrate_Intercept)                           0.01      0.27    -0.52     0.54 1.00    13834     6815
cor(Lipid_treatmentPolyandry,Carbohydrate_Intercept)                  0.00      0.27    -0.52     0.53 1.00     9816     7196
cor(Lipid_Intercept,Carbohydrate_treatmentPolyandry)                 -0.00      0.28    -0.53     0.53 1.00    13922     7281
cor(Lipid_treatmentPolyandry,Carbohydrate_treatmentPolyandry)         0.00      0.28    -0.53     0.55 1.00    12566     7569
cor(Carbohydrate_Intercept,Carbohydrate_treatmentPolyandry)           0.00      0.28    -0.54     0.53 1.00    11563     7714
cor(Lipid_Intercept,Protein_Intercept)                                0.00      0.28    -0.52     0.54 1.00    13637     6712
cor(Lipid_treatmentPolyandry,Protein_Intercept)                       0.00      0.28    -0.53     0.53 1.00    11022     7065
cor(Carbohydrate_Intercept,Protein_Intercept)                         0.00      0.28    -0.53     0.53 1.00    10145     7426
cor(Carbohydrate_treatmentPolyandry,Protein_Intercept)               -0.00      0.28    -0.53     0.53 1.00     9156     6841
cor(Lipid_Intercept,Protein_treatmentPolyandry)                       0.00      0.28    -0.53     0.54 1.00    15294     6636
cor(Lipid_treatmentPolyandry,Protein_treatmentPolyandry)             -0.00      0.27    -0.53     0.52 1.00    12057     6512
cor(Carbohydrate_Intercept,Protein_treatmentPolyandry)                0.00      0.28    -0.53     0.53 1.00    10481     7316
cor(Carbohydrate_treatmentPolyandry,Protein_treatmentPolyandry)      -0.01      0.28    -0.54     0.53 1.00     9051     7446
cor(Protein_Intercept,Protein_treatmentPolyandry)                     0.00      0.28    -0.53     0.54 1.00     8856     7479
cor(Lipid_Intercept,Glycogen_Intercept)                               0.01      0.28    -0.52     0.54 1.00    14706     7112
cor(Lipid_treatmentPolyandry,Glycogen_Intercept)                      0.00      0.28    -0.53     0.54 1.00    12127     7024
cor(Carbohydrate_Intercept,Glycogen_Intercept)                        0.00      0.27    -0.52     0.54 1.00    11292     6363
cor(Carbohydrate_treatmentPolyandry,Glycogen_Intercept)              -0.00      0.28    -0.53     0.53 1.00     9910     7085
cor(Protein_Intercept,Glycogen_Intercept)                            -0.00      0.28    -0.54     0.54 1.00     8748     7275
cor(Protein_treatmentPolyandry,Glycogen_Intercept)                   -0.00      0.28    -0.54     0.52 1.00     7251     7812
cor(Lipid_Intercept,Glycogen_treatmentPolyandry)                      0.00      0.28    -0.53     0.54 1.00    15138     7138
cor(Lipid_treatmentPolyandry,Glycogen_treatmentPolyandry)             0.00      0.27    -0.51     0.53 1.00    12441     7367
cor(Carbohydrate_Intercept,Glycogen_treatmentPolyandry)               0.00      0.27    -0.52     0.54 1.00    10449     7529
cor(Carbohydrate_treatmentPolyandry,Glycogen_treatmentPolyandry)      0.00      0.28    -0.53     0.54 1.00     9418     7092
cor(Protein_Intercept,Glycogen_treatmentPolyandry)                   -0.00      0.28    -0.53     0.54 1.00     8620     7282
cor(Protein_treatmentPolyandry,Glycogen_treatmentPolyandry)          -0.00      0.27    -0.53     0.52 1.00     7272     6969
cor(Glycogen_Intercept,Glycogen_treatmentPolyandry)                  -0.00      0.28    -0.54     0.53 1.00     6255     7043
cor(Lipid_Intercept,Chitin_Intercept)                                -0.00      0.28    -0.54     0.54 1.00    13268     7280
cor(Lipid_treatmentPolyandry,Chitin_Intercept)                       -0.00      0.27    -0.53     0.52 1.00    11731     7629
cor(Carbohydrate_Intercept,Chitin_Intercept)                         -0.00      0.28    -0.53     0.54 1.00    10469     7643
cor(Carbohydrate_treatmentPolyandry,Chitin_Intercept)                -0.01      0.28    -0.54     0.52 1.00     8100     7306
cor(Protein_Intercept,Chitin_Intercept)                               0.00      0.28    -0.52     0.54 1.00     8134     8168
cor(Protein_treatmentPolyandry,Chitin_Intercept)                     -0.00      0.28    -0.53     0.53 1.00     8115     7497
cor(Glycogen_Intercept,Chitin_Intercept)                              0.01      0.28    -0.53     0.54 1.00     7361     8201
cor(Glycogen_treatmentPolyandry,Chitin_Intercept)                    -0.01      0.28    -0.53     0.53 1.00     6437     8302
cor(Lipid_Intercept,Chitin_treatmentPolyandry)                       -0.01      0.28    -0.54     0.53 1.00    13334     7468
cor(Lipid_treatmentPolyandry,Chitin_treatmentPolyandry)              -0.00      0.27    -0.52     0.53 1.00    13046     7663
cor(Carbohydrate_Intercept,Chitin_treatmentPolyandry)                -0.00      0.28    -0.54     0.53 1.00    10428     7286
cor(Carbohydrate_treatmentPolyandry,Chitin_treatmentPolyandry)        0.00      0.28    -0.53     0.54 1.00     9408     7132
cor(Protein_Intercept,Chitin_treatmentPolyandry)                      0.00      0.28    -0.53     0.53 1.00     8664     7507
cor(Protein_treatmentPolyandry,Chitin_treatmentPolyandry)            -0.00      0.28    -0.53     0.53 1.00     8111     7681
cor(Glycogen_Intercept,Chitin_treatmentPolyandry)                     0.00      0.28    -0.54     0.53 1.00     6966     8175
cor(Glycogen_treatmentPolyandry,Chitin_treatmentPolyandry)           -0.00      0.28    -0.54     0.54 1.00     6497     7897
cor(Chitin_Intercept,Chitin_treatmentPolyandry)                      -0.00      0.28    -0.53     0.54 1.00     6219     7985
cor(Lipid_Intercept,Dryweight_Intercept)                             -0.01      0.28    -0.52     0.52 1.00    13442     7316
cor(Lipid_treatmentPolyandry,Dryweight_Intercept)                    -0.00      0.28    -0.54     0.54 1.00    10824     7108
cor(Carbohydrate_Intercept,Dryweight_Intercept)                       0.00      0.28    -0.52     0.52 1.00     9437     6945
cor(Carbohydrate_treatmentPolyandry,Dryweight_Intercept)              0.01      0.27    -0.51     0.53 1.00     8050     8002
cor(Protein_Intercept,Dryweight_Intercept)                            0.00      0.28    -0.53     0.53 1.00     8664     7933
cor(Protein_treatmentPolyandry,Dryweight_Intercept)                  -0.00      0.28    -0.54     0.52 1.00     7988     7892
cor(Glycogen_Intercept,Dryweight_Intercept)                          -0.00      0.28    -0.53     0.53 1.00     7131     8108
cor(Glycogen_treatmentPolyandry,Dryweight_Intercept)                 -0.01      0.28    -0.54     0.53 1.00     6788     7768
cor(Chitin_Intercept,Dryweight_Intercept)                            -0.01      0.28    -0.55     0.52 1.00     6101     7577
cor(Chitin_treatmentPolyandry,Dryweight_Intercept)                    0.00      0.28    -0.53     0.54 1.00     5527     7602
cor(Lipid_Intercept,Dryweight_treatmentPolyandry)                     0.01      0.28    -0.53     0.55 1.00    12880     7422
cor(Lipid_treatmentPolyandry,Dryweight_treatmentPolyandry)            0.00      0.27    -0.53     0.52 1.00    12106     7046
cor(Carbohydrate_Intercept,Dryweight_treatmentPolyandry)              0.00      0.28    -0.53     0.53 1.00    10910     7333
cor(Carbohydrate_treatmentPolyandry,Dryweight_treatmentPolyandry)     0.01      0.28    -0.52     0.54 1.00     8704     7439
cor(Protein_Intercept,Dryweight_treatmentPolyandry)                   0.00      0.28    -0.54     0.54 1.00     8369     7795
cor(Protein_treatmentPolyandry,Dryweight_treatmentPolyandry)         -0.00      0.28    -0.52     0.53 1.00     7772     7856
cor(Glycogen_Intercept,Dryweight_treatmentPolyandry)                 -0.00      0.28    -0.53     0.53 1.00     7041     7735
cor(Glycogen_treatmentPolyandry,Dryweight_treatmentPolyandry)         0.00      0.28    -0.53     0.53 1.00     6473     7736
cor(Chitin_Intercept,Dryweight_treatmentPolyandry)                   -0.01      0.28    -0.53     0.54 1.00     6425     7813
cor(Chitin_treatmentPolyandry,Dryweight_treatmentPolyandry)          -0.00      0.27    -0.53     0.52 1.00     5625     7451
cor(Dryweight_Intercept,Dryweight_treatmentPolyandry)                 0.00      0.28    -0.54     0.54 1.00     5710     7350

Population-Level Effects: 
                                        Estimate Est.Error l-95% CI u-95% CI Rhat Bulk_ESS Tail_ESS
Lipid_Intercept                            -0.12      0.24    -0.59     0.36 1.00     6932     7152
Carbohydrate_Intercept                      0.22      0.27    -0.32     0.76 1.00     8961     7440
Protein_Intercept                           0.02      0.28    -0.53     0.56 1.00     9467     8065
Glycogen_Intercept                         -0.07      0.26    -0.58     0.45 1.00     9134     7728
Chitin_Intercept                           -0.06      0.25    -0.55     0.44 1.00     7653     8105
Dryweight_Intercept                         0.63      0.11     0.42     0.85 1.00     7256     7086
Lipid_sexMale                              -0.12      0.41    -0.93     0.68 1.00     5583     6918
Lipid_treatmentPolyandry                    0.39      0.28    -0.16     0.92 1.00     6242     6327
Lipid_Dryweight                             0.54      0.25     0.04     1.03 1.00     4680     6226
Lipid_sexMale:treatmentPolyandry           -0.05      0.31    -0.67     0.55 1.00     7546     6786
Carbohydrate_sexMale                        0.02      0.43    -0.81     0.86 1.00     7608     7494
Carbohydrate_treatmentPolyandry            -0.25      0.30    -0.83     0.35 1.00     8609     7096
Carbohydrate_Dryweight                      0.10      0.27    -0.42     0.62 1.00     6376     6979
Carbohydrate_sexMale:treatmentPolyandry    -0.41      0.35    -1.09     0.26 1.00     8926     7472
Protein_sexMale                            -0.01      0.44    -0.86     0.85 1.00     6467     7640
Protein_treatmentPolyandry                 -0.22      0.31    -0.82     0.38 1.00     8496     7777
Protein_Dryweight                          -0.21      0.27    -0.74     0.34 1.00     5492     7121
Protein_sexMale:treatmentPolyandry          0.35      0.36    -0.35     1.06 1.00     9640     7873
Glycogen_sexMale                           -0.27      0.43    -1.10     0.57 1.00     6445     7335
Glycogen_treatmentPolyandry                 0.22      0.30    -0.37     0.79 1.00     8260     7660
Glycogen_Dryweight                          0.33      0.27    -0.18     0.85 1.00     5430     6925
Glycogen_sexMale:treatmentPolyandry         0.39      0.35    -0.30     1.07 1.00     9674     8182
Chitin_sexMale                              0.40      0.42    -0.43     1.21 1.00     5956     7056
Chitin_treatmentPolyandry                  -0.11      0.28    -0.67     0.45 1.00     7677     7040
Chitin_Dryweight                           -0.49      0.26    -1.00     0.02 1.00     5296     6576
Chitin_sexMale:treatmentPolyandry          -0.32      0.33    -0.96     0.32 1.00     8787     7616
Dryweight_sexMale                          -1.61      0.14    -1.90    -1.33 1.00     6937     6906
Dryweight_treatmentPolyandry                0.53      0.16     0.22     0.83 1.00     6826     6910
Dryweight_sexMale:treatmentPolyandry       -0.35      0.20    -0.73     0.03 1.00     6057     6748

Family Specific Parameters: 
                   Estimate Est.Error l-95% CI u-95% CI Rhat Bulk_ESS Tail_ESS
sigma_Lipid            0.74      0.09     0.58     0.94 1.00     6443     7012
sigma_Carbohydrate     1.00      0.11     0.80     1.25 1.00     8636     7372
sigma_Protein          1.02      0.12     0.82     1.29 1.00     9523     6888
sigma_Glycogen         0.95      0.11     0.76     1.19 1.00    11707     7446
sigma_Chitin           0.84      0.10     0.67     1.06 1.00     7464     7642
sigma_Dryweight        0.36      0.04     0.29     0.46 1.00     9207     7629

Residual Correlations: 
                               Estimate Est.Error l-95% CI u-95% CI Rhat Bulk_ESS Tail_ESS
rescor(Lipid,Carbohydrate)        -0.33      0.14    -0.59    -0.04 1.00     5091     6469
rescor(Lipid,Protein)             -0.06      0.15    -0.35     0.23 1.00     9533     7092
rescor(Carbohydrate,Protein)       0.04      0.15    -0.25     0.32 1.00    10144     7494
rescor(Lipid,Glycogen)             0.04      0.15    -0.26     0.32 1.00     6330     6923
rescor(Carbohydrate,Glycogen)     -0.01      0.15    -0.30     0.28 1.00    10140     6808
rescor(Protein,Glycogen)          -0.14      0.14    -0.41     0.15 1.00     8731     7742
rescor(Lipid,Chitin)              -0.06      0.15    -0.35     0.23 1.00     7493     7682
rescor(Carbohydrate,Chitin)       -0.42      0.13    -0.64    -0.15 1.00     9009     6900
rescor(Protein,Chitin)             0.07      0.15    -0.22     0.35 1.00     8593     7175
rescor(Glycogen,Chitin)           -0.03      0.15    -0.32     0.26 1.00     8371     7499
rescor(Lipid,Dryweight)            0.16      0.18    -0.21     0.49 1.00     5252     6335
rescor(Carbohydrate,Dryweight)    -0.00      0.18    -0.35     0.34 1.00     6169     7470
rescor(Protein,Dryweight)         -0.04      0.17    -0.38     0.30 1.00     5852     7018
rescor(Glycogen,Dryweight)         0.01      0.18    -0.33     0.35 1.00     5373     6886
rescor(Chitin,Dryweight)           0.26      0.18    -0.10     0.58 1.00     4795     7120

Samples were drawn using sampling(NUTS). For each parameter, Bulk_ESS
and Tail_ESS are effective sample size measures, and Rhat is the potential
scale reduction factor on split chains (at convergence, Rhat = 1).

Posterior effect size of treatment on metabolite abundance, for each sex

Here, we use the model to predict the mean concentration of each metabolite (in standard units) in each treatment and sex (averaged across the eight replicate selection lines). We then calculate the effect size of treatment by subtracting the (sex-specific) mean for the M treatment from the mean for the P treatment; thus a value of 1 would mean that the P treatment has a mean that is larger by 1 standard deviation. Thus, the y-axis in the following graphs essentially shows the posterior estimate of standardised effect size (Cohen’s d), from the model shown above.

Because the model contains dry weight as a mediator variable, we created these predictions two different ways, and display the answer for both using tabs in the following figures/tables. Firstly, we predicted the means controlling for differences in dry weight between sexes and treatments; this was done by deriving the predictions dry weight set to its global mean, for both sexes and treatments. Secondly, we derived predictions without controlling for dry weight. This was done by deriving the predictions with dry weight set to its average value for the appropriate treatment-sex combination.

By clicking the tabs and comparing, one can see that the estimates of the treatment effect hardly change when differences in dry weight are controlled for. This indicates that dry mass does not have an important role in mediating the effect of treatment on metabolite composition, even though body size differs between treatments. Thus, we conclude that the M vs P treatments caused metabolite composition to evolve, through mechanisms other than the evolution of dry weight.

Figure

Not controlling for differences in dry weight between treatments

new <- expand_grid(sex = c("Male", "Female"),
                   treatment = c("Monogamy", "Polyandry"),
                   Dryweight = NA, line = NA) %>%
  mutate(type = 1:n())

levels <- c("Carbohydrate", "Chitin", "Glycogen", "Lipid", "Protein", "Dryweight")

# Estimate mean dry weight for each of the 4 sex/treatment combinations
evolved_mean_dryweights <- data.frame(
  new[,1:2], 
  fitted(brms_metabolite_SEM, re_formula = NA,
         newdata = new %>% select(-Dryweight), 
         summary = TRUE, resp = "Dryweight")) %>%
  as_tibble()

# Find the mean dry weight for males and females (across treatments)
male_dryweight <- mean(evolved_mean_dryweights$Estimate[1:2])
female_dryweight <- mean(evolved_mean_dryweights$Estimate[3:4])

new_metabolites <- bind_rows(
  expand_grid(sex = c("Male", "Female"),
              treatment = c("Monogamy", "Polyandry"),
              Dryweight = c(male_dryweight, female_dryweight), line = NA) %>%
    filter(sex == "Male" & Dryweight == male_dryweight |
             sex == "Female" & Dryweight == female_dryweight) %>%
    mutate(type = 1:4),
  evolved_mean_dryweights %>% select(sex, treatment, Dryweight = Estimate) %>%
    mutate(line = NA, type = 5:8)
)


# Predict data from the SEM of metabolites...

# Because we use sum contrasts for "line" and line=NA in the new data, 
# this function predicts at the global means across the 4 lines (see ?posterior_epred)
fitted_values <- posterior_epred(
  brms_metabolite_SEM, newdata = new_metabolites, re_formula = NA,
  summary = FALSE, resp = c("Carbohydrate", "Chitin", "Glycogen", "Lipid", "Protein")) %>% 
  reshape2::melt() %>% rename(draw = Var1, type = Var2, variable = Var3) %>% 
  as_tibble() %>%
  left_join(new_metabolites, by = "type") %>%
  select(draw, variable, value, sex, treatment, Dryweight) %>%
  mutate(variable = factor(variable, levels))


treat_diff_standard_dryweight <- fitted_values %>%
  filter(Dryweight %in% c(male_dryweight, female_dryweight)) %>%
  spread(treatment, value) %>%
  mutate(`Difference in means (Poly - Mono)` = Polyandry - Monogamy) 

treat_diff_actual_dryweight <- fitted_values %>%
  filter(!(Dryweight %in% c(male_dryweight, female_dryweight))) %>% 
  select(-Dryweight) %>%
  spread(treatment, value) %>%
  mutate(`Difference in means (Poly - Mono)` = Polyandry - Monogamy) 

summary_dat1 <- treat_diff_actual_dryweight %>%
  filter(variable != 'Dryweight') %>%
  rename(x = `Difference in means (Poly - Mono)`) %>%
  group_by(variable, sex)  %>%
  summarise(`Difference in means (Poly - Mono)` = median(x),
            `Lower 95% CI` = quantile(x, probs = 0.025), 
            `Upper 95% CI` = quantile(x, probs = 0.975),
            p = 1 - as.numeric(bayestestR::p_direction(x)),
            ` ` = ifelse(p < 0.05, "\\*", ""),
            .groups = "drop")

summary_dat2 <- treat_diff_standard_dryweight %>%
  filter(variable != 'Dryweight') %>%
  rename(x = `Difference in means (Poly - Mono)`) %>%
  group_by(variable, sex)  %>%
  summarise(`Difference in means (Poly - Mono)` = median(x),
            `Lower 95% CI` = quantile(x, probs = 0.025), 
            `Upper 95% CI` = quantile(x, probs = 0.975),
            p = 1 - as.numeric(bayestestR::p_direction(x)),
            ` ` = ifelse(p < 0.05, "\\*", ""),
            .groups = "drop")

sampled_draws <- sample(unique(fitted_values$draw), 100)
ylims <- c(-1.8, 1.8)

p1 <- treat_diff_actual_dryweight %>%
  filter(variable != 'Dryweight') %>% 
  ggplot(aes(x = sex, y = `Difference in means (Poly - Mono)`,fill = sex)) +
  geom_hline(yintercept = 0, linetype = 2) +
  stat_halfeye() + 
  geom_line(data = treat_diff_actual_dryweight %>%
              filter(draw %in% sampled_draws) %>%
              filter(variable != 'Dryweight'), 
            alpha = 0.8, size = 0.12, colour = "black", aes(group = draw)) +
  geom_point(data = summary_dat1, pch = 21, colour = "black", size = 3.1) + 
  scale_fill_brewer(palette = 'Pastel1', direction = 1, name = "") +
  scale_colour_brewer(palette = 'Pastel1', direction = 1, name = "") +
  facet_wrap( ~ variable,  nrow = 1) +
  theme_bw() +
  theme(legend.position = 'none',
        strip.background = element_blank(),
        text = element_text(family = nice_font),
        panel.grid.major.x = element_blank()) +
  coord_cartesian(ylim = ylims) + 
  ylab("Difference in means between\nselection treatments (P - M)") + xlab("Sex")


ggsave("output/metabolite_plot.pdf", p1, height=4, width=6)
p1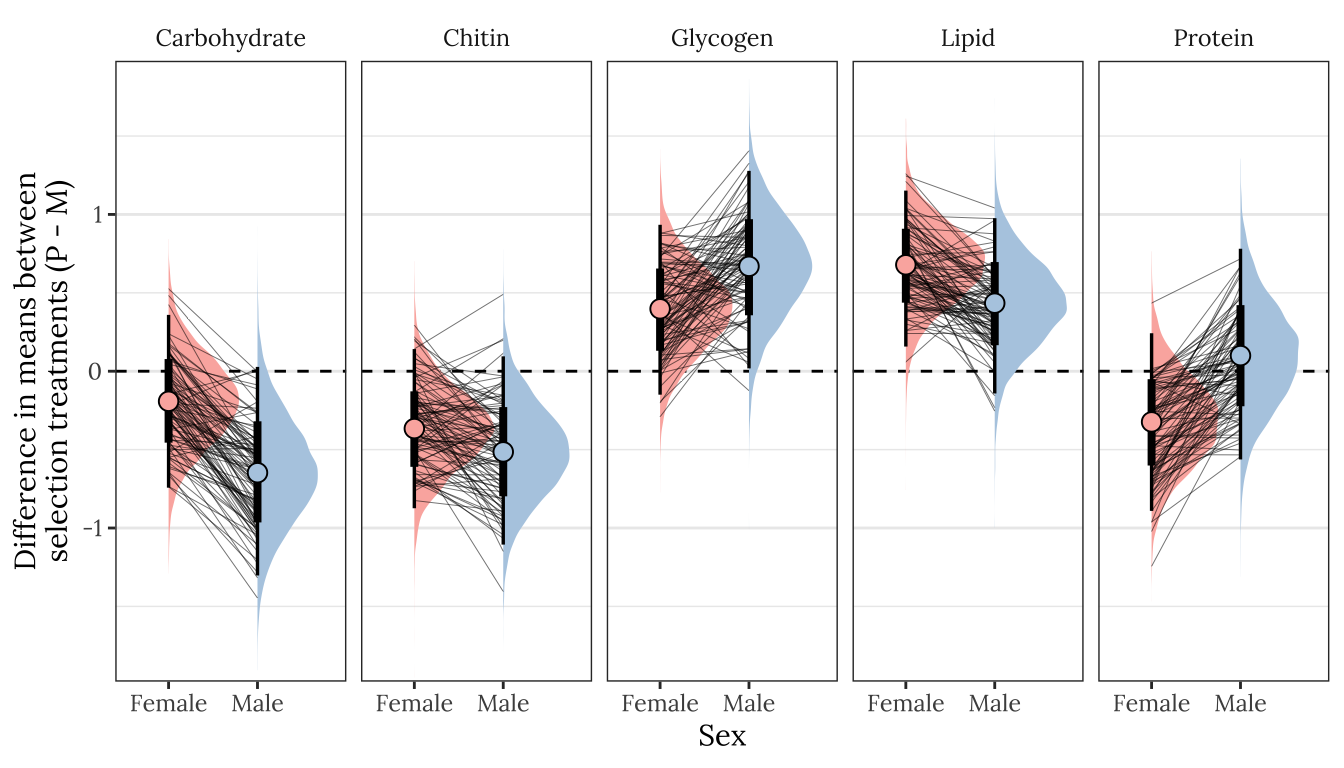

Version	Author	Date
b6cf554	lukeholman	2020-12-11
a88f037	lukeholman	2020-12-11
bb96acf	lukeholman	2020-12-11
e5c580f	lukeholman	2020-12-11
7fca240	lukeholman	2020-12-10
f7c88a2	lukeholman	2020-12-10
43cc270	lukeholman	2020-12-09

Figure XX: Posterior estimates of the treatment effect size for both sexes, for each of the five metabolites. A positive value means that the mean metabolite concentration is higher in the P treatment than the M treatment, while a negative effects denotes M > P. A strongly supported treatment effect is implied by the majority of the posterior lying to one side of zero. The error bars summarise the 66% and 95% quantiles of the posterior. This plot was created used posterior predictions of the means that were not adjusted for differences in dry weight between treatments.

Controlling for differences in dry weight between treatments

treat_diff_standard_dryweight %>%
  filter(variable != 'Dryweight') %>% 
  ggplot(aes(x = sex, y = `Difference in means (Poly - Mono)`,fill = sex)) +
  geom_hline(yintercept = 0, linetype = 2) +
  stat_halfeye() + 
  geom_line(data = treat_diff_standard_dryweight %>%
              filter(draw %in% sampled_draws) %>%
              filter(variable != 'Dryweight'), 
            alpha = 0.8, size = 0.12, colour = "black", aes(group = draw)) +
  geom_point(data = summary_dat2, pch = 21, colour = "black", size = 3.1) + 
  scale_fill_brewer(palette = 'Pastel1', direction = 1, name = "") +
  scale_colour_brewer(palette = 'Pastel1', direction = 1, name = "") +
  facet_wrap( ~ variable,  nrow = 1) +
  theme_bw() +
  theme(legend.position = 'none',
        strip.background = element_blank(),
        text = element_text(family = nice_font),
        panel.grid.major.x = element_blank()) +
  coord_cartesian(ylim = ylims) + 
  ylab("Difference in means between\nselection treatments (P - M)") + xlab("Sex")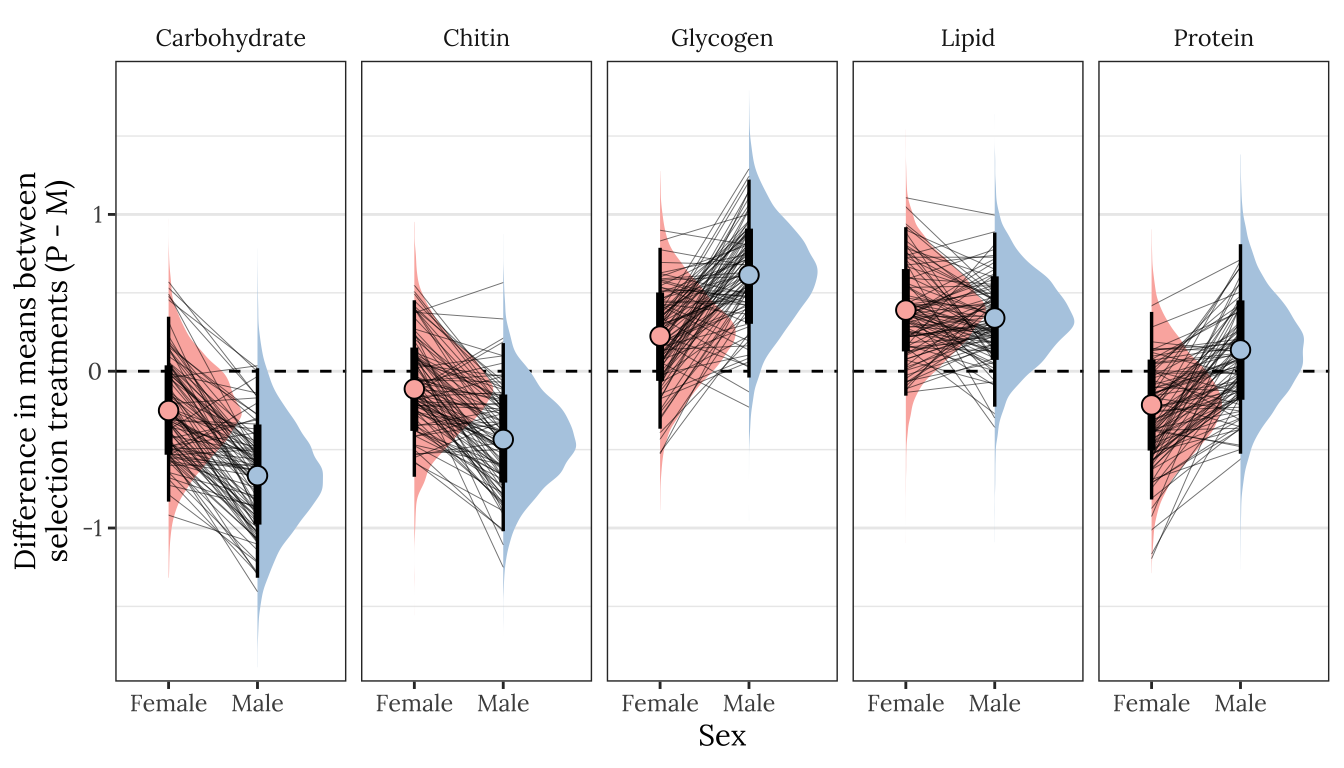

Version	Author	Date
b6cf554	lukeholman	2020-12-11
a88f037	lukeholman	2020-12-11
bb96acf	lukeholman	2020-12-11
e5c580f	lukeholman	2020-12-11
7fca240	lukeholman	2020-12-10
f7c88a2	lukeholman	2020-12-10

Figure XX: Posterior estimates of the treatment effect size for both sexes, for each of the five metabolites. A positive value means that the mean metabolite concentration is higher in the P treatment than the M treatment, while a negative effects denotes M > P. A strongly supported treatment effect is implied by the majority of the posterior lying to one side of zero. The error bars summarise the 66% and 95% quantiles of the posterior. This plot was created used posterior predictions of the means that were adjusted for differences in dry weight between treatments.

Table

Not controlling for differences in dry weight between treatments

summary_dat1 %>%
  kable(digits = 3) %>%
  kable_styling(full_width = FALSE)

variable	sex	Difference in means (Poly - Mono)	Lower 95% CI	Upper 95% CI	p
Carbohydrate	Female	-0.192	-0.743	0.359	0.249
Carbohydrate	Male	-0.647	-1.303	0.028	0.031	*
Chitin	Female	-0.366	-0.874	0.141	0.077
Chitin	Male	-0.515	-1.106	0.095	0.044	*
Glycogen	Female	0.398	-0.150	0.934	0.077
Glycogen	Male	0.669	0.018	1.278	0.022	*
Lipid	Female	0.679	0.157	1.152	0.006	*
Lipid	Male	0.434	-0.142	0.976	0.063
Protein	Female	-0.323	-0.891	0.242	0.128
Protein	Male	0.100	-0.563	0.781	0.385

Controlling for differences in dry weight between treatments

summary_dat2 %>%
  kable(digits = 3) %>%
  kable_styling(full_width = FALSE)

variable	sex	Difference in means (Poly - Mono)	Lower 95% CI	Upper 95% CI	p
Carbohydrate	Female	-0.251	-0.832	0.348	0.207
Carbohydrate	Male	-0.666	-1.317	0.019	0.028	*
Chitin	Female	-0.113	-0.673	0.453	0.340
Chitin	Male	-0.435	-1.020	0.179	0.078
Glycogen	Female	0.224	-0.367	0.787	0.224
Glycogen	Male	0.613	-0.040	1.222	0.033	*
Lipid	Female	0.390	-0.156	0.919	0.077
Lipid	Male	0.339	-0.226	0.885	0.110
Protein	Female	-0.215	-0.818	0.378	0.241
Protein	Male	0.136	-0.526	0.810	0.344

Posterior difference in treatment effect size between sexes

This section essentially examines the treatment \(\times\) sex interaction term, by calculating the difference in the effect size of the P/M treatment between sexes, for each of the five metabolites. We find no strong evidence for a treatment \(\times\) sex interaction, i.e. the treatment effects did not differ detectably between sexes.

Figure

Not controlling for differences in dry weight between treatments

treatsex_interaction_data1 <- treat_diff_actual_dryweight %>%
  select(draw, variable, sex, d =  `Difference in means (Poly - Mono)`) %>%
  arrange(draw, variable, sex) %>%
  group_by(draw, variable) %>%
  summarise(`Difference in effect size between sexes (male - female)` = d[2] - d[1],
            .groups = "drop") # males - females


p2 <- treatsex_interaction_data1 %>%
  filter(variable != 'Dryweight') %>% 
  ggplot(aes(x = `Difference in effect size between sexes (male - female)`, y = 1, fill = stat(x < 0))) +
  geom_vline(xintercept = 0, linetype = 2) +
  stat_halfeyeh() +
  facet_wrap( ~ variable) +
  scale_fill_brewer(palette = 'Pastel2', direction = 1, name = "") +
  theme_bw() +
  theme(legend.position = 'none',
        text = element_text(family = nice_font),
        strip.background = element_blank()) +
  ylab("Posterior density")

ggsave("output/metabolite_interaction_plot.pdf", p2, height=4, width=6)
p2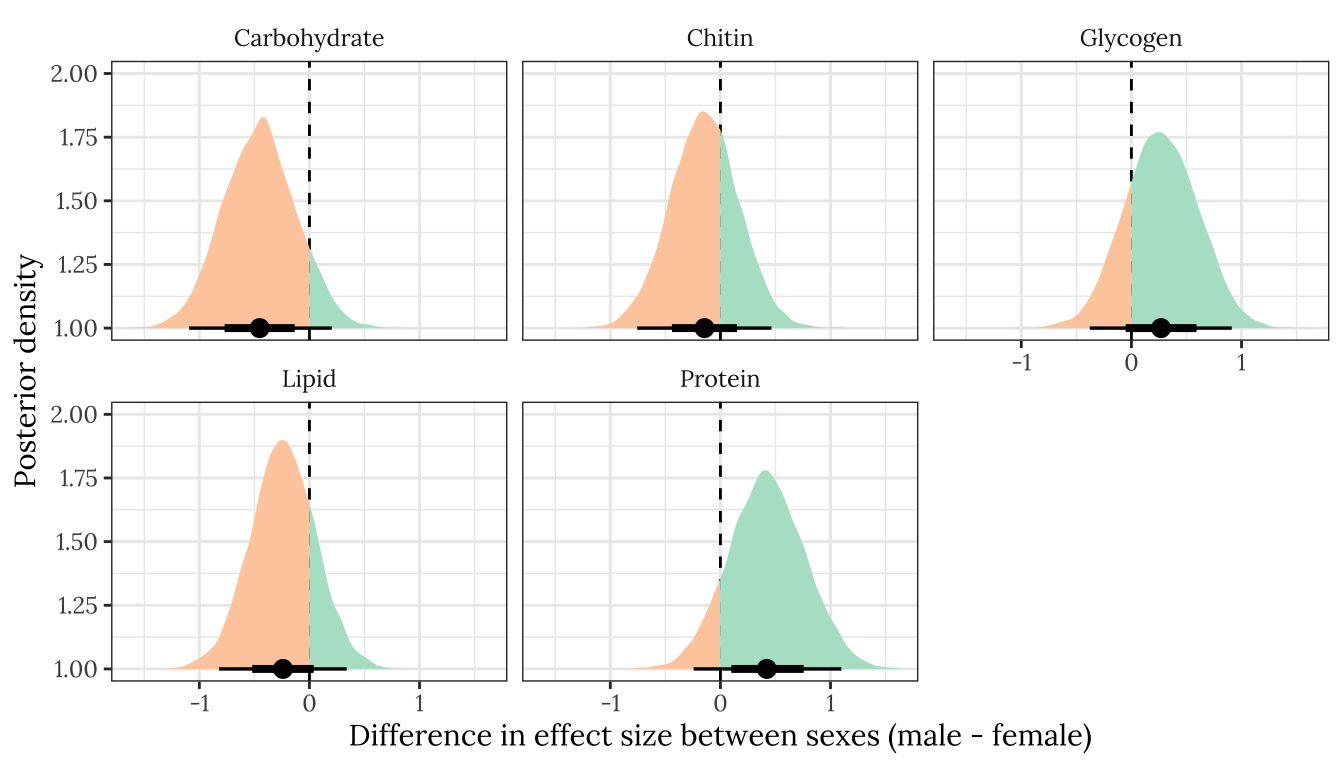

Version	Author	Date
e5c580f	lukeholman	2020-12-11
f7c88a2	lukeholman	2020-12-10
43cc270	lukeholman	2020-12-09

Figure XX: Posterior estimates of the difference in the treatment effect size (i.e. mean of P minus mean of M) between males and females, for each of the five metabolites. A positive value means that the effect size is more positive in males, and negative means it is more positive in females. A strongly supported sex difference in effect size would be implied by the majority of the posterior lying to one side of zero. The error bars summarise the 66% and 95% quantiles of the posterior. This plot was created used posterior predictions of the means that were not adjusted for differences in dry weight between treatments.

Controlling for differences in dry weight between treatments

treatsex_interaction_data2 <- treat_diff_standard_dryweight %>%
  select(draw, variable, sex, d =  `Difference in means (Poly - Mono)`) %>%
  arrange(draw, variable, sex) %>%
  group_by(draw, variable) %>%
  summarise(`Difference in effect size between sexes (male - female)` = d[2] - d[1],
            .groups = "drop") # males - females

treatsex_interaction_data2 %>%
  filter(variable != 'Dryweight') %>% 
  ggplot(aes(x = `Difference in effect size between sexes (male - female)`, y = 1, fill = stat(x < 0))) +
  geom_vline(xintercept = 0, linetype = 2) +
  stat_halfeyeh() +
  facet_wrap( ~ variable) +
  scale_fill_brewer(palette = 'Pastel2', direction = 1, name = "") +
  theme_bw() +
  theme(legend.position = 'none',
        text = element_text(family = nice_font),
        strip.background = element_blank()) +
  ylab("Posterior density")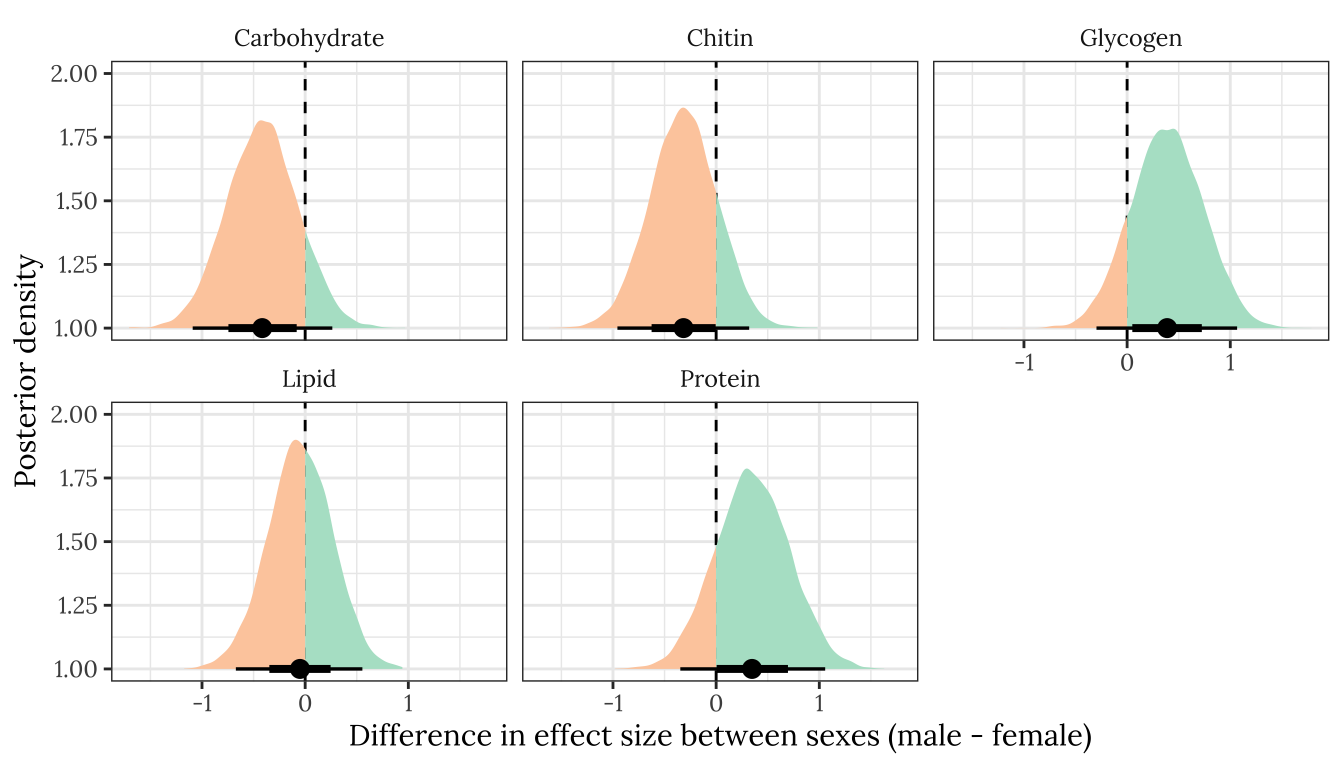

Version	Author	Date
e5c580f	lukeholman	2020-12-11
f7c88a2	lukeholman	2020-12-10

Figure XX: Posterior estimates of the difference in the treatment effect size (i.e. mean of P minus mean of M) between males and females, for each of the five metabolites. A positive value means that the effect size is more positive in males, and negative means it is more positive in females. A strongly supported sex difference in effect size would be implied by the majority of the posterior lying to one side of zero. The error bars summarise the 66% and 95% quantiles of the posterior. This plot was created used posterior predictions of the means that were adjusted for differences in dry weight between treatments.

Table

Not controlling for differences in dry weight between treatments

treatsex_interaction_data1 %>%
  filter(variable != 'Dryweight') %>%
  rename(x = `Difference in effect size between sexes (male - female)`) %>%
  group_by(variable)  %>%
  summarise(`Difference in effect size between sexes (male - female)` = median(x),
            `Lower 95% CI` = quantile(x, probs = 0.025), 
            `Upper 95% CI` = quantile(x, probs = 0.975),
            p = 1 - as.numeric(bayestestR::p_direction(x)),
            ` ` = ifelse(p < 0.05, "\\*", ""),
            .groups = "drop") %>%
  kable(digits=3) %>%
  kable_styling(full_width = FALSE)

variable	Difference in effect size between sexes (male - female)	Lower 95% CI	Upper 95% CI	p
Carbohydrate	-0.452	-1.092	0.203	0.091
Chitin	-0.145	-0.756	0.463	0.321
Glycogen	0.269	-0.379	0.911	0.212
Lipid	-0.240	-0.821	0.338	0.208
Protein	0.421	-0.244	1.099	0.111

Controlling for differences in dry weight between treatments

treatsex_interaction_data2 %>%
  filter(variable != 'Dryweight') %>%
  rename(x = `Difference in effect size between sexes (male - female)`) %>%
  group_by(variable)  %>%
  summarise(`Difference in effect size between sexes (male - female)` = median(x),
            `Lower 95% CI` = quantile(x, probs = 0.025), 
            `Upper 95% CI` = quantile(x, probs = 0.975),
            p = 1 - as.numeric(bayestestR::p_direction(x)),
            ` ` = ifelse(p < 0.05, "\\*", ""),
            .groups = "drop") %>%
  kable(digits=3) %>%
  kable_styling(full_width = FALSE)

variable	Difference in effect size between sexes (male - female)	Lower 95% CI	Upper 95% CI	p
Carbohydrate	-0.416	-1.090	0.263	0.117
Chitin	-0.316	-0.957	0.320	0.166
Glycogen	0.388	-0.297	1.066	0.139
Lipid	-0.050	-0.672	0.555	0.437
Protein	0.348	-0.347	1.057	0.167

sessionInfo()

R version 4.0.3 (2020-10-10)
Platform: x86_64-apple-darwin17.0 (64-bit)
Running under: macOS Catalina 10.15.4

Matrix products: default
BLAS:   /Library/Frameworks/R.framework/Versions/4.0/Resources/lib/libRblas.dylib
LAPACK: /Library/Frameworks/R.framework/Versions/4.0/Resources/lib/libRlapack.dylib

locale:
[1] en_AU.UTF-8/en_AU.UTF-8/en_AU.UTF-8/C/en_AU.UTF-8/en_AU.UTF-8

attached base packages:
[1] stats     graphics  grDevices utils     datasets  methods   base     

other attached packages:
 [1] showtext_0.9-1   showtextdb_3.0   sysfonts_0.8.2   knitrhooks_0.0.4 knitr_1.30       kableExtra_1.1.0 DT_0.13          tidybayes_2.0.3  brms_2.14.4     
[10] Rcpp_1.0.4.6     ggridges_0.5.2   gridExtra_2.3    GGally_1.5.0     forcats_0.5.0    stringr_1.4.0    dplyr_1.0.0      purrr_0.3.4      readr_1.3.1     
[19] tidyr_1.1.0      tibble_3.0.1     ggplot2_3.3.2    tidyverse_1.3.0  workflowr_1.6.2 

loaded via a namespace (and not attached):
  [1] readxl_1.3.1         backports_1.1.7      plyr_1.8.6           igraph_1.2.5         svUnit_1.0.3         splines_4.0.3        crosstalk_1.1.0.1   
  [8] TH.data_1.0-10       rstantools_2.1.1     inline_0.3.15        digest_0.6.25        htmltools_0.5.0      rsconnect_0.8.16     fansi_0.4.1         
 [15] magrittr_2.0.1       modelr_0.1.8         RcppParallel_5.0.1   matrixStats_0.56.0   xts_0.12-0           sandwich_2.5-1       prettyunits_1.1.1   
 [22] colorspace_1.4-1     blob_1.2.1           rvest_0.3.5          haven_2.3.1          xfun_0.19            callr_3.4.3          crayon_1.3.4        
 [29] jsonlite_1.7.0       lme4_1.1-23          survival_3.2-7       zoo_1.8-8            glue_1.4.2           gtable_0.3.0         emmeans_1.4.7       
 [36] webshot_0.5.2        V8_3.4.0             pkgbuild_1.0.8       rstan_2.21.2         abind_1.4-5          scales_1.1.1         mvtnorm_1.1-0       
 [43] DBI_1.1.0            miniUI_0.1.1.1       viridisLite_0.3.0    xtable_1.8-4         stats4_4.0.3         StanHeaders_2.21.0-3 htmlwidgets_1.5.1   
 [50] httr_1.4.1           DiagrammeR_1.0.6.1   threejs_0.3.3        arrayhelpers_1.1-0   RColorBrewer_1.1-2   ellipsis_0.3.1       farver_2.0.3        
 [57] pkgconfig_2.0.3      reshape_0.8.8        loo_2.3.1            dbplyr_1.4.4         labeling_0.3         tidyselect_1.1.0     rlang_0.4.6         
 [64] reshape2_1.4.4       later_1.0.0          visNetwork_2.0.9     munsell_0.5.0        cellranger_1.1.0     tools_4.0.3          cli_2.0.2           
 [71] generics_0.0.2       broom_0.5.6          evaluate_0.14        fastmap_1.0.1        yaml_2.2.1           processx_3.4.2       fs_1.4.1            
 [78] nlme_3.1-149         whisker_0.4          mime_0.9             projpred_2.0.2       xml2_1.3.2           compiler_4.0.3       bayesplot_1.7.2     
 [85] shinythemes_1.1.2    rstudioapi_0.11      gamm4_0.2-6          curl_4.3             reprex_0.3.0         statmod_1.4.34       stringi_1.5.3       
 [92] highr_0.8            ps_1.3.3             Brobdingnag_1.2-6    lattice_0.20-41      Matrix_1.2-18        nloptr_1.2.2.1       markdown_1.1        
 [99] shinyjs_1.1          vctrs_0.3.0          pillar_1.4.4         lifecycle_0.2.0      bridgesampling_1.0-0 estimability_1.3     insight_0.8.4       
[106] httpuv_1.5.3.1       R6_2.4.1             promises_1.1.0       codetools_0.2-16     boot_1.3-25          colourpicker_1.0     MASS_7.3-53         
[113] gtools_3.8.2         assertthat_0.2.1     rprojroot_1.3-2      withr_2.2.0          shinystan_2.5.0      multcomp_1.4-13      bayestestR_0.6.0    
[120] mgcv_1.8-33          parallel_4.0.3       hms_0.5.3            grid_4.0.3           coda_0.19-3          minqa_1.2.4          rmarkdown_2.5       
[127] git2r_0.27.1         shiny_1.4.0.2        lubridate_1.7.8      base64enc_0.1-3      dygraphs_1.1.1.6

Metabolite composition

Load packages

Load metabolite composition data

Inspect the raw data

Raw numbers

Simple plots

Plot of correlations between variables

Mean dry weight

Directed acyclic graph (DAG)

Fit brms structural equation model

Define Priors

Define the SEM’s sub-models

Running the model

Posterior predictive check of model fit

Table of model parameter estimates

Formatted table

Complete output from summary.brmsfit()

Posterior effect size of treatment on metabolite abundance, for each sex

Figure

Not controlling for differences in dry weight between treatments

Controlling for differences in dry weight between treatments

Table

Not controlling for differences in dry weight between treatments

Controlling for differences in dry weight between treatments

Posterior difference in treatment effect size between sexes

Figure

Not controlling for differences in dry weight between treatments

Controlling for differences in dry weight between treatments

Table

Not controlling for differences in dry weight between treatments

Controlling for differences in dry weight between treatments

Fit `brms` structural equation model

Complete output from `summary.brmsfit()`