Last updated: 2025-01-14

Checks: 6 1

Knit directory: PODFRIDGE/

This reproducible R Markdown analysis was created with workflowr (version 1.7.1). The Checks tab describes the reproducibility checks that were applied when the results were created. The Past versions tab lists the development history.

R Markdown file: uncommitted changes

The R Markdown file has unstaged changes. To know which version of the R Markdown file created these results, you’ll want to first commit it to the Git repo. If you’re still working on the analysis, you can ignore this warning. When you’re finished, you can run wflow_publish to commit the R Markdown file and build the HTML.

Environment: empty

Great job! The global environment was empty. Objects defined in the global environment can affect the analysis in your R Markdown file in unknown ways. For reproduciblity it’s best to always run the code in an empty environment.

Seed: set.seed(20230302)

The command set.seed(20230302) was run prior to running the code in the R Markdown file. Setting a seed ensures that any results that rely on randomness, e.g. subsampling or permutations, are reproducible.

Session information: recorded

Great job! Recording the operating system, R version, and package versions is critical for reproducibility.

Cache: none

Nice! There were no cached chunks for this analysis, so you can be confident that you successfully produced the results during this run.

File paths: relative

Great job! Using relative paths to the files within your workflowr project makes it easier to run your code on other machines.

Repository version: 159a638

Great! You are using Git for version control. Tracking code development and connecting the code version to the results is critical for reproducibility.

The results in this page were generated with repository version 159a638. See the Past versions tab to see a history of the changes made to the R Markdown and HTML files.

Note that you need to be careful to ensure that all relevant files for the analysis have been committed to Git prior to generating the results (you can use wflow_publish or wflow_git_commit). workflowr only checks the R Markdown file, but you know if there are other scripts or data files that it depends on. Below is the status of the Git repository when the results were generated:


Ignored files:
    Ignored:    .DS_Store
    Ignored:    .Rhistory
    Ignored:    .Rproj.user/
    Ignored:    analysis/.Rhistory
    Ignored:    data/.DS_Store

Unstaged changes:
    Modified:   analysis/relative-distribution.Rmd

Note that any generated files, e.g. HTML, png, CSS, etc., are not included in this status report because it is ok for generated content to have uncommitted changes.

These are the previous versions of the repository in which changes were made to the R Markdown (analysis/relative-distribution.Rmd) and HTML (docs/relative-distribution.html) files. If you’ve configured a remote Git repository (see ?wflow_git_remote), click on the hyperlinks in the table below to view the files as they were in that past version.

File	Version	Author	Date	Message
Rmd	159a638	linmatch	2025-01-13	Update relative-distribution.Rmd
Rmd	5280afb	linmatch	2025-01-13	fix test mean family size
Rmd	9778698	linmatch	2025-01-09	update
html	9778698	linmatch	2025-01-09	update
Rmd	0c90de8	linmatch	2024-12-18	clean and organize the document
Rmd	f567c4a	linmatch	2024-12-16	update
html	f567c4a	linmatch	2024-12-16	update
Rmd	231390a	linmatch	2024-12-11	update analysis
html	231390a	linmatch	2024-12-11	update analysis
Rmd	8007864	linmatch	2024-12-03	update workflow page
html	8007864	linmatch	2024-12-03	update workflow page
Rmd	e553adc	linmatch	2024-11-21	Update relative-distribution.Rmd
Rmd	e76576b	linmatch	2024-11-21	Update relative-distribution.Rmd
Rmd	21f0f4f	linmatch	2024-11-19	Update relative-distribution.Rmd
Rmd	f583798	linmatch	2024-11-14	Update relative-distribution.Rmd
Rmd	900b2e4	linmatch	2024-11-14	Update relative-distribution.Rmd
Rmd	776920f	linmatch	2024-11-12	update the model fit analysis in children’s part
html	776920f	linmatch	2024-11-12	update the model fit analysis in children’s part
Rmd	06a8f96	linmatch	2024-11-05	update sibling’s part
html	06a8f96	linmatch	2024-11-05	update sibling’s part
Rmd	1741cb1	linmatch	2024-11-05	fix test
Rmd	4e68621	linmatch	2024-11-05	fix chisq-test in cohort stability
html	4e68621	linmatch	2024-11-05	fix chisq-test in cohort stability
Rmd	6fb5b40	linmatch	2024-10-29	update sibling’s distribution plot
Rmd	570abb0	linmatch	2024-10-22	update sibling part
Rmd	2e09e08	linmatch	2024-10-22	workflow build
html	2e09e08	linmatch	2024-10-22	workflow build
Rmd	bb2c61b	linmatch	2024-10-21	complete fertility shift analysis
Rmd	842d935	linmatch	2024-10-17	update fertility shift
Rmd	2ae8460	linmatch	2024-10-16	fix the chisq-test
Rmd	9632ae1	linmatch	2024-10-12	update cohort stability
Rmd	9852339	linmatch	2024-10-08	update cohort stability
html	9852339	linmatch	2024-10-08	update cohort stability
Rmd	7ec169f	linmatch	2024-10-03	update sibling distribution
Rmd	27b986f	linmatch	2024-10-01	update stability cohort analysis
Rmd	57a97db	linmatch	2024-09-30	Update relative-distribution.Rmd
Rmd	52aa7f8	linmatch	2024-09-27	improving code on Part1
Rmd	c54a746	linmatch	2024-09-26	update and fix step 2
Rmd	94d00b3	linmatch	2024-09-24	fix step1
Rmd	1225480	linmatch	2024-09-23	update on step1
Rmd	83174c0	Tina Lasisi	2024-09-22	Instructions and layout for relative distribution
html	83174c0	Tina Lasisi	2024-09-22	Instructions and layout for relative distribution
Rmd	78c1621	Tina Lasisi	2024-09-21	Update relative-distribution.Rmd
Rmd	f4c2830	Tina Lasisi	2024-09-21	Update relative-distribution.Rmd
Rmd	2851385	Tina Lasisi	2024-09-21	rename old analysis
html	2851385	Tina Lasisi	2024-09-21	rename old analysis

Introduction

The relative genetic surveillance of a population is influenced by the number of genetically detectable relatives individuals have. First-degree relatives (parents, siblings, and children) are especially relevant in forensic analyses using short tandem repeat (STR) loci, where close familial searches are commonly employed. To explore potential disparities in genetic detectability between African American and European American populations, we examined U.S. Census data from four census years (1960, 1970, 1980, and 1990) focusing on the number of children born to women over the age of 40.

Data Sources

We used publicly available data from the Integrated Public Use Microdata Series (IPUMS) for the U.S. Census years 1960, 1970, 1980, and 1990. The datasets include information on:

AGE: Age of the respondent.
RACE: Self-identified race of the respondent.
chborn_num: Number of children ever born to the respondent.

Data citation: Steven Ruggles, Sarah Flood, Matthew Sobek, Daniel Backman, Annie Chen, Grace Cooper, Stephanie Richards, Renae Rogers, and Megan Schouweiler. IPUMS USA: Version 14.0 [dataset]. Minneapolis, MN: IPUMS, 2023. https://doi.org/10.18128/D010.V14.0

Data Preparation

Filtering Criteria: We selected women aged 40 and above to ensure that most had completed childbearing.

Due to the terms of agreement for using this data, we cannot share the full dataset but our repo contains the subset that was used to calculate the mean number of offspring and variance.

Race Classification: We categorized individuals into two groups:

African American: Those who identified as “Black” or “African American”.
European American: Those who identified as “White”.

Calculating Number of Siblings: For each child of these women, the number of siblings (n_sib) is one less than the number of children born to the mother:

\[ n_{sib} = chborn_{num} - 1 \]

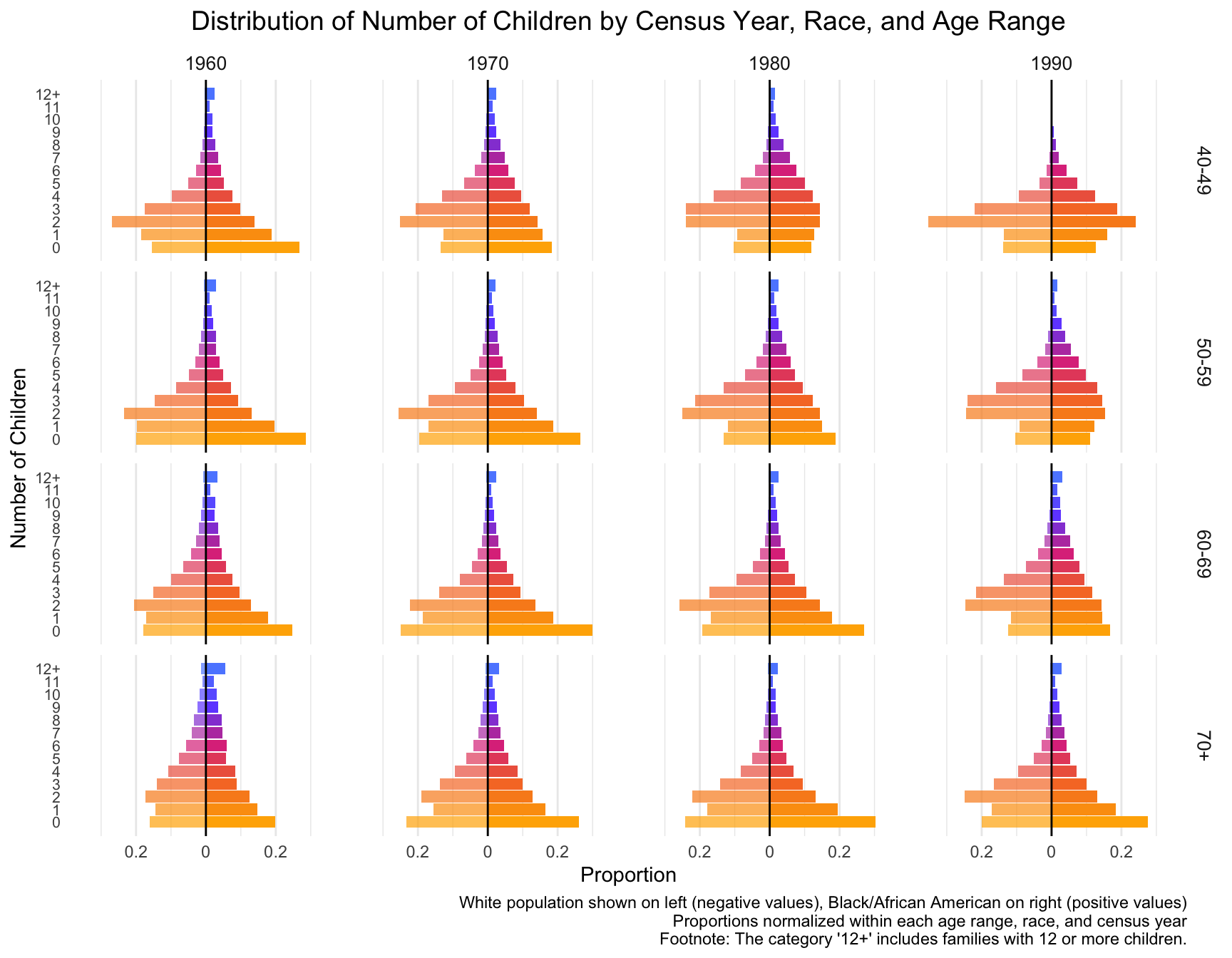
Distribution of Number of Children Across Census Years

First we visualize the general trends in the frequency of the number of children for African American and European American mothers across the Census years by age group.

Version	Author	Date
f567c4a	linmatch	2024-12-16

With this visualization of the distribution of the data, we can see that there are differences between White and Black Americans.

We will now test for differences in 1) the mean and variance, and 2) zero-inflation.

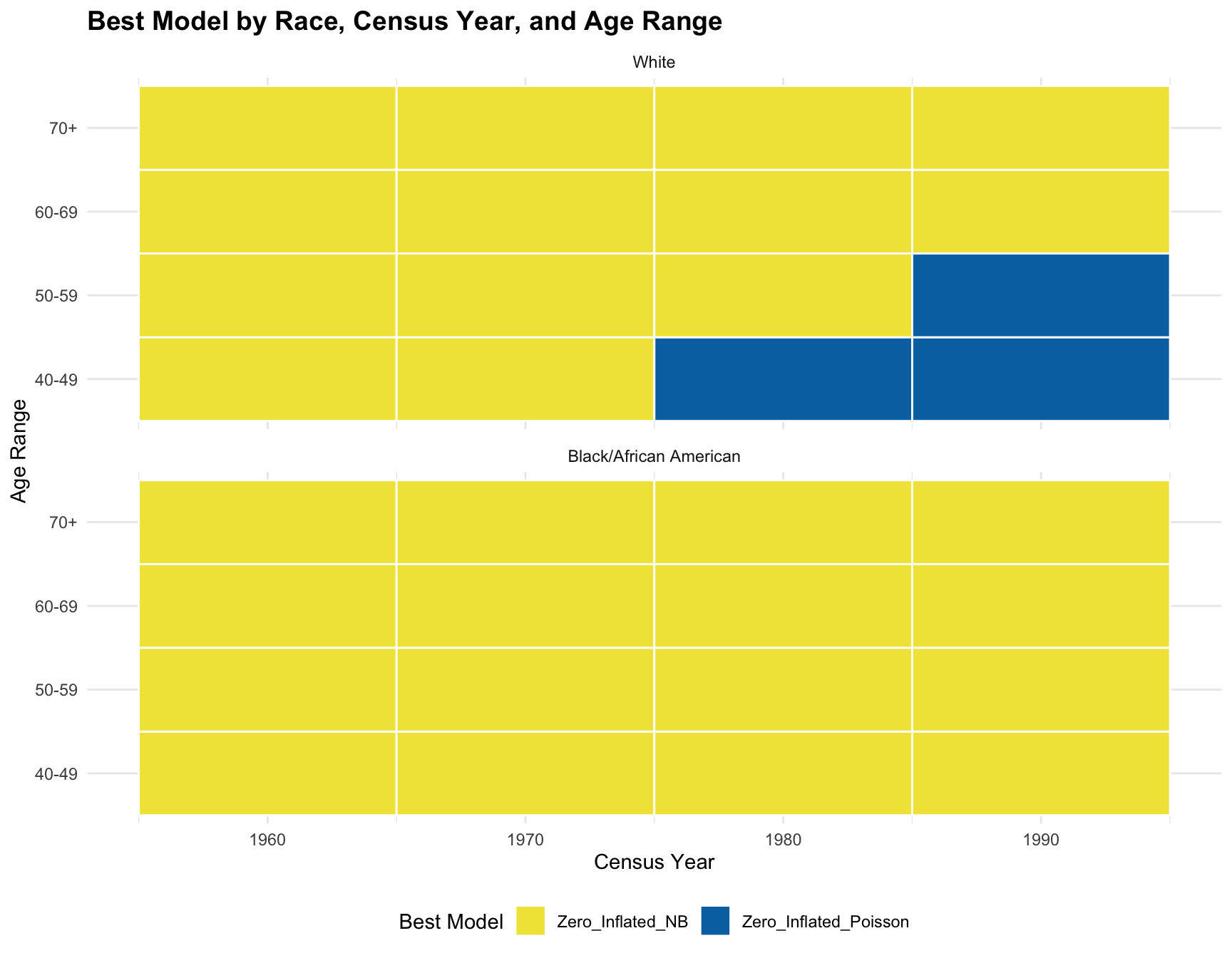
Model Fit Across Census Years

For each combination of race, census year, and age range, we fit the following candidate models:

Poisson Model
Negative Binomial (NB) Model
Zero-Inflated Poisson (ZIP) Model
Zero-Inflated Negative Binomial (ZINB) Model

Fit and Compare Models

Record the Best Model for Each Subset

                     Race Census_Year Age_Range            Best_Model
1                   White        1960     40-49      Zero_Inflated_NB
2                   White        1960     50-59      Zero_Inflated_NB
3                   White        1960     60-69      Zero_Inflated_NB
4                   White        1960       70+      Zero_Inflated_NB
5  Black/African American        1960     40-49      Zero_Inflated_NB
6  Black/African American        1960     50-59      Zero_Inflated_NB
7  Black/African American        1960     60-69      Zero_Inflated_NB
8  Black/African American        1960       70+      Zero_Inflated_NB
9                   White        1970     40-49      Zero_Inflated_NB
10                  White        1970     50-59      Zero_Inflated_NB
11                  White        1970     60-69      Zero_Inflated_NB
12                  White        1970       70+      Zero_Inflated_NB
13 Black/African American        1970     40-49      Zero_Inflated_NB
14 Black/African American        1970     50-59      Zero_Inflated_NB
15 Black/African American        1970     60-69      Zero_Inflated_NB
16 Black/African American        1970       70+      Zero_Inflated_NB
17                  White        1980     40-49 Zero_Inflated_Poisson
18                  White        1980     50-59      Zero_Inflated_NB
19                  White        1980     60-69      Zero_Inflated_NB
20                  White        1980       70+      Zero_Inflated_NB
21 Black/African American        1980     40-49      Zero_Inflated_NB
22 Black/African American        1980     50-59      Zero_Inflated_NB
23 Black/African American        1980     60-69      Zero_Inflated_NB
24 Black/African American        1980       70+      Zero_Inflated_NB
25                  White        1990     40-49 Zero_Inflated_Poisson
26                  White        1990     50-59 Zero_Inflated_Poisson
27                  White        1990     60-69      Zero_Inflated_NB
28                  White        1990       70+      Zero_Inflated_NB
29 Black/African American        1990     40-49      Zero_Inflated_NB
30 Black/African American        1990     50-59      Zero_Inflated_NB
31 Black/African American        1990     60-69      Zero_Inflated_NB
32 Black/African American        1990       70+      Zero_Inflated_NB

Analyze the Effect of Race, Census Year, and Age Range


Call:
glm(formula = Best_Model_Binary ~ Race + Census_Year + Age_Range, 
    family = binomial(), data = best_models)

Coefficients:
                             Estimate Std. Error z value Pr(>|z|)
(Intercept)                 8.741e+03  7.710e+06   0.001    0.999
RaceBlack/African American  8.903e+01  8.227e+04   0.001    0.999
Census_Year                -4.426e+00  3.902e+03  -0.001    0.999
Age_Range50-59              4.390e+01  5.002e+04   0.001    0.999
Age_Range60-69              8.990e+01  1.045e+05   0.001    0.999
Age_Range70+                8.990e+01  1.045e+05   0.001    0.999

(Dispersion parameter for binomial family taken to be 1)

    Null deviance: 1.9912e+01  on 31  degrees of freedom
Residual deviance: 2.4509e-09  on 26  degrees of freedom
AIC: 12

Number of Fisher Scoring iterations: 25

RESULT:The p-value for each variable is larger than 0.05, indicating non-significant effects on best model fitting.

Visualize the Results

Version	Author	Date
2851385	Tina Lasisi	2024-09-21

Conclusion

The logistics regression shows that there isn’t a significant association between the predictors(races, age ranges, and census year) and the best-fitting model. According to the resulting visualization, the ZINB model is the best fit for the black population across census year and age group. However, the ZINB model perform the best among the white population only across year 1960 and 1970, and age group 60-69 and 70+.

Cohort Stability Analysis

The goal is to determine if there is a significant change in zero inflation, family size, or model fit for the same cohort across different census years, given race.

Table with Birth-Year (Cohort)

                     Race Census_Year Age_Range            Best_Model    Cohort
1                   White        1960     40-49      Zero_Inflated_NB 1911-1920
2                   White        1960     50-59      Zero_Inflated_NB 1901-1910
3                   White        1960     60-69      Zero_Inflated_NB 1891-1900
4                   White        1960       70+      Zero_Inflated_NB -Inf-1890
5  Black/African American        1960     40-49      Zero_Inflated_NB 1911-1920
6  Black/African American        1960     50-59      Zero_Inflated_NB 1901-1910
7  Black/African American        1960     60-69      Zero_Inflated_NB 1891-1900
8  Black/African American        1960       70+      Zero_Inflated_NB -Inf-1890
9                   White        1970     40-49      Zero_Inflated_NB 1921-1930
10                  White        1970     50-59      Zero_Inflated_NB 1911-1920
11                  White        1970     60-69      Zero_Inflated_NB 1901-1910
12                  White        1970       70+      Zero_Inflated_NB -Inf-1900
13 Black/African American        1970     40-49      Zero_Inflated_NB 1921-1930
14 Black/African American        1970     50-59      Zero_Inflated_NB 1911-1920
15 Black/African American        1970     60-69      Zero_Inflated_NB 1901-1910
16 Black/African American        1970       70+      Zero_Inflated_NB -Inf-1900
17                  White        1980     40-49 Zero_Inflated_Poisson 1931-1940
18                  White        1980     50-59      Zero_Inflated_NB 1921-1930
19                  White        1980     60-69      Zero_Inflated_NB 1911-1920
20                  White        1980       70+      Zero_Inflated_NB -Inf-1910
21 Black/African American        1980     40-49      Zero_Inflated_NB 1931-1940
22 Black/African American        1980     50-59      Zero_Inflated_NB 1921-1930
23 Black/African American        1980     60-69      Zero_Inflated_NB 1911-1920
24 Black/African American        1980       70+      Zero_Inflated_NB -Inf-1910
25                  White        1990     40-49 Zero_Inflated_Poisson 1941-1950
26                  White        1990     50-59 Zero_Inflated_Poisson 1931-1940
27                  White        1990     60-69      Zero_Inflated_NB 1921-1930
28                  White        1990       70+      Zero_Inflated_NB -Inf-1920
29 Black/African American        1990     40-49      Zero_Inflated_NB 1941-1950
30 Black/African American        1990     50-59      Zero_Inflated_NB 1931-1940
31 Black/African American        1990     60-69      Zero_Inflated_NB 1921-1930
32 Black/African American        1990       70+      Zero_Inflated_NB -Inf-1920

Summary Statistics for Each Subset

Test for Significant Changes Over Time Within Each Cohort

The goal is to determine if there is a significant change in any of the following across census years for the same cohort:

Zero Inflation: Check if the proportion of women with zero children changes significantly over time for the same cohort.
Family Size: Test if the mean or variance in the number of children changes for the same cohort over time.
Model Fit: Analyze if the best-fitting model for the cohort changes over time.

a. Zero-Inflation Analysis

Version	Author	Date
8007864	linmatch	2024-12-03
2851385	Tina Lasisi	2024-09-21

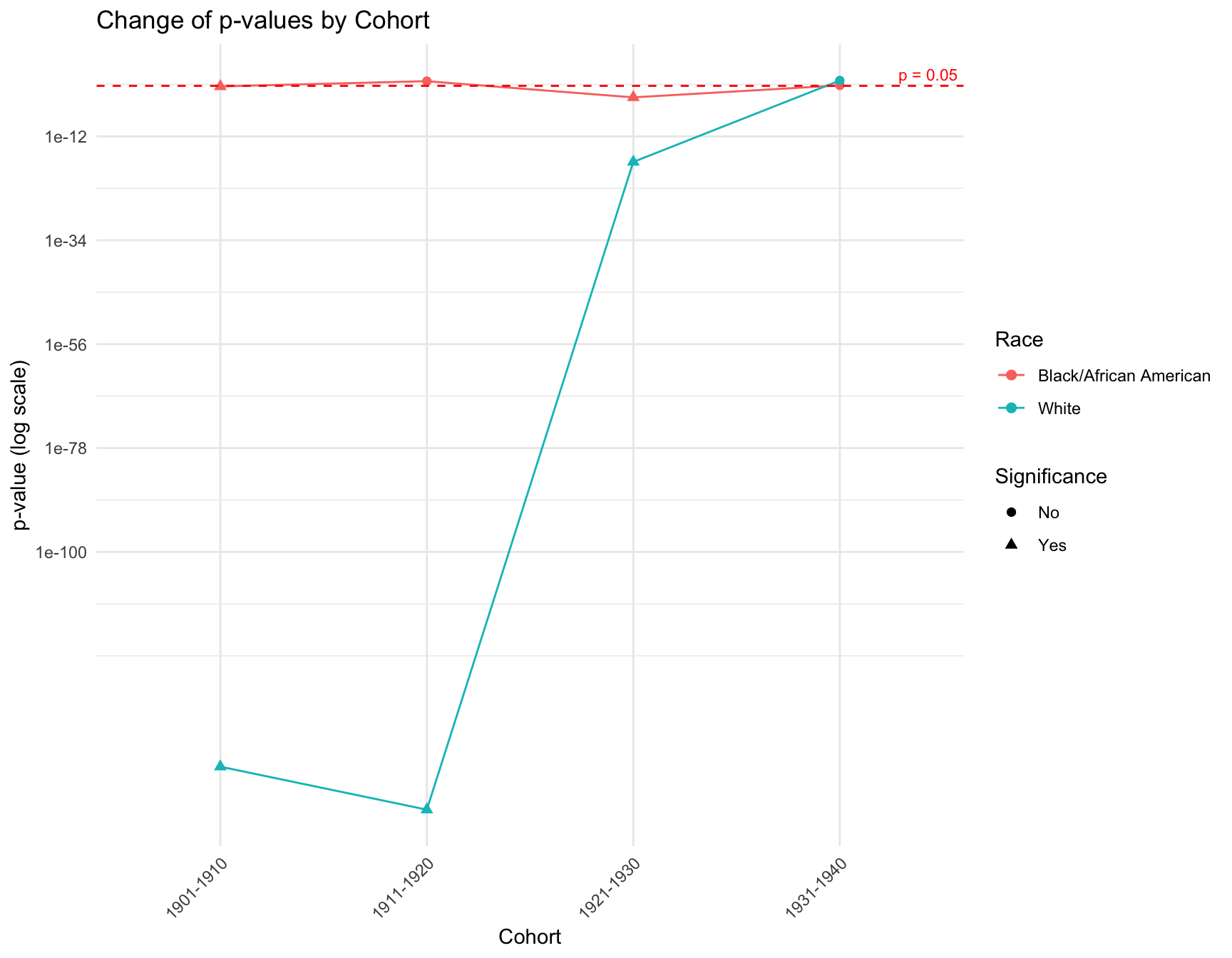
RESULT: The graph shows that there is a discrepancy in the p-value within the cohorts like 1901-1910, 1911-1920 and 1921-1930 by race. However, in cohort 1931-1941, the p-value of each race is pretty close to each other. The overall trend of the p-value for black population is stable across cohort, while the trend for white population fluctuate a lot.

b. Family Size Analysis


Cohort: 1891-1900 has only 1 Census Year. Skipping ANOVA.

Cohort: -Inf-1890 has only 1 Census Year. Skipping ANOVA.

Cohort: -Inf-1900 has only 1 Census Year. Skipping ANOVA.

Cohort: -Inf-1910 has only 1 Census Year. Skipping ANOVA.

Cohort: 1941-1950 has only 1 Census Year. Skipping ANOVA.

Cohort: -Inf-1920 has only 1 Census Year. Skipping ANOVA.

                     RACE    Cohort  Statistic      p_value Significance
1  Black/African American 1911-1920  0.2935745 7.455953e-01           No
t  Black/African American 1901-1910  2.8577289 4.272684e-03          Yes
11 Black/African American 1921-1930 21.4153393 5.058954e-10          Yes
t1 Black/African American 1931-1940 -0.0665138 9.469694e-01           No


Cohort: 1891-1900 has only 1 Census Year. Skipping ANOVA and t-test.

Cohort: -Inf-1890 has only 1 Census Year. Skipping ANOVA and t-test.

Cohort: -Inf-1900 has only 1 Census Year. Skipping ANOVA and t-test.

Cohort: -Inf-1910 has only 1 Census Year. Skipping ANOVA and t-test.

Cohort: -Inf-1920 has only 1 Census Year. Skipping ANOVA and t-test.

Cohort: 1941-1950 has only 1 Census Year. Skipping ANOVA and t-test.

    RACE    Cohort  Statistic      p_value Significance
1  White 1911-1920 68.7034766 1.472553e-30          Yes
t  White 1901-1910 16.2673142 1.889832e-59          Yes
11 White 1921-1930 83.5688313 5.178495e-37          Yes
t1 White 1931-1940  0.7361998 4.616101e-01           No

RESULT: 1.In both racial group, the ANOVA and t-test is not applicable for the following cohort since there is only one census year available in the data for those cohorts:-Inf-1910, 1941-1950, -Inf-1920, -Inf-1890, -Inf-1900, and 1891-1900 2.By looking at the ANOVA and t-test for mean family size in white population, the p-value of cohorts 1901-1910, 1911-1920 and 1921-1930 are smaller than 0.05. In the black population, the p-value of cohorts 1901-1910 and 1921-1930 are smaller than 0.05. These results indicate mean family size for these cohort has significantly changed over different census years in different racial population.

c. Model Fit Analysis

Version	Author	Date
9778698	linmatch	2025-01-09
2851385	Tina Lasisi	2024-09-21

RESULT: Based on the heatmap created, we can see that the model fit for each cohort(cohort with 2+ corresponding census year) across year does not change.

Conclusion

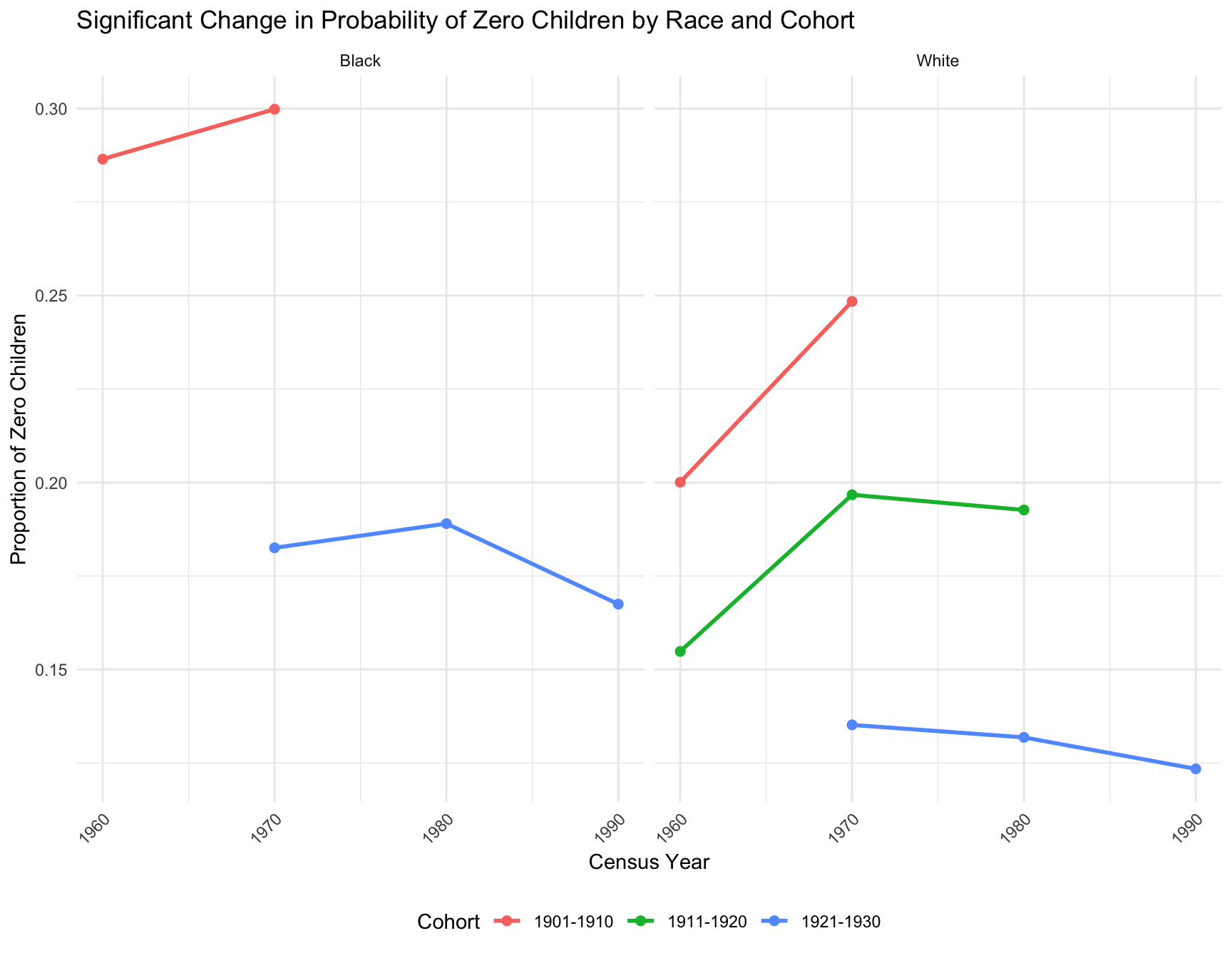
Zero-inflation: We observe that the proportion of women with zero children change significantly across census year in the following cohort by race: -black population:1901-1910, 1921-1930 -white population:1901-1910, 1911-1920, 1921-1930
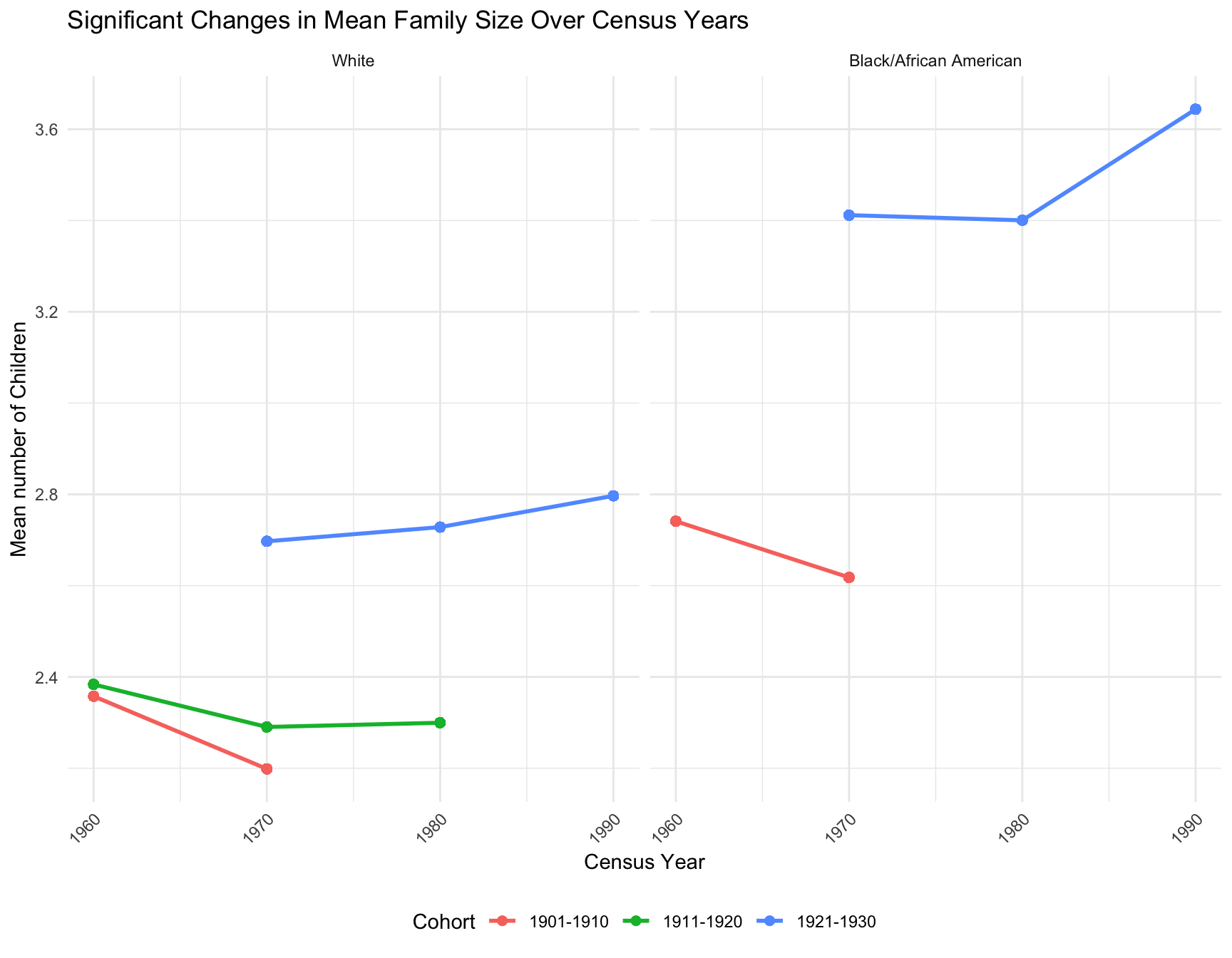
Family size: Cohorts 1901-1910, 1911-1920, 1921-1930, and 1931-1940 present significant change in mean family size across year for both races.
Best-fitting Model: Model fit for each cohort(cohort with 2+ corresponding census year) across year does not change in both racial group.

Analyzing and Visualizing Significant Fertility Shifts

The goal is to summarize the previous information and create visualization that illustrates significant fertility shifts in cohorts, compares fertility patterns of 40-49 year-olds to 50-59 year-olds in the 1990 census so we can pick the set of fertility distributions we want to use to visualize the sibling distribution and do the math on the genetic surveillance.

Panel A: Fertility Distribution Shifts Across Cohorts

Cohorts with Significant Change in Zero Inflation

Version	Author	Date
9778698	linmatch	2025-01-09
2851385	Tina Lasisi	2024-09-21

Cohorts with Significant Change in Mean Family Size

Version	Author	Date
9778698	linmatch	2025-01-09
2851385	Tina Lasisi	2024-09-21

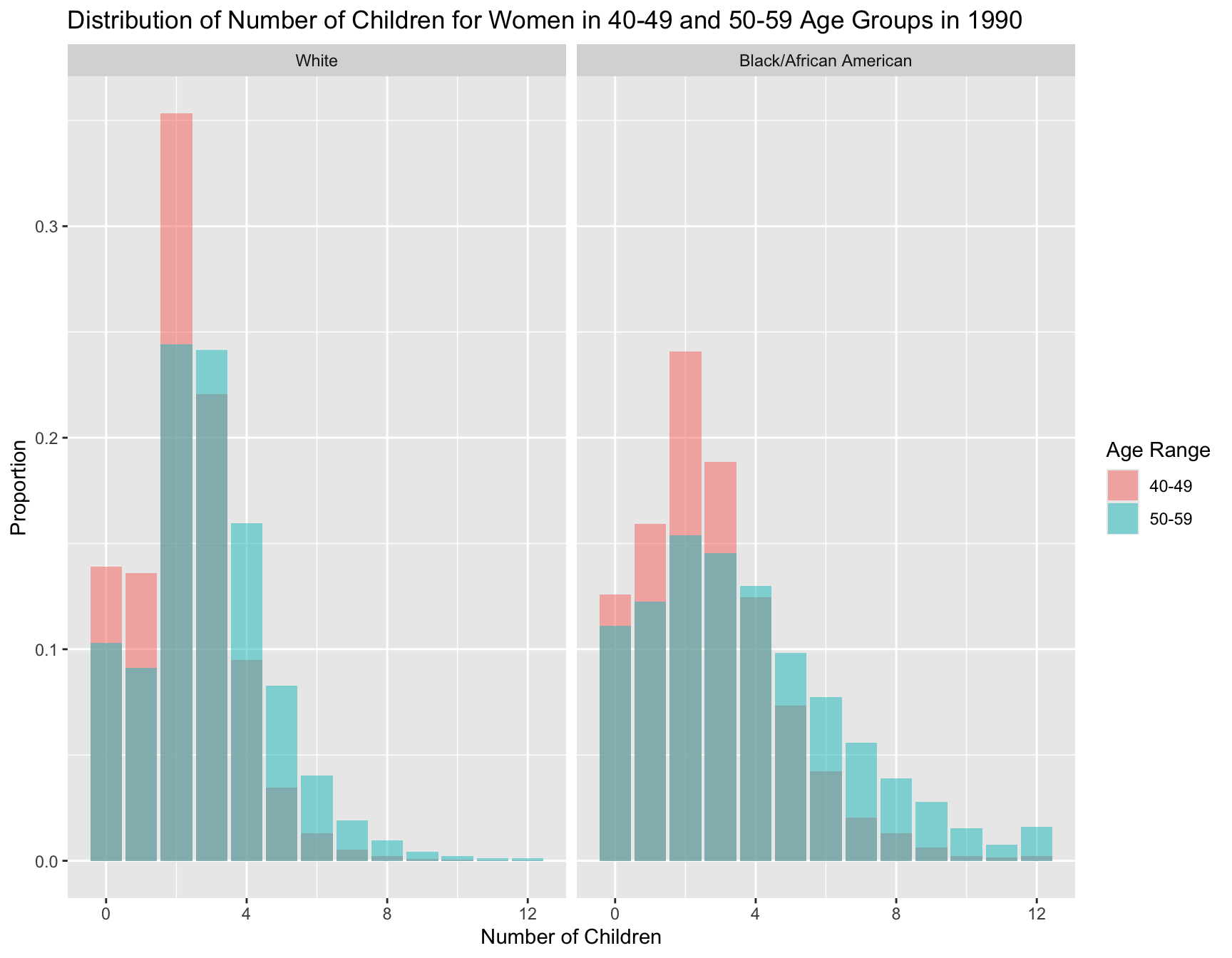
Panel B: Comparison of 40-49 and 50-59 Age Groups in 1990

Visulization of Distribution

Summary Statistics Table

`summarise()` has grouped output by 'AGE_RANGE'. You can override using the
`.groups` argument.

# A tibble: 4 × 5
# Groups:   AGE_RANGE [2]
  AGE_RANGE RACE                  mean_children variance_children zero_inflation
  <chr>     <fct>                         <dbl>             <dbl>          <dbl>
1 40-49     White                          2.20              2.09          0.139
2 40-49     Black/African Americ…          2.69              3.96          0.126
3 50-59     White                          2.89              3.35          0.103
4 50-59     Black/African Americ…          3.72              7.74          0.111

Test for Difference in Means

Since the data for black population and white population violate normality assumption, we perform a Mann-Whitney U test for both racial groups in the follwoing:

[1]  1.012022e-31 3.463246e-126

RESULT: These p-values are both extremely small (close to zero), meaning there is a very strong statistical difference between the two age groups (40-49 and 50-59) in terms of the mean number of children within each racial group.

Test for Difference in Variances

Levene's Test for Homogeneity of Variance (center = median)
          Df F value    Pr(>F)    
group      3  93.887 < 2.2e-16 ***
      176718                      
---
Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

Levene's Test for Homogeneity of Variance (center = median)
           Df F value    Pr(>F)    
group       3  4205.8 < 2.2e-16 ***
      1740751                      
---
Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

RESULT: Since the p values are smaller than 0.05 for both racial group, we have enough evidence to reject the null hypothesis, indicating that the variances of the number of children between the two age groups within each racial group are significantly different.

Chi-Square Test for Difference in Zero Inflation

`summarise()` has grouped output by 'RACE', 'AGE_RANGE'. You can override using
the `.groups` argument.

# A tibble: 8 × 4
# Groups:   RACE, AGE_RANGE [4]
  RACE                   AGE_RANGE childlessness count
  <fct>                  <chr>     <chr>         <int>
1 White                  40-49     0 Children    15945
2 White                  40-49     1+ Children   98807
3 White                  50-59     0 Children     9906
4 White                  50-59     1+ Children   86173
5 Black/African American 40-49     0 Children     1645
6 Black/African American 40-49     1+ Children   11430
7 Black/African American 50-59     0 Children     1215
8 Black/African American 50-59     1+ Children    9730

[1] 0.0004515422

[1] 8.34736e-138

RESULT: The p-values for both tests are extremely low, suggests that there is a significant difference in the proportion of women with 0 children across age ranges (40-49 vs. 50-59) for both the Black/African American and White racial groups. The results imply that childlessness is not uniformly distributed across age groups.

Step 4: Summarize Findings

Write a clear and concise summary addressing the following points.

4.1 Significant Fertility Shifts Across Cohorts

Identify Timing of Shifts:
- Specify when significant fertility shifts occurred for each racial group based on your analysis in Question 2.
Describe Nature of Shifts:
- Detail the characteristics of the shifts, such as:
  - Decrease in mean number of children
  - Increase in childlessness (zero inflation)
  - Changes in variance or distribution shape
Highlight Differences Between Racial Groups:
- Compare the timing and nature of shifts between African American and European American women.
- Discuss any patterns or discrepancies observed.

4.2 Comparison of 40-49 and 50-59 Age Groups in 1990

Summarize Key Differences:
- Present the differences in fertility patterns between the two age groups for each racial group.
- Include comparisons of:
  - Distribution shapes
  - Mean number of children
  - Variance
  - Zero inflation
Report Statistical Test Results:
- Provide the results of the t-tests, F-tests, and chi-square tests.
- Interpret the significance of these results in the context of your analysis.
Discuss Implications:
- Consider what these differences suggest about fertility trends and behaviors.
- Reflect on whether the older age group represents completed fertility patterns.

4.3 Synthesis and Implications

Integrate Findings:
- Connect the insights from the cohort analysis with the age group comparison.
- Discuss how the patterns observed in the 1990 census relate to the shifts identified across cohorts.
Consider Contributing Factors:
- Explore potential social, economic, or policy factors that may have contributed to the observed fertility shifts.
  - For example, changes in access to education, employment opportunities, or family planning resources.
Reflect on Broader Implications:
- Discuss how these fertility trends might impact your broader research topic, such as genetic surveillance disparities.
- Consider the implications for future demographic research or policy development.

Additional Considerations

Visual Clarity:
- Ensure all visualizations are easy to interpret.
- Use clear labels, legends, and annotations.
Contextualize Statistical Significance:
- Explain not just whether results are statistically significant, but also what they mean in practical terms.
Acknowledge Data Limitations:
- Discuss any limitations or biases in the data that could affect your findings.
  - For instance, sample size constraints or missing data.
Ethical Considerations:
- Approach discussions of race and fertility sensitively and responsibly.
- Avoid drawing causal conclusions without robust evidence.

Integration with Previous Work

Leverage Previous Analyses:
- Use the visualizations and statistical summaries from Questions 1 and 2 as foundations for this analysis.
Create a Cohesive Narrative:
- Ensure that your findings from all questions are connected and build upon each other.
- Tell a comprehensive story about fertility trends across cohorts and racial groups.

Final Deliverables

Multi-Panel Visualization:
- Panel A: Fertility distribution shifts across cohorts with highlighted significant shifts.
- Panel B: Comparative distribution plots for 40-49 and 50-59 age groups in 1990, including summary statistics.
Written Summary:
- A concise report that addresses the points outlined in Step 4.
- Include interpretations of statistical analyses and discuss broader implications.
Statistical Analysis Documentation:
- Provide details of the statistical tests conducted, including test assumptions, results, and interpretations.
Annotated Code (if applicable):
- While not the focus, include any new code used for this analysis with appropriate comments.

Distribution of Number of Siblings Across Census Years

Having analyzed the distribution of the number of children, we now turn our attention to the distribution of the number of siblings. We will explore the trends in the frequency of the number of siblings for African American and European American mothers across the Census years by age group.

Frequency of siblings is calculated as follows.

\[ \text{freq}_{n_{\text{sib}}} = \text{freq}_{\text{mother}} \cdot \text{chborn}_{\text{num}} \]

For example, suppose 10 mothers (generation 0) have 7 children, then there will be 70 children (generation 1) in total who each have 6 siblings.

We take our original data and calculate the frequency of siblings for each mother based on the number of children they have. We then aggregate this data to get the frequency of siblings for each generation along with details on the birth years of the relevant children to visualize the distribution of the number of siblings across generations.

Data Preparation

Calculate Sibling Frequencies

Aggregate Sibling Data

Check Normalization

Visualization of Distribution of Number of Siblings

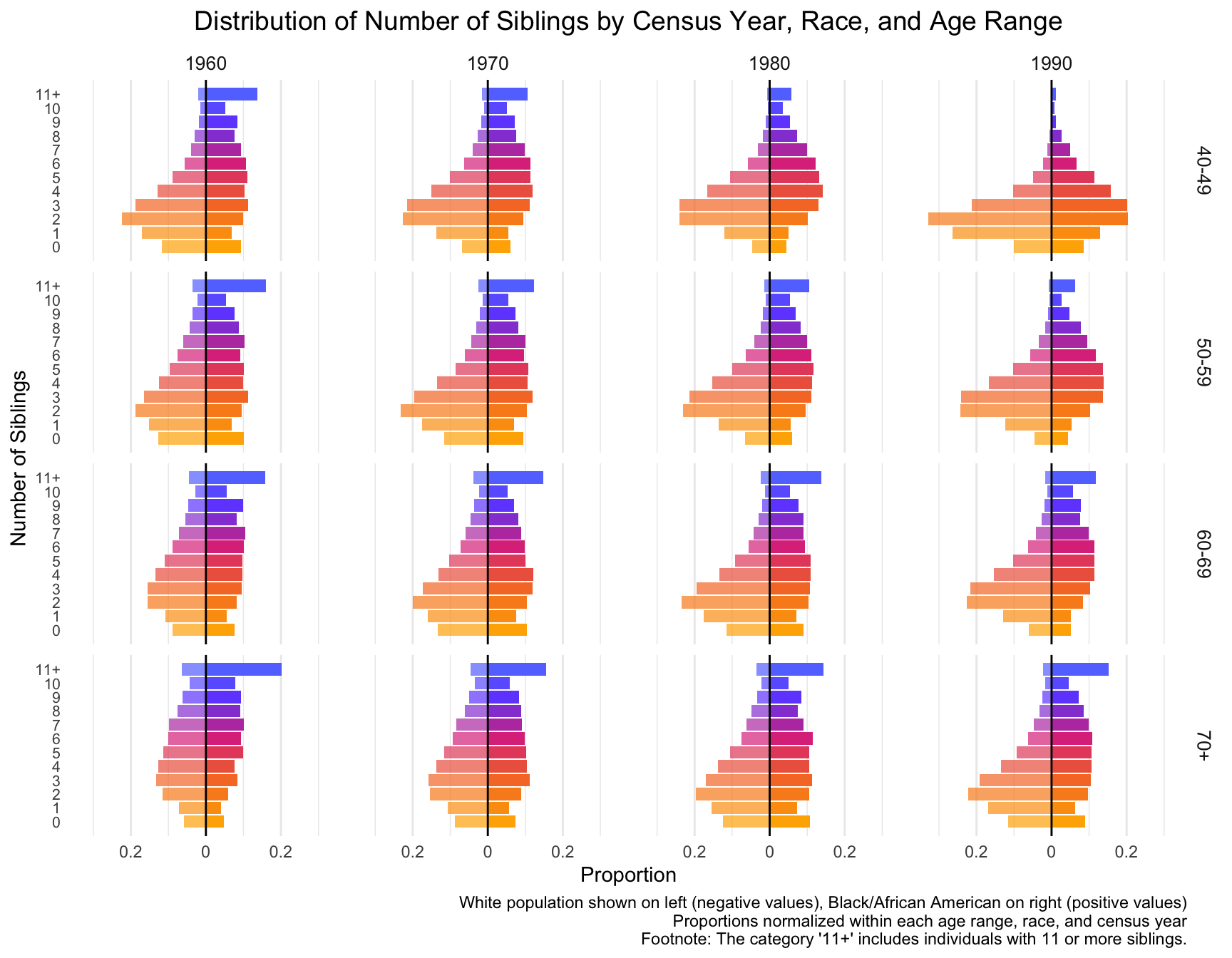
RESULT:

-By Census Year: In 1960 and 1970, individuals are more likely to have higher number of siblings, especially in the 5-10 range. This trend diminishes over time.

By 1980 and 1990, the distribution shifts toward smaller family sizes, with a growing proportion of individuals having fewer siblings.

-By age range:

40-49 Age Group: For this group, the number of individuals with 0-2 siblings increases across census years, especially in 1980 and 1990, while the proportion of individuals with larger sibling counts decreases.

50-59 and 60-69 Age Groups: These groups show a similar shift toward smaller family sizes, but the trend is slightly more gradual compared to the younger age group.

70+ Age Group: The shift to fewer siblings is noticeable, although the trend is less pronounced. The distribution remains relatively stable across the census years, with a significant portion of individuals still coming from large families in 1960 and 1970.

Compare the distributions between White and Black/African American populations.

RESULT: -Black/African American Populations (right side of each pair) consistently show a higher proportion of individuals with larger sibling counts (5-10 siblings) compared to White populations. However, similar to the White population, the number of individuals with fewer siblings increases over time.

Note any significant changes or trends in the number of siblings over time.

RESULT: -White Populations: (left side of each pair) have a more marked shift toward smaller families by 1990, with a larger proportion of individuals having 0-2 siblings compared to the Black/African American population. The decline in larger family sizes (5+ siblings) is more pronounced among Whites, particularly by 1980 and 1990.

Consider how these sibling distributions might differ from the children distributions you analyzed earlier, and think about potential reasons for these differences.

RESULT: While both distributions show a trend toward smaller families, the sibling distribution is more spread out across different sibling counts, suggesting potential difference in the distribution.

Model Fit Across Census Years

We repeat the model fitting process we performed for the children distribution, this time using the sibling distribution data.

Identify Best-Fitting Models by comparing AIC

Visualize Results

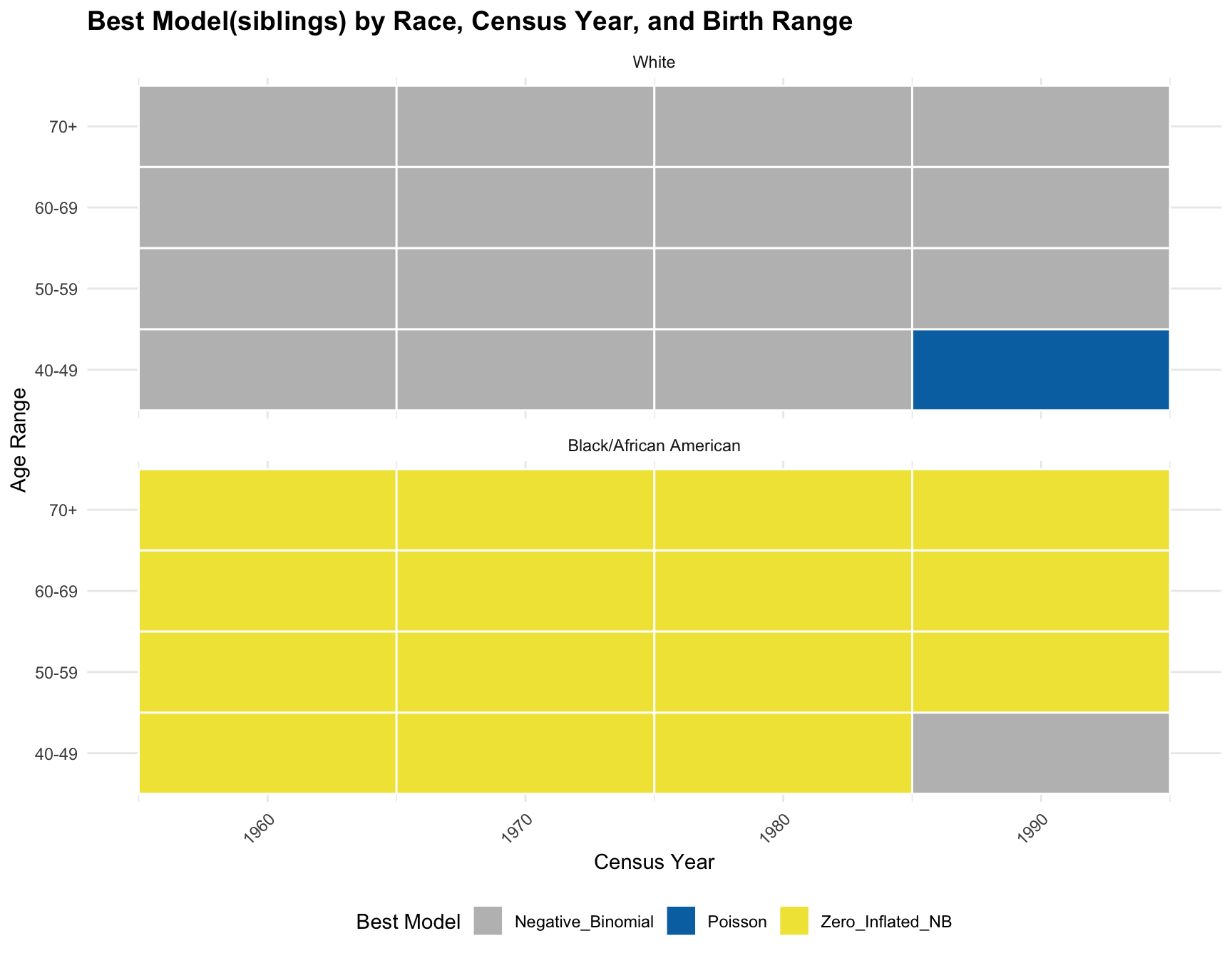
RESULT: By comparing the pattern of best-fitting models between the sibling and children distributions, we observe that the best model for black population has the same best model(zero-inlfated NB) across year and age range except on one subset(age 40-49 in 1990) in siblings distribution. However, there is a large difference in best model for white population. A large portion of best model in children distribution for white population is zero-inlfated NB, while negative-binomial is the best model fitted for siblings distribution except for one subset(age 40-49 in 1990).

Cohort Stability Analysis Siblings

Analyze the stability of sibling distributions across cohorts, similar to the analysis performed for children.

Zero Inflation: Check if the proportion of individuals with zero siblings changes significantly over time for the same cohort
Family Size: Test if the mean or variance in the number of siblings changes for the same cohort over time.
Model Fit: Analyze if the best-fitting model for the cohort changes over time.

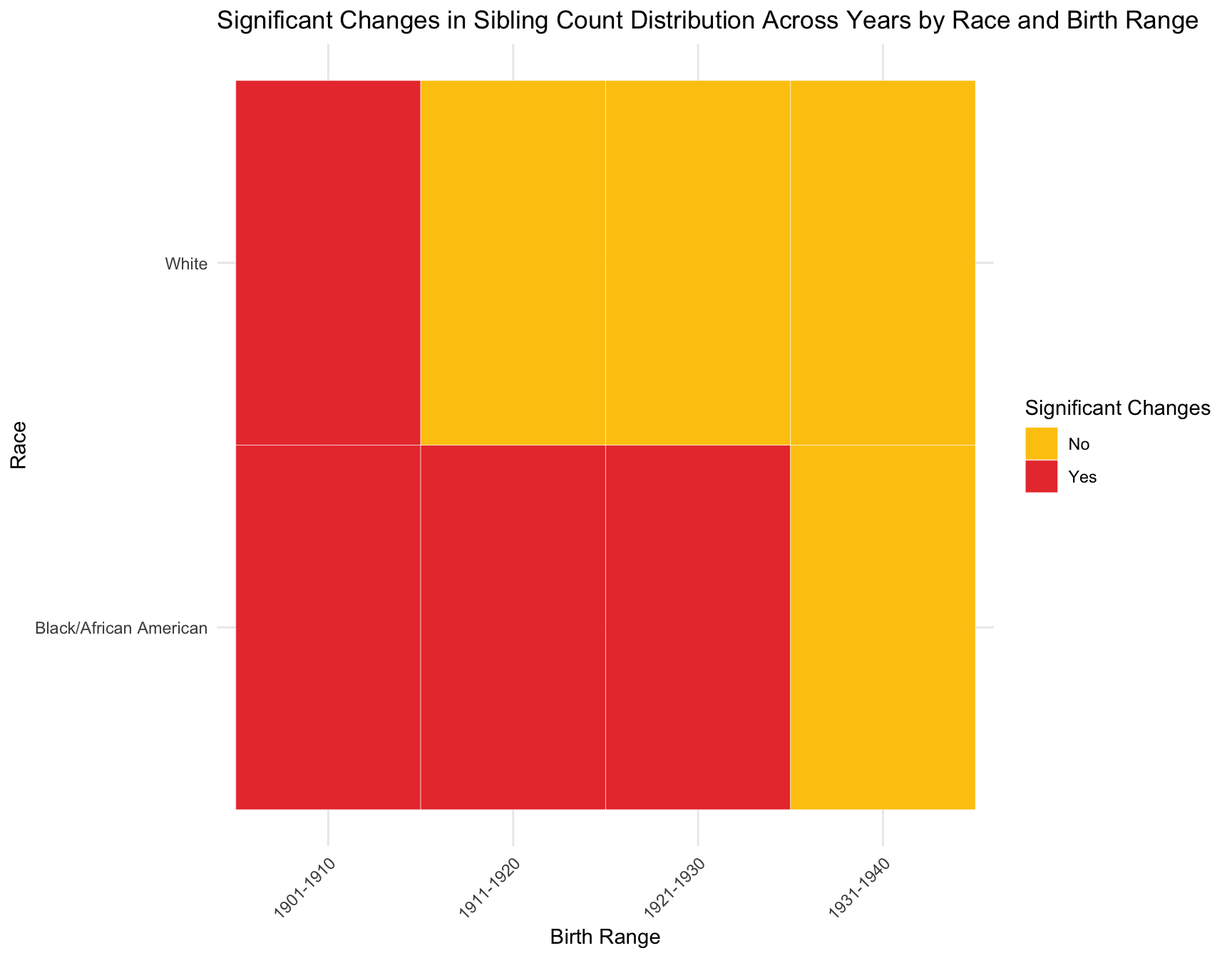
a. Zero-Inflation Analysis

                             RACE    Cohort Chi_Square    p_value Significance
X-squared  Black/African American 1901-1910  2.7595148 0.09667755           No
X-squared1 Black/African American 1911-1920  3.1588986 0.20608856           No
X-squared2 Black/African American 1921-1930  6.4474388 0.03980673          Yes
X-squared3 Black/African American 1931-1940  0.8166152 0.36617166           No

RESULT: The table shows that only the cohort 1921-1930 has significant change in probability of individuals with zero siblings in black population.

            RACE    Cohort Chi_Square      p_value Significance
X-squared  White 1901-1910  46.930953 7.353216e-12          Yes
X-squared1 White 1911-1920 120.015145 8.690450e-27          Yes
X-squared2 White 1921-1930  79.061388 6.792628e-18          Yes
X-squared3 White 1931-1940   2.776021 9.568561e-02           No

RESULT: The table shows that cohorts 1901-1910, 1911-1920, 1921-1930 have significant change in probability of individuals with zero siblings in white population.

b. Family Size Analysis


Cohort: 1891-1900 has only 1 Census Year. Skipping ANOVA.

Cohort: -Inf-1890 has only 1 Census Year. Skipping ANOVA.

Cohort: -Inf-1900 has only 1 Census Year. Skipping ANOVA.

Cohort: -Inf-1910 has only 1 Census Year. Skipping ANOVA.

Cohort: 1941-1950 has only 1 Census Year. Skipping ANOVA.

Cohort: -Inf-1920 has only 1 Census Year. Skipping ANOVA.

                     RACE    Cohort Statistic      p_value Significance
1  Black/African American 1911-1920  1.420923 2.415084e-01           No
t  Black/African American 1901-1910  2.041113 4.126381e-02          Yes
11 Black/African American 1921-1930 13.940627 8.872689e-07          Yes
t1 Black/African American 1931-1940  0.951569 3.413272e-01           No

RESULT: The mean number of siblings change significantly in cohorts 1901-1910 and 1921-1930 in black population.


Cohort: -Inf-1890 has only 1 Census Year. Skipping ANOVA and t-test.

Cohort: 1891-1900 has only 1 Census Year. Skipping ANOVA and t-test.

Cohort: -Inf-1900 has only 1 Census Year. Skipping ANOVA and t-test.

Cohort: -Inf-1910 has only 1 Census Year. Skipping ANOVA and t-test.

Cohort: -Inf-1920 has only 1 Census Year. Skipping ANOVA and t-test.

Cohort: 1941-1950 has only 1 Census Year. Skipping ANOVA and t-test.

    RACE    Cohort Statistic      p_value Significance
1  White 1911-1920  7.438832 5.880808e-04          Yes
t  White 1901-1910  2.126441 3.346854e-02          Yes
11 White 1921-1930 46.149409 9.125672e-21          Yes
t1 White 1931-1940  1.151129 2.496808e-01           No

RESULT: The mean number of siblings change significantly in cohorts 1901-1910, 1911-1920, 1921-1930 in white population.

c. Model Fit Analysis

Version	Author	Date
8007864	linmatch	2024-12-03

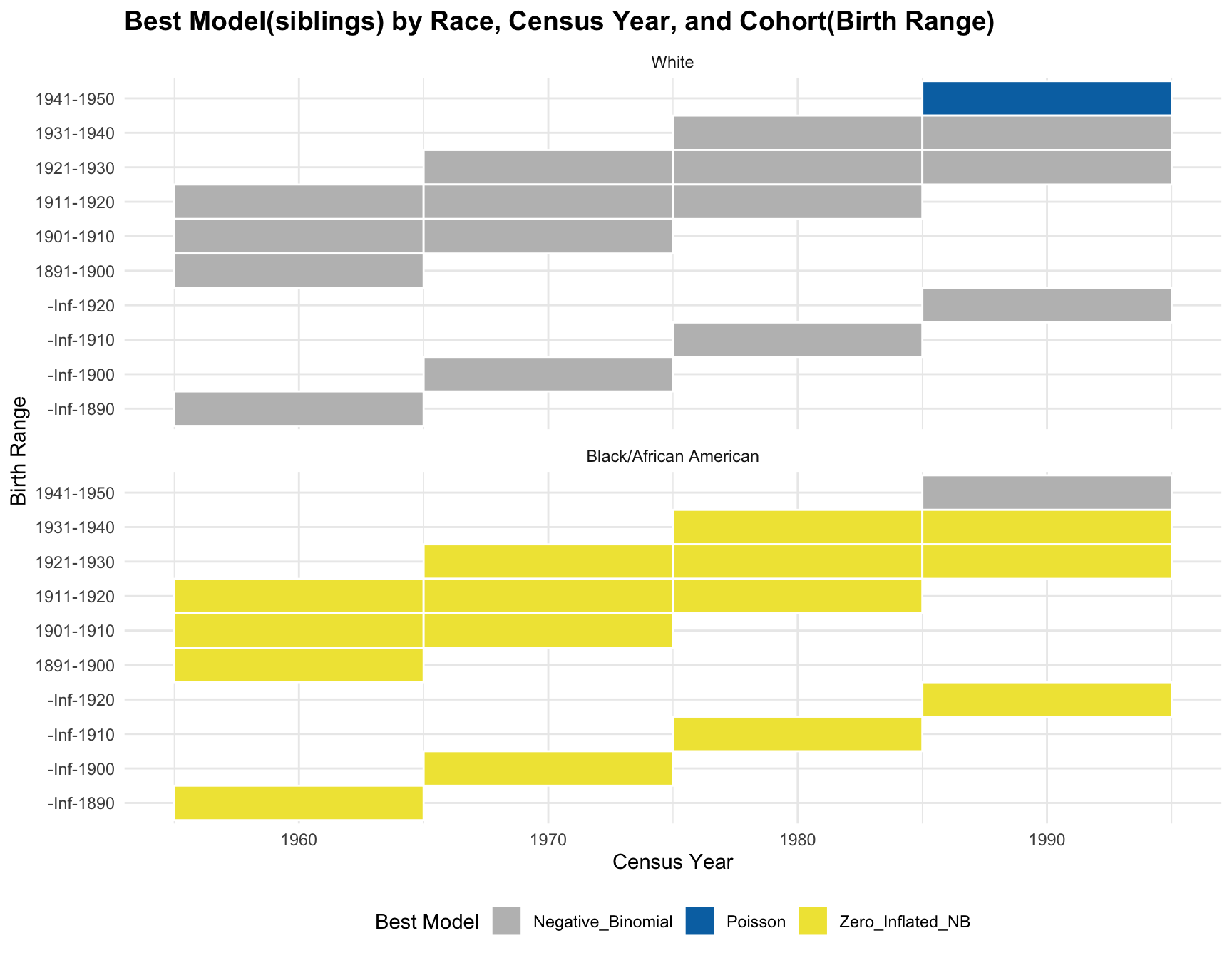
RESULT: The best model for each cohort(those with 1+ corresponding census year) is stable over time.

Addtional Analysis on Overall Distribution

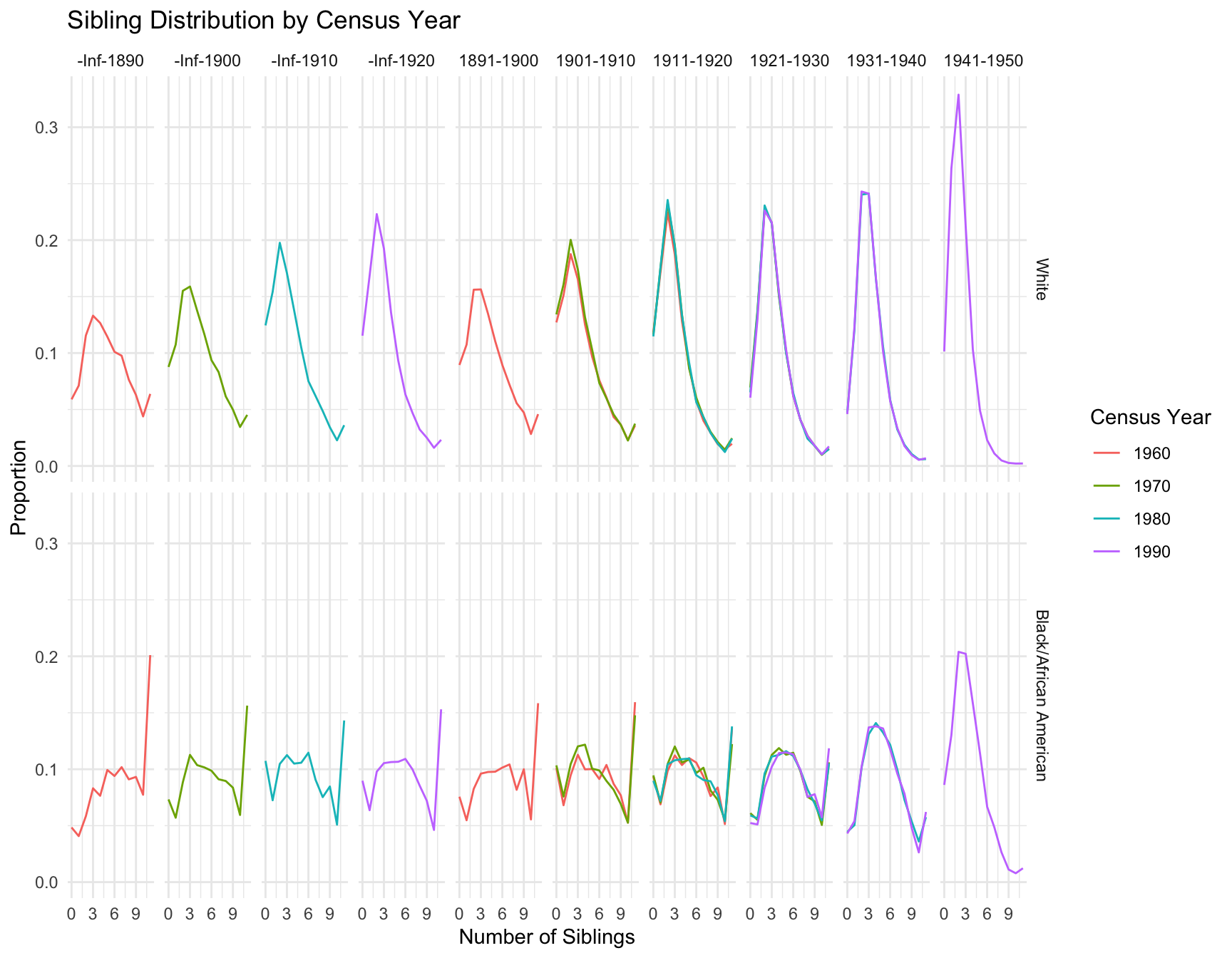
We also perform additional analysis to see if the overall distribution is stable across census year for the same cohort

Version	Author	Date
f567c4a	linmatch	2024-12-16
8007864	linmatch	2024-12-03

$`1901-1910`

    Kruskal-Wallis rank sum test

data:  sibling_count by YEAR
Kruskal-Wallis chi-squared = 13.23, df = 1, p-value = 0.0002755


$`1911-1920`

    Kruskal-Wallis rank sum test

data:  sibling_count by YEAR
Kruskal-Wallis chi-squared = 22.761, df = 2, p-value = 1.141e-05


$`1921-1930`

    Kruskal-Wallis rank sum test

data:  sibling_count by YEAR
Kruskal-Wallis chi-squared = 18.893, df = 2, p-value = 7.895e-05


$`1931-1940`

    Kruskal-Wallis rank sum test

data:  sibling_count by YEAR
Kruskal-Wallis chi-squared = 0.21333, df = 1, p-value = 0.6442

$`1901-1910`

    Kruskal-Wallis rank sum test

data:  sibling_count by YEAR
Kruskal-Wallis chi-squared = 3.8533, df = 1, p-value = 0.04965


$`1911-1920`

    Kruskal-Wallis rank sum test

data:  sibling_count by YEAR
Kruskal-Wallis chi-squared = 4.9189, df = 2, p-value = 0.08548


$`1921-1930`

    Kruskal-Wallis rank sum test

data:  sibling_count by YEAR
Kruskal-Wallis chi-squared = 2.7072, df = 2, p-value = 0.2583


$`1931-1940`

    Kruskal-Wallis rank sum test

data:  sibling_count by YEAR
Kruskal-Wallis chi-squared = 0.21333, df = 1, p-value = 0.6442

                    RACE    Cohort Stable_Distribution Significant_Changes
1 Black/African American 1901-1910                  No                 Yes
2 Black/African American 1911-1920                  No                 Yes
3 Black/African American 1921-1930                  No                 Yes
4 Black/African American 1931-1940                 Yes                  No
5                  White 1901-1910                  No                 Yes
6                  White 1911-1920                 Yes                  No
7                  White 1921-1930                 Yes                  No
8                  White 1931-1940                 Yes                  No

Visualize stability

Version	Author	Date
231390a	linmatch	2024-12-11
8007864	linmatch	2024-12-03

Result

From the plot above, we can see the distribution of sibling is stable in the following cohorts by race: -black population:1901-1919, 1911-1920, 1921-1930 -white population:1901-1910

R version 4.3.2 (2023-10-31)
Platform: x86_64-apple-darwin20 (64-bit)
Running under: macOS Sonoma 14.5

Matrix products: default
BLAS:   /Library/Frameworks/R.framework/Versions/4.3-x86_64/Resources/lib/libRblas.0.dylib 
LAPACK: /Library/Frameworks/R.framework/Versions/4.3-x86_64/Resources/lib/libRlapack.dylib;  LAPACK version 3.11.0

locale:
[1] en_US.UTF-8/en_US.UTF-8/en_US.UTF-8/C/en_US.UTF-8/en_US.UTF-8

time zone: America/Detroit
tzcode source: internal

attached base packages:
[1] stats     graphics  grDevices utils     datasets  methods   base     

other attached packages:
 [1] ggpubr_0.6.0      rstatix_0.7.2     car_3.1-3         carData_3.0-5    
 [5] nnet_7.3-19       pscl_1.5.9        MASS_7.3-60       gridExtra_2.3    
 [9] ggnewscale_0.5.0  patchwork_1.2.0   rempsyc_0.1.8     scales_1.3.0     
[13] knitr_1.45        viridis_0.6.5     viridisLite_0.4.2 lubridate_1.9.3  
[17] forcats_1.0.0     stringr_1.5.1     purrr_1.0.2       readr_2.1.5      
[21] tidyr_1.3.1       tibble_3.2.1      ggplot2_3.5.1     tidyverse_2.0.0  
[25] dplyr_1.1.4       workflowr_1.7.1  

loaded via a namespace (and not attached):
 [1] gtable_0.3.4      xfun_0.41         bslib_0.6.1       processx_3.8.3   
 [5] callr_3.7.3       tzdb_0.4.0        vctrs_0.6.5       tools_4.3.2      
 [9] ps_1.7.6          generics_0.1.3    fansi_1.0.6       highr_0.10       
[13] pkgconfig_2.0.3   lifecycle_1.0.4   farver_2.1.1      compiler_4.3.2   
[17] git2r_0.33.0      munsell_0.5.0     getPass_0.2-4     httpuv_1.6.14    
[21] htmltools_0.5.7   sass_0.4.8        yaml_2.3.8        Formula_1.2-5    
[25] later_1.3.2       pillar_1.9.0      jquerylib_0.1.4   whisker_0.4.1    
[29] cachem_1.0.8      abind_1.4-8       tidyselect_1.2.1  digest_0.6.34    
[33] stringi_1.8.3     labeling_0.4.3    rprojroot_2.0.4   fastmap_1.1.1    
[37] grid_4.3.2        colorspace_2.1-0  cli_3.6.2         magrittr_2.0.3   
[41] utf8_1.2.4        broom_1.0.6       withr_3.0.0       backports_1.5.0  
[45] promises_1.2.1    timechange_0.3.0  rmarkdown_2.25    httr_1.4.7       
[49] ggsignif_0.6.4    hms_1.1.3         evaluate_0.23     rlang_1.1.3      
[53] Rcpp_1.0.12       glue_1.7.0        rstudioapi_0.15.0 jsonlite_1.8.9   
[57] R6_2.5.1          fs_1.6.3

Estimating Differences in the Distribution of First-degree Relatives

Manqing Lin, Tina Lasisi

2025-01-14 10:55:41

Introduction

Data Sources

Data Preparation

Distribution of Number of Children Across Census Years

Model Fit Across Census Years

Fit and Compare Models

Record the Best Model for Each Subset

Analyze the Effect of Race, Census Year, and Age Range

Visualize the Results

Conclusion

Cohort Stability Analysis

Table with Birth-Year (Cohort)

Summary Statistics for Each Subset

Test for Significant Changes Over Time Within Each Cohort

a. Zero-Inflation Analysis

b. Family Size Analysis

c. Model Fit Analysis

Conclusion

Analyzing and Visualizing Significant Fertility Shifts

Panel A: Fertility Distribution Shifts Across Cohorts

Cohorts with Significant Change in Zero Inflation

Cohorts with Significant Change in Mean Family Size

Panel B: Comparison of 40-49 and 50-59 Age Groups in 1990

Visulization of Distribution

Summary Statistics Table

Test for Difference in Means

Test for Difference in Variances

Chi-Square Test for Difference in Zero Inflation

Step 4: Summarize Findings

4.1 Significant Fertility Shifts Across Cohorts

4.2 Comparison of 40-49 and 50-59 Age Groups in 1990

4.3 Synthesis and Implications

Additional Considerations

Integration with Previous Work

Final Deliverables

Distribution of Number of Siblings Across Census Years

Data Preparation

Calculate Sibling Frequencies

Aggregate Sibling Data

Check Normalization

Visualization of Distribution of Number of Siblings

Model Fit Across Census Years

Identify Best-Fitting Models by comparing AIC

Visualize Results

Cohort Stability Analysis Siblings

a. Zero-Inflation Analysis

b. Family Size Analysis

c. Model Fit Analysis

Addtional Analysis on Overall Distribution

Visualize stability

Result